火车车厢重排问题

基于、XML与Flash架构的火车车厢重排问题虚拟实验开发摘要：当前，XML（Extensible Makeup Language）是跨平台数据结构的最佳选择，应用广泛。

它是一种通用的、跨平台的数据描述方法，相比于一般的记事本文件，完全采用了Unicode 编码和条理清晰的分层标签。

介绍了和Flash之间通过XML文件传递信息解决火车重排堆栈问题。

Flash使抽象的数据结构问题转化为具象的动画呈现给学生，有助于学生理解问题、编写程序。

关键词：XML；；Flash；虚拟实验；火车车厢重排0引言当前，XML是跨平台数据结构的最佳选择。

XML全称为可扩展标记语言（Extensible Makeup Language）。

它是一种通用的、跨平台的数据描述方法，也是未来存储信息的方式，其应用无处不在。

XML是可扩展的、与平台无关的语言，相比于一般记事本文件，它完全采用Unicode 编码和条理清晰的分层标签并且支持国际化。

Flash是专业的动画创作工具，可以开发有吸引力、表现力的用户界面和丰富的应用程序。

它开发的文件数据量小，可以以插件方式工作、“流”形式文件播放以及实时交互。

因此，Flash成功地渗入到网络动画、音乐电视、广告、教学、游戏等多个领域。

是基于通用语言的编译运行程序，其强大的适应性，几乎可以使它运行在Web 应用软件开发者全部的平台上。

通用语言的基本库、消息机制、数据接口的处理都能无缝整合到的Web应用中。

也是languageindependent（语言独立化）的，支持C#（C++和Java的结合体）、VB、Jscript、C++、F++等语言。

与Flash之间传值在中对数据进行处理后，生成XML树，然后通过XML 文件在Flash端接收XML文件，解析XML树后，根据传入的参数进行操作。

^[1]其通信原理如图1所示。

端生成XML文件的代码如下：System.Xml.XmlTextWriter xmlWriter = new XmlTextWriter （Server.MapPath（"./1234.xml"），System.Text.Encoding.UTF8）；//声明一个xmlWriter变量用于编写XML文件xmlWriter.Formatting = Formatting.Indented；//用于生成良好的显示格式，增强可读性xmlWriter.WriteStartDocument（）；xmlWriter.WriteStartElement（"数据"）；//生成一个结点xmlWriter.WriteStartElement（"单次"）；xmlWriter.WriteAttributeString（"车厢"，firstNum.ToString（））；//写入节点的属性xmlWriter.WriteAttributeString（"铁轨"，secondNum.ToString（））；xmlWriter.WriteAttributeString（"出入"，thirdNum.ToString（））；xmlWriter.WriteEndElement（）；xmlWriter.WriteEndDocument（）；//写文档结束xmlWriter.Close（）；//关闭textWriterFlash端接收XML文件的代码如下：var myXML：XML= new XML；var XML_URL：String = "1234.xml"；var myXMLURL：URLRequest = new URLRequest（XML_URL）；public var myLoader：URLLoader = new URLLoader （myXMLURL）；public function Motion（）{myLoader.addEventListener（"complete"，xmlLoaded）；}2火车重排堆栈问题动画实现笔者在学习数据结构时发现授课内容比较抽象，需要具体的图解动态地描述问题。

计算机科学与工程学院
《算法与数据结构》试验报告[一]
专业班级10级计算机工程02 试验地点计算机大楼计工教研室学生学号1005080222 指导教师蔡琼
学生姓名肖宇博试验时间2012-4-21
试验项目算法与数据结构
试验类别基础性（）设计性（）综合性（√）其它（）试
验目的及要求（1）掌握队列的特点及其存储方法；（2）掌握队列的常见算法和程序实现。

成绩评定表
类别评分标准分值得分合计
上机表现积极出勤、遵守纪律
主动完成设计任务
30分
程序与报告程序代码规范、功能正确
报告详实完整、体现收获
70分
goto label2;
}
else if(r!=0)
{
printf("重排前的序列为\n");
for(i=1;i<=k;i++)
{
printf("%d\t",a[i]);
}
printf("\n");
printf("排列后的车厢号为：\n");
reset(q,w1,w2,k);
}
else
{
printf("我也不知道错哪了？'");
}
}
四、测试用例（尽量覆盖所有分支）
1.输入正确的序列后得到结果如图：
2.倒输这几个数如图：
3.顺序输这个序列
4.如果输入的车厢数有误的时候（为负数或零）
5.如果输入的序列不是连续自然数。

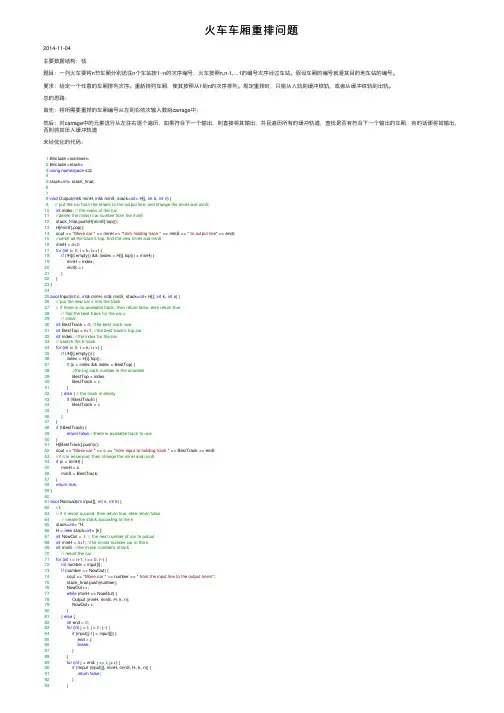
⽕车车厢重排问题2014-11-04主要数据结构：栈题⽬：⼀列⽕车要将n节车厢分别送往n个车站按1~n的次序编号，⽕车按照n,n-1,…1的编号次序经过车站。

假设车厢的编号就是其⽬的地车站的编号。

要求：给定⼀个任意的车厢排列次序。

重新排列车厢，使其按照从1到n的次序排列。

规定重排时，只能从⼊轨到缓冲铁轨，或者从缓冲铁轨到出轨。

总的思路：⾸先：将所需要重排的车厢编号从左到右依次输⼊数组carrage中；然后：对carrage中的元素进⾏从左往右逐个遍历，如果符合下⼀个输出，则直接将其输出，并且遍历所有的缓冲轨道，查找是否有符合下⼀个输出的车厢，有的话便将其输出，否则将其压⼊缓冲轨道未经优化的代码：1 #include <iostream>2 #include <stack>3using namespace std;45 stack<int> stack_final;678void Output(int& minH, int& minS, stack<int> H[], int k, int n) {9// put the car from the strack to the output line, and change the minH and minS10int index; // the index of the car11//delete the minist car number from the minS12 stack_final.push(H[minS].top());13 H[minS].pop();14 cout << "Move car " << minH << "from holding track " << minS << " to output line" << endl;15//serch all the track's top, find the new minH and minS16 minH = n+2;17for (int i= 0; i < k; i++) {18if (!H[i].empty() && (index = H[i].top()) < minH) {19 minH = index;20 minS = i;21 }22 }23 }2425bool Input(int c, int& minH, int& minS, stack<int> H[], int k, int n) {26// put the new car c into the track27// if there is no available track, then return false, else return true28// find the best track for the car c29// initial30int BestTrack = 0; //the best track now31int BestTop = n+1; //the best track's top car32int index; //the index for the car33// search the k track34for (int i= 0; i < k; i++) {35if (!H[i].empty()) {36 index = H[i].top();37if (c < index && index < BestTop) {38//the top car's number is the smallest39 BestTop = index;40 BestTrack = i;41 }42 } else { // the track is empty43if (!BestTrack) {44 BestTrack = i;45 }46 }47 }48if (!BestTrack) {49return false; //there is available track to use50 }51 H[BestTrack].push(c);52 cout << "Move car " << c << "from input to holding track " << BestTrack << endl;53//if it is essencial, then change the minH and minS54if (c < minH) {55 minH = c;56 minS = BestTrack;57 }58return true;59 }6061bool Railroad(int input[], int n, int k) {62//k63// if it resort succed, then return true, else return false64// create the stack according to the k65 stack<int> *H;66 H = new stack<int> [k];67int NowOut = 1; // the next number of car to putout68int minH = n+1; //the minist number car in the k69int minS; //the minist number's strack70// resort the car71for (int i = n-1; i >= 0; i--) {72int number = input[i];73if (number == NowOut) {74 cout << "Move car " << number << " from the input line to the output line\n";75 stack_final.push(number);76 NowOut++;77while (minH == NowOut) {78 Output (minH, minS, H, k, n);79 NowOut++;80 }81 } else {82int end = 0;83for (int j = i; j > 0; j--) {84if (input[j-1] < input[j]) {85 end = j;86break;87 }88 }89for (int j = end; j <= i; j++) {90if (!Input (input[j], minH, minS, H, k, n)) {91return false;92 }93 }94if (end) {95 i = end;96 }97 }98 }99return true;100 }101102int main() {103int n, *input;104 cin >> n;105 input = new int[n];106for (int i = 0; i < n; i++) {107 cin >> input[i];108 }109if (Railroad(input, n, n-1)) {110 cout << "resort succed!\n";111while (!stack_final.empty()) {112 cout << stack_final.top() << "";113 stack_final.pop();114 }115 } else {116 cout << "failed\n";117 }118 }View Code经过优化之后的代码：增加的条件：车厢可以从排在后⾯的缓冲轨道移到前⾯的缓冲轨道。

火车车厢重排问题1.1火车车厢重排问题一列货运列车共有n节车厢，每节车厢将停放在不同的车站。

假定n个车站的编号分别为1~n,货运列车按照第n站至第1站的顺序经过这些车站。

车厢编号与他们的目的地一样。

为了便于从列车上卸掉相应的车厢，必须重排车厢顺序，使得各车厢从前往后按编号1到n的次序排列。

当所有车厢按照这种次序排列时，在每个车站只需卸掉最后一个车厢即可。

1.2想法一列火车的每个车厢按顺序从入轨进入不同缓冲轨，缓冲轨重排后的进入出轨，重新编排成一列货车。

比如：编号为3的车厢进入缓冲轨1，则下一个编号小于3的车厢则必须进入下一个缓冲轨2，而编号大于3的车厢则进入缓冲轨1，排在3号车厢的后面，这样，出轨的时候才可以按照从小到大的顺序重新编排我们在一个转轨站里完成重拍的工作，在转轨站有一个入轨，一个出轨和k个缓冲轨（位于入轨和出轨之间）。

下面的图示就是一个转轨站，其中有3个缓冲轨，H1,H2,H3。

（PPT中有动态演示）1.3算法描述：那么缓冲轨就不是FILO 而是FIFO了那么就要用队列来实现车厢重排了，算法的描述和栈实现的基本一样的，只是OutPut和Hold 函数改了一下，将一截车厢移动到缓冲轨时，车厢c应该移动到这样的缓冲轨中：该缓冲轨中现有各车厢的编号均小于c，如果有多个缓冲轨都满足这一条件，那么选择其中左端车厢编号最大的那个缓冲轨，否则选择一个空的缓冲轨(如果存在的话)1.4代码：#include<iostream>#include<stack>usingnamespace std;template<class T>void PrintfNum(T a[], constint& n);// move cars from holding track to output trackvoid OutPut(stack<int> t[],int n, int totalStack,int& min){//move car from holding trackfor(int x = 0;x <totalStack; ++x){if(!t[x].empty() && t[x].top() == min){cout<<"Move car "<< t[x].top() <<" from holding track "<< x <<" to output"<<endl;t[x].pop();++min;x = -1; // find next car from the first holding track 0}}}// move cars from input track to holding trackbool Hold(stack<int> t[],int n , int totalStack){for(int i = 0;i <totalStack; ++i){if(t[i].empty() || (!t[i].empty() && t[i].top() > n)){cout<<"holding track "<<i<<" hold car "<< n <<endl;t[i].push(n);returntrue; // we already find a holding track, so break the loop. }}returnfalse;}int main(int argc, char* argv[]){constint NUM = 9;constint STACKNUM = 3;stack<int> t[STACKNUM];int min = 1;int a[NUM] = {5,8,1,7,4,2,9,6,3};PrintfNum(a,NUM);for(int i = NUM - 1; i>= 0; --i){if(a[i] == min){// try to move cars from input track or holding track cout<<"Move car "<< a[i] <<" from input to output"<<endl;++min;OutPut(t,a[i],STACKNUM,min);}else{// move cars from input track to holding trackif(!Hold(t,a[i],STACKNUM)){cout<<"Not enough holding track"<<endl;break;}}} getchar();return 0;}template<class T>void PrintfNum(T a[], constint& n){for(int i = 0; i< n; ++i){cout<< a[i] <<",";}cout<<endl;}1.5火车车厢重排问题决策过程H1H2H31.5.1初始数组H1 H2 H31.5.2H1H2H3H1 H2 H3H1 H2 H3H1 H2 H3H1 H2 H3H1 H2 H3H1H2 H3H1 H2 H3H1 H2 H3H1 H2 H3H1 H2 H3 1．6程序运行截图。

3.顺序输这个序列
4.如果输入的车厢数有误的时候（为负数或零）
5.如果输入的序列不是连续自然数
五、实验总结
先后学习了 C/C++,对编程语言基本上有一些了解，但在数据结构试验程序 设计过程中还是学到了很多。
经过两天的设计，在不断翻阅以前资料的情况下，有针对性的复习了 C/C++ 中指针、循环的相关理论知识和的基础知识和应用技巧，最后比较成功的完成 了本次的设计。 这次的实验是完成火车厢重徘问题，依旧采用的检查用户的错误输入机制，充 分考虑了用户的各种错误，比如输入的序列不是连续自然数，如果输入的车厢 数有误的时候（为负数或零）等等的情况，完成了该次实验，主要出现的问题 在于数组的下标问题，老是出现越界访问错误等等，这要在下次的实验当中多 加注意！
return q->data[q->front+1]; }
int getrear(squeue *&q) {
{ return q->data[q->rear];
} }
void reset(squeue *&q,squeue *&w1,squeue *&w2,int k) {
int nowout=1; int n1=0,n2=0; for(int i=0;i<50;i++) {
出轨
H1
1
入轨
H3
出轨
H2 (d) 将 6789 移至出轨
火车车厢重排算法伪代码如下：
1. 分别对k个队列初始化； 2. 初始化下一个要输出的车厢编号nowOut = 1; 3. 依次取入轨中的每一个车厢的编号；
如果入轨中的车厢编号等于nowOut，则 输出该车厢； nowOut++；

火车车厢重排问题栈c语言以下是一个用C语言实现火车车厢重排问题的代码：```c#include <stdio.h>#include <stdlib.h>#define MAX_SIZE 100typedef struct {int val;struct Node* next;} Node;typedef struct {Node* top;} Stack;Stack* createStack() {Stack* stack = (Stack*)malloc(sizeof(Stack));stack->top = NULL;return stack;}int isEmpty(Stack* stack) {return (stack->top == NULL);}void push(Stack* stack, int val) {Node* newNode = (Node*)malloc(sizeof(Node));newNode->val = val;newNode->next = stack->top;stack->top = newNode;}int pop(Stack* stack) {if (isEmpty(stack)) {printf("Stack is empty.\n");return -1;}int val = stack->top->val;Node* temp = stack->top;stack->top = stack->top->next;free(temp);return val;}int peek(Stack* stack) {if (isEmpty(stack)) {printf("Stack is empty.\n");return -1;}return stack->top->val;}int canReorder(int numCars, int cars[]) { Stack* stationStack = createStack(); Stack* branchStack = createStack(); int nextCar = 1;for (int i = 0; i < numCars; i++) {// 如果当前车厢和需要出站的车厢一致，直接出站if (cars[i] == nextCar) {nextCar++;continue;}// 将从站台出来的车厢压入分支轨道while (!isEmpty(stationStack) && peek(stationStack) == nextCar) {push(branchStack, pop(stationStack));nextCar++;}// 当前车厢进站push(stationStack, cars[i]);}// 如果分支轨道中的车厢可以按顺序出站，则返回1，否则返回0while (!isEmpty(branchStack)) {if (pop(branchStack) != nextCar) {return 0;}nextCar++;}return 1;}int main() {int numCars;int cars[MAX_SIZE];printf("Enter the number of train cars: ");scanf("%d", &numCars);printf("Enter the train car numbers: ");for (int i = 0; i < numCars; i++) {scanf("%d", &cars[i]);}int result = canReorder(numCars, cars);if (result) {printf("Yes, it is possible to reorder the train cars.\n"); } else {printf("No, it is not possible to reorder the train cars.\n"); }return 0;}```输入示例：```Enter the number of train cars: 5Enter the train car numbers: 3 1 2 4 5```输出示例：```Yes, it is possible to reorder the train cars. ```。

第１ ２ 卷 第１ ０ 期
２ ０ １ ３ １ ｏ ） ｑ
软 件 导 刊
Ｓｏ ｆ ｔ ｗａ ｒ ｅ Ｇｕｉ ｄ ｅ
Ｖｏ１ ．１ ２Ｎ０．１ Ｏ Ｏｃ ｔ ．２ ０１ ３
基 于 Ａｓ ｐ ． ｎ ｅ ｔ 、 ＸＭ Ｌ与 Ｆ ｌ ａ ｓ ｈ架 构 的 火 车 车 厢 重 排 问 题 虚 拟 实 验 开 发
ｘ ｍｌ Ｗｒ ｉ ｔ ｅ ｒ ． Ｗｒ ｉ ｔ ｅ Ｓ ｔ ａ ｒ ｔ Ｅ ｌ ｅ ｍｅ ｎ ｔ （ ” 数据 ” ） ； ／ ／ 生 成 一 个 结 点
ｘ ｍｌ Ｗｒ ｉ ｔ ｅ ｒ ． Ｗｒ ｉ ｔ ｅ Ｓ ｔ ａ ｒ ｔ Ｅｌ ｅ ｍｅ ｎ ｔ （ ” 单 次” ） ； ｘ ｍｌ Ｗｒ ｉ ｔ ｅ ｒ ． Ｗｒ ｉ ｔ ｅ Ａｔ ｔ ｒ ｉ ｈ ｕ ｔ ｅ Ｓ ｔ ｒ ｉ ｎ ｇ（” 车 厢 ｔ ｒ ｉ ｎ ｇ（ ） ）；／ ／ 写 入 节 点 的属 性
交 互 。因 此 ， Ｆ ｌ ａ ｓ ｈ成 功 地 渗 入 到 网 络 动 画 、 音 乐 电视 、 广 告、 教学 、 游戏等多个领域 下 ：
Ｓ ｙ ｓ ｔ ｅ ｍ． Ｘｍ １ ． Ｘｍｌ Ｔｅ ｘ ｔ Ｗｒ ｉ ｔ ｅ ｒ ｘ ｍｌ Ｗｒ ｉ ｔ ｅ ｒ— ｎ ｅ ｗ Ｘｍｌ Ｔｅ ｘ ｔ —
给学生 ， 有 助 于 学 生理 解 问题 、 编写程序 。
关键 词 ： ＸＭＩ ； Ａｓ ｐ ． ｎ ｅ ｔ ； Ｆ ｌ ａ ｓ ｈ ； 虚 拟 实验 ； 火 车 车 厢 重 排
中图分类号 ： ＴＰ ３ １ １
文献 标 识 码 ： Ａ
文章编号 ： １ ６ ７ ２ — ７ ８ ０ ０ （ ２ ０ １ ３ ） ０ ０ １ ０ — ０ ｌ １ ４ — ０ ３

火车车厢重排问题栈c语言火车车厢重排问题是一个经典的问题，考验了数据结构和算法的运用。

这个问题可以很好地帮助我们了解如何使用栈这种数据结构来解决实际问题，并且可以通过编写C语言程序对其进行求解。

在本文中，我们将深入探讨火车车厢重排问题，并编写C语言程序实现问题的求解。

首先，让我们来了解一下火车车厢重排问题的具体描述。

假设有一列火车车厢按照编号从1到n的顺序排列在轨道上。

现在我们需要将这些车厢按照特定的顺序重新排列，给定一个目标排列，我们需要找出一种排列车厢的方法，使得最终的排列符合目标排列。

具体而言，对于每一个车厢，我们可以将其从原来的位置移动到一个临时的缓冲轨道中，然后再将其移动到目标位置。

这个问题的关键在于如何确定每个车厢应该如何移动才能满足最终的目标排列。

为了解决这个问题，我们可以使用栈这种数据结构来辅助实现。

栈是一种先进后出的数据结构，这样的特性非常适合用来模拟火车车厢的重排过程。

具体而言，我们可以将原始轨道上的车厢编号序列作为输入，然后使用栈来模拟车辆的移动过程，最终得到目标排列。

下面我们将通过C语言程序来实现这个过程。

首先，我们需要定义一个栈的数据结构，来模拟车厢的移动过程。

我们可以使用数组来实现这个栈，同时需要定义一个栈顶指针来表示当前栈顶元素的位置。

另外，我们还需要定义一个函数来模拟入栈和出栈的过程。

接下来，让我们来具体实现这个栈的数据结构和相关的函数。

```c#include <stdio.h>#include <stdlib.h>#define MAX_SIZE 100typedef struct {int data[MAX_SIZE];int top;} Stack;void init(Stack *s) {s->top = -1;}void push(Stack *s, int value) { if (s->top < MAX_SIZE - 1) {s->top++;s->data[s->top] = value;} else {printf("Stack overflow\n");}}int pop(Stack *s) {if (s->top >= 0) {int value = s->data[s->top];s->top--;return value;} else {printf("Stack underflow\n"); return -1;}}int main() {Stack s;init(&s);//对栈进行入栈和出栈操作push(&s, 1);push(&s, 2);push(&s, 3);printf("%d\n", pop(&s)); //输出3printf("%d\n", pop(&s)); //输出2printf("%d\n", pop(&s)); //输出1printf("%d\n", pop(&s)); //输出Stack underflow，表示栈已空return 0;}```在这段代码中，我们定义了一个栈的数据结构，并实现了栈的初始化、入栈和出栈操作。

目录1．题目： (2)1-1.队列的应用——火车厢重排问题 (2)1-2.简单指导 (2)2.设计目的及内容 (3)2-1.目的 (3)2-2.内容 (3)设计内容 (3)3.概要设计 (4)3-1.函数调用的关系图 (4)3-2.流程图 (4)3-2-1. 总体程序设计流程图 (4)3-2-2 Output函数的流程图. (5)3-2-3. Hold函数的流程图 (6)4. 算法描述 (8)4-1. 模块一：LinkQueue() 构造函数 (8)初始化一个空的链队列 (8)4-2. 模块二：析构函数 (8)释放链队列中的各结点的存储空间 (8)4-3. 模块三：EnQueue函数 (9)将队头元素x入队 (9)4-4. 模块四：DeQueue函数 (9)将队头元素出队 (9)4-5.模块五：GetQueue函数 (9)取链队列的队头元素 (9)4-6. 模块六：Empty函数 (10)判断链队列是否为空 (10)4-7. 模块七：Outputput 函数 (10)该函数调用6个函数模板来实现火车厢重排问题，预设K个缓冲轨道，通过运用函数模板来比较各个缓冲轨道的队头元素，确定队列的出队、入队元素，最后通过输入和输出函数来实现火车厢由小到大的顺序出轨 (10)5.源程序 (11)6. 运行结果及性能分析 (15)6-1. 运行结果及性能分析 (15)6-1-1.开始后的界面 (15)6-1-2. 输入火车总数i=5和缓冲轨数j=3后的界面 (16)6-1-3.随机输入1.2.3.4.5的进入顺序后开始进入重排界面 (16)6-2. 性能分析 (16)7.心得体会 (17)1．题目：1-1.队列的应用——火车厢重排问题假设一列货运列车共有n节编号分别为1~n的车厢，在进站前这n节车厢并不是按其编号有序排列；现要求重新排列各车厢，使该列车在进入车站时，所有车厢从前到后按编号1~n的次序排列，以便各车厢能够停靠在与其编号一致的站点。

江西理工大学软件学院《数据结构》课程设计报告20xx—20xx学年第x学期课程名称数据结构设计题目火车车厢重排问题专业班级xxxxxxxxxx姓名xxxxx学号xxxxxxxxx指导教师xxxxxxxx同伴xxxxxxxxxxxx年xx 月xx 日目录一、问题描述 (1)二、基本要求 (1)三、概要设计 (1)四、详细设计 (3)五、运行与测试 (8)六、总结与心得 (10)课程设计题目：火车车厢重排问题一、问题描述一列货运列车共有 n 节车厢，每节车厢将停放在不同的车站。

假定 n 个车站的编号分别为 1 ~ n ，即货运列车按照第 n 站至第 1 站的次序经过这些车站。

为了便于从列车上卸掉相应的车厢，车厢的编号应与车站的编号相同，这样，在每个车站只需卸掉最后一节车厢。

所以，给定任意次序的车厢，必须重新排列他们。

车厢的重排工作可以通过转轨站完成。

在转轨站中有一个入轨、一个出轨和k 个缓冲轨，缓冲轨位于入轨和出轨之间。

假定缓冲轨按先进先出的方式运作，设计算法解决火车车厢重排问题。

二、基本要求1.设计存储结构表示n个车厢，k个缓冲轨以及入轨和出轨；2.设计并实现车厢重排算法；3.分析算法的时间性能。

三、概要设计为了重排车厢，若有k个缓冲轨，缓冲轨Hk为可直接将车厢从入轨移动到出轨的通道，则可用来暂存车厢的缓冲轨的数目为k-1。

假定有3个缓冲轨，入轨中有9节车厢，其初始次序为5, 8, 1, 7, 4, 2, 9, 6, 3，重排后，9节车厢出轨次序为9，8，7，6，5，4，3，2，1。

重排过程如下：3号车厢不能直接移动到出轨（因为1号车厢和2号车厢必须排在3号车厢之前），因此，把3号车厢移动至H1。

6号车厢可放在H1中3号车厢之后（因为6号车厢将在3号车厢之后出轨）。

9号车厢可以继续放在H1中6号车厢之后，而接下来的2号车厢不能放在9号车厢之后（因为2号车厢必须在9号车厢之前出轨）。

因此，应把2号车厢放在H2。

一、试验课题队列的应用实验目的：（1）掌握队列的特点及其存储方法；（2）掌握队列的常见算法和程序实现。

二、试验内容(1)问题描述：一列货运列车共有n节车厢，每节车厢将停放在不同的车站。

假定n个车站的编号分别为1~n，即货运列车按照第n站至第1站的次序经过这些车站。

为了便于从列车上卸掉相应的车厢，车厢的编号应与车站的编号相同，这样，在每个车站只要卸掉最后一节车厢。

所以，给定任意次序的车厢，必须重新排列它们。

车厢的重排工作可以通过国转轨站完成。

在转轨站中有一个入轨、一个出轨和k个缓冲轨，缓冲轨位于入轨和出轨之间。

假定缓冲轨按先进先出飞方式运作，设计算法解决火车车厢重排问题。

(2)基本要求：设计存储结构表示n个车厢、k个缓冲轨以及入轨和出轨;设计并实现车厢重排算法；分析算法的时间性能三、试验分析实验说明：转轨站示意图如下：2222(a) 将369、247依次入缓冲轨(b) 将1移至出轨，234移至出轨(c) 将8入缓冲轨，5移至出轨(d) 将6789移至出轨火车车厢重排过程如下：火车车厢重排算法伪代码如下：四、源程序代码#include<iostream>using namespace std;const MS=100;template <class T>struct QNode{T data;QNode<T> *next;};template <class T>class LiQueue{public:LiQueue( ); //构造函数，初始化一个空的链队列~LiQueue( ); //析构函数，释放链队列中各结点的存储空间void EnQueue(T x); //将元素x入队T DeQueue( ); //将队头元素出队T GetFront( ); //取链队列的队头元素T GetRear();bool Empty( ); //判断链队列是否为空QNode<T> *front, *rear; //队头和队尾指针，分别指向头结点和终端结点};template <class T>LiQueue<T>::LiQueue( ){QNode <T> *s;s=new QNode<T>;s->next=NULL;front=rear=s;}template <class T>LiQueue<T>::~LiQueue( ){QNode <T> *p;while(front){p=front;front=front->next;delete p;}}template <class T>void LiQueue<T>::EnQueue(T x){QNode<T> *s;s=new QNode<T>;s->data=x; //申请一个数据域为x的结点ss->next=NULL;rear->next=s; //将结点s插入到队尾rear=s;}template <class T>T LiQueue<T>::DeQueue(){QNode <T> *p; int x;if (rear==front) throw "下溢";p=front->next;x=p->data; //暂存队头元素front->next=p->next; //将队头元素所在结点摘链if (p->next==NULL) rear=front; //判断出队前队列长度是否为1delete p;return x;}template <class T>T LiQueue<T>::GetFront(){if (rear!=front)return front->next->data;}template <class T>T LiQueue<T>::GetRear(){if(rear!=front)return rear->data;}template <class T>bool LiQueue<T>::Empty( ){if(front==rear) return 0;else return 1;}class Train{private :int n,k,th;public :Train();void ChongPai();};Train::Train(){cout<<"请输入火车(货运列车）的车厢个数为："<<endl;cin>>n;cout<<"请输入转轨站的缓冲轨个数为："<<endl;cin>>k;}void Train::ChongPai(){int a[MS];LiQueue<int>*b;b=new LiQueue<int>[k+2];cout<<"请输入车厢入轨编号次序："<<endl;for(int i=0;i<n;i++)cin>>a[i];for(i=n-1;i>=0;i--)b[k].EnQueue(a[i]);cout<<"则进行车厢重排过程如下:"<<endl;th=1;while(b[k].Empty()){int xx=b[k].DeQueue();if(xx==th){cout<<th<<"号车厢直接移至出轨"<<endl;b[k+1].EnQueue(th);th++;int j=0;while(b[j].Empty()){int x=b[j].GetFront();if(x==th){cout<<x<<"号车厢从"<<j+1<<"号缓冲轨出轨"<<endl;b[j].DeQueue();b[k+1].EnQueue(x);j=0;th++;}elsej++;}continue;}else{int j=0,u=5;while(b[j].Empty()&&j<k){if(xx<b[j].GetRear())j++;else{cout<<xx<<"号车厢移至"<<j+1<<"号缓冲轨"<<endl;b[j].EnQueue(xx);u=1;break;}}if(u==5&&j<k){cout<<xx<<"号车厢移至"<<j+1<<"号缓冲轨"<<endl;b[j].EnQueue(xx);}if(j==k-1){cout<<"\n缓冲轨不够，重排车厢失败\n";return;}}}cout<<"车厢依次出轨的编号为：";while(b[k+1].Empty())cout<<b[k+1].DeQueue()<<" ";cout<<endl;}void main(){Train a;a.ChongPai();}五、测试用例1.当有9个火车车厢，3个缓冲轨道时，运行结果如下：2. 当有12个火车车厢，3个缓冲轨道时，运行结果如下：3. 当有12个火车车厢，5个缓冲轨道，运行结果如下：4. 当有12个火车车厢，7个缓冲轨道时，运行结果如下：几次测试都表明试验设计的正确性。

实验报告了便于从列车上卸掉相应的车厢，车厢的编号应与车站的编号相同，这样，在每个车站只要卸掉最后一节车厢。

所以，给定任意次序的车厢，必须重新排列它们。

车厢的重排工作可以通过转轨站完成。

在转轨站中有一个入轨、一个出轨和k个缓冲轨，缓冲轨位于入轨和出轨之间。

假定缓冲轨按先进先出的方式运作，设计算法解决火车车厢重排问题。

②基本要求●设计存储结构表示n个车厢、k个缓冲轨以及入轨和出轨；●设计并实现车厢重排算法；●分析算法的时间性能。

③思考●如果缓冲轨按后进先出的方式工作，即用栈表示缓冲轨，应如何解决火车车厢重排问题？二、数据结构设计迷宫问题和火车重排问题可以通过栈与队列实现的。

迷宫的进出和车厢的出入轨和缓冲轨主要是对栈与队列的判断和操作。

int empty( STLink top[],int n) /*判断是否为空*/{return (top[n]==NULL);}int push(STLink top[],int A,int m) /*入栈*/{STLink p;if(!(p=(STLink)malloc(LEN)))return 0;else{p->data=A;p->link=top[m];top[m]=p;return 1;}}int pop(STLink top[],int m) /*出栈*/{int A;STLink p;p=top[m];A=p->data;top[m]=top[m]->link;free(p);return A;}struct Node{ /定义队列int data;Node* next;};三、算法设计1.迷宫问题：进入格子后，需要判断此时格子位置周围障碍物的位置，对其进行压栈，判断，然后看是否满足条件，满足就进栈，不满足就弹出，然后输出不能通过建立迷宫：typedef struct LStack{Element elem;struct LStack *next;}*PLStack;int InitStack(PLStack &S){S=NULL;return 1;}int StackEmpty(PLStack S){if(S==NULL)return 1;elsereturn 0;}int Push(PLStack &S, Element e){PLStack p;p=(PLStack)malloc(sizeof(LStack));p->elem=e;p->next=S;S=p;return 1;}（2）.输出路径2.火车车厢排序六、实验收获与思考通过本次实验，进一步增强了对栈和队列的理解，明白的栈的先进后出和队列先进先出的方式，对压栈和出入栈与队列有了深刻认识。

一年级数学练习题火车厢火车旅行一直是孩子们喜欢的事情之一。

而对一年级的孩子们来说，通过数学习题来了解火车厢的数量和顺序，不仅可以培养他们的数学能力，还可以激发他们对火车旅行的好奇心和探索欲。

本文将为一年级孩子们准备一些有关火车厢的数学练习题，通过解题的方式让他们更好地理解火车厢的排列和顺序。

问题一：火车厢的数量小明参加了一次火车旅行，他所乘坐的火车共有8节车厢。

请问火车上一共有几节车厢？解答：小明所乘坐的火车共有8节车厢。

问题二：火车厢的顺序小红所乘坐的火车有4节车厢，记为A、B、C、D。

请问有多少种不同的排列方式能够组成这4节火车厢？解答：小红所乘坐的火车有4节车厢，共有以下6种不同的排列方式：ABCD，ABDC，ACBD，ACDB，ADBC，ADCB。

问题三：火车厢的排序小杰想坐一辆由5节车厢组成的火车，但他希望第一节车厢是红色，最后一节车厢是蓝色。

请问有多少种满足条件的排序方式？解答：根据题意，我们需要找到满足条件的排列方式。

我们可以先确定第一节车厢和最后一节车厢的位置，然后对其余3节车厢进行排列。

根据排列的原则，我们有4种选择来确定第一节车厢（A、B、C、D），同样有4种选择来确定最后一节车厢。

因此，一共有4 × 4 = 16种满足条件的排序方式。

问题四：火车厢的数量与顺序小华所乘坐的火车共有6节车厢，其中蓝色车厢3节，红色车厢2节，绿色车厢1节。

请问有多少种不同的排列方式能够组成这6节火车厢？解答：根据题意，我们需要找到满足条件的排列方式。

我们可以先确定相同颜色的车厢的位置，然后对其余车厢进行排列。

根据排列的原则，我们有3种选择来确定蓝色车厢的位置，然后有2种选择来确定红色车厢的位置，最后只有1种选择来确定绿色车厢的位置。

因此，一共有3 × 2 × 1 = 6种不同的排列方式。

通过以上的数学练习题，孩子们可以加深理解火车厢数量和顺序的概念。

同时，通过解题的方式，他们还可以培养逻辑思维和解决问题的能力。

实验报告1．实验要求利用队列结构实现车厢重排问题。

车厢重排问题如下：一列货车共有n节车厢，每个车厢都有自己的编号，编号范围从1~n。

给定任意次序的车厢，的车厢编号。

提示：一列火车的每个车厢按顺序从入轨进入不同缓冲轨，缓冲轨重排后的进入出轨，重新编排成一列货车。

比如：编号为3的车厢进入缓冲轨1，则下一个编号小于3的车厢则必须进入下一个缓冲轨2，而编号大于3的车厢则进入缓冲轨1，排在3号车厢的后面，这样，出轨的时候才可以按照从小到大的顺序重新编排。

2. 程序分析2.1 存储结构本程序采用单链表结构，具体为链队列结构，使用队列结构的先进先出原则可以较好地处理车厢重排问题。

链队列结构示意图如下：2.2 关键算法分析一、本程序的关键算法主要为处理车厢重排问题的函数TrainPermute()，其伪代码如下：void TrainPermute():1. 初始化条件:计数器i=0,与非门aa=12. 判断是否能入轨while(用i<n判断是否n节车厢都入缓冲轨)&&(用aa=1判断是否有合适的缓冲轨可入)2.1将aa置空；2.2用for循环，依次取入入轨中的每一个车厢的编号进入合适的缓冲轨；2.2.1如果缓冲轨中尾指针比进入缓冲轨元素小，则进入该缓冲轨；计数器i+1;有合适缓冲轨，将aa变为真;跳出for循环并进入while循环；2.2.2如果缓冲轨中第一个元素为空，则进入缓冲轨成为第一个元素；计数器i+1;有合适缓冲轨，将aa变为真;跳出for循环并进入while循环；2.3 用aa判断是否有进入合适的缓冲轨2.3.1 aa=0即没有合适的缓冲轨，则输出无法排列；2.3.2 aa=1即有合适的缓冲轨，则2.3.2.1遍历缓冲轨，输出每个缓冲轨按顺序存储的车厢；2.3.2.2 按从小到大的顺序出轨for(引入输出轨计数器newOut=1;newOut<n; newOut+1;)newOut与每个队列的头元素比较若相等，则元素出队；输出显示；具体代码如下：void TrainPermute(int arr[],LinkQueue<int> a[],int n,int k){int i=0;bool aa=1;while((i<n)&&(aa)) //当入轨中有车厢时{for(int m=0;m<k;m++){if(a[m].GetRear()<arr[i]){a[m].EnQueue(arr[i]);i++;}if(a[m].front->next==NULL){a[m].EnQueue(arr[i]);aa=1;i++;break;}}}if(aa==0) //当无法将入轨中队头车厢移至合适缓冲轨中时，程序结束{cout<<"车厢无法重排,算法结束"<<endl;}else //当入轨中已经没有车厢时{for(int m=0;m<k;m++){cout<<"第"<<(m+1)<<"个缓冲轨的列车编号";a[m].Trans();cout<<endl;}cout<<"火车车厢出轨顺序为:"<<endl;for(int newOut=1;newOut<=n;newOut++){for(int j=0;j<k;j++) //扫描缓冲轨，将其队头元素依次由小到大输出{if(a[j].GetFront()==newOut){cout<<a[j].DeQueue()<<" ";}}}}}二、主函数伪代码如下：1. 输入n与k值，若输入值错误，则程序结束；2. 通过循环结构为数组array[]赋值，具体分析见代码；3. 输出入轨中火车车厢号码排列；4. 调用TrainPermute()函数；三、为array[]随机赋值的基本思想为：设置计数器count=0，设置数组ifmark[]来标记array[]赋值情况，依次将1至n等n个数随机赋给array[]，其中，若array[t]未被赋值，即ifmark[t]=0，则将值赋给array[t]，计数器加一；若array[t]已被赋值，即ifmark[t]=1，则重新开始循环。

一、试验课题队列的应用实验目的：（1）掌握队列的特点及其存储方法；（2）掌握队列的常见算法和程序实现。

二、试验内容(1)问题描述：一列货运列车共有n节车厢，每节车厢将停放在不同的车站。

假定n个车站的编号分别为1~n，即货运列车按照第n站至第1站的次序经过这些车站。

为了便于从列车上卸掉相应的车厢，车厢的编号应与车站的编号相同，这样，在每个车站只要卸掉最后一节车厢。

所以，给定任意次序的车厢，必须重新排列它们。

车厢的重排工作可以通过国转轨站完成。

在转轨站中有一个入轨、一个出轨和k个缓冲轨，缓冲轨位于入轨和出轨之间。

假定缓冲轨按先进先出飞方式运作，设计算法解决火车车厢重排问题。

(2)基本要求：设计存储结构表示n个车厢、k个缓冲轨以及入轨和出轨;设计并实现车厢重排算法；分析算法的时间性能三、试验分析实验说明：转轨站示意图如下：2222(a) 将369、247依次入缓冲轨 (b) 将1移至出轨，234移至出轨(c)将8入缓冲轨，5移至出轨 (d) 将6789移至出轨火车车厢重排过程如下：火车车厢重排算法伪代码如下：四、源程序代码#include<iostream>using namespace std;const MS=100;template <class T>struct QNode{T data;QNode<T> *next;};template <class T>class LiQueue{public:LiQueue( ); //构造函数，初始化一个空的链队列~LiQueue( ); //析构函数，释放链队列中各结点的存储空间void EnQueue(T x); //将元素x入队T DeQueue( ); //将队头元素出队T GetFront( ); //取链队列的队头元素T GetRear();bool Empty( ); //判断链队列是否为空QNode<T> *front, *rear; //队头和队尾指针，分别指向头结点和终端结点};template <class T>LiQueue<T>::LiQueue( ){QNode <T> *s;s=new QNode<T>;s->next=NULL;front=rear=s;}template <class T>LiQueue<T>::~LiQueue( ){QNode <T> *p;while(front){p=front;front=front->next;delete p;}}template <class T>void LiQueue<T>::EnQueue(T x){QNode<T> *s;s=new QNode<T>;s->data=x; //申请一个数据域为x的结点ss->next=NULL;rear->next=s; //将结点s插入到队尾 rear=s;}template <class T>T LiQueue<T>::DeQueue(){QNode <T> *p; int x;if (rear==front) throw "下溢";p=front->next;x=p->data; //暂存队头元素front->next=p->next; //将队头元素所在结点摘链if (p->next==NULL) rear=front; //判断出队前队列长度是否为1 delete p;return x;}template <class T>T LiQueue<T>::GetFront(){if (rear!=front)return front->next->data;}template <class T>T LiQueue<T>::GetRear(){if(rear!=front)return rear->data;}template <class T>bool LiQueue<T>::Empty( ){if(front==rear) return 0;else return 1;}class Train{private :int n,k,th;public :Train();void ChongPai();};Train::Train(){cout<<"请输入火车(货运列车）的车厢个数为："<<endl;cin>>n;cout<<"请输入转轨站的缓冲轨个数为："<<endl;cin>>k;}void Train::ChongPai(){int a[MS];LiQueue<int>*b;b=new LiQueue<int>[k+2];cout<<"请输入车厢入轨编号次序："<<endl;for(int i=0;i<n;i++)cin>>a[i];for(i=n-1;i>=0;i--)b[k].EnQueue(a[i]);cout<<"则进行车厢重排过程如下:"<<endl;th=1;while(b[k].Empty()){int xx=b[k].DeQueue();if(xx==th){cout<<th<<"号车厢直接移至出轨"<<endl;b[k+1].EnQueue(th);th++;int j=0;while(b[j].Empty()){int x=b[j].GetFront();if(x==th){cout<<x<<"号车厢从"<<j+1<<"号缓冲轨出轨"<<endl;b[j].DeQueue();b[k+1].EnQueue(x);j=0;th++;}elsej++;}continue;}else{int j=0,u=5;while(b[j].Empty()&&j<k){if(xx<b[j].GetRear())j++;else{cout<<xx<<"号车厢移至"<<j+1<<"号缓冲轨"<<endl;b[j].EnQueue(xx);u=1;break;}}if(u==5&&j<k){cout<<xx<<"号车厢移至"<<j+1<<"号缓冲轨"<<endl;b[j].EnQueue(xx);}if(j==k-1){cout<<"\n缓冲轨不够，重排车厢失败\n";return;}}}cout<<"车厢依次出轨的编号为：";while(b[k+1].Empty())cout<<b[k+1].DeQueue()<<" ";cout<<endl;}void main(){Train a;a.ChongPai();}五、测试用例1.当有9个火车车厢，3个缓冲轨道时，运行结果如下：2. 当有12个火车车厢，3个缓冲轨道时，运行结果如下：3. 当有12个火车车厢，5个缓冲轨道，运行结果如下：4. 当有12个火车车厢，7个缓冲轨道时，运行结果如下：几次测试都表明试验设计的正确性。

cout<<endl; cout<<"请问是手动输入车厢号还是随机产生？ \n1 手动 2 随机 " <<endl;
cin>>h; switch(h) {case 1: cout<<endl; for(a=0;a<n;a++) cin>>array[a]; break; case 2: srand((unsigned)time(NULL)); int count=0; int *m; m=new int[n]; while(count!=n) { t=rand()%n; if(m[t]!=1) { array[t]=count+1; m[t]=1; count++; } } break;
}
cout<<endl; cout<<"火车车厢入轨顺序为:"<<endl; for(int i=0;i<n;i++) cout<<array[i]<<" "; cout<<endl; LinkQueue *buffer; buffer=new LinkQueue[k]; cout<<endl; TrainPermute(array,buffer,n,k); cout<<endl;} //缓冲轨
bool Empty() {if(front==NULL) return 1; else return 0;}
//判断队空
friend void TrainPermute(int arr[],LinkQueue a[],int n,int k); private: Node *front,*rear; };

⽕车车厢重排问题问题描写叙述：⼀列货运⽕车从出发站出发时⽕车上⼀共同拥有n节车厢，编号各⾃是1到n。

运货的各节车厢是在⼊轨上时是随机的顺序，⽕车头在出轨处，如今要将各节车厢按编号从⼤到⼩挂到车头上。

当中在⼊轨与出轨之间有k条缓冲铁轨，将通过缓冲铁轨完毕本次的⽕车车厢的重排。

详细规则：⼀、车厢从⼊轨的前部（即右端）仅仅能够移动到⼀个缓冲铁轨的顶端或出轨的右端。

⼆、缓冲铁轨的顶端的车厢仅仅能够移动到出轨的最左端三、车厢不能从⼀个缓冲铁轨移动到还有⼀个缓冲铁轨或者再移动到⼊轨四、车厢移动到出轨的最左端（即⽕车头端）后不能再移动解决步骤：⼀、从⼊轨端開始移除最右边的车厢假设该车厢正好能够挂在出轨端则直接移到⼊轨端。

然后再在缓冲铁轨中查找是否有接到出轨上的车厢如有则移出如⽆则開始步骤四。

否则先在每条缓冲铁轨中查找。

⼆、假设能找到⼀条缓冲铁轨顶端的车厢编号正好⽐它⼤并且和它最接近则移动到该条缓冲铁轨上三、假设每⼀条有车厢的缓冲铁轨的顶端车厢编号都⽐它⼩，则再查找有没有空的缓冲铁轨假设有则移动到缓冲铁轨上，否则返回false。

四、继续開始从⼊轨端移除最右端的车厢⽽且開始反复步骤⼀。

应⽤的数据结构：因为对于每个缓冲铁轨来说都是LIFO后进先出的特点所以能够考虑採⽤栈的数据结构。

详细实现代码及结果例如以下：#include<iostream>#include<vector>#include<stack>#include<deque>#include<iterator>#include<algorithm>using namespace std;//辅函数：更新缓冲铁轨上的min_buf、min_travoid updata(vector<stack<int>> & tracks_buf,int & min_buf,int & min_tra){for (int i = 0;i<tracks_buf.size();i++){if(!tracks_buf[i].empty() && min_buf>tracks_buf[i].top()){min_buf = tracks_buf[i].top();min_tra = i;}}}//辅函数：将车厢移到缓冲铁轨上bool trans(int n,int d,vector<stack<int>> & tracks_buf,int & min_buf,int & min_tra){//先查找最优缓冲铁轨int min_gap = n+1;//d与个缓冲铁轨顶端上⼤于的车厢与d之间的最⼩间隔int prefer_track = -1;//最优铁轨for (int i = 0;i<tracks_buf.size();i++){if (!tracks_buf[i].empty() && tracks_buf[i].top()>d && (tracks_buf[i].top()-d)<min_gap){min_gap = tracks_buf[i].top()-d;prefer_track = i;}}if(-1!=prefer_track)//找到最优缓冲铁轨{tracks_buf[prefer_track].push(d);updata(tracks_buf,min_buf,min_tra);return true;}else{//再查找是否存在空铁轨for (int i = 0;i<tracks_buf.size();i++){if(tracks_buf[i].empty()){tracks_buf[i].push(d);updata(tracks_buf,min_buf,min_tra);return true;}}//否则返回false;return false;}}/* ⽕车车厢重排问题* datas：⽕车车厢在⼊轨上时的序列* n : ⽕车车厢的总节数* k ：缓冲铁轨的条数*///主要函数bool fun(vector<int> &datas,deque<int> & results,int n,int k){int min_buf = n+1;//缓冲铁轨上最⼩的车厢号int min_tra = 0;//最⼩的车厢所在的缓冲铁轨编号vector<stack<int>> tracks_buf(k);//缓冲铁轨数组int need = 1;//出轨处须要挂上的车厢号while (!datas.empty()){int d = datas.back();datas.pop_back();if (d==need)//符合要求直接移到出轨{results.push_front(need);need++;//再到缓冲铁轨中查找是否有下⼀个符合的车厢while(min_buf == need)//找到{results.push_front(need);need++;//移除缓冲铁轨tracks_buf[min_tra].pop();//更新min_buf、min_tramin_buf = n+2;min_tra = 0;updata(tracks_buf,min_buf,min_tra);}}else//不符合要求移到缓冲铁轨上{if(!trans(n,d,tracks_buf,min_buf,min_tra)){return false;}}}return true;}int main(){int array[] = {5,8,1,7,4,2,9,6,3};deque<int> results;vector<int> vec(array,array+sizeof(array)/sizeof(array[0]));int n = vec.size();int k = 3;//3条缓冲铁轨if (fun(vec,results,n,k)){cout<<k<<"条缓冲铁轨能够将依照";copy(vec.begin(),vec.end(),ostream_iterator<int>(cout));cout<<"此序列的"<<n<<"节车厢⼜⼀次排好挂到⽕车头上。