【备考2020】北师大初中数学中考总复习：正多边形与圆的有关的证明和计算--巩固练习(提高)

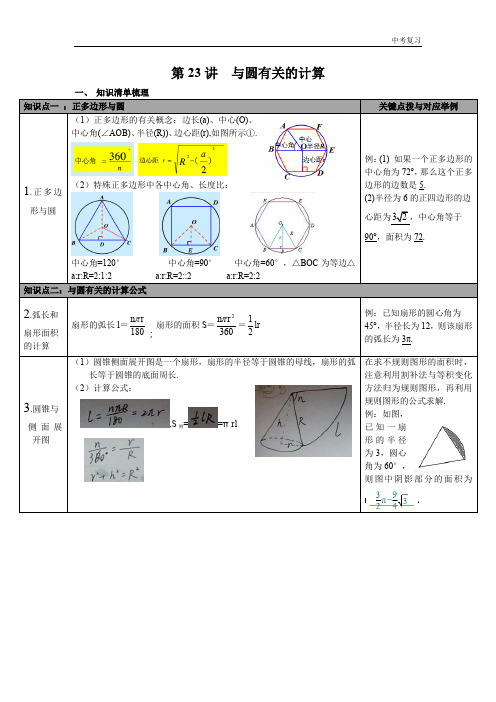
中考总复习正多边形与圆的有关的证明和计算--知识讲解【正多边形与圆的有关的证明和计算】一、正多边形的定义与性质：正多边形是指所有边相等、所有角相等的多边形。

正多边形的性质如下：1.所有边相等，所有角相等；2.任意两条边之间的夹角相等；3.对角线相等；4.中心角等于外角。

二、正多边形的内角与外角的关系：1.由正多边形的定义可知，正多边形的内角和为180°(n-2)，其中n 为正多边形的边数；2.正多边形的外角和为360°，由此可得正多边形的内角和与外角和之间的关系：内角和=外角和/2三、正多边形的周长和面积的计算：1.正多边形的周长为边长×边数；2.正多边形的面积为面积公式：面积=1/2×边长×边数×正弦(360°/边数)。

四、正多边形内接圆的半径和面积：2.正多边形内接圆的面积等于正多边形面积的一半。

五、正多边形外接圆的半径和面积：1.正多边形外接圆的半径等于正多边形的边长的一半乘以正弦(180°/边数)；2.正多边形外接圆的面积等于正多边形边长的平方乘以正弦(360°/边数)乘以1/2六、正多边形的对称轴：正多边形有旋转对称轴和镜像对称轴两类：1.正多边形的旋转对称轴有n条，其中n为正多边形的边数；2.正多边形的镜像对称轴有2n条，其中n为正多边形的边数。

七、圆的性质及计算：1.圆是由一个动点到一个定点的距离保持不变的动点集；2.圆的半径是动点到圆心的距离；3.圆的直径是通过圆心的一条线段，且长度等于半径的两倍；4.圆的周长等于直径的乘以π，即周长=2×半径×π；5.圆的面积等于半径的平方乘以π，即面积=半径×半径×π。

八、正多边形与圆的关系：1.正多边形的内接圆同时是这个正多边形的外接圆，即正多边形的内接圆与外接圆重合；3.正多边形的外接圆的半径等于正多边形的边长的一半乘以正弦(180°/边数)；4.正多边形的外接圆的面积等于正多边形边长的平方乘以正弦(360°/边数)乘以1/2；5.正多边形的内接圆和外接圆的关系可以用于计算正多边形的周长和面积。

中考总复习：正多边形与圆的有关的证明和计算—巩固练习（提高）【巩固练习】一、选择题1. 将一个底面半径为5 cm ，母线长为12 cm 的圆锥形纸筒沿一条母线剪开并展平，所得的侧面展开图的圆心角是（ ）度．A.60B.90C.120D.1502．某盏路灯照射的空间可以看成如图所示的圆锥，它的高AO ＝8米，母线AB 与底面半径OB 的夹角为α，4tan 3α=，则圆锥的底面积是（ ）平方米．A.9πB.16πC. 25πD.36π3．某花园内有一块五边形的空地如图所示，为了美化环境，现计划在五边形各顶点为圆心，2m 长为半径的扇形区域内（阴影部分）种上花草，那么种上花草的扇形区域总面积是（ ）A ．6πm 2B ．5πm 2C ．4πm 2D ．3πcm 2 4．如图所示，直径AB 为6的半圆，绕A 点逆时针旋转60°，此时点B 到了点B '，则图中阴影部分的面积是（ ）A ．6πB ．5πC ．4πD ．3π5．如图所示，从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC ，将剪下的扇形围成一个圆锥，则圆锥的底面圆半径为 （ ）A ．13B ．6C ．3D ．4 6．（2015•威海）如图，正六边形A 1B 1C 1D 1E 1F 1的边长为2，正六边形A 2B 2C 2D 2E 2F 2的外接圆与正六边形A 1B 1C 1D 1E 1F 1的各边相切，正六边形A 3B 3C 3D 3E 3F 3的外接圆与正六边形A 2B 2C 2D 2E 2F 2的各边相切，…按这样的规律进行下去，A 10B 10C 10D 10E 10F 10的边长为（ ）A ．B ．C ．D ．二、填空题7．若一个圆锥的侧面积是18π，侧面展开图是半圆，则该圆锥的底面圆半径是________．8．如图，已知⊙O 是边长为2的等边△ABC 的内切圆，则⊙O 的面积为________．9．如图是一条水平铺设的直径为2米的通水管道横截面，其水面宽为1.6米，则这条管道中此时水最深为__________米．10．将半径为10cm ，弧长为12π的扇形围成圆锥(接缝忽略不计)，那么圆锥的母线与圆锥高的夹角的余弦值是________．11．如图所示是一个用来盛爆米花的圆锥形纸杯，纸杯开口圆的直径EF 长为10cm ．在母线OF 上的点A 处有一块爆米花残渣，且FA ＝2cm ，一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点，则此蚂蚁爬行的最短距离为________cm ．12．（2015•深圳校级模拟）如图一组有规律的正多边形，各正多边形中的阴影部分面积均为a，按此规律，则第n个正多边形的面积为．三、解答题13．如图所示，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连结EF、EO，若DE＝DPA＝45°．(1)求⊙O的半径；(2)求图中阴影部分的面积．14. 如图AB是⊙O的直径，点D在⊙O上，∠DAB＝45°，BC∥AD，CD∥AB．(1)判断直线CD与⊙O的位置关系，并说明理由；(2)若⊙O的半径为1，求图中阴影部分的面积(结果保留π)．15．已知：如图，△ABC内接于⊙O，AB为直径，弦CE⊥AB于F，C是AD的中点，连结BD并延长交EC的延长线于点G，连结AD，分别交CE、BC于点P、Q．(1)求证：P 是△ACQ 的外心；(2)若3tan 4ABC ∠=，CF ＝8，求CQ 的长； (3)求证：(FP+PQ)2＝FP ·FG ．16. （2014•碑林区校级模拟）如图，圆O 的半径为r ．（1）在图①中，画出圆O 的内接正△ABC ，简要写出画法；求出这个正三角形的周长．（2）在图②中，画出圆O 的内接矩形ABCD ，简要写出画法；若设AB=x ，则矩形的周长为 ．（3）如图③，六边形ABCDEF 内接于半径为r （常数）的⊙O ，其中AD 为直径，且AB=CD=DE=FA ．设AB=x ，求六边形ABCDEF 的周长L 关于x 的函数关系式，并探究L 是否有最大值，若有，请指出x 为何值时，L 取得最大值；若没有，请说明理由．【答案与解析】一、选择题1.【答案】D ；【解析】圆锥的底面周长为22510r πππ=⨯=，所以它的侧面展开图的圆心角 是1801015012n ππ⨯==°． 2.【答案】D ； 【解析】因为4tan 3AO BO α==，AO ＝8，所以BO ＝6，所以圆锥的底面积是2636ππ=． 3.【答案】A ；【解析】五个扇形的半径都为2cm ，设其圆心角分别为1n °，2n °，3n °，4n °，5n °，则无法直接利用扇形面积公式求解，可以整体考虑，123455n n n n n ++++=°°°°°边形形内角和＝(5-2)×180°＝540°，∴ 2254026(m )360S ππ⨯==阴影． 4.【答案】A ；【解析】如果分别求S Ⅰ和S Ⅲ得阴影面积则很复杂，由旋转前后图形全等，易得S Ⅰ＝S Ⅱ，∴ 26066360ABB S S S S S S ππ'⨯=+====ⅠⅢⅡⅢ阴影扇形+． 5.【答案】B ；【解析】要求围成的圆锥的底面圆半径，只要求出扇形ABC 中BC 的弧长，该弧长即为围成的圆锥的底面圆的周长，再根据周长即可以求出半径．∵ 直径为2，∠BAC ＝60°∴ AC ，∴ BC 的弧长为6，设底面圆的半径为r ，则由26r π=解得6r = 6.【答案】D ；【解析】连结OE 1，OD 1，OD 2，如图，∵六边形A 1B 1C 1D 1E 1F 1为正六边形，∴∠E 1OD 1=60°，∴△E 1OD 1为等边三角形，∵正六边形A 2B 2C 2D 2E 2F 2的外接圆与正六边形A 1B 1C 1D 1E 1F 1的各边相切， ∴OD 2⊥E 1D 1，∴OD 2=E 1D 1=×2，∴正六边形A 2B 2C 2D 2E 2F 2的边长=×2，同理可得正六边形A 3B 3C 3D 3E 3F 3的边长=（）2×2，则正六边形A 10B 10C 10D 10E 10F 10的边长=（）9×2=．故选D ．二、填空题7．【答案】3；【解析】设圆锥的母线长为R ，侧面展开图半圆弧长为l ，圆锥底面积半径为r ， 则有：218018360R ππ=． ∴ R 2＝36，R ＝6．又1182Rl π=． ∴ 2l π=，∴ 2πr ＝6π，r ＝3．8．【答案】3π； 【解析】设⊙O 与BC 切于D 点，连接OD ，OC ．在Rt △ODC 中，112122DC BC ==⨯=．∠OCD ＝30°．∴ tan 30OD DC ==°．∴ 3OD =，则22O 33S r πππ⎛⎫=== ⎪ ⎪⎝⎭⊙． 9．【答案】0.4；【解析】如图，过O 作OC ⊥AB 于C ，并延长并AB 于D ．在Rt △OBC 中，212OB ==，11 1.60.822BC AB ==⨯=．∴ 20.6OC ==．∴ CD ＝OD-OC ＝1-0.6＝0.4(米)．10．【答案】45； 【解析】如图，因为2πR＝12π，所以R ＝6．由勾股定理，得8h =． 所以84cos 105AO CAO AC ∠===．11．【答案】【解析】底圆周长为2πr ＝10π，设圆锥侧面展开图的扇形所对圆心角为n °， 有2180n R r ππ=，即1010180n ππ⨯=， ∴ n ＝180°，如图所示，FA ＝2，OA ＝8，在Rt△OEA中由勾股定理可得EA即为所求最短距离．∴EA=== 12．【答案】a；【解析】第一个：正多边形的面积等于a；第二个：如图作AE⊥BD于E，设正六边形的边长为2，∵正六边形的一个内角为120°，∴∠ABE=30°，则AE=1，BE=，△ABD的面积为：×2×1=，a=2×2=4，∴正六边形的面积为：a，第三个：如图，∵正八边形的一个内角为135°，∴∠ABD=45°，设正八边形的边长为2，则BD=AD=，△ABD的面积为1，四边形ABEF的面积为1+2+1=2+2，a=2×（2+2）=4+4，∴正八边形的面积为2a，通过计算可以看出：第n个正多边形的面积为a．三、解答题13.【答案与解析】（1）∵直径AB⊥DE，∴ 12CE DE == ∵ DE 平分半径OA ，∴ 1122CE AO OE ==． 在Rt △OCE 中，∵ ∠CEO ＝30°．∴ OE ＝2．即⊙O 的半径为2．（2）连OF ，在Rt △DCP 中，∵ ∠DPC ＝45°．∠D ＝90°-45°＝45°∴ ∠EOF ＝2∠D ＝90°．∵ 2902360S ππ=⨯⨯=扇形OEF ． 1122222OEF S OE OF ∆==⨯⨯= ∴ 2OEF OEF S S S π∆=-=-阴影扇形． 14.【答案与解析】解：(1)直线CD 与⊙O 相切．如图，连接OD ．∵ OA ＝OD ，∠DAB ＝45°，∴ ∠ODA ＝45°．∴ ∠AOD ＝90°．∵ CD ∥AB ，∴ ∠ODC ＝∠AOD ＝90°，即OD ⊥CD ．又∵ 点D 在⊙O 上，∴ 直线CD 与⊙O 相切．(2)∵ BC ∥AD ，CD ∥AB ， ∴ 四边形ABCD 是平行四边形．∴ CD ＝AB ＝2．∴ ()(12)13222OBCD OB CD OD S +⨯+⨯===梯形． ∴ 图中阴影部分的面积等于 231312424OBD OBCD S S ππ-=-⨯⨯=-扇形梯形．15.【答案与解析】(1)证明：∵ C 是AD 的中点，∴ AC CD =．∴ ∠CAD ＝∠ABC ．∵ AB 是⊙O 的直径，∴ ∠ACB ＝90°．∴ ∠CAD+∠AQC ＝90°．又 CE ⊥AB ，∴ ∠ABC+∠PCQ ＝90°．∴ ∠AQC ＝∠PCQ ．∴ 在△PCQ 中，有PC ＝PQ ．∵ CE ⊥直径AB ，∴ AC AE =．∴ AE CD =．∴ ∠CAD ＝∠ACE ．∴ 在△APC 中，有PA ＝PC ．∴ PA ＝PC ＝PQ ．∴ P 是△ACQ 的外心．(2)解：∵ CE ⊥直径AB 于F ，∴ 在Rt △BCF 中， 由3tan 4CF ABC BF ∠==，CF ＝8， 得 43233BF CF ==．∴ 由勾股定理，得403BC ==． ∵ AB 是⊙O 直径，∴ 在Rt △ACB 中，由3tan 4AC ABC BC ∠==，403BC =， 得 3104AC BC ==．易知Rt△ACB∽Rt△QCA，∴ AC2＝CQ·BC．∴2152ACCQBC==．(3)证明：∵ AB是⊙O直径，∴∠ACB＝90°．∴∠DAB+∠ABD＝90°．又CF⊥AB，∴∠ABG+∠G＝90°．∴∠DAB＝∠G．∴ Rt△AFP∽Rt△GFB．∴AF FPFG BF=，即AF·BF＝FP·FG．易知Rt△ACF∽Rt△CBF，∴ FC2＝AF·BF(或由射影定理得)∴ FC2＝FP·FG．由(1)，知PC＝PQ，∴ FP+PQ＝FP+PC＝FC．∴ (FP+PQ)2＝FP·FG．16.【答案与解析】解：（1）首先把圆六等份，然后连接三个不相邻的顶点即可作出．△ABC就是所求的三角形；（2）在直角△ABD中，AD==，则BC=AD=，CD=AB=x．则矩形的周长是：2x+2，故答案是：2x+2；（3）连接AC，∵AD是直径，∴∠ACD=90°，又∵CG⊥AD于点G．∴CD2=DG•AD，∴DG==，∴BC=EF=AD﹣2DG=2r﹣．则L=4x+4r﹣．当x=﹣=r时，L取得最大值．最大值是：6r．。

中考数学复习指导《正多边形与圆》知识点归纳一、正多边形的定义正多边形是指所有边相等，所有角相等的多边形。

我们以正n边形来进行讨论，其中n表示边的个数。

二、正多边形的性质1.角的个数：正n边形有n个内角和n个外角。

2.外角和：正n边形的外角和为360°。

3.内角和：正n边形的内角和为(2n-4)×90°。

4.中心角和：正n边形的中心角和为360°。

5. 半径和边长之间的关系：正n边形的边长为a，半径为R，则有R=a/(2×sin(π/n))。

三、正多边形的对称性正n边形有n条对称轴，每条对称轴都把正多边形分成两个对称的部分。

四、圆的性质1.圆心角：圆心角是圆的半径所对应的圆弧所夹的角。

圆心角的大小等于其对应的圆弧的度数。

2.弧长：圆心角对应的圆弧的长度称为弧长。

如果圆的半径为R，圆心角的大小为θ，那么圆弧的长度S=R×θ。

3.弦长：弦是圆上的两点之间的线段，弦长可以通过两角的正弦来计算。

4.弦割定理：圆上的一弦分割出的弧长等于该圆的半径与该弦分割出的小弧的两圆心角的和。

即S=S1+S2=R×θ1+R×θ25.弧度制：弧度制是一种角度的度量方式，将角度定义为弧长与半径的比值：角度=弧长/半径。

单位为弧度。

6.周长和面积：圆的周长等于2πR，面积等于πR²。

五、圆与正多边形的关系1.正多边形逼近圆：正多边形的边数越多，逼近的程度越高，其内接圆越接近于外接圆。

2.正多边形的周长与圆的周长：正n边形的周长与内接圆的周长之比约为n/2π。

3. 正多边形的面积与圆的面积：正n边形的面积与内接圆的面积之比约为(1/2•n•sin(2π/n))/π）。

以上就是《正多边形与圆》的一些重要知识点的归纳。

在复习时，可以通过理论学习、练习习题以及解决实际问题的应用题来巩固和提升自己的理解能力。

加油！。

【2020中考数学专项复习】：正多边形与圆的有关的证明和计算【考纲要求】1．了解正多边形的概念，掌握用等分圆周画圆的内接正多边形的方法；会计算弧长及扇形的面积、圆锥的侧面积及全面积；2．结合相关图形性质的探索和证明，进一步培养合情推理能力，发展逻辑思维能力和推理论证的表达能力；通过这一章的学习，进一步培养综合运用知识的能力，运用学过的知识解决问题的能力.【知识网络】【考点梳理】考点一、正多边形和圆1、正多边形的有关概念：(1) 正多边形：各边相等，各角也相等的多边形叫做正多边形.(2)正多边形的中心——正多边形的外接圆的圆心.(3)正多边形的半径——正多边形的外接圆的半径.(4)正多边形的边心距——正多边形中心到正多边形各边的距离.（正多边形内切圆的半径.）(5)正多边形的中心角——正多边形每一边所对的外接圆的圆心角.2、正多边形与圆的关系：(1)将一个圆n(n≥3)等分(可以借助量角器)，依次连结各等分点所得的多边形是这个圆的内接正多边形.(2)这个圆是这个正多边形的外接圆.（3）把圆分成n(n≥3)等分，经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.这个圆叫做正n边形的内切圆.（4）任何正n边形都有一个外接圆和一个内切圆，这两个圆是同心圆.3、正多边形性质：(1)任何正多边形都有一个外接圆.(2) 正多边形都是轴对称图形，一个正n边形共有n条对称轴，每条对称轴都通过正n边形的中心．当边数是偶数时，它又是中心对称图形，它的中心就是对称中心.(3)边数相同的正多边形相似.它们周长的比，边心距的比，半径的比都等于相似比，面积的比等于相似比的平方．（4）任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆.要点诠释：（1）正n边形的有n个相等的外角，而正n边形的外角和为360度，所以正n边形每个外角的度数是360n；所以正n边形的中心角等于它的外角.（2）边数相同的正多边形相似.周长的比等于它们边长（或半径、边心距）的比.面积比等于它们边长（或半径、边心距）平方的比.考点二、圆中有关计算1．圆中有关计算圆的面积公式：，周长.圆心角为、半径为R的弧长.圆心角为，半径为R，弧长为的扇形的面积.弓形的面积要转化为扇形和三角形的面积和、差来计算.圆柱的侧面图是一个矩形，底面半径为R，母线长为的圆柱的体积为，侧面积为，全面积为.圆锥的侧面展开图为扇形，底面半径为R，母线长为，高为的圆锥的侧面积为，全面积为，母线长、圆锥高、底面圆的半径之间有.弓形的面积（1）由弦及其所对的劣弧组成的图形，S弓形=S扇形-S△OAB；（2）由弦及其所对的优弧组成的弓形，S弓形=S扇形+S△OAB.要点诠释：(1)对于扇形面积公式，关键要理解圆心角是1°的扇形面积是圆面积的，即；(2)在扇形面积公式中，涉及三个量：扇形面积S、扇形半径R、扇形的圆心角，知道其中的两个量就可以求出第三个量.(3)扇形面积公式，可根据题目条件灵活选择使用，它与三角形面积公式有点类似，可类比记忆；(4)扇形两个面积公式之间的联系：.【典型例题】类型一、正多边形有关计算1．如图，矩形ABCD中，AB=4，以点B为圆心，BA为半径画弧交BC于点E，以点O为圆心的⊙O 与弧AE，边AD，DC都相切．把扇形BAE作一个圆锥的侧面，该圆锥的底面圆恰好是⊙O，则AD的长为（）A.4B.92C.112D.5【思路点拨】首先求得弧AE的长，然后利用弧AE的长正好等于圆的底面周长，求得⊙O的半径，则BE 的长加上半径即为AD的长．【答案】D；【解析】解：∵AB=4，∠B=90°，∴9042180AEππ⨯==，∵圆锥的底面圆恰好是⊙O，∴⊙O的周长为2π，∴⊙O的半径为1，∴AD=BC=BE+EC=4+1=5.故选D．【总结升华】本题考查了圆锥的计算及相切两圆的性质，解题的关键是熟记弧长的计算公式. 举一反三：【高清课堂：正多边形与圆的有关证明与计算自主学习7】【变式1】如图，两个相同的正六边形，其中一个正多边形的顶点在另一个正多边形外接圆圆心O处．求重叠部分面积与阴影部分面积之比.【答案】解：连结OA、OB、OC，设OA′交AB于K，OE′交CD于H，∵∠AOK=∠AOC-∠KOC=120°-∠KOC，∠COH=120°-∠KOC，∴∠AOK=∠COH，又∠OAK=∠OCH=60°，OA=OC，∴△AOK≌△COH，由△AOK≌△COH，得S五边形OKBCH=S四边形ABCO=2S△OBC，∴S阴影=S正六边形ABCDEF-S五边形OKBCH′=6S△OBC-2S△OBC=4S△OBC.S五边形OKBCH：S阴影= 21=42.即重叠部分面积与阴影部分面积之比为：12 .【高清课堂：正多边形与圆的有关证明与计算 自主学习8】【变式2】 已知：正十边形的半径是R ，求证：它的边长为1011)2a R =.【答案】证明：作∠OAB 的平分线AM 交OB 于M ，则∠O=∠OAM=36°，∠AMB=∠B=72°， ∴OM=MA=AB ，则△ABM ∽△OAB 得：OA AB=AB BM用R ，a 10分别表示OA ，AB ，BM ，代入以上比例式整理得a 102+ Ra 10-R 2=0,解关于a 10的一元二次方程得1011)2a R =（负值已舍去）.类型二、正多边形与圆综合运用2．如图所示，AB 是半圆的直径，AB ＝2r ，C 、D 为半圆的三等分点，求阴影部分的面积．【思路点拨】图中阴影部分是一个不规则图形，可利用C 、D 是半圆的三等分点，得到AC BD =，从而 有∠CDA ＝∠DAB ，进而CD ∥AB ，故有△ACD 与△OCD 的面积相等，将阴影部分的面积转化为 扇形OCD 的面积． 【答案与解析】解：连接OC 、OD 、CD ．∵ AC BD =，∴ ∠CDA ＝∠DAB ．∴ CD ∥AB ，∴ ACD OCD S S =△△． ∴ OCD S S =阴影扇形．又∵ ∠COD ＝13∠AOB ＝60°， ∴ 2226013603606OCDn r r S S r πππ====阴影扇形．【总结升华】本题容易误认为阴影部分是扇形，对扇形的定义、图形理解不准确，此阴影部分为不规则图形，应利用等积转化法转化为规则图形——扇形．举一反三：【变式】如图所示，在△ABC 中，BC ＝4，以点A 为圆心，2为半径的⊙A 与BC 相切于点D ，交AB 于E ，交AC 于F ，点P 是⊙A 上的一点，且∠EPF ＝40°，则图中阴影部分的面积是( )A ．449π-B ．849π-C ．489π-D ．889π- 【答案】连接AD ，则AD ⊥BC ，阴影部分面积ABC EAF S S =-△扇．故21802842423609S ππ⨯=⨯⨯-=-阴影． 答案：B3．有一个两直角边分别为15cm 和20cm 的直角三角形，若绕一边旋转一周，可得到几种几何体？你能分别求出其全面积吗？【思路点拨】可将直角三角形绕边长为15cm 的直角边旋转一周，所得几何体是底面半径为20cm ，锥高为15cm 的圆锥体；绕边长为20cm 的直角边旋转一周，可得底面半径为15cm ，锥高为20cm 的圆锥体；绕斜边旋转一周，可得两个圆锥的组合体，按这三种情况分别计算全面积即可． 【答案与解析】解：三种．由图①可知，以AC ＝15cm 为轴旋转一周，则其全面积22020S S S ππ=+=⨯⨯侧底 2900(cm )π=．由图②可知，以BC ＝20为轴旋转一周，则其全面积21515S S S ππ=+=⨯⨯圆侧 2375225600(cm )πππ=+=．如图③所示，以AB 为轴旋转一周，得一个圆锥组合体，其全面积S 是上下两个锥体的侧面积之和． 作CD ⊥AB 于D ，则1122ABC S AC BC AB CD ∆==， ∴ 201512cm 25CD ⨯==，即底面半径为12cm ． ∴ S ＝π×12×20+π×12×15＝240π+180π＝420π(cm 2)．【总结升华】利用面积公式计算时，要仔细分析题意，找准已知量和未知量，特别注意全面考虑问题，分情况逐一计算，防止漏解．4．如图所示，有一圆锥形粮堆，其正视图是边长为6cm 的正三角形ABC ，粮堆母线AC 的中点P 处有一老鼠正在偷吃粮食，此时小猫正在B 处，它要沿圆锥侧面到达P 处捕捉老鼠，则小猫所经过的最短路程是多少？【思路点拨】小猫所经过的路程要最短，应该求圆锥侧面展开后两点B 、P 之间的线段长度. 【答案与解析】解：设圆锥底面半径为r ，母线长为l ，展开后圆心角度数为n °，则底面圆的周长为2πr ，侧面展开图的弧长为180n l π，∴ 2180n ll ππ=． ∵ 轴截面△ABC 为等边三角形， ∴ AB ＝BC ，即26l r ==． ∴ r ＝3． ∴ 623180n ππ⨯⨯=． ∴ n ＝180，即其侧面展开图为半圆，如图所示，则△ABP 为直角三角形，BP 为最短路线．在Rt △ABP 中，BP ===．答：小猫所经过的最短路程为． 【总结升华】将所求问题转化为平面上两点之间线段最短的问题，充分利用圆锥底面周长等于侧面展开图的弧长沟通空间元素与平面元素之间的关系．5．如图，在正方形ABCD 中，AB ＝4，O 为对角线BD 的中点，分别以OB ，OD 为直径作⊙O 1，⊙O 2．(1)求⊙O 1的半径；(2)求图中阴影部分的面积．【思路点拨】连接O 1E ，求出一个小弓形的面积再乘以4即可.【答案与解析】解：(1)在正方形ABCD 中，AB ＝AD ＝4，∠A ＝90°，∴ BD ==．∴ ⊙O 1的半径为1144BD =⨯=即⊙O 1．(2)连接O 1E ，∵ BD 为正方形ABCD 的对角线，∴ ∠ABO ＝45°．∵ O 1E ＝O 1B ，∴ ∠BEO 1＝∠EBO 2＝45°．∴ ∠BO 1E ＝90°．∴ 111O BE O BE S S S =-=△扇形211122π⨯=-． 根据图形的对称性得 S 1＝S 2＝S 3＝S 4，∴ 1424S S π==-阴影．【总结升华】求阴影部分面积时，一般要将阴影部分面积转化为几个规则图形的面积求差或和.举一反三：【变式】已知：如图所示，水平地面上有一面积为30πcm2的扇形AOB，半径OA＝6cm，且OA与地面垂直．在没有滑动的情况下，将扇形向右滚动至OB与地面垂直为止，求O点移动的距离．【答案】解：观察图形可知O点移动距离即为扇形滚动距离，而扇形滚动距离为优弧AOB的弧长．∵12S l R=⨯弧扇，∴223010(cm)6SlRππ⨯===弧．答：O点移动的距离为10π cm．6．如图，已知在⊙O中，43AB=，AC是⊙O的直径，AC⊥BD于F，∠A＝30°．(1)求图中阴影部分的面积；(2)若用阴影扇形OBD 围成一个圆锥侧面，请你出这个圆锥的底面圆的半径．【思路点拨】（1）阴影部分是一个扇形，扇形圆心角∠BOD ＝2∠BOC ＝2×2×30°＝120°，只需通过解直角三角形求出OB 的长，即可利用扇形面积2360n r π=求出阴影部分面积．（2）扇形弧长是圆锥的底面周长，由条件求出BCD 的长l ，利用2l r π=可求出半径r 的长．【答案与解析】解：(1)过O 作OE ⊥AB 于E，则12AE AB == 在Rt △AEO 中，∠BAC ＝30°，cos30AE OA =°． ∴4cos302A OA ===°．又∵ OA ＝OB ，∴ ∠ABO ＝30°．∴∠BOC＝60°．∵ AC⊥BD，∴BC CD=．∴∠COD＝∠BOC＝60°．∴∠BOD＝120°．∴221201643603603n OASπππ==⨯=阴影．(2)设圆锥的底面圆的半径为r，则周长为2πr，∴12024180rππ=⨯．∴43r=．【总结升华】用扇形围成圆锥，扇形的半径是圆锥的母线，扇形的弧长是圆锥的底面周长.中考总复习：正多边形与圆的有关的证明和计算—巩固练习（提高）【巩固练习】一、选择题1. 将一个底面半径为5 cm，母线长为12 cm的圆锥形纸筒沿一条母线剪开并展平，所得的侧面展开图的圆心角是（）度．A.60B.90C.120D.1502．某盏路灯照射的空间可以看成如图所示的圆锥，它的高AO＝8米，母线AB与底面半径OB的夹角为α，4tan3α=，则圆锥的底面积是（）平方米．A.9πB.16πC. 25πD.36π3．某花园内有一块五边形的空地如图所示，为了美化环境，现计划在五边形各顶点为圆心，2m 长为半径的扇形区域内（阴影部分）种上花草，那么种上花草的扇形区域总面积是（ ）A ．6πm 2B ．5πm 2C ．4πm 2D ．3πcm 24．如图所示，直径AB 为6的半圆，绕A 点逆时针旋转60°，此时点B 到了点B ，则图中阴影部分的面积是（ ）A ．6πB ．5πC ．4πD ．3π5．如图所示，从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC ，将剪下的扇形围成一个圆锥，则圆锥的底面圆半径为 （ ）A ．13B ．6C ．3D ．4 6．已知三角形的三边长分别为3，4，5，则它的边与半径为1的圆的公共点个数所有可能的情况是( )A ．0，1，2，3B ．0，1，2，4C ．0，1，2，3，4D ．0，1，2，3，4，5二、填空题7．若一个圆锥的侧面积是18π，侧面展开图是半圆，则该圆锥的底面圆半径是________．8．如图，已知⊙O是边长为2的等边△ABC的内切圆，则⊙O的面积为________．9．如图是一条水平铺设的直径为2米的通水管道横截面，其水面宽为1.6米，则这条管道中此时水最深为__________米．10．将半径为10cm，弧长为12π的扇形围成圆锥(接缝忽略不计)，那么圆锥的母线与圆锥高的夹角的余弦值是________．11．如图所示是一个用来盛爆米花的圆锥形纸杯，纸杯开口圆的直径EF长为10cm．在母线OF上的点A 处有一块爆米花残渣，且FA＝2cm，一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点，则此蚂蚁爬行的最短距离为________cm．12．如图，扇形OAB，∠AOB＝90°，⊙P与OA、OB分别相切于点F、E，并且与弧AB切于点C，则扇形OAB的面积与⊙P的面积比是________．三、解答题13．如图所示，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，连结EF、EO，若DE＝DPA＝45°．(1)求⊙O的半径；(2)求图中阴影部分的面积．14.如图AB是⊙O的直径，点D在⊙O上，∠DAB＝45°，BC∥AD，CD∥AB．(1)判断直线CD与⊙O的位置关系，并说明理由；(2)若⊙O的半径为1，求图中阴影部分的面积(结果保留π)．15．已知：如图，△ABC 内接于⊙O ，AB 为直径，弦CE ⊥AB 于F ，C 是AD 的中点，连结BD 并延长交EC 的延长线于点G ，连结AD ，分别交CE 、BC 于点P 、Q ．(1)求证：P 是△ACQ 的外心；(2)若3tan 4ABC ∠=，CF ＝8，求CQ 的长； (3)求证：(FP+PQ)2＝FP ·FG ．16. 如图，△ABC 内接于⊙O ，且∠B ＝60°．过点C 作圆的切线l 与直径AD 的延长线交于点E ，AF ⊥l ，垂足为F ，CG ⊥AD ，垂足为G ．(1)求证：△ACF ≌△ACG ；(2)若AF ＝AF =，求图中阴影部分的面积．【答案与解析】一、选择题1.【答案】D ；【解析】圆锥的底面周长为22510r πππ=⨯=，所以它的侧面展开图的圆心角是1801015012n ππ⨯==°． 2.【答案】D ； 【解析】因为4tan 3AO BO α==，AO ＝8，所以BO ＝6，所以圆锥的底面积是2636ππ=． 3.【答案】A ； 【解析】五个扇形的半径都为2cm ，设其圆心角分别为1n °，2n °，3n °，4n °，5n °，则无法直接利用扇形面积公式求解，可以整体考虑，123455n n n n n ++++=°°°°°边形形 内角和＝(5-2)×180°＝540°，∴ 2254026(m )360S ππ⨯==阴影． 4.【答案】A ；【解析】如果分别求S Ⅰ和S Ⅲ得阴影面积则很复杂，由旋转前后图形全等，易得S Ⅰ＝S Ⅱ，∴ 26066360ABB S S S S S S ππ'⨯=+====ⅠⅢⅡⅢ阴影扇形+． 5.【答案】B ；【解析】要求围成的圆锥的底面圆半径，只要求出扇形ABC 中BC 的弧长，该弧长即为围成的圆锥的底面圆的周长，再根据周长即可以求出半径．∵ 直径为2，∠BAC ＝60°∴ AC ，∴ BC ，设底面圆的半径为r ，则由2r π=解得r = 6.【答案】C ；【解析】∵ 32+42＝52，∴ 这个三角形是直角三角形，且其内切圆半径34512r +-==．则这个三角形的边与半径为1的圆的公共点个数有如下情况：共有0，1，2，3，4五种情况．二、填空题7．【答案】3；【解析】设圆锥的母线长为R ，侧面展开图半圆弧长为l ，圆锥底面积半径为r ， 则有：218018360R ππ=． ∴ R 2＝36，R ＝6．又1182Rl π=． ∴ 2l π=，∴ 2πr ＝6π，r ＝3．8．【答案】3π； 【解析】设⊙O 与BC 切于D 点，连接OD ，OC ．在Rt △ODC 中，112122DC BC ==⨯=．∠OCD ＝30°．∴ tan 303OD DC ==°．∴ 3OD =，则22O 3S r πππ===⎝⎭⊙．9．【答案】0.4；【解析】如图，过O 作OC ⊥AB 于C ，并延长并AB 于D ．在Rt △OBC 中，212OB ==，11 1.60.822BC AB ==⨯=．∴ 20.6OC ==．∴ CD ＝OD-OC ＝1-0.6＝0.4(米)．10．【答案】45； 【解析】如图，因为2πR ＝12π，所以R ＝6．由勾股定理，得8h ==． 所以84cos 105AO CAO AC ∠===．11．【答案】【解析】底圆周长为2πr ＝10π，设圆锥侧面展开图的扇形所对圆心角为n °， 有2180n R r ππ=，即1010180n ππ⨯=， ∴ n ＝180°，如图所示，FA ＝2，OA ＝8，在Rt △OEA 中由勾股定理可得EA 即为所求最短距离．∴ EA ====12．【答案】 34+； 【解析】连接OC ，PE ，PF ，则四边形OEPF 是正方形．设PE ＝r ，则OP ，OC ＝1)r +．∴ 2S r ==扇形．∴ OAB S 扇形:234S r +=⊙P :2r π34+=．三、解答题13.【答案与解析】（1）∵ 直径AB ⊥DE ，∴ 12CE DE == ∵ DE 平分半径OA ，∴ 1122CE AO OE ==． 在Rt △OCE 中，∵ ∠CEO ＝30°．∴ OE ＝2．即⊙O 的半径为2．（2）连OF ，在Rt △DCP 中，∵ ∠DPC ＝45°．∠D ＝90°-45°＝45°∴ ∠EOF ＝2∠D ＝90°．∵ 2902360S ππ=⨯⨯=扇形OEF ． 1122222OEF S OE OF ∆==⨯⨯= ∴ 2OEF OEF S S S π∆=-=-阴影扇形．14.【答案与解析】解：(1)直线CD 与⊙O 相切．如图，连接OD ．∵ OA ＝OD ，∠DAB ＝45°，∴ ∠ODA ＝45°．∴ ∠AOD ＝90°．∵ CD ∥AB ，∴ ∠ODC ＝∠AOD ＝90°，即OD ⊥CD ．又∵ 点D 在⊙O 上，∴ 直线CD 与⊙O 相切．(2)∵ BC ∥AD ，CD ∥AB ，∴ 四边形ABCD 是平行四边形．∴ CD ＝AB ＝2．∴ ()(12)13222OBCD OB CD OD S +⨯+⨯===梯形． ∴ 图中阴影部分的面积等于231312424OBD OBCD S S ππ-=-⨯⨯=-扇形梯形．15.【答案与解析】(1)证明：∵ C 是AD 的中点，∴ AC CD =．∴ ∠CAD ＝∠ABC ．∵ AB 是⊙O 的直径，∴ ∠ACB ＝90°．∴ ∠CAD+∠AQC ＝90°．又 CE ⊥AB ，∴ ∠ABC+∠PCQ ＝90°．∴ ∠AQC ＝∠PCQ ．∴ 在△PCQ 中，有PC ＝PQ ．∵ CE ⊥直径AB ，∴ AC AE =．∴ AE CD =．∴∠CAD＝∠ACE．∴在△APC中，有PA＝PC．∴ PA＝PC＝PQ．∴ P是△ACQ的外心．(2)解：∵ CE⊥直径AB于F，∴在Rt△BCF中，由3tan4CFABCBF∠==，CF＝8，得43233 BF CF==．∴由勾股定理，得403 BC==．∵ AB是⊙O直径，∴在Rt△ACB中，由3tan4ACABCBC∠==，403BC=，得3104AC BC==．易知Rt△ACB∽Rt△QCA，∴ AC2＝CQ·BC．∴2152ACCQBC==．(3)证明：∵ AB是⊙O直径，∴∠ACB＝90°．∴∠DAB+∠ABD＝90°．又CF⊥AB，∴∠ABG+∠G＝90°．∴∠DAB＝∠G．∴ Rt△AFP∽Rt△GFB．∴AF FPFG BF=，即AF·BF＝FP·FG．易知Rt△ACF∽Rt△CBF，∴ FC2＝AF·BF(或由射影定理得)∴ FC2＝FP·FG．由(1)，知PC＝PQ，∴ FP+PQ＝FP+PC＝FC．∴ (FP+PQ)2＝FP·FG．16.【答案与解析】(1)证明：如图，连接CD，OC，则∠ADC＝∠B＝60°．∵ AC⊥CD，CG⊥AD，∴∠ACG＝∠ADC＝60°．由于∠ODC＝60°，OC＝OD，∴△OCD为正三角形，得∠DCO＝60°．由OC l⊥，得∠ECD＝30°，∴∠ECG＝30°+30°＝60°．进而∠ACF＝180°-2×60°＝60°，∴△ACF≌△ACG．(2)解：在Rt △ACF 中，∠ACF ＝60°，AF ＝CF ＝4．在Rt △OCG 中，∠COG ＝60°，CG ＝CF ＝4，得3OC ==．在Rt △CEO 中，23OE OC ==．于是2160)23609CEO COD OC S S S OE CG ππ=-=-=△阴影扇形．。

初中数学中考复习正多边形与圆的有关的证明和计算正多边形与圆的关系是初中数学中重要的内容。

在中考复习中，我们需要掌握正多边形与圆的有关知识，并能够进行证明和计算。

一、正多边形的性质与计算：1.正多边形的定义：正多边形是指所有边相等，所有角也相等的多边形。

2.正多边形的计算：正n边形的内角和为180°(n-2)，每个内角为(180°(n-2))/n。

正n边形的外角和为360°，每个外角为360°/n。

正n边形的中心角为360°/n。

例题1：求正六边形的内角和。

解：内角和为180°(6-2)=720°。

例题2：求正五边形的每个内角大小。

解：每个内角为(180°(5-2))/5=108°。

二、正多边形与圆的关系：1.圆的定义：圆是平面上一组到一个固定点(圆心)距离相等的点的集合。

2.正多边形与圆的关系：正多边形的顶点均在圆上，且正多边形的外接圆和内切圆都满足以下性质：①外接圆：正多边形的外接圆的圆心与正多边形的中心重合。

②内切圆：正多边形的内切圆的圆心与正多边形的中心重合，且内接圆的半径等于正多边形的边长的一半。

3.正多边形与圆的证明：①外接圆的证明：由正多边形的定义可知，正多边形的每个顶点到圆心的距离都相等，即正多边形的顶点在圆上。

而圆心与正多边形的中心重合，所以正多边形的外接圆的圆心与正多边形的中心重合。

②内切圆的证明：首先，通过正多边形的定义，可以证明正多边形的每个顶点到圆心的距离都相等，即正多边形的顶点在圆上。

其次，由于正多边形的边长相等，所以正多边形的中心到各个顶点的距离也相等。

而内切圆的半径等于正多边形中心到任意一个顶点的距离，所以正多边形的内切圆的圆心与正多边形的中心重合，且内切圆的半径等于正多边形的边长的一半。

例题3：如图，正六边形ABCD中，O为外接圆的圆心，求AB的长。

解：由于正六边形的外接圆的圆心与正多边形的中心重合，所以O即为正六边形的中心。

正多边形与圆的有关的证明和计算知识讲解及典型例题解析【考纲要求】1．了解正多边形的概念，掌握用等分圆周画圆的内接正多边形的方法；会计算弧长及扇形的面积、圆锥的侧面积及全面积；2．结合相关图形性质的探索和证明，进一步培养合情推理能力，发展逻辑思维能力和推理论证的表达能力；通过这一章的学习，进一步培养综合运用知识的能力，运用学过的知识解决问题的能力.【知识网络】【考点梳理】考点一、正多边形和圆1、正多边形的有关概念：(1) 正多边形：各边相等，各角也相等的多边形叫做正多边形.(2)正多边形的中心——正多边形的外接圆的圆心.(3)正多边形的半径——正多边形的外接圆的半径.(4)正多边形的边心距——正多边形中心到正多边形各边的距离.（正多边形内切圆的半径）(5)正多边形的中心角——正多边形每一边所对的外接圆的圆心角.2、正多边形与圆的关系：(1)将一个圆n(n≥3)等分(可以借助量角器)，依次连结各等分点所得的多边形是这个圆的内接正多边形.(2)这个圆是这个正多边形的外接圆.（3）把圆分成n(n≥3)等分，经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.这个圆叫做正n边形的内切圆.（4）任何正n边形都有一个外接圆和一个内切圆，这两个圆是同心圆.3、正多边形性质：(1)任何正多边形都有一个外接圆.(2) 正多边形都是轴对称图形，一个正n边形共有n条对称轴，每条对称轴都通过正n边形的中心．当边数是偶数时，它又是中心对称图形，它的中心就是对称中心.(3)边数相同的正多边形相似.它们周长的比，边心距的比，半径的比都等于相似比，面积的比等于相似比的平方．（4）任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆.要点诠释：（1）正n边形的有n个相等的外角，而正n边形的外角和为360度，所以正n边形每个外角的度数是360n；所以正n边形的中心角等于它的外角.（2）边数相同的正多边形相似.周长的比等于它们边长（或半径、边心距）的比.面积比等于它们边长（或半径、边心距）平方的比.考点二、圆中有关计算1．圆中有关计算圆的面积公式：，周长.圆心角为、半径为R的弧长.圆心角为，半径为R，弧长为的扇形的面积.弓形的面积要转化为扇形和三角形的面积和、差来计算.圆柱的侧面图是一个矩形，底面半径为R，母线长为的圆柱的体积为，侧面积为，全面积为.圆锥的侧面展开图为扇形，底面半径为R，母线长为，高为的圆锥的侧面积为，全面积为，母线长、圆锥高、底面圆的半径之间有.要点诠释：(1)对于扇形面积公式，关键要理解圆心角是1°的扇形面积是圆面积的，即；(2)在扇形面积公式中，涉及三个量：扇形面积S、扇形半径R、扇形的圆心角，知道其中的两个量就可以求出第三个量.(3)扇形面积公式，可根据题目条件灵活选择使用，它与三角形面积公式有点类似，可类比记忆；(4)扇形两个面积公式之间的联系：.【典型例题】类型一、正多边形有关计算1．图①是我们常见的地砖上的图案，其中包含了一种特殊的平面图形﹣正八边形．（1）如图②，AE是⊙O的直径，用直尺和圆规作⊙O的内接正八边形ABCDEFGH（不写作法，保留作图痕迹）；（2）在（1）的前提下，连接OD，已知OA=5，若扇形OAD（∠AOD＜180°）是一个圆锥的侧面，则这个圆锥底面圆的半径等于．【思路点拨】（1）作AE的垂直平分线交⊙O于C，G，作∠AOG，∠EOG的角平分线，分别交⊙O于H，F，反向延长 FO，HO，分别交⊙O于D，B顺次连接A，B，C，D，E，F，G，H，八边形ABCDEFGH即为所求；（2）由八边形ABCDEFGH是正八边形，求得∠AOD=3=135°得到的长=，设这个圆锥底面圆的半径为R，根据圆的周长的公式即可求得结论．【答案与解析】（1）如图所示，八边形ABCDEFGH即为所求，（2）∵八边形ABCDEFGH是正八边形，∴∠AOD=3=135°，∵OA=5，∴的长=，设这个圆锥底面圆的半径为R，∴2πR=，∴R=，即这个圆锥底面圆的半径为．故答案为：．【总结升华】本题考查了尺规作图，圆内接八边形的性质，弧长的计算，圆的周长公式的应用，会求八边形的内角的度数是解题的关键．举一反三：【变式1】如图是三根外径均为1米的圆形钢管堆积图和主视图，则其最高点与地面的距离是______米．【答案】31+.解析：如图，以三个圆心为顶点等边三角形O1O2O3的高O1C＝3，所以AB＝AO1+O1C+BC＝1313122++=+．【变式2】同一个圆的内接正三角形、正方形、正六边形的边长的比是__________.32：：【变式3】一张圆心角为45°的扇形纸板和圆形纸板按如图方式剪得一个正方形，边长都为2，则扇形纸板和圆形纸板的面积比是（）A．5：4 B．5：2 C．：2 D．：【答案】A.【解析】解：如图1，连接OD，∵四边形ABCD是正方形，∴∠DCB=∠ABO=90°，AB=BC=CD=2，∵∠AOB=45°，∴OB=AB=2，由勾股定理得：OD==2，∴扇形的面积是=π；如图2，连接MB、MC，∵四边形ABCD是⊙M的内接四边形，四边形ABCD是正方形，∴∠BMC=90°，MB=MC，∴∠MCB=∠MBC=45°，∵BC=2，∴MC=MB=，∴⊙M的面积是π×（）2=2π，∴扇形和圆形纸板的面积比是π÷（2π）=．故选：A．类型二、正多边形与圆有关面积的计算2．(1)如图(a)，扇形OAB 的圆心角为90°，分别以OA ，OB 为直径在扇形内作半圆，P 和Q分别表示阴影部分的面积，那么P 和Q 的大小关系是( )．A ．P ＝QB ．P ＞QC ．P ＜QD ．无法确定(2)如图(b)，△ABC 为等腰直角三角形，AC ＝3，以BC 为直径的半圆与斜边AB 交于点D ，则图中阴影部分的面积是________．(3)如图(c)，△AOB 中，OA ＝3cm ，OB ＝1cm ，将△AOB 绕点O 逆时针旋转90°到△A ′OB ′，求AB 扫过的区域(图中阴影部分)的面积．(结果保留π)【思路点拨】 直接使用公式计算阴影部分面积比较困难时，可采用和差法、转化法、方程法等，有时也需要运用变换的观点来解决问题．【答案与解析】解：(1)阴影部分的面积直接求出十分困难，可利用几个图形面积的和差进行计算：2OAB OCA P S S Q =-+扇形半圆2211()42R R Q Q ππ=-+=； (2)(转化法“凑整”)利用BmD CnD S S =弓形弓形，则阴影部分的面积可转化为△ACD 的面积，等于△ABC 面积的一半，答案为94； (3)(旋转法)将图形ABM 绕点O 逆时针旋转到A ′B ′M ′位置，则A OA MOM S S S ''=-阴影扇形扇形2211244OA OM πππ=-=． 【总结升华】求阴影面积的几种常用方 (1)公式法；(2)割补法；（3）旋转法；(4)拼凑法；(5)等积变形法；(6)构造方程法．举一反三：【变式】如图，在△ABC 中，AB ＝AC ，AB ＝8，BC ＝12，分别以AB 、AC 为直径作半圆，则图中阴影部分的面积是( )A ．64π127-B ．16π32-C ．16π247-D ．16π127-【答案】解：如图，由AB ，AC 为直径可得AD ⊥BC ，则BD ＝DC ＝6．在Rt △ABD 中，228627AD =-=，∴ 211246271612722S ππ⎛⎫=⨯⨯⨯-⨯⨯=-⎪⎝⎭阴影． 答案选D.3．如图所示，A 是半径为2的⊙O 外一点，OA ＝4，AB 是⊙O 的切线，B 为切点，弦BC ∥OA ，连AC ，求阴影部分的面积．【思路点拨】图中的阴影是不规则图形，不易直接求出，如果连接OB 、OC ，由BC ∥OA ，根据同底等高的三角形面积相等，于是所求阴影可化为扇形OBC 去求解．【答案与解析】解：如图所示，连OB 、OC∵ BC ∥OA ．∴ △OBC 和△ABC 同底等高，∴ S △ABC ＝S △OBC ，∴∵ AB 为⊙O 的切线，∴ OB ⊥AB ．∵ OA ＝4，OB ＝2，∴ ∠AOB ＝60°．∵ BC ∥OA ，∴ ∠AOB ＝∠OBC ＝60°．∵ OB ＝OC ，∴ △OBC 为正三角形．∴ ∠COB ＝60°，∴ 260223603OBC S S ππ⨯===阴影扇形．【总结升华】通过等积替换化不规则图形为规则图形，在等积转化中①可根据平移、旋转或轴对称等图形变换；②可根据同底（等底）同高（等高）的三角形面积相等进行转化．举一反三：【变式】如图所示，半圆的直径AB ＝10，P 为AB 上一点，点C ，D 为半圆的三等分点，则阴影部分的面积等于________．【答案】 解：连接OC 、OD 、CD ．∵ C 、D 为半圆的三等分点，∴ ∠AOC ＝∠COD ＝∠DOB ＝180603=°°． 又∵ OC ＝OD ，∴ ∠OCD ＝∠ODC ＝60°，∴ DC ∥AB ，∴ PCD OCD S S =△△，∴ 2605253606S S ππ===g g 阴影扇形OCD ．4．如图，在边长为4的正方形ABCD中，以AB为直径的半圆与对角线AC交于点E．（1）求弧BE所对的圆心角的度数．（2）求图中阴影部分的面积（结果保留π）．【思路点拨】（1）连接OE，由条件可求得∠EAB=45°，利用圆周角定理可知弧BE所对的圆心角∠EOB=2∠E AB=90°；（2）利用条件可求得扇形AOE的面积，进一步求得弓形的面积，利用Rt△ADC的面积减去弓的面积可求得阴影部分的面积．【答案与解析】解：（1）连接OE，∵四边形ABCD为正方形，∴∠EAB=45°，∴∠EOB=2∠EAB=90°；（2）由（1）∠EOB=90°，且AB=4，则OA=2，∴S扇形AOE==π，S△AOE=OA2=2，∴S弓形=S扇形AOE﹣S△AOE=π﹣2，又∵S△ACD=AD•CD=×4×4=8，∴S阴影=8﹣（π﹣2）=10﹣π．【总结升华】本题主要考查扇形面积的计算和正方形的性质，掌握扇形的面积公式是解题的关键，注意弓形面积的计算方法．»AB）对应5．将一块三角板和半圆形量角器按图中方式叠放，重叠部分（阴影）的量角器圆弧（的中心角（∠AOB）为120°，AO的长为4cm，求图中阴影部分的面积.【思路点拨】看是否由“规则的”三角形、四边形、圆、扇形、弓形等可求面积的图形，经过怎样的拼凑、割补、叠合而成，这是解决这类题的关键．【答案与解析】阴影部分的面积可看成是由一个扇形AOB 和一个Rt △BOC 组成，其中扇形AOB 的中心角是120°，AO 的长为4，Rt △BOC 中，OB ＝OA ＝4，∠BOC ＝60°，∴ 可求得BC 长和OC 长，从而可求得面积，阴影部分面积＝扇形AOB 面积+△BOC 面积＝21623cm 3π⎛⎫+ ⎪⎝⎭． 【总结升华】本题是求简单组合图形的面积问题，解答时，常常是寻找这些“不规则的图形”是由哪些“可求面积的、规则的图形”组合而成.举一反三：【变式】如图，矩形ABCD 中，AB ＝1，2AD =．以AD 的长为半径的⊙A 交BC 于点E ，则图中阴影部分的面积为________．【答案】1224π--. 解析：连接AE ，易证AB ＝BE ＝1，∠BAE ＝45°，所以∠EAD ＝45°， 所以21112(2)22824ABE ABCD DAE S S S S ππ=--=--=--△阴影矩形扇形．6．如图，AB 是⊙O 的直径，点P 是AB 延长线上一点，PC 切⊙O 于点C ，连接AC ，过点O 作AC 的垂线交AC 于点D ，交⊙O 于点E ．已知AB ﹦8，∠P=30°．（1）求线段PC 的长；（2）求阴影部分的面积．【思路点拨】（1）连接OC，由PC为圆O的切线，根据切线的性质得到OC与PC垂直，可得三角形OCP为直角三角形，同时由直径AB的长求出半径OC的长，根据锐角三角函数定义得到tanP为∠P的对边OC与邻边PC的比值，根据∠P的度数，利用特殊角的三角函数值求出tanP的值，由tanP及OC的值，可得出PC 的长；（2）由直角三角形中∠P的度数，根据直角三角形的两个锐角互余求出∠AOC的度数，进而得出∠BOC的度数，由OD与BC垂直，且OC=OB，利用等腰三角形的三线合一得到OD为∠BOC的平分线，可求出∠COD度数为60°，再根据直角三角形中两锐角互余求出∠OCD度数为30°，根据30°角所对的直角边等于斜边的一半，由斜边OC的长求出OD的长，先由∠COD的度数及半径OC的长，利用扇形的面积公式求出扇形COE的面积，再由OD与CD的长，利用直角三角形两直角边乘积的一半求出直角三角形COD 的面积，用扇形COE的面积减去三角形COD的面积，即可求出阴影部分的面积．【答案与解析】解：（1）连接OC，∵PC切⊙O于点C，∴OC⊥PC，∵AB=8，∴OC=12AB=4，又在直角三角形OCP中，∠P=30°，∴tanP=tan30°=OCPC，即PC=433=43；（2）∵∠OCP=90°，∠P=30°，∴∠COP=60°，∴∠A OC=120°，又AC⊥OE，OA=OC，∴OD为∠AOC的平分线，∴∠COE=12∠AOC=60°，又半径OC=4，∴S扇形OCE=26048=3603ππ⨯，在Rt△OCD中，∠COD=60°，∴∠OCD=30°，∴OD=12OC=2，根据勾股定理得：CD=22OC-OD=23，【总结升华】此题考查了切线的性质，含30°角的直角三角形的性质，等腰三角形的性质，锐角三角函数定义，以及扇形的面积公式，遇到已知切线的类型题时，常常连接圆心与切点，利用切线的性质得出垂直，利用直角三角形的性质来解决问题．。

与圆有关的计算弧长： 扇形面积阴影部分面积 圆锥侧面积： 180r n l π=R l R n S 弧扇213602==π白整阴S S S -=母侧l S r π=计算 对称性 定义正多边形与圆 周长、面积、中心角、半径 画法：等分圆 正多形都是轴对称图形 正n 边形有n 条对称轴，都经过中心 若n 是偶数，则正n 边形还是中心对称图形备 课 笔 记备课时间：20 年 月 日课题 第24课时：正多边形与圆、与圆有关的计算课型 复习课课时1教学 目标 1.知道正多边形、正多边形的中心等概念，掌握正多边形的对称性；2.会用尺规作圆的内接正方形和正六边形，知道用正多边形进行平面图形的镶嵌；3.会计算圆的周长、扇形的弧长及简单组合图形的周长；4.会计算圆的面积、扇形的面积及简单组合图形的面积；5.知道圆锥当中的量与侧面展开图－扇形当中的量的对应关系，以及利用其解决相关问题.教学 重点 计算扇形的弧长、面积以及圆锥中的有关计算.教学 难点 利用圆锥当中的量与侧面展开图－扇形当中的量的对应关系解决问题.教学 准备导学案、多媒体课件教 学 内 容三次备课教 学 过 程一次备课 活动一、知识梳理活动二、基础检测1．（1）给出下列说法：①正多边形的各条边相等；②各边相等的多边形是正多边形；③各角相等的多边形是正多边形；④各边相等的圆的内接多边形是正多边形；⑤既是轴对称又是中心对称的多边形是正多边形．其中正确说法的个数是 ( ) A ．1 B ．2 C ．3 D ．4布置学生复习教材：九上第二章P77-P95 学生活动：组内讨论，回顾知识点,完善知识体系. 教师活动：课堂上多媒体展示知识点，组织小组讨论，完善知识体系，建构知识框架.教学过程一次备课（2）张明同学设计了四种正多边形的瓷砖图案，在这四种瓷砖图案中，不能铺满地面的是( )A B C D（3）正多边形的一个外角为15°，则边数为；正n边形的一个内角是156°，则n＝；正n边形的一个外角与一个内角的比为1：3，则n＝．2.（1）在半径为1的⊙O中，120°的圆心角所对的弧长是,面积是．（2）如果一个扇形的半径是1，弧长是3，那么此扇形的圆心角的大小为．(3) 一个扇形的圆心角为135°，弧长为3πcm，则此扇形的面积是cm2．3.（1）已知圆锥的底面半径为4cm，母线长为6cm，则它的侧面展开图的面积等于．（2）用一个半径为30，圆心角为120°的扇形围成一个圆锥，则这个圆锥的底面半径是．活动三、综合检测4.如图，五边形ABCDE是正五边形．若l1∥l2，则∠1﹣∠2＝°．5.如图，有一个⊙O和两个正六边形T1，T2．T1的6个顶点都在圆周上，T2的6条边都和⊙O相切(我们称T1，T2分别为⊙O的内接正六边形和外切正六边形)．设T1，T2的边长分别为a，b，正六边形T1，T2的面积分别为S1，S2，则S1：S2＝．6.如图，AB是圆锥的母线，BC为底面直径，已知BC＝6cm，圆锥的侧面积为15πcm2，则sin∠ABC的值为（）A．B．C．D．7.如图，正方形ABCD内接于⊙O，⊙O的半径为2，以点A为圆心，以AC长为半径画弧交AB的延长线于点E，交AD的延长线于点F，则图中阴影部分的面积为（）A．4π﹣4 B．4π﹣8 C．8π﹣4 D．8π﹣8学生活动：独立思考，自主完成.教师活动：请学生结合性质和判定，分析问题并解决问题,对暴露出来的问题及时提醒.学生活动：1、独自练习；2、小组交流.教师活动：1、指导学生在分析问题中总结注意点；2、对学生进行友情提醒；3、对难点问题加强指导、纠错．第6题第4题第5题第7题教学过程一次备课8.如图，已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上，过点C作CD⊥AB，分别交AB、AO的延长线于点D、E，AE交半圆O于点F，连接CF．（1）判断直线DE与半圆O的位置关系，并说明理由；（2）求证：CF=OC；（3）若半圆O的半径为12，求阴影部分的周长与面积．活动四、拓展提升9.如图，在△ABC中，AB=5，将△ABC绕点A逆时针旋转30°后得到△ADE，点B经过的路径为，则图中阴影部分的面积为（）A．πB．πC．πD．π10. 如图，△OAC的顶点O在坐标原点，OA边在x轴上，OA＝2，AC＝1，把△OAC绕点A按顺时针方向旋转到△O′AC′，使得点O′的坐标是（1，），则在旋转过程中线段OC扫过部分（阴影部分）的面积为．11. 一块等边三角形木板，边长为1，现将木板沿水平线翻滚，如图所示，若翻滚了2017次，则B点所经过的路径长度为．学生活动：独立思考、自主探索、学生展示．教师活动：适时点拨、评价．第9题第10题第11题。

初中数学中考复习正多边形与圆的有关的证明和计算正多边形与圆的有关证明和计算是初中数学中的基础知识，掌握这些知识将有助于学生在中考中取得好成绩。

下面将详细介绍正多边形与圆的证明和计算相关内容。

一、多边形的内角和在初中数学中，我们首先要了解正多边形的内角和的计算方式。

一个n边形（n≥3）的内角和公式为：(n-2)×180度，也可以写成(n-2)×π弧度。

例如，一个三角形的内角和为(3-2)×180度=180度；一个四边形的内角和为(4-2)×180度=360度。

二、正多边形的性质1.正多边形的内角是相等的。

这是因为正多边形的所有边长和内角都相等。

2.正多边形的外角是相等的。

外角是指在多边形外部，相邻两边的夹角。

3.正多边形的对角线个数为n(n-3)/2，其中n为多边形的边数。

例如，一个六边形有6(6-3)/2=9条对角线。

4.正多边形的对角线长度相等。

如果我们连接正多边形的一个顶点和非相邻顶点，得到的线段即为对角线。

所有对角线的长度均相等。

5.正多边形的中心到顶点的距离称为半径，正多边形的中心到边的距离称为中线。

一个正多边形的半径和中线相等。

三、正多边形的外接圆和内切圆1. 正n边形的外接圆半径r的计算公式为：r = a/2sin(π/n)，其中a为正n边形的边长。

例如，一个正六边形的边长为a，那么它的外接圆的半径为r = a/2sin(π/6)。

2. 正n边形的内切圆半径R的计算公式为：R = a/2tan(π/n)。

例如，一个正六边形的边长为a，那么它的内切圆的半径为R =a/2tan(π/6)。

四、正多边形与圆的面积1. 正n边形的面积公式为：S = (1/4) × n × a² × cot(π/n)，其中a为正n边形的边长。

例如，一个正六边形的边长为a，那么它的面积为S = (1/4) × 6 × a² × cot(π/6)。

正多边形和圆有什么关系？答案：解：把圆分成n（n≥3)等份(1）依次连接各分点所得的多边形是这个圆的圆内接正n边形；（2)经过各分点作圆的切线，以相邻切线的交点炎顶点的多边形是这个圆的外切正n边形；(3）每个正n边形都有一个内切圆和一个外接圆，它们是同心圆.【举一反三】典题:如图24。

3—1，⊙O的内接等腰△ABC，AB=AC，弦BD、CE分别平分∠ABC、∠ACB，BE=BC，求证：五边形AEBCD是正五边形.思路导引:由等腰三角形的性质,得两底角相等。

又BD、CE分别平分∠ABC、∠ACB，从而说明圆周角相等，相等的圆周角所对和弧相等,从而说明A、B、C、D、E是圆的五等分点,所以五边形AEBCE是正五边形.标准答案：证明：∵AB=AC，∴五边形AEBCD是正五边形.尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文档在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

文中部分文字受到网友的关怀和支持，在此表示感谢！在往后的日子希望与大家共同进步，成长。

This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be someunsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。