魔考大师讲义

《国际MBA大师高层论坛――――全部演讲讲义》准MBA阵线——伴你MBA备考每一天╔---------------------------------------------------------------------------------╗┆数学资料下载英语资料下载管理资料下载语文资料下载┆┆逻辑资料下载政治资料下载历年联考真题模拟试题下载┆┆电子图书下载免费在线讲座备考经验分享最新联考资讯┆┆学习交流论坛资料共享论坛学校专区论坛管理实战论坛┆╚---------------------------------------------------------------------------------╝╭═══════════════════════════════════════╮声明：本文件由站长收集制作发布或网友提供，准MBA阵线整理后提供下载，本站提供的各类文件，只为方便考友备考学习之用，请勿用做任何其他商业用途，如本文件侵犯你的版权，请在论坛“本站站务”区告知，我们将在第一时间删除。

说明：要获得更多的最新免费MBA备考资料,请随时关注和准MBA论坛推荐：准MBA阵线（MBA备考资料下载，自荐一下） MBAHOME网站（MBA资讯，拥有最火的MBA论坛）中国MBA网（中国MBA的官方新闻发布网站）中国SMBA网（可以说是目前中国最好的SMBA网站）中国MBA培训网（有很多打折的MBA辅导课程出售）╰═══════════════════════════════════════╯整合营销传播的策略与发展——唐E·舒尔茨整合营销传播的策略与发展唐E·舒尔茨的演讲同学们、老师们晚上好！我的发音不太准，请大家原谅。

非常高兴来到这个学校，今天下午我们来杭州的路上，有人告诉我杭州最有名的有三件东西，他们是茶叶、丝绸、美女。

我可以肯定关于美女肯定是正确的。

今天晚上我和大家一起来探讨一下整合营销传播和它怎样将会在今后的营销体系中改变我们的新的概念。

《悟空申论大魔笈4.0版本》我不是教你写申论我是教你考申论史上最贴近实战的申论魔幻秘笈目录序言-------------------------------------------------------------------------------------------------------- 6 第一章：公务员考试必须坚持“三心并用” -------------------------------------------------------------------- 9 第二章：不要错过任何一次考试机会 --------------------------------------------------------- 错误!未定义书签。

第三章：通过一个例子明白申论为什么哪样考? --------------------------------------------------------------- 12 第四章：为什么申论比行测更要引起重视？ -------------------------------------------------- 错误!未定义书签。

第五章：唯有申论可以在短时间内提高------------------------------------------------------- 错误!未定义书签。

第六章：万能模板到底还有没有用？ --------------------------------------------------------- 错误!未定义书签。

第七章：你的身份是公务员而不是原来的你 -------------------------------------------------- 错误!未定义书签。

第八章：材料是“根”--------------------------------------------------------------------------------------- 15 第九章：想看看申论阅卷时的照片吗 --------------------------------------------------------- 错误!未定义书签。

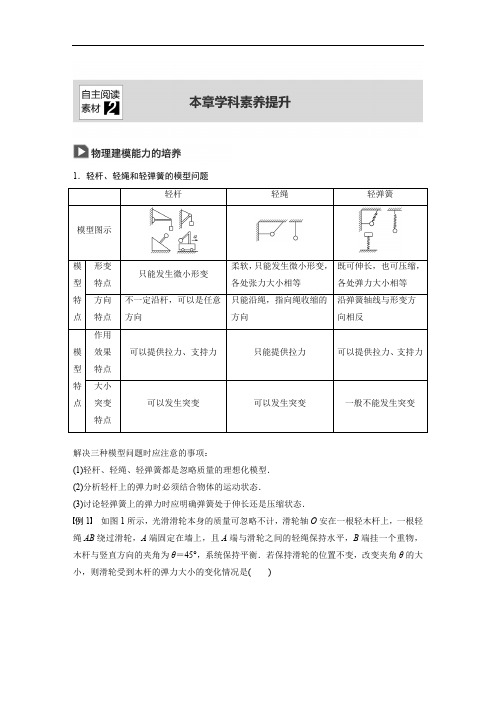
1．轻杆、轻绳和轻弹簧的模型问题轻杆轻绳轻弹簧模型图示形变特点只能发生微小形变柔软，只能发生微小形变，各处张力大小相等既可伸长，也可压缩，各处弹力大小相等模型特点方向特点不一定沿杆，可以是任意方向只能沿绳，指向绳收缩的方向沿弹簧轴线与形变方向相反作用效果特点可以提供拉力、支持力只能提供拉力可以提供拉力、支持力模型特点大小突变特点可以发生突变可以发生突变一般不能发生突变解决三种模型问题时应注意的事项：(1)轻杆、轻绳、轻弹簧都是忽略质量的理想化模型．(2)分析轻杆上的弹力时必须结合物体的运动状态．(3)讨论轻弹簧上的弹力时应明确弹簧处于伸长还是压缩状态．例1　如图1所示，光滑滑轮本身的质量可忽略不计，滑轮轴O 安在一根轻木杆上，一根轻绳AB 绕过滑轮，A 端固定在墙上，且A 端与滑轮之间的轻绳保持水平，B 端挂一个重物，木杆与竖直方向的夹角为θ＝45°，系统保持平衡．若保持滑轮的位置不变，改变夹角θ的大小，则滑轮受到木杆的弹力大小的变化情况是( )图1A．只有θ变小，弹力才变大B．只有θ变大，弹力才变大C．无论θ变大还是变小，弹力都变大D．无论θ变大还是变小，弹力都不变解析　无论θ变大还是变小，水平段轻绳和竖直段轻绳中的拉力不变，所以这两个力的合力不变，合力与木杆对滑轮的弹力平衡，故滑轮受到木杆的弹力不变，故D正确．答案　D例2　如图2所示，水平轻杆的一端固定在墙上，轻绳与竖直方向的夹角为37°，小球的重力为12 N，轻绳的拉力为10 N，水平轻弹簧的弹力为9 N，小球处于静止状态，求轻杆对小球的作用力．(取sin 37°＝0.6，cos 37°＝0.8)图2解析　设轻杆的弹力大小为F，与水平方向的夹角为α.(1)弹簧向左拉小球时，小球受力如图甲所示．由平衡条件知：F cos α＋F T sin 37°＝F弹F sin α＋F T cos 37°＝G代入数据解得：F＝5 N，α＝53°即杆对小球的作用力大小为5 N，方向与水平方向成53°角斜向右上方．(2)弹簧向右推小球时，小球受力如图乙所示：由平衡条件得：F cos α＋F T sin 37°＋F 弹＝0F sin α＋F T cos 37°＝G代入数据解得：F ＝15.5 N ，α＝π－arctan .415即杆对小球的作用力大小为15.5 N ，方向与水平方向成π－arctan斜向左上方．415答案　见解析2．轻绳套轻环的动态平衡模型物理的学习特别强调分析、推理和建模能力的培养，特别是对于题目隐含条件的挖掘，找到解决问题的突破口，此称为破题能力．在本章有一类典型的共点力平衡问题，即轻绳套光滑轻环的动态平衡分析问题，如图3所示．图3绳上套的是光滑轻环，作用在绳上形成“活结”，此时绳上的拉力处处相等，平衡时与水平面所成夹角相等，即α＝β.当动点P 移至P ′时，绳长保持不变，夹角α＝β也保持不变，Q 移至Q ′，这与绳“死结”模型截然不同．此类问题破题关键有两点：(1)不计轻环与绳间的摩擦时，左右两段绳中张力相等，左右两段绳与竖直方向的夹角也相等．(2)总绳长度不变时，sin θ＝，绳中张力和绳与竖直方向的夹角θ随两悬点水平距离d 的变d l 化而变化．例3　如图4所示为建筑工地一个小型起重机起吊重物的示意图．一根轻绳跨过光滑的动滑轮，轻绳的一端系在位置A 处，动滑轮的下端挂上重物，轻绳的另一端挂在起重机的吊钩C 处，起吊重物前，重物处于静止状态．起吊重物过程是这样的：先让吊钩从位置C 竖直向上缓慢地移动到位置B ，然后再让吊钩从位置B 水平向右缓慢地移动到D ，最后把重物卸在某一个位置．则关于轻绳上的拉力大小变化情况，下列说法正确的是( )图4A ．吊钩从C 向B 移动过程中，轻绳上的拉力不变B ．吊钩从B 向D 移动过程中，轻绳上的拉力变小C ．吊钩从C 向B 移动过程中，轻绳上的拉力变大D ．吊钩从B 向D 移动过程中，轻绳上的拉力不变解析　由C 到B 时，两绳夹角不变，由滑轮受力平衡知，绳子拉力不变，由B 到D 时，两绳夹角θ增大，由滑轮受力平衡得2F T cos ＝mg ，绳子拉力变大．故A 正确．θ2答案　A例4　(2018·山东省济南一中期中)如图5，竖直放置的П形支架上，一根不可伸长的轻绳通过轻质滑轮悬挂一重物G ，现将轻绳的一端固定于支架上的A 点，另一端从与A 点等高的B 点沿支架缓慢地向C 点移动，则绳中拉力大小变化的情况是( )图5A ．先变小后变大B ．先不变后变小C ．先不变后变大D ．先变大后变小解析　当轻绳从B 端移动到直杆的最上端的过程中，设两绳的夹角为2α，绳子总长为L ，两直杆间的距离为s ，由数学知识得到sin α＝，L 、s 不变，则α保持不变．s L再根据平衡条件可知，两绳的拉力F 保持不变．当轻绳的右端从直杆的最右上端移动到C 时，设两绳的夹角为2θ.以滑轮为研究对象，分析受力情况，作出力的示意图如图所示．根据平衡条件得2F cos θ＝mg得到绳子的拉力F＝mg2cos θ所以在当轻绳的右端从直杆的最右上端移动到C的过程中，θ减小，cos θ增大，则F变小，所以B正确．答案　B。

小高考讲义专题2考点目的要求1.了解物质的量的含义和单位，了解阿伏加德罗常数的含义。

2.了解摩尔质量、气体摩尔体积、物质的量浓度的含义。

3.学会配制一定物质的量浓度的溶液。

4.了解物质的质量、摩尔质量、物质的微粒数、物质的量、气体摩尔体积、物质的量浓度等物理量之间的关系，能用它们停止复杂的化学计算。

一、物质的量1.物质的量(n)基本物理量之一，表示含有一定数目微观粒子的集合体，用符号________表示。

物质的量的单位是________，符号为________。

2.阿伏加德罗常数(1)概念：______中所含碳原子数。

符号为______，单位为______，近似值约为______。

(2)有关N、N A、n的计算公式：n＝________。

3.摩尔质量(1)概念：单位物质的量的物质所具有的____________，符号：M，单位：________。

(2)M以g·mol－1为单位时，其数值与________________________________相等。

(3)有关m、M、n的计算公式：n＝________ 、m＝________。

二、气体摩尔体积1.影响物质体积大小的要素(1)影响物质体积的要素：_______________、_______________、_______________。

(2)决议气体体积大小的要素：____________________、__________________。

2.气体摩尔体积(V m)(1)概念：单位物质的量的气体所占的体积，单位：________。

(2)影响要素：气体摩尔体积数值不是固定不变的，它取决于________和________。

在规范状况下约为________。

(3)有关V、V m、n的计算公式：V m＝________。

三、物质的量浓度1.物质的量浓度的概念(1)物质的量浓度(c B)：表示单位体积溶液里所含溶质的物质的量。

(2)单位：__________________。

粉笔高中美术科目三讲义英文文档内容：Chalk High School Art Course Three Lecture Notes1.Introduction to Art HistoryThis lecture will introduce students to the history of art, including ancient civilizations, the Renaissance, and modern art movements.Students will learn about famous artists, their works, and the cultural contexts in which they created.2.Drawing TechniquesIn this lecture, students will learn various drawing techniques, such as perspective, shading, and rendering.The instructor will demonstrate these techniques and provide students with hands-on practice opportunities.Students will also learn how to use different types of chalk to achieve different effects in their drawings.3.Color Theory and ApplicationThis lecture will cover the basics of color theory, including primary colors, secondary colors, and complementary colors.Students will learn how to mix colors and use them in their artwork.The instructor will also demonstrate how to use chalk to create vibrant and visually appealing compositions.中文文档内容：粉笔高中美术科目三讲义1.艺术史简介本讲将向学生介绍艺术史，包括古代文明、文艺复兴和现代艺术运动。

《刻意练习：如何从新手到大师》阅读记录目录一、书籍概述 (2)1. 书籍简介 (2)2. 作者介绍 (3)二、第一章 (4)1. 成长心态 (5)1.1 定义与特点 (6)1.2 成长心态的重要性 (8)2. 刻意练习 (9)2.1 刻意练习的概念 (10)2.2 如何进行刻意练习 (11)三、第二章 (12)1. 新手阶段 (13)1.1 特点与困境 (14)1.2 新手如何开始学习 (15)2. 提升阶段 (16)2.1 技能提升的途径 (17)2.2 如何克服瓶颈期 (18)3. 大师阶段 (19)3.1 大师的特点与素质 (20)3.2 大师的成长经历与教训 (21)四、第三章 (23)1. 确定目标 (25)1.1 设定明确的目标 (25)1.2 目标分解与计划制定 (26)2. 技能拆解与逐步攻克 (27)2.1 技能拆解的方法 (28)2.2 逐步攻克每个技能点 (29)3. 持续反馈与调整策略 (30)3.1 获取反馈的渠道 (31)3.2 根据反馈调整练习策略 (33)五、第四章 (34)1. 音乐领域 (36)1.1 音乐学习与演奏技巧 (37)1.2 刻意练习在音乐中的应用案例 (39)2. 编程领域 (40)2.1 编程技能的学习与提升方法 (42)2.2 刻意练习在编程中的应用案例 (43)一、书籍概述《刻意练习：如何从新手到大师》是一本由心理学家安德斯艾利克森（Anders Ericsson）所著的书籍，探讨了如何通过刻意练习来提高技能和专业知识。

这本书的核心观点是，通过长期的、有目的的、集中式的训练，人们可以突破自己的局限，达到卓越的水平。

传统的技能学习方式往往缺乏针对性，导致学习效率低下。

而刻意练习则要求我们有意识地将注意力集中在特定的技能上，不断挑战自己的极限，从而实现技能的提升。

刻意练习还需要有效的反馈机制，以便我们能够及时了解自己的不足之处，并进行针对性的改进。

高昆仑考点精讲讲义2024【引言】在备考过程中，选择一本好的辅导资料至关重要。

今天，我们要为大家推荐的就是这样一本被誉为“备考神器”的高昆仑考点精讲讲义2024。

这本讲义不仅具有很高的知名度，而且在广大考生中赢得了极高的好评。

下面，我们就来详细了解一下这本讲义的核心内容和特点。

【主体部分】1.全面覆盖考试重点高昆仑考点精讲讲义2024严格按照考试大纲编写，全面覆盖了考试的重点内容。

讲义内容系统、严谨，有助于考生梳理知识体系，为考试做好充分准备。

2.深入浅出地讲解难点讲义在阐述考点时，力求简洁明了，用易懂的语言将复杂问题讲清楚。

对于考试中的难点，讲义更是进行了深入剖析，帮助考生更好地理解和掌握。

3.实用性强，注重培养应试能力高昆仑考点精讲讲义2024注重实用性，以提高考生的应试能力为目标。

讲义中附有大量真题解析，让考生了解考试趋势，熟悉出题思路。

此外，讲义还提供了丰富的练习题，方便考生进行自我检测。

4.案例丰富，提高理解力讲义中采用了丰富的案例，使理论知识更加生动形象。

考生在学习过程中，可以通过案例加深对知识点的理解，提高自己的理论素养。

【讲义的优势】相比其他辅导资料，高昆仑考点精讲讲义2024具有以下优势：1.知名度高，权威性强高昆仑老师在考试辅导领域具有很高的声誉，其讲义权威性不言而喻。

2.内容丰富，针对性强讲义内容丰富，不仅包括理论知识，还包括真题解析、练习题等，针对性强。

3.更新及时，紧跟考试趋势讲义会根据考试大纲和考试趋势进行及时更新，确保考生掌握最新、最实用的知识。

【适用人群与使用建议】高昆仑考点精讲讲义2024适合各类考试考生使用，尤其是希望提高考试成绩、系统学习知识点的考生。

使用建议如下：1.结合考试大纲，明确学习重点。

2.认真阅读讲义，做好笔记，加深理解。

3.针对讲义中的难点和考点，多做练习，巩固知识。

4.定期进行自我检测，提高应试能力。

【结语】总之，高昆仑考点精讲讲义2024是一本值得推荐的备考辅导资料。

新课标高考大一轮复习讲义·数学(文)第一章集合与常用逻辑用语1．1集合的概念与运算[考纲考情分析] 1.了解集合的含义，体会元素与集合的属于关系；能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.2.理解集合之间包含与相等的含义，能识别给定集合的子集；在具体情境中，了解全集与空集的含义.3.(1)理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集．(2)理解在给定集合中一个子集的补集的含义，会求给定子集的补集．(3)能使用Venn图表达集合间的基本关系及集合的基本运算.4.集合的交、并、补运算及两集合间的包含关系是考查的重点，在集合的运算中经常与不等式、函数相结合，解题时常用到数轴和韦恩(Venn)图，考查学生的数形结合思想和计算推理能力，题型以选择题为主，低档难度．[知识梳理]1．集合与元素(1)集合中元素的三个特征：确定性、互异性、无序性.(2)元素与集合的关系是属于或不属于两种，用符号∈或∉表示．(3)集合的表示法：列举法、描述法、图示法.(4)常见数集的记法集合自然数集正整数集整数集有理数集实数集符号N N*(或N＋)Z Q R2.集合间的基本关系关系自然语言符号语言Venn图子集集合A中所有元素都在集合B中(即若x∈A，则x∈B)A⊆B(或B．⊇．A．)．真子集集合A是集合B的子集，且集合B中至少有一个元素不在集合A中A B(或B A)集合相等集合A，B中的元素相同或集合A，B互为子集A＝B3.集合的基本运算运算自然语言符号语言Venn图交集由属于集合A且属于集合B的所有元素组成的集合A∩B＝{x|x∈A且x∈B}并集由所有属于集合A或属于集合B的元素组成的集合A∪B＝{x|x∈A或x∈B}补集由全集U中不属于集合A的所有元素组成的集合∁U A＝{x|x∈U且x∉A}知识拓展(1)若有限集A中有n个元素，则集合A的子集个数为2n，真子集的个数为2n－1.(2)A⊆B⇔A∩B＝A⇔A∪B＝B.(3)A∩∁U A＝∅；A∪∁U A＝U；∁U(∁U A)＝A.[小题速练]1．判断下列结论是否正确(请在括号中打“√”或“×”)(1){x|x≤1}＝{t|t≤1}．(√)(2){x|y＝x2＋1}＝{y|y＝x2＋1}＝{(x，y)|y＝x2＋1}．(×)(3)若{x2,1}＝{0,1}，则x＝0,1.(×)(4)若A∩B＝A∩C，则B＝C.(×)(5)对于任意两个集合A，B，关系(A∩B)⊆(A∪B)恒成立．(√)2．若集合A＝{x∈N|x≤10}，a＝22，则下列结论正确的是()A．{a}⊆A B．a⊆AC．{a}∈A D．a∉AD[由题意知A＝{0,1,2,3}，由a＝22，知a∉A.]3．(2018·课标全国Ⅰ，1)已知集合A＝{0,2}，B＝{－2，－1，0,1,2}，则A∩B＝() A．{0,2} B．{1,2}C．{0} D．{－2，－1,0,1,2}A[本题主要考查集合的基本运算．∵A＝{0,2}，B＝{－2，－1,0,1,2}，∴A∩B＝{0,2}，故选A.]4．已知集合A＝{1,3，m}，B＝{1，m}，A∪B＝A，则m等于()A．0或 3 B．0或3C．1或 3 D．1或3或0B[A＝{1,3，m}，B＝{1，m}，A∪B＝A，故B⊆A，所以m＝3或m＝m，即m＝3或m＝0或m＝1，其中m＝1不符合题意，所以m＝0或m＝3，故选B.]5．设集合M＝{x|－1≤x＜2}，N＝{x|x－k≥0}，若M⊆N，则k的取值范围是() A．k≥－1 B．k＞－1C．k≤2 D．k≥2A[由题意可知：N＝{x|x≥k}，结合M⊆N可得：则k的取值范围是k≥－1.故选A.]考点一集合的基本概念【例1】(1)(2019·广东佛山顺德学情调研，1)若A＝{1,2}，B＝{(x，y)|x∈A，y∈A}，则集合B中元素的个数为()A．1 B．2C．3 D．4D[由题意得B＝{(1,1)，(1,2)，(2,1)，(2,2)}，所以集合B中元素的个数为4，故选D.](2)若集合A ＝{x ∈R |ax 2－3x ＋2＝0}中只有一个元素，则a ＝( ) A.92 B ．98C ．0D ．0或98D [若集合A 中只有一个元素，则方程ax 2－3x ＋2＝0只有一个实根或有两个相等实根．当a ＝0时，x ＝23，符合题意；当a ≠0时，由Δ＝(－3)2－8a ＝0，得a ＝98，所以a 的取值为0或98.] 规律总结 (1)第(2)题集合A 中只有一个元素，要分a ＝0与a ≠0两种情况进行讨论，此题易忽视a ＝0的情形． (2)用描述法表示集合，先要弄清集合中代表元素的含义，再看元素的限制条件，明确集合类型，是数集、点集还是其他的集合． 【针对训练1】 (1)设a ，b ∈R ，集合{1，a ＋b ，a }＝⎩⎨⎧⎭⎬⎫0，b a ，b ，则b －a ＝________. 2 [因为{1，a ＋b ，a }＝⎩⎨⎧⎭⎬⎫0，b a ，b ，a ≠0， 所以a ＋b ＝0，且b ＝1，所以a ＝－1，b ＝1，所以b －a ＝2.](2)(2018·上海黄浦4月模拟(二模)，1)已知集合A ＝{1,2,3}，B ＝{1，m }，若3－m ∈A ，则非零实数m 的值是________．2 [若3－m ＝1，则m ＝2，符合题意；若3－m ＝2，则m ＝1，此时集合B 中的元素不满足互异性，故m ≠1；若3－m ＝3，则m ＝0，不符合题意．故答案为2.]考点二 集合的基本关系【例2】 (1)(2019·山东济宁第一次模拟，1)已知集合A ＝{x ∈Z |x 2＋3x <0}，则满足B ⊆A 的集合B 的个数为( )A ．2B ．3C ．4D ．8C [A ＝{x ∈Z |x 2＋3x <0}＝{－1，－2}，由于B ⊆A ，所以集合B 的个数为22＝4，故选C.](2)已知集合A ＝{x |x 2－2 019x ＋2 018<0}，B ＝{x |x <a }，若A ⊆B ，则实数a 的取值范围是________．[2 018，＋∞) [由x 2－2 019x ＋2 018<0，解得1<x <2 018，故A ＝{x |1<x <2 018}．又B ＝{x |x <a }，A ⊆B ，如图所示，可得a ≥2 018.]规律总结 (1)空集是任何集合的子集，在涉及集合关系时，必须优先考虑空集的情况，否则会造成漏解．(2)已知两个集合间的关系求参数时，关键是将条件转化为元素或区间端点间的关系，进而转化为参数所满足的关系，常用数轴、Venn 图等来直观解决这类问题．【针对训练2】 (1)已知集合A ＝{x ∈R |x 2＋x －6＝0}，B ＝{x ∈R |ax －1＝0}，若B ⊆A ，则实数a 的值为( )A.13或－12 B ．－13或12C.13或－12或0 D ．－13或12或0 D [由题意知，A ＝{2，－3}．当a ＝0时，B ＝∅，满足B ⊆A ；当a ≠0时，ax －1＝0的解为x ＝1a ， 由B ⊆A ，可得1a ＝－3或1a＝2， ∴a ＝－13或a ＝12. 综上可知，a 的值为－13或12或0.] (2)已知集合A ＝{x |－2≤x ≤7}，B ＝{x |m ＋1<x <2m －1}，若B ⊆A ，则实数m 的取值范围是________．(－∞，4] [当B ＝∅时，有m ＋1≥2m －1，则m ≤2；当B ≠∅时，若B ⊆A ，如图，则⎩⎪⎨⎪⎧ m ＋1≥－2，2m －1≤7，m ＋1<2m －1，解得2<m ≤4.综上，m 的取值范围是(－∞，4]．]考点三 集合的基本运算考向一 集合的运算【例3】 (1)(2017·全国Ⅰ)已知集合A ＝{x |x <1}，B ＝{x |3x <1}，则( )A ．A ∩B ＝{x |x <0} B ．A ∪B ＝RC ．A ∪B ＝{x |x >1}D ．A ∩B ＝∅A [∵B ＝{x |3x <1}，∴B ＝{x |x <0}．又A ＝{x |x <1}，∴A ∩B ＝{x |x <0}，A ∪B ＝{x |x <1}．](2)已知集合A ＝{(x ，y )|x 2＝4y }，B ＝{(x ，y )|y ＝x }，则A ∩B 的真子集个数为( )A ．1B ．3C ．5D ．7B [因为抛物线x 2＝4y 的图象与直线y ＝x 的图象有两个交点，所以A ∩B 有两个元素，故A ∩B 的真子集个数为22－1＝3，故选B.]考向二 利用集合的运算求参数【例4】 (1)设集合A ＝{x |－1≤x <2}，B ＝{x |x <a }，若A ∩B ≠∅，则a 的取值范围是( )A ．－1<a ≤2B ．a >2C ．a ≥－1D ．a >－1D [因为A ∩B ≠∅，所以集合A ，B 有公共元素，作出数轴，如图所示，易知a >－1.](2)(2018·广东二模，3)已知x ∈R ，集合A ＝{0,1,2,4,5}，集合B ＝{x －2，x ，x ＋2}，若A ∩B ＝{0,2}，则x ＝( )A ．－2B ．0C ．1D ．2B [因为A ＝{0,1,2,4,5}，B ＝{x －2，x ，x ＋2}且A ∩B ＝{0,2}，所以⎩⎪⎨⎪⎧ x －2＝0，x ＝2或⎩⎪⎨⎪⎧x ＝0，x ＋2＝2，当x ＝2时，B ＝{0,2,4}，A ∩B ＝{0,2,4}(舍)； 当x ＝0时，B ＝{－2,0,2}，A ∩B ＝{0,2}．综上，x ＝0.故选B.]规律总结 (1)一般来讲，集合中的元素若是离散的，则用Venn 图表示；集合中的元素若是连续的，则用数轴表示，此时要注意端点的情况．(2)运算过程中要注意集合间的特殊关系的使用，灵活使用这些关系，会使运算简化．【针对训练3】 (1)(2019·广东佛山质量检测(二)，1)已知全集U ＝{0,1,2,3,4}，若A ＝{0,2,3}，B ＝{2,3,4}，则(∁U A )∩(∁U B )＝( )A ．∅B ．{1}C ．{0,2}D ．{1,4}B [因为全集U ＝{0,1,2,3,4}，A ＝{0,2,3}，B ＝{2,3,4}，所以∁U A ＝{1,4}，∁U B ＝{0,1}，因此(∁U A )∩(∁U B )＝{1}，选B.](2)设集合A ＝{0，－4}，B ＝{x |x 2＋2(a ＋1)x ＋a 2－1＝0，x ∈R }．若A ∩B ＝B ，则实数a 的取值范围是________．(－∞，－1]∪{1} [因为A ＝{0，－4}，所以B ⊆A 分以下三种情况：①当B ＝A 时，B ＝{0，－4}，由此可知，0和－4是方程x 2＋2(a ＋1)x ＋a 2－1＝0的两个根，由根与系数的关系，得⎩⎪⎨⎪⎧ Δ＝4(a ＋1)2－4(a 2－1)>0，－2(a ＋1)＝－4，a 2－1＝0，解得a ＝1；②当B ≠∅且B A 时，B ＝{0}或B ＝{－4}，并且Δ＝4(a ＋1)2－4(a 2－1)＝0，解得a ＝－1，此时B ＝{0}满足题意；③当B ＝∅时，Δ＝4(a ＋1)2－4(a 2－1)<0，解得a <－1.综上所述，所求实数a 的取值范围是(－∞，－1]∪{1}．]课时作业(一)[基础巩固]1．(2018·课标全国Ⅱ，2)已知集合A ＝{1,3,5,7}，B ＝{2,3,4,5}，则A ∩B ＝( )A ．{3}B ．{5}C ．{3,5}D ．{1,2,3,4,5,7}C [由题意得A ∩B ＝{3,5}，故选C.]2．已知全集U ＝{1,2,3,4,5,6}，集合P ＝{1,3,5}，Q ＝{1,2,4}，则(∁U P )∪Q ＝( )A ．{1}B ．{3,5}C ．{1,2,4,6}D ．{1,2,3,4,5}C [∵U ＝{1,2,3,4,5,6}，P ＝{1,3,5}，∴∁U P ＝{2,4,6}，∵Q ＝{1,2,4}，∴(∁U P )∪Q ＝{1,2,4,6}，故选C.]3．(2019·齐鲁名校教科研协作体山东、湖北部分重点中学高考冲刺模拟(三)，1)若集合M ＝{(x ，y )|x ＋y ＝0}，N ＝{(x ，y )|x 2＋y 2＝0，x ∈R ，y ∈R }，则有( )A ．M ∪N ＝MB ．M ∪N ＝NC ．M ∩N ＝MD ．M ∩N ＝∅A [N ＝{(x ，y )|x 2＋y 2＝0，x ∈R ，y ∈R }＝{(0,0)}，且点(0,0)满足直线x ＋y ＝0，所以M ∪N ＝M ，故选A.]4．已知集合A ＝{x |x 2－x －6＜0}，B ＝{x |3x ＞1}，则A ∩B ＝( )A ．(1,2)B ．(1,3)C ．(0,2)D ．(0,3)D [集合A ＝{x |x 2－x －6＜0}＝{x |－2＜x ＜3}，B ＝{x |3x ＞1}＝{x |x ＞0}，A ∩B ＝{x |0＜x ＜3}＝(0,3)，故选D.]5．(2019·潍坊调研)已知全集U ＝R ，集合A ＝{1,2,3,4,5}，B ＝{x ∈R |x ≥2}，则图中阴影部分所表示的集合为( )A ．{0,1}B ．{1}C ．{1,2}D ．{0,1,2}B [因为A ∩B ＝{2,3,4,5}，而图中阴影部分为集合A 去掉A ∩B 部分，所以阴影部分所表示的集合为{1}，故选B.]6．已知集合M ＝{1,2,3,4}，则集合P ＝{x |x ∈M ，且2x ∉M }的子集的个数为( )A ．8B ．4C ．3D ．2B [由题意得P ＝{3,4}，∴集合P 有4个子集，故选B.]7．(2017·全国Ⅱ)设集合A ＝{1,2,4}，B ＝{x |x 2－4x ＋m ＝0}．若A ∩B ＝{1}，则B 等于( )A ．{1，－3}B ．{1,0}C ．{1,3}D ．{1,5}C [∵A ∩B ＝{1}，∴1∈B .∴1－4＋m ＝0，即m ＝3.∴B ＝{x |x 2－4x ＋3＝0}＝{1,3}．故选C.]8．已知集合A ＝{x |－1<x <0}，B ＝{x |x ≤a }，若A ⊆B ，则a 的取值范围为( )A ．(－∞，0]B ．[0，＋∞)C ．(－∞，0)D ．(0，＋∞)B [用数轴表示集合A ，B (如图)，由A ⊆B ，得a ≥0.]9．已知集合P ＝{x |x 2－2x ≥0}，Q ＝{x |1＜x ≤2}，则(∁R P )∩Q ＝________.(1,2) [∵P ＝{x |x ≥2或x ≤0}，∁R P ＝{x |0＜x ＜2}，∴(∁R P )∩Q ＝{x |1＜x ＜2}．]10．若{3,4，m 2－3m －1}∩{2m ，－3}＝{－3}，则m ＝ ________ .1 [由集合中元素的互异性，可得⎩⎪⎨⎪⎧ m 2－3m －1＝－3，2m ≠－3，2m ≠3，2m ≠4， 所以m ＝1.]11．集合A ＝{x |x <0}，B ＝{x |y ＝lg [x (x ＋1)]}，若A －B ＝{x |x ∈A ，且x ∉B }，则A －B ＝________.[－1,0) [由x (x ＋1)>0，得x <－1或x >0，∴B ＝(－∞，－1)∪(0，＋∞)，∴A －B ＝[－1,0)．]12．已知集合A ＝{x |y ＝lg (x －x 2)}，B ＝{x |x 2－cx <0，c >0}，若A ⊆B ，则实数c 的取值范围是________．[1，＋∞) [由题意知，A ＝{x |y ＝lg (x －x 2)}＝{x |x －x 2>0}＝(0,1)，B ＝{x |x 2－cx <0，c >0}＝(0，c )．由A ⊆B ，画出数轴，如图所示，得c ≥ 1.][能力提升]13．定义一种新的集合运算△：A △B ＝{x |x ∈A ，且x ∉B }．若集合A ＝{x |x 2－4x ＋3<0}，B ＝{x |2≤x ≤4}，则按运算△，B △A 等于( )A ．{x |3<x ≤4}B ．{x |3≤x ≤4}C ．{x |3<x <4}D ．{x |2≤x ≤4}B [A ＝{x |1<x <3}，B ＝{x |2≤x ≤4}，由题意知，B △A ＝{x |x ∈B ，且x ∉A }＝{x |3≤x ≤4}，故选B.]14．已知集合A ＝{x |1<x <3}，B ＝{x |2m <x <1－m }，若A ∩B ＝∅，则实数m 的取值范围是( )A ．[13，＋∞)B ．[0，13) C ．(－∞，0] D ．[0，＋∞)D [∵A ∩B ＝∅，①若2m ≥1－m ，即m ≥13时，B ＝∅，符合题意； ②若2m <1－m ，即m <13时， 需满足⎩⎪⎨⎪⎧ m <13，1－m ≤1或⎩⎪⎨⎪⎧m <13，2m ≥3， 解得0≤m <13或∅，即0≤m <13. 综上，实数m 的取值范围为[0，＋∞)，故选D.]15．已知集合A ＝{x |x 2－2x ＋a >0}，且1∉A ，则实数a 的取值范围是________．(－∞，1] [∵1∉{x |x 2－2x ＋a >0}，∴1∈{x |x 2－2x ＋a ≤0}，即1－2＋a ≤0，∴a ≤1.]16．设A 是整数集的一个非空子集，对于k ∈A ，如果k －1∉A ，且k ＋1∉A ，那么称k 是A 的一个“孤立元”．给定S ＝{1,2,3,4,5,6,7,8}，由S 的3个元素构成的所有集合中，不含“孤立元”的集合共有________个．6 [依题意可知，由S 的3个元素构成的所有集合中，不含“孤立元”时，这三个元素一定是连续的三个自然数．故这样的集合共有6个．]1.2 命题及其关系、充分条件与必要条件[考纲考情分析] 1.理解命题的概念.2.了解“若p ，则q ”形式的命题及其逆命题、否命题与逆否命题，会分析四种命题的相互关系.3.理解必要条件、充分条件与充要条件的含义.4.命题的真假判断和充分必要条件的判定是考查的主要形式，多与集合、函数、不等式、立体几何中的线面关系相交汇，考查学生的推理能力，题型为选择、填空题，低档难度．[知识梳理]1．命题用语言、符号或式子表达的，可以 判断真假 的陈述句叫做命题，其中 判断为真 的语句叫做真命题， 判断为假 的语句叫做假命题．2．四种命题及其相互关系(1)四种命题间的相互关系(2)四种命题的真假关系①两个命题互为逆否命题，它们具有 相同 的真假性．②两个命题为互逆命题或互否命题时，它们的真假性 没有关系 .3．充分条件、必要条件与充要条件的概念若p ⇒q ，则p 是q 的 充分 条件，q 是p 的 必要 条件p 是q 的 充分不必要 条件p ⇒q 且q ⇒/ p p 是q 的 必要不充分 条件p ⇒/ q 且q ⇒p p 是q 的 充要 条件p ⇔q p 是q 的 既不充分也不必要 条件p ⇒/q 且q ⇒/ p知识拓展1．否命题与命题的否定：否命题是既否定条件，又否定结论，而命题的否定是只否定命题的结论．2．区别A 是B 的充分不必要条件(A ⇒B 且BD ⇒/A )，与A 的充分不必要条件是B (B ⇒A 且AD ⇒/B )两者的不同．3．A 是B 的充分不必要条件⇔¬B 是¬A 的充分不必要条件．4．充要关系与集合的子集之间的关系，设A ＝{x |p (x )}，B ＝{x |q (x )}，①若A ⊆B ，则p 是q 的充分条件，q 是p 的必要条件．②若A B ，则p 是q 的充分不必要条件，q 是p 的必要不充分条件．③若A ＝B ，则p 是q 的充要条件．[小题速练]1．判断下列结论是否正确(请在括号中打“√”或“×”)(1)“x 2＋2x －3<0”是命题．( × )(2)命题“若p ，则q ”的否命题是“若p ，则¬q ”．( × )(3)当q 是p 的必要条件时，p 是q 的充分条件．( √ )(4)当p 是q 的充要条件时，也可说成q 成立当且仅当p 成立．( √ )(5)若p 是q 的充分不必要条件，则¬p 是¬q 的必要不充分条件．( √ )2．下列说法正确的是( )A ．命题“若x 2＝1，则x ≠1”的否命题是“若x 2＝1，则x ＝1”B ．命题“∃x 0∈R ，x 20－x 0＜0”的否定是“∀x ∈R ，x 2－x ＞0”C ．命题“若函数f (x )＝x 2－ax ＋1有零点，则“a ≥2或a ≤－2”的逆否命题为真命题D ．“y ＝f (x )在x 0处有极值”是“f (x 0)＝0”的充要条件C [选项A, 命题“若x 2＝1，则x ≠1”的否命题是“若x 2＝1，则x ＝1”，错误；选项B, 命题“∃x 0∈R ，x 20－x 0＜0”的否定是“∀x ∈R ，x 2－x 0≤0”，错误；选项C, 命题“若函数f (x )＝x 2－ax ＋1有零点，则“a ≥2或a ≤－2”的逆否命题与原命题同真假， 函数f (x )＝x 2－ax ＋1有零点，即方程x 2－ax ＋1＝0有解，Δ≥0解得a ≥2或a ≤－2，故原命题正确；选项D ，“y ＝f (x )在x 0处有极值”是“f ′(x 0)＝0”的既不充分也不必要条件，如y ＝|x |在x ＝0处有极值，但不可导，y ＝x 3在x ＝0处满足f ′(0)＝0，但在定义域内单调递增；综上可知，选C.]3．命题“若α＝π4，则tan α＝1”的逆否命题是( ) A ．若α≠π4，则tan α≠1 B ．若α＝π4，则tan α≠1 C ．若tan α≠1，则α≠π4 D ．若tan α≠1，则α＝π4C [命题“若p ，则q ”的逆否命题是“若¬q ，则¬p ”，显然¬q ：tan α≠1，¬p ：α≠π4，所以该命题的逆否命题是“若tan α≠1，则α≠π4”，故选C.] 4．(2018·天津，3)设x ∈R ，则“x 3>8”是“|x |>2”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件A [由x 3>8得x >2，由|x |>2得x >2或x <－2.所以“x 3>8”是“|x |>2”的充分而不必要条件．故选A.]5．已知p ：x >a 是q ：2＜x ＜3的必要不充分条件，则实数a 的取值范围是________． (－∞，2] [由已知，可得{x |2＜x ＜3}{x |x ＞a }，∴a ≤2.]考点一 命题及其关系【例1】 (1)(2019·广东广雅中学联考)给出下列命题：①“∃x 0∈R ，x 20－x 0＋1≤0”的否定；②“若x 2＋x －6≥0，则x >2”的否命题；③命题“若x 2－5x ＋6＝0，则x ＝2”的逆否命题．其中真命题的个数是( )A ．0B ．1C ．2D ．3C [①的否定是“∀x ∈R ，x 2－x ＋1>0”是真命题，①正确；②的否命题是“若x 2＋x －6<0，则x ≤2”，由x 2＋x －6<0，得－3<x <2，∴x ≤2成立，②正确；③由x 2－5x ＋6＝0，得x ＝2或x ＝3，原命题是假命题，因此可知逆否命题为假命题，③错误．综上可知，真命题是①，②，故选C.](2)设m ∈R ，命题“若m ＞0，则方程x 2＋x －m ＝0有实根”的逆否命题是________． 答案 若方程x 2＋x －m ＝0没有实根，则m ≤0规律总结 (1)对于不是“若p ，则q ”形式的命题，需先改写；(2)若命题有大前提，写其他三种命题时需保留大前提．(3)判断一个命题为真命题，要给出推理证明；判断一个命题是假命题，只需举出反例即可．(4)根据“原命题与逆否命题同真同假，逆命题与否命题同真同假”这一性质，当一个命题直接判断不易进行时，可转化为判断其等价命题的真假．【针对训练1】 (1)下列命题是真命题的是( )A ．若1x ＝1y，则x ＝y B ．若x 2＝1，则x ＝1 C ．若x ＝y ，则x ＝y D ．若x ＜y ，则x 2＜y 2答案 A(2)(2018·衡水金卷A 信息卷(五)，14)命题p ：若x >0，则x >a ；命题q ：若m ≤a －2，则m <sin x (x ∈R )恒成立．若p 的逆命题，q 的逆否命题都是真命题，则实数a 的取值范围是 ________ .[0,1) [命题p 的逆命题是若x >a ，则x >0，故a ≥0.因为命题q 的逆否命题为真命题，所以命题q 为真命题，则a －2<－1，解得a <1.则实数a 的取值范围是[0,1)．]考点二 充分必要条件的判定【例2】 (1)(2018·北京，4)设a ，b ，c ，d 是非零实数，则“ad ＝bc ”是“a ，b ，c ，d 成等比数列”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件B [由a ，b ，c ，d 成等比数列，可得ad ＝bc ，即必要性成立；当a ＝1，b ＝－2，c ＝－4，d ＝8时，ad ＝bc ，但a ，b ，c ，d 不成等比数列，即充分性不成立，故选B.](2)已知条件p ：x >1或x <－3，条件q ：5x －6>x 2，则¬p 是¬q 的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件A [由5x －6>x 2，得2<x <3，即q ：2<x <3.所以q ⇒p ，pD ⇒/q ，所以¬p ⇒¬q ，¬q ⇒/¬p ，所以¬p 是¬q 的充分不必要条件，故选A.]规律总结 充分条件、必要条件的三种判定方法(1)定义法：根据p ⇒q ，q ⇒p 进行判断，适用于定义、定理判断性问题．(2)集合法：根据p ，q 成立的对象的集合之间的包含关系进行判断，多适用于命题中涉及字母范围的推断问题．(3)等价转化法：根据一个命题与其逆否命题的等价性，进行判断，适用于条件和结论带有否定性词语的命题．【针对训练2】 (1)“sin α＝cos α”是“cos 2α＝0”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要A [cos 2α＝0⇒cos 2α－sin 2α＝0⇒(cos α－sin α)·(cos α＋sin α)＝0，所以sin α＝cos α或sin α＝－cos α，故答案选A. ](2)(2018·浙江，6)已知平面α，直线m ，n 满足m ⊄α，n ⊂α，则“m ∥n ”是“m ∥α”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件A [∵m ⊄α，n ⊂α，m ∥n ，∴m ∥α，故充分性成立．而由m ∥α，n ⊂α，得m ∥n 或m 与n 异面，故必要性不成立．故选A.](3)设x ∈R ，i 是虚数单位，则“x ＝2”是“复数Z ＝(x 2－4)＋(x ＋2)i 为纯虚数”的( )A ．充分不必要条件B ．充要条件C ．必要不充分条件D ．既不充分也不必要条件B [由复数z ＝(x 2－4)＋(x ＋2)i 为纯虚数，则⎩⎪⎨⎪⎧x 2－4＝0x ＋2≠0，解得x ＝2， 所以x ＝2是复数z ＝(x 2－4)＋(x ＋2)i 为纯虚数的充要条件，故选B.]考点三 充分必要条件的应用【例3】 已知集合A 是函数y ＝lg(20＋8x －x 2)的定义域，集合B 是不等式x 2－2x ＋1－a 2≥0(a ＞0)的解集，p ：x ∈A ，q ：x ∈B .(Ⅰ)若A ∩B ＝∅，求a 的取值范围；(Ⅱ)若¬p 是q 的充分不必要条件，求a 的取值范围．解 (Ⅰ)A ＝{x |－2＜x ＜10}，B ＝{x |x ≥1＋a 或x ≤1－a }． 若A ∩B ＝∅，则必须满足⎩⎪⎨⎪⎧ 1＋a ≥10，1－a ≤－2，a ＞0，解得a ≥9，所以a 的取值范围是a ≥9.(Ⅱ)易得¬p ：x ≥10或x ≤－2.∵¬p 是q 的充分不必要条件，∴{x |x ≥10或x ≤－2}是B ＝{x |x ≥1＋a 或x ≤1－a }的真子集，即⎩⎪⎨⎪⎧ 10≥1＋a ，－2≤1－a ，a ＞0，解得0＜a ≤3，∴a 的取值范围是0＜a ≤3.【针对训练3】 (1)已知p ：(x －m )2＞3(x －m )是q ：x 2＋3x －4＜0的必要不充分条件，则实数m 的取值范围为________．(－∞，－7]∪[1，＋∞) [p 对应的集合A ＝{x |x ＜m 或x ＞m ＋3}，q 对应的集合B ＝{x |－4＜x ＜1}，由p 是q 的必要不充分条件可知，B A ，∴m ≥1或m ＋3≤－4，即m ≥1或m ≤－7.](2)设n ∈N *，一元二次方程x 2－4x ＋n ＝0有整数根的充要条件是n ＝________. 3或4 [由Δ＝16－4n ≥0，得n ≤4，又n ∈N *，则n ＝1,2,3,4.当n ＝1,2时，方程没有整数根；当n ＝3时，方程有整数根1,3，当n ＝4时，方程有整数根2.综上可知，n ＝3或4.]课时作业(二)[基础巩固]1．(2019·河南八市联考)命题“若a ＞b ，则a ＋c ＞b ＋c ”的否命题是( )A ．若a ≤b ，则a ＋c ≤b ＋cB ．若a ＋c ≤b ＋c ，则a ≤bC ．若a ＋c ＞b ＋c ，则a ＞bD ．若a ＞b ，则a ＋c ≤b ＋cA [否命题是将原命题的条件和结论都否定，故命题“若a ＞b ，则a ＋c ＞b ＋c ”的否命题是“若a ≤b ，则a ＋c ≤b ＋c ”，故选A.]2．设p ：f (x )＝x 3－2x 2＋mx ＋1在(－∞，＋∞)上单调递增；q ：m ＞43，则p 是q 的( ) A ．充要条件 B ．充分不必要条件C ．必要不充分条件D ．以上都不对C [∵f (x )＝x 3－2x 2＋mx ＋1在(－∞，＋∞)上单调递增，∴f ′(x )＝3x 2－4x ＋m ，即3x 2－4x ＋m ≥0在R 上恒成立，∴Δ＝16－12m ≤0，即m ≥43，即p ：m ≥43，又因为q ：m ＞43，∴根据充分必要条件的定义可判断：p 是q 的必要不充分条件，故选C.]3．(2019·广东名校模拟)王昌龄的《从军行》中两句诗为“黄沙百战穿金甲，不破楼兰终不还”，其中后一句中“攻破楼兰”是“返回家乡”的( )A ．充分条件B ．必要条件C ．充要条件D ．既不充分也不必要条件B [“攻破楼兰”是“返回家乡”的必要条件．故选B.]4．(2018·河南4月高考适应性考试，3)下列说法中，正确的是( )A ．命题“若am 2<bm 2，则a <b ”的逆命题是真命题B ．命题“∃x 0∈R ，x 20－x 0>0”的否定是“∀x ∈R ，x 2－x ≤0”C ．命题“p 或q ”为真命题，则命题“p ”和命题“q ”均为真命题D ．已知x ∈R ，则“x >1”是“x >2”的充分不必要条件B [选项A 的逆命题为“若a <b ，则am 2<bm 2”，则m ＝0时，不成立，所以是假命题；易知选项B 正确；对于选项C ，命题“p 或q ”为真命题，则命题“p ”和命题“q ”至少有一个是真命题，所以是假命题；对于选项D ，“x >1”是“x >2”的必要不充分条件，所以是假命题．故选B.]5．(2019·广东佛山教学质量检测(二)，3)已知函数f (x )＝3x －3－x ，∀a ，b ∈R ，则“a >b ”是“f (a )>f (b )”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件C [因为f (x )＝3x －3－x ，所以f ′(x )＝3x ln 3－3－x ln 3×(－1)＝3x ln 3＋3－x ln 3，易知f ′(x )>0，所以函数f (x )＝3x －3－x 为(－∞，＋∞)上的单调递增函数，从而由“a >b ”可得“f (a )>f (B )”，由“f (a )>f (b )”可得“a >b ”，即“a >b ”是“f (a )>f (b )”的充分必要条件，选C.]6．已知直线a ，b 分别在两个不同的平面α，β内，则“直线a 和直线b 相交”是“平面α和平面β相交”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件A [若直线a 和直线b 相交，则平面α和平面β相交；若平面α和平面β相交，那么直线a 和直线b 可能平行或异面或相交，故选A.]7．已知命题p ：x 2＋2x －3＞0；命题q ：x ＞a ，且¬q 的一个充分不必要条件是¬p ，则a 的取值范围是( )A ．[1，＋∞)B ．(－∞，1]C ．[－1，＋∞)D ．(－∞，－3]A [由x 2＋2x －3＞0，得x ＜－3或x ＞1，由¬q 的一个充分不必要条件是¬p ，可知¬p 是¬q 的充分不必要条件，等价于q 是p 的充分不必要条件．故a ≥1，故选A.]8．下列结论错误的是( )A ．命题“若x 2－3x －4＝0，则x ＝4”的逆否命题为“若x ≠4，则x 2－3x －4≠0”B ．“x ＝4”是“x 2－3x －4＝0”的充分条件C ．命题“若m ＞0，则方程x 2＋x －m ＝0有实根”的逆命题为真命题D ．命题“若m 2＋n 2＝0，则m ＝0且n ＝0”的否命题是“若m 2＋n 2≠0，则m ≠0或n ≠0”C [C 项命题的逆命题为“若方程x 2＋x －m ＝0有实根，则m ＞0”．若方程有实根，则Δ＝1＋4m ≥0，即m ≥－14，不能推出m ＞0，所以不是真命题，故选C.] 9．“若a ≤b ，则ac 2≤bc 2”，则原命题及命题的逆命题、否命题和逆否命题中真命题的个数是________．2 [其中原命题和逆否命题为真命题，逆命题和否命题为假命题．]10．设p ：实数x ，y 满足x >1且y >1，q ：实数x ，y 满足x ＋y >2，则p 是q 的________条件．(选填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)充分不必要 [当x >1，y >1时，x ＋y >2一定成立，即p ⇒q ，当x ＋y >2时，可令x ＝－1，y ＝4，即q ⇒D ⇒/p ，故p 是q 的充分不必要条件．]11．直线x －y －k ＝0与圆(x －1)2＋y 2＝2有两个不同交点的充要条件是________．(－1,3) [直线x －y －k ＝0与圆(x －1)2＋y 2＝2有两个不同交点等价于|1－0－k |2<2，解之得－1<k <3.]12．有下列几个命题：①“若a ＞b ，则a 2＞b 2”的否命题；②“若x ＋y ＝0，则x ，y 互为相反数”的逆命题；③“若x 2＜4，则－2＜x ＜2”的逆否命题．其中真命题的序号是________．②③ [①原命题的否命题为“若a ≤b ，则a 2≤b 2”，错误；②原命题的逆命题为“若x ，y 互为相反数，则x ＋y ＝0”，正确；③原命题的逆否命题为“若x ≥2或x ≤－2，则x 2≥4”，正确．][能力提升]13．使不等式2x>1成立的一个充分不必要条件是( ) A ．0<x <2 B ．x >0C ．0<x <1D ．x <1C [不等式2x>1的解为0<x <2， 依题意，选项是0<x <2的充分不必要条件，所以选项表示的集合是{x |0<x <2}的真子集，故选C.]14．(2018·华大新高考联盟4月教学质量检测，6)设函数f (x )＝⎩⎪⎨⎪⎧2mx ＋1，x ≥0，－x －1x ，x <0，则“m >1”是“f [f (－1)]>4”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件A [当m >1时，f [f (－1)]＝f ⎣⎡⎦⎤－(－1)－1(－1)＝f (2)＝22m ＋1>4，当f [f (－1)]>4时，f [f (－1)]＝f ⎣⎡⎦⎤－(－1)－1(－1)＝f (2)＝22m ＋1>4＝22，∴2m ＋1>2，解得m >12.故“m >1”是“f [f (－1)]>4”的充分不必要条件．故选A.]15．已知条件p ：2x 2－3x ＋1≤0，条件q ：x 2－(2a ＋1)x ＋a (a ＋1)≤0.若¬p 是¬q 的必要不充分条件，则实数a 的取值范围是________．⎣⎡⎦⎤0，12 [方法一 命题p 为⎩⎨⎧ x ⎪⎪⎭⎬⎫12≤x ≤1， 命题q 为{x |a ≤x ≤a ＋1}．¬p 对应的集合A ＝⎩⎨⎧x ⎪⎪⎭⎬⎫x >1或x <12， ¬q 对应的集合B ＝{x |x >a ＋1或x <a }．∵¬p 是¬q 的必要不充分条件， ∴⎩⎪⎨⎪⎧ a ＋1≥1，①a ≤12，②或⎩⎪⎨⎪⎧ a ＋1≥1，①a ≥12，② ∴0≤a ≤12. 方法二 命题p ：A ＝⎩⎨⎧x ⎪⎪⎭⎬⎫12≤x ≤1， 命题q ：B ＝{x |a ≤x ≤a ＋1}．∵¬p 是¬q 的必要不充分条件，∴p 是q 的充分不必要条件，即A B ，∴⎩⎪⎨⎪⎧ a ＋1≥1，a ≤12或⎩⎪⎨⎪⎧a ＋1≥1，a ≤12，∴0≤a ≤12.] 16．设a ，b 为正数，则“a －b >1”是“a 2－b 2>1”的 ________ 条件．(选填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)充分不必要 [∵a －b >1，即a >b ＋1.又∵a ，b 为正数，∴a 2>(b ＋1)2＝b 2＋1＋2b >b 2＋1，即a 2－b 2>1成立；反之，当a ＝3，b ＝1时，满足a 2－b 2>1，但a －b >1不成立．所以“a －b >1”是“a 2－b 2>1”的充分不必要条件．]1．3 简单的逻辑联结词、全称量词与存在量词[考纲考情分析] 1.了解逻辑联结词“或”“且”“非”的含义.2.理解全称量词与存在量词的意义.3.能正确地对含有一个量词的命题进行否定.4.逻辑联结词和含有一个量词的命题的否定是高考的重点；命题的真假判断常以函数、不等式为载体，考查学生的推理判断能力，题型为选择、填空题，低档难度．[知识梳理]1．简单的逻辑联结词(1)命题中的 且 、 或 、 非 叫做逻辑联结词．(2)命题p q 、p 或q 、非p 的真假判断p q p 且q p 或q非p 真 真 真 真假 真 假 假 真 假2.(1)全称量词：短语“所有的”“任意一个”等在逻辑中通常叫做全称量词，用符号“ ∀ ”表示．(2)存在量词：短语“存在一个”“至少有一个”等在逻辑中通常叫做存在量词，用符号“ ∃ ”表示．知识拓展1．含有逻辑联结词的命题真假的判断规律(1)p ∨q ：p ，q 中有一个为真，则p ∨q 为真，即有真为真．(2)p ∧q ：p ，q 中有一个为假，则p ∧q 为假，即有假即假．(3)¬p ：与p 的真假相反，即一真一假，真假相反．2．含有一个量词的命题的否定的规律是“改量词，否结论”．3．命题的否定和否命题的区别：命题“若p ，则q ”的否定是“若p ，则¬q ”，否命题是“若¬p ，则¬q ”．[小题速练]1．判断下列结论是否正确(请在括号中打“√”或“×”)(1)命题“5>6或5>2”是假命题．( × )(2)命题p 和¬p 不可能都是真命题．( √ )(3)若命题p ，q 中至少有一个是真命题，则p ∨q 是真命题．( √ )(4)“长方形的对角线相等”是特称命题．( × ) (5)若命题¬(p ∧q )是假命题，则命题p ，q 中至少有一个是真命题．( × )2．命题“∃x ∈R ，x 2－2x ＋1＜0”的否定是( )A ．∃x ∈R ，x 2－2x ＋1≥0B ．∃x ∈R ，x 2－2x ＋1＞0C ．∃x ∈R ，x 2－2x ＋1≥0D ．∀x ∈R ，x 2－2x ＋1＜0答案 C3．给出下列四个结论：①命题“∀x ＞0，x ＋1x ≥2”的否定是“∃x 0＞0，x 0＋1x 0＜2”； ②“若θ＝π3，则sin θ＝32”的否命题是“若θ≠π3，则sin θ≠32”； ③p ∨q 是真命题，p ∨q 是假命题，则命题p ，q 中一真一假；④若p ：1x≤1，q ：ln x ≥0，则p 是q 的充分不必要条件，其中正确结论的个数为( ) A ．1 B ．2C ．3D ．4答案 C4．(2019·贵阳调研)下列命题中的假命题是( )A ．∃x 0∈R ，lg x 0＝1B ．∃x 0∈R ，sin x 0＝0C ．∀x ∈R ，x 3＞0D ．∀x ∈R,2x ＞0C [当x ＝10时，lg 10＝1，则A 为真命题；当x ＝0时，sin 0＝0，则B 为真命题；当x ＜0时，x 3＜0，则C 为假命题；由指数函数的性质知，∀x ∈R,2x ＞0，则D 为真命题．故选C.]5．若“∀x ∈⎣⎡⎦⎤0，π4，tan x ≤m ”是真命题，则实数m 的最小值为________． 1 [∵函数y ＝tan x 在⎣⎡⎦⎤0，π4上是增函数， ∴y max ＝tan π4＝1.依题意知，m ≥y max ，即m ≥1. ∴m 的最小值为1.]考点一 含有逻辑联结词的命题的真假判断【例1】 (1)已知命题p ：∃x ∈R ，x 2－x ＋1≥0；命题q ：若a 2＜b 2，则a <b .下列命题为真命题的是( )A ．p ∧qB ．p ∧¬qC ．¬p ∧qD ．¬p ∧¬qB [由x ＝0时x 2－x ＋1≥0成立知p 是真命题，由12＜(－2)2,1＞－2可知q 是假命题，所以p ∧¬q 是真命题，故选B.](2)(2018·安徽淮北第二次(4月)模拟，3)命题p ：若向量a ·b <0，则a 与b 的夹角为钝角，命题q ：若cos α·cos β＝1，则sin(α＋β)＝0.下列命题为真命题的是( )A ．pB ．¬qC ．p ∧qD ．p ∨qD [当a ，b 方向相反时，a ·b <0，但夹角是180°，不是钝角，命题p 是假命题；若cos αcos β＝1，则cos α＝cos β＝1或cos α＝cos β＝－1，所以sin α＝sin β＝0，从而sin(α＋β)＝0，命题q 是真命题，所以p ∨q 是真命题，故选D.] 规律总结 “p ∨q ”“p ∧q ”“¬p ”等形式命题真假的判断步骤 (1)确定命题的构成形式；(2)判断其中命题p 、q 的真假；(3)确定“p ∧q ”“p ∨q ”“¬p ”等形式命题的真假．【针对训练1】 (1)已知命题p ：函数y ＝－tan ⎝⎛⎭⎫x ＋π6在定义域上为减函数，命题q ：在△ABC 中，若A ＞30°，则sin A ＞12，则下列命题为真命题的是( ) A ．(¬p )∧q B ．(¬p )∧(¬q )C ．p ∧(¬q )D ．p ∨q答案 B(2)命题“存在一个无理数，它的平方是有理数”的否定是( )A ．任意一个有理数，它的平方是有理数B ．任意一个无理数，它的平方不是有理数C ．存在一个有理数，它的平方是有理数D ．存在一个无理数，它的平方不是有理数答案 B考点二 含有一个量词命题的否定及真假判定【例2】 (1)命题“∀n ∈N *，f (n )∈N *且f (n )≤n ”的否定形式是( )A ．∀n ∈N *，f (n )∉N *且f (n )＞nB ．∀n ∈N *，f (n )∉N *或f (n )＞nC ．∃n 0∈N *，f (n 0)∉N *且f (n 0)＞n 0D ．∃n 0∈N *，f (n 0)∉N *或f (n 0)＞n 0D [全称命题的否定为特称命题，∴命题的否定是：∃n 0∈N *，f (n 0)∉N *或f (n 0)>n 0.](2)下列命题中的假命题是( )A ．∀x ∈R,2x －1>0B ．∀x ∈N *，(x －1)2>0C ．∃x 0∈R ，lg x 0<1D ．∃x 0∈R ，tan x 0＝2B [当x ∈N *时，x －1∈N ，可得(x －1)2≥0，当且仅当x ＝1时取等号，故B 不正确；易知A ，C ，D 正确，故选B.]规律总结 (1)判定全称命题“∀x ∈M ，p (x )”是真命题，需要对集合M 中的每一个元素x ，证明p (x )成立；要判断特称命题是真命题，只要在限定集合内找到一个x ＝x 0，使p (x 0)成立．(2)对全(特)称命题进行否定的方法①找到命题所含的量词，没有量词的要结合命题的含义先加上量词，再改变量词； ②对原命题的结论进行否定．【针对训练2】 (1)已知命题p ：“∃x 0∈R ，e x 0－x 0－1≤0”，则¬p 为( )A ．∃x 0∈R ，e x 0－x 0－1≥0B ．∃x 0∈R ，e x 0－x 0－1>0C ．∀x ∈R ，e x －x －1>0D ．∀x ∈R ，e x －x －1≥0C [根据全称命题与特称命题的否定关系，可得¬p 为“∀x ∈R ，e x －x －1>0”，故选C.](2)(2018·江西师范大学附属中学4月月考，3)已知定义域为R 的函数f (x )不是偶函数，则下列命题一定为真命题的是( )A ．∀x ∈R ，f (－x )≠f (x )B ．∀x ∈R ，f (－x )≠－f (x )C ．∃x 0∈R ，f (－x 0)≠f (x 0)D ．∃x 0∈R ，f (－x 0)≠－f (x 0)C [∵定义域为R 的函数f (x )不是偶函数，∴∀x ∈R ，f (－x )＝f (x )为假命题，∴∃x 0∈R ，f (－x 0)≠f (x 0)为真命题，故选C.]考点三 由命题的真假求参数的取值范围【例3】 (1)已知命题p ：“∀x ∈[0,1]，a ≥e x ”，命题q ：“∃x 0∈R ，x 20＋4x 0＋a ＝0”．若命题“p ∧q ”是真命题，则实数a 的取值范围是( )A ．(4，＋∞)B ．[1,4]C ．[e,4]D ．(－∞，－1)C [由题意知p 与q 均为真命题，由p 为真，可知a ≥e ，由q 为真，知x 2＋4x ＋a ＝0有解，则Δ＝16－4a ≥0，∴a ≤4.综上可知e ≤a ≤4.](2)若命题“∃x 0∈R ，使得3x 20＋2ax 0＋1＜0”是假命题，则实数a 取值范围是( )A ．(－3，3)B ．(－∞，－3]∪[3，＋∞)C ．[－3，3]D ．(－∞，－3)∪(3，＋∞)C [命题“∃x 0∈R ，使得3x 20＋2ax 0＋1＜0”是假命题，则∀x ∈R,3x 2＋2ax ＋10为真命题，Δ＝4a 2－12≤0，解得x ∈[－3，3]，故选C.]规律总结 (1)解参数的取值范围．(2)对于含量词的命题中求参数的取值范围的问题，可根据命题的含义，利用函数值域(或最值)解决．【针对训练3】 设p ：∃x ∈⎝⎛⎭⎫1，52，使f (x )＝lg(ax 2＋4x －4)有意义．若¬p 为假命题，则实数a 的取值范围是______________．(－1，＋∞) [根据题意，由¬p 为假命题，则p 为真命题，即∃x ∈⎝⎛⎭⎫1，52，使ax 2＋4x －4＞0成立，若a ＝0，则⎩⎪⎨⎪⎧ 42a ≤1f (1)＞0或⎩⎨⎧－42a ≥52f ⎝⎛⎭⎫52＞0，解得a ＞0；若a ＝0，则当x ∈⎝⎛⎭⎫1，52，总有4x －4＞0成立； 若a ＜0，则⎩⎪⎨⎪⎧Δ＝42＋16a ＞01＜－2a ＜52⇒a ＞－1，即－1＜a ＜0. 综上得，所求实数a 的取值范围为(－1，＋∞)．]课时作业(三)[基础巩固]1．已知命题p ：∀x ＞1，log 2x ＋4log x 2＞4，则¬p 为( )A ．¬p ：∀x ≤1，log 2x ＋4log x 2≤4B ．¬p ：∃x ≤1，log 2x ＋4log x 2≤4C ．¬p ：∃x ＞1，log 2x ＋4log x 2＝4D ．¬p ：∃x ＞1，log 2x ＋4log x 2≤4D [命题是全称命题，则命题的否定是特称命题，即：¬p ：∃x ＞1，log 2x ＋4log x 2≤4，故选D.]2．设命题p ：函数y ＝sin 2x 的最小正周期为π2；命题q ：函数y ＝cos x 的图象关于直线x ＝π2对称，则下列判断正确的是( ) A ．p 为真 B ．¬q 为假C ．p ∧q 为假D ．p ∨q 为真C [函数y ＝sin 2x 的最小正周期为2π2＝π，故命题p 为假命题；x ＝π2不是y ＝cos x 的对称轴，故命题q 为假命题，故p ∧q 为假．故选C.]3．命题p ：若sin x >sin y ，则x >y ；命题q ：x 2＋y 2≥2xy .下列命题为假命题的是( )A ．p ∨qB ．p ∧qC ．qD ．¬pB [命题p 假，q 真，故命题p ∧q 为假命题．]4．下列命题中的真命题是( )A ．∃x 0∈R ，使得sin x 0＋cos x 0＝32B ．∀x ∈(0，＋∞)，e x >x ＋1C ．∃x 0∈(－∞，0)，2x 0<3x 0D ．∀x ∈(0，π)，sin x >cos xB [∵sin x ＋cos x ＝2sin ⎝⎛⎭⎫x ＋π4≤2<32，故A 错误；设f (x )＝e x －x －1，则f ′(x )＝e x －1，∴f (x )在(0，＋∞)上为增函数，又f (0)＝0，∴∀x ∈(0，＋∞)，f (x )>0，即e x >x ＋1，故B 正确；当x <0时，y ＝2x 的图象在y ＝3x 的图象上方，故C 错误；∵当x ∈⎝⎛⎭⎫0，π4时，sin x <cos x ，故D 错误．故选B.]5．设命题p ：∃x 0∈(0，＋∞)，x 0＋1x 0＞3；命题q ：∀x ∈(2，＋∞)，x 2＞2x ，则下列命题为真的是( )A ．p ∧(¬q )B ．(¬p )∧qC ．p ∧qD ．(¬p )∨qA [对于命题p ，当x 0＝4时，x 0＋1x 0＝174＞3，故命题p 为真命题；对于命题q ，当x ＝4时，24＝42＝16，即∃x 0∈(2，＋∞)，使得2x 0＝x 20成立，故命题q 为假命题，所以p ∧(¬q )。

2020届九年级中考复习浙教版科学讲义：九年级上册12功和功率第12课时功与功率一、功(c)物体在力的方向上通过一段距离。

作用在物体上的力，1．做功的两个必要因素：功等于力跟物体在力的方向上通过距离的乘积。

2．公式：W＝Fs………定义式………克服重力做功＝Gh fs………克服摩擦力做功＝………已知功率和做功时间求功＝Pt功的单位是焦耳，简称焦，符号是J。

【知识拓展】三种情况不做功：一是有力而无距离；二是有距离而无力；三是有力也有距．1 离，但力的方向和距离垂直。

13/ 1．2020届九年级中考复习浙教版科学讲义：九年级上册12功和功率2．计算功的大小时，一要注意是哪个力在做功，二要注意是在力的方向上通过的距离。

二、功率(c)1．含义：功率是单位时间内做的功，用字母P表示。

功率是用来描述做功快慢的物理量。

2．公式：P＝W/t＝Fs/t＝Fv3．单位：瓦特，简称瓦，符号是W。

常用单位：kW。

3W 10单位换算：1kW＝三、杠杆(b)1．五要素——组成杠杆示意图－112图O表示。

①支点：杠杆绕着转动的固定点，用字母表示。

F②动力：使杠杆转动的力，用字母1表示。

F③阻力：阻碍杠杆转动的力，用字母2表示。

L④动力臂：从支点到动力作用线的距离，用字母1表示。

L⑤阻力臂：从支点到阻力作用线的距离，用字母213/ 2．2020届九年级中考复习浙教版科学讲义：九年级上册12功和功率2．研究杠杆的平衡条件：杠杆平衡指杠杆处于__静止__或__匀速转动__状态。

实验前应调节杠杆两端的螺母，使杠杆在__水平位置__平衡，目的是便于从杠杆上直接量出力臂。

L＝FL__(用公式表示)。

F或杠杆原理)是：__通过实验可得出杠杆的平衡条件(2121 3．分类：四、滑轮(a)1．定滑轮定滑轮实质是一个等臂杠杆。

其特点是使用定滑轮不能省力但是能改变力的方向。

(或速度v)＝重s。

：理想的定滑轮(不计轮轴间摩擦)F＝G绳子自由端移动距离FF(或速度v)。