浙江大学847结构力学历年考研试题

《结构力学Ⅰ》考研2021考研结构力学真题库对于准备考研结构力学的同学来说，掌握历年真题是至关重要的。

2021 年的考研结构力学真题能够为大家提供宝贵的复习方向和重点。

首先，让我们来看看 2021 年结构力学考研真题中的常见题型。

其中，静定结构的内力分析是基础且重要的部分。

例如，会给定一个简单的梁、刚架或者桁架结构，要求计算其在特定荷载作用下的支座反力、内力（轴力、剪力、弯矩）。

这部分题目通常需要同学们熟练掌握截面法、节点法等基本的计算方法，并且要对各种静定结构的受力特点有清晰的认识。

在超静定结构的分析方面，力法和位移法是重点考查的内容。

真题中可能会出现一个多次超静定的结构，要求同学们用力法或位移法求解其内力。

这不仅考验对基本原理的理解，还需要具备正确建立基本方程和求解方程的能力。

例如，会涉及到如何确定基本未知量、如何绘制单位弯矩图和荷载弯矩图，以及如何利用公式计算系数和自由项等。

影响线的问题也是常见的考点之一。

可能会要求绘制某个量值（如支座反力、某截面内力）的影响线，或者根据影响线求最不利荷载位置及相应的最大量值。

这需要同学们理解影响线的概念和绘制方法，能够灵活运用机动法、静力法等。

在结构的动力分析方面，单自由度体系的自由振动和受迫振动经常出现在真题中。

需要掌握自振频率的计算、振型的概念，以及在简谐荷载作用下的动力响应等知识。

另外，矩阵位移法也是近年来的一个重要考点。

涉及到如何将结构离散化、建立单元刚度矩阵和整体刚度矩阵，以及求解节点位移和内力等。

下面我们通过具体的题目来进一步分析。

【题目】如图所示的静定梁，已知 q ＝ 10kN/m，l ＝ 6m，求支座A 和B 的反力。

【解析】这是一道典型的静定梁的内力分析题目。

首先，对整个梁进行受力分析，以 A 点为矩心，由ΣM A＝ 0 可得：B 支座的竖向反力为 30kN（向上）。

然后，由ΣF y ＝ 0 可得 A 支座的竖向反力为30kN（向上）。

目　录
2007年浙江大学457结构力学考研真题2008年浙江大学847结构力学考研真题2009年浙江大学847结构力学考研真题2010年浙江大学847结构力学考研真题2011年浙江大学847结构力学考研真题2012年浙江大学847结构力学考研真题2013年浙江大学847结构力学考研真题2014年浙江大学847结构力学考研真题2015年浙江大学847结构力学考研真题
（含参考答案）
2007年浙江大学457结构力学考研真题
2008年浙江大学847结构力学考研真题
2009年浙江大学847结构力学考研真题
2010年浙江大学847结构力学考研真题
2011年浙江大学847结构力学考研真题
2012年浙江大学847结构力学考研真题。

浙大847结构力学大高分学长考研心得我是从去年8月1号开始准备复习的，但是由于G20的关系，我们不能留校，只能回去，在家复习效率巨低，根本看不进书，我白天加起来大概学3个小时左右，晚上不学，这种状态一直持续到9月15号开学为止。

但是这一个多月的时间里我还是把以前的课本都看了一遍（微积分，线代，概率论，结构力学），还有数学的复习全书（我数学复习资料用的是李永乐的），只看知识点，题目没怎么认真看，随意扫了下。

到学校后开始出去自习了，晚上一般学到9点，归根结底还是心还没静下来，非常抗拒考研，毕竟大一大二玩的比较多，一个玩惯了的人再让他去捡起课本认真学习真的很难，考试周是没办法，不看容易挂，而且考试周持续时间短，不像考研，战线实在太长了，刚开始的时候真的感觉遥遥无期。

所以后来学校开始做保研工作的时候我被诱惑了。

我当时的成绩是肯定保不了研的，但是光按专业成绩来说直博是稳的，虽然我以前不想直博，因为我不是那种静下心来能搞科研的人，而且直博时间太久，硕士比起博士来说要水很多，文凭也比较好拿（不要说我功利心重。

这社会没办法，本科生不好找工作，尤其是土木，你没个实习经验，被人家赏识，大部分只能去施工方，很多公司招聘的起步也是硕士及其以上）。

我申请了保研后，拿到了名额，通过了面试，万万没想到，在要签字的时候，老师才告诉我，我六级分数没到480，直不了博。

当时真的很无语，那何必还要通知我面试呢。

在此想劝学弟学妹们不管你要不要直博，先尽量把六级过了，或者雅思托福过了，这个分数可以抵的，具体看要求我忘记了。

因为你不清楚你以后想法会不会转变，所以尽量把能准备的都准备好，给自己留个后路。

我的后路被封死了，考研成了我唯一的选择。

那天之后，我再没想过别的，一心考研。

头一个月还抱怨，每天9点就回来了，根本看不进去，每次想着怎么还有90多天的时候就很烦躁。

一开始我是一个人复习的，后来觉得太孤单了，找了另外两个同学一起复习。

那个时候我大概已经学了一个月了，麻木了，心也静下来了，再加上跟同学一起的原因，我每天晚上都能学到10点，听完图书馆闭馆的音乐再走。

结构力学考研真题整理详解一、填空题1在平面体系中，联结______的铰称为单铰，联结______的铰称为复铰。

[哈尔滨工业大学2007研]【答案】两个刚片；两个以上的刚片查看答案【解析】根据定义，单铰是指联结两个刚片的一个铰；复铰是指同时联结两个以上刚片的一个铰。

2互等定理只适用于______体系。

反力互等定理、位移互等定理是以______定理为基础导出的。

[哈尔滨工业大学2007研]【答案】线弹性；功的互等查看答案【解析】因为互等定理中采用的位移计算公式都是在线弹性假定下求出的，所以互等定理只适用于线弹性结构。

互等定理包括功的互等定理、位移互等定理及反力互等定理，其中反力互等定理、位移互等定理均基于功的互等定理导出，是功的互等定理的特殊情况。

二、选择题1在温度改变下，静定结构将（）。

[宁波大学2009研]A．有内力、有位移、无应变B．有内力、有位移、有应变C．有内力、无位移、无应变D．无内力、无位移、有应变【答案】B查看答案【解析】在温度改变下，静定结构不会产生内力，但会发生变形，即产生应变和位移。

2用图乘法求位移的必要条件之一是（）。

[宁波大学2009研]A．单位荷载下的弯矩图为一直线B．结构可分为等截面直杆C．所有杆件EI为常数且相同D．结构必须是静定的【答案】B查看答案【解析】图乘法求位移的必要条件包括：①杆轴为直线；②EI为常数；③M—和MP两个弯矩图中至少有一个是直线图形。

B项，变截面直杆可根据截面刚度不同分段利用图乘法求解位移，因此B项不是图乘法求位移的必要条件。

3力法基本方程使用条件是（）构成的超静定结构。

[宁波大学2009研]A．弹塑性材料B．任意变形的任何材料C．微小变形且线弹性材料D．任意变形的线性弹性材料【答案】C查看答案【解析】力法是指解除超静定结构的多余联系而得到静定的基本结构，以多余未知力作为基本未知量，根据基本体系应与原结构变形相同而建立的位移条件，首先求出多余未知力，然后由平衡条件计算其余反力、内力的方法。

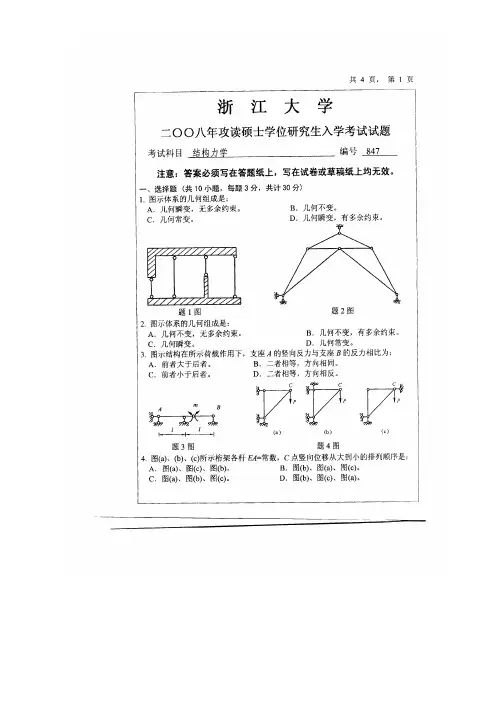
浙江大学2012年攻读硕士学位研究生入学考试试题考试科目结构力学（A卷）编号 847 注意：答案必须写在答题纸上，写在试卷或草稿纸上均无效。

一、选择题（共10小题，每题3分，共计30分）1.图示平面体系的几何组成是：A．几何不变，无多余约束。

B.几何不变，有多余约束。

C．几何瞬变。

D. 几何常变。

2.以下关于瞬变体系的论述，正确的是：A．瞬变体系的总体约束数目不足，从而导致体系瞬时可变。

B.瞬变体系经微笑位移后即成为几何不变，故可作为结构使用。

C．瞬变体系必定存在多余约束。

D. 瞬变体系必定存在瞬铰。

3.图示结构的弯矩图轮廓是（选项见图）：4.图示桁架，杆件C的内力是：A．0。

B. /2-。

PC．/2-。

D. P。

P5. 图示结构，各杆EI EA 、均为常数，线膨胀系数为α。

若各杆温度均匀升高t 度，则D 点的竖向位移（向下为正）为：A ．ta α。

B. ta α- 。

C ．2ta α。

D. 0。

6. 图示结构，若改变B 点链杆的方向（不通过A 铰），下列叙述正确的是：A ．全部内力没有变化。

B.弯矩有变化 。

C ．剪力有变化。

D.轴力有变化 。

7. 图示结构，分别采用力法、位移法计算，其中力法取静定的基本结构，位移法忽略轴向变形，则基本未知量数目分别为：A ．3、4。

B.4、4 。

C ．4、5。

D.5、5。

8. 图示四种单跨梁，其材料、截面均相同，则极限荷载值最大的是：9. 题8中，极限荷载值最小的是：10.以下关于杆件结构极限荷载的论述，错误的是：A ．极限状态可能不唯一，但极限荷载时唯一的。

B. 极限荷载的计算不仅要考虑结构的最终平衡状态，还需要考虑其变形状态。

C ．极限荷载既是可破坏荷载，又是可接受荷载。

D. 极限荷载的大小与结构的温度改变、支座移动、制造误差无关。

二、填空题（共7小题，每空2分，共计26分）11.图示三铰拱，拱轴线方程为2y=4()/fx l x l -，其中4,16f m l m ==，则D 截面弯矩 D M = 11A (下侧受拉为正)，D 截面剪力QD F = 11B 。

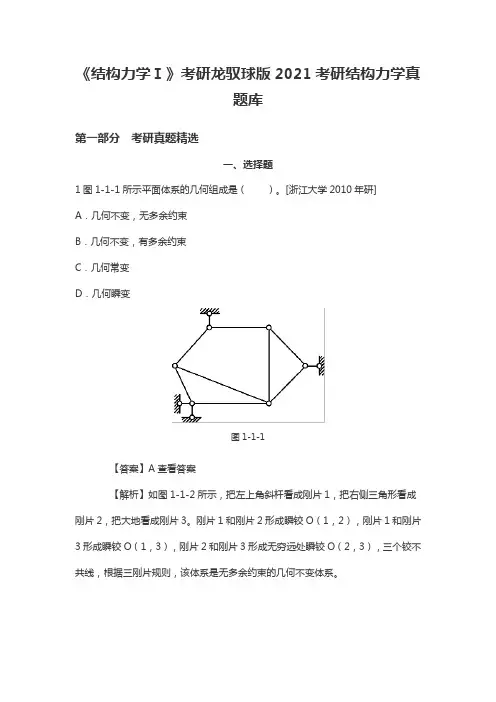
《结构力学Ⅰ》考研龙驭球版2021考研结构力学真题库第一部分考研真题精选一、选择题1图1-1-1所示平面体系的几何组成是（）。

[浙江大学2010年研]A．几何不变，无多余约束B．几何不变，有多余约束C．几何常变D．几何瞬变图1-1-1【答案】A查看答案【解析】如图1-1-2所示，把左上角斜杆看成刚片1，把右侧三角形看成刚片2，把大地看成刚片3。

刚片1和刚片2形成瞬铰O（1，2），刚片1和刚片3形成瞬铰O（1，3），刚片2和刚片3形成无穷远处瞬铰O（2，3），三个铰不共线，根据三刚片规则，该体系是无多余约束的几何不变体系。

图1-1-22图1-1-3（a）所示体系的几何组成是（）。

[武汉大学2012年研、郑州大学2010年研、华南理工大学2007年研、河海大学2007年研]A．无多余约束的几何不变体系B．几何可变体系C．有多余约束的几何不变体系D．瞬变体系图1-1-3【答案】A查看答案【解析】在几何构造分析时，可以将曲杆替换为直杆进行简化，所以可将图1-1-3（a）所示体系替换为图1-1-3（b）所示体系。

在任一体系上添加或去除二元体不改变体系的几何构造，因此依次去除C支座链杆与CE杆、D支座链杆与DE杆所组成的二元体，以及二元体A—E—B后，可知原体系为无多余约束的几何不变体系。

3如图1-1-4所示结构在所示荷载作用下，其支座A的竖向反力与支座B的反力相比为（）。

[郑州大学2010年研、哈尔滨工业大学2008年研]A．前者大于后者B．二者相等，方向相同C．前者小于后者D．二者相等，方向相反图1-1-4【答案】B查看答案【解析】根据静力平衡条件，对C点取矩，∑M C＝0，R A·l－R B·l＝0，解得R A＝R B，即支座A的竖向反力与支座B的反力大小相等，方向也相同。

4图1-1-5所示结构，当高度h增加时，杆件1的内力（）。

[南京理工大学2012年研]A．增大B．减小C．不确定D．不变【答案】D查看答案【解析】根据零杆判别法，图示结构是对称结构受到对称荷载作用，杆件1、2与底下两根水平杆件组成“K”形结点，所以杆件1、2均为零杆，与结构高度h 增加与否无关。