解方程的一般步骤
- 格式:ppt
- 大小:2.55 MB
- 文档页数:33

解整式方程的步骤
解整式方程的步骤主要包括以下几个方面:
1、去分母:方程两边同时乘以最简公分母,将分式方程化为整式方程。
这是解分式方程的基本方法,通过这一步,可以消除方程中的分母,使得方程更容易求解。
2、去括号:当方程中含有括号时,需要将括号内的项移到一边,使其成为一个整体。
如果括号前有"+",则括号内不变符号;如果括号前有"-",则括号内变号。
3、移项:对于含有未知数的项,将其移动到方程的左边,而常数项移动到方程右边。
这样做是为了简化方程,便于求解。
4、合并同类项:合并方程中的同类项,即将相同系数的项放在一起,以简化方程的结构。
5、系数化为1:对于含有未知数的项,将其系数化为1,这样可以直接求得未知数的值。
6、验根:最后一步是检验方程的解是否正确。
如果最简公分母为0,说明原方程无解,需要重新计算。
这个步骤确保了解题过程的正确性和有效性。

解方程的步骤解方程是数学中非常重要的内容之一。
在方程中,我们需要找到一个或多个数值,使得方程两边的值相等。
通过解方程,我们可以解决各种实际问题,例如计算小费,计算利润等。
首先,让我们来看一下一元一次方程。
一元一次方程指的是只有一个未知数(通常用x表示)且次数为一的方程。
一元一次方程的一般形式为ax+b=c,其中a、b、c是已知数。
解一元一次方程的基本步骤如下:1. 将方程的形式转化为 ax=b-c。
这一步可以通过移项来实现,将常数项移动至方程的另一侧。
2. 化简方程,将方程化简为 ax=d的形式,其中d=b-c。
3. 除以系数a,得到 x=d/a。
这一步的目的是消除方程中未知数的系数。
通过这些步骤,我们可以得到方程的解。
下面,我们通过一个具体的例子来说明解一元一次方程的过程。
假设有一个一元一次方程 2x+3=9。
首先,我们需要将方程的形式转化为 ax=b-c。
在这个例子中,我们把方程转化为 2x=9-3。
然后,化简方程,得到 2x=6。
接下来,我们除以系数2,得到 x=3。
所以,方程的解为 x=3。
除了一元一次方程,还有许多其他类型的方程需要解决。
例如,二次方程、多项式方程等。
每种类型的方程都有相应的解法。
对于二次方程,一般形式为 ax^2+bx+c=0。
解二次方程有两种常见的方法:配方法和求根公式。
根据具体的情况选择适合的方法来解决问题。
对于多项式方程,我们可以使用因式分解法来解决。
该方法的目的是将方程分解为一个或多个乘法因子的积。
解方程在数学中起着重要的作用。
通过解方程,我们可以解决各种实际问题,并推导出更复杂的数学概念和定理。
因此,掌握解方程的方法和技巧对于学习数学以及在日常生活中运用数学知识都非常重要。
总结起来,解方程是数学中的重要内容之一。
通过解方程,我们可以找到方程的解,解决实际问题,并推导出更深入的数学概念。
无论是一元一次方程、二次方程还是多项式方程,都有相应的解法。
掌握解方程的方法和技巧对于学习数学和应用数学知识都至关重要。

一般解一元一次方程的基本步骤是什么?解一元一次方程的一般步骤是:
去分母:在方程两边都乘以各分母的最小公倍数.
去括号:先去小括号,再去中括号,最后去大括号.
移项:把含有未知数的项都移到方程的一边,其他项都移到方程的另一边.合并同类项:把方程化成ax=b(a≠0)的形式.
系数化成1:在方程两边都除以未知数的系数a,得到方程的解x=b a
以上是解一元一次方程的大体步骤,某些题中,也许某一步骤就用不到,有些题也可不按上面的步骤顺序进行方程的变形,要根据具体问题的特点,灵活运用这些步骤,尽量找到较简便的解方程途径。
[例1] 解方程:
解:原方程变形为
去分母,得4(50x+200)-12x=9(x+4)-131
去括号,得200x+800-12x=9x+36-131
移项,得200x-12x-9x=36-131-800
合并同类项,得179x=-895
系数化成1,得x=-5
[例2] 解方程:
解:原方程变形为
去分母,得18x-5=10x-10
移项,得18x-10x=-10+5
合并同类项,得8x=-5
方程的形式可能是多种多样的,要细心观察特点,灵活安排具体步骤,解得简便。

四年级解方程的步骤解方程是数学中一个重要的内容,四年级的解方程步骤相对简单,让我们来一起学习解方程的基本步骤。
步骤一:了解方程的含义我们需要了解什么是方程。
方程是一个等式,其中包含未知数和已知数,并且未知数的值是我们要解出来的。
例如,2x + 3 = 7,这就是一个方程,其中x是未知数。
步骤二:观察方程观察方程的左右两边是否有已知数和未知数。
在观察的过程中,我们要注意等号两边的数是否相等,如果相等,那么我们得出的解就是正确的。
步骤三:解方程1.首先,我们需要把方程中的常数移到等号的一边,未知数移到等号的另一边。
例如,2x + 3 = 7,我们需要把3移到等号的另一边,变成2x = 7 - 3。
2.其次,我们要根据方程的要求,进行运算。
例如,2x = 7 - 3,我们需要计算等号两边的值。
计算后,我们得到2x = 4。
3.然后,我们需要根据方程的要求,解出未知数的值。
例如,2x= 4,我们需要计算未知数x的值。
计算后,我们得到x = 4 ÷ 2,即x = 2。
步骤四:验证解在解完方程后,我们需要对解进行验证,确保解是正确的。
验证的方法就是把解代入原方程中,观察两边是否相等。
例如,我们把解x = 2代入原方程2x + 3 = 7,得到2 × 2 + 3 = 7。
计算后,我们得到4 + 3 = 7,等号两边相等,说明解是正确的。
步骤五:总结完成解方程的步骤后,我们需要总结这个过程。
解方程的步骤可以通过以下的方式进行总结:-观察方程,分析已知数和未知数的位置。
-移项,将常数移到等号的一边,未知数移到等号的另一边。
-运算,根据方程的要求进行计算。
-解未知数,解出未知数的值。
-验证解,验证解是否正确。
四年级解方程的步骤相对简单,但是要注意细节。
在解方程时,我们要运用已学的数学知识,灵活运用加减乘除等基本运算。
通过多做练习,我们可以更加熟练地解方程。
通过以上的步骤,我们可以解方程,求出未知数的值。

一元一次方程怎么解详细过程
解一元一次方程的步骤:
1、去分母:方程两边同时乘各分母的最小公倍数。
2、去括号:一般先去小括号,再去中括号,最后去大括号,但顺序有时可依据情况而定使计算简便,可根据乘法分配律。
3、移项:把方程中含有未知数的项移到方程的另一边,其余各项移到方程的另一边移项时别忘记了要变号。
一般都是这样:(比方)从5x=4x+8得到5x-4x=8,把未知数移到一起!
4、合并同类项:将原方程化为ax=b(a≠0)的形式。
5、化系数为一:方程两边同时除以未知数的系数。
6、得出方程的解。

解一元一次方程的五步步骤
解一元一次方程的五步骤如下:
步骤一:将方程化为标准形式
将方程整理成形如ax + b = 0的形式,其中a和b分别是常数。
步骤二:合并同类项
将方程中的同类项合并,得到ax = -b的形式。
步骤三:消去系数
将方程两边同时除以系数a,消去x的系数,得到x = -b/a的
形式。
步骤四:验证解是否正确
将x = -b/a代入原方程,验证方程的两边是否相等。
若相等,
则解为正确;若不相等,则解为错误。
步骤五:表示解的特征
根据方程的解的特征,可以判断解的形式:
- 若a = 0且b = 0,方程有无数解。
- 若a = 0且b ≠ 0,方程无解。
- 若a ≠ 0,方程有唯一解x = -b/a。

初中解方程的步骤及格式解方程是数学中的一种重要方法,也是初中数学学习中的一项重要内容。
解方程的步骤和格式可以总结为以下几个方面:1.式子分析:首先对给定的方程进行仔细分析,确定其形式(一次方程、二次方程等),了解方程中的各个元素及其含义。
2.去括号和合并同类项:对于包含有括号的方程,首先要去掉括号,然后进行合并同类项的运算。
3.移项和化简:将含有未知数的项移至一侧,将常数项移到另一侧,使方程化为形如"未知数=数字"的形式。
4.清除分母:如果方程中存在分母,将方程的两侧乘以分母的公倍数,从而消去分母。
5.解方程:根据方程的形式和题目的要求,采用不同的方法进行解方程。
-如果是一次方程(线性方程),可以采用等式相减法、等式相加法、代入法等解法。
-如果是二次方程,可以采用配方法、因式分解法、求根公式等解法。
-如果是分式方程,可以采用通分、求最小公倍数等解法。
-如果是含有绝对值的方程,可以根据绝对值的性质进行分情况讨论。
6.检验答案:将求得的解代入原方程,检验是否满足原方程,以确保解的正确性。
对于初中解方程的步骤和格式,可以举一个具体的例子来说明:题目:解方程2x - 5 = 3x + 8步骤1:对方程进行分析,确定为一次方程。
其中2x和3x是未知数x的系数,-5和8是常数项。
步骤2:去括号和合并同类项,方程变为2x - 5 = 3x + 8。
步骤3:移项和化简,将3x移至左侧,将常数项5和8移到右侧,方程变为2x - 3x = 8 + 5。
步骤4:化简,方程变为-x = 13。
步骤5:解方程,由于这是一次方程,可以采用等式相加法。
将方程两侧同时加上x,得到0 = 13 + x。
步骤6:移项,得到x = -13。
步骤7:检验答案,将x = -13代入原方程,得到2*(-13) - 5 = 3*(-13) + 8,计算得到-26 - 5 = -39 + 8,-31 = -31,等式成立,说明解正确。

解方程一.具体步骤 1.去分母——> 2.去括号——> 3.移项——> 4.合并同类项——> 5.未知数x 的系数化为1二.例子: 3x+23 =2x-151.去分母: (原理:等式两边同时乘以或除以同一个数,等式依然成立) 3和5的最小公倍数是15,等式的两边同时乘以15:15ⅹ(3x+23 )=15ⅹ(2x-15) ——>5(3x+2)=3(2X-1); 2.去括号 (注意,去括号的时候,如果括号前是负号,则括号里的符号要变号) 5(3x+2)=3(2X-1);——>15x+10=6x-33.移项 (原理,等式两边同时加上或减去同一个数,等式依然成立)15x+10=6x-3;先移x :15x+10-6x =6x-6x-3——>15x+10-6x =-3在移+10:15x-10+10-6x =-3-10——>15x-6x=-3-10以上两步骤只是原理,它等效于把6x 从等式右边移到左边并变号-6x : 15x+10-6x=-3把+10从等式左边移到等式右边变号-10: 15x-6x=-3-104,合并同类项 (什么是同类项:所含字母相同,并且相同字母的指数也分别相同的项:如2x 与3x ,4y 与6y ,像6x 与3x 2就不是同类项,它们x 的指数不一样)15x-6x=-3-10——>9x=-135.未知数的系数化为1:x=-139例题2: 3x+23 +2=2x-151:去分母 15ⅹ(3x+23 +2)=15ⅹ2x-15(等式两边乘以15,不要忘了2也要乘) 5(3x+2)+30=3(2x-1)2.去括号 15x+10+30=6x-33.移项 15x-6x=-3-10-304.合并同类项 9x=-435.未知数x 的系数化1 x=-439例题3:3x+23 -2x-15=-2 1:去分母 15ⅹ(3x+23 -2x-15)=15ⅹ-2 (等式两边乘以15,不要忘了2也要乘) 5(3x+2)-3(2x -1)=-302.去括号 15x+10-6x +3 =-30 (去括号的时候,如果括号前是负号,则括号里的符号要变号)3.移项 15x-6x=-3-10-304.合并同类项 9x=-435.未知数x 的系数化1 x=-439。

解方程书写格式范例解方程是数学中一项重要的技能,它在不同学科以及日常生活中都有广泛的应用。
解方程的书写格式对于清晰和准确地表达解的过程和结果非常重要。
下面是解一元一次方程、一元二次方程和一元三次方程的书写格式范例。
一、解一元一次方程一元一次方程是形如ax + b = 0的方程,其中a和b是已知的实数,x是未知数。
解一元一次方程的一般步骤如下:1.清除方程中的常数项,使得等式左边为0;2.把方程化为ax = c的形式,其中c是常数;3.把方程写成x = c/a的形式,即解出x的值。
例如,解方程2x + 3 = 7的步骤如下:1.减去3,得到2x = 4;2.除以2,得到x = 2。
所以方程2x + 3 = 7的解为x = 2。
二、解一元二次方程一元二次方程是形如ax^2 + bx + c = 0的方程,其中a、b和c 是已知的实数,x是未知数。
解一元二次方程的一般步骤如下:1.计算判别式D = b^2 - 4ac的值;2.如果D > 0,那么方程有两个不等的实数解,可以使用求根公式x = (-b ± √D) / (2a)求解;3.如果D = 0,那么方程有两个相等的实数解,可以使用求根公式x = -b / (2a)求解;4.如果D < 0,那么方程没有实数解。
例如,解方程x^2 - 4x + 3 = 0的步骤如下:1.计算判别式D = (-4)^2 - 4(1)(3) = 16 - 12 = 4;2.因为D > 0,所以方程有两个不等的实数解;3.使用求根公式x = (4 ± √4) / (2*1) = (4 ± 2) / 2 = 3或1;所以方程x^2 - 4x + 3 = 0的解为x = 3或x = 1。
三、解一元三次方程一元三次方程是形如ax^3 + bx^2 + cx + d = 0的方程,其中a、b、c和d是已知的实数,x是未知数。
解一元三次方程的一般步骤如下:1.首先,使用合适的方法将方程转化为形如y^3 + py + q = 0的方程;2.利用数值法或其他方法求解y的值;3.把y的值代入x = u - (b/3a)的公式中,其中u = y - (b^2 / 3a),可以求出x的值。

解方程的基本方法与步骤解方程是数学中的重要内容,它是研究方程的根或变量的取值的过程。
正确应用解方程的方法和步骤,能够帮助我们解决各种问题,从而推进数学的发展。
本文将介绍解方程的基本方法与步骤,帮助读者更好地理解和应用解方程的技巧。
一、一元一次方程的解法一元一次方程是形如ax + b = 0的方程,其中a和b是已知常数,x 是未知数。
解一元一次方程的方法有多种,下面将介绍两种常用的方法。
1.1 直接法直接法是最常见和最简便的解一元一次方程的方法。
以ax + b = 0为例,具体步骤如下:步骤一:将方程两边的常数项移到一个侧,使方程等号两边的系数相等。
得到ax = -b。
步骤二:将方程两边同时除以x的系数a,得到x = -b/a。
1.2 代入法代入法是通过代入一个已知数的值来求解方程的方法。
以ax + b = 0为例,具体步骤如下:步骤一:选取一个已知数,用该已知数代替方程中的未知数,得到一个新的方程。
步骤二:解这个新方程,得到一个值。
步骤三:将求得的值代入原方程中,验证是否满足原方程。
如果满足原方程,即为方程的解;如果不满足,则选取其他已知数进行代入。
二、一元二次方程的解法一元二次方程是形如ax^2 + bx + c = 0的方程,其中a、b和c是已知常数,x是未知数。
解一元二次方程的方法有多种,下面将介绍两种常用的方法。
2.1 因式分解法因式分解法是通过将方程因式分解为两个一元一次方程的乘积来求解方程的方法。
以ax^2 + bx + c = 0为例,具体步骤如下:步骤一:对方程进行因式分解,得到(ax + m)(nx + n) = 0的形式。
步骤二:令括号中的每个一元一次方程等于零,解出x的值,得到x1和x2(可能重根)。
2.2 公式法公式法是通过利用一元二次方程的求根公式来求解方程的方法。
以ax^2 + bx + c = 0为例,具体步骤如下:步骤一:计算方程的判别式D = b^2 - 4ac。
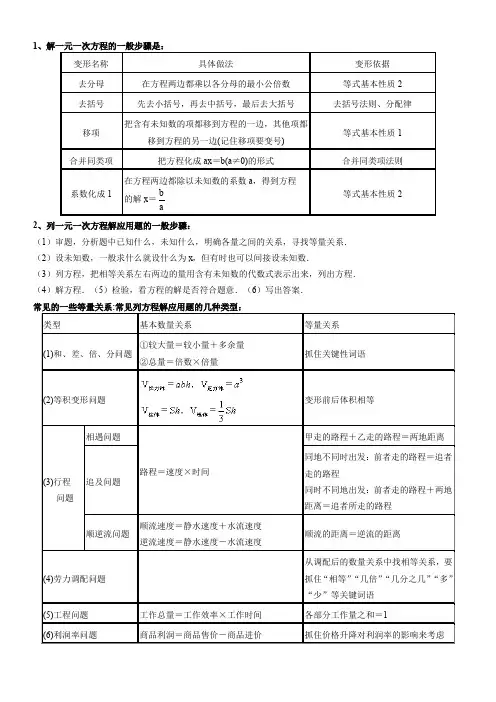
12、列一元一次方程解应用题的一般步骤:(1)审题,分析题中已知什么,未知什么,明确各量之间的关系,寻找等量关系.(2)设未知数,一般求什么就设什么为x,但有时也可以间接设未知数.(3)列方程,把相等关系左右两边的量用含有未知数的代数式表示出来,列出方程.(4)解方程.(5)检验,看方程的解是否符合题意.(6)写出答案.商品利润率=1.商品销售此类问题主要涉及的关键量:进价,标价,实际售价,利润,利润率。
熟记这些量间的基本关系式:商品的利润=商品的实际售价-商品的进价.(这里不考虑其它因素)商品的利润率=商品打折后的售价=商品的标价÷10×折扣数.另外在解决商品的利润率的问题中,还涉及如下关系式.注意会由基本关系式推出式子的变形,以便于解决问题.例:由×100%=利润率,可得商品的实际售价=商品的进价×(1+利润率).例1、商店里的皮上衣每件标价为2200元,在一次促销活动中,它打八折销售,结果仍获利10%,求此商品的进价.分析:题中的相等关系是商品的进价×(1+利润率)=商品的实际售价.解:设此商品的进价为x元,依题意(1+10%)x=2200×0.8.解这个方程,得x=1600.答:此商品的进价为1600元.例2、以现价销售一件商品的利润率为30%,如果商家在现有的价格基础上先提价40%,后降价50%的方法进行销售,商家还能有利润吗?为什么?依题意其后来折扣后的售价为(1+30%)a×(1+40%)(1-50%)=0.91a.∵0.91a-a=-0.09a,∴×100%=-9%.答:商家不仅没有利润,而且亏损的利润率为9%.2.银行存贷款例3、夏老师欲购买一辆汽车,销售商告诉夏老师,若采取分期付款方式:一种付款方式是第一月付4万元,以后每月付款一万元;另一种付款方式是前一半时间每月付款1万四千元,后一半时间,每月付款1万1千元;两种付款方式中付款钱数和付款时间都相同。
小学解方程的步骤解方程是数学学科中的基本内容之一,也是培养学生思维能力和解决问题能力的重要环节。
小学阶段,学生开始接触代数,初步学习解一元一次方程。
解方程的过程需要遵循一定的步骤,下面将介绍小学解方程的常用步骤。
步骤一:观察并列方程在解一元一次方程的过程中,首先需要观察并列方程。
并列方程是由等号将两个表达式连接起来的算式,通常包括未知数和已知数。
例如,一个简单的并列方程可以写作:2x + 3 = 7。
步骤二:移项整理接下来,需要对方程进行移项整理。
移项整理是将未知数移到等号的一侧,已知数移到等号的另一侧,使方程的形式更加简洁明确。
例如,对于上面的方程,可以将3移动到等号的右边,得到:2x = 7 - 3。
步骤三:合并同类项移项整理后,需要进行合并同类项的操作。
合并同类项是将方程中相同的项进行合并,得到更简化的方程。
例如,对于上面的方程,可以合并等号右边的常数项,得到:2x = 4。
步骤四:消元求解合并同类项后,需要进行消元求解的操作。
消元是通过运算将未知数的系数合并或约简到1的过程。
例如,对于上面的方程,可以将未知数2x的系数2除以2,得到:x = 2。
步骤五:检验解的正确性最后一步是检验解的正确性。
检验解是将求得的解回代到原方程中,看是否能使方程两边相等。
例如,将x = 2代入原方程2x + 3 = 7中,得到2*2 + 3 = 7,计算得到左边等于右边,说明解x = 2是正确的。
以上就是小学解方程的常用步骤。
在解方程的过程中,需要学生熟练掌握观察并列方程、移项整理、合并同类项、消元求解和检验解的技巧和方法。
通过不断的练习和实践,学生可以提高解方程的能力,培养出良好的数学思维和解决问题的能力。
希望以上内容对小学解方程的学习有所帮助!。
按照解分式方程的一般步骤
解分式方程的一般步骤如下:
1. 将分式中的分子和分母都化简成最简形式;
2. 如果方程中有括号,先将括号内的式子进行展开和化简;
3. 将方程中的分母乘到等式两侧,消去分母;
4. 将方程化为一元一次方程,即将所有变量放在等号左边,所有常数放在等号右边;
5. 化简方程,解出未知数的值;
6. 将所得的解带入原分式中检验,若成立,则解为正确答案,若不成立,则说明所得的解不是原分式的解。
以上是解分式方程的一般步骤,可以通过这些步骤来解决分式方程问题。
解二元一次方程的一般步骤:解二元一次方程的一般步骤解二元一次方程是数学中常见的问题,它涉及到两个未知量的关系。
以下是解决二元一次方程的一般步骤:1. 确定方程的形式:二元一次方程的一般形式为`ax + by = c`,其中a、b和c是已知数或常数,x和y是未知量。
确定方程的形式:二元一次方程的一般形式为`ax + by = c`,其中a、b和c是已知数或常数,x和y是未知量。
2. 消去一个未知量:通过消去其中一个未知量,将方程化简为只含有一个未知量的一元一次方程。
消去一个未知量:通过消去其中一个未知量,将方程化简为只含有一个未知量的一元一次方程。
- 如果系数a或b之一为0,可以直接得到另一个未知量的值。
例如,如果a = 0,则可以得到y = c/b。
- 如果系数a和b都不为0,则可以通过以下两种方法消去其中一个未知量:- 代入法:选择一个未知量的值,将其代入方程中,从而得到另一个未知量的值。
代入法:选择一个未知量的值,将其代入方程中,从而得到另一个未知量的值。
- 消元法:通过方程的加减等运算,消去一个未知量的系数,从而得到另一个未知量的值。
消元法:通过方程的加减等运算,消去一个未知量的系数,从而得到另一个未知量的值。
3. 求解另一个未知量:将经过第2步处理后得到的一元一次方程,求解出另一个未知量的值。
求解另一个未知量:将经过第2步处理后得到的一元一次方程,求解出另一个未知量的值。
4. 验证解的正确性:将求解得到的两个未知量的值代入原方程,验证等式是否成立。
验证解的正确性:将求解得到的两个未知量的值代入原方程,验证等式是否成立。
下面是一个解二元一次方程的示例:假设有以下二元一次方程:2x + 3y = 74x - 5y = -1我们将使用消元法来解这个方程。
首先,通过乘以适当的数值,使得两个方程中y的系数的绝对值相同。
这样,在两个方程相减时,y的项将会消失:2(4x - 5y) = 2(-1)4x - 5y = -2接下来,将第一个方程和第二个方程相加,消去x的系数:(2x + 3y) + (4x - 5y) = 7 + (-2)6x - 2y = 5现在,我们得到了一个只含有一个未知量的一元一次方程。