时间和位移

匀变速直线运动的位移与时间的关系公式
匀变速直线运动的位移与时间的关系公式可以由运动学公式推导得到，具体分为两种情况：
1. 匀速直线运动的位移与时间的关系公式：
位移 = 速度 ×时间
其中，位移表示物体在运动过程中从起点到终点的距离，速度表示物体的运动速度，时间表示运动的时间长度。

2. 变速直线运动的位移与时间的关系公式：
位移 = 初速度 ×时间 + 0.5 ×加速度 ×时间²
其中，初速度表示运动开始时的速度，加速度表示运动过程中的加速度。

这个公式描述了的位移与时间的关系可以用来计算变速直线运动下物体在不同时间点的位置。

注意，这个公式的适用条件是运动过程中加速度是一个常量。

另外还有一种特殊情况，匀变速直线运动中，如果物体的位移与时间的关系符合二次函数的形式，可以使用二次函数公式来描述位移与时间的关系。

例如：位移 = a ×时间² + b ×时间 + c，其中a、b和c是常数。

位移与时间的公式
物理学中，位移与时间的公式是衡量物体在一个特定的时间内位移的基本方程。

它的公式为 s＝v＊t，其中s表示位移（d），v表示速度（m/s），t表示时间（S）。

公式s＝v＊t表明，当物体在一定的时间内，得到同等位移，则其速度必然是一致的。

反之，当物体在一定的时间内，做出不定速度的非连续运动，那么它将有不同的位移量。

这个公式也能用来检查一个物体在给定的一段时间内，有多少位移量。

这个公式也能帮助人们理解物理学中的简单的概念。

例如，当球从高处自由落下时，它的速度会随时间的推移而增加。

而从这个公式中可以推导出，只要时间不变，其位移量必定是恒定的。

这个公式也能帮助人们了解其他物理学概念，如加速度。

当物体处于加速度状态时，其速度随时间的变化而变化，但并不是恒定的，而是根据加速度值而变化，这个公式也能被用来求出加速运动物体在一定时间内，所做的位移量。

总之，物理学中的位移与时间的公式非常重要，它不仅能帮助人们理解物理学的概念，还能帮助人们检查物体在给定的一段时间内有变化时，所做的位移量。

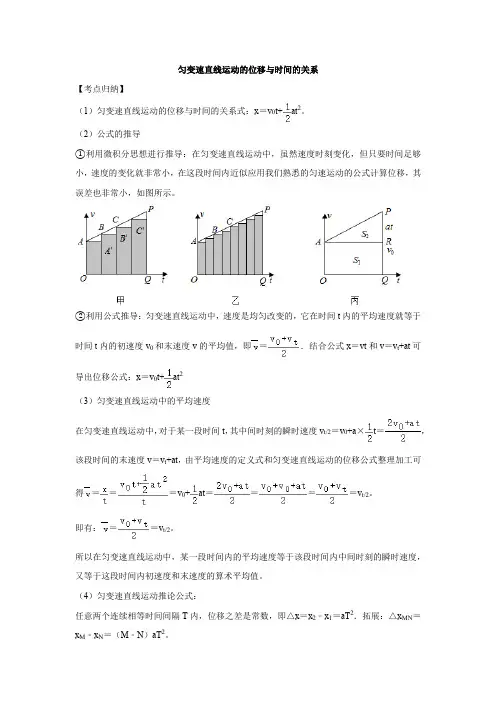
匀变速直线运动的位移与时间的关系【考点归纳】（1）匀变速直线运动的位移与时间的关系式：x＝v0t+at2。

（2）公式的推导①利用微积分思想进行推导：在匀变速直线运动中，虽然速度时刻变化，但只要时间足够小，速度的变化就非常小，在这段时间内近似应用我们熟悉的匀速运动的公式计算位移，其误差也非常小，如图所示。

②利用公式推导：匀变速直线运动中，速度是均匀改变的，它在时间t内的平均速度就等于时间t内的初速度v0和末速度v的平均值，即＝．结合公式x＝vt和v＝v t+at可导出位移公式：x＝v0t+at2（3）匀变速直线运动中的平均速度在匀变速直线运动中，对于某一段时间t，其中间时刻的瞬时速度v t/2＝v0+a×t＝，该段时间的末速度v＝v t+at，由平均速度的定义式和匀变速直线运动的位移公式整理加工可得＝＝＝v0+at＝＝＝＝v t/2。

即有：＝＝v t/2。

所以在匀变速直线运动中，某一段时间内的平均速度等于该段时间内中间时刻的瞬时速度，又等于这段时间内初速度和末速度的算术平均值。

（4）匀变速直线运动推论公式：任意两个连续相等时间间隔T内，位移之差是常数，即△x＝x2﹣x1＝aT2．拓展：△x MN＝x M﹣x N＝（M﹣N）aT2。

推导：如图所示，x1、x2为连续相等的时间T内的位移，加速度为a。

【命题方向】例1：对基本公式的理解汽车在平直的公路上以30m/s的速度行驶，当汽车遇到交通事故时就以7.5m/s2的加速度刹车，刹车2s内和6s内的位移之比（）A.1：1B.5：9C.5：8D.3：4分析：求出汽车刹车到停止所需的时间，汽车刹车停止后不再运动，然后根据位移时间公式求出2s内和6s内的位移。

解：汽车刹车到停止所需的时间＞2s所以刹车2s内的位移＝45m。

t0＜6s，所以刹车在6s内的位移等于在4s内的位移。

＝60m。

所以刹车2s内和6s内的位移之比为3：4．故D正确，A、B、C错误。

时间和位移举例引出时间和位移火车从北京到上海，需多长时间，走了多远例如：13时开始上课，14时20分下课，中间休息10分钟，14时30分上课1.时刻指的是某个时间点，指某一瞬间。

时间间隔又是指两个不同瞬时之间的一段时间时间间隔就是两个时间点之间的部分也就是通常人们所说的时间的长短。

时间和时间间隔可在时间数轴上表示出来，时刻用点表示，时间间隔用线段表示，我们平时所说的时间，有时指的是时刻，有时指的是时间间隔，要根据上下文认清它的含义！属于时刻的有：第几秒初；第几秒末；前几秒末；后几秒初属于时间间隔的有：第几秒内；几秒内；前几秒；后几秒内。

注意：第一秒末也是第三秒出第一秒是从0到1 第二秒内是从1到2 前三秒是从0到3举例：火车从上海到北京，坐飞机，坐火车，轨迹不一样2.初中就知道，路程是物体运动轨迹的长度，可见他所经过的路程是不相同的，但都是从北京到上海，位置的变动是相同的，当物体从某一点运动到另一点时，尽管可以沿不同的轨迹、走过不同的路程，但位置的变动是相同的，物理学中用一个叫位移的物理量来表示位置的变化。

位移：描述质点位置改变的物理量，方向由初位置指向末位置；大小是从初位置到末位置的线段长度。

3.矢量：既有大小，又有方向例：位移力速度标量：只有大小，没有方向例：路程质量、密度、温度、功、功率、动能、势能、体积、时间、热量、电阻、力矩、电流等等矢量加减用平行四边形定则或三角形定则标量的加减，用代数求和4.位移-时间图像在平面直角坐标系中，用横轴表示时间t，用纵轴表示位移x，给据给出的数据，作出几个点的坐标，用平滑的曲线将几个点连接起来，则这条曲线就表示了物体的运动特点，这种图像就叫做位移-时间图像.如图甲表示的位移-时间图像（1）x-t图像描述的是物体运动的位移随时间变化的规律。

一般以出发点为坐标原点来描述物体的位移，所以在直线运动中位移-时间图像有时可以理解为位置-时间图像，但并不表示图像是物体运动的轨迹。

如何计算物体的位移和位移时间要计算物体的位移和位移时间，首先需要清楚位移和位移时间的概念。

位移是指物体从一个位置到另一个位置的距离，而位移时间是指物体完成这个位移所花费的时间。

下面将介绍如何计算物体的位移和位移时间的方法。

一、位移的计算方法物体的位移可以通过以下的方法进行计算：1. 直线运动的位移计算在直线运动的情况下，可以使用以下的公式来计算位移：位移 = 终点位置 - 起点位置2. 曲线运动的位移计算在曲线运动的情况下，物体的位移可以通过对物体的运动轨迹进行积分来计算。

具体的计算方法会涉及到数学上的微积分原理和方法。

二、位移时间的计算方法物体的位移时间可以通过以下的方法进行计算：1. 直线运动的位移时间计算在直线运动的情况下，位移时间可以通过以下的公式计算：位移时间 = 终点时间 - 起点时间2. 曲线运动的位移时间计算在曲线运动的情况下，位移时间可以通过对物体的运动轨迹进行微分来计算。

具体的计算方法同样涉及到数学上的微积分原理和方法。

三、实例演示下面通过一个实例来演示如何计算物体的位移和位移时间。

假设一个汽车在 t=0 时刻从起点位置出发，经过 2 小时后到达终点位置，我们想要计算汽车的位移和位移时间。

根据直线运动的位移计算公式，我们可以得到：位移 = 终点位置 - 起点位置假设起点位置为 0 米，终点位置为 100 米，则位移为：位移 = 100 米 - 0 米 = 100 米根据直线运动的位移时间计算公式，我们可以得到：位移时间 = 终点时间 - 起点时间假设起点时间为 0 小时，终点时间为 2 小时，则位移时间为：位移时间 = 2 小时 - 0 小时 = 2 小时通过以上的计算，我们得到汽车在 2 小时内的位移为 100 米，位移时间为 2 小时。

四、总结计算物体的位移和位移时间是物理学中的基本问题之一。

在直线运动的情况下，可以通过位移的差值直接计算；在曲线运动的情况下，需要运用微积分原理进行计算。

位移时间公式变形位移时间公式是物理学中常见的一个公式，用于计算物体在给定加速度下的位移所需的时间。

它可以表示为：位移 = 1/2 * 加速度 * 时间的平方这个公式可以通过变形得到不同的表达方式，方便我们根据已知条件求解未知量。

下面将介绍几种常见的变形形式。

1. 时间的平方 = 2 * 位移 / 加速度这个变形形式可以通过已知位移和加速度来求解所需时间的平方。

将已知的位移和加速度代入公式中，通过计算得到时间的平方。

2. 时间 = 平方根(2 * 位移 / 加速度)这个变形形式是通过对上述公式求平方根得到的。

已知位移和加速度的值，可以通过计算得到所需的时间。

3. 加速度 = 2 * 位移 / 时间的平方这个变形形式是通过对原公式进行代数变换得到的。

已知位移和时间的值，可以通过计算得到加速度的大小。

4. 位移 = 加速度 * 时间的平方 / 2这个变形形式是通过对原公式进行代数变换得到的。

已知加速度和时间的值，可以通过计算得到位移的大小。

这些变形形式可以根据具体的问题来选择使用，以便更方便地求解所需的物理量。

例如，在计算自由落体运动中，我们可以根据已知的加速度和时间来求解位移，或者根据已知的位移和时间来求解加速度。

除了这些基本的变形形式，还可以根据具体问题进行更复杂的变形。

例如，在考虑空气阻力的情况下，位移时间公式需要进行修正，以考虑空气阻力对物体运动的影响。

位移时间公式的变形形式可以帮助我们根据已知条件求解未知量，从而更深入地理解物体在给定加速度下的运动规律。

在实际应用中，我们可以根据具体问题选择合适的变形形式来进行求解。

同时，我们也可以通过这些变形形式来推导出其他与位移、时间和加速度相关的公式，进一步扩展我们对物体运动规律的认识。

高中物理时间和位移在我们的日常生活中，时间和位移的概念是如此基础和普遍，我们几乎意识不到它们的存在。

然而，在物理学的微观世界中，时间和位移变得极其重要，它们是构建宇宙模型的基本元素。

本文将探讨高中物理中的时间和位移概念。

我们要理解什么是时间。

在物理学中，时间是一个测量事件顺序或持续时间的量。

它是绝对的，意味着无论在何处，时间的流逝都是一致的。

例如，不论在地球还是火星上，一秒的时间都是相同的。

时间单位可以是秒、分钟、小时、天等，它们根据特定的需求和场合被使用。

接下来，我们要探讨位移。

位移是物体从初始位置到终止位置的直线距离。

它描述了物体在空间中移动的距离和方向。

位移是一个矢量，因为它包含方向和大小两个要素。

例如，如果你从家里的位置走到公园，位移就是从家到公园的距离。

在这个过程中，如果你改变了行走的方向，那么你的位移也会相应地改变。

时间和位移的概念在物理学中有着广泛的应用。

例如，在研究物体的运动时，我们需要了解物体的速度和加速度，这些都是时间和位移的函数。

速度是描述物体在单位时间内移动的距离，而加速度是描述物体速度变化快慢的量。

通过使用这些概念，我们可以理解并预测物体的运动行为。

时间和位移的概念也与能量和动量等物理量密切相关。

例如，动能和势能是描述物体由于运动或位置而具有的能量形式。

同样地，动量和冲量也是描述物体运动和力作用的物理量。

这些概念都与时间和位移有着直接或间接的关系。

时间和位移是物理学的基本概念，它们对于理解物体的运动、能量转换以及许多其他物理现象都至关重要。

通过在高中阶段学习和掌握这些概念，我们可以为未来的学习和职业生涯打下坚实的基础。

高中物理时间和位移》高中物理时间和位移时间是指时间的长度，在单位时间内所完成的时间长度。

具有瞬时性和不可逆性。

时间瞬时即逝，无法被人们控制和改变。

在物理学中，时间是一个非常重要的概念，它与位移、速度等物理量密切相关。

位移是指物体在空间中所处位置的变化，通常用矢量表示。

位移与时间关系公式位移与时间关系公式是描述物体在运动过程中位移与时间之间的数学关系的公式。

在物理学中，位移通常用符号Δx表示，表示物体从初始位置到最终位置之间的距离。

时间用符号t表示，表示物体运动所经过的时间。

位移与时间之间的关系可以通过速度来描述。

速度是物体在单位时间内所经过的位移。

如果物体的速度是恒定的，那么位移与时间之间的关系可以用简单的公式来表示。

当物体的速度恒定时，位移与时间之间的关系可以用以下公式表示：Δx = v × t其中，Δx表示位移，v表示速度，t表示时间。

这个公式的意思是物体的位移等于物体的速度乘以物体运动所经过的时间。

如果物体的速度不是恒定的，那么位移与时间之间的关系就需要通过速度的变化来描述。

在这种情况下，可以使用平均速度来表示位移与时间之间的关系。

平均速度是物体在一段时间内的位移与时间的比值。

如果物体在时间t1内的位移为x1，在时间t2内的位移为x2，那么位移与时间之间的关系可以用以下公式表示：Δx = (x2 - x1) / (t2 - t1)这个公式的意思是物体的位移等于物体在时间t2和t1之间的位移差除以时间t2和t1之间的时间差。

除了上述的线性关系，位移与时间之间的关系还可以通过其他的函数关系来描述。

例如，当物体的加速度恒定时，位移与时间之间的关系可以用以下公式表示：Δx = v0 × t + (1/2) × a × t^2其中，Δx表示位移，v0表示物体的初始速度，t表示时间，a表示物体的加速度。

这个公式的意思是物体的位移等于物体的初始速度乘以时间加上物体的加速度乘以时间的平方的一半。

除了上述的公式，位移与时间之间的关系还可以通过其他的函数关系来描述，这些函数关系会因物体运动的特性而不同。

例如，当物体的加速度不恒定时，位移与时间之间的关系可以通过物体的加速度函数来描述。

总结起来，位移与时间之间的关系可以通过不同的公式来描述，这些公式的选择取决于物体运动的特性以及速度和加速度是否恒定。

位移-时间关系2021at t v x +=是匀变速直线运动的位移-时间关系，也可以称之为位移-时间函数，简称位移（而不是路程）公式。

关于这个公式，我们也可以进行以下两方面的探讨：1. 公式的推导：我们知道位移等于平均速度乘以时间，即：t v =x ，而平均速度又等于初速度加末速度除以2，即：20v v v +=，所以，200002122x at t v t at v v t v v t v +=++=+== 你可能认为 t v 0x =，事实上，若物体做匀加速直线运动，它越来越快，这样算得结果就会比实际的位移小，同理若写成 vt =x ，这样结果又会偏大，所以这里的速度既不能取初速度，也不能取末速度，只能取这一过程的平均速度。

又考虑到物体做匀变速直线运动，它的速度均匀地变化，所以平均速度就等于初速度加末速度除以2，很好理解。

只有物体的速度均匀地变化，或者说物体做匀变速直线运动时，某一过程的平均速度才等于这一过程初、末速度的平均值，否则，上述结论是不成立的。

这个也好理解，假设我们想知道这次月考咱们班物理总分是多少?有一个简单的方法就是物理平均分乘以总人数，而且平均分就等于最高分加最低分除以2，看是不是很简单？这样操作可不可以？你可能意识到了，这样做有时是不可以的，除非咱们班这次的物理成绩与学生人数是按一次函数规律变化的。

例如咱（班级人数40人）的物理成绩从低分到高分依次是2分、4分、6分、8分……80分，这样算是没有问题的。

2. 2021at t v x +=公式中的x 是位移，而不是路程。

例如，有物体做匀减速直线运动，初速度为30 m/s ，加速度为-10 m/s 2，也就是说物体的速度每秒增加-10 m/s ，代入位移公式即可求得它在前1、3、5、7秒内的位移分别如下：25m s)1(m/s 10(21s 130m/s 212221101=⨯-⨯+⨯=+=）at t v x 45m s)3(m/s 10(21s 330m/s 212222202=⨯-⨯+⨯=+=）at t v x 25m s)5(m/s 10(21s 530m/s 212223303=⨯-⨯+⨯=+=）at t v x 5m 3s)7(m/s 10(21s 730m/s 212224404-=⨯-⨯+⨯=+=）at t v x当然还可以这样算，我们以求前7秒内的位移为例，因为物体的加速度为-10 m/s 2，所以它的速度每秒减小10 m/s ，初速度为30 m/s ，经3时间速度即可以减为0，或者说3 s 末物体静止，不难算出这一过程物体发生的位移为x 2=45m ；接下来物体还得运动4秒，速度变化的快慢还是-10 m/s 2，所以，4s 末物体的速度为-10 m/s ，5 s 末物体的速度为-20 m/s ，7 s 末物体的速度为-40 m/s 。

匀变速直线运动的位移与时间的关系【知识整合】1．匀变速直线运动的位移公式 根据平均速度的定义式，做任何变速运动的位移都可以表示为t v x =，则匀变速直线运动的位移公式为2001()/22t s vt v v t v t at ==+=+ （1）位移公式说明匀变速直线运动的位移与时间是二次函数关系，式中的0v 是初速度，时间t 应是物体实际运动的时间。

（2）在取初速度0v 方向为正方向的前提下，匀加速度直线运动a 取正值，匀减速直线运动a 取负值；计算的结果0s >，说明位移的方向与初速度的方向相同；0s <说明位移的方向与初速度的方向相反。

（3）对于初速度为零（00v =）的匀变速直线运动，位移公式为211122s v t at == 即位移s 与时间t 的二次方成正比。

（4）速度—时间图像下的面积表示位移的大小，且t 轴上方的面积表示正位移，t 轴下方的面积表示负位移。

2.逆向转换法将末速度为 0的匀减速直线运动转化初速度为0的匀加速直线运动，进行计算【典例分析】例1某做直线运动的质点的位移随时间变化的关系式为242,x t t x =+与t 的单位分别是m 和s ，则质点的初速度和加速度分别是（ ）A ．4/m s 和22/m sB ．0和42/m sC ．4/m s 和42/m sD ．4/m s 和0例2一辆汽车在笔直的公路上做匀变速直线运动，该公路每隔15m 安置一个路标，如图1所示，汽车通过AB 两相邻路标用了2s ，通过BC两路标用了3s ，求汽车通过A 、B 、C 三个路标时的速度。

例3以18/m s 的速度行驶的汽车，紧急刹车后做匀减速直线运动，其加速度大小为62/m s ，求：（1）汽车在2s 内通过的距离；（2）汽车在6s 内通过的距离。

图1例4有一个做匀变速直线运动的质点，它在两段连续相等时间内通过的位移分别是24m 和64m ，连续相等的时间为4s ，求质点的初速度和加速度的大小。

物理匀变速直线运动的位移和时间的关系物理中的匀变速直线运动是指物体在相等时间内位移的增量是逐渐增加的运动。

在这种运动中，位移与时间之间存在着一定的关系。

我们来了解一下匀变速直线运动的基本概念。

匀变速直线运动是指物体在相等时间间隔内，其位移的增量是逐渐增加的运动。

这意味着物体在单位时间内的位移是不断增加的，即速度在变化。

而这种变化是有规律可循的。

在匀变速直线运动中，位移与时间之间的关系可以通过速度来描述。

速度是指物体在单位时间内位移的增量，可以用公式v = Δx/Δt来表示，其中v表示速度，Δx表示位移的增量，Δt表示时间的增量。

根据速度的定义，我们可以得出位移与时间的关系。

假设物体的初始位移为x0，初始时间为t0，位移的增量为Δx，时间的增量为Δt，那么根据速度的定义，我们可以得到以下关系：v = Δx/Δt将上述公式稍作变形，可以得到：Δx = v * Δt这个公式表明，位移的增量等于速度乘以时间的增量。

也就是说，位移的增量与时间的增量成正比，且比例系数为速度。

进一步地，我们可以将上述公式进行积分，得到位移与时间之间的具体关系。

假设物体的初始位移为x0，初始时间为t0，位移为x，时间为t，速度为v，则有：x - x0 = ∫(v dt)这个公式表示，位移与时间之间的关系可以通过速度的积分来描述。

通过对速度关于时间的积分，我们可以得到位移与时间之间的具体关系。

匀变速直线运动的位移与时间之间存在着一定的关系。

位移的增量等于速度乘以时间的增量，而位移与时间之间的具体关系可以通过速度的积分来描述。

这些关系可以帮助我们更好地理解和分析匀变速直线运动的特性和规律。

希望本文对您有所帮助，谢谢阅读！。

高一物理时间和位移笔记时间和位移是物理中非常重要的概念，两者也是密切相关的。

1. 时间：时间是一个基本的物理量，用来描述物体运动的持续时间。

在物理中，时间通常用t表示，单位是秒（s）。

时间的测量是比较相对的，即一段时间是相对于其他时间的长度来衡量的。

2. 位移：位移是物体在一段时间内运动的变化距离和方向。

位移用Δx表示，单位是米（m）。

位移是一个矢量量，它包含了大小和方向两个方面的信息。

3. 平均速度：平均速度是指物体在一段时间内所走过的距离与时间的比值。

平均速度用v表示，单位是米每秒（m/s）。

平均速度的计算公式为v = Δx / Δt，其中Δx是位移，Δt是时间。

4. 瞬时速度：瞬时速度是指物体在某一瞬间的短时间间隔内所走过的位移距离。

瞬时速度可以通过计算物体的瞬时位移与这段瞬间的时间间隔的比值来获得。

5. 平均加速度：平均加速度是指物体在一段时间内速度变化的大小与时间的比值。

平均加速度用a表示，单位是米每秒的平方（m/s^2）。

平均加速度的计算公式为a = Δv / Δt，其中Δv是速度的变化量，Δt是时间。

6. 瞬时加速度：瞬时加速度是指物体在某一瞬间的短时间间隔内速度变化的大小。

瞬时加速度可以通过计算物体的瞬时速度的变化率来获得。

7. 物体的运动可以分为匀速运动和变速运动两种情况。

在匀速运动中，物体的速度始终保持不变，即加速度为零；而在变速运动中，物体的速度会随时间变化而变化，即加速度不为零。

总结起来，时间和位移是描述物体运动的两个重要概念。

时间描述了物体运动的持续时间，而位移描述了物体在一段时间内的距离和方向的变化。

速度和加速度则是与时间和位移密切相关的物理量，它们描述了物体运动的快慢和变化情况。

等分时间和等分位移的公式在物理学中，我们经常遇到需要等分时间或等分位移的情况。

这些情况下，我们可以利用一些公式来帮助我们计算和解决问题。

让我们来看看等分时间的公式。

当我们需要在一段时间内等分成n 个小时间段时，我们可以使用以下公式：Δt = (t₂ - t₁) / n其中，Δt表示等分的小时间段的长度，t₂表示时间段的结束时间，t₁表示时间段的开始时间，n表示我们要等分成的小时间段的个数。

举个例子，假设我们有一个时间段从8:00到9:00，我们想要将这个时间段等分成6个小时间段。

我们可以使用上述公式来计算每个小时间段的长度。

假设t₂为9:00，t₁为8:00，n为6，带入公式计算得到：Δt = (9:00 - 8:00) / 6 = 1/6小时 = 10分钟所以，我们可以将这个时间段等分成6个小时间段，每个小时间段的长度为10分钟。

接下来，让我们来看看等分位移的公式。

当我们需要在一个位移中等分成n个小位移时，我们可以使用以下公式：Δx = (x₂ - x₁) / n其中，Δx表示等分的小位移的长度，x₂表示位移的结束位置，x₁表示位移的开始位置，n表示我们要等分成的小位移的个数。

举个例子，假设我们有一段位移从0到100，我们想要将这段位移等分成5个小位移。

我们可以使用上述公式来计算每个小位移的长度。

假设x₂为100，x₁为0，n为5，带入公式计算得到：Δx = (100 - 0) / 5 = 20所以，我们可以将这段位移等分成5个小位移，每个小位移的长度为20。

通过上述公式，我们可以在物理学中解决一些等分时间和等分位移的问题。

这些公式可以帮助我们计算小时间段的长度和小位移的长度，从而更好地理解和分析物理现象。

需要注意的是，这些公式仅适用于等分时间和等分位移的情况。

在其他情况下，我们可能需要使用不同的公式来计算和解决问题。

因此，在应用公式时，我们需要根据具体情况选择合适的公式进行计算。

总结起来，等分时间和等分位移的公式可以帮助我们在物理学中解决一些问题。