菲涅尔双面镜干涉法
- 格式:docx
- 大小:789.55 KB
- 文档页数:5


菲涅尔双棱镜实验报告一、实验目的本实验旨在通过菲涅尔双棱镜实验,观察光的干涉现象,测量光波波长,并加深对光的波动性的理解。
二、实验原理菲涅尔双棱镜是由两个折射角很小的直角棱镜底边相接而成。
当一束单色平行光垂直照射在双棱镜的棱脊上时,经双棱镜折射后,其折射光可视为由两个虚光源发出的相干光。
这两个虚光源发出的光在空间相遇,会产生干涉条纹。
根据光的干涉原理,相邻两亮条纹或暗条纹之间的距离与光波波长、双棱镜到观察屏的距离以及两虚光源之间的距离有关。
通过测量条纹间距、双棱镜到观察屏的距离以及两虚光源之间的距离,就可以计算出光波波长。
三、实验仪器钠光灯、菲涅尔双棱镜、凸透镜、测微目镜、光具座等。
四、实验步骤1、调节光具座上各元件,使其共轴。
将钠光灯、双棱镜、凸透镜和测微目镜依次放置在光具座上,调节它们的高度和位置,使它们的中心大致在同一水平轴线上。
2、调整钠光灯的位置,使其发出的平行光垂直照射在双棱镜的棱脊上。
3、移动凸透镜,使通过双棱镜折射后的光线在测微目镜中形成清晰的像。
4、调节测微目镜,使其十字叉丝清晰,并使干涉条纹清晰可见。
5、测量条纹间距。
通过测微目镜测量相邻十条亮条纹或暗条纹之间的距离,多次测量取平均值。
6、测量双棱镜到测微目镜的距离。
使用直尺测量双棱镜到测微目镜的距离,同样多次测量取平均值。
7、测量两虚光源之间的距离。
利用凸透镜成像法测量两虚光源之间的距离。
五、实验数据及处理1、条纹间距的测量测量次数 1:_____mm测量次数 2:_____mm测量次数 3:_____mm平均值:_____mm2、双棱镜到测微目镜的距离的测量测量次数 1:_____cm测量次数 2:_____cm测量次数 3:_____cm平均值:_____cm3、两虚光源之间的距离的测量测量次数 1:_____mm测量次数 2:_____mm测量次数 3:_____mm平均值:_____mm根据实验原理,光波波长的计算公式为:\\lambda =\frac{d \times \Delta x}{D}\其中,\(\lambda\)为光波波长,\(d\)为两虚光源之间的距离,\(\Delta x\)为条纹间距,\(D\)为双棱镜到测微目镜的距离。

菲涅耳双棱镜干涉实验
菲涅耳双棱镜干涉实验是一种利用干涉现象观察光波特性的实验。
在此实验中,将一束单色光通过一个菲涅耳双棱镜,光线将被分成两束,每一束光线都沿不同的路径传输,在某一点再次相交而产生干涉。
在干涉产生的区域,由于两束光线在该区域的相位差,干涉有时是增强的,有时是减弱的。
这种干涉可观察到明暗相间的条纹,称为干涉条纹。
通过观察干涉条纹的形态和位置,可以确定光波的波长和相位差。
菲涅耳双棱镜干涉实验在工业、医学、物理学、测量学、地质学和天文学等领域有广泛的应用。

菲涅尔双镜条纹间距公式推导
菲涅尔双镜条纹间距公式推导如下:
在双棱镜干涉实验中:
所用双棱镜折射角a很小(a=△0/LO)并且主截面垂直于作为光源的狭缝S:借助于双棱镜的折射,将自S发出的波阵面分为向不同方向传播的两个部分,这两部分波阵面好象自图中所示虚光源S1和S2点发出的一样在两波相交的区域P1P'2产生干涉两相干光源的距离t可由折射角为a的棱镜对光线产生的偏向角公式=(n-1)a 算出:t =2(n -1)aL1 ①
其中n为棱镜玻璃折射率
将t及值(L=L1+L2)代入双缝干涉间隔公式L=L/t中,则得双棱镜干涉相邻条纹间距:ΔL=(L1+L2)λ/2(n -1)aL12。

菲涅耳双棱镜干涉实验一、实验目的了解菲涅耳双棱镜干涉的原理,掌握用这种棱镜来测量波长的方法 二、实验仪器菲涅耳双棱镜 读数显微镜 会聚透镜 狭缝屏 光具座 氦氖激光器 三、实验原理菲涅耳双棱镜是利用分波前的方法实现干涉的常用器件。
它是由玻璃制成的等腰三角棱镜,有两个小的约为1℃锐角和一个大的钝角。
从狭缝S 出射光束经过双棱镜的折射产生狭缝的两个虚光源1S 和2S ,它们是相干光源。
经过双棱镜的两束折射光在重合区域将发生干涉,结果在屏上形成明暗相间的直线形的干涉条纹。
任意相邻的两亮纹或者暗纹之间的间隔δ是:λδdD =上式中D 为虚光源到屏之间的距离,d 为两虚光源的间距,λ是光源的波长。
由此可知,我们只要测定D d δ就可测出光源的波长。
四、实验步骤1. 先将激光束调节到与导轨的棱脊相平行:移动观察屏调节激光束的俯仰角度使得在观察屏的光斑位置不发生变化。
2. 然后将读数显微镜安装到导轨上使得激光光斑落在物镜的中央位置。
3. 接着将透镜安装到导轨上使激光光斑落在物镜的位置不变就说明它们共轴。
4. 再将狭缝添置到导轨上,最后把双棱镜安装到导轨上,让双棱镜的平面正对激光束,倘若反射的光斑从原路返回,则说明光束是垂直入射的,水平调节支架的底座使得双棱镜平分激光束。
5. 现在要做的工作就是将激光器换成钠光灯,再做微调就可以精确对准了。
—6. 将狭缝调小些,调节三棱镜的棱边与狭缝严格平行,此时可从读数显微镜里头看到直线状明暗相间的干涉条纹。
7. 移动透镜让狭缝的虚像经透镜成两次像,测出两次所称像的间隔分别为l 和'l ,则虚光源的间隔'll d =。
8. 测好虚光源的间隔数据后,将会聚透镜放置在狭缝的前面可使得光线更为集中入射到狭缝,并将读数显微镜的叉丝其中一条旋转到与干涉条纹相平行,记下读数显微镜的位置。
9. 进行测量,每隔5条暗条纹测一次,并记下相应的读数,多读几个数据。
10. 挪去双棱镜,移动读数显微镜靠近狭缝知道看清狭缝的边缘,记下此时的读数显微镜的位置,那么狭缝离干涉条纹形成位置的距离就等于这两次读数显微镜位置的差值的绝对值。
实验五 菲涅耳双棱镜干涉[实验目的]1. 观察和研究菲涅耳双棱镜产生的干涉现象; 2. 测量干涉滤光片的透射波长(λ0)。
[仪器和装置]白炽灯,干涉滤光片,可调狭缝,柱面镜,菲涅耳双棱镜,双胶合成像物镜,测微目镜。
[实验原理]如图1a 所示,菲涅耳双棱镜装置由两个相同的棱镜组成。
两个棱镜的折射角α很小,一般约为5 ~ 30'。
从点(或缝)光源S 发出的一束光,经双棱镜折射后分为两束。
从图中可以看出,这两折射光波如同从棱镜形成的两个虚像S 1和S 2发出的一样。
S 1和S 2构成两相干光源,在两光波的迭加区产生干涉。
a、从图1b 看出,若棱镜的折射率为n ,则两虚像S 1、S 2之间的距离a n l d )1(2-= (5-1)干涉条纹的间距λan l l l e )1(2'-+=(5-2)式中,λ为光波的波长。
对于玻璃材料的双棱镜有n =1.50,则λal l l e '+=(5-3) 可得到e l l la'+=λ (5-4) 在迭加区内放置观察屏E ,就可接收到平行于脊棱的等距直线条纹。
若用白光照明,可接收到彩色条纹。
对于扩展光源,由图2可导出干涉孔径角:''l l al +=β (5-5) 和光源临界宽度:⎪⎭⎫⎝⎛+=='1l l a b λβλ (5-6) 从式(5-5)和(5-6)看出,当l'=0时,β=0,则光源的临界宽度b 变为无穷大。
此时,干涉条纹定域在双棱镜的脊棱附近。
b 为有限值时,条纹定域在以下区域内:λαλ-≤b ll ' (5-7)a) 图 1 双棱镜干涉原理图[内容和步骤]1.调整光路,观察和研究双棱镜干涉现象(1) 按图3所示,将光学元件置于光学平台上。
调整光学元件,使其满足同轴等高的要求。
(2) 取l ≈200mm ,l '≈1200mm ,按λ=550nm ,α=30',n =1.50计算出b 的数值。
实验七 菲涅耳双棱镜干涉一、实验目的1.掌握菲涅耳双棱镜获得双光束干涉的方法2.观察双棱镜产生的双光束干涉现象,进一步理解产生干涉的条件3.结合杨氏实验理解菲涅耳双棱镜实验的原理,弄清有关物理量之间的关系二、实验原理菲涅耳双棱镜实验是一种分波阵面的干涉实验,实验装置简单,但设计思想巧妙。
它通过测量毫米量级的长度,可以推算出小于微米量级的光波波长。
1881年菲涅耳用双棱镜实验和双面镜实验再次证明了光的波动性质,为波动光学奠定了坚实的基础。
如图7—1所示,将一块平玻璃板的上表面加工成两楔形,两端与棱脊垂直,楔角较小(一般小于1度)。
当单色光源照射在双棱镜表面时,经其折射后形成两束好像由两个光源发出的光,即两列光波的频率相同,传播方向几乎相同,相位差不随时间变化,那么,在两列光波相交的区域内,光强的分布是不均匀的,满足光的相干条件,称这种棱镜为双棱镜。
菲涅儿利用图7—2所示的装置,获得了双光束的干涉现象。
图中双棱镜AB 是一个分割波前的分束器。
从单色光源M 发出的光波,经透镜L 会聚于狭缝S ,使S 成为具有较大亮度的线状光源。
当狭缝S 发出的光波投射到双棱镜AB 上时,经折射后,其波前便被分割成两部分,形成沿不同方向传播的两束相干柱波。
通过双棱镜观察这两束光,就好像它们是由1S 和2S 发出的一样,故在其相互交叠区域21P P 内产生干涉。
如果狭缝的宽度较小,双棱镜的棱脊与光源平行,就能在白屏P 上观察到平行与狭缝的等间距干涉条纹。
x 图7—2棱脊端面楔角图7—1设'd 代表两虚光源1S 和2S 间的距离,d 为虚光源所在的平面(近视地在光源狭缝S 的平面内)至观察屏的距离,且'd <<d ,干涉条纹宽度为x δ,则实验所用光波波长λ可由下式确定x d d δλ'= (7—1) (7—1)式表明,只要测出'd 、d 和x δ,便可计算出光波波长。
通过使用简单的米尺和测微目镜,进行毫米级的长度测量,推算出微米级的光波波长,所以,这是一种光波波长的绝对测量。
实验38 光的干涉实验(三)——双棱镜干涉实验利用菲涅尔(A.J.Fresnel )双棱镜可以实现光的干涉。
菲涅尔双棱镜干涉实验曾在历史上为确立光的波动学说起到过重要作用,它提供了一种用简单仪器测量光的波长的方法。
【重点、难点提示】光的波动性;双棱镜干涉现象;双棱镜干涉测波长;光路的调整【目的和要求】1.观察由双棱镜所产生的干涉现象,并测定单色光波长。
2.加深对光的波动性的了解,学习调节光路的一些基本知识和方法。
【实验仪器】1.光源;2.光具座;3.狭缝;4.双棱镜;5.凸透镜;6.测微目镜。
【实验原理】双棱镜形状如图6.38.1所示,其折射角很小,因而折射棱角接近180 。
今设有一平行于折射棱的缝光源S 产生的光束照射到双棱镜上,则光线经过双棱镜折射后,形成两束犹如从虚光源S 1和S 2发出的相干光束。
它们在空间 传播时有一部分重叠而发生干涉(画有双斜线的区域), 图6.38.1 双棱镜示意图 结果在屏幕E 上显现干涉条纹,如图6.38.2所示。
SS 1S 2O E图6.38.2 双棱镜产生的相干光束示意图干涉条纹以O 点为对称点上下交错地配置。
用不同的单色光源作实验时,各亮条纹的距离也不同,波长越短的单色光,条纹越密;波长越长的单色光,条纹越稀。
如果用白色光作实验,则只有中央亮条纹是白色的,其余条纹在中央白条纹两边,形成由紫而红的彩色条纹。
利用干涉条纹可测出单色光的波长。
单色光的波长λ由下式决定x Da ∆=2λ (6.38.1) 式中2a 为S 1S 2间的距离、D 为S 1S 2到E 幕的距离,∆x 为任意两条暗条纹之间距离。
【实验内容与步骤】一、调整光路 本实验的具体装置如图6.38.3所示,由光源发出的光通过狭缝变为缝光源,再经双棱镜折射,就可获得两个相干光源,因而能在测微目镜里看到干涉条纹。
测微目镜的构造和使用参见第三章§3.3.4“常用光学仪器”4。
图6.38.3 双棱镜干涉装置图1.开亮光源,先将狭缝稍放大点,观察光通过狭缝后是否照射到双棱镜的棱背和射入目镜,若不能,则须调整光源及目镜的位置以达到上述目的。
全息光栅制作方法的设计和研究
全息光学元件(HOE)是指采用全息方法(包括计算全息方法)制作的,可以完成准直、聚焦、分束、成像、光束偏转光
束扫描等功能的元件。
在完成上述功能时,它不是基于光的反射
和规律折射,而是基于光的衍射和干涉原理。
所以全息光学元件
又称为衍射元件。
常用的全息光学元件包括全息透镜、全息光栅
和全息空间滤波器等。
全息光栅是一种重要的分光元件。
作为光
谱分光元件,与传统的刻划光栅相比,具有以下优点:光谱中
无鬼线、杂散光少、分辨率高、有效孔径大、生产效率高、价格
便宜等,已广泛应用于各种光栅光谱仪中,供科研、教学、产
品开发之用。
作为光束分束器件,在集成光学和光通信中用作
光束分束器、光互连器、耦合器和偏转器等。
在光信息处理中,
可作为滤波器用于图像相减、边沿增强等。
本实验主要进行平
面全息光栅的设计和制作实验。
一. 实验目的
1.学习掌握制作全息光栅的原理和方法。
2.学习掌握制作全息复合光栅的原理和方法,观察其莫尔条
纹。
3.设计制作全息光栅并测出其光栅常数(要求所制作的光栅
不少于100条/毫米)
二、实验原理
1.全息光栅
全息光学元件是指基于光的衍射和干涉原理,采用全息方法
制作的,可以完成准直、聚焦、分束、成像、光束偏转、光束扫
描等功能的元件。
光全息技术主要利用光相干迭加原理,简单讲
就是通过对复数项(时间项)的调整,使两束光波列的峰值迭加,峰谷迭加,达到相干场具有较高的对比度的技术。
常用的全息光
学元件包括全息透镜、全息光栅和全息空间滤波器等。
其中全息
光栅就是利用全息照相技术制作的光栅,在科研、教学以及产品开发等领域有着十分广泛用途。
一般在光学稳定的平玻璃坯件上涂上一层给定型厚度的光致抗蚀剂或其他光敏材料的涂层,由激光器发生两束相干光束,使其在涂层上产生一系列均匀的干涉条纹,光敏物质被感光,然后用特种溶剂溶蚀掉被感光部分,即在蚀层上获得干涉条纹的全息像,所制得为透射式衍射光栅。
如在玻璃坯背面镀一层铝反射膜,可制成反射式衍射光栅。
作为光谱分光元件,全息光栅与传统的刻划光栅相比,具有以下优点:光谱中无鬼线、杂散光少、分辨率高、有效孔径大、价格便宜等;全息光栅已广泛应用于各种光栅光谱仪中。
作为光束分束器件,全息光栅在集成光学和光学通信中用作光束分束器、光互连器、耦合器和偏转器等;在光信息处理中,可作为滤波器用于图像相减、边沿增强等。
2.光栅条纹
光栅,也称衍射光栅,是基于多缝衍
射原理的重要光学元件。
光栅是一块刻有
大量平行等宽、等距狭缝(刻线)的平面
玻璃或金属片,其狭缝数量很大,一般每
毫米几十至几千条。
单色平行光通过光栅
会形成暗条纹很宽、明条纹很细的图样,
而这些锐细而明亮的条纹称作谱线。
谱线
的位置随波长而异,因此当复色光通过光
栅时,不同波长光所产生的谱线在不同位
置出现而形成光谱。
也就是说,光通过光
栅形成光谱是单缝衍射和多缝干涉的共同
结果(如图1)。
3.光栅方程 光栅方程sin d k θλ=描述了光栅结构
与光的入射角和衍射角之间的关系,它表示当衍射角θ满足sin d k θλ=的时候发生干涉加强现象,其中d 即为光栅常数。
而当光以入射角i θ入射时,光栅方程写为 (sin sin )i d k θθλ+=。
4.光栅常数
图1 光通过光栅形成光谱
光栅常数是光栅两刻线之间的距离。
一个理想的光栅可以认为由一组等间距的
无限长无限窄的狭缝组成,
而狭缝之间的间距称为光栅
常数,在图2中用d 表示。
全息光栅的光栅常量大
小取决于两束平行光与全息
干板的夹角。
设两列相干的
平行光分别以1θ和2θ角入射
全息干板,则光栅常数
12(sin sin )d λθθ=+;若两
列相干的平面波的夹角
12θθθ=+很小,则光栅常数d λθ≈。
5.全息光栅制作原理
两束具有特定波面形状的光束干涉,在记录平面上形成亮暗相间的干涉条纹,用全息记录介质记录干涉条纹,经处理得到全息光栅。
而采用不同波面形状的光束或不同的全息记录介质和处理过程可以得到不同类型或不同用途的全息光栅。
根据两束相干平行光产生机理的不同,制作全息光栅的光路可分为两类。
一种称为“分振幅法” ,该类方法是利用分束镜使一束光波一分为二;另一类称为 “分波面法” ,该类方法是利用一定的仪器将一束光波的波面一分为二。
其中在实际制作时通常采取分振幅法,但分振幅法制作全息光栅光栅常数通常较小。
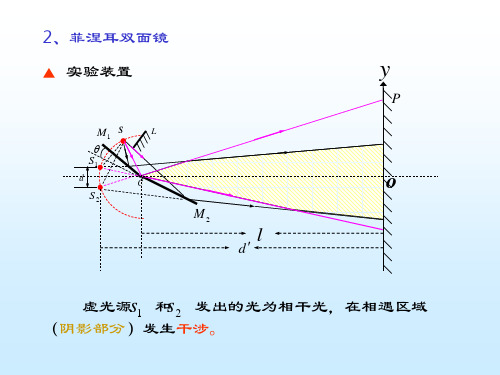
菲涅尔双面镜是分波面获的相干光常用的实
验仪器,其典型光路如图4 所示。
图中S 为缝光
源,M 1、M 2为菲涅尔双面镜。
其干涉条纹近似为等
图2 光栅光路
图3 菲涅尔双面镜
间距的平行直条纹,将其进行记录便可制得全息光栅。
菲涅尔双面镜干涉法的制作光路如图5所示。
激光器发出的
光经扩束准直后得到平行光,然后入射到菲涅尔双面镜上,其反
射光在全息干板上进行相干叠加。
光栅常数决定
于双镜的夹角。
该方法具有与杨氏双缝干涉法相似的优点,
光程差小、干涉效果好,光栅常数易于控制且光
栅常数较大,但其光路调节复杂,如果用准直透
镜则干涉光斑面积较小,如果不用准直透镜则相
干光仅为近平行光。
图4菲涅尔双面镜干涉法三、实验步骤
1.制作全息光栅
(1)按照如图4摆放实验器材
(2)打开激光器,使激光器发出的光经扩束镜后得到平行光,
然后入射到菲涅尔双面镜上,其反射光在全息干板上进行相干叠
加
(3)调节双面镜的夹角以此来调节光栅常数
2.拍摄全息光栅
(1)在黑暗环境中,挡住激光束,把干片放在架子上;
(2)让激光束照射在干片上2秒,再重新挡住激光束,把干片取
下带到暗房中;
(3)把干片泡在显影液中大约10秒钟,取出,用清水冲洗;
(4)泡在定影液中约5分钟,取出,冲洗后晾干;
(5)用激光束检验冲洗好的干片,若能看见零级、一级的光斑,
说明此干片可以用于测定光栅常数
3.注意事项
(1)半导体激光器工作电压为直流电压3V,应用专用220V/3V
直流电源工作(该电源可避免接通电源瞬间电感效应产生高电压
的功能),以延长半导体激光器的工作寿命;
(2)不要正对着激光束观察,以免损坏眼睛;
(3)曝光时间要掌握好,曝光面切勿放反了;
(4)由于有多组同学一起实验,处理干片的时候切勿将干片混淆;
(5)在处理干片时注意避免光源(手机等)。