菲涅尔双棱镜干涉测波长

一、引言法国科学家菲涅尔用几个自己设计的新实验，在当时令人信服地证明了光的干涉现象的存在，这些实验之一就有他在1826年进行的双棱镜实验。

与杨氏双缝干涉借助衍射形成分波面干涉不同，它利用棱镜形成“双缝”，并用毫米级的精度测量出纳米级的精度，它的物理思想、实验方法和测量技巧至今仍值得我们学习，并且对于以后微观物理学方面的实验仍然具有巨大的作用。

在本实验中通过用菲涅尔双棱镜对纳光波长的测量，要求我们掌握光的干涉有关原理及光学测量的基本技巧，特别要学习在光学实验中计算测量结果不确定度的各种方法。

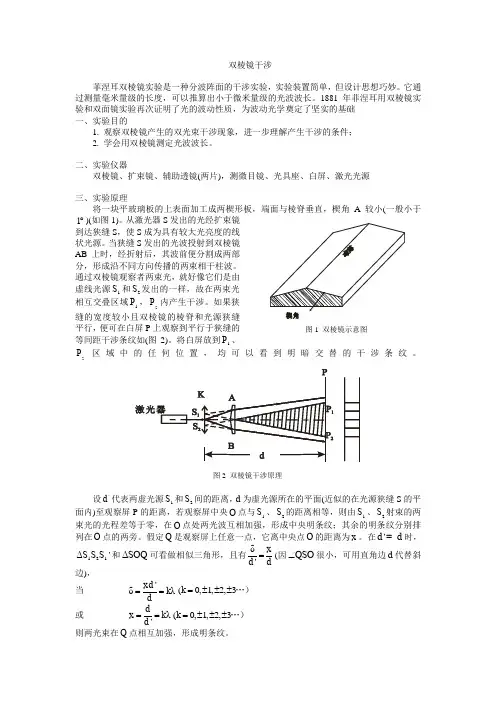
二、实验原理1)菲涅尔双棱镜实际上是一个顶角A极大的等腰三棱镜,如下图所示，当S点处的单色点光源从BC面入射时，通过ABD的光向下偏折，通过ACD的光向上偏折，形成如图所示的交叠区，并产生S1、S2两个虚的点光源，于是在交叠区两个虚光源发出的相干光发生干涉；干涉条纹间距为X=Dλ/d (1)；其中d是两个虚光源之间的间距；D是光源到观察屏的距离；λ是光的波长。

用测微目镜的分划板作为观察屏可直接读出条纹间距X的值，D可直接由导轨上的直尺读出。

观察屏 S点光源通过双棱镜的折射2)虚光源间距的测量：使用二次成像法，光路图如下图所示：在双棱镜与测微目镜之间加一个焦距为f的凸透镜L，当D>4f时，可以移动L在测微目镜中观察到两虚光源的放大像和缩小像，读出虚光源像的间距d1,d2；有几何光学可知：d=(d 1d 2) 1/2；带入即可求出虚光源间距d 的值。

（由于制图不太准，图上显示的两个焦距f 略有差异,实际是相同的）3) 实验时我们利用以上原理来对未知量条纹间距X ,及虚光源间距d ；并且将点光源换成线光源使衍射条纹由点变线，增强了条纹的亮度，方便读数测量。

三、实验装置及实验过程实验装置双棱镜、测微目镜、光具座、线光源和透镜； 右图为测微目镜的结构图：使用时调节目镜与分划板之间的距离使之能清晰地看到分划板的准线及刻度线；而后调节测微目镜与待测实像的距离使像清晰无视差并且便于测量。

用双棱镜干涉测光波波长的实验报告【实验目的】1．掌握用双棱镜获得双光束干涉的方法，加深对干涉条件的理解．2．学会用双棱镜测定钠光的波长．【实验仪器】光具座，单色光源(钠灯)，可调狭缝，双棱镜，辅助透镜(两片)，测微目镜，白屏．【实验原理】如果两列频率相同的光波沿着几乎相同的方向传播，并且它们的位相差不随时间而变化，那么在两列光波相交的区域，光强分布是不均匀的，而是在某些地方表现为加强，在另一些地方表现为减弱(甚至可能为零)，这种现象称为光的干涉．菲涅耳利用图1所示的装置，获得了双光束的干涉现象．图中AB 是双棱镜，它的外形结构如图2所示，将一块平玻璃板的一个表面加工成两楔形板，端面与棱脊垂直，楔角A 较小(一般小于10)．从单色光源发出的光经透镜L 会聚于狭缝S ，使S 成为具有较大亮度的线状光源．从狭缝S 发出的光，经双棱镜折射后，其波前被分割成两部分，形成两束光，就好像它们是由虚光源S1和S2发出的一样，满足相干光源条件，因此在两束光的交叠．区域P1P2内产生干涉．当观察屏P 离双棱镜足够远时，在屏上可观察到平行于狭缝S 的、明暗相间的、等间距干涉条纹．图1 图2 设两虚光源S1和S2之间的距离为d '，虚光源所在的平面(近似地在光源狭缝S 的平面内)到观察屏P 的距离为d ，且d d <<'，干涉条纹间距为x ∆，则实验所用光源的波长λ为 x d d ∆'=λ因此，只要测出d '、d 和x ∆，就可用公式计算出光波波长．【实验内容】1．调节共轴(1)按图1所示次序，将单色光源M ，会聚透镜L ，狭缝S ，双棱镜AB 与测微目镜P 放置在光具座上．用目视法粗略地调节它们中心等高、共轴，棱脊和狭缝S 的取向大体平行．(2)点亮光源M ，通过透镜L 照亮狭缝S ，用手执白纸屏在双棱镜后面检查：经双棱镜折射后的光束，有否叠加区P1P2 (应更亮些)?叠加区能否进入测微目镜?当移动白屏时，叠加区是否逐渐向左、右(或上、下)偏移?根据观测到的现象，作出判断，进行必要的调节使之共轴．2．调节干涉条纹(1)减小狭缝S 的宽度，绕系统的光轴缓慢地向左或右旋转双棱镜AB ，当双棱镜的棱脊与狭缝的取向严格平行时，从测微目镜中可观察到清晰的干涉条纹．(2)在看到清晰的干涉条纹后，为便于测量，将双棱镜或测微目镜前后移动，使干涉条纹的宽度适当．同时只要不影响条纹的清晰度，可适当增加狭缝S 的缝宽，以保持干涉条纹有足够的亮度．(注：双棱镜和狭缝的距离不宜过小，因为减小它们的距离，S1、S2间距也将减小，这对d '的测量不利．)3．测量与计算(1)用测微目镜测量干涉条纹的间距x ∆．为了提高测量精度，可测出n 条(10～20条) 干涉条纹的间距x ，除以n ，即得x ∆．测量时，先使目镜叉丝对准某亮纹(或暗纹)的中心，然后旋转测微螺旋，使叉丝移过n 个条纹，读出两次读数．重复测量几次，求出x ∆． (2)用光具座支架中心间距测量狭缝至观察屏的距离d ．由于狭缝平面与其支架中心不重合，且测微目镜的分划板(叉丝)平面也与其支架中心不重合，所以必须进行修正，以免导致测量结果的系统误差．测量几次，求出d ．(3)用透镜两次成像法测两虚光源的间距d '．参见图3，保持狭缝S 与双棱镜AB 的位置不变，即与测量干涉条纹间距x ∆时的相同(问：为什么不许动?)，在双棱镜与测微目镜之间放置一已知焦距为f '的会聚透镜L '，移动测微目镜使它到狭缝S 的距离f d '>4，然后维持恒定．沿光具座前后移动透镜L '，就可以在L '的两个不同位置上从测微目镜中看到两虚光源S1和S2经透镜所成的实像1S '和2S '，其中一组为放大的实像，另一组为缩小的实像．分别测得两放大像的间距1d 和两缩小像的间距2d ，则按下式即可求得两虚光源的间距值d '． d '．多测几次，取平均21d d d ='图3 (4)用所测得的x ∆、d '、d 值，代入式(7-1)，求出光源的波长λ．(5)计算波长测量值的标准不确定度．【注意事项】(1)使用测微目镜时，首先要确定测微目镜读数装置的分格精度，要注意防止回程差，旋转读数鼓轮时动作要平稳、缓慢，测量装置要保持稳定．(2)在测量d 值时，因为狭缝平面和测微目镜的分划板平面均不和光具座滑块的读数准线(支架中心)共面，必须引人相应的修正(例如，GP 一78型光具座，狭缝平面位置的修正量为42.5mm ，MCU 一15型测微目镜分划板平面的修正量为27.0mm)，否则将引起较大的系统误差．(3)测量d1、d2时，由于透镜像差的影响，将引入较大误差，可在透镜L '上加一直径约lcm 的圆孔光阑(用黑纸)以增加d1、d2测量的精确度．(可对比一下加或不加光阑的测量结果．)【思考】1．双棱镜和光源之间为什么要放一狭缝?为何缝要很窄且严格平行于双棱镜脊才可以得到清晰的干涉条纹?2．试证明公式21d d d ='THANKS致力为企业和个人提供合同协议，策划案计划书，学习课件等等打造全网一站式需求欢迎您的下载，资料仅供参考。

双棱镜干涉菲涅耳双棱镜实验是一种分波阵面的干涉实验，实验装置简单，但设计思想巧妙。

它通过测量毫米量级的长度，可以推算出小于微米量级的光波波长。

1881年菲涅耳用双棱镜实验和双面镜实验再次证明了光的波动性质，为波动光学奠定了坚实的基础 一、实验目的1. 观察双棱镜产生的双光束干涉现象，进一步理解产生干涉的条件；2. 学会用双棱镜测定光波波长。

二、实验仪器双棱镜、扩束镜、辅助透镜(两片)，测微目镜、光具座、白屏、激光光源三、实验原理将一块平玻璃板的上表面加工成两楔形板，端面与棱脊垂直，楔角A 较小(一般小于1︒)(如图1)。

从激光器S 发出的光经扩束镜到达狭缝S ，使S 成为具有较大光亮度的线状光源。

当狭缝S 发出的光波投射到双棱镜AB 上时，经折射后，其波前便分割成两部分，形成沿不同方向传播的两束相干柱波。

通过双棱镜观察者两束光，就好像它们是由虚线光源1S 和2S 发出的一样，故在两束光相互交叠区域1P ，2P 内产生干涉。

如果狭缝的宽度较小且双棱镜的棱脊和光源狭缝平行，便可在白屏P 上观察到平行于狭缝的等间距干涉条纹如(图2)。

将白屏放到1P 、2P区域中的任何位置，均可以看到明暗交替的干涉条纹。

设'd代表两虚光源1S 和2S 间的距离，d 为虚光源所在的平面(近似的在光源狭缝S 的平面内)至观察屏P 的距离，若观察屏中央O 点与1S 、2S 的距离相等，则由1S 、2S 射束的两束光的光程差等于零，在O 点处两光波互相加强，形成中央明条纹；其余的明条纹分别排列在O 点的两旁。

假定Q 是观察屏上任意一点，它离中央点O 的距离为x 。

在'd d =时，121Δ'S S S 和ΔS O Q可看做相似三角形，且有δ'x d d=(因Q S O ∠很小，可用直角边d 代替斜边)， 当 'δλx d k d==(0,1,2,3k =±±±…）或λ'd x k d ==(0,1,2,3k =±±±…）则两光束在Q 点相互加强，形成明条纹。

北京航空航天大学基础物理实验------研究性实验实验题目双棱镜干涉测钠光波长一、摘要法国科学家菲涅耳（Augustin J.Fresnel）在1826年进行的双棱镜实验证明了光的干涉现象的存在，它不借助光的衍射而形成分波面干涉，用毫米级的测量得到纳米级的精度，其物理思想、实验方法与测量技巧至今仍然值得我们学习。

二、实验原理如果两列频率相同的光波沿着几乎相同的方向传播，并且这两列光波的位相差不随时间而变化，那么在两列光波相交的区域内，光强的分布不是均匀的，而是在某些地方表现为加强，在另一些地方表现为减弱(甚至可能为零)，这种现象称为光的干涉。

菲涅尔镜双棱镜可以看作是由两块底面相接、棱角很小的直角棱镜合成。

若置单色光源S于双棱镜的正前方，则从S射来的光束通过双棱镜的折射后，变成两束相互重叠的光，这两束光放佛是从光源的两个虚像S1 和S2是两个相干光源，所以若在两束光想重叠的区域内放置一屏，即可观察到明暗相间的干涉条纹。

菲涅耳利用如图1所示装置，获得了双光束的干涉现象．图中双棱镜B是一个分割波前的分束器，它的外形结构如图2所示．将一块平玻璃板的上表面加工成两楔形板，端面与棱脊垂直，楔角较小(一般小于1°). 当狭缝S发出的光波投射到双棱镜B上时，借助棱镜界面的两次折射，其波前便分割成两部分，形成沿不同方向传播的两束相干柱波．通过双棱镜观察这两束光，就好像它们是由虚光源和发出的一样，故在两束光相互交叠区域内产生干涉．如果狭缝的宽度较小且双棱镜的棱脊和光源狭缝平行，便可在光屏上观察到平行于狭缝的等间距干涉条纹。

双棱镜的干涉条纹图设代表两虚光源和间的距离，为虚光源所在的平面(近似地在光源狭缝S的平面内)至观察屏Q的距离，且，任意两条相邻的亮（或暗）条纹间的距离为，则实验所用光波波长可由下式表示：（根据形成明、暗条纹的条件，当光程差为半波长的偶数倍时产生明条纹，当光程差为半波长的奇数倍时产生暗条纹）(1)上式表明，只要测出、和，就可算出光波波长。

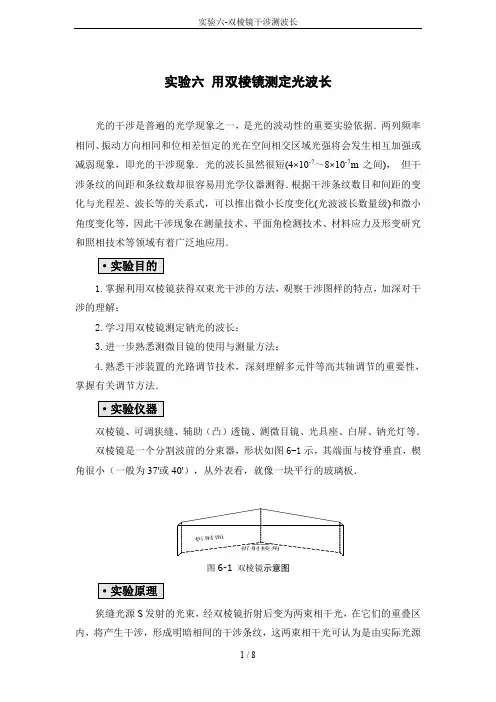
实验六用双棱镜测定光波长光的干涉是普遍的光学现象之一，是光的波动性的重要实验依据．两列频率相同、振动方向相同和位相差恒定的光在空间相交区域光强将会发生相互加强或减弱现象，即光的干涉现象．光的波长虽然很短(4×10-7～8×10-7m之间)，但干涉条纹的间距和条纹数却很容易用光学仪器测得．根据干涉条纹数目和间距的变化与光程差、波长等的关系式，可以推出微小长度变化(光波波长数量级)和微小角度变化等，因此干涉现象在测量技术、平面角检测技术、材料应力及形变研究和照相技术等领域有着广泛地应用．·实验目的1.掌握利用双棱镜获得双束光干涉的方法，观察干涉图样的特点，加深对干涉的理解；2.学习用双棱镜测定钠光的波长；3.进一步熟悉测微目镜的使用与测量方法；4.熟悉干涉装置的光路调节技术，深刻理解多元件等高共轴调节的重要性，掌握有关调节方法．·实验仪器双棱镜、可调狭缝、辅助（凸）透镜、测微目镜、光具座、白屏、钠光灯等．双棱镜是一个分割波前的分束器，形状如图6-1示，其端面与棱脊垂直，楔角很小（一般为37'或40'），从外表看，就像一块平行的玻璃板．折射面折射棱角图6-1 双棱镜示意图·实验原理狭缝光源S发射的光束，经双棱镜折射后变为两束相干光，在它们的重叠区内，将产生干涉，形成明暗相间的干涉条纹，这两束相干光可认为是由实际光源S的两个虚像S1、S2发出的，称S1、S2为虚光源．如图6-2所示．S S1 S2O Ex2a图6-2 双棱镜产生的相干光束示意图干涉条纹以O点为对称点上下展开．用不同的单色光源作实验时，各亮条纹的距离也不同，波长越短的单色光，条纹越密；波长越长的单色光，条纹越疏．如果用白色光作实验，则只有中央亮条纹是白色的，其余条纹在中央白条纹两边，形成由紫到红的彩色条纹．利用干涉条纹可测出单色光的波长．单色光的波长λ由下式决定：xDd∆=λ（6-1）式中d为两虚光源S1、S2间的距离、x∆为干涉条纹间距、D为虚光源到观察屏的距离．由（6-1）式可知，测得相邻条纹间距x∆、狭缝（光源）到测微目镜分化板的距离D及两虚光源之间的距离d，便可求出入射光的波长λ．·实验内容与步骤一、调整光路按图6-3布置光路，由光源发出的光通过狭缝变为缝光源，再经双棱镜折射，就可获得两个相干光源，因而能在测微目镜里看到干涉条纹．图6-3 双棱镜干涉装置图1．光学元件同轴等高的调节点亮光源，先将狭缝稍放大点，光具座上只放光源、狭缝、透镜，观察屏放在测微目镜位置．调狭缝中心与透镜的主光轴共轴，并使主光轴平行于导轨（共轴等高调节方法见薄透镜焦距的测定）．再放入双棱镜，并调节左右高低，使屏上出现两个强度相同、等高并列的虚光源的像．最后用测微目镜代替观察屏，调节测微目镜，使两个虚光源的像位于测微目镜中心．2．调节狭缝与双棱镜的棱脊平行调节狭缝架上的方向旋钮，观察者在双棱镜的另一侧，逆着光路透过双棱镜观察，直到同时看到两个虚光源为止． 二、调出清晰的干涉条纹取下透镜，缩小狭缝，并用目镜观察是否有干涉条纹出现．若没有，调节狭缝架上的方向旋钮，使能清楚地看出干涉条纹为止，再适当调节缝宽，使干涉条纹较清晰．三、测干涉条纹宽度∆x调节狭缝、双棱镜及测微目镜的相对位置，使目镜视野中至少能够看清15条以上的干涉条纹（条纹宽度不能过窄）．将双棱镜和测微目镜锁紧，（在后期的整个测量过程中，都不能移动双棱镜的位置）将目镜叉丝对准所选定的某条暗纹的一侧，从镜里的标尺及旋钮上记下读数x 1，再转动旋钮，使叉丝经10条暗纹的同侧，记下读数x 2，由（6-2）式即可求得x ∆，如图6-4．测3-5组，取平均．10||21x x x -=∆ （6-2）x∆四、测虚光源到观察屏的距离D双棱镜的楔角小于1°，可近似认为虚光源与狭缝在同一平面，测量过程中，我们是用测微目镜进行观察的，因此D 实际上应该为狭缝到测微目镜分划板的距离．由于狭缝所在平面与光具座滑座的中心不重合，并且测微目镜分划板平面也不与光具座滑座的中心重合，因此必须进行修正．如图6-5所示,e s Y Y D s e ∆+∆+-= （6-3）式中s Y 为狭缝滑座中心的位置；e Y 为测微目镜滑座中心的位置；s ∆为狭缝到滑座中心的距离，00.42≈∆s mm ；e ∆为测微目镜分划板到滑座中心的距离，15.37≈∆e mm ．图6-5 狭缝到观察屏的修正距离五、测两虚光源之间的距离d将测微目镜取下，插入光屏，移动光屏使狭缝到光屏的距离大于辅助透镜焦距的4倍，固定光屏．将凸透镜置于双棱镜与光屏之间，移动透镜，在光屏上可有两次呈像，此时可利用二次呈像法测虚光源的距离．测量之前要利用小像追大像法再次调共轴（调节过程见薄透镜焦距测定）．而若光具座较短或透镜焦距过小，此时虚光源经透镜只能呈一次像，此时只能用物距像距法测虚两光源的距离（两虚光源的像，应为两条亮度相同的平行线）．YeYs Ye-YsΔSΔeD1．二次呈像法两虚光源之间的距离d 需借助透镜将两条虚光源成像在测微目镜叉丝板上进行测量．当虚光源平面与测微目镜的叉丝板相距大于4倍透镜焦距值时，透镜在物、像平面之间有两个共轭成像点，透镜在这两点分别将虚光源放大或缩小成像在测微目镜的叉丝板上，用测微目镜分别测量在这两次成像时像面上的两条亮线的距离（两虚光源像的距离），两虚光源之间的距离为：21d d d = （6-4）式中为1d 为虚光源两放大像之间的距离；2d 为虚光源两缩小像之间的距离．放大像与缩小像各测5组，求其平均值．2．物距像距法在双棱镜与目镜间加上凸透镜，调节透镜高度，并前后移动透镜，在目镜中看到二虚光源S 1、S 2的像S 1'、S 2'．将目镜叉丝先后对准S 1'和S 2'，测出其间之距离为d '（如图6-6所示）．然后根据透镜成像公式（5），即可求得二虚光源的距离d ．'d BAd =（6-5） 2a S 1S 22a'S 1'S 2'AB图6-6 测虚光源成像光路图式中A 为物距（狭缝到透镜距离），B 为像距（透镜到测微目镜分划板距离）．A 和B 可从光具座上测出，注意修正狭缝和测微目镜的附加距离．·实验数据测量1.干涉条纹间距测量数据记录表 单组测量条纹间距数n =条纹序号 1 2 3 4 5 条纹位置X i (mm )条纹序号1+n2+n3+n4+n5+nd d '条纹位置X i +n (mm )X i +n - X i (mm ) 条纹间距Δx i (mm )2.狭缝平面与测微目镜叉丝面之间的距离D 测量数据表狭缝座位置 Y s (mm) 目镜座位置 Y e (mm) 狭缝面相对座中心 偏移Δs (mm) 叉丝面相对座中心 偏移Δe (mm) D =|Y e -Y s |+Δs +Δe(mm)3.两次成像法测两虚光源的间距d 数据记录表测量对象 放大像间距d 1测量 缩小像间距d 2测量第i 次 1 23412 34左像位置x li (mm)右像位置x ri (mm)d 1i / d 2i (mm)=1d mm =2d mm ==21d d d mm·实验注意事项1.严格进行共轴调节，该实验对共轴性要求非常严格，调节时可用白屏在外观察双缝所产生之光束是否亮波均匀，狭缝宽度必须适当；2.测微目镜读数时，读数鼓轮必须顺一个方向旋转，动作要平稳、缓慢，以免产生回程误差；3.测虚光源到测微目镜之距离时要注意修正；4.注意直接测量量与间接测量量单位的统一．·历史渊源与应用前景自1801年起，托马斯·杨在英国皇家学会连续宣读了数篇基于光的波动说分析干涉现象的论文，他所进行的著名的分波前双孔（缝）干涉实验以后被称为杨氏实验．杨氏实验在物理学史上有着重要的地位，将波动的空间周期性转化成干涉条纹的间距，通过对干涉条纹特性的分析得出了许多具有重要理论及实际意义的结论，从而大大丰富和深化了人们对干涉原理及光场相干性的认识．托马斯·杨让一束狭窄的日光通过不透明屏上的两个靠得很近的小缝后，再投到另一个屏上，此时屏上会出现彩色干涉条纹．历史上第一次用该方法获得了彩色干涉图样．菲涅尔双棱镜干涉实验就是在杨氏实验的基础上改进而来的，增加了相干波面的有效照明面积，从而增强了入射光强，使干涉现象明显，易于测量．该实验曾在历史上为确立光的波动学说起到了重要作用，它提供了一种直观、简捷、准确的测量光波长的方法．·与中学物理的衔接中学物理课标对双缝干涉及相关内容的要求是：1.通过实验认识光的干涉现象以及在生活、生产中的应用；2.用激光笔进行光的干涉实验；3.此实验是高考选考实验之一．·自主学习本实验的构思亮点：菲涅尔双棱镜干涉实验是分波面干涉实验的基本原型，非常巧妙地利用了光的空间相干性从自然光中获得了相干光源，不足之处是两束相干光路基本不能分开，难以实现广泛意义上的光学测量。

双棱镜干涉测波长填空题1．光的干涉现象说明光具有光具有波动性，两束光相干的条件是其频率相同，振动方向相同，相位相同或位相差恒定。

2．通常，产生相干光的方式有两种，即分振幅法和分波阵面法。

在双棱镜干涉实验中通过分波阵面法获得相干光。

3．用测微目镜测量时，为消除螺距间隙误差，应把测微目镜鼓轮沿一个方向旋转，中途不能反转。

为准确测量条纹间距及两虚光源间距，应使目镜分划板竖线与条纹及虚光源的像平行。

简答题：1.如果干涉条纹不清晰，采取那些措施可以使它变清晰？答：①狭缝宽窄合适；②狭缝与双棱镜的棱脊平行；2.用双棱镜干涉装置测单色光的波长，需要测哪些物理量？如何测得这些物理量？答：双棱镜干涉装置测单色光的波长公式为，我们需要测量相邻两明条纹的间距∆x，α是两相干光源的间距，直接测量相干光源的大像间距b和小像间距b'，即可求出α，，狭缝到测微目镜之间的距离D。

∆X合α可用测微目镜测量；D可从光轨上读出。

3. 本实验干涉条纹和测微目镜分划板之间是否存在视差？为什么？答：本实验干涉条纹和测微目镜分划板之间不存在视差。

因为本实验的干涉条纹为非定域条纹，在两相干光束相交叠的区域内，处处都有干涉条纹。

测微目镜置于干涉场内任何地方，都有干涉条纹落在分划板上，所以干涉条纹和分划板之间不存在视差，测量时不需做“消视差”调节。

菲涅尔双棱镜数据处理数据表格, mm干涉条纹间距实验数据2：, 相干光源间距实验数据3：狭缝滑块位置: 71.65cm 测微目镜滑块位置: 138.15cm 狭缝平面至滑块中心修正值=3.5cm测微目镜分划板至滑块中心修正值= 651.0mm数据处理及不确定度计算：1.干涉条纹间距d的不确定度（测微目镜仪器误差）2.相干光源间距a的不确定度对线误b=1.384mm, =0.414mm3.D的不确定度光轨上米尺的读数误差=1mm4.计算单色光波长及不确定度5.实验结果：。