预习思考题_用双棱镜测钠光波长
- 格式:doc
- 大小:25.50 KB
- 文档页数:1

北京师范大学物理实验教学中心 基础物理实验 预习思考题
【实验题目】用菲涅耳双棱镜测量钠光波波长
1. 双棱镜是怎样实现双光束干涉的?干涉条纹是怎样分布的?干涉条纹的宽度、在视野中
的数目由哪些因素决定?
试验原理:菲涅尔双棱镜可以看成是有两块底面相接、棱角很小的直角棱镜合成。
若置单色单色光源S0于双棱镜的正前方,则从S0射来的光束通过双棱镜的折射后,变为两束相重叠的光,这两束光仿佛是从光源S0的两个虚像S1和S2射出的一样。
由于S1和S2是两个相关光源,所以若在两束相重叠的区域内放置一个屏,即可观察到明暗相间的干涉条纹。
干涉条纹的分布:基本成等宽分布。
条纹宽度:干涉条纹的间距与光源的波长成正比。
条纹数目影响因素:在视野中的数目由光源的波长和光源、双棱镜和屏幕之间的相对距离决定。
2. 在实验时,双棱镜和光源之间为什么要放一狭缝?为什么狭缝很窄时,才可以得到清晰的
干涉条纹?
放一狭缝:保证通过双棱镜折射的两束光来自同一光源,射出的两束光是相干的。
狭缝要很窄:如果狭缝不够窄,来自狭缝两个边缘的光会分别通过双棱镜折射,不能保证光源的相干性。
3. 光路调整的基本原则是什么?
狭缝、凸透镜、目镜、透镜、双棱镜等各个元件等高共轴。
4. 画出光路图,试证明公式21'd d d 。
(d ′为两虚光源的距离;d1、d2分别为两个虚光
源的放大的像和缩小像的距离)
成绩(满分20 分):。


/d U ud x D d ⋅=∆=,λ,UDx u d x D d ∆=∆=/λ222/22)()()()()(/v u u u du x u D u u v u d x D +++∆+=∆λλ双棱镜干涉测光波波长[预习思考题]1、公式 中各量的物理意义是什么?实验中需测哪些物理量?答:二式中各量的物理意义:λ是待测光波长;d 是狭缝的两个虚像之间的距离;D 为狭缝到观察屏的距离;ΔX 为干涉条纹间距;U 为物距(狭缝到透镜的距离);υ为像距(透镜到测微目镜的距离。
目镜视场中有d 的像); d /为虚光源间距d 的像。
实验中需要测量的量有:D 、ΔX 、U 、υ、d 。
2、导出λ的不确定度传播式。
解:对上式取对数,求偏导,作方均根处理后即可得到:3、导轨上的光学器件都等高共轴后,仍看不到干涉条纹,可能的原因主要有哪两个?答:① 狭缝过宽;② 双棱镜棱脊未与狭缝平行。
4、使用测微目镜时应注意什么?答:① 消除目的物与叉丝之间的视差(二者处于同一平面);② 消除空回误差(鼓轮应沿一个方向转动,中途不能反转);③ 叉丝的移动范围必须控制在毫米标度线所示的区域内(视场中的,dD λ,x Dd∆=λ0~8mm 以内),以防损坏读数机构。
[实验后思考题]1、为什么双棱镜的折射角α必须很小?答:双棱镜的折射角α如过大,形成的虚光源的像就大而散,导致干涉条纹不清晰;另外,干涉条纹间距ΔX= 若折射角α增大,虚光源间距d 就随之增大,ΔX 就会变小,ΔX 太小则无法分辨,故双棱镜折射角α一般为0.5°~1°。
2、根据实际情况,说明狭缝宽度与干涉效果的关系。
答:狭缝过宽,则干涉条纹不清晰;狭缝过窄,又会因光通量太少使视场过暗,干涉条纹亮处不亮。
3、移动双棱镜,增大或缩小双棱镜与狭缝的间距、干涉条纹的疏密将如何变化?为什么?答:当狭缝和测微目镜都固定后,若增大双棱镜与狭缝的距离,干涉条纹将变密,反之变稀。
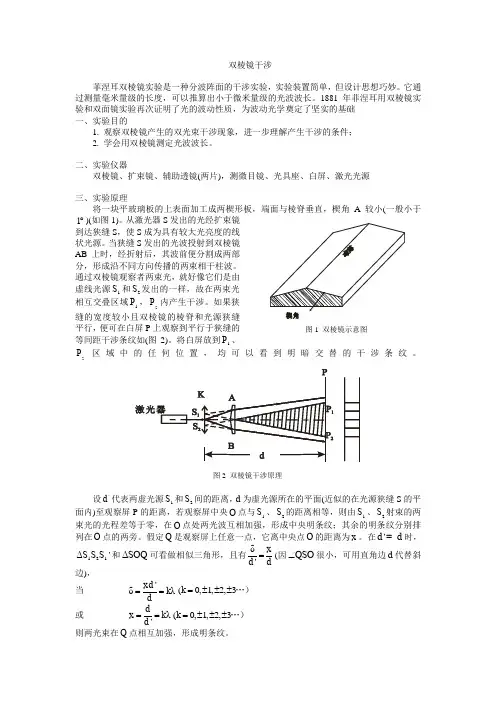
双棱镜干涉菲涅耳双棱镜实验是一种分波阵面的干涉实验,实验装置简单,但设计思想巧妙。
它通过测量毫米量级的长度,可以推算出小于微米量级的光波波长。
1881年菲涅耳用双棱镜实验和双面镜实验再次证明了光的波动性质,为波动光学奠定了坚实的基础 一、实验目的1. 观察双棱镜产生的双光束干涉现象,进一步理解产生干涉的条件;2. 学会用双棱镜测定光波波长。
二、实验仪器双棱镜、扩束镜、辅助透镜(两片),测微目镜、光具座、白屏、激光光源三、实验原理将一块平玻璃板的上表面加工成两楔形板,端面与棱脊垂直,楔角A 较小(一般小于1︒)(如图1)。
从激光器S 发出的光经扩束镜到达狭缝S ,使S 成为具有较大光亮度的线状光源。
当狭缝S 发出的光波投射到双棱镜AB 上时,经折射后,其波前便分割成两部分,形成沿不同方向传播的两束相干柱波。
通过双棱镜观察者两束光,就好像它们是由虚线光源1S 和2S 发出的一样,故在两束光相互交叠区域1P ,2P 内产生干涉。
如果狭缝的宽度较小且双棱镜的棱脊和光源狭缝平行,便可在白屏P 上观察到平行于狭缝的等间距干涉条纹如(图2)。
将白屏放到1P 、2P区域中的任何位置,均可以看到明暗交替的干涉条纹。
设'd代表两虚光源1S 和2S 间的距离,d 为虚光源所在的平面(近似的在光源狭缝S 的平面内)至观察屏P 的距离,若观察屏中央O 点与1S 、2S 的距离相等,则由1S 、2S 射束的两束光的光程差等于零,在O 点处两光波互相加强,形成中央明条纹;其余的明条纹分别排列在O 点的两旁。
假定Q 是观察屏上任意一点,它离中央点O 的距离为x 。
在'd d =时,121Δ'S S S 和ΔS O Q可看做相似三角形,且有δ'x d d=(因Q S O ∠很小,可用直角边d 代替斜边), 当 'δλx d k d==(0,1,2,3k =±±±…)或λ'd x k d ==(0,1,2,3k =±±±…)则两光束在Q 点相互加强,形成明条纹。

实验八 用双棱镜测钠光波长【实验目的】:1.观察双棱镜产生的光的干涉现象和特点,掌握获得双束光干涉的一种方法,进一步理解产生干涉的条件。
2.用双棱镜测定钠光的波长;3.学习测微目镜等光学仪器的使用与调整方法。
4.观察光的干涉现象【实验仪器】:双棱镜、可调狭缝、辅助透镜、测微目镜、光具座、白屏、钠光灯。
【实验原理】:由双棱镜干涉条件,光源发射的单色光经会聚透镜后会聚于单缝S 而成线光源,光从S 发出经双棱镜后,形成二虚光源S 1、S 2,该虚光源所发出的光满足干涉条件,在交迭区内产生干涉,成为平行于狭缝的等间距干涉条纹,由此可得:xDd ∆=λ 其中:λ :光源之波长。
∆x :干涉条纹的间距。
d :虚光源S 1、S 2间距。
D :虚光源(狭缝S )至观察处之距离。
∆x :可由测微目镜测量求出;D :可由光具座标尺读数读出;d :由二次成像法求出: 21d d d =其中:d 1、d 2为辅助透镜二次成像成像到测微目镜分划板的二虚光源S 1、S 2之间的距离。
【实验步骤与内容】:一、测钠光波长:1.按实验要求安置光学元件,进行共轴调节 ,使光束能对称地照射于双棱镜之棱脊上;2.调节测微目镜,使之能观察到清晰的干涉条纹;3.按要求测量n 条条纹间距x ,测量5—7组数据(填入记录表格)。
测虚光源到测微目镜之距离(单次测量) D , ∆ D (填入记录表格)。
按二次成像法测d 1d 2测量3—5组数据(填入记录表格)二、数据处理要求:参照相关教材不确定度计算举例处理数据。
【注意事项】:1.严格进行共轴调节该实验对共轴性要求非常严格,调节时可用白屏在外观察双缝所产生之光束是否亮波均匀,狭缝宽度必须适当;2.测微目镜读数时,必须顺一个方向旋转,以免产生回程误差;3.旋转读数鼓轮时,动作要平稳、缓慢。
4.测虚光源到测微目镜之距离时要注意修正值。
复习思考题:1、双棱镜和光源之间为什么要放一狭缝?为什么狭缝要很窄才可以看到清晰的干涉条纹?2、试证明公式21'd d d。

实验二十七 动力学共振法测定材料的杨氏弹性模量【预习题】1.外延测量法有什么特点?使用时应注意什么问题?答:所谓外延测量法,就是所需要的数据在测量数据范围之外,一般很难测量,为了求得这个数,采用作图外推求值的方法。
具体地说就是先使用已测数据绘制出曲线,再将曲线按原规律延长到待求值范围,在延长线部分求出所要的值。
使用外延测量法时应注意:外延法只适用于在所研究范围内没有突变的情况,否则不能使用2.悬丝的粗细对共振频率有何影响?答:在一定范围内,悬丝的直径越大时,共振频率反而越小。
因为共振频率与阻尼的关系为2202βωω-=,悬丝直径大时,阻尼相应较大,即β大,则共振频率应该较小。
当然,悬丝直径也不可过粗,太粗的悬丝对于棒振动时振幅的影响很大,即2222204)(p p mA ωβωω+-=变小,而不利于信号的拾取。
【思考题】1.在实际测量过程中如何辨别共振峰真假?答:理论上认为,“改变信号发生器输出信号的频率,当其数值与试样棒的某一振动模式的频率一致时发生共振,这时试样振动振幅最大,拾振器输出电信号也达到最大”。
实验中,并非示波器检测到信号峰值处频率都为样品棒的共振频率,由样品支架和装置其它部分的振动也会导致示波器检测到极值信号。
因此正确真假判别共振信号对于测量相当重要。
真假共振峰的判别方法有好几种,如预估法和撤耦法,预估法指利用已知的金属杨氏模量,利用公式估算出共振频率,撤耦法指用手托起试样棒,此时拾振信号应消失,反之为假信号。
预估法和撤耦法结合起来用比较好:预估法可判断出共振频率的大致范围,而撤耦法则可做进一步精确判断。
另外,还可以在不放铜棒的情况下先做一个粗略检测,即将可能的干扰信号频率做一个排除。
2.如何测量节点的共振频率。
答:从实验装置图中可以看出,试样振动时,由于悬丝的作用,棒的振动并非原理中要求的自由振动,而是存在阻尼下的受迫振动,所检测共振频率随悬挂点到节点的距离增大而增大。
若要测量(27-1)式中所需的试样棒基频共振频率,只有将悬丝挂在节点处,处于基频振动模式时,试样棒上存在两个节点,它们的位置距离分别为0.224L 和0.776L 处。




![实验五 双棱镜干涉及光波波长测量_大学物理实验_[共4页]](https://uimg.taocdn.com/c9decb3d998fcc22bdd10dd6.webp)
133 七、思考题(1)迈克尔逊干涉仪是利用什么方法获得相干光的?(2)简述迈克尔逊干涉仪的调整方法。
读数前怎样调整干涉仪的零点?(3)实验中如何利用干涉测量单色光的波长?(4)调出等倾干涉和等厚干涉的条件是什么?(5)在调整等倾干涉条纹时,为什么有一个由直变圆的渐变过程?实验五 双棱镜干涉及光波波长测量自从1801年英国科学家杨(T.Young )用双缝做了光的干涉实验后,光的波动说开始为许多学者接受,但仍有不少反对意见。
有人认为杨氏条纹不是干涉所致,而是双缝的边缘效应,二十多年后,法国科学家菲涅耳做了几个新实验,令人信服地证明了光的干涉现象的存在,这些新实验就包括他在1826年进行的双棱镜实验。
该实验不借助光的衍射而形成分波面干涉,用毫米级的测量得到纳米级的精度,其物理思想、实验方法与测量技巧至今仍然值得我们学习。
本实验通过用菲涅耳双棱镜对钠灯波长的测量,要求掌握光的干涉的有关原理和光学测量的一些基本技巧,特别要学习在光学实验中如何计算测量结果的不确定度。
一、实验目的(1)掌握光具组的光路同轴等高调节方法。
(2)观察光的双棱镜干涉现象,并掌握干涉测量光波波长的方法。
二、实验仪器FD-FBI-B 型双棱镜光干涉实验仪,半导体激光器,钠光灯及电源。
三、实验原理菲涅耳双棱镜(简称双棱镜)是一个顶角A 极大的等腰三棱镜,如图6-24所示。
它可看成由两个楔角很小的直角三棱镜ABD 和ACD 所组成,故名双棱镜。
当一个单色点光源S 从它的BC 面入射时,通过上半个棱镜ABD 的光束向下偏折,通过下半个棱镜ACD 的光束向上偏折,相当于形成S 1和S 2两个虚光源。
与杨氏实验中的两个小孔形成的干涉一样,把观察屏放在两光束的交叠区,就可看到干涉条纹。
图中,d 是两虚光源的间距,D 是光源到观察屏的距离。
测量d 的方法很多,其中之一是“二次成像法”,如图6-25所示,即在双棱镜与测微目镜之间加入一个焦距为f 的凸透镜L ,当4D f >时,可移动L 而在测微目镜中看到两虚光源的缩小像或放大像。
光学实验思考题一、 薄透镜焦距的测定⒈远方物体经透镜成像的像距为什么可视为焦距? 答:根据高斯公式v fu f'+=1,有其空气中的表达式为'111f v u =+-,对于远方的物体有u =-∞,代入上式得f ´=v ,即像距为焦距。
⒉如何把几个光学元件调至等高共轴?粗调和细调应怎样进行?答:对于几个放在光具座上的光学元件,一般先粗调后细调将它们调至共轴等高。
⑴ 粗调将光学元件依次放在光具座上,使它们靠拢,用眼睛观察各光学元件是否共轴等高。
可分别调整:1) 等高。
升降各光学元件支架,使各光学元件中心在同一高度。
2) 共轴。
调整各光学元件支架底座的位移调节螺丝,使支架位于光具座中心轴线上,再调各光学元件表面与光具座轴线垂直。
⑵细调(根据光学规律调整)利用二次成像法调节。
使屏与物之间的距离大于4倍焦距,且二者的位置固定。
移动透镜,使屏上先后出现清晰的大、小像,调节透镜或物,使透镜在屏上成的大、小像在同一条直线上,并且其中心重合。
⒊能用什么方法辨别出透镜的正负?答:方法一:手持透镜观察一近处物体,放大者为凸透镜,缩小者为凹透镜。
方法二:将透镜放入光具座上,对箭物能成像于屏上者为凸透镜,不能成像于屏上者为凹透镜。
⒋测凹透镜焦距的实验成像条件是什么?两种测量方法的要领是什么?答: 一是要光线近轴,这可通过在透镜前加一光阑档去边缘光线和调节共轴等高来实现;二是由于凹透镜为虚焦点,要测其焦距,必须借助凸透镜作为辅助透镜来实现。
物距像距法测凹透镜的要领是固定箭物,先放凸透镜于光路中,移动辅助凸透镜与光屏,使箭物在光屏上成缩小的像(不应太小)后固定凸透镜,记下像的坐标位置(P );再放凹透镜于光路中,并移动光屏和凹透镜,成像后固定凹透镜(O 2),并记下像的坐标位置(P ´);此时O 2P =u ,O 2P ´=v 。
用自准法测凹透镜焦距的要领是固定箭物,取凸透镜与箭物间距略小于两倍凸透镜的焦距后固定凸透镜(O 1),记下像的坐标位置(P );再放凹透镜和平面镜于O 1P 之间,移动凹透镜,看到箭物平面上成清晰倒立实像时,记下凹透镜的坐标位置(O 2),则有f 2 =O 2P 。
实验五 利用双棱镜干涉测红光波长一、实验目的:1、观察双棱镜产生的双光束干涉现象,进一步理解产生干涉的条件2、学会使用双棱镜测定光波波长二、实验仪器:双棱镜,可调狭缝,辅助透镜(两片),测微目镜,光具座,白屏,单色光源三、实验原理:两列的光波如果频率相同,传播方向相同,位相差恒定,那么在两列光波相交的区域将形成明暗相间的干涉条纹。
利用双棱镜干涉测钠光波长如图所示从单色光源M 发出的光经过透镜L 会聚于狭缝S ,使S 成为具有较大亮度的线状光源。
当狭缝S 发出的光投射到双棱镜上时,经折射后,其波前便分割成两部分,形成沿不同方向传播的两束相干柱波。
通过双棱镜观察这两束光,就好像它们是由虚光源S 1和S 2发出的一样,故在两束光相互交叠区域P 1P 2内产生干涉。
干涉条纹间距x ∆和光波波长λ之间关系有下式表示: xDd∆=λ其中,d 为两虚光源S 1和S 2的距离;D 为狭缝S 到测微目镜的距离。
实验中,只要测出d 、D 和x ∆的值,就可以光波的波长λ。
四、实验步骤:1、参照原理图在光学平台上安置各仪器,调节共轴等高,使钠光通过透镜L 会聚在狭缝S 上。
双棱镜的棱脊与狭缝须平行地置于光轴上,以获得清晰的干涉条纹。
2、用测微目镜测量干涉条纹间距x ∆,并测出狭缝到目镜的距离D 。
3、保持狭缝和双棱镜的位置不动,用二次成像法测出虚光源的距离d 。
4、根据公式计算钠光波长。
五、实验数据及处理:表1 10条条纹间距(单位 mm)表2 狭缝到目镜的距离D (单位 cm)表3 虚光源的距离d (单位 mm)六、注意事项:使用测微目镜时,首先要确定测微目镜读数装置的分格精度;要注意防止回程误差;旋转读数鼓轮时动作要平稳、缓慢;测量装置要保持稳定。
x Dd ∆=λ。
利用双棱镜测定光波波长【实验目的】1.掌握利用分割波前实现双光束干涉的方法;2. 观察光场空间相干性;3.用菲涅耳双棱镜测量钠光光波波长。
【仪器及用具】钠光灯、双棱镜、光具座、凸透镜、测微目镜、单缝、辅助棒。
【实验原理】一般情况下两个独立的光源(除激光光源外)不可能产生干涉。
要观察干涉现象必须用光学方法将一个原始光点(振源)分成两个位相差不变的辐射中心,即造成“相干光源”。
分割的方法有两种,即波前分割法和振辐分割法,波前分割的装置有双面镜,双棱镜等,。
本实验采用菲涅耳双棱镜进行波前分割,从而获得相干光,实现光的干涉。
Q-钠光灯 1L -透镜 S-单缝 B-双棱镜 2L -辅助成像透镜 M-测微目 图18-1用菲涅耳双棱镜测量钠光波长实验装置实验装置如图18-1所示。
,各器件均安置在光具座上,Q 为钠光灯;S 为宽度及取向可调单缝;透镜1L 将光源Q 发出的光会聚于单缝S 上,以提高照明单缝上的光强度;B 为双棱镜;1L 为辅助成像透镜,用来测量两虚光源1S 、2S 之间的距离d ;M 为测微目镜。
菲涅耳双棱镜是由两块底边相接、折射棱角 小于1°的直角棱镜组成的。
从单缝发出的光经双棱镜折射后,形成两束犹如从虚光源发出的频率相同、振动方向相同、并且在相遇点有恒定相位差的相干光束,它们在空间传播时,有一部分彼此重叠而形成干涉场。
如图18-2所示.图18-2设由双棱镜B 所产生的两相干虚光源1S 、2S 间距为d ,观察屏P 到1S 、2S 平面的距离为D 。
若P 上的0P 点到1S 和2S 的距离相等,则1S 和2S 发出的光波到0P 的光程也相等,因而在0P 点相互加强而形成中央明条纹(零级干涉条纹)。
设1S 和2S 到屏上任一点k P 的光程差为D ,k P 与的距0P 离为k X ,则当d <<D 和k X <<D 时,可得到kX d D∆=(18-1) 当光程差为∆波长的整数倍,即(K =0、1、2、···)时,得到明条纹。
【实验题目】 用菲涅耳双棱镜测钠光波长
【实验记录】
狭缝到测微目镜的距离的D=530mm
【数据处理与分析】
钠光波长: =
=
D
ad λ576nm 相对误差 2%
不确定度分析:(各个直接测量量的A 类、B 类不确定的估算,以及综合不确定度的估算。
从而根据不确定度的传播公式得到间接测量量(波长)的不确定度) 10a 不确定度为:综合不确定度:max{ |A – Ai}|=0.677 A 类不确定度:0.0460 B 类不确定度:0.672 D1不确定度:0.672 D1a 类不确定度:0.0837 D1b 类不确定度:0.682 D2不确定度:0.0677 D2a 类不确定度:0.682 D2b 类不确定度:0.0577 【课后问题】
试用双棱镜劈尖角A,光源与棱镜的距离d, 双棱镜折射率n, 把两个虚光源s1和s2的间距表示出来。
2dtan【arcsin(n*sinA)】
报告成绩(满分30分):⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽指导教师签名:⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽日期:⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽。
1院(系)名称物理系 班别 姓名 专业名称物理学 学号 实验课程名称普通物理实验 实验项目名称用双棱镜测定光波波长 内容包含:实验目的、实验原理简述、实验中注意事项、实验预习中的问题探讨一.实验目的 1.观察双棱镜产生的干涉现象2.掌握求得双光束干涉的一种方法,进一步理解产生干涉的条件3.学会用双凌静测定光波波长二.实验原理简述双棱镜是在一块玻璃薄板上,将其上表面加工成两块楔角很小(小于1º)的楔形板。
如图4.2.12-1(a )所示,可将它看成是由两个顶角很小、底边相连的直角棱角构成,其公共棱边与端面垂直。
利用双棱镜产生双光束干涉的原理如图 4.2.12-1(b )所示。
用单色光源(钠灯)照亮狭缝S ,从狭缝S 射出的光波,经双棱镜B (双棱镜的邻边与狭缝平行)折射后分成两束光,按各自的方向传播。
经过双棱镜观察时,这两束光好像是从虚光源S1和S2发出的。
因为这两束光来自同一光源,故是干涉光,在他们互相叠加的空间区域P1P2内产生干涉,将白屏M 置于该区域任意位置,均可观察到平行于狭缝的等间距干涉条纹.图4.2.12-1 设S1、S2间的距离为d ,由S1和S2所在的平面到白屏M 的距离为D ,且D>>d ,如图4.2.12-2所示。
单色光波波长为λ,若白屏M 上某点P2为亮点,则两束光在该点的光程差Δ满足Δ=K λ,K=0,1,2,………为干涉条纹的级数。
因该点离屏中心的距离X<<D ,且Δ<<d ,故有D XK K d λ= (12-1) 若P 为暗点,则该点到O 点的距离为2(2k 1)2D XK d λ=+ (12-2)可见屏上两相邻亮条纹(或暗条纹)之间的距离(即干涉条纹的宽度)为 D X d λ∆=d X D λ=∆(12-3)图4.2.12-2三.实验注意事项1.严格进行共轴调节:该实验对共轴性要求非常严格,调节时可用白屏在外观察双缝所产生之光束是否亮波均匀,狭缝宽度必须适当2.测量目镜读数时,必须顺一个方向旋转,以免产生回程差。
实验十三用双棱镜干涉测钠光波长法国科学家菲涅耳(Augustin J.Fresnel)在1826年进行的双棱镜实验,证明了光的干涉现象的存在,它不借助光的衍射而形成分波面干涉,用毫米级的测量得到纳米级的精度,其物理思想、实验方法与测量技巧至今仍然值得我们学习。
本实验通过用菲涅耳双棱镜对钠光波长的测量,要求掌握光的干涉的有关原理和光学测量的一些基本技巧,特别要学习在光学实验中如何计算测量结果的不确定度。
【实验目的】1.观察双棱镜产生的双光束干涉现象,进一步理解产生干涉的条件;2.学会用双棱镜测定光波波长.【实验原理】如果两列频率相同的光波沿着几乎相同的方向传播,并且这两列光波的位相差不随时间而变化,那么在两列光波相交的区域内,光强的分布不是均匀的,而是在某些地方表现为加强,在另一些地方表现为减弱(甚至可能为零),这种现象称为光的干涉。
图12-1 双棱镜的干涉条纹图菲涅耳利用图12-1所示装置,获得了双光束的干涉现象.图中双棱镜B是一个分割波前的分束器,它的外形结构如图12-2所示.将一块平玻璃板的上表面加工成两楔形板,端面与棱脊垂直,楔角较小(一般小于1°). 当狭缝S发出的光波投射到双棱镜B上时,借助棱镜界面的两次折射,其波前便分割成两部分,形成沿不同方向传播的两束相干柱波.通过双棱镜观察这两束光,就好像它们是由虚光源1S 和2S 发出的一样,故在两束光相互交叠区域内产生干涉.如果狭缝的宽度较小且双棱镜的棱脊和光源狭缝平行,便可在光屏Q 上观察到平行于狭缝的等间距干涉条纹.设d 代表两虚光源1S 和2S 间的距离,D 为虚光源所在的平面(近似地在光源狭缝S 的平面内)至观察屏Q 的距离,且d 《D ,任意两条相邻的亮(或暗)条纹间的距离为ΔX ,则实验所用光波波长λ可由下式表示:X D d ∆=λ (12-1)上式表明,只要测出d ,、D 和ΔX ,就可算出光波波长。
由于干涉条纹宽度ΔX 很小,必须使用测微目镜进行测量.两虚光源间的距离d ,可用一已知焦距为f 的会聚透镜L ,置于双棱镜与测微目镜之间,如图12-3所示,由透镜两次成像法求得.只要使测微目镜到狭缝的距离大于4f ,前后移动透镜,就可以在透镜的两个不同位置上从测微目镜中看到两虚光源1S 和2S 经透镜所成的实像,其中之一为放大的实像,另一个为缩小的实像.如果分别测得两放大像的间距1d ,和两缩小像的间距2d ,则根据下式 d= 21d d (12-2)即可求得两虚光源之间的距离d .图12-3 双棱镜干涉实验装置图12-2 双棱镜B 外形结构图【实验装置】本实验装置由双棱镜、测微目镜、光具座、线光源和透镜等组成。
北京师范大学物理实验教学中心 基础物理实验 预习思考题
【实验题目】用菲涅耳双棱镜测量钠光波波长
1. 双棱镜是怎样实现双光束干涉的?干涉条纹是怎样分布的?干涉条纹的宽度、在视野中
的数目由哪些因素决定?
试验原理:菲涅尔双棱镜可以看成是有两块底面相接、棱角很小的直角棱镜合成。
若置单色单色光源S0于双棱镜的正前方,则从S0射来的光束通过双棱镜的折射后,变为两束相重叠的光,这两束光仿佛是从光源S0的两个虚像S1和S2射出的一样。
由于S1和S2是两个相关光源,所以若在两束相重叠的区域内放置一个屏,即可观察到明暗相间的干涉条纹。
干涉条纹的分布:基本成等宽分布。
条纹宽度:干涉条纹的间距与光源的波长成正比。
条纹数目影响因素:在视野中的数目由光源的波长和光源、双棱镜和屏幕之间的相对距离决定。
2. 在实验时,双棱镜和光源之间为什么要放一狭缝?为什么狭缝很窄时,才可以得到清晰的
干涉条纹?
放一狭缝:保证通过双棱镜折射的两束光来自同一光源,射出的两束光是相干的。
狭缝要很窄:如果狭缝不够窄,来自狭缝两个边缘的光会分别通过双棱镜折射,不能保证光源的相干性。
3. 光路调整的基本原则是什么?
狭缝、凸透镜、目镜、透镜、双棱镜等各个元件等高共轴。
4. 画出光路图,试证明公式21'd d d 。
(d ′为两虚光源的距离;d1、d2分别为两个虚光
源的放大的像和缩小像的距离)
成绩(满分20 分):。