四年级组合图形周长的计算

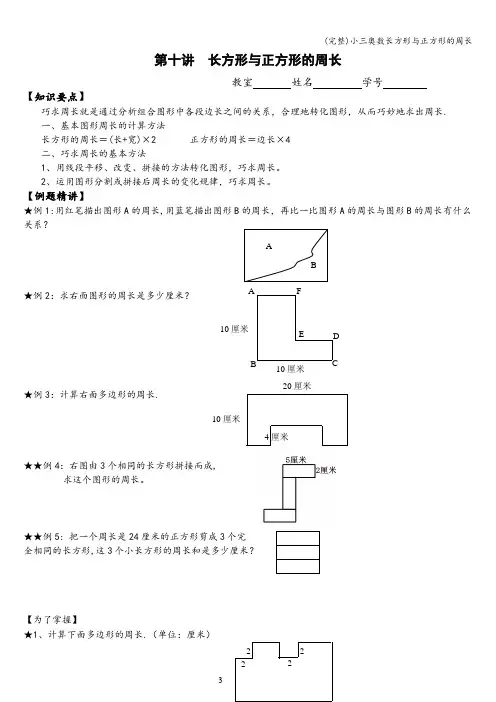
第十讲 长方形与正方形的周长教室 姓名 学号【知识要点】巧求周长就是通过分析组合图形中各段边长之间的关系，合理地转化图形，从而巧妙地求出周长. 一、基本图形周长的计算方法长方形的周长＝(长+宽)×2 正方形的周长＝边长×4 二、巧求周长的基本方法1、用线段平移、改变、拼接的方法转化图形，巧求周长。

2、运用图形分割或拼接后周长的变化规律，巧求周长。

【例题精讲】★例1:用红笔描出图形A 的周长,用蓝笔描出图形B 的周长，再比一比图形A 的周长与图形B 的周长有什么关系？★例2：求右面图形的周长是多少厘米？★例3：计算右面多边形的周长.★★例4：右图由3个相同的长方形拼接而成,求这个图形的周长。

★★例5: 把一个周长是24厘米的正方形剪成3个完 全相同的长方形,这3个小长方形的周长和是多少厘米？【为了掌握】★1、计算下面多边形的周长.（单位：厘米）ABAFBCED 10厘米10厘米 20厘米10厘米4厘米322 22★2、一个正方形的边长是2厘米，由6个这样的正方形拼成一个长方形,周长最长是几厘米？★3、右面多边形的周长是几厘米？（单位:厘米)★4、两个大小相同的正方形拼成一个长方形后，周长比原来的两个正方形周长的和减少了18厘米，则拼成的长方形的周长是多少？★5、计算下列图形（左图）的周长(单位:厘米)。

【为了优秀】★★1、如图，阴影部分是正方形,求出图中长方形ABCD 的周长.★★2、如图所示，用4个一样大的长方形和一个小正方形，拼成一个边长为56厘米的正方形,每个长方形的周长是多少厘米?★★3、正方形A 的周长是28，B 的周长是20，求由A 、B 组成的图形周长（如下图）。

43 12810厘米7厘米32★★4、一张长方形纸，长是31厘米，宽是16厘米。

先剪下一个最大的正方形，再从余下的纸片中剪下一个最大的正方形。

问最后余下的长方形的周长是多少？【为了竞赛】★★★1、一个正方形被分成了三个相同的长方形。

第3讲 巧求周长【知识点拔】 姓名:数学活动课上，李老师出了这样一道题：小华和小兵玩打仗游戏，每人占据了一块地，（如图所示），请问：谁占地的边界线长？小马说：“小华所占地的边界线长。

”小虎说：“小兵所占地的边界线长。

”两人争论不休，谁也说服不了谁。

小聪说：“你们两人别争了，小华和小兵所占地的边界线一样长。

”李老师微笑着点点头。

这究竟是怎么回事呢？这个问题实际上是牵涉到如何求一个平面图形的周长。

要想顺利解决此类问题，通常要用到平移、转化、分解等方法，以及灵活运用我们已经学过的长方形、正方形的周长计算公式。

【典型例题】【例子】如右图，若每个小正方形的周长为12厘米，则它们组合而成的“十”字图形的周长为多少厘米?【练一练】从一个周长是20厘米的正方形中，剪下一个周长是6厘米的正方形，剩下的图形的周长是多少厘米？（写出所有可能的结果）【例2】下图是一座楼房的平面图，求这个平面图的周长。

【练一练】某人以每分钟150米的速度绕右图所示跑一圈，需要多少分钟？【例3】有一个长方形纸片，长比宽多2厘米，周长是36厘米。

用剪刀剪3下（如右图），这六个长方形的周长之和是多少？【练一练】如右图，把一个长是12厘米，宽是10厘米的长方形横切3刀，竖切2刀，共切成了12个小长方形。

所有这些小长方形的周长之和是多少？【例4】 如图，用5个小正方形和1个大正方形拼成一个更大的正方形，若此最大正方形的周长为120厘米，则图中的5个小正方形周长之和是多少厘米？【练一练】如右图，一个正方形被分成了4个同样大小的长方形，每个长方形的周长都是60厘米，求正方形的周长是多少厘米？【例5】 一个小长方形纸的长是20厘米,宽是16厘米,现把若干个这样的小长方形纸片,按右图所示的方法,1层、2层、3层……摆下去，共摆了80层.摆好后的这个图形周长为 厘米。

【练一练】有一批长20厘米，宽12厘米的长方形纸片按图中所示方法一层、二层、三层的摆下去，共要摆成四层，求摆好后图形的周长。

平面图形面积————圆的面积班级XX 上课时间专题简析：在进行组合图形的面积计算时，要仔细观察，认真思考，看清组合图形是由几个基本单位组成的，还要找出图中的隐蔽条件与已知条件和要求的问题间的关系。

并且同学们应该牢记几个常见的圆与正方形的关系量：在正方形里的最大圆的面积占所在正方形的面积的3.144 ,而在圆内的最大正方形占所在圆的面积的23.14,这些知识点都应该常记于心，并牢牢掌握！.例题1。

求图中阴影部分的面积（单位：厘米）。

[分析]如图所示的特点，阴影部分的面积可以拼成1/4圆的面积。

62×3.14×1/4＝28.26（平方厘米） . 练习1求下面各个图形中阴影部分的面积（单位：厘米）。

例题2。

求图中阴影部分的面积（单位：厘米）。

[分析]形的面积减去大三角形面积的一半。

2×1/4－4×4÷2÷2＝8.56（平方厘米）练习2: 计算下面图形中阴影部分的面积（单位：厘米，正方形边长4）。

例题3。

在正方形ABCD 中，AC ＝6厘米。

求阴影部分的面积。

[分析]这道题的难点在于正方形的边长未知，这样扇形的半径也就不知道。

但我们可以看出，AC 是等腰直角三角形ACD的斜边。

根据等腰直角三角形的对称性可知，斜边上的高等于斜边的一半（如图所示），我们可以求出等腰直角三角形ACD 的面积，进而求出正方形ABCD 的面积，即扇形半径的平方。

这样虽然半径未求出，但可以求出半径的平方，也可以把半径的平方直接代入圆面积公式计算。

既是正方形的面积，又是半径的平方为：6×（6÷2）×2＝18（平方厘米）阴影部分的面积为：18－18×3.14÷4＝3.87（平方厘米）答：阴影部分的面积是3.87平方厘米。

.练习3 1、如图所示，图形中正方形的面积是50平方厘米，分别求出每个图形中阴影部分的面积。

2、如图所示，正方形中对角线长10厘米，过正方形两个相对的顶点以其边长为半径分别做弧。

组合图形中圆的周长与面积一、学习目标：1．巩固加深对圆的周长与面积的理解与计算，掌握在组合图形中求圆的周长及面积的方法。

2．提高自己思维的灵活性。

二、知识基础：1．什么叫圆的周长？围成圆的曲线的长叫圆的周长。

什么叫圆的面积？圆所占平面的大小叫圆的面积？2．怎样求圆的周长和面积？圆的周长：c=πd 或c=2πr 。

圆的面积：2r S π=3．一个边长2分米的正方形剪下一个最大的圆，圆的周长为（6.28）分米。

面积为（3.14）平方分米。

4．在一个正方形内做一个最大的圆，圆的面积是正方形面积的（4π） 正方形的边长就是圆的直径，设圆的直径为2r ，半径为r ，圆面积为2r π正方形边长就为2r ，正方形面积为24)2()2(r r r =⨯ 所以4422ππ==÷r r 正方形面积圆面积三、方法例谈例1：将半径分别为3厘米和2厘米的两个半圆如图放置，求阴影部分周长。

请认真看图：阴影部分周长是由哪些组合起来的？怎样分别求出这几部分的长度？厘米31=B O厘米1231212=-=-=O O A O A OAC=2—1=1厘米112r C O π=； 1121r C O π= 2221r C O π= cm r r C C O O 7.15214.3314.321212121=⨯+⨯=+=+ππ 阴影部分周长：厘米两个半圆7.197.15131=++=++AC B O答：阴影部分周长为19.7厘米例2：如图：从点A 到点B 沿大圆周长和沿着中、小圆的周长走，路程相同吗？①认真看图：大圆周是由哪几部分组成？中、小圆周是由哪几部分组成？②这题是要我们求什么？求大圆的半周长，求中、小圆的半周长，然后进行比较大小③怎样进行计算呢？设中圆直径为D ，小圆直径为d ，则：大圆直径为D+d ，所以d D d D C πππ2121)(21+=+=大 D C π21=中 d C π21=小 d D C C ππ2121+=+小中 所以：小中大C C C +=这就是说两种求法经过的路程是相同的。

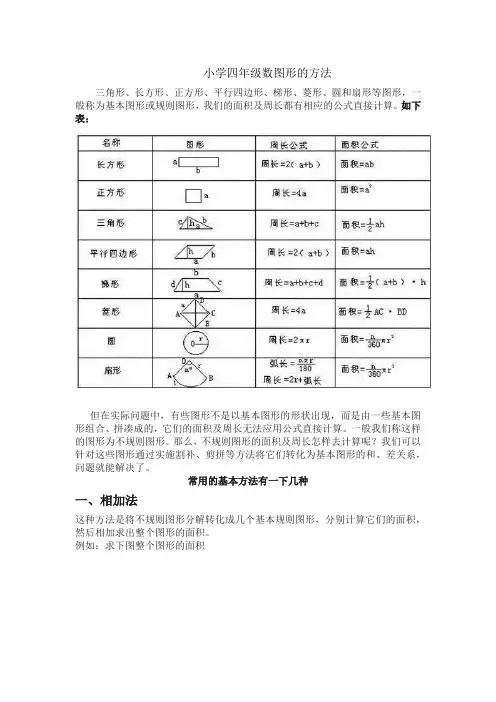
小学四年级数图形的方法三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形，我们的面积及周长都有相应的公式直接计算。

如下表：但在实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算。

一般我们称这样的图形为不规则图形。

那么，不规则图形的面积及周长怎样去计算呢？我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系，问题就能解决了。

常用的基本方法有一下几种一、相加法这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积。

例如：求下图整个图形的面积一句话：半圆的面积+正方形的面积=总面积二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。

例如：下图，求阴影部分的面积。

一句话：先求出正方形面积再减去里面圆的面积即可.三、直接求法这种方法是根据已知条件，从整体出发直接求出不规则图形面积。

例如：下图，求阴影部分的面积。

一句话：通过分析发现阴影部分就是一个底是2、高是4的三角形四、重新组合法这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可例如：下图，求阴影部分的面积。

一句话：拆开图形，使阴影部分分布在正方形的4个角处，如下图。

五、辅助线法这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可例如：下图，求两个正方形中阴影部分的面积。

一句话：此题虽然可以用相减法解决，但不如添加一条辅助线后用直接法作更简便（如下图）根据梯形两侧三角形面积相等原理（蝴蝶定理），可用三角形丁的面积替换丙的面积，组成一个大三角ABE，这样整个阴影部分面积恰是大正方形面积的一半.六、割补法法这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形，从而使问题得到解决。

知识精讲一、知识点概述我们已经学习了长方形和正方形周长的计算，会运用长方形和正方形周长的计算公式计算长方形和正方形的周长，本周我们要进一步学习和运用长方形和正方形的周长公式，巧求表面上看起来根本不是长方形或正方形的图形的周长，提高我们空间想象能力和解决问题的能力。

2、复习长方形的周长＝长×2＋宽×2＝ (长＋宽)×2正方形的周长＝边长×43、求不规则图形的周长的方法运用长方形和正方形的周长公式，巧求表面上看起来根本不是长方形或正方形的图形的周长，这就必须掌握“转化”的思考方法。

所谓“转化”，这里主要是指把某个图形转变成标准的长方形或正方形，以便计算它们的周长。

特别提示：在运用转化的思维方法时，必须仔细观察题目所给的图形是不是一个直角多边形，即所有的角是不是都为直角。

因为任意直角多边形，总可以弥补成一个长方形或正方形。

三、新授例1、计算右边图形的周长。

(单位：厘米)分析：要想求出这个图形的周长，乍看起来，似乎缺少条件。

因为这个图形不是一个正方形，而是一个六边形。

要求这个六边形的周长，只有把所有的边长相加，然而条件不足。

怎么办呢?我们先仔细观察这个图形，发现它的六个角都是直角，因此，我们可以把图中右上缺角处的线段分别向上、向右平行移到虚线外(见下图)。

这样，正好移补成一个正方形，问题得到了解决。

解答：30×4＝120(厘米)答：这个图形的周长是120厘米。

巩固练习：1．如图是由三个长方形组成的。

求这个组合图形的周长。

3、下图是一个楼梯的侧剖面图，已知每步台阶宽3分米，高2分米。

求这个楼梯侧面的周长是多少米。

分析：要求楼梯侧面的周长，表面看起来似乎缺少条件。

但是，如果认真观察，就可以发现把每层台阶的宽度向上移到和最上层同样高的地方，把每层台阶的高度右移到和下层台阶的高度一致的地方，这样原图就转化成一个长方形，这时长方形的长＝3×10＝30(分米)，宽＝2×10＝20(分米)，根据求长方形周长的计算公式(注意将分米换算成米)就可以求出图形的周长了。

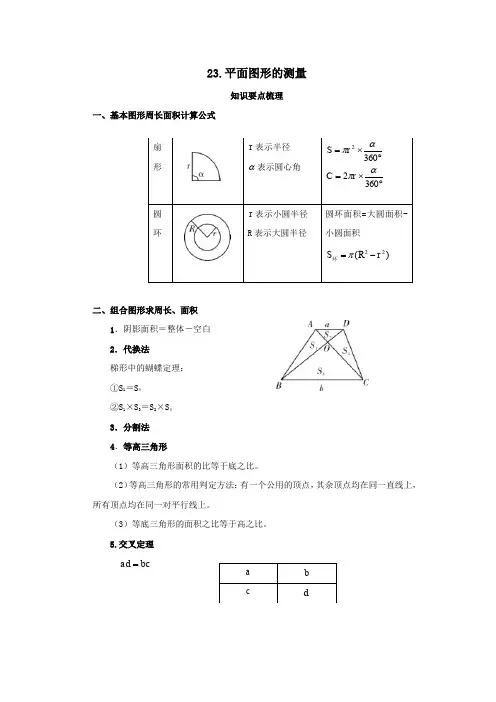
23.平面图形的测量知识要点梳理一、基本图形周长面积计算公式二、组合图形求周长、面积 1．阴影面积＝整体－空白 2．代换法梯形中的蝴蝶定理： ①S 1＝S 4 ②S 1×S 3＝S 2×S 4 3．分割法 4．等高三角形（1）等高三角形面积的比等于底之比。

（2）等高三角形的常用判定方法：有一个公用的顶点，其余顶点均在同一直线上，所有顶点均在同一对平行线上。

（3）等底三角形的面积之比等于高之比。

5.交叉定理 bc ad =考点精讲分析典例精讲考点1组合图形的周长和面积【例1】 求下面图形的周长和面积。

（单位：米） 【精析】 要求它的周长，可用长方形的2个长＋1个宽＋圆的周长的一半；要求它的面积，可用图中长方形的面积加上半圆的面积即可。

【答案】 周长：2.5×2＋2＋3.14×2÷2 ＝5＋2＋3.14 ＝10.14（米）面积：2.5×2＋3.14×2)22(÷2 ＝5＋3.14×1÷2 ＝5＋1.57 ＝6.57（平方米）答：这个图形的周长是10.14米，面积是6.57平方米【归纳总结】 组合图形的计算，一般都要把它分割成规则图形再进行计算。

考点2 等积变换法求面积【例2】 如图，ABCD 是直角梯形，AB ＝3厘米，AD ＝4厘米，BC ＝6厘米，求阴影部分的面积。

【精析】 阴影部分的面积为三角形ABE 和三角形DEC 的面积之和，利用△ABE 和△DEC 是等高三角形则阴影部分的面积可以变换为BC 边的长乘以高，再除以2。

【答案】 6×3÷2＝9（平方厘米）【归纳总结】 高一定，阴影部分面积＝底之和×高÷2。

考点3 割补法求面积【例3】 如图，是一块长方形草地，长方形的长是16，宽是10，中间有两条道路，一条是长方形，一条是平行四边形，那么，阴影部分的面积是多大？【精析】如果按常规解法，此题较麻烦，如果用割补法、平移法则较简单。

三年级上册数学《求组合图形的周长》专项练习，附答案参考答案：1、从一个长20厘米，宽12厘米的长方形，剪下最大的正方形，剩下小长方形周长是多少？剩下的小长方形，长为12，宽为20-12=8（12+8）×2=40（厘米）2、两个边长是8cm的正方形组合后的图形周长是多少？组合后是一个长方形，长为16cm，宽为8cm（16+8）=48（cm）3、两个长方形的长是12cm，宽是8cm，组合后的图形周长最小是多少？把两个长方形的长组合在一起，组成的图形是一个长方形长为16cm,宽为12cm（16+12）×2=56（cm）4、如图所示：从一个长12厘米，宽8厘米的长方形，剪下一个边长为1厘米的小正方形，剩下图形的周长是多少？(12+8)×2+2×1=42（厘米）5、长方形的长是12cm，宽是8cm，与边长是8cm的正方形组合成下面的这个图形,组合后的图形周长是多少？（12+8+8）×2=56（cm）6、长方形的长是12cm，与边长是8cm的正方形组合成下面的这个图形。

重叠部分刚好是正方形边长的一半，组合后的图形周长是多少？（12+8÷2+8）×2=48（cm）7、下图中，阴影部分是正方形，图中大长方形的周长是多少？（24+16）×2=80（cm）8、长方形的长是12cm，宽是8cm，与边长是10cm的正方形组合成下面的这个图形，组合后的图形周长是多少？(10+12+10)×2=64（cm）9、长方形的长是12cm，宽是8cm，与边长是10cm的正方形组合成下面的这个图形。

重叠部分刚好是正方形边长的一半，组合后的图形周长是多少？(10+12-10÷2+10)×2=54（cm）10、长方形的长是12cm，与边长是10cm的正方形组合成下面的这个图形。

组合后的图形周长是多少？(12+10)×2=44（cm）11、两个长方形的长是10cm，宽是4cm，求重叠后的周长是多少？10×4=40（cm）12、一个正方形被两条线段分成4个长方形，这四个长方形的周长是16分米，求原来正方形的边长是多少？16÷2÷4=2（分米）13、一个周长为48厘米的长方形被两条线段分成4个长方形，四个小长方形的周长是多少？48×2=96（厘米）。

小学奥数专题之—————组合图形一、平移与转化空白部分的短边长2cm，求阴影部分面积？求图形周长是多少？求阴影部分面积？两个完全一样的三角形重叠在一起，求阴影面积？四边形为正方形，M，N为中点，求阴影面积？求阴影的面积（单位；厘米）求阴影面积（单位；厘米）小圆半径为1cm，花瓣图形的周长和面积是多少？正方形的边长为4cm，求阴影的面积？求梯形的面积？正方形的边长为4cm，求阴影面积？正方形的边长为4cm，求阴影周长和面积？正方形的边长为4cm，求阴影面积？正方形的边长为4cm，求阴影面积？正方形的边长为4cm，求阴影面积？三个圆的半径相等都是2cm，求阴影的面积？正方形的面积是16平方厘米求阴影面积？求阴影的面积？（单位；厘米）下图中圆的半径是4厘米，O是圆心，AB和正方形的边长为4cm，求阴影部分周长和面积？DC互相垂直，OE=1厘米，EF=2厘米，那么图中阴影部分的面积是多少平方厘米？求阴影部分面积？平行四边形面积是24 平方厘米，求阴影部分面积？求阴影部分面积？圆的半径是6厘米，求图中的阴影面积。

大小正方形的边长分别为5cm，4cm 长方形的面积与圆的面积相等，已知圆的半径为3cm，求阴影部分面积？求阴影部分面积？求阴影面积？（单位；厘米）三角形ABC和三角形都是等腰直角三角形，阴影部分是正方形。

三角形ABC与三角形DEC的面积比是多少？梯形的面积是54平方厘米，求图中阴影部分的面积？圆的直径是16cm，求阴影部分的面积？阴影部分为正方形，求大长方形的周长？图中两个正方形的边长都为4厘米，求阴影部分面积？求阴影部分面积？图中三角形为等腰直角三角形，求阴影部分面积？求阴影部分面积？ 求阴影部分面积？ 重叠类如下图，两个41圆扇形AOB 与A ′O ′B ′重叠放在一起，其中POQO ′的面积是5平方厘米的正方形，那么阴影部分的面积是多少？大圆半径为4cm ，小圆半径为2cm ，求大圆白色部分比小圆白色部分面积多多少平方厘米如图平行四边形的长边是6cm ，短边 有红黄绿三块大小相同的正方形纸片，放在一个底为正方形 是3cm ，长边上的高是2.6cm ，求阴 的盒子内，他们相互重叠，在露出部分的中红色面积是，黄色 影部分的面积？ 面积是17，绿色面积是7，求正方形盒子底的面积？ABCD 是边长为a 的正方形， 每个小圆的半径都是2cm ，求阴影部分面积？利用割补法求阴影的面积（单位；厘米）小圆半径为2 小圆半径为3加减法求下面阴影面积（单位：厘米）6旋转法求下列各图阴影部分面积（单位厘米）梯形上底为3厘米，下底是5厘米，高是4厘米，E是DC的中点，求阴影部分的面积是多少？一个等腰三角形的斜边长6厘米，求它的面积？一个正方形的对角线长5厘米，求这个正方形的面积?一个三角形的斜边长是10厘米，两直角边的差是3厘米，求这个直角三角形的面积？一个直角三角形的斜边长是15厘米，两直角边的差是4厘米，求这个直角三角形的面积？小正方形的边长是3厘米，大正方形的边长是5厘米，求阴影部分的面积是多少？四边形的对角线，将四边形分成四个小三角形，已知其中的三个三角形的面积分别是15平方米，75平方米，65平方米，求阴影部分的面积？一个长方形被两条直线分成四个长方形，其中三个的面积是20平方米，25平方米，30平方米，另一个长方形的面积是多少平方米？一个长方形被四条直线分成九个长方形，其中五个的面积分别是1,2,3,4,5平方厘米，求阴影部分的面积是多少平方厘米？图形内所标数据分别为各长方形的面积，那么大长方形的面积是多少？在梯形ABCD中，两条对角线相交于O，下底是上底的3倍，三角形AOD的面积是12平方厘米，那么梯形的面积是多少平方厘米？已知梯形中两个小三角形的面积分别为3平方厘米，9平方厘米，求梯形ABCD的面积？在梯形ABCD中，三角形CDE的面积为20,AE:CD=2:5，求梯形ABCD的面积？在梯形ABCD中，三角形ACE的面积为60，AB:CD=1:3,求梯形ABCD的面积？在正方形中方了三个同样大的小正方形，已知绿色部分的面积是20，蓝色部分的面积是14，红色部分的面积是10，求大正方形的面积？如图数据为各三角形部分的面积，求阴影部分的面积。

小升初数学组合图形的面积+数学趣题+分数计算技巧+奥数题训练及答案解析组合图形的面积一、 知识要点：1. 我们学过的常见多边形的周长和面积求法:2.计算不规则图形的面积，常用到哪些方法？二、知识运用典型例题。

例题1：如图，两条对角线把梯形ABCD 分割成四个三角形，（1） 请写出图中面积相等的三角形？（2） 已知两个三角形的面积，求另两个三角形的面积各是多少？ （3） 求梯形ABCD 的面积？B C例2：长方形ABCD 的面积是24平方厘米，三角形EBC 的面积是30平方厘米，两块阴影部分的面积相差多少?例3：如下图，长方形ABCD 的面积是20平方厘米，三角形ADF 的面积为5平方厘米，三角形ABE 的面积为7平方厘米，求三角形AEF 的面积。

例4：如下图，已知四条线段长分别是AB=2，CE=6，CD=5，AF=4，并有两个直角，求四边形ABCD 的面积。

D BCA D三、知识运用课堂练习。

1、三角形EBC的面积是40平方厘米，且阴影部分面积比三角形EFG的面积大10平方厘米。

求平行四边形ABCD的面积？2、如下图，长方形的长和宽分别是12和9，把三角形的三条边分别平均分成三段，得到A，B，C，D，E，F六个点，连接AF、BC、DE，得到一个六边形。

这个六边形的面积是多少？3、在右图中，AB=8厘米，CD=4厘米，BC=6厘米，三角形AFB比三角形EFD 的面积大18厘米2。

求ED的长。

4、下图是由大、小两个正方形组成的，小正方形的边长是4厘米，求三角形ABC的面积。

课后练习 等级1、下图中的甲和乙都是正方形，求阴影部分的面积。

2、下图中，矩形ABCD 的边AB 为4厘米，BC 为6厘米，三角形ABF 比三角形E DF 的面积大9厘米2，求ED 的长。

3、（动手操作题）右图是一个4×4的方格纸，请在保持每个小方格完整的情况下，将它分割成大小、形状完全相同的两部分。

（至少要有4种不同的方法）甲乙生活中的数学趣题一、知识要点。

四年级周长计算公式周长是指封闭图形一周的长度。

不同的图形有不同的周长计算公式。

1. 正方形：边长为5 厘米，周长= 边长×4，即5×4 = 20 厘米。

解释：正方形的四条边长度相等，所以周长等于边长乘以4。

2. 长方形：长为8 厘米，宽为3 厘米，周长= （长+ 宽）×2，即（8 + 3）×2 = 22 厘米。

解释：长方形相对的两条边长度相等，所以周长等于（长+ 宽）乘以2。

3. 三角形：三条边分别为4 厘米、5 厘米、6 厘米，周长= 4 + 5 + 6 = 15 厘米。

解释：三角形的周长就是三条边长度的总和。

4. 等边三角形：边长为7 厘米，周长= 边长×3，即7×3 = 21 厘米。

解释：等边三角形三条边长度相等，所以周长等于边长乘以3。

5. 等腰三角形：腰长为6 厘米，底边长为4 厘米，周长= 6×2 + 4 = 16 厘米。

解释：等腰三角形两条腰长度相等，周长等于两条腰的长度加上底边的长度。

6. 平行四边形：相邻两边分别为5 厘米和3 厘米，周长= （5 + 3）×2 = 16 厘米。

解释：平行四边形对边长度相等，周长等于相邻两边长度之和乘以2。

7. 菱形：边长为8 厘米，周长= 边长×4，即8×4 = 32 厘米。

解释：菱形的四条边长度相等，周长等于边长乘以4。

8. 梯形：上底为3 厘米，下底为7 厘米，腰分别为4 厘米和5 厘米，周长= 3 + 7 + 4 + 5 = 19 厘米。

解释：梯形的周长等于上底、下底和两条腰长度的总和。

9. 圆形：半径为5 厘米，周长= 2×π×半径，即2×3.14×5 = 31.4 厘米。

解释：圆的周长等于2 乘以圆周率乘以半径。

10. 半圆：半径为6 厘米，周长= π×半径+ 2×半径，即3.14×6 + 2×6 = 30.84 厘米。

一、选择题1. 下图中正方形部分是一个水池，其余部分是草坪，已知正方形的面积是300平方米，草坪的面积是（）平方米。

A．B．C．D．不能确定2. 观察图形，对于两个图中阴影部分的叙述，（）是正确的。

A．周长、面积都不相等B．周长、面积都相等C．周长相等，面积不相等D．周长不相等，面积相等3. 如图，在长方形中有三个大小相等的圆，下列说法错误的是（）。

A．长方形的宽是4cmB．圆的半径是12cm的C．阴影部分的面积等于长方形的面积减去三个圆的面积4. 如图中阴影部分的面积是9平方厘米，图中圆环的面积是（）平方厘米。

A．18.84 B．56.52 C．81 D．28.265. 下面两个图中，关于涂色部分的描述正确的是（）。

A．周长和面积都不相等B．周长相等，但面积不相等C．周长不相等，但面积相等二、填空题6. 等腰直角三角形的一腰长是8厘米，以它的两腰为直径分别画两个半圆，那么，阴影部分的面积共有________平方厘米。

7. 如图：已知正方形的面积是10平方分米，那么阴影部分的面积是_____平方分米。

8. 如图，外侧大正方形的边长是10厘米，图中阴影部分的面积是27.5平方厘米，那么圆内大正方形面积是小正方形面积的________倍。

9. 如图，一个正方形边长为10cm，一个直径为2cm的圆在正方形内部沿正方形四条边滚动一周，它所扫过的面积为( )cm2。

10. 下图有( )条对称轴，如果圆的直径是20dm，那么阴影部分的面积是( )。

三、解答题11. 如图，O是圆心，OD＝4，C是OB的中点，阴影部分面积是14π，求三角形OAB的面积。

12. 沈阳方圆大厦是一座古钱币造型的建筑。

小新模仿它设计了一个模型，模型的正面是铜钱的形状，其圆的直径是24cm，中间正方形的边长是0.8dm。

这个模型正面的面积是多少平方厘米？13. 求阴影部分的面积．（单位：厘米）14. 下图是一面我国唐代外圆内方的铜镜。