理论力学 第十章振动

理论力学中的杆件的振动分析杆件是理论力学中经常研究的一个重要物体。

它可以是直杆、曲杆或者弯折杆。

振动分析是研究杆件在外力作用下的动态响应，对于杆件在工程实践中的应用具有重要的意义。

本文将从理论力学的角度出发，对杆件的振动分析进行探讨。

一、杆件的自由振动杆件的自由振动是指在无外力作用下，杆件在某一固有频率下产生的振动。

对于直杆而言，自由振动可以通过解杆件的振动微分方程来求解。

对于曲杆或弯折杆，由于其几何形状的复杂性，需要借助数值求解方法进行分析。

自由振动的频率可以通过求解杆件的固有值问题得到。

根据杆件的几何形状和材料性质，可以导出杆件的振动微分方程。

然后，通过合适的边界条件，解出振动微分方程的特征方程，进而求解杆件的固有频率和振型。

二、杆件的受迫振动杆件的受迫振动是指在外力作用下，杆件产生的振动响应。

外力可以是静力荷载、动力荷载或者周期性激励力，例如谐振激励力。

在杆件的受迫振动分析中，需要建立动力学方程，考虑杆件的质量、刚度和阻尼等影响因素。

对于直杆而言，可以利用振动方程和边界条件求解出杆件的受迫振动响应。

对于曲杆或弯折杆，受迫振动的分析较为复杂。

通常需要借助有限元方法进行数值模拟，得到杆件的动态响应。

在模拟前，需要对杆件进行网格划分，并设置适当的材料参数和边界条件。

通过求解有限元方程，可以得到杆件的受迫振动响应。

三、振动分析的应用理论力学中的杆件振动分析在工程实践中有着广泛的应用。

以下列举几个典型的应用场景：1. 结构设计优化：通过对杆件的振动分析，可以评估结构的动态性能，从而优化设计。

例如，在桥梁工程中，振动分析可以用于评估桥梁的抗震性能，确保其在地震等外力作用下的稳定性。

2. 装配工艺分析：在装配过程中，杆件的振动响应可能会引起误差或者装配不良。

通过振动分析，可以识别潜在的装配问题，并采取相应的措施进行改进。

3. 动力学仿真：在机械系统或者工艺设备中，杆件的振动会对系统的动力学性能产生重要影响。

如何理解理论力学中的自由振动和强迫振动？在理论力学的世界里，自由振动和强迫振动是两个非常重要的概念。

它们不仅在物理学、工程学等领域有着广泛的应用，也深深影响着我们对自然界中各种振动现象的理解。

首先，让我们来谈谈自由振动。

想象一下，你有一个弹簧，一端固定，另一端连接着一个质量块。

当你把这个质量块拉离平衡位置然后松手，它就会开始振动，这种振动就是自由振动。

在自由振动中，系统仅依靠其自身的初始能量和内部特性来维持振动。

自由振动的特点之一是其振动频率是由系统本身的物理参数决定的，这个频率被称为固有频率。

比如说，弹簧的劲度系数和质量块的质量就会影响固有频率。

而且，在没有外界干扰的理想情况下，自由振动会一直持续下去，但由于不可避免的阻尼作用，振动的幅度会逐渐减小，最终停止。

阻尼是自由振动中一个不可忽视的因素。

阻尼可以来自于空气阻力、摩擦力等。

它就像是一个“能量消耗者”，不断地把振动系统的机械能转化为热能等其他形式的能量，导致振动逐渐减弱。

举个简单的例子，一个秋千如果没有人推动，在摆动的过程中就会因为空气阻力和秋千与支架之间的摩擦力而逐渐减慢，最终停下来，这就是一种自由振动受到阻尼影响的表现。

接下来，我们再看看强迫振动。

强迫振动与自由振动最大的不同在于，它是由外部周期性的驱动力作用于系统而产生的振动。

比如说，一个发动机运转时产生的周期性力作用在机器的某个部件上，导致该部件产生振动，这就是强迫振动。

在这种情况下，振动的频率是由外部驱动力的频率决定的，而不是系统的固有频率。

强迫振动有一个很有趣的现象，叫做共振。

当外部驱动力的频率与系统的固有频率相等时，振动的幅度会达到极大值，这就是共振现象。

共振在很多领域都有着重要的应用，同时也可能带来一些潜在的危险。

比如，在桥梁设计中，如果桥梁的固有频率与过往车辆的振动频率接近，就可能在特定情况下发生共振，导致桥梁的损坏。

但在另一方面，我们也可以利用共振来实现一些有益的目的，比如在无线电通信中，通过调整电路的参数，使其与接收信号的频率产生共振，从而提高信号的接收效果。

如何通过理论力学解决振动问题？在我们的日常生活和工程实践中，振动现象无处不在。

从桥梁的晃动到机械零件的微小振动，从建筑物在风中的摇摆到电子设备中的振动噪声，振动问题的研究和解决具有重要的意义。

理论力学作为力学的基础学科，为我们提供了强大的工具和方法来分析和解决这些振动问题。

首先，让我们来了解一下什么是振动。

简单来说，振动就是物体在平衡位置附近的往复运动。

这种运动可以是周期性的，也可以是非周期性的。

而要解决振动问题，我们需要明确振动的几个关键要素，比如振幅、频率、周期和相位等。

理论力学中，解决振动问题的第一步通常是建立力学模型。

这就像是给我们要研究的振动系统画一幅清晰的“画像”。

我们需要确定系统的组成部分，包括质量、弹簧和阻尼器等，并分析它们之间的相互作用。

以一个简单的弹簧振子为例，它由一个质量块和一个弹簧组成。

在这种情况下，我们可以根据牛顿第二定律来建立运动方程。

假设质量为 m 的物体受到弹簧的弹性力 F ＝ kx（其中 k 是弹簧的劲度系数，x 是物体相对于平衡位置的位移），并且考虑到可能存在的阻尼力（比如摩擦力），其大小通常与速度成正比，方向相反，假设为 cv（其中c 是阻尼系数，v 是速度），那么根据牛顿第二定律 F ＝ ma（其中 a 是加速度），我们可以得到方程：m a ＝ kx cv通过一些数学处理和假设（比如假设阻尼较小，振动为简谐振动等），我们可以将这个方程转化为一个更便于分析的形式，从而求出振动的特征，比如频率和振幅。

但实际的振动问题往往比简单的弹簧振子要复杂得多。

例如，在多自由度系统中，可能存在多个质量和多个弹簧相互连接，这时候就需要用到矩阵的方法来建立和求解方程。

除了建立方程，求解方程也是至关重要的一步。

对于一些简单的线性常系数微分方程，我们可以通过经典的方法，如特征方程法来求解。

但对于更复杂的方程，可能需要借助数值方法，比如龙格库塔法等。

在解决振动问题时，能量方法也是非常有用的。

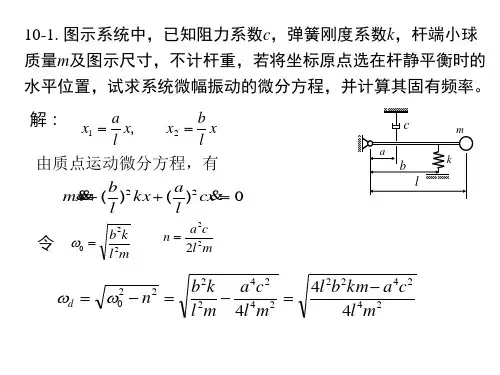
理论力学中的振动力学分析振动力学是理论力学的重要分支，研究物体在受到激励或固有力的作用下发生的振动现象。

它在物理学、工程学和其他领域中有着广泛的应用。

本文将探讨理论力学中的振动力学分析，包括自由振动、受迫振动、阻尼振动以及共振等方面。

自由振动是指物体在没有外界激励的情况下的振动。

它的频率和振幅是由物体的固有属性决定的。

根据振动系统的性质不同，可以分为单自由度振动和多自由度振动。

单自由度振动是指只有一个自由度的振动系统，比如简谐振子。

多自由度振动是指有多个自由度的振动系统，比如梁的弯曲振动和齿轮系统的振动。

在振动力学分析中，我们可以通过求解系统的运动微分方程来得到振动的解析解，从而获得物体的振动模态。

受迫振动是指物体在外力作用下的振动。

外力可以是周期性的，也可以是非周期性的。

对于受迫振动的分析，我们可以利用拉格朗日方程和牛顿第二定律进行分析。

通过求解运动微分方程，我们可以得到物体在受迫振动下的运动规律，进而确定其响应和频率特性。

阻尼振动是指物体在有摩擦力或阻尼器存在下的振动。

阻尼力会消耗物体的振动能量，使得振动逐渐减弱并最终趋向于稳定状态。

阻尼振动的分析可以采用阻尼振动微分方程进行。

根据阻尼力与速度之间的关系，可以分为线性阻尼、非线性阻尼和阻抗阻尼。

线性阻尼是指阻尼力与速度成正比，非线性阻尼指阻尼力与速度的平方成正比，而阻抗阻尼则是指阻尼力与速度的高次方的乘积成正比。

共振是指物体在受到与其固有频率相同的外力激励时振幅达到最大的现象。

共振可以引起物体的失稳和破坏，因此在工程设计中，需要避免共振现象的出现。

共振的分析可以通过计算系统的频率响应函数来实现。

频率响应函数可以描述物体对不同频率外力的响应情况，从而确定共振频率和共振幅值。

综上所述，振动力学在理论力学中具有重要的地位和应用价值。

通过对振动力学的深入研究和分析，我们可以理解物体在振动过程中的特性和行为，进而为工程设计和科学研究提供有力的支持。

懂得振动力学的基本原理和方法，对于处理实际问题和解决振动相关的工程难题具有重要的意义。

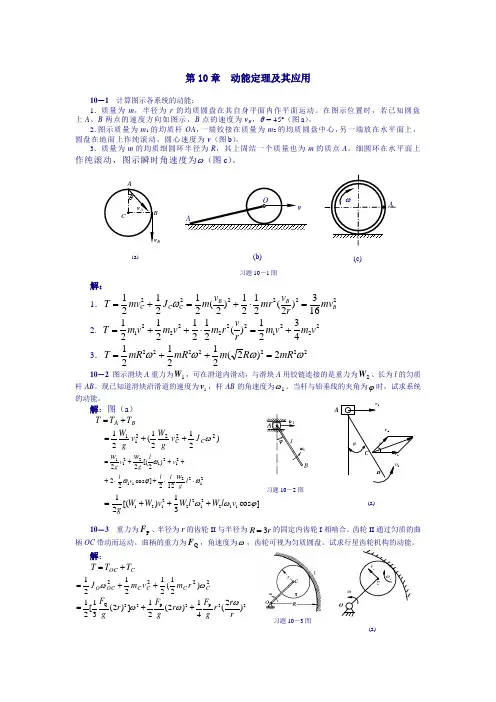
(a)A(a)O第10章 动能定理及其应用10－1 计算图示各系统的动能：1．质量为m ，半径为r 的均质圆盘在其自身平面内作平面运动。

在图示位置时，若已知圆盘上A 、B 两点的速度方向如图示，B 点的速度为v B ，θ = 45º（图a ）。

2．图示质量为m 1的均质杆OA ，一端铰接在质量为m 2的均质圆盘中心，另一端放在水平面上，圆盘在地面上作纯滚动，圆心速度为v（图b ）。

3．质量为m 的均质细圆环半径为R ，其上固结一个质量也为m 的质点A 。

细圆环在水平面上作纯滚动，图示瞬时角速度为ω（图c ）。

解：1．222222163)2(2121)2(212121BB BC C C mv r v mr v m J mv T =⋅+=+=ω 2．222122222214321)(21212121v m v m r v r m v m v m T +=⋅++=3．22222222)2(212121ωωωωmR R m mR mR T =++=10－2 图示滑块A 重力为1W ，可在滑道内滑动，与滑块A 用铰链连接的是重力为2W 、长为l 的匀质杆AB 。

现已知道滑块沿滑道的速度为1v ，杆AB 的角速度为1ω。

当杆与铅垂线的夹角为ϕ时，试求系统的动能。

解：图（a ）B A T T T +=)2121(21222211ωC C J v g W v g W ++=21221121212211122]cos 22)2[(22ωϕωω⋅⋅+⋅++++=l gW l l v l v l g W v g W]cos 31)[(2111221222121ϕωωv l W l W v W W g +++=10－3 重力为P F 、半径为r 的齿轮II 与半径为r R 3=的固定内齿轮I 相啮合。

齿轮II 通过匀质的曲柄OC 带动而运动。

曲柄的重力为Q F ，角速度为ω，齿轮可视为匀质圆盘。

试求行星齿轮机构的动能。

理论力学中的振动现象理论分析振动是物体在某一参考点附近周期性地往复运动的现象。

在理论力学中，振动现象是一种重要的研究对象，对于理解物体的运动规律和解决实际问题具有重要意义。

本文将从理论力学的角度，对振动现象进行理论分析。

一、振动的基本概念和特征振动是物体在某一平衡位置附近往复运动的现象。

振动的基本特征包括周期性、往复性和谐波性。

周期性意味着振动现象具有一定的周期，即在一定时间内重复发生；往复性指物体在振动过程中来回运动；谐波性表示振动的运动规律可以用正弦或余弦函数来描述。

二、单自由度振动的理论分析单自由度振动是指物体在一个自由度上进行振动，常见的例子包括弹簧振子和简谐振子。

弹簧振子是通过弹簧连接的质点在重力作用下进行振动，而简谐振子是指受到恢复力作用的质点进行的振动。

对于单自由度振动，可以通过运动方程和力学原理进行理论分析。

运动方程可以通过牛顿第二定律得到，即质点的加速度与作用力之间的关系。

对于弹簧振子和简谐振子，运动方程可以表示为mx'' + kx = 0，其中m是质点的质量，x是质点的位移，k是恢复力的劲度系数。

通过求解运动方程，可以得到振动的解析解。

对于弹簧振子和简谐振子，解析解可以表示为x = Acos(ωt + φ)，其中A是振幅，ω是角频率，t是时间，φ是初相位。

解析解可以描述振动的幅度、频率和相位等特征。

三、多自由度振动的理论分析多自由度振动是指物体在多个自由度上进行振动，常见的例子包括双摆和弦上的驻波。

对于多自由度振动，可以通过运动方程和线性代数的方法进行理论分析。

对于双摆，可以通过运动方程得到两个摆角的运动方程，然后通过线性代数的方法求解。

通过求解本征值和本征向量，可以得到双摆的固有频率和振型。

固有频率表示双摆的振动频率，振型表示双摆的形状和运动规律。

对于弦上的驻波，可以通过波动方程和边界条件进行理论分析。

波动方程可以描述弦上的波动现象，边界条件可以表示弦的两端的约束条件。

第十章 机械振动和机械波一、基本知识点机械振动：物体在平衡位置附近的往复运动叫做。

胡克定律: 弹簧弹性力F 的大小与位移x 的大小成正比，而且F 的方向与位移方向相反，即F kx =-式中，k 为弹簧的劲度系数。

具有这种性质的力称为线性回复力。

简谐振动的运动学方程:cos()x A t ωϕ=+式中A 为振幅，表示振动物体离开平衡位置的最大位移的绝对值；()t ωϕ+是决定简谐振动状态的物理量，称为在t 时刻振动的相位，单位是弧度()rad ；ϕ为初相位，是0t =时刻的相位；ω=角频率。

简谐振动的动力学方程:2220d x x dtω+=简谐振动的频率：振动物体在单位时间内完整振动的次数，单位是赫兹()Hz 。

简谐振动的周期：振动物体完成一次完整振动所经历的时间，单位是秒()s 。

关系：周期T 是频率ν的倒数；ω=2πν=2π/T简谐振动物体的速度:sin()cos()2dx A t A t dt πυωωϕωωϕ==-+=++ 简谐振动物体的加速度:22222cos()cos()d xa A t x A t dtωωϕωωωϕπ==-+=-=++振幅：A = 初相位：arctanx υϕω-= 式中，0x 为t=0时刻的初始位移，0υ为t=0s 时刻的初始速度。

旋转矢量法: 用一个旋转矢量末端在一条轴线上的投影点的运动来表示简谐振动的方法。

以简谐振动的平衡位置O 作为x 轴的坐标原点，自O 点出发作一矢量A（其长度等于简谐振动振幅A ）。

设0t = 时刻，矢量A 与x 轴所成的角等于初相位ϕ。

若矢量A以角速度ω（其大小等于简谐振动角频率ω）匀速绕O 点逆时针旋转，则在任一时刻矢量A末端在x 轴上的投影点P 相对原点的位移为cos()x A t ωϕ=+，显然，P 在x 轴上做简谐振动。

如图10-1所示。

cos()x A t ωϕ=+图10-1 简谐振动的旋转矢量法弹簧振子的弹性势能：222211cos ()22p E kx mA t ωωϕ==+弹簧振子的动能：222211sin ()22k E m mA t υωωϕ==+ 系统的总机械能：2212p k E E E mA ω=+=表明总机械能总量守恒。

理论力学中的波动与振动分析波动与振动是理论力学中重要的研究方向，涉及到许多实际应用和科学理论。

本文将从经典力学和量子力学两个方面，对波动与振动进行深入分析。

一、经典力学中的波动与振动在经典力学中，波动可以用以下形式的波动方程来描述：ψ(x, t) = A * sin(kx - ωt + φ)其中，ψ是波函数，A代表振幅，k是波数，x表示位置变量，ω代表角频率，t为时间变量，φ为相位角。

振动是波动的一种特殊形式，当振动发生在一维系统中时，可以用简谐振动方程来描述：x(t) = A * cos(ωt + φ)其中，x为位移，A为最大位移量，ω为角频率，t为时间，φ为初相位角。

二、量子力学中的波动与振动在量子力学中，粒子的波动性由波函数来描述，而波函数的演化满足薛定谔方程：i * ℏ * ∂ψ/∂t = -Ĥψ其中，Ĥ为哈密顿算符，ℏ为普朗克常数除以2π。

量子力学中的波动性表现为粒子的波粒二象性，即既具有粒子性又具有波动性。

粒子的波函数通过薛定谔方程得到后，可以用波包的形式表示。

波包是一个由多个简谐波组合而成的波动形式，可以用高斯波包表达。

对于振动来说，在量子力学中，可以用谐振子模型进行描述。

谐振子模型是量子力学中的一个重要模型，它是简谐振动的量子版本。

谐振子的哈密顿算符表达式为：Ĥ = (ℏω/2) * (a^†a + aa^†)其中，a和a^†分别是谐振子的湮灭算符和产生算符，ℏ是普朗克常数除以2π，ω为角频率。

谐振子的能级由能量本征值给出。

三、波动与振动的应用波动和振动在物理学、工程学和其他学科中有广泛的应用。

以下是一些常见的应用领域：1.声学：声音是通过空气中的波动传播的，声学研究了声音的起源、传播和感知。

声波的频率和振幅可以影响我们对声音的感知。

2.光学：光是一种电磁波，光学研究了光的传播、反射、折射等现象。

波动光学理论可以解释光的干涉、衍射等现象。

3.无线通信：通过调制载波的振幅和频率，可以实现无线信号的传输。

理论力学中的自由振动分析正文：自由振动是理论力学中重要的研究内容，对于许多物理系统的描述和分析具有重要意义。

本文将从理论力学的角度出发，对自由振动的分析进行探讨。

1.自由振动的概念及特点自由振动指的是在没有外力作用下，物体相对平衡位置发生来回运动的现象。

它具有一定的特点，包括振幅恒定、周期恒定、频率恒定、起始相位任意等。

2.单自由度谐振子的分析单自由度谐振子是理论力学中最简单的模型，它的运动方程可以用简谐振动方程来描述。

在给定势能函数和初始条件的情况下，可以通过求解运动方程得到振动的解析解。

3.动力学平衡法在自由振动分析中的应用动力学平衡法是一种常用的分析自由振动的方法，它基于动力学原理，通过建立动力学方程和适当的边界条件，可以求解系统的自由振动频率和振型。

4.拉格朗日方程在自由振动中的应用拉格朗日方程也是分析自由振动的强大工具，它将系统的动力学问题转化为虚功原理的极值问题。

通过求解拉格朗日方程，可以得到系统的自由振动方程及其解析解。

5.自由振动的能量及其守恒定律自由振动过程中，系统会在动能和势能之间不断转化。

根据能量守恒定律，系统的总能量在振动过程中保持不变。

通过能量的分析可以更加深入地理解自由振动的特点和规律。

6.自由振动的实际应用自由振动的研究不仅仅局限于理论推导和分析，其在实际应用中也具有广泛的价值。

例如，在工程领域中，通过对结构物自由振动特性的研究，可以预测和评估其振动响应，为设计和改进结构提供依据。

结语：自由振动是理论力学的重要研究内容，通过对自由振动的分析，可以揭示物体运动的规律和特性。

同时，自由振动的研究也具有实际应用价值，为工程设计和结构优化提供了理论支持。

通过对自由振动的深入研究，我们可以更好地理解物体的振动行为，并为相关领域的发展做出贡献。