下载文档原格式
高中数学知识点树形图总结一、数与代数1. 数的基本概念- 整数s与有理数- 实数与复数- 绝对值与相反数- 乘法口诀与乘除法规则2. 代数表达式- 单项式与多项式- 因式分解- 代数式的加减乘除- 完全平方公式与立方和差公式3. 一元一次方程与不等式- 方程与方程的解- 解一元一次方程- 一元一次不等式及其解集- 线性函数的图像与性质4. 二元一次方程组- 方程组的解- 消元法- 代入法- 线性方程组的图像解法5. 一元二次方程- 一元二次方程的标准形式- 配方法- 公式法- 因式分解法- 根的判别式与根与系数的关系6. 不等式与不等式组- 不等式的性质- 解一元二次不等式- 含绝对值的不等式- 不等式组及其解集的确定二、平面几何1. 点、线、面- 点的位置关系- 直线的方程- 射线与线段- 平面的基本性质2. 三角形与四边形- 三角形的基本性质- 特殊三角形（等腰、等边、直角） - 四边形的分类与性质- 多边形的内角和与外角和3. 圆的基本性质- 圆的定义与性质- 圆的方程- 切线与割线- 圆与圆的位置关系4. 相似与全等- 全等三角形的判定- 相似三角形的判定与性质- 比例与相似比- 相似多边形5. 三角函数- 正弦、余弦、正切函数- 三角函数的基本关系- 三角函数的图像与性质- 解三角形问题6. 几何变换- 平移与旋转- 轴对称与中心对称- 相似变换与全等变换三、立体几何1. 空间几何体- 棱柱、棱锥与圆柱、圆锥 - 长方体与正方体- 球的体积与表面积- 多面体的表面积与体积 2. 空间位置关系- 点与直线的位置关系- 直线与平面的位置关系 - 直线与直线的位置关系 - 平面与平面的位置关系 3. 空间向量- 向量的加法与数乘- 向量的点积与叉积- 向量的模与方向余弦- 向量在立体几何中的应用四、概率与统计1. 概率的基本概念- 随机事件与概率的定义 - 事件的概率计算- 条件概率与独立事件2. 随机变量及其分布- 离散型随机变量- 连续型随机变量- 概率分布与概率密度函数3. 统计量与统计图表- 均值、中位数与众数- 方差与标准差- 直方图、饼图与箱线图4. 抽样与估计- 抽样分布- 参数估计- 置信区间5. 假设检验与回归分析- 假设检验的基本概念- 单样本与双样本假设检验- 线性回归与相关性分析五、数学思维与方法1. 合情推理与演绎推理- 归纳法与类比法- 反证法与归谬法2. 数学证明方法- 直接证明与间接证明- 构造性证明- 极限概念在证明中的应用3. 数学建模与问题解决- 数学建模的基本步骤- 问题解决策略- 数学在实际问题中的应用以上是高中数学知识点的树形图总结，涵盖了高中数学课程的主要。
高一数学集合知识点归纳树状图数学是一门综合性学科，其知识点繁多而复杂。
在高中阶段，学生们需要对各个数学分支的知识点进行系统的学习和掌握。
其中，集合论作为数学的一部分，也是高中数学的重要内容之一。
本文将通过归纳整理，展示高一数学集合知识点的树状图，帮助读者更好地理解和掌握这一领域的知识。
一、集合的定义与基本概念集合是数学中一个基本的概念，它是指由确定的元素所构成的整体。
在集合的定义中，常见的符号有大括号“{}”和“∈”表示“属于”。
例如，{1, 2, 3}表示一个由元素1、2和3构成的集合，而1∈{1, 2, 3}表示元素1属于该集合。
二、集合之间的关系在集合论中，有几个重要的关系需要了解。
其中，包括交集、并集、差集和补集。
1. 交集：表示两个集合的共同元素组成的集合。
使用符号“∩”表示。
例如，A∩B表示集合A和集合B的交集。
2. 并集：表示两个集合的所有元素组成的集合。
使用符号“∪”表示。
例如，A∪B表示集合A和集合B的并集。
3. 差集：表示集合A中有而集合B中没有的元素组成的集合。
使用符号“-”表示。
例如，A-B表示集合A和集合B的差集。
4. 补集：表示全集中不属于某个集合的元素组成的集合。
使用符号“c”表示。
例如，A’表示集合A的补集。
三、集合的特殊性质除了基本概念和关系外，集合还有一些特殊的性质需要了解。
1. 空集：不包含任何元素的集合称为空集，使用符号“Φ”表示。
2. 全集：包含所有可能元素的集合称为全集。
3. 子集：如果一个集合中的所有元素都属于另一个集合，那么这个集合是另一个集合的子集。
4. 幂集：集合的幂集是指所有子集所构成的集合。
四、集合运算与集合关系的性质在集合的运算和关系中，存在一些重要的性质。
1. 交换律和结合律：交换律表示交集和并集的操作次序不影响结果；结合律表示交集和并集具有结合性质。
2. 分配律：交集和并集之间存在分配律，可以用来简化复杂的运算。
3. 同一律和零元律：集合的交集和并集与全集、空集之间具有同一律和零元律。
高一高二数学知识点框架数学是一门基础性学科，在高中阶段，学生需要掌握一系列的数学知识点，为今后进一步学习和应用数学打下坚实的基础。
本文将按照高一和高二学年，对数学知识点进行框架性的概述，以帮助学生系统地了解和学习这些知识点。
高一数学知识点框架：1. 函数与方程- 函数的概念及性质- 一次函数与二次函数- 指数函数与对数函数- 三角函数- 一元二次方程与不等式- 二元一次方程组2. 平面几何- 平面几何基本概念- 各种图形的性质与计算 - 空间几何初步认识3. 三角函数- 三角函数的定义和性质 - 三角函数的图像与性质 - 三角函数的变换与应用4. 概率与统计- 概率的基本概念与计算 - 统计的基本概念与应用 - 统计图表的绘制与分析5. 数列与数列的应用- 等差数列与等比数列- 数列的通项公式及求和公式 - 数列在实际问题中的应用6. 其他重要知识点- 特殊函数的性质与应用- 数据分析与概率- 平面解析几何初步认识高二数学知识点框架：1. 微积分初步- 极限与连续- 导数与微分- 函数与导数- 微分中值定理与导数应用2. 三角函数与复数- 三角函数的进阶概念与性质 - 三角函数的图像与性质- 复数的基本概念与计算3. 空间几何与向量- 空间中的点线面- 向量的基本概念与运算- 平面与直线方程4. 概率与统计进阶- 随机事件与概率计算- 离散型随机变量与概率分布- 正态分布与抽样- 统计推断与假设检验5. 数列与数列的应用进阶- 递推数列与其它数列- 数列的极限与收敛性- 数列在实际问题中的应用6. 其他重要知识点- 函数与方程的进阶概念与性质- 平面解析几何的进阶认识- 微积分在实际问题中的应用以上只是对高一和高二数学知识点进行了简要的概述，实际上每个知识点都非常广泛而深入。
在学习过程中，学生需要通过课堂学习、课后练习以及辅导材料的阅读来巩固和加深对数学知识点的理解与应用。
同时，老师和家长的指导与帮助也是至关重要的。
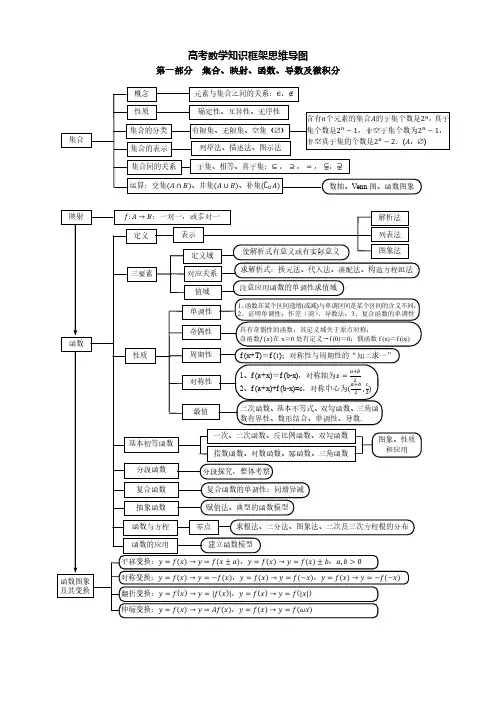
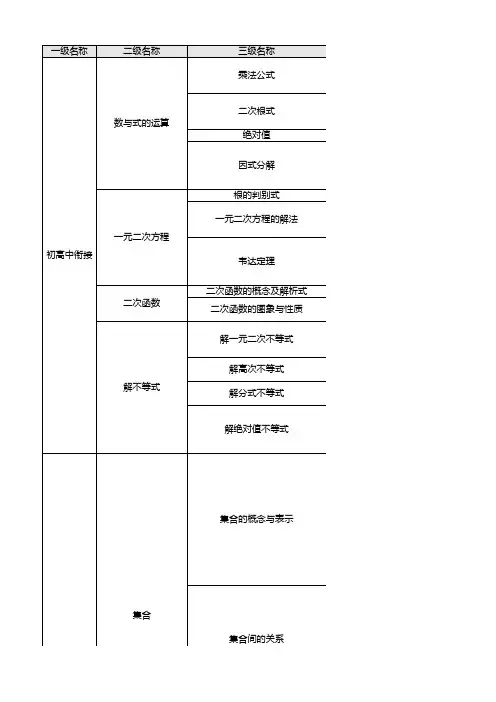
高一数学全部知识点框架高一数学是中学阶段的重要学科之一，它为后续的学习打下了基础。
在高一数学学习中，我们将学习多个不同的知识点。
下面是高一数学全部知识点的框架：1. 数学基础知识1. 数的集合及运算2. 数的性质与计算3. 整式与分式4. 数与式的计算与运算5. 近似数与有效数字2. 一次函数与方程1. 一次函数及其性质2. 一次方程及其解法3. 一次函数的图像与应用3. 二次函数与方程1. 二次函数及其性质2. 二次方程及其解法3. 二次函数的图像与应用4. 平方根与无理方程4. 不等式与线性规划1. 不等式及其性质2. 一元一次不等式的解法3. 一元二次不等式的解法4. 线性规划问题的解法5. 数列与数学归纳法1. 数列及其性质2. 等差数列与等比数列3. 数列的通项公式与求和公式4. 数学归纳法的应用6. 平面向量与解析几何1. 平面向量的定义与运算2. 平面向量的性质与判定3. 平面向量的应用4. 解析几何中的直线与圆7. 三角函数与解三角形1. 三角函数的概念与性质2. 三角函数的图像与变换3. 特殊角与三角恒等式4. 解三角形的基本原理与方法8. 概率与统计1. 随机事件与概率2. 随机变量与概率分布3. 统计与统计图表4. 抽样与统计推断9. 空间几何与立体几何1. 空间中点、距离与斜率2. 点、直线、平面的位置关系3. 空间几何中的相交与垂直4. 立体几何中的体积与表面积10. 三角函数在坐标系中的应用1. 三角函数与坐标系2. 正弦定理与余弦定理3. 平面向量与三角形的关系4. 三角函数的应用问题以上是高一数学全部知识点的框架，通过系统学习和巩固这些知识点，将为我们打下坚实的数学基础，为高中数学学习奠定良好的基础。
希望每位同学都能努力学好高一数学，为未来的学习铺平道路。
高一到高三数学知识点框架数学作为一门科学，是一种用来研究数量、结构、变化以及空间等概念的学科。
在高中阶段，数学的学习变得更加深入和广泛，包含了许多重要的数学知识点。
以下是高一到高三数学知识点的框架概述。
一、高一数学知识点1. 初识代数- 复数与复数运算- 一次函数与二次函数- 不等式与不等式运算2. 平面直角坐标系- 点、直线、圆、抛物线、双曲线的方程与性质- 点、直线、圆、抛物线、双曲线的位置关系3. 三角函数- 各三角函数的定义、性质与图像- 三角函数的运算与解三角形4. 解析几何- 向量的概念与运算- 直线、平面的方程与性质- 圆、二次曲线的方程与性质5. 立体几何- 点、线、面的位置关系与垂直公理- 空间直角坐标系- 直线、平面与空间曲线的方程与性质二、高二数学知识点1. 函数与导数- 函数的极限与连续性- 导数的定义、性质与计算法则- 函数的单调性与凹凸性2. 数列与数列极限- 数列的表示与性质- 数列的极限与极限计算- 等差数列与等比数列3. 三角函数与导数- 三角函数的极限与连续性- 三角函数的导数与导数计算- 三角函数的单调性与凹凸性4. 微分学应用- 函数的最值与最值问题- 异常点与拐点- 近似计算与线性化5. 空间解析几何- 空间中的直线与平面- 空间曲线的切线与法平面- 空间曲面的法向量三、高三数学知识点1. 函数与导数（复习与拓展）- 反函数与复合函数- 高阶导数与导数应用- 导数与函数的图像2. 不等式与极值- 不等式的性质与求解方法- 不等式组与解集表示- 函数极值的判定与应用3. 积分学基础- 定积分的性质与计算方法- 曲线下面积与面积应用- 平均值与均值定理4. 函数与积分- 反常积分与变限积分- 曲线长度与曲面旋转体积- 平面图形的面积与曲线的弧长5. 排列与组合- 排列与排列组合- 不同排列与重复排列- 置换与选择问题以上是高一到高三数学知识点的框架概述。
这些知识点构成了高中数学学科的核心内容，每个知识点都有其自身的重要性和应用价值。
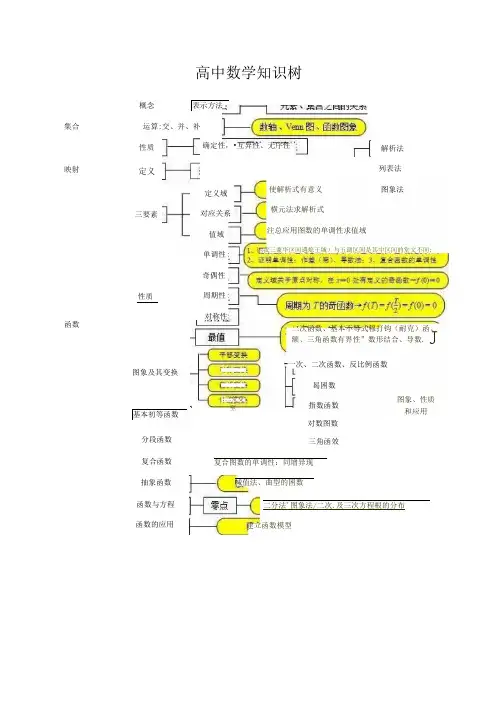
集合映射函数概念性质高中数学知识树表示方法性质定义三要素运算:交、并、补确定性，•互异性、无序性解析法列表法使解析式有意义图象法定义域横元法求解析式对应关系注总应用图数的单调性求值域值域单调性奇偶性周期性对称性图象及其变换曷困数:三荒芟至指数函数对数图数图象、性质和应用困我三兼华区间遇熄王城）与五调区间是其中区间的堂文不间;二次函数、基本不等式穆打钩（耐克）函、额、三角函数有界性”数形结合、导数. J基本初等函数分段函数复合函数-一次、二次函数、反比例函数三角函效复合图数的单调性：同增异现抽象函数函数与方程函数的应用建立函数模型喊值法、曲型的困数二分法'图象法/二次.及三次方程根的分布甬的概念弧度制强长公式、扇形面租公式任意用的三角图数的定义•—三用国数级②圉象也可以用五点作圉法+电用整体代换求单调区间f注意那符号”金最小正周期丁= ⑤对称轴工=--+ 2,对称中心为Jy，出csn 平面向重+ i 转为通 庭用吕加法黑访求粕击错包相加法可行垃 目标臼舞 应用期 最值问照基本不等式士 几何憨文： 二是H 毓，+与 ””「，正1胜甑 ，困支括一轴上能舞里H 措」 第打顶和 一畤》［+—）范三的形 -I 立院由甲除等比螂蚯%+去｝T 简单的名研生规制 ⑥加“7口产%一 %7⑤小■户尸什小 d 公式法：应用等差.等比数列的前也顶和公式）（借助二次曲数的图象X7^十二次的美蔡） 解析法；s*"|-Q 列g 特触厩射）图象法 L_|等型列卜速报公式答型刷 ~~（等嚏翱列三阍七重列的停世;）T 短触：i —tn+fy .*i 书： 通炳公式梅脸式二=4口-疔+u -汴：相道距离的d =/（»）不等式的性感 一元二次不源式 正弦定理卜（醒的1■野的法诺）余弦定理 羊庭增＞ 租演文：积定位L 粕展小应用时上黄：-正二定三相萼 常见建推类型及方法 常见求和方法 -Q 》组求和一 ）不答式 班到圆锥曲线充分舞必要条件、必要mE充分条件、充要条件全构里同局■点0口一比,乃一）。
