当前位置：文档之家 › 量子力学(第六章)

量子力学(第六章)

  • 格式：ppt
  • 大小：1.77 MB
  • 文档页数：71

下载文档原格式

  / 71

合集下载

量子力学导论第6章答案

量子力学导论第6章答案

第六章 中心力场6.1) 利用6.1.3节中式（17）、（18），证明下列关系式相对动量 ()21121p m p m Mr p-==∙μ （1） 总动量1p p R M P+==∙ （2）总轨迹角动量p r P R p r p r L L L⨯+⨯=⨯+⨯=+=221121 （3）总动能 μ222222222121pMP m p m p T +=+= （4）反之，有 ,11r m R rμ+= r m R r22μ-= （5） p P m p +=21μ，p P m p -=12μ（6）以上各式中，()212121 ,m m m m m m M +=+=μ证： 212211m m r m r m R ++=， （17） 21r r r -=， （18）相对动量 ()21122121211p m p m M r r m m m m r p-=⎪⎪⎭⎫ ⎝⎛-+==∙∙∙μ （1’）总动量 ()2121221121p p m m r m r m m m R M P+=+++==∙∙∙ （2’）总轨迹角动量 221121p r p r L L L⨯+⨯=+=)5(2211p r m u R p r m u R ⨯⎪⎪⎭⎫⎝⎛-+⨯⎪⎪⎭⎫ ⎝⎛+= ()()2112211p m p mMr p p R -⨯++⨯=)2)(1(p r P R ⨯+⨯=由（17）、(18)可解出21,r r，即（5）式；由（1’）（2’）可解出（6）。

总动能()22112262221212222m p P m m p P m m p m p T ⎪⎪⎭⎫⎝⎛-+⎪⎪⎭⎫⎝⎛+=+=μμ2122222122112222122222m m p P u m pPm m um m p P u m pPm m u⋅-++⋅++=()()⎪⎪⎭⎫⎝⎛+++++=2122221222211112122m m p Pm m m Pm m m μ2222pMP +=（4’）［从（17），(18)式可解出（5）式；从（1），(2)式可解出（6）式］.6.2) 同上题，求坐标表象中p 、P 和L 的算术表示式r i p ∇-= R i P ∇-= ，p r P R L⨯+⨯=解： ()()211221121r r m mMi p m p mMp ∇-∇-=-=（1）其中 1111z k y j x ir ∂∂+∂∂+∂∂=∇，而x X M m x x x X x X x ∂∂+∂∂=∂∂∂∂+∂∂∂∂=∂∂1111，同理，y YM m y ∂∂+∂∂=∂∂11zZM m z ∂∂+∂∂=∂∂11；（利用上题（17）（18）式。

量子力学答案(第二版)苏汝铿第六章课后答案6.16-6#8

量子力学答案(第二版)苏汝铿第六章课后答案6.16-6#8
代入薛定鄂方程： i
(s x + s y + s y ) ？？
sin qe- iwt ÷ ÷ ÷ - cos q ÷
，设 f (t )＝ç ç
¶f = Hf ¶t
骣 a(t )÷ ÷，则有 ç ÷ b(t )÷ 桫
i d a(t ) = cos qa(t ) + sin qe- iwt b(t )......(1) - m0 B dt i d b(t ) = - cos qb(t ) + sin qeiwt a(t ).....(2) - m0 B dt
c1' = iw1e- iwt c2
化简得： 其中：
c2' = iw1eiwt c1
cos q, w1 = m0 B sin q, w2 = w + 2w0
w0 =
m0 B
a(t ) = c1eiwt b(t ) = c2e- iwt
解得： c2 '' = iw2c2 '- w12c2 （＊） 由初始条件：
( S1z - S 2 z )c 1 = 0 ( S1z - S 2 z )c 2 = 0 c 4 ( S1z - S 2 z )c 3 = c 3 ( S1z - S2 z )c 4 = 2 2
骣1 2 ç A ç ç 4 ç ç ç ç ç ç 0 ç 所以得到： H ' = ç ç eB ç ç ç ç mc 2 ç ç ç ç ç 0 ç 桫
eB ( S1z - S2 z ) mc 解： eB ＝H 0 + A( sx 2 + s y 2 + sz 2 ) + ( S1z - S2 z ) mc H = H 0 + AS1 S2 +

量子力学答案(第二版)苏汝铿第六章课后答案6.10-6#6 @

量子力学答案(第二版)苏汝铿第六章课后答案6.10-6#6 @
点), 这样就有 L
1 N L 2
耦合之后总磁矩
1 1 N L J ( g p g N )N S J J 2 2 R J ( J 1)
因 J LS 有
N 3 ( g p g N ) N (1) J / 2
旋 S , 然后总自旋再与轨道角动量 l 耦合形成总角动量 J , 用核磁子表示你的结果. 已知质子和 中子的磁矩分别是 2.79 和-1.91 核磁子. 解: (i) S,D 态的宇称为正, 而 P 态的宇称为负, 由于宇称守恒, 开始时为 S 态的量子态在任何 时刻都不可能有 P 态混入 (ii)
1 1 1.5 ( g p g N ) N J 0.31 N J 2 2
取 J 方向的投影并使 J s 为最大值 J 1 , 从而有 0.31 N 6.11 一个 介子(赝标粒子, 自旋为零, 奇宇称)最初别束缚在氘核周围, 并处在最低库仑态
的角分布是多少? (i). 反应前后宇称守恒, 有
p( ) p(d )(1) L1 p(n) p(n)(1) L
L1 , L2 分 别 是 d 及n+n 的 轨 道角 动量 . 但反 应 前 是 在库 仑 势的 最低 能 态
中, L1 0 , 且已知: p( ) 1, p(d ) 1 有
2/3 c , 2/ d 3 , 1/ 3
p 1,1 p 1, 1 0 n 1, 0
查 C G 系数表, 可得
a 1 / 3b ,
共振态的 I 3/ 2 , 经过此面的截面比为 1 2 4 2 a : b : c 1: a : ac 1: : 9 9
能的, 因为 L 1 , 所以几率为 0 (iii) 从而有 初始态为 J , J z 1,1 , 将其变成非耦合表象 L 1, S 1, L, L3 , S , S z

量子力学答案(第二版)苏汝铿第六章课后答案6.7-6#15

量子力学答案(第二版)苏汝铿第六章课后答案6.7-6#15

1 的本征态，粒子 2
1 2 的本征态，取 =1 ，求体系总自旋 S 的可能值及相应的概率。 2
解： S x ;
1 Sz ; Sz ; 2
1 2

（1）
Sz ; Sx ;
（2）
系统处于 S1z ; S2 x ; 的态上，将其写到 S z 的表象中为
S1z ;
编辑者：霍团长 6— 7
对于两个自旋 1/2 的例子组成的体系，证明张量算符
S12
3 (σ1 r )(σ2 r ) σ1 σ2 r2
和 S 2 及 J 对易。 S 为总自旋， J 是总角动量 J = S + l ，l 是体系的轨迹角动量，在质心坐 标系中， l 的算符形式是：
l r p i r , r = r1 - r2
而 S s( s 1)
2
1 S2 z ; S2 z ; 2

其可能值为 0或2 总自旋为零的态可表示为：
0
1 S1z ; S2 z ; S1z ; S2 z ; 2
0
1 1 1 S2 z ; S1z ; S1z ; S2 z ; 2 2 2
证明： （1）
3 2 , σ1 3, ( 1n )2 1 4 1 S s1 s2 (σ1 σ2 ) 2 3 1 ∴ S 2 σ1 σ 2 2 2 1 1 Sn S n (σ1 n σ2 n) ( 1n 2 n ) 2 2 1 1 1 ∴ Sn 2 ( 1n 2 2 n 2 2 1n 2 n ) 1n 2 n 4 2 2
2 解：取系统的力学量完全集为 ( H , S12 , S 2 , Sz )

量子力学 6-1 电子自旋的实验证据

量子力学 6-1 电子自旋的实验证据
1
6-1 电子自旋的实验证据
第六章 电子自旋 全888—1969），
1888年2月17日出生于德国。1906年开 始学习物理化学，1912年在布雷斯劳大 学获博士学位。同年他到布拉格当爱因 斯坦的助手，以后又随爱因斯坦转到苏 黎世，1913年成为物理化学私人讲师。 1943年诺贝尔物理学奖授予斯特恩，表 彰他发展分子束方法和发现了质子的磁矩。
M sz e Sz
7

S
自旋回旋磁比率：
6-1 电子自旋的实验证据
第六章 电子自旋 全同粒子 能级排列
注意
此节重点
(1)理解电子自旋是一种纯粹的量子力学效应，没有经 典图象与之对应。（不是电子自转之类的空间运动）
(2)验证电子自旋存在的实验是斯特恩—盖拉赫实验 (3)每个电子具有自旋角动量 向的取值只能有两个 S z 。 2
1922年，他和合作，成功地做了斯特恩-盖 拉赫实验，通过这个著名实验，他们用分 子束方法证明了空间量子化的真实性，并 为进一步测定质子之类的亚原子粒子的磁 矩奠定了基础。
2
6-1 电子自旋的实验证据
第六章 电子自旋 全同粒子 能级排列
格拉赫（Walther Gerlach）
1889出生于德国. 1912年于图宾根大学获得物理学博士学位。 他的研究对象是黑体辐射和光电效应。一战期间, 盖拉赫和 维恩一起发展无线电报技术。在工业界呆了一段时间后, 盖 拉赫于1920年在法兰克福的实验物理研究所谋到了一个助手 的位置, 该所紧捱着玻恩的理论物理所。后来和斯特恩合作 完成了斯特恩-盖拉赫实验. 3
6-1 电子自旋的实验证据
第六章 电子自旋 全同粒子 能级排列
从薛定谔方程出发可以解释许多微观现象，例如计 算谐振子和氢原子的能级从而得出它们的谱线频率 等。计算结果在相当精确的范围内与实验符合。

量子力学概论第6章 不含时微扰理论

量子力学概论第6章 不含时微扰理论

6.4.3 中间情况的塞曼效应
表6.2 存在精细结构和塞曼分裂的氢原子n=2能级
图6.12 弱场、中间场、强场下，氢 原子n=2能态的塞曼分裂
6.5 超精细分裂图6.1 基态氢原子的超精细分裂图6.14 两个相邻的极化原子
图6.6 例题6.2中的简并的消除
6.3 氢原子的精细结构
6.3.1 相对论修正 6.3.2 自旋-轨道耦合
表6.1 氢原子玻尔能量修正量级图
6.3.2 自旋-轨道耦合
图6.7 从电子看质子运动
图6.8 带电圆环绕轴旋转
图6.9 考虑了精细结构的氢原子能级图(未按比例大小给出)
6.4 塞曼效应
第6章 不含时微扰理论
6.1 非简并微扰理论 6.2 简并微扰理论 6.3 氢原子的精细结构 6.4 塞曼效应 6.5 超精细分裂
6.1 非简并微扰理论
6.1.1 6.1.2 6.1.3
一般公式 一级近似理论 二级能量修正
6.1.1 一般公式
图6.1 受到小微扰的无限深方势阱
对于零级(λ0)项1有H0ψ0n=E0nψ0n, 有 H0ψ0n=E0nψ0n,(6.1)
对于一级项(λ1)有，
H0ψ1n+H′ψ0n=E0nψ1n+E1nψ0n.(6.7)
对于二级项(λ2)有，
H0ψ2n+H′ψ1n=E0nψ2n+E1nψ1n+E2nψ0n， (6.8)
依次类推。(方程中并没有λ——它仅仅用来 更清楚地按数量级分出各方程——所以现在 把λ取为1。)
6.1.2 一级近似理论
E0nxnynz=π2ћ22ma2(n2x+n2y+n2z).(6.32) 注意到基态(ψ111)是非简并的；它的能量为：

第六章 散射

散射
• 具有确定动量的粒子从远处而来，通过另一个粒子（称 为散射中心）附近，相互作用后而发生偏转，又向远处而 去，这就是散射。量子力学中，散射又称碰撞。在碰撞过 程中，如果两粒子内部状态均未发生改变，则称为弹性散 射；反之，称为非弹性散射。
• • 我们仅限于讨论弹性散射。 为方便起见，采用质心坐标系，并假定散射中心的质量 远大于入射粒子的质量，即由碰撞引起的散射中心的运动 可以略去。这样，入射粒子发生弹性散射后，只有运动方 向发生改变，动量大小并未发生改变。 另外，入射粒子与散射中心的相互作用只发生在很小的 空间区域内，在这小区域外，入射粒子（初态）及散射粒 子（末态）均处于自由粒子状态。
微分散射截面的表达式为
q( ) f ( )
2 2
l
（20）

1 k2
(2l 1) P (cos )e
i l 0 l
sin l
（21）
由此可以看出：求散射振幅 f ( )的问题归结为求相移 l ，而 l 的获得需要根据U (r ) 的具体情况解径向方程求 Rl (r ) ，然 后取其渐近解，并写成 Rl (r )
(r , , ) Rl (r )Ylm ( , )
l ,m
若选取粒子入射方向并通过散射中心的轴线为极轴，则 中心力场的散射问题具有轴对称性，波函数及散射振幅都与 无关，即 m 0 ，所以有
(r , , ) Rl (r )Pl (cos )
l
（11）
l 0
2
l Ql
l 0
（22） （23） （24）
Ql
4 k
2
(2l 1) sin 2 l
Q
4 Im f (0) k

量子力学习题

第六章 角动量初步6-1 分别用球坐标和直角坐标证明zL ˆ是厄米算符 6-2 试证明：ϕθϕθψ33sin )(),,(i e r f r =为2ˆL 和zL ˆ的共同本征函数，并求相应的本征值。

说明当体系处于此状态时，yx L L ˆ,ˆ有无确定值。

6-3 设体系处在102111Y C Y C +=ψ的状态中，试：（1）将此波函数归一化；（2）求力学量2L的测量值及相应的几率；（3）求力学量z L 的可能值及相应的几率；（4）x L 和y L 的可能值及相应的几率。

6-4 设在2ˆL 和z L ˆ的共同表象中，算符y L 的矩阵表示为⎪⎪⎪⎭⎫⎝⎛--=0000022i i i i L y ，求它的本征值和归一化的本征函数，并将它表示成m Y 1的线性叠加。

6-5 求粒子处在态lm Y 时，轨道角动量的x 分量和y 分量的平均值x L 和y L ，并证明)(2)()(2222m l l L L y x -+=∆=∆ 6-6 设体系处于zL ˆ的本征态lm Y ，求证轨道角动量沿与z 轴成θ角方向上的分量的平均值为θcos m 了。

6-7 设体系处于某一状态，在该状态中测量力学量L 2 得到的值是22 ，测量力学量zL ˆ得到的值为 -，求测量力学量x L 和y L 的可能值。

6-8 求L 2 ，x L 的共同本征函数，限定222 =L 。

6-9 对于11Y ，求x L 的取值及相应的几率。

6-10 试证明：（1）{}x r L L r i L x x L x )ˆˆ()ˆˆ(ˆˆˆˆ22 ⨯-⨯=- （2）{}xx x x p L L p i L p p L )ˆˆ()ˆˆ(ˆˆˆˆ22 ⨯-⨯=- 6-11 证明： （1）p i p L L pˆ2ˆˆˆˆ =⨯+⨯ （2）⎥⎦⎤⎢⎣⎡=⨯-⨯p L p L L p i ˆ,ˆ)ˆˆˆˆ(2 6-12 证明：p r i p r p r L∙+∙-=2222)(ˆ，进而证明rr r r Lr p ∂∂∂∂-=2222221ˆ1ˆ6-13 对于（z L L ˆ,ˆ2）的共同本征态),(ϕθlm Y ，计算2x L 和2yL 的平均值，以及y x L L ∆∆,，验证测不准关系。

量子力学曾谨言习题解答第六章

第六章：中心力场[1]质量分别为 m 1,m 2的两个粒子组成的体系，质心座标及相对座R标r为：R =212211m m r m r m ++ (1)r 12r r r-= (2)试求总动量21p p P+=及总角动量21l l L +=在R ,r表象中的算符表示。

1. [解] （a ）合动量算符21p p P+=。

根据假设可以解出1r ，2r令21m m m +≡ ： r m m R r121-= （３）r m m R r212+= （４）设各个矢量的分量是),,(1111z y x r ，),(22,22z y x r ,),,(z y x r和),,(Z Y X R 。

为了计算动量的变换式先求对1x ， 2x 等的偏导数：xX m m x x x X x X x ∂∂-∂∂=∂∂∂∂+∂∂∂∂=∂∂1111 （5）xX m m x x x X x X x ∂∂+∂∂=∂∂∂∂+∂∂∂∂=∂∂2222 （6） 关于1y ∂∂，2y ∂∂，1z ∂∂，2z ∂∂ 可以写出与（5）（6）类似的式子，因而： )()(212^1^^2^1^x x i p p p p P x x x x ∂∂+∂∂=+=+==Xi x X m m x X m m i ∂∂=∂∂+∂∂+∂∂-∂∂ )(21 RiZ i k Y i j X i i P ∇=∂∂+∂∂+∂∂= ^(b)总角动量)(2211^2^1^∇⨯+∇⨯=+=r r il l Lx x r r iL )(2211^∇⨯+∇⨯==)()(2222111y z z y i z z y i ∂∂-∂∂+-∂∂ 利用（3），（4），（5），（6）： ))({(12^zZ m m y m m Y i L x ∂∂-∂∂-=))((12y Y m m z m m Z ∂∂-∂∂-- ))((21zZ m m y m m Y ∂∂+∂∂++ )})((21yY m m z m m Z ∂∂+∂∂+- =)()({1y Z z Y Y Z Z Y m m i ∂∂-∂∂-∂∂-∂∂ )()(221y z z y m m Y z Z y m m m ∂∂-∂∂+∂∂-∂∂-)()(2yZ z Y Y Z Z Y m m ∂∂-∂∂+∂∂-∂∂+)}()(2221yz z y m m Y z Z y m m m ∂∂-∂∂+∂∂-∂∂+=)}(){(yz z y Y Z Z Yi∂∂-∂∂+∂∂-∂∂ =x r R r iR i )(∇⨯+∇⨯因而 r R r iR i L ∇⨯+∇⨯=^[2]证明r r r ∂∂+=∇1],[212，∇=∇],[212r（证明）第一式ψ)(2122∇-∇r r =))((21222222222ψz y x zy x ++∂∂+∂∂+∂∂ )(21222222222zy x z y x ∂∂+∂∂+∂∂++-ψψψ但xz y x z y x x z y x x∂∂+++++=++∂∂ψψψ222222222)( 22222222()(z y x x x z y x x ++∂∂=++∂∂ψψ+)222xzy x ∂∂++ψ =232222222)())((z y x x x xz y x ++-+∂∂++ψψψ+2222223222)(xz y x z y x x x∂∂+++++∂∂ψψ即2222222222x z y x z y x x ∂∂++-++∂∂ψψ=232222222)(2z y x x zy x x x++-+++∂∂ψψψ同样写出关于y,z 的式子，相加得：22222222{21)(21zy x zz y y x xr r ++∂∂+∂∂+∂∂=∇-∇ψψψψ+}3222zy x ++-ψψ=r z r z y r y x r x ψψψψ+∂∂+∂∂+∂∂ =ψ)1(rr +∂∂ 因ψ是任意函数，因而第一式得证。

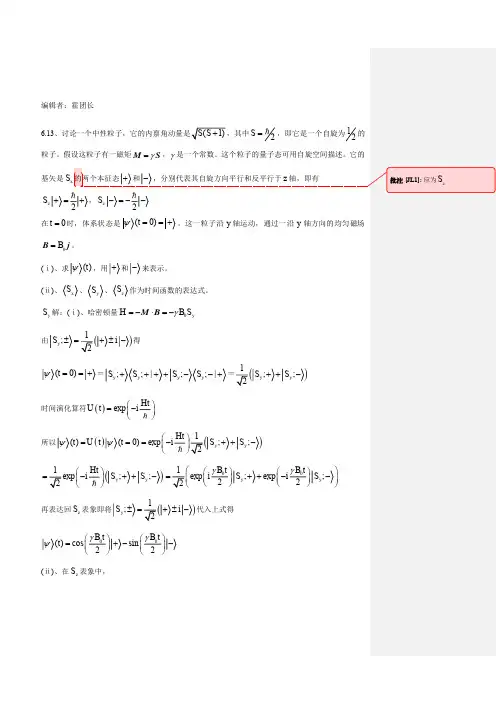
量子力学答案(第二版)苏汝铿第六章课后答案6.13-6#1

2 2

1 1 2 2 2 1 1 x 2 cos s c 4s 2c 2 cos E2 E3 t / 2 2 2 2 1 x 2

1 x 2 Et /

1
1 sin 2 1 x2

1 x 2 Et / 2
批注 [JL1]: 应为 S z
Sz
2
， Sz
2

在 t 0 时，体系状态是
(t 0) 。这一粒子沿 y 轴运动，通过一沿 y 轴方向的均匀磁场
B B0 j 。
(ⅰ)、求
(t ) ，用 和 来表示。
(ⅱ)、 S x 、 S y 、 S z 作为时间函数的表达式。

i
i

B0t B0t 1 S x (t ) | S x | (t ) cos sin B0t ， sin ＝ 2 2 2
S y (t ) | S y | (t ) 0 ，
2 2 2 1 2 2 2 2 1 d i qB ( eB )2 2 E 2u d c 2c 2 2 2 z 2

1 ，所以
在极限情况 0 H / E
1 ，则 x
E g1 g 2 1 0 H g1 g 2 0 H , 4 2 2 E E 1 E2 2 1 x2 1 2 x g1 g 2 0 H ， 4 4 2 E 1 E3 1 2 1 x2 g 2 g1 0 H ， 4 2 E g1 g 2 1 E4 0 H g1 g2 0 H 4 2 2 E1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

i ( ) t 2 2 q 1 p p A p A p c 2


1 q p p p p A 2 c 2q i p p A 2 c
代入正则方程
H H ,P r P r
(2)
即可得出
式中
1 r q E v B (3) c 1 E A (电场强度) (4) c t
B A (磁感应强度)
c
• H和 p 的关系一样。这里 p 为正则动量。由这
个原理和正则量子化规则可知，有电磁场时， 量子化规则应当变更为
i i q t t q i A c
• 这就将电磁势引进了 Schrodinger 方程 。于是， 有电磁场时的 Schrodinger 方程为
的电子的速度 v 远小于光速 c ( v / c 102 ),辐
射场中磁场对电子的作用远小于电场,一般只
考虑电场的作用 。
本章将讨论恒定磁场中原子能级和光谱
的变化(Zeeman效应)以及自由荷电粒子在恒
定磁场中的运动(Lanbau能级)。 下面首先给出给出荷电粒子在恒定电磁 场中的Schrodinger方程。
A A A ( r , t ) 1 (r , t ) (16) c t 电场强度 E 和磁场强度 B 都不改变。
可以证明Schrodinger方程(9)在规范变换(16)
式下，只需波函数也同时经受如下定域相位变
因而Schrodinger方程为
q 2 1 i (i A) q (9) t c 2 q q 1 (i A) (i A) q c c 2 一般说来， 与 A 不对易
换(注意，此时相因子依赖于空间坐标，是定
域的)
e
则方程(9)形式不变
iq ／c

(17)
2 1 q i P A q t c 2
(18)
这说明，电磁场中Schrödinger方程具有定域
§近似看成在一个中心 平均场中运动，能级一般有m简并。实验发现， 如把原子(光源)置于强磁场中，原子发出的 每条光谱线都分裂为三条，此即正常Zeeman 效应，光谱线的分裂反映原子的简并能级发 生分裂，即能级简并被解除或部分解除 。
在原子大小范围中，实验室里常用的磁 场都可视为均匀磁场，记为 B，不依赖于电 子的坐标，于是，相应的矢势 A 可写为: 1 A B r （对称规范） (1) 2 不难验证 A B, A 0 。 取磁场方向为z轴方向，则
但若利用电磁场的横波条件 A 0
p A A p i A
P
(10) ，则方
程(9)也可以表示为
2 2 1 q q 2 i p A p+ A +q 2 t c 2 c 2 (11)
附：最小电磁耦合原理及电磁场 中的 Schrodinger 方程
• 在建立 Schrodinger 方程的一次量子化中，我 们使用了以下对应
E i t p i
•
有电磁场时，电磁势表示为 ( A ) ( A, i ). 。按经
典的最小耦合原理，对电荷为 q 的粒子，其 q ( H q )和（p A) 之间的关系如同无电磁场时
第六章 电磁场中粒 子的运动
本章所讲的主要内容
电磁场中荷电粒子运动，两类动量(6.1) 正常Zeeman效应(6.2)
Landau能级(6.3)
氢原子问题,即电子在原子核的Coulomb
引力 势中的运动。原子核结构问题原则上可
以归结为彼此有Coulomb斥力的多电子体系在
原子核Coulomb引力势中的运动。由于原子中
式(3)即荷电q的粒子在电磁场中的Newton方 程,式(3)右边第二项即Lorentz力。由（1） 和（2）不难 得到 H 1 q x ( px Ax ), (5) px c
所以 q q Ax x Ax px x c c 因而 q p A , (6) c
1 q 2 H ( p A) e(r ) V (r ) （2） 2 c
其中 是标量电磁势，而V (r )是由非电磁 力（例如核力）所引起的任何另外的势。 将 p 换成算符i ，经典表示式（2）就可 以转换成量子力学的表示式。因此我们得 到推广的薛定谔方程








即
式中
j 0 t
(13)
1 q j p p A 2 c




1 q q p A p A 2 c c
i
将这些表示式代入到式(6)，按(7)同时用 代替 ，则得 A, A,
2 i 2 2 2 e H { 2i i ( ) } 2 iq { A i A i c 1 2 1 ( A) } 2 2 2 q 2 2 {A 2 A ( ) } 2 2 c q （11） (q ) V c t
（其中 是时间和空间的任意函数），而不 会改变场强 1 A B A; E （8） c t 如果物理现象仅仅决定于场强而不决定于势， 则这个规范不变性在量子理论中也必须成立。 现在如果我们简单的将(7)代入哈密顿量 (6)，当然会得到一些破坏薛定鄂方程规范不 变性的附加项。为了可能消去这些项，只有 让波函数也参与规范变换，但是由于 有 * 确定的物理意义，因此它和场强一样不会由 于变换而改变，唯一的可能是设
iq 2 其中 H ( A A ) 2 2 c 2 q 2 （4） A q V 2 2 c
2
i H t
（3）
由于
( A ) A A
（5）
上式子可化为 2 iq 1 2 H ( A A) 2 c 2 q2 2 A q V （6） 2 2 c 在麦克斯韦的经典理论中还证明，矢势 A 和标势 可以同时进行如下的规范变换 1 A A A ; c t （7）
规范不变性。此外，容易证明， , j, v
等都具有规范不变性。
附：关于电磁场中Schrodinger 方程的规 范不变性的证明 在经典电动力学中已经证明，用矢势 A q 的任意粒子的动 描述的磁场使得电荷为 量 p 要用
q P p A c
（1）
来代替，于是非相对论性的哈密顿量变成
i e
（9）
其中 仍然可以是r 和t的任意适当的函数。 这样一来
i
e { i} 2 i 2 2 2 e { 2i i ( ) } （10）
e { i }
1 q 2 i [ (i A) V q ] t 2 c
q p A 是机械（普通）动量 这里 V 为其它势能项， c
算符， p i 为正则动量算符。注意，现在机械 动量 正则动量。

2.规范不变性 作下 电磁场具有规范不变性，即当A， 列规范变换时，
重新整理后可得 iq c i e H H ( ) c q
q 如果令 c
iq 2 c q 2 c { ( ) 2 A ( )} 22 c q mc q 2 2 e c c 2 2 {( ) 2 ( ) } 2 2 2 c q q q （ 12 ） c t
1 v v Re( v ) 2
(14)
q 1 q 1 v p A i A (15) c c
可理解为粒子的速度算 与式(6)比较，v 符，而 j 为流密度算符。
讨论
1.定域的概率守恒与流密度 式(11)取复共轭(注意，A 与 为实，在坐
标表象中 p p )
2 2 1 q q 2 i p A p+ A +q 2 t c 2 c 2 (12) (11) (12) 利用 A 0 ,得
§6.1
电磁场中荷电粒子的运动, 两类动量
考虑质量为 ,荷电 q 的粒子在电磁场 中的运动。在经典力学中,其Hamilton量为: (1) 其中 A , 分别是电磁矢势和标势,P 称为正则 动量,Hamilton量这样写法的理由如下:把式(1)
2 1 q H P A q 2 c
（12a）
则上述表示式就可化简成
e
i
q H H c t
（13）
由于在同样的变换下薛定谔方程式(3)的左 边给出 q i ie i ( i ) i （14）
t t t t c t
上二式中右边第二项互相抵消，于是得到 i t H 。这就证明了，当 按照 (11,12a)变换时，薛定鄂方程具有规范不变 性。