空气过滤器的能耗计算模型
- 格式:doc
- 大小:28.50 KB
- 文档页数:6

过滤组件过滤效率计算公式过滤组件是一种常见的工业设备,用于将固体颗粒、液体或气体中的杂质分离出来。
过滤效率是衡量过滤组件性能的重要指标之一,它反映了过滤组件对杂质的分离能力。
在工业生产中,正确计算过滤效率对于选择合适的过滤组件、优化生产过程具有重要意义。
本文将介绍过滤效率的计算公式及其相关知识。
过滤效率定义。
过滤效率是指过滤组件在一定条件下对特定颗粒或物质的分离能力。
通常用百分比表示,表示在一定时间内过滤组件对杂质的分离率。
过滤效率越高,说明过滤组件对杂质的分离能力越强。
过滤效率计算公式。
过滤效率的计算公式通常采用以下形式:过滤效率(%)=(1-(C/C0))100%。
其中,C0表示进入过滤组件前的杂质浓度,单位为mg/L或μg/m3;C表示通过过滤组件后的杂质浓度,单位同样为mg/L或μg/m3。
过滤效率的计算公式是基于杂质浓度的变化来描述的。
当杂质浓度C0和C确定后,就可以通过公式计算出过滤效率。
这个公式简单直观,易于理解和应用。
过滤效率影响因素。
过滤效率的高低受到多种因素的影响,主要包括以下几个方面:1. 过滤介质的选择,不同的过滤介质对于不同颗粒或物质的分离效果不同,因此过滤介质的选择对过滤效率有重要影响。
2. 过滤速度,过滤速度是指单位时间内通过过滤介质的流体体积。
过快的过滤速度可能导致颗粒通过过滤介质,从而降低过滤效率。
3. 过滤压力,过滤压力是指在过滤过程中对流体施加的压力。
适当的过滤压力可以提高过滤效率,但过高的过滤压力可能损坏过滤介质,降低过滤效率。
4. 过滤介质的清洗和更换,过滤介质在长时间使用后会积累大量杂质,影响过滤效率。
定期清洗和更换过滤介质对于保持过滤效率至关重要。
过滤效率的应用。
过滤效率是一个重要的工业指标,它在多个领域都有着广泛的应用。
在水处理领域,过滤效率是衡量水处理设备性能的重要指标。
通过正确计算和评估过滤效率,可以选择合适的水处理设备,保证出水质量符合相关标准。
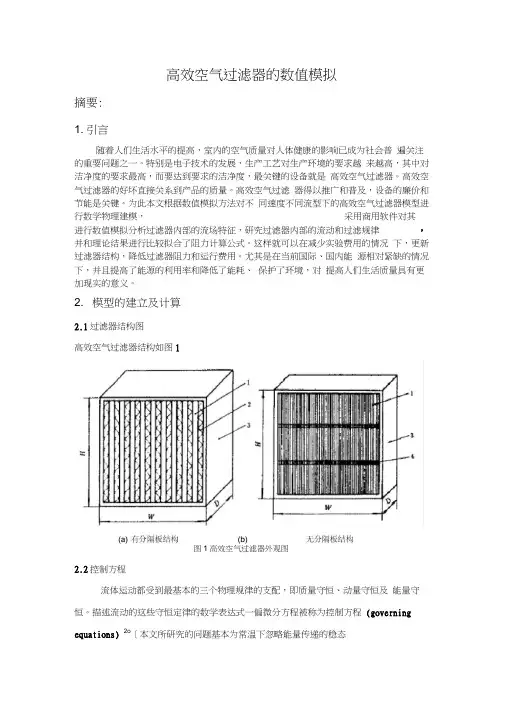
高效空气过滤器的数值模拟摘要:1. 引言随着人们生活水平的提高,室内的空气质量对人体健康的影响已成为社会普遍关注的重要问题之一。
特别是电子技术的发展,生产工艺对生产环境的要求越来越高,其中对洁净度的要求最高,而要达到要求的洁净度,最关键的设备就是高效空气过滤器。
高效空气过滤器的好坏直接关系到产品的质量。
高效空气过滤器得以推广和普及,设备的廉价和节能是关键。
为此本文根据数值模拟方法对不同速度不同流型下的高效空气过滤器模型进行数学物理建模,采用商用软件对其进行数值模拟分析过滤器内部的流场特征,研究过滤器内部的流动和过滤规律,并和理论结果进行比较拟合了阻力计算公式。
这样就可以在减少实验费用的情况下,更新过滤器结构,降低过滤器阻力和运行费用。
尤其是在当前国际、国内能源相对紧缺的情况下,并且提高了能源的利用率和降低了能耗、保护了环境,对提高人们生活质量具有更加现实的意义。
2. 模型的建立及计算2.1过滤器结构图高效空气过滤器结构如图1图1高效空气过滤器外观图2.2控制方程流体运动都受到最基本的三个物理规律的支配,即质量守恒、动量守恒及能量守恒。
描述流动的这些守恒定律的数学表达式一偏微分方程被称为控制方程(governing equations) 2o〔本文所研究的问题基本为常温下忽略能量传递的稳态流动。
所以控制方程可以写为: 连续性方程(质量守恒):d 、U =0动量方程:di 、. uU 二 di 、.gradu - 一,:-t :- rd i 、. U 二 d 「grad 、、 其中p 为压力,T 为流体的密度,」为流体的动力粘度,为流体的运动粘度。
2.3网格划分及计算模型网格划分如图2所示,边界条件具体设置为:进口为速度进口;出口采用自由出 口边界条件;壁面均采用选择无滑移固体壁面。
分别采用层流模型核湍流模型进行求解, 壁面函数采用壁面函数处理,求解算法采用 Simplec 算法,Pressure 采用 Standard, Momentum 采用 Power Law , Turbulent Kinetic Energy 采用 First Order Upwind ,Turbulent Dissipation Rate 采用 First Order Upwi nd 。



空气过滤器的滤速与面风速计算公式首先,我们需要了解以下几个概念:1. 滤速(Filter Velocity):指空气通过过滤器的速度,一般以米/秒(m/s)为单位。
滤速的大小对过滤器的性能有重要影响,过高的滤速可能导致过滤器堵塞或漏滤,而过低的滤速则可能导致过滤效果不好。
2. 面风速(Face Velocity):指空气进入过滤器的速度,一般以米/秒(m/s)为单位。
面风速也是评估过滤器性能的指标之一,通常会根据具体应用需求进行设计。
下面介绍两种常见的空气过滤器滤速与面风速计算公式:1.手动设计公式:滤速与面风速之间的关系可以通过以下公式计算:滤速=Q/(A×V)其中,Q表示空气流量,单位为立方米/秒(m³/s);A表示过滤器的有效施工面积,单位为平方米(m²);V表示过滤器的体积,单位为立方米(m³)。
2.自动设计公式:滤速与面风速之间的关系也可以通过以下公式计算:滤速=Q/A其中,Q表示空气流量,单位为立方米/秒(m³/s);A表示过滤器的有效施工面积,单位为平方米(m²)。
这两个公式都是根据空气流量与过滤器面积之间的关系推导得出的,通过调整空气流量和过滤器面积可以实现滤速的控制。
需要注意的是,这两个公式都是理论值,实际应用时还需要考虑其他因素,如过滤器结构设计、空气流动特性等。
除了滤速与面风速之间的关系,还需要考虑过滤器的阻力和压损。
过滤器的阻力与空气流速成正比,通常可以通过实验测量或厂家提供的数据进行获取。
过滤器的压损是指空气通过过滤器时由于阻力造成的气体压力损失,一般以帕斯卡(Pa)为单位。
通过以上公式和概念,可以根据具体应用需求来计算空气过滤器的滤速与面风速,以满足过滤效果以及能耗的要求。

无尘室能量消耗计算公式
无尘室的能量消耗计算公式涉及多个因素,包括空气处理设备、温度控制、空气过滤等。
一般来说,无尘室的能量消耗可以通过以
下公式进行估算:
能量消耗 = 空气处理设备能耗 + 温度控制能耗 + 空气过滤能耗 + 照明能耗 + 其他设备能耗。
其中,空气处理设备能耗包括空调、通风设备等的能耗,通常
可以通过设备的额定功率和运行时间来计算;温度控制能耗涉及到
保持无尘室内稳定温度所需的能量,可以通过温度控制设备的能耗
参数进行估算;空气过滤能耗是指空气过滤设备的能耗,可以根据
过滤设备的额定功率和运行时间来计算;照明能耗则是指无尘室内
照明设备的能耗,通常可以根据照明设备的功率和使用时间来计算;其他设备能耗包括无尘室内其他设备的能耗,如监控设备、生产设
备等。
需要注意的是,以上公式只是对无尘室能量消耗的一种简化估
算方式,实际情况可能会更为复杂。
在实际应用中,还需要考虑到
能耗的季节变化、设备的能效比、能源价格等因素,以及对能耗进
行精细化的监控和管理,以实现能耗的最小化和优化。
因此,在实际应用中,可能需要结合具体的无尘室设计和运行情况,采用更为复杂的能耗计算模型来进行准确的能耗估算和管理。


初效过滤器的风阻计算公式初效过滤器是空气处理系统中的重要组成部分,其主要作用是过滤空气中的颗粒物和杂质。
在空气处理系统中,初效过滤器的风阻是一个重要参数,它直接影响着系统的能耗和运行效率。
因此,正确计算初效过滤器的风阻是非常重要的。
初效过滤器的风阻计算公式可以通过以下公式来计算:风阻 = (0.5 ρ V^2 A C) / 1000。
其中,ρ为空气密度,单位为kg/m^3;V为空气流速,单位为m/s;A为过滤器的有效过滤面积,单位为m^2;C为过滤器的阻力系数,无单位;1000为换算系数。
通过这个公式,我们可以计算出初效过滤器的风阻,从而评估系统的能耗和运行效率。
首先,我们需要计算空气密度ρ。
空气密度受温度和湿度的影响,一般情况下可以通过以下公式计算:ρ = P / (R T)。
其中,P为大气压力,单位为Pa;R为气体常数,单位为J/(kg·K);T为空气温度,单位为K。
大气压力P可以通过气象站或者气象数据获取,一般情况下为101325Pa。
气体常数R为287.05 J/(kg·K)。
空气温度T可以通过温度传感器测量得到。
接下来,我们需要计算空气流速V。
空气流速是指空气在过滤器中的流动速度,一般情况下可以通过风速仪或者流量计测量得到。
在实际计算中,我们需要考虑到空气流速的变化,取平均值作为计算参数。
然后,我们需要计算过滤器的有效过滤面积A。
过滤器的有效过滤面积是指空气在过滤器中被过滤的有效面积,一般情况下可以通过过滤器的尺寸和结构参数计算得到。
最后,我们需要确定过滤器的阻力系数C。
过滤器的阻力系数是指过滤器在过滤空气时所产生的阻力,一般情况下可以通过厂家提供的数据或者实验测量得到。
通过以上步骤,我们可以得到初效过滤器的风阻值。
在实际应用中,我们可以根据风阻值来评估系统的能耗和运行效率,从而优化空气处理系统的设计和运行。
除了通过公式计算初效过滤器的风阻,我们还可以通过实验方法来测量初效过滤器的风阻。

两种空气净化设备效能的数学建模一、基于HEPA过滤器的空气净化设备效能数学建模HEPA过滤器是一种高效的空气净化设备,其主要作用是过滤空气中的微小颗粒物,如灰尘、花粉、烟雾等,从而提高室内空气质量。
为了评估HEPA过滤器的效能,我们可以采用以下数学模型:1. 空气净化效率模型空气净化效率是指HEPA过滤器能够过滤掉的颗粒物的百分比。
假设HEPA过滤器的过滤效率为E,空气中的颗粒物浓度为C,过滤器的空气流量为Q,则空气净化效率可以表示为:空气净化效率 = E × C × Q2. 过滤器寿命模型HEPA过滤器的寿命取决于其过滤效率和使用时间。
假设HEPA过滤器的过滤效率为E,使用时间为T,则过滤器的寿命可以表示为:过滤器寿命 = E × T3. 能耗模型HEPA过滤器的能耗取决于其空气流量和电力消耗。
假设HEPA过滤器的空气流量为Q,电力消耗为P,则能耗可以表示为:能耗 = Q × P二、基于光触媒技术的空气净化设备效能数学建模光触媒技术是一种新型的空气净化技术,其主要作用是利用光触媒材料催化分解空气中的有害气体,如甲醛、苯等,从而提高室内空气质量。
为了评估光触媒空气净化设备的效能,我们可以采用以下数学模型:1. 空气净化效率模型光触媒空气净化效率是指光触媒材料催化分解有害气体的百分比。
假设光触媒空气净化设备的净化效率为E,空气中有害气体的浓度为C,则空气净化效率可以表示为:空气净化效率 = E × C2. 光触媒材料寿命模型光触媒材料的寿命取决于其催化分解有害气体的效率和使用时间。
假设光触媒材料的催化分解效率为E,使用时间为T,则光触媒材料的寿命可以表示为:光触媒材料寿命 = E × T3. 能耗模型光触媒空气净化设备的能耗取决于其电力消耗和光源的使用时间。
假设光触媒空气净化设备的电力消耗为P,光源的使用时间为T,则能耗可以表示为:能耗 = P × T基于HEPA过滤器和光触媒技术的空气净化设备都可以通过数学建模来评估其效能。

根据80000m3空气净化装置计算。
根据m3空气净化装置计算根据给定的m3空气净化装置的体积,我们可以进行一些基本的计算来帮助你更好地了解和使用该装置。
1. 空气净化效率空气净化装置的主要功能是净化空气,去除其中的污染物。
要确定该装置的净化效率,需要考虑以下因素:- 空气中的污染物种类和浓度- 空气净化装置的技术和过滤器类型- 空气净化装置的运行时间和保养情况根据这些因素,你可以参考厂商提供的规格表或咨询相关专业人士来确定空气净化装置的净化效率。
2. 换气次数换气次数是指在一定时间内,空气净化装置将整个空间的空气清洁一次的次数。
换气次数的计算方法如下:换气次数 = 空气净化装置的风量 / 空间的总体积根据给定的m3空气净化装置的体积,可以将该装置的风量和换气次数进行相应的计算。
3. 滤芯更换频率空气净化装置的滤芯是核心组成部分,用于捕捉和过滤空气中的污染物。
滤芯的使用寿命通常取决于以下几个因素:- 空气中的污染物浓度和种类- 使用环境的清洁程度- 空气净化装置的运行时间根据厂商提供的指导,你可以计算出滤芯的更换频率,以确保空气净化装置的正常运行。
4. 能耗空气净化装置的能耗是一个重要的指标,在选购和使用过程中需要加以考虑。
你可以参考以下几点来评估空气净化装置的能耗:- 厂商提供的能耗参数和测试结果- 不同空气净化装置的能源利用效率比较- 空气净化装置的运行时间和风速调节通过对能耗的评估,你可以选择符合需求的节能型空气净化装置。
以上是根据80000m3空气净化装置进行的一些基本计算和相关指导。
在实际选购和使用中,建议你参考厂商提供的详细说明书,并咨询专业人士的意见,以确保使用该装置的安全和有效性。

空压机空气滤清器寿命计算方法
空压机空气滤清器的使用寿命取决于多个因素,包括新过滤器的初阻力、过滤材料的蓬松度、过滤器所具备的滤料面积、空气中含尘浓度、过滤器所使用的风量等。
理论上,空气滤清器的使用寿命可以通过一个特定的公式来计算:T=P/(N1×10-3 ×Qtη)。
在这个公式中,T代表滤清器的使用寿命,P
代表滤清器的积尘量,N1代表过滤器前空气的含尘浓度(mg/m3),Q代
表过滤器的风量(m3/h),t代表滤清器一天的运行时间(h),η代表滤清
器的效率。
此外,国产滤纸与进口滤纸相比,其最大缺陷在于脱毛和滤料本底积尘高,这与其生产环境及工艺欠精细有关。
国产滤纸在常用滤速下高效滤纸阻力高,而超高效滤纸则阻力偏高更普遍。
由于国产滤纸的积尘高,所以使用寿命也就没有进口滤纸长。
请注意,上述公式仅供参考,实际使用中可能需要根据具体情况进行调整。
如果需要更准确的信息,建议咨询相关行业专家或查阅有关技术文献。
空气过滤器的"过滤效率"是被捕捉的粉尘量与原空气含尘量之比:过滤效率=过滤器捕集粉尘量/上游空气含尘量=1-下游空气含尘量/上游空气含尘量
效率的意义看似简单,可它的含义和数值却因试验方法的不同而大不一样.
在决定过滤效率的因素中,粉尘"量"的含义多种多样,由此计算和测量出来的过滤器效率数值也就五花八门.实用中, 粉尘的总重量,粉尘的颗粒数量;有时是针对某一典型粒径粉尘的量,有进是所有粒径粉尘的量;还有用特定方法间接地反映浓度的通光量(比色法),荧光量(荧光法);有某种状态下的瞬时量,也有发尘试验全过程变化效率值的加权平均量。
对同一只过滤器采用不同的方法进行测试,测得的效率值就会不一样。
各国家,各厂商使用的测试方法不统一,对过滤器效率的解释和表达大相径庭。
离开测试方法,过滤效率就无从谈起。
历史上,搞通风和洁净室过滤器的人是一伙人,搞汽车滤清器的是另一伙人,此外还有搞除尘器的,搞液体过滤的,他们各用各的方法,各说各的效率。
当空气过滤器厂掺和汽车滤清器的买卖时,或除尘器厂开发空气过滤器时,他们自已也难免会被自已所说的过滤效率搞糊涂。
为了省事并减少误解,国外出现了一此用代号表示效率的方法那些代号既明胡了试验方法也确定了效率指标,详见2.1节“过滤效率标识”和2.2节“过滤效率规格比较”。
如今,全世界的过滤器厂商都来挤占中国市场,国内厂商为了向各种背景的用户推销产品,也随心所欲地使用效率标识。
各种各样的效率数值和效率名词使用户,设计师和制造厂云山雾罩。
东莞和生工业服装有限公司
空气过滤器技术参数介绍
1、过滤器效率
空气过滤器的过滤效率是被捕捉的粉尘量与原空气含尘量之比:
过滤效率=过滤器捕集粉尘量/上游空气含尘量= 1 -下游空气含尘量/上游空气含尘量过滤器效率只能通过相关检测才能得知,亚高效、高效必须经过逐台检测,合格品才能使用。
2、过滤器的阻力
过滤器的阻力是当过滤材质过滤掉污染物时对产生气流力量,当阻力增加时,容尘量变小,使用时间也相应减少,终阻力达到某规定值时过滤器报废,所以终阻力直接关系到过滤器的效率变化、过滤器使用寿命、系统送风量变化范围、系统能耗等。
3、过滤器的额定风量
额定风量是在过滤器达到设计效率时的最大风量。
过滤器不同使用风量下有不同的阻力,
在选择过滤器要小于额定风量,这样可以保证其过滤效率的稳定。
4、容尘量
容尘量是并非过滤器报废时容纳大气粉尘的重量,它是过滤器在特定试验条件下容纳特定试验粉尘的重量,容尘量与过滤器实际容纳粉尘重量没有直接对应关系。
5、面速度(面风速)和过滤速度
速度指迎风截面上通过气流的速度,一般以m/s表示;
面速度=风量÷迎风截面积
过滤速度指过滤材料上通过气流的速度,一般以cm/s表示;
过滤速度=风量÷过滤面积
过滤面积指所用的过滤材料的面积,只有当过滤材料为平面状垂直于气流方向时,该过滤器的迎风截面积和过滤面积是一样的,而装在吸尘器中的滤材往往都是打折成形的。
国外也用英制风速单位表示:fpm(foot per minute) 英尺/分钟,1000 fpm≈5.08m/s
东莞和生工业服装有限公司。
两种空气净化设备效能的数学建模
随着人们环境保护意识的提高,空气净化设备越来越受到重视。
为了评估不同的空气净化设备的效能,我们需要进行数学建模。
第一种空气净化设备是静电除尘器。
静电除尘器采用电场作用原理,将负电荷的颗粒物吸附在正极板上,达到净化空气的目的。
设静电除尘器的净化效率为E1,收集器距离电极板的距离为d,电极板间的电压为U,颗粒物直径为d0。
则静电除尘器的效能数学模型为:
E1 = 1 - exp[-K * (U/d) ^ 2 * d0 ^ 3]
其中,K为常数。
第二种空气净化设备是HEPA过滤器。
HEPA过滤器采用纤维材料对空气中的颗粒物进行过滤,能够有效去除直径为0.3微米以上的颗粒物。
设HEPA过滤器的净化效率为E2,纤维直径为d1,空气流速为v,纤维间距为d2。
则HEPA过滤器的效能数学模型为:
E2 = 1 - exp[-K * (v * d1 / d2) ^ n]
其中,K和n为常数。
通过数学建模,我们可以对不同类型的空气净化设备进行效能评估,选择合适的设备进行空气净化,保障人们的健康。
- 1 -。
空气净化器效能计算公式空气净化器是一种能够过滤空气中有害颗粒物和气体的设备,它可以帮助改善室内空气质量,保护人们的健康。
在选择空气净化器时,了解其效能是非常重要的。
效能计算公式可以帮助我们评估空气净化器的性能,从而选择最适合自己需求的产品。
在空气净化器效能的计算中,有几个关键参数需要考虑,包括CADR(清洁空气传递率)、CFM(立方英尺每分钟)和AHC(空气清洁率)。
CADR是指空气净化器在单位时间内去除空气中颗粒物的能力,通常以立方英尺每分钟(CFM)为单位。
CFM是指空气净化器每分钟处理的空气量,而AHC则是指空气净化器在单位时间内去除空气中污染物的百分比。
根据以上参数,我们可以使用以下公式来计算空气净化器的效能:效能 = CADR × AHC ÷ CFM。
在这个公式中,CADR代表清洁空气传递率,AHC代表空气清洁率,CFM代表立方英尺每分钟。
通过这个公式,我们可以很容易地计算出空气净化器的效能,从而对不同产品进行比较和评估。
在实际应用中,我们可以通过以下步骤来计算空气净化器的效能:1. 首先,我们需要查看空气净化器的CADR数值,这通常可以在产品说明书或者官方网站上找到。
CADR数值越大,表示空气净化器去除空气中颗粒物的能力越强。
2. 其次,我们需要了解空气净化器的CFM数值,这也可以在产品说明书或者官方网站上找到。
CFM数值越大,表示空气净化器处理空气的能力越强。
3. 最后,我们需要查看空气净化器的AHC数值,这同样可以在产品说明书或者官方网站上找到。
AHC数值越大,表示空气净化器去除空气中污染物的能力越强。
通过以上步骤,我们就可以得到空气净化器的效能值,从而对不同产品进行比较和评估。
通过效能值的比较,我们可以更加准确地选择适合自己需求的空气净化器,从而保障室内空气质量,保护自己和家人的健康。
除了以上的计算公式,还有一些其他因素也会影响空气净化器的效能,比如空气净化器的过滤器类型、过滤器的更换周期、空气净化器的使用环境等。
空气过滤器效率标准一、空气过滤器的不同效率表示方法当被过滤气体中的含尘浓度以计重浓度表示时,则效率为计重效率;以计数浓度表示时,则效率为计效效率;以其它物理量作相对表示时,则为比色效率或浊度效率等。
最常用的表示方法是用过滤器进出口气流中的尘粒浓度表示的计数效率。
1.在额定风量下,按国家标准GB/T14295-93《空气过滤器》及GB13554-92《高效空气过滤器》的规定,不同过滤器的效率范围如下:2.由于现在许多企业选用的是进口的过滤器,而它们表示效率的方法与国内的不同,为便于比较,将它们之间的换算关系列表如下:二、空气过滤器的规格与额定风量各类过滤器的一些标准尺寸、风量及初阻力如下表:空气过滤器的不同效率表示方法,空气过滤器的效率表示方法,空气过滤器效率空气过滤器效率规格比较表,空气过滤器效率表示方法容尘量:容尘量是在特定试验条件下,过滤器容纳特定人工粉尘的重量。
所谓“特定”,指的是:a. 标准试验风洞,以及相关试验与测量设备;b. 比实际大气粉尘颗粒大得多的标准人工尘;c. 标准规定,或委托方与试验方商定的试验方法与计算方法;d. 委托方与试验方商定的终止试验的条件。
只有在试验条件相同时,才能根据容尘量来粗略估计哪只过滤器的使用寿命会比另一只更长一些。
“容尘量”与过滤器实际容纳粉尘的重量没有直接对应关系,孤立的“容尘量”数据对用户没有任何意义。
例如,一只过滤器的试验容尘量为600g,报废时它可能会容纳2.5kg的大气粉尘;另一只的容尘量为900g,到了你手里,它可能只能兜住1.5kg 粉尘。
过滤器厂家和专业试验室在评估一般通风用过滤器产品时,要对过滤器进行破坏性发尘试验,其主要目的是评估过滤器在整个试验过程中的平均效率。
容尘量是通过这种试验得到的一组数据中的一个数据。
如果某个实验室曾对一大批过滤器进行过发尘试验,试验者可以利用一批容尘量数据来比较相关的过滤器。
外人很难搞清那些容尘量的实际意义。
空气过滤器的能耗计算模型
摘要:文章介绍了三种计算空气过滤器能耗的模型,用于估算过滤器的耗能情况,并进行了模拟计算。
关键词: 空气过滤器, 压力损失, 能耗
Abstract: The paper introduces three kinds of calculation model of the air filter energy consumption, used to estimate the energy dissipation filter, and by simulation calculation.
Key Words: air filter, loss of pressure, energy consumption
引言:在通风系统中,空气过滤器用于过滤空气中的尘粒。
普通集中空调系统中,过滤器能耗约占风机总能耗的10%(办公建筑)~30%(制药厂等洁净空调中)[1]。
过滤器的能耗与以下几个因素有关:过滤器的数量、类型、气流速度、尘粒的积累程度和过滤器的更换状况等。
River(1996)提出了过滤器压力损失模型,即过滤器总压力损失为空气进出口压力损失和通过过滤器压力损失之和。
该模型假定通过过滤器的气流形式为层流,空气进出口压力损失与气流的动压头成比例,通过过滤媒介的压力损失与空气流速成比例[2]。
River和Murphy在2000年的研究中又进一步考虑到空气通过过滤媒介被压缩的因素[3]。
过滤器的压力损失模型可以利用生产厂家提供的数据建立,当安装日期和气流状况确定后,这个模型理论上可以得到压力损失的精确解。
然而在这些模型中都假设气流的温度和压力是恒定的,而许多通风和空调系统的实际运行状况,空气流速是随时间变化的。
尽管我们可以根据过滤器寿命期空气的平均流速和平均压力来大致估算过滤器的能耗,但是由于变量之间的非线性关系,得出的结果可能与实际情况相去甚远。
本文介绍了三种计算空气过滤器能耗的方法,这些方法可以克服以前的压力损失模型存在的不足,后两种方法还可用来估算过滤器寿命周期和能耗,进行寿命周期成本分析的研究。
1.压力损失模型
对于一个选定的过滤器,压力损失模型应该反映空气流速和过滤器尘粒积累程度的影响。
为了建立压力损失模型,进行以下假定:
对于固定的过滤器尘粒积累度,过滤器的有效面积A,压力损失Δp和空气质量流速m的关系为:
(1)
式中b为回归因子;
压力损失因子n与过滤器尘粒积累度G是相对独立的;
过滤器的有效面积A与尘粒积累度G有关,可表示:
(2)
式中c-回归因子,A0-过滤器设计有效面积;
过滤器的尘粒积累度与单个过滤器的运行时间成比例, ,无因次时间因子为使用时间τ与使用寿命τl的比值;
基于以上假定,压力损失Δp可表示为:
(3)
其中
(4)
(5)
过滤器的压力损失特性与压力损失因子n,初阻力Δp0,终阻力Δpe有关。
m0为设计质量流速。
1.1瞬时法
过滤器的能耗P和空气质量流速m与压力损失Δp的乘积成比例,也和风机的效率η有关,过滤器的功率的表达式为:
(6)
式中ρ-空气密度kg/m3
把式(3)引入到式(4)中,得到风机功率比表达式:
(7)
其中
(8)
当空气流速和过滤器的更换状况已知,那么式(7)和(8)可以计算风机功率。
由式(7)可知,随着过滤器尘粒积累度的增加,风机的功率呈指数形式增加,并与空气质量流速的n+1次方成正比。
由于这些变量是非线性关系,所以不能由平均空气流速和平均过滤器尘粒积累度来计算平均风机功率。
图1a表示在典型过滤器(n=1.52,Δp0=83Pa,Δpe=470Pa)中不同过滤器尘粒积累度下风机功率比与空气质量流速比的关系。
图1b表示不同空气流速下与过滤器尘粒积累度G的关系;他们都不是线性关系。
可以看出:当过滤器尘粒积累度最大时,风机功率将增加到初始功率的5.6倍。
图1 风机功率随流速和尘粒累积程度的变化
1.2区间法:
为了简化计算,区间法把过滤器的寿命周期分成等长的区间,通过缩小时间间隔来减小风量变化的影响,过滤器的能耗通过每个区间进行计算,总能耗等于各个区间能耗的总和。
当各等距区间的使用情况比较规律时可用区间法来计算。
用统计规律来考虑各区间中空气质量流速和过滤器尘粒积累度的变化对风机能耗的影响,如果在第i个时间间隔,空气质量流速最大为mmini,最小为mmaxi,平均流速为mai,则平均过滤器的功率可表示为:
(9)
式中的
(10)
fi(m)是质量流速在时间上的分布函数,与在这个区间内质量流速m经历的时间有关:
(11)
由于尘粒积累度和其他参数的改变,流速随时间而变化。
时间跨度小时,质量流速可以作为定值来考虑。
如果时间跨度很大,空气状况有较大变化,那么可以假定一个气流密度分布函数。
这里引入三种模式,可以根据实际应用作出适当选择。
第一种模式假定气流以平均流速通过过滤器,其质量流速概率密度fi(m)表示为:
(12)
其中
(13)
第二种模式假定空气质量流速呈平均分布:
(14)
第三种模式假定空气质量流速呈正态分布:
(15)
其中σ为平均标准方差;
把时间和空气质量流速密度引入公式9,则过滤器在第i区间的功率比分别为
平均分布模式
平均值模式(16)
正态分布模式
其中
(17)
(18)
过滤器的能耗即为各区间能耗之和,表示为:
(19)
式中:τe-过滤器的寿命。
气流模式的选择对风机功率的计算有巨大影响。
图二表示风机功率比(piu/pic),即平均分布模式的功率piu与平均值模式的功率pic之比。
正态分布模式的功率比与平均分布模式具有相同的特征。
因此,在风机功率的计算中流量模式的选择必须仔细选择以达到最准确的计算结果。
图二
1.3不等距区间法
在这种模型中,区间的跨度各不相等,此种方法适于系统使用灵活的场合,时间间隔各不相等
(19)
式中:τa-过滤器平均寿命
引入时间和质量密度(公式10,11,12)到公式6中,过滤器能耗比(第i区间)表示为
平均分布模式
平均值模式(20)
正态分布模式
其中
(21)
(22)
年度过滤器能耗Ef即为各个区间之和,表示为
(23)
在一年中使用的过滤器的寿命τe不等时,过滤器寿命期的能耗Ef表示为
(24)
1.4计算实例
下表总结了一个标准状况下等距区间法的计算结果。
在这个算例中,过滤器的寿命期分为六个区间,每个区间跨度为1个月。
空气的质量流速由风机给出。
假定过滤器是1月安装的,无因次时间由每个区间的开始到寿命期的结束决定,能耗比则按每月进行计算。
过滤器的阻力随尘粒积累度的增加而增加,及时更换过滤器能减小风机能耗,增加空气的流速。
结果表明,选择平均分布模式计算得到的风机能耗稍大于平均值模式。