离散数学-2007`2008(2)-试卷B参考答案及评分细则

离散数学考试试题（A、B卷及答案）离散数学考试试题(A卷及答案)一、证明题(10分)1) (P∧Q∧A→C)∧(A→P∨Q∨C)? (A∧(P?Q))→C。

P<->Q=(p->Q)合取(Q->p)证明: (P∧Q∧A→C)∧(A→P∨Q∨C)(?P∨?Q∨?A∨C)∧(?A∨P∨Q∨C)((?P∨?Q∨?A)∧(?A∨P∨Q))∨C反用分配律((P∧Q∧A)∨(A∧?P∧?Q))∨C( A∧((P∧Q)∨(?P∧?Q)))∨C再反用分配律( A∧(P?Q))∨C(A∧(P?Q))→C2) ?(P↑Q)??P↓?Q。

证明:?(P↑Q)??(?(P∧Q))??(?P∨?Q))??P↓?Q。

二、分别用真值表法与公式法求(P→(Q∨R))∧(?P∨(Q?R))的主析取范式与主合取范式,并写出其相应的成真赋值与成假赋值(15分)。

主析取范式与析取范式的区别:主析取范式里每个括号里都必须有全部的变元。

主析取范式可由析取范式经等值演算法算得。

证明:公式法:因为(P→(Q∨R))∧(?P∨(Q?R))(?P∨Q∨R)∧(?P∨(Q∧R)∨(?Q∧?R))(?P∨Q∨R)∧(((?P∨Q)∧(?P∨R))∨(?Q∧?R))分配律(?P∨Q∨R)∧(?P∨Q∨?Q)∧(?P∨Q∨?R)∧(?P∨R∨?Q)∧(?P ∨R∨?R) (?P∨Q∨R)∧(?P∨Q∨?R)∧(?P∨?Q∨R)4M使(非P析取Q析取R)为0所赋真值,即100,二进制为4M∧6M∧50m∨1m∨2m∨3m∨7m所以,公式(P→(Q∨R))∧(?P∨(Q?R))为可满足式,其相应的成真赋值为000、001、010、011、111:成假赋值为:100、101、110。

真值表法:0 0 1 0 1 00 1 11 0 0 1 0 1 1 1 0 1 1 1 0111111111111111111为000、001、010、011、111:成假赋值为:100、101、110。

《离散数学》试题带答案试卷九试题与答案一、 填空 30% （每空 3分）1、 选择合适的论域和谓词表达集合A=“直角坐标系中，单位元（不包括单位圆周）的点集”则A= 。

2、 集合A={Φ,{Φ}}的幂集P (A) = 。

3、 设A={1，2，3，4}，A 上二元关系R={<1，2>，<2，1>，<2，3>，<3，4>}画出R的关系图。

4、 设A={<1,2>,<2 , 4 >,<3 , 3 >} , B={<1,3>,<2,4>,<4,2>},则B A ⋃= 。

B A = 。

5、 设|A|=3，则A 上有 个二元关系。

6、 A={1，2，3}上关系R= 时，R 既是对称的又是反对称的。

7、 偏序集><≤R A ,的哈斯图为，则≤R = 。

8、 设|X|=n ，|Y|=m 则（1）从X 到Y 有 个不同的函数。

（2）当n , m 满足 时，存在双射有 个不同的双射。

9、 2是有理数的真值为 。

10、Q ：我将去上海，R ：我有时间，公式)()(Q R R Q →∧→的自然语言为 。

11、公式)()(Q P P Q ∧⌝∧→的 主合取范式是 。

12、 若} ,, , {21m S S S S =是集合A 的一个分划，则它应满足 。

二、 选择 20% （每小题 2分）1、 设全集为I ，下列相等的集合是（ ）。

A 、} |{是偶数或奇数x x A =；B 、)}2( |{y x I y y x B =∧∈∃=；C 、)}12( |{+=∧∈∃=y x I y y x C ；D 、},4,4,3,3,2,2,1,1,0|{ ----=x D 。

2、 设S={N ，Q ，R}，下列命题正确的是（ ）。

A 、S S N N ∈∈∈2 ,2则； B 、S N S Q Q N ⊂∈⊂则 ,； C 、R N R Q Q N ⊂⊂⊂则 ,； D 、S N S N ⋂⊂Φ⊂Φ⊂Φ则 ,。

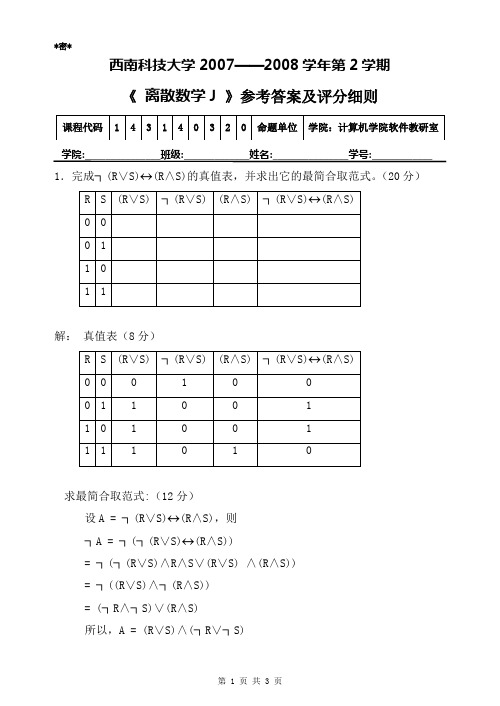
西南科技大学2007——2008学年第2学期《离散数学J 》参考答案及评分细则学院:_______________班级:_____________姓名:_______________学号:____________ 1．完成┐(R∨S)↔(R∧S)的真值表，并求出它的最简合取范式。

（20分）解：真值表（8分）求最简合取范式:（12分）设A = ┐(R∨S)↔(R∧S)，则┐A = ┐(┐(R∨S)↔(R∧S))= ┐(┐(R∨S)∧R∧S∨(R∨S) ∧(R∧S))= ┐((R∨S)∧┐(R∧S))= (┐R∧┐S)∨(R∧S)所以，A = (R∨S)∧(┐R∨┐S)2．“同班同学有同一个班主任，张三和李四的班主任不是同一个人，所以张三和李四不是同班同学。

”将上述命题谓词符号化，并证明。

(20分)其中P(x,y):x和y是同班同学，Q(x,y):x和y有同一个班主任，a:张三，b:李四。

解：符号化：（5分）前提：∀x∀y(P(x,y)→Q(x,y)), ┐Q(x,y)结论：┐P(a,b)推理证明：（15分）(1)∀x∀y(P(x,y)→Q(x,y)) P(2)∀y(P(a,y)→Q(a,y)) T,(1),US(3)P(a,b)→Q(a,b) T,(2),US(4)┐Q(a,b) P(5)┐P(a,b) T,(3,4),I43．写出集合{{φ,a},{a}}的全部子集合（8分）解：子集有：φ，{{φ,a}},{{φ}},{{φ,a},{a}}4．某班学生40人，会排球的有20人，会篮球的15人，以上两种运动都会的5人，问两种运动都不会的有几人？（12分）解：设会排球的是集合A，会篮球的是集合B。

则|A∪B|＝|A|＋|B|－|A∩B|＝20＋15－5＝30所以，两种运动都不会的有40-30＝10人。

5．设R是从集合A到集合B的关系，S,T是从集合B到集合C的关系，试证明R(S∩T)⊆(RS)∩(RT) （15分）证明：对任意<a,c>∈Rο(S∩T)，则由合成运算知，至少存在b∈B,使得：<a,b>∈R ,<b,c>∈(S∩T)，即：<b,c>∈S,且<b,c>∈T。

离散数学考试题(后附详细答案)一、命题符号化（共6小题，每小题3分，共计18分）1.用命题逻辑把下列命题符号化a)假如上午不下雨，我去看电影，否则就在家里读书或看报。

b)我今天进城，除非下雨。

c)仅当你走，我将留下。

2.用谓词逻辑把下列命题符号化a)有些实数不是有理数b)对于所有非零实数x，总存在y使得xy=1。

c) f 是从A到B的函数当且仅当对于每个a∈A存在唯一的b∈B，使得f(a)=b.二、简答题（共6道题，共32分）1.求命题公式(P→(Q→R)) (R→(Q→P))的主析取范式、主合取范式，并写出所有成真赋值。

（5分）2.设个体域为{1,2,3}，求下列命题的真值（4分）a)x y(x+y=4)b)y x (x+y=4)3.求x(F(x)→G(x))→(xF(x)→xG(x))的前束范式。

（4分）4.判断下面命题的真假，并说明原因。

（每小题2分，共4分）a)（A B）－C=(A-B) (A-C)b)若f是从集合A到集合B的入射函数，则|A|≤|B|5.设A是有穷集，|A|=5，问（每小题2分，共4分）a)A上有多少种不同的等价关系？b)从A到A的不同双射函数有多少个？6.设有偏序集<A,≤>，其哈斯图如图1，求子集B={b,d,e}的最小元，最大元、极大元、极小元、上界集合、下界集合、上确界、下确界，(5分)f g图17.已知有限集S={a1,a2,…,a n},N为自然数集合，R为实数集合，求下列集合的基数S;P(S);N,N n;P(N);R,R×R,{o,1}N（写出即可）(6分)三、证明题（共3小题，共计40分）1.使用构造性证明，证明下面推理的有效性。

（每小题5分，共10分）a)A→(B∧C),(E→ F)→ C, B→(A∧ S) B→Eb)x(P(x)→ Q(x)), x(Q(x)∨R(x))，x R(x) x P(x)2.设R1是A上的等价关系，R2是B上的等价关系，A≠ 且B≠ ，关系R满足：<<x1,y1>,<x2,y2>>∈R，当且仅当< x1, x2>∈R1且<y1,y2>∈R2。

离散数学考试题(后附详细答案)一、命题符号化（共6小题，每小题3分，共计18分）1.用命题逻辑把下列命题符号化a)假如上午不下雨，我去看电影，否则就在家里读书或看报。

b)我今天进城，除非下雨。

c)仅当你走，我将留下。

2.用谓词逻辑把下列命题符号化a)有些实数不是有理数b)对于所有非零实数x，总存在y使得xy=1。

c) f 是从A到B的函数当且仅当对于每个a∈A存在唯一的b∈B，使得f(a)=b.二、简答题（共6道题，共32分）1.求命题公式(P→(Q→R)) (R→(Q→P))的主析取范式、主合取范式，并写出所有成真赋值。

（5分）2.设个体域为{1,2,3}，求下列命题的真值（4分）a)x y(x+y=4)b)y x (x+y=4)3.求x(F(x)→G(x))→(xF(x)→xG(x))的前束范式。

（4分）4.判断下面命题的真假，并说明原因。

（每小题2分，共4分）a)（A B）－C=(A-B) (A-C)b)若f是从集合A到集合B的入射函数，则|A|≤|B|5.设A是有穷集，|A|=5，问（每小题2分，共4分）a)A上有多少种不同的等价关系？b)从A到A的不同双射函数有多少个？6.设有偏序集<A,≤>，其哈斯图如图1，求子集B={b,d,e}的最小元，最大元、极大元、极小元、上界集合、下界集合、上确界、下确界，(5分)f g图17.已知有限集S={a1,a2,…,a n},N为自然数集合，R为实数集合，求下列集合的基数S;P(S);N,N n;P(N);R,R×R,{o,1}N（写出即可）(6分)三、证明题（共3小题，共计40分）1.使用构造性证明，证明下面推理的有效性。

（每小题5分，共10分）a)A→(B∧C),(E→ F)→ C, B→(A∧ S) B→Eb)x(P(x)→ Q(x)), x(Q(x)∨R(x))，x R(x) x P(x)2.设R1是A上的等价关系，R2是B上的等价关系，A≠ 且B≠ ，关系R满足：<<x1,y1>,<x2,y2>>∈R，当且仅当< x1, x2>∈R1且<y1,y2>∈R2。

天津师范大学考试试卷2009 —2010学年第一 学期期末考试试卷（B 卷）科目： 离散数学学院： 管理学院专业：08信管、物流一、 单项选择题:在每小题的备选答案中选出一个正确答案，并将正确答案的代（每小题 分，本大题共 分）1.谓词公式(∀x)(P(x) ( ∃y)R(y)) → Q(x)中量词(∀x)的辖域是（ ）。

A. (∀x) (P(x) ( ∃y)R(y))B. P(x)C. P(x) ( ∃y)R(y)D. P(x),Q(x)2. 下列公式中哪些公式不是前束范式（ ）。

A. x ∀∃y(P(x) q(y))B. ∀x ∀y(P(x) Q(y) ( ∃z)S(z))C.Q(a,b)D. P3. 给定解释N 如下：个体域为自然数D N ；D N 上特定元素a = 0；D N 上特定函数f(x,y) = x+y , g(x,y) = x ∙y ； D N 上特定谓词E(x,y)为x=y ,下列公式为真的是（ ）。

A. ∀xE(g(x,a),x) B. ∀x ∀y ∀zE(f(x,y),z) C. ∀x ∀yE(f(x,y),g(x,y)) D. ∃x ∃yE(f(x,y),g(x,y))4. 设集合X≠∅，则空关系∅不具备的性质是（）。

xA.反自反性B.自反性C.对称性D.传递性5. 下列各式中，哪个不成立（）。

A.(∀x) (P(x) Q(x))⇔(∀x) (P(x) (∀x)Q(x))B.(∃x)(P(x) Q(x))⇔(∃x) (P(x) (∃x)Q(x)C.(∀x) (P(x) Q(x))⇔(∀x) (P(x) (∀x)Q(x)D.(∀x) (P(x) Q)⇔(∀x) (P(x) Q)6. 设个体域A={a,b},则∃x(F(x) G(x))消去量词为（）。

A. F(a) G(a)B. F(b) G(b)C. ( F(a) G(a) (F(b) G(b)))D. F(a) G(b)7. 给定A={1,2,3,4}，A上的关系R={<1,3>,<1,4>,<2,3>,<2,4>,<3,4>}满足的性质是（）。

北京交通大学2007-2008学年第二学期《离散数学基础（信科专业）》期末考试卷（A）学院：____________ _专业：___________________ 班级____________姓名：学号：□选修□必修一、填空题（共10分，每空1分）1.在推理理论中，推导过程中如果一个或多个公式重言蕴涵某个公式，则这个公式就可以引入推导过程中，这一推理规则叫做（T规则）。

2.设A={a，{b}}，则A的幂集是P (A)= {Φ, a，{b}, {a，{b}}；3.设R 是集合A上的二元关系，如果关系R同时具有自反性、反对称性和传递性，则称R是A上的一个偏序关系。

4.既是满射，又是单射的映射称为1-1映射（双射）。

5.设S为非空有限集,代数系统<P(S),∪>的单位元和零元分别为S和φ。

6.具有n个顶点的无向完全图共有n(n-1)/2条边。

7.简单图是指无环、无重边的图。

8.k-正则图是指所有顶点的度数均为k的的图。

9.Hamilton通路是指通过图中所有顶点一次且仅一次的通路。

10.设G=（E，V）是图，如果G是连通的，则P（G）= 1 。

11.命题公式(P→Q) ∧ (P→R)的主析取范式中包含极小项（ A ）A．P∧Q∧R；B．P∧Q∧⌝R；C ．P ∧⌝Q ∧R ；D ．P ∧⌝Q ∧⌝R12. 下列谓词公式中（ A ）不正确。

A ．(∃x)(A(x) →B) ⇔ (∃x) A(x) →B ； B ．(∃x)(B →A(x)) ⇔ B →(∃x) A(x)；C ．(∀x)(B →A(x)) ⇔ B →(∀x) A(x)；D ．(∀x)(A(x)∨B) ⇔(∀x)A(x)∨B ；13. 设S = {2，a ，{3}，4}，R ={{a}，3，4，1}，指出下面的写法中正确的是（ D ）（A ）R=S ； （B ）{a,3}⊆S ； （C ）{a}⊆R ；（D ）φ⊆R ；14. 下列命题公式不是重言式的是 C 。

离散考试试题及答案一、选择题（每题5分，共20分）1. 在离散数学中，下列哪个概念不是布尔代数的基本运算？A. 与B. 或C. 非D. 模答案：D2. 集合论中，下列哪个符号表示“属于”关系？A. ∈B. ∉C. ⊆D. ⊂答案：A3. 命题逻辑中，下列哪个符号表示“蕴含”关系？A. ∧B. ∨C. →D. ↔答案：C4. 关系R在集合A上是自反的，意味着什么？A. 对于所有a∈A，(a, a)∈RB. 对于所有a∈A，(a, a)∉RC. 对于所有a∈A，(a, b)∈RD. 对于所有a∈A，(a, b)∉R答案：A二、填空题（每题5分，共20分）1. 一个集合的基数是集合中元素的________。

答案：数量2. 在有向图中，如果存在一条从顶点u到顶点v的路径，则称顶点v 是顶点u的________。

答案：可达的3. 一个图是连通的，当且仅当图中任意两个顶点都是________。

答案：连通的4. 在命题逻辑中，一个命题的否定是________。

答案：它的对立命题三、简答题（每题10分，共30分）1. 请解释什么是图的哈密顿回路。

答案：哈密顿回路是一个图中的闭合回路，它恰好访问图中的每个顶点一次。

2. 描述一下什么是二元关系，并给出一个例子。

答案：二元关系是定义在两个集合上的一个关系，它关联了第一个集合中的元素和第二个集合中的元素。

例如，小于关系是数字集合上的一个二元关系。

3. 什么是图的生成树？答案：图的生成树是图的一个子图，它包含图中的所有顶点，并且是一棵树，即它是连通的且没有环。

四、计算题（每题15分，共30分）1. 给定一个集合A={1,2,3,4,5}，计算它的幂集。

答案：幂集P(A)={∅, {1}, {2}, {3}, {4}, {5}, {1,2}, {1,3}, {1,4}, {1,5}, {2,3}, {2,4}, {2,5}, {3,4}, {3,5}, {4,5},{1,2,3}, {1,2,4}, {1,2,5}, {1,3,4}, {1,3,5}, {1,4,5}, {2,3,4}, {2,3,5}, {2,4,5}, {3,4,5}, {1,2,3,4}, {1,2,3,5}, {1,2,4,5}, {1,3,4,5}, {2,3,4,5}, {1,2,3,4,5}, A}。