人教B版高中数学理八立体几何(B)名师精编单元测试

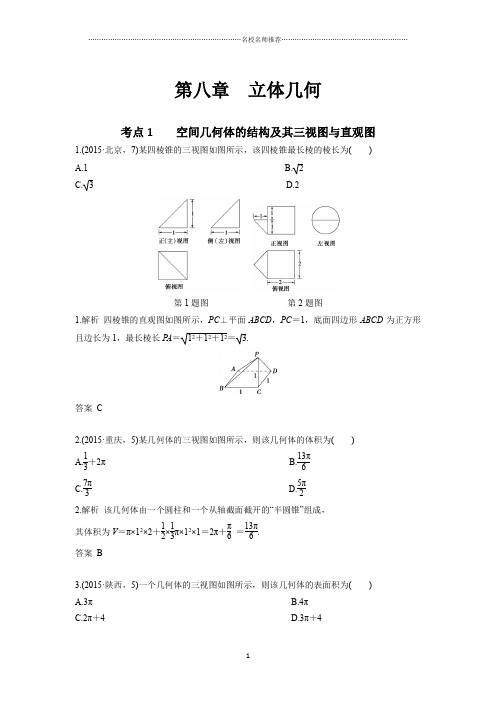
第八章 立体几何考点1 空间几何体的结构及其三视图与直观图1.(2015·北京，7)某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为( ) A.1 B. 2 C. 3 D.2第1题图 第2题图1.解析 四棱锥的直观图如图所示，PC ⊥平面ABCD ，PC ＝1，底面四边形ABCD 为正方形且边长为1，最长棱长P A ＝12＋12＋12＝ 3.答案 C2.(2015·重庆，5)某几何体的三视图如图所示，则该几何体的体积为( ) A.13＋2π B.13π6 C.7π3 D.5π2 2.解析 该几何体由一个圆柱和一个从轴截面截开的“半圆锥”组成， 其体积为V ＝π×12×2＋12×13π×12×1＝2π＋π6 ＝13π6.答案 B3.(2015·陕西，5)一个几何体的三视图如图所示，则该几何体的表面积为( ) A.3π B.4π C.2π＋4D.3π＋4第3题图 第4题图3.解析 由三视图可知原几何体为半圆柱，底面半径为1，高为2， 则表面积为：S ＝2×12π×12＋12×2π×1×2＋2×2＝π＋2π＋4＝4＋3π.答案 D4.(2015·浙江，2)某几何体的三视图如图所示(单位：cm)，则该几何体的体积是( ) A ．8 cm 3 B ．12 cm 3 C.323 cm 3 D.403cm 34.解析 由三视图可知该几何体是由棱长为2 cm 的正方体与底面为边长为2 cm 正方形、高为2 cm 的四棱锥组成，V ＝V 正方体＋V 四棱锥＝8 cm 3＋83 cm 3＝323 cm 3.故选C.答案 C5.(2015·福建，9)某几何体的三视图如图所示，则该几何体的表面积等于( )A.8＋2 2B.11＋2 2C.14＋2 2D.155.解析 该几何体为底面是直角梯形的直四棱柱．S 表＝2×12(1＋2)×1＋2×1＋2×1＋2×2＋2×2＝11＋22，故选B.答案 B6.(2014·辽宁，7)某几何体三视图如图所示，则该几何体的体积为( )A.8－π4B.8－π2C.8－πD.8－2π 6.解析 该几何体是一个正方体截去两个四分之一圆柱形成的组合体， 其体积V ＝23－14×π×12×2×2＝8－π，故选C.答案 C7.(2014·浙江，3)某几何体的三视图(单位：cm)如图所示，则该几何体的体积是( ) A.72 cm 3 B.90 cm 3 C.108 cm 3D.138 cm 37.解析 由三视图可知，该几何体的直观图如图所示，则该几何体的体积V ＝V 四棱柱＋V 三棱柱＝4×6×3＋12×4×3×3＝90(cm 3)．答案 B8.(2014·新课标全国Ⅰ，8)如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是( )A.三棱锥B.三棱柱C.四棱锥D.四棱柱8.解析 由题知，该几何体的三视图为一个三角形，两个四边形，分析可知该几何体为三棱柱. 答案 B9.(2014·新课标全国Ⅱ，6)如图，网格纸上正方形小格的边长为1(表示1 cm)，图中粗线画出的是某零件的三视图，该零件由一个底面半径为3 cm ，高为6 cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.139.解析 由三视图可知该零件是一个底面半径为2、高为4的圆柱和一个底面半径为3、高为2的圆柱的组合体，所以该组合体的体积V 1＝π·22·4＋π·32·2＝34π，原来的圆柱体毛坯的体积为V ＝π·32·6＝54π，则切削掉部分的体积为V 2＝54π－34π＝20π，所以切削掉部分的体积与原来的圆柱体毛坯体积的比值为20π54π＝1027.故选C.答案 C10．(2015·天津，10)一个几何体的三视图如图所示(单位：m)，则该几何体的体积为________m 3.10.解析 由所给三视图可知，该几何体是由相同底面的两圆锥和一圆柱组成，底面半径为1，圆锥的高为1，圆柱的高为2，所以其体积V ＝2×13×π×12×1＋π×12×2＝83π.答案 83π11.(2014·北京，11)某三棱锥的三视图如图所示，则该三棱锥最长棱的棱长为________．11.解析 三视图所表示的几何体的直观图如图所示．结合三视图知，P A ⊥平面ABC ，P A ＝2，AB ＝BC ＝2，AC ＝2， 所以PB ＝P A 2＋AB 2＝4＋2＝6，PC ＝P A 2＋AC 2＝22， 所以该三棱锥最长棱的棱长为2 2. 答案 22考点2 空间几何体的表面积和体积1.(2016·新课标全国Ⅱ，4)体积为8的正方体的顶点都在同一球面上，则该球面的表面积为( ) A.12π B.323π C.8πD.4π1.解析 由题可知正方体的棱长为2，其体对角线23即为球的直径， 所以球的表面积为4πR 2＝(2R )2π＝12π，故选A. 答案 A2.(2016·新课标全国Ⅱ，7)如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为( )A.20πB.24πC.28πD.32π2.解析 由三视图可知，组合体的底面圆的面积和周长均为4π，圆锥的母线长l ＝（23）2＋22＝4，所以圆锥的侧面积为S 锥侧＝12×4π×4＝8π，圆柱的侧面积S 柱侧＝4π×4＝16π，所以组合体的表面积S ＝8π＋16π＋4π＝28π，故选C. 答案 C3.(2016·新课标全国Ⅲ，10)如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为( )A.18＋365B.54＋18 5C.90D.81 3.解析 由题意知，几何体为平行六面体，边长分别为3，3，45， 几何体的表面积S ＝3×6×2＋3×3×2＋3×45×2＝54＋18 5. 答案 B4.(2016·新课标全国Ⅲ，11)在封闭的直三棱柱ABCA 1B 1C 1内有一个体积为V 的球， 若AB ⊥BC ，AB ＝6，BC ＝8，AA 1＝3，则V 的最大值是( ) A.4π B.9π2 C.6πD.32π34.解析 由题意知，底面三角形的内切圆直径为4，三棱柱的高为3， 所以球的最大直径为3，V 的最大值为9π2.答案 B5.(2016·新课标全国Ⅰ，7)如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3，则它的表面积是( )A.17πB.18πC.20πD.28π5.解析 由题知，该几何体的直观图如图所示，它是一个球(被过球心O 且互相垂直的三个平面)切掉左上角的18后得到的组合体，其表面积是球面面积的78和三个14圆面积之和.易得球的半径为2，则得S ＝78×4π×22＋3×14π×22＝17π，故选A.答案 A6.(2016·山东，5)一个由半球和四棱锥组成的几何体，其三视图如图所示.则该几何体的体积为( )A.13＋23πB.13＋23π C.13＋26π D.1＋26π 6.解析 由三视图知，半球的半径R ＝22，四棱锥为底面边长为1，高为1的正四棱锥， ∴V ＝13×1×1×1＋12×43π×⎝⎛⎭⎫223＝13＋26π，故选C.答案 C7.(2015·新课标全国Ⅰ，11)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为16＋20π，则r ＝( )A.1B.2C.4D.87.解析 由题意知，2r ·2r ＋12·2πr ·2r ＋12πr 2＋12πr 2＋12·4πr 2＝4r 2＋5πr 2＝16＋20π，∴r ＝2.答案 B8.(2015·新课标全国Ⅱ，10)已知A ，B 是球O 的球面上两点，∠AOB ＝90°，C 为该球面上的动点．若三棱锥OABC 体积的最大值为36，则球O 的表面积为( ) A.36π B.64π C.144π D.256π 8.解析 如图，要使三棱锥OABC 即COAB 的体积最大，当且仅当点C 到平面OAB 的距离，即三棱锥COAB 底面OAB 上的高最大，其最大值为球O 的半径R ， 则V OABC 最大＝V COAB 最大＝13×12S △OAB ×R ＝13×12×R 2×R ＝16R 3＝36，所以R ＝6，得S 球O ＝4πR 2＝4π×62＝144π.选C. 答案 C9.(2015·安徽，9)一个四面体的三视图如图所示，则该四面体的表面积是( )A.1＋ 3B.1＋2 2C.2＋ 3D.2 2 9.解析 由几何体的三视图可知空间几何体的直观图如图所示．∴其表面积S 表＝2×12×2×1＋2×34×(2)2＝2＋3，故选C.答案C10.(2015·新课标全国Ⅰ，6)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问：积及为米几何？”其意思为：“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有( ) A.14斛 B.22斛 C.36斛 D.66斛10.解析 由题意知：米堆的底面半径为163(尺)，体积V ＝13×14πR 2·h ＝3209(立方尺)．所以堆放的米大约为3209×1.62≈22(斛)．答案 B11.(2015·新课标全国Ⅱ，6)一个正方体被一个平面截去一部分后，剩余部分的三视图如下图，则截去部分体积与剩余部分体积的比值为( )A.18B.17C.16D.1511.解析 如图，由题意知，该几何体是正方体ABCDA 1B 1C 1D 1被过三点A 、B 1、D 1的平面所截剩余部分，截去的部分为三棱锥AA 1B 1D 1.设正方体的棱长为1，则截去部分体积与剩余部分体积的比值为 VAA 1B 1D 1VB 1C 1D 1ABCD ＝VAA 1B 1D 1VA 1B 1C 1D 1ABCD －VAA 1B 1D 1＝13×12×12×113－13×12×12×1＝15.选D.答案 D12.(2015·山东，9)已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( ) A.22π3B.42π3C.22πD.42π12.解析 如图，设等腰直角三角形为△ABC ，∠C ＝90°，AC ＝CB ＝2，则AB ＝2 2.设D 为AB 中点，则BD ＝AD ＝CD ＝ 2.∴所围成的几何体为两个圆锥的组合体，其体积V ＝2×13×π×(2)2×2＝42π3.答案 B13.(2015·湖南，10)某工件的三视图如图所示，现将该工件通过切削，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件的利用率为(材料利用率＝新工件的体积/原工件的体积)( )A.8B.8C.2－3πD.2－3π13.解析 欲使正方体最大，则其上底面四个顶点需在圆锥上． 圆锥体积V 1＝13π×12×22＝223π.作几何体截面图，则内接正方体棱长a ＝223，正方体体积V 2＝a 3＝⎝⎛⎭⎫2233＝16227，∴V 2V 1＝16227×322π＝89π.故选A.答案 A14.(2014·新课标全国Ⅱ，7)正三棱柱ABCA 1B 1C 1的底面边长为2,侧棱长为3,D 为BC 中点,则三棱锥AB 1DC 1的体积为( )A.3B.32C.1D.3214.解析 由题意可知AD ⊥BC ，由面面垂直的性质定理可得AD ⊥平面DB 1C 1， 又AD ＝2·sin 60°＝3，所以11AB DC V ＝13AD ·S △11B DC ＝13×3×12×2×3＝1，故选C. 答案 C15.(2014·重庆，7)某几何体的三视图如图所示，则该几何体的体积为( )A.12B.18C.24D.3015.解析 此几何体是由一个三棱柱截去一个三棱锥得到的，三棱柱和三棱锥的底面都是直角三角形，两直角边长分别为3和4，其面积为6，三棱柱的高为5，三棱锥的高为3，所以该几何体的体积为6×5－13×6×3＝24，选择C.答案 C16.(2014·陕西，5)将边长为1的正方形以其一边所在直线为旋转轴旋转一周，所得几何体的侧面积是( )A.4πB.3πC.2πD.π16.解析 由几何体的形成过程知所得几何体为圆柱，底面半径为1，高为1，其侧面积S ＝2πrh ＝2π×1×1＝2π. 答案 C17.(2016·浙江，9)某几何体的三视图如图所示(单位：cm)，则该几何体的表面积是________cm 2，体积是________cm 3.17.解析 由三视图可知该几何体由一个正方体和一个长方体组合而成， 上面正方体的边长为2 cm ，下面长方体的底面边长为4 cm ，高为2 cm ， 其直观图如右图，其表面积S ＝6×22＋2×42＋4×2×4－2×22＝80(cm 2)， 体积V ＝2×2×2＋4×4×2＝40(cm 3). 答案 80 4018.(2016·四川，12)已知某三棱锥的三视图如图所示，则该三棱锥的体积是________.18.解析 由三视图可大致画出三棱锥的直观图如图，由正、俯视图可知，△ABC为等腰三角形，且AC ＝23，AC 边上的高为1，∴S △ABC ＝12×23×1＝ 3.由侧视图可知：三棱锥的高h ＝1，∴V SABC ＝13h s ABC ＝33.答案 3319.(2016·北京，11)某四棱柱的三视图如图所示，则该四棱柱的体积为________.19.解析 由三视图知该四棱柱为直四棱柱，底面积S ＝（1＋2）×12＝32，高h ＝1，所以四棱柱体积V ＝S ·h ＝32×1＝32.答案 3220.(2015·四川，14)在三棱柱ABCA 1B 1C 1中，∠BAC ＝90°，其正视图和侧视图都是边长为1的正方形，俯视图是直角边长为1的等腰直角三角形，设点M ，N ，P 分别是AB ，BC ，B 1C 1的中点，则三棱锥P A 1MN 的体积是________．20.解析 由题意知还原后的几何体是一个直放的三棱柱，三棱柱的底面是直角边长为1的等腰直角三角形，高为1的直三棱柱.∵1PA MN V ＝1A PMN V ，又AA 1∥平面PMN ，∴1A PMN V ＝APMN V ， ∴V APMN ＝13×12×1×12×12＝124，故1PA MN V ＝124.答案 12421．(2014·天津，10)一个几何体的三视图如图所示(单位：m)，则该几何体的体积为________m 3.21.解析 由三视图可得该几何体是组合体，上面是底面圆的半径为2 m 、高为2 m 的圆锥，下面是底面圆的半径为1 m 、高为4 m 的圆柱，所以该几何体的体积是13×4π×2＋4π＝20π3(m 3)．答案 20π322.(2014·山东，13)一个六棱锥的体积为23，其底面是边长为2的正六边形，侧棱长都相等，则该六棱锥的侧面积为________． 22.解析 由题意可知，该六棱锥是正六棱锥，设该六棱锥的高为h ，则13×6×34×22×h ＝23，解得h ＝1，底面正六边形的中心到其边的距离为3， 故侧面等腰三角形底边上的高为3＋1＝2， 故该六棱锥的侧面积为12×12×2＝12.答案 1223.(2015·新课标全国Ⅱ，19)如图，长方体ABCD-A 1B 1C 1D 1中AB ＝16，BC ＝10，AA 1＝8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E ＝D 1F ＝4.过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形． (1)在图中画出这个正方形(不必说明画法和理由)； (2)求平面α把该长方体分成的两部分体积的比值． 23.解 (1)交线围成的正方形EHGF 如图：(2)作EM ⊥AB ，垂足为M ，则AM ＝A 1E ＝4，EB 1＝12，EM ＝AA 1＝8. 因为EHGF 为正方形，所以EH ＝EF ＝BC ＝10. 于是MH ＝EH 2－EM 2＝6，AH ＝10，HB ＝6.因为长方体被平面α分成两个高为10的直棱柱，所以其体积的比值为97(79也正确)．24.(2015·湖南，18)如图，直三棱柱ABC-A1B 1C 1的底面是边长为2的正三角形，E ，F 分别是BC ，CC 1的中点． (1)证明：平面AEF ⊥平面B 1BCC 1；(2)若直线A 1C 与平面A 1ABB 1所成的角为45°，求三棱锥F AEC 的体积． 24.(1)证明 ∵△ABC 为正三角形，E 为BC 中点，∴AE ⊥BC ，∴又B 1B ⊥平面ABC ，AE ⊂平面ABC ，∴B 1B ⊥AE ， ∴由B 1B ∩BC ＝B 知，AE ⊥平面B 1BCC 1，又由AE ⊂平面AEF ，∴平面AEF ⊥平面B 1BCC 1. (2)解 设AB 中点为M ，连接CM ，则CM ⊥AB ，由平面A 1ABB 1⊥平面ABC ，且平面A 1ABB 1∩平面ABC ＝AB 知，CM ⊥面A 1ABB 1， ∴∠CA 1M 即为直线A 1C 与平面A 1ABB 1所成的角， ∴∠CA 1M ＝45°. 易知CM ＝32×2＝3，在等腰Rt △CMA 中，AM ＝CM ＝3， 在Rt △A 1AM 中，A 1A ＝A 1M 2－AM 2＝ 2.∴FC ＝12A 1A ＝22，又S △AEC ＝12×34×4＝32，∴V 三棱锥F AEC ＝13×32×22＝612.25.(2014·广东，18)如图1，四边形ABCD 为矩形，PD ⊥平面ABCD ，AB ＝1，BC ＝PC ＝2.作如图2折叠：折痕EF ∥DC ，其中点E ，F 分别在线段PD ，PC 上，沿EF 折叠后点P 叠在线段AD 上的点记为M ，并且MF ⊥CF .(1)证明：CF ⊥平面MDF ； (2)求三棱锥MCDE 的体积．25.(1)证明 ∵PD ⊥平面ABCD ，AD ⊂平面ABCD ，∴PD ⊥AD ，又四边形ABCD 是矩形，∴CD ⊥AD .∵PD ⊂平面PCD ，CD ⊂平面PCD ，且PD ∩CD ＝D ， ∴AD ⊥平面PCD ，∵CF ⊂平面PCD ，∴AD ⊥CF ，又MF ⊥CF ，MF ∩AD ＝M ，∴CF ⊥平面MDF . (2)解 ∵PD ⊥平面ABCD ，∴PD ⊥CD ， 又CD ＝AB ＝1，PC ＝2，∴PD ＝ 3. 由(1)知CF ⊥平面MDF ，∴CF ⊥DF .∴由S △PCD ＝12PD ×CD ＝12PC ×DF 得DF ＝32，∴CF ＝CD 2－DF 2＝12.∵EF ∥CD ，∴DE DP ＝CF CP ，∴DE ＝CF CP ×DP ＝34.∴S △CDE ＝12CD ×DE ＝12×1×34＝38.∵AD ⊥平面PCD ，即MD ⊥平面CDE ，且ME ＝PE ＝PD －ED ＝334，∴MD ＝ME 2－ED 2＝2716－316＝62，∴三棱锥MCDE 的体积为V MCDE ＝13S △CDE ×MD ＝13×38×62＝216.考点3 点、线、面的位置关系1.(2016·新课标全国Ⅰ，11)平面α过正方体ABCDA 1B 1C 1D 1的顶点A ，α∥平面CB 1D 1， α∩平面ABCD ＝m ，α∩平面ABB 1A 1＝n ，则m ，n 所成角的正弦值为( ) A.32 B.22C.33D.131.解析 如图所示，设平面CB 1D 1∩平面ABCD ＝m 1，∵α∥平面CB 1D 1，∴m 1∥m ，又∵平面ABCD ∥平面A 1B 1C 1D 1，平面CB 1D 1∩平面A 1B 1C 1D 1＝B 1D 1，∴B 1D 1∥m 1，∴B 1D 1∥m ，同理可得CD 1∥n .故m 、n 的所成角的大小与B 1D 1、CD 1所成角的大小相等，即∠CD 1B 1的大小. 而B 1C ＝B 1D 1＝CD 1(均为面对角线)，∴∠CD 1B 1＝π3，∴sin ∠CD 1B 1＝32，故选A.答案 A2.(2016·浙江，2)已知互相垂直的平面α，β交于直线l .若直线m ，n 满足m ∥α，n ⊥β，则( ) A.m ∥l B.m ∥n C.n ⊥lD.m ⊥n2.解析由已知，α∩β＝l，∴l⊂β，又∵n⊥β，∴n⊥l，C正确.故选C.答案 C3.(2015·广东，6)若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是()A．l与l1,l2都不相交B．l与l1,l2都相交C．l至多与l1,l2中的一条相交D．l至少与l1,l2中的一条相交3.解析若l与l1，l2都不相交则l∥l1，l∥l2，∴l1∥l2，这与l1和l2异面矛盾，∴l至少与l1，l2中的一条相交．答案D4.(2015·湖北，5)l1,l2表示空间中的两条直线,若p：l1,l2是异面直线,q：l1,l2不相交,则() A．p是q的充分条件,但不是q的必要条件B．p是q的必要条件,但不是q的充分条件C．p是q的充分必要条件D．p既不是q的充分条件，也不是q的必要条件4.解析由l1，l2是异面直线，可得l1，l2不相交，所以p⇒q；由l1，l2不相交，可得l1，l2是异面直线或l1∥l2，所以q⇒/p.所以p是q的充分条件，但不是q的必要条件．故选A.答案A5.(2015·浙江，4)设α，β是两个不同的平面，l，m是两条不同的直线，且l⊂α，m⊂β()A.若l⊥β，则α⊥βB.若α⊥β，则l⊥mC.若l∥β，则α∥βD.若α∥β，则l∥m5.解析选项A：∵l⊥β，l⊂α，∴α⊥β，A正确；选项B：α⊥β，l⊂α，m⊂β，l与m位置关系不固定；选项C，∵l∥β，l⊂α，∴α∥β或α与β相交；选项D：∵α∥β，l⊂α，m⊂β.∴此时l与m位置关系不固定，故选A.答案A6.(2015·四川，18) 一个正方体的平面展开图及该正方体的直观图的示意图如图所示．(1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由)；(2)判断平面BEG与平面ACH的位置关系．并证明你的结论．(3)证明：直线DF⊥平面BEG.6.(1) 解点F，G，H的位置如图所示．(2)证明平面BEG∥平面ACH，证明如下：因为ABCDEFGH为正方体，所以BC∥FG，BC＝FG，又FG∥EH，FG＝EH，所以BC∥EH，BC＝EH，于是BCHE为平行四边形，所以BE∥CH，又CH⊂平面ACH，BE⊄平面ACH，所以BE∥平面ACH，同理BG∥平面ACH，又BE∩BG＝B，所以平面BEG∥平面ACH.(3)证明连接FH，因为ABCDEFGH为正方体，所以DH⊥平面EFGH，因为EG⊂平面EFGH，所以DH⊥EG，又EG⊥FH，EG∩FH＝O，所以EG⊥平面BFHD，又DF⊂平面BFHD，所以DF⊥EG，同理DF⊥BG，又EG∩BG＝G，所以DF⊥平面BEG.7.(2014·陕西，17)四面体ABCD及其三视图如图所示，平行于棱AD，BC的平面分别交四面体的棱AB，BD，DC，CA于点E，F，G，H.(1)求四面体ABCD 的体积； (2)证明：四边形EFGH 是矩形．7.(1)解 由该四面体的三视图可知，BD ⊥DC ，BD ⊥AD ，AD ⊥DC ，BD ＝CD ＝2，AD ＝1，∴AD ⊥平面BDC ，∴四面体体积V ＝13×12×2×2×1＝23.(2)证明 ∵BC ∥平面EFGH ，平面EFGH ∩平面BDC ＝FG ，平面EFGH ∩平面ABC ＝EH ， ∴BC ∥FG ，BC ∥EH ， ∴FG ∥EH .同理EF ∥AD ，HG ∥AD ， ∴EF ∥HG ，∴四边形EFGH 是平行四边形． 又∵AD ⊥平面BDC ， ∴AD ⊥BC ，∴EF ⊥FG ， ∴四边形EFGH 是矩形．8.(2014·新课标全国Ⅱ，18)如图，四棱锥P ABCD 中，底面ABCD 为矩形，P A ⊥平面ABCD ，E 为PD 的中点．(1)证明：PB ∥平面AEC ；(2)设AP ＝1，AD ＝3，三棱锥P ABD 的体积V ＝34，求A 到平面PBC 的距离． 8.(1)证明 设BD 与AC 的交点为O ，连接EO . 因为ABCD 为矩形，所以O 为BD 的中点． 又E 为PD 的中点，所以E O ∥PB.又因为E O ⊂平面AEC ，PB ⊄平面AEC ， 所以PB ∥平面AEC.(2)解 V ＝16P A ·AB ·AD ＝36AB ，由V ＝34，可得AB ＝32.作AH ⊥PB 交PB 于H ，由题设知BC ⊥平面P AB ，所以BC ⊥AH ，所以AH ⊥平面PBC . 在Rt △P AB 中， PB ＝132，所以AH ＝P A ·AB PB ＝31313，即A 到平面PBC 的距离为31313. 考点4 线面平行的判定与性质1.(2014·辽宁，4)已知m ，n 表示两条不同直线，α表示平面．下列说法正确的是( ) A.若m ∥α，n ∥α，则m ∥n B.若m ⊥α，n ⊂α，则m ⊥n C.若m ⊥α，m ⊥n ，则n ∥α D.若m ∥α，m ⊥n ，则n ⊥α1.解析 若m ∥α，n ∥α，则m 与n 可能平行、相交或异面，故A 错； B 正确；若m ⊥α，m ⊥n ，则n ∥α或n ⊂α，故C 错误；若m ∥α，m ⊥n ，则n 与α可能平行、相交或n ⊂α，故D 错误．因此选B. 答案 B2.(2016·新课标全国Ⅲ，19)如图，四棱锥P ABCD 中，P A ⊥底面ABCD ，AD ∥BC ，AB ＝AD ＝AC ＝3，P A ＝BC ＝4，M 为线段AD 上一点，AM ＝2MD ，N 为PC 的中点.(1)证明：MN ∥平面P AB ； (2)求四面体NBCM 的体积. 2.(1)证明 由已知得AM ＝23AD ＝2.取BP 的中点T ，连接AT ，TN ，由N 为PC 中点知TN ∥BC ，TN ＝12BC ＝2.又AD ∥BC ，故TN 綊AM ，四边形AMNT 为平行四边形，于是MN ∥A T. 因为AT ⊂平面PAB ，MN ⊄平面PAB ，所以MN ∥平面PAB.(2)解 因为PA ⊥平面ABCD ，N 为PC 的中点，所以N 到平面ABCD 的距离为12PA.取BC 的中点E ，连接AE.由AB ＝AC ＝3得AE ⊥BC ，AE ＝AB2－BE2＝ 5. 由AM ∥BC 得M 到BC 的距离为5，故S △BCM ＝12×4×5＝2 5.所以四面体NBCM 的体积VNBCM ＝13×S △BCM×PA 2＝453.3.(2015·北京，18)如图，在三棱锥V-ABC 中，平面V AB ⊥平面ABC ，△V AB 为等边三角形，AC ⊥BC ，且AC ＝BC ＝2，O ，M 分别为AB ，VA 的中点． (1)求证：VB ∥平面MOC ；(2)求证：平面MOC ⊥平面VAB ； (3)求三棱锥VABC 的体积．3.解 (1)因为O ，M 分别为AB ，V A 的中点，所以OM ∥VB ， 又因为VB ⊄平面MOC ，所以VB ∥平面MOC.(2)因为AC ＝BC ，O 为AB 的中点，所以OC ⊥AB.又因为平面VAB ⊥平面ABC ，且OC ⊂平面ABC ，所以OC ⊥平面V AB. 所以平面MOC ⊥平面V AB.(3)在等腰直角三角形ACB 中，AC ＝BC ＝2，所以AB ＝2，OC ＝1， 所以等边三角形VAB 的面积S △VAB ＝ 3.又因为OC ⊥平面VAB .所以三棱锥CVAB 的体积等于13·OC ·S △VAB ＝33，又因为三棱锥VABC 的体积与三棱锥CVAB 的体积相等，所以三棱锥VABC 的体积为33.4.(2015·广东，18)如图，三角形PDC 所在的平面与长方形ABCD 所在的平面垂直，PD ＝PC ＝4，AB ＝6，BC ＝3. (1)证明：BC ∥平面PDA ； (2)证明：BC ⊥PD ；(3)求点C 到平面PDA 的距离．4.解 (1)因为四边形ABCD 是长方形，所以BC ∥AD ， 因为BC ⊄平面PDA ，AD ⊂平面PDA ，所以BC ∥平面PDA.(2)因为四边形ABCD 是长方形，所以BC ⊥CD ，因为平面PDC ⊥平面ABCD ，平面PDC∩平面ABCD ＝CD ，BC ⊂平面ABCD ， 所以BC ⊥平面PDC ，因为PD ⊂平面PDC ，所以BC ⊥PD. (3)取CD 的中点E ，连接AE 和PE. 因为PD ＝PC ，所以PE ⊥CD ，在Rt △PED 中，PE ＝PD2－DE2＝42－32＝7.因为平面PDC ⊥平面ABCD ，平面PDC∩平面ABCD ＝CD ，PE ⊂平面PDC ， 所以PE ⊥平面ABCD ，由(2)知：BC ⊥平面PDC ，由(1)知：BC ∥AD ，所以AD ⊥平面PDC ， 因为PD ⊂平面PDC ，所以AD ⊥PD.设点C 到平面PDA 的距离为h ，因为V 三棱锥CPDA ＝V 三棱锥PACD ， 所以13S △PDA·h ＝13S △ACD·PE ，即h ＝S △ACD·PE S △PDA ＝12×3×6×712×3×4＝372，所以点C 到平面PDA 的距离是372.5.(2015·江苏，16)如图，在直三棱柱ABC-A 1B 1C 1中，已知AC ⊥BC ，BC ＝CC 1.设AB 1的中点为D ，B 1C ∩BC 1＝E . 求证：(1)DE ∥平面AA 1C 1C ； (2)BC 1⊥AB 1.5.证明 (1)由题意知，E 为B 1C 的中点， 又D 为AB 1的中点，所以DE ∥AC.又因为DE ⊄平面AA 1C 1C ，AC ⊂平面AA 1C 1C ， 所以DE ∥平面AA 1C 1C.(2)因为棱柱ABCA 1B 1C 1是直三棱柱， 所以CC 1⊥平面ABC.因为AC ⊂平面ABC，所以AC ⊥CC 1.又因为AC⊥BC，CC1⊂平面BCC1B1，BC⊂平面BCC1B1，BC∩CC1＝C，所以AC⊥平面BCC1B1.又因为BC1⊂平面BCC1B1，所以BC1⊥AC.因为BC＝CC1，所以矩形BCC1B1是正方形，所以BC1⊥B1C.因为AC，B1C⊂平面B1AC，AC∩B1C＝C，所以BC1⊥平面B1AC.又因为AB1⊂平面B1AC，所以BC1⊥AB1.6.(2015·山东，18)如图，三棱台DEF-ABC中，AB＝2DE，G，H分别为AC，BC的中点．(1)求证：BD∥平面FGH；(2)若CF⊥BC，AB⊥BC，求证：平面BCD⊥平面EGH.6.证明(1)方法一连接DG，CD，设CD∩GF＝M，连接MH.在三棱台DEF ABC中，AB＝2DE，G为AC的中点，可得DF∥GC，DF＝GC，所以四边形DFCG为平行四边形．则M为CD的中点，又H为BC的中点，所以HM∥BD，又HM⊂平面FGH，BD⊄平面FGH，所以BD∥平面FGH.方法二在三棱台DEFABC中，由BC＝2EF，H为BC的中点，可得BH∥EF，BH＝EF，所以四边形HBEF为平行四边形，可得BE∥HF.在△ABC中，G为AC的中点，H为BC的中点，所以GH∥AB.又GH∩HF＝H，所以平面FGH∥平面ABED.又因为BD⊂平面ABED，所以BD∥平面FGH.(2)连接HE，因为G，H分别为AC，BC的中点，所以GH∥AB.由AB⊥BC，得GH⊥BC.又H为BC的中点，所以EF∥HC，EF＝HC，因此四边形EFCH是平行四边形，所以CF∥HE.又CF⊥BC，所以HE⊥BC.又HE，GH⊂平面EGH，HE∩GH＝H，所以BC⊥平面EGH.又BC⊂平面BCD，所以平面BCD⊥平面EGH.A1和ACC1A1都为矩形．7.(2014·四川，18)在如图所示的多面体中,四边形ABB(1)若AC⊥BC,证明：直线BC⊥平面ACC1A1；(2)设D,E分别是线段BC,CC1的中点,在线段AB上是否存在一点M,使直线DE∥平面A1MC？请证明你的结论．7.(1)证明因为四边形ABB1A1和ACC1A1都是矩形，所以AA1⊥AB，AA1⊥AC.因为AB，AC为平面ABC内两条相交直线，所以AA1⊥平面ABC.因为直线BC⊂平面ABC，所以AA1⊥BC.又由已知，AC⊥BC，AA1，AC为平面ACC1A1内两条相交直线，所以BC⊥平面ACC1A1.(2)解取线段AB的中点M，连接A1M，MC，A1C，AC1，设O为A1C，AC1的交点．由已知可知，O为AC1的中点．连接MD，OE，则MD，OE分别为△ABC，△ACC1的中位线，所以，MD 平行且等于12AC ，OE 平行且等于12AC ，所以MD 平行且等于OE.连接OM ，从而四边形MDEO 为平行四边形， 则DE ∥MO.因为直线DE ⊄平面A1MC ，MO ⊂平面A 1MC ， 所以直线DE ∥平面A1MC.即线段AB 上存在一点M(线段AB 的中点)，使直线DE ∥平面A1MC.8.(2014·山东，18)如图，四棱锥P ABCD 中，AP ⊥平面PCD ，AD ∥BC ，AB ＝BC ＝12AD ，E ，F 分别为线段AD ，PC 的中点．(1)求证：AP ∥平面BEF ； (2)求证：BE ⊥平面P AC .8.证明 (1)设AC ∩BE ＝O ，连接OF ，EC . 由于E 为AD 的中点，AB ＝BC ＝12AD ，AD ∥BC ，所以AE ∥BC ，AE ＝AB ＝BC ，所以四边形ABCE 为菱形，所以O 为AC 的中点． 又F 为PC 的中点，所以在△PAC 中，可得AP ∥OF. 又OF ⊂平面BEF ，AP ⊄平面BEF ，所以AP ∥平面BEF.(2)由题意知ED ∥BC ，ED ＝BC.所以四边形BCDE 为平行四边形，所以BE ∥CD. 又AP ⊥平面PCD ，所以AP ⊥CD ，所以AP ⊥BE. 因为四边形ABCE 为菱形，所以BE ⊥AC.又AP∩AC ＝A ，AP 、AC ⊂平面PAC ，所以BE ⊥平面PAC.9.(2014·安徽，19)如图，四棱锥P-ABCD 的底面是边长为8的正方形，四条侧棱长均为217.点G ，E ，F ，H 分别是棱PB ，AB ，CD ，PC 上共面的四点，平面GEFH ⊥平面ABCD ，BC ∥平面GEFH . (1)证明：GH ∥EF ；(2)若EB ＝2，求四边形GEFH 的面积．9.(1)证明 因为BC ∥平面GEFH ，BC ⊂平面PBC ，且平面PBC∩平面GEFH ＝GH ， 所以GH ∥BC.同理可证EF ∥BC ，所以GH ∥EF.(2)解 连接AC ，BD 交于点O ，BD 交EF 于点K ，连接OP ，GK. 因为PA ＝PC ，O 是AC 的中点， 所以PO ⊥AC ，同理可得PO ⊥BD.又BD∩AC ＝O ，且AC ，BD 都在底面内，所以PO ⊥底面ABCD. 又因为平面GEFH ⊥平面ABCD ，且PO ⊄平面GEFH ， 所以PO ∥平面GEFH.因为平面PBD∩平面GEFH ＝GK ，所以PO ∥GK ，且GK ⊥底面ABCD ， 所以GK ⊥EF ，所以GK 是梯形GEFH 的高． 由AB ＝8，EB ＝2得EB ∶AB ＝KB ∶DB ＝1∶4， 所以KB ＝14DB ＝12OB ，即K 为OB 的中点．再由PO ∥GK 得GK ＝12PO ，即G 是PB 的中点，且GH ＝12BC ＝4.由已知可得OB ＝42，PO ＝PB2－OB2＝68－32＝6，所以GK ＝3. 故四边形GEFH 的面积S ＝GH ＋EF 2·GK ＝4＋82×3＝18.考点5 线面垂直的判定与性质1.(2014·浙江，6)设m ，n 是两条不同的直线，α，β是两个不同的平面( ) A.若m ⊥n ，n ∥α，则m ⊥α B.若m ∥β，β⊥α，则m ⊥α C.若m ⊥β，n ⊥β，n ⊥α，则m ⊥α D.若m ⊥n ，n ⊥β，β⊥α，则m ⊥α 1.解析 选项A 、B 、D 中m 均可能与平面α平行、垂直、斜交或在平面α内，故选C. 答案C2.(2016·新课标全国Ⅰ，18)如图，已知正三棱锥PABC 的侧面是直角三角形，PA ＝6，顶点P 在平面ABC 内的正投影为点D ，D 在平面PAB 内的正投影为点E ，连接PE 并延长交AB 于点G.(1)证明：G 是AB 的中点；(2)作出点E 在平面PAC 内的正投影F(说明作法及理由)，并求四面体PDEF 的体积. 2.(1)证明 因为P 在平面ABC 内的正投影为D ，所以AB ⊥PD . 因为D 在平面P AB 内的正投影为E ，所以AB ⊥DE . 所以AB ⊥平面PED ，所以AB ⊥PG .又由已知可得P A ＝PB ，从而G 是AB 的中点.(2)解 在平面P AB 内，过点E 作PB 的平行线交P A 于点F ，F 即为E 在平面P AC 内的正投影.理由如下：由已知可得PB ⊥P A ，PB ⊥PC ，又EF ∥PB ， 所以EF ⊥P A ，EF ⊥PC ，所以EF ⊥平面P AC ，即点F 为E 在平面P AC 内的正投影. 连接CG ，因为P 在平面ABC 内的正投影为D ， 所以D 是正三角形ABC 的中心.由(1)知，G 是AB 的中点，所以D 在CG 上，所以CD ＝23CG .由题设可得PC ⊥平面P AB ，DE ⊥平面P AB ， 所以DE ∥PC ，所以PE ＝23PG ，DE ＝13PC .由已知，正三棱锥的侧面是直角三角形且P A ＝6，可得DE ＝2，PE ＝2 2. 在等腰直角三角形EFP 中，可得EF ＝PF ＝2.所以四面体PDEF 的体积V ＝13×12×2×2×2＝43.3.(2016·新课标全国Ⅱ，19)如图，菱形ABCD 的对角线AC 与BD 交于点O ，点E ，F 分别在AD ，CD 上，AE ＝CF ，EF 交BD 于点H ，将△DEF 沿EF 折到△D ′EF 的位置.(1)证明：AC ⊥HD ′；(2)若AB ＝5，AC ＝6，AE ＝54，OD ′＝22，求五棱锥D ′ABCFE 的体积.3.(1)证明 由已知得AC ⊥BD ，AD ＝CD ，又由AE ＝CF 得AE AD ＝CFCD ，故AC ∥EF ，由此得EF ⊥HD ，折后EF 与HD 保持垂直关系，即EF ⊥HD ′， 所以AC ⊥HD ′.(2)解 由EF ∥AC 得OH DO ＝AE AD ＝14.由AB ＝5，AC ＝6得DO ＝BO ＝AB 2－AO 2＝4， 所以OH ＝1，D ′H ＝DH ＝3，于是OD ′2＋OH 2＝(22)2＋12＝9＝D ′H 2，所以OD ′⊥OH .由(1)知AC ⊥HD ′，又AC ⊥BD ，BD ∩HD ′＝H ， 所以AC ⊥平面DHD ′，于是AC ⊥OD ′，又由OD ′⊥OH ，AC ∩OH ＝O ， 所以OD ′⊥平面ABC . 又由EF AC ＝DH DO 得EF ＝92，五边形ABCFE 的面积S ＝12×6×8－12×92×3＝694，所以五棱锥D ′ABCFE 的体积V ＝13×694×22＝2322.4.(2016·北京，18)如图，在四棱锥P ABCD 中，PC ⊥平面ABCD ，AB ∥DC ，DC ⊥AC .(1)求证：DC ⊥平面P AC ； (2)求证：平面P AB ⊥平面P AC ；(3)设点E 为AB 的中点，在棱PB 上是否存在点F ，使得P A ∥平面CEF ？说明理由. 4.(1)证明 ∵PC ⊥平面ABCD ，DC ⊂平面ABCD ， ∴PC ⊥DC.又AC ⊥DC ，PC∩AC ＝C ，PC ⊂平面PAC ，AC ⊂平面PAC ， ∴CD ⊥平面PAC.(2)证明 ∵AB ∥CD ，CD ⊥平面PAC ， ∴AB ⊥平面PAC ， 又AB ⊂平面PAB ， ∴平面PAB ⊥平面PAC.(3)解 棱PB 上存在点F ，使得PA ∥平面CEF. 证明如下：取PB 的中点F ，连接EF ，CE ，CF ， 又因为E 为AB 的中点， ∴EF 为△PAB 的中位线， ∴EF ∥PA.又PA ⊄平面CEF ，EF ⊂平面CEF ， ∴PA ∥平面CEF.5.(2016·浙江，18)如图，在三棱台ABCDEF 中，平面BCFE ⊥平面ABC ，∠ACB ＝90°，BE ＝EF ＝FC ＝1，BC ＝2，AC ＝3. (1)求证：BF ⊥平面ACFD ；(2)求直线BD 与平面ACFD 所成角的余弦值.5.(1)证明 延长AD ，BE ，CF 相交于一点K ，如图所示，因为平面BCFE ⊥平面ABC ，且AC ⊥BC ， 所以AC ⊥平面BCK ， 所以BF ⊥AC .又因为EF ∥BC ，BE ＝EF ＝FC ＝1，BC ＝2，所以△BCK 为等边三角形，且F 为CK 的中点，则BF ⊥CK. 所以BF ⊥平面ACFD.(2)解 因为BF ⊥平面ACK ，所以∠BDF 是直线BD 与平面ACFD 所成的角.在Rt △BFD 中，BF ＝3，DF ＝32，得cos ∠BDF ＝217.所以直线BD 与平面ACFD 所成角的余弦值为217.6.(2016·四川，17)如图，在四棱锥P ABCD 中，P A ⊥CD ，AD ∥BC ，∠ADC ＝∠P AB ＝90°，BC ＝CD ＝12AD .(1)在平面P AD 内找一点M ，使得直线CM ∥平面P AB ，并说明理由. (2)证明：平面P AB ⊥平面PBD .6.(1)解 取棱AD 的中点M (M ∈平面P AD )，点M 即为所求的一个点，理由如下：因为AD ∥BC ，BC ＝12AD ，所以BC ∥AM ，且BC ＝AM .所以四边形AMCB 是平行四边形，所以CM ∥AB. 又AB ⊂平面PAB ，CM ⊄平面PAB ， 所以CM ∥平面PAB.(说明：取棱PD 的中点N ，则所找的点可以是直线MN 上任意一点) (2)证明 由已知，PA ⊥AB ，PA ⊥CD.因为AD ∥BC ，BC ＝12AD ，所以直线AB 与CD 相交，所以PA ⊥平面ABCD ，所以PA ⊥BD. 因为AD ∥BC ，BC ＝12AD ，所以BC ∥MD ，且BC ＝MD ， 所以四边形BCDM 是平行四边形， 所以BM ＝CD ＝12AD ，所以BD ⊥AB.又AB∩AP ＝A ，所以BD ⊥平面PAB.又BD ⊂平面PBD ，所以平面PAB ⊥平面PBD.7.(2015·新课标全国Ⅰ，18)如图，四边形ABCD 为菱形，G 是AC 与BD 的交点，BE ⊥平面ABCD .(1)证明：平面AEC ⊥平面BED ；(2)若∠ABC ＝120°，AE ⊥EC ，三棱锥EACD 的体积为63，求该三棱锥的侧面积． 7.解 (1)因为四边形ABCD 为菱形，所以AC ⊥BD. 因为BE ⊥平面ABCD ，所以AC ⊥BE. 所以AC ⊥平面BED ，又AC ⊂平面AEC ， 所以平面AEC ⊥平面BED.(2)设AB ＝x ，在菱形ABCD 中，由∠ABC ＝120°，可得AG ＝GC ＝32x ，GB ＝GD ＝x 2. 因为AE ⊥EC ，所以在Rt △AEC 中，可得EG ＝32x. 由BE ⊥平面ABCD ，知△EBG 为直角三角形，可得BE ＝22x. 由已知得，三棱锥EACD 的体积VEACD ＝13×12AC·GD·BE ＝624x3＝63.故x ＝2，从而可得AE ＝EC ＝ED ＝ 6.所以△EAC 的面积为3，△EAD 的面积与△ECD 的面积均为5， 故三棱锥EACD 的侧面积为3＋2 5.8.(2015·安徽，19)如图，三棱锥P -ABC 中，P A ⊥平面ABC ，P A ＝1，AB ＝1，AC ＝2，∠BAC ＝60°. (1)求三棱锥P -ABC 的体积；(2)证明：在线段PC 上存在点M ，使得AC ⊥BM ，并求PMMC的值．8.(1)解 由题设AB ＝1，AC ＝2，∠BAC ＝60°，可得S △ABC ＝12·AB·AC·sin 60°＝32.由PA ⊥平面ABC ，可知PA 是三棱锥P-ABC 的高， 又PA ＝1，所以三棱锥P-ABC 的体积V ＝13·S △ABC·PA ＝36.(2)证明 在平面ABC 内，过点B 作BN ⊥AC ，垂足为N ， 在平面PAC 内，过点N 作MN ∥PA 交PC 于点M ，连接BM. 由PA ⊥平面ABC 知PA ⊥AC ，所以MN ⊥AC. 由于BN∩MN ＝N ，故AC ⊥平面MBN ， 又BM ⊂平面MBN ，所以AC ⊥BM.在Rt △BAN 中，AN ＝AB·cos ∠BAC ＝12，从而NC ＝AC －AN ＝32，由MN ∥PA 得PM MC ＝AN NC ＝13.9.(2015·湖北，20)《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称 之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．在如图所示的阳马P-ABCD 中，侧棱PD ⊥底面ABCD ，且PD ＝CD ，点E 是PC 的中点，连接DE 、BD 、BE . (1)证明：DE ⊥平面PBC .试判断四面体EBCD 是否为鳖臑．若是，写出其每个面的直角(只需写出结论)；若不是，请说明理由； 9.解 (1)因为PD ⊥底面ABCD ，所以PD ⊥BC ， 由底面ABCD 为长方形，有BC ⊥CD ， 而PD∩CD ＝D ，所以BC ⊥平面PCD. 而DE ⊂平面PCD ，所以BC ⊥DE.又因为PD ＝CD ，点E 是PC 的中点，所以DE ⊥PC. 而PC∩BC ＝C ，所以DE ⊥平面PBC.由BC ⊥平面PCD ，DE ⊥平面PBC ，可知四面体EBCD 的四个面都是直角三角形， 即四面体EBCD 是一个鳖臑，其四个面的直角分别是∠BCD ，∠BCE ，∠DEC ，∠DEB. (2)由已知，PD 是阳马PABCD 的高，所以V1＝13SABCD·PD ＝13BC·CD·PD ；由(1)知，DE 是鳖臑DBCE 的高，BC ⊥CE ，所以V2＝13S △BCE·DE ＝16BC·CE·DE.在Rt △PDC 中，因为PD ＝CD ，点E 是PC 的中点，所以DE ＝CE ＝22CD ， 于是V1V2＝13BC·CD·PD 16BC·CE·DE ＝2CD·PD CE·DE＝4.记阳马P-ABCD 的体积为V1，四面体EBCD 的体积为V2，求V1V2的值．10.(2015·浙江，18)如图，在三棱柱ABC-A 1B 1C 1中，∠BAC ＝90°，AB ＝AC ＝2，A 1A ＝4，A 1在底面ABC 的射影为BC 的中点，D 为B 1C1的中点．。

○………………内………………○………………装………………○………………订………………○………………线………………○………………○………………外………………○………………装………………○………………订………………○………………线………………○………………学校：______________姓名：_____________班级：_______________考号：______________________绝密★启用前第八单元 立体几何初步单元测试卷高一数学（考试时间：120分钟 试卷满分：150分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上。

写在本试卷上无效。

4．测试范围：人教必修二2019第八单元 立体几何初步。

5．考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷一、单项选择题：（本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1．（2022·辽宁朝阳·高二开学考试）若m ，n ，l 为空间三条不同的直线，,,αβγ为空间三个不同的平面，则下列为真命题的是（ ） A ．若,m l n l ⊥⊥，则m n ∥ B ．若,m m αβ∥∥，则αβ∥ C ．若,αγβγ⊥⊥，则αβ∥ D ．若,,m n m n αβ⊥⊥∥，则αβ∥【答案】D 【解析】 【分析】对于A ：由m ，n 的位置关系是相交，平行或者异面即可判断；对于B:举反例：m 是平面,αβ外的直线，当m l ∥时，满足,m m αβ∥∥，不满足αβ∥.即可判断； 对于C ：由,αβ可能相交，可能平行即可判断； 对于D ：利用线面垂直的性质可以证明. 【详解】对于A ：,m l n l ⊥⊥时，m ，n 的位置关系是相交，平行或者异面.故A 错；对于B:若l αβ=，m 是平面,αβ外的直线，当m l ∥时，满足,m m αβ∥∥，不满足αβ∥.故B 错；对于C ：若,αγβγ⊥⊥，则,αβ可能相交，可能平行.故C 错；对于D ：由,m m n α⊥∥，则n α⊥，又n β⊥，由线面垂直的性质可得：αβ∥.故D 正确.故选：D2．（2022·河北张家口·一模）下图是战国时期的一个铜镞，其由两部分组成，前段是高为2cm ､底面边长为1cm 的正三棱锥，后段是高为0.6cm 的圆柱，圆柱底面圆与正三棱锥底面的正三角形内切，则此铜镞的体积约为（ ）A ．30.25cmB ．30.65cmC ．30.15cmD ．30.45cm【答案】D 【解析】 【分析】先求出内切圆半径为r ，再分别利用三棱锥体积与圆柱体积公式即可求出总体积. 【详解】因为正三棱锥的底面边长为1，设其内切圆半径为r ，由等面积法，可得：()1111sin 6011122r ⨯⨯⨯︒=++，解得：3r =3由三棱锥体积与圆柱体积公式可得：()2311311sin 6020.60.45cm 32V π=⨯⨯⨯⨯︒⨯+⨯⨯≈⎝⎭. 故选：D.3．（2021·陕西·西安市远东一中高一期末）如图，在正四棱柱1111ABCD A B C D -中，122AA AD ==，点E 为棱1BB 的中点，过A ，E ，1C 三点的平面截正四棱柱1111ABCD A B C D -所得的截面面积为（ ）○………………内………………○………………装………………○………………订………………○………………线………………○…………○………………外………………○………………装………………○………………订………………○………………线………………○………… 学校：______________姓名：_____________班级：_______________考号：______________________A ．2 B．2C ．23D 3【答案】D【解析】 【分析】根据题意画出截面，得到截面为菱形1AEC F ，从而可求出截面的面积. 【详解】取1DD 的中点F ， 1CC 的中点G，连接1,,,,AF FC BG FG EF ，因为该几何体为正四棱柱， ∴////,,AB CD FG AB CD FG == 故四边形ABGF 为平行四边形， 所以//AF BG ，又1//BG EC ，∴1//AF EC ，同理1//AE FC ，且112AF EC AE FC EF ====所以过A ，E ，1C 三点的平面截正四棱柱1111ABCD A B C D -所得的截面为菱形1AEC F ，所以该菱形1AEC F 的面积为23223=故选：D4．（2022·北京市第一六一中学高三阶段练习）如图，有一个水平放置的透明无盖的正方体容器，容器高8cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm ，如果不计容器的厚度，则该球的半径为( )A ．5cmB ．6cmC ．7cmD ．8cm【答案】A 【解析】 【分析】作出球的正视图，根据已知条件构造直角三角形，列关于球半径R 的方程求解即可．【详解】如图为球的一个正视图，AB 长度等于正方体棱长，AB 中点为M ，则MB ＝4，球面恰好接触水面时测得水深为6cm ，862MD ∴=-=cm ，设球的半径为R ，则CM ＝R －2，CB ＝R ，○………………内………………○………………装………………○………………订………………○………………线………………○…………○………………外………………○………………装………………○………………订………………○………………线………………○………… 学校：______________姓名：_____________班级：_______________考号：______________________故选：A.5．（2021·江苏苏州·高三阶段练习）用一平面截圆柱，得到如图所示的几何体，截面椭圆的长轴两端点到底面的距离分别为3和5，圆柱的底面直径为4，则该几何体的体积为（ ）A ．16πB ．32πC ．8πD ．64π【答案】A 【解析】 【分析】由图形可知所求几何体是由底面直径相同，高为3的圆柱和高为2的圆柱的一半拼成，由圆柱体积公式可求得结果. 【详解】作出几何体的轴截面如下图所示：则所求几何体是由一个底面直径为4，高为3的圆柱与一个底面直径为4，高为2的圆柱的一半构成，∴所求几何体体积2212322162V πππ=⋅⨯+⋅⨯=.故选：A.6．（2022·云南昭通·高三阶段练习（文））如图所示，在正方体1111-ABCD A B C D 中，点F 是棱1AA 上的一个动点，平面1BFD 交棱1CC 于点E ，则下列命题中假命题是（ ）A ．存在点F ，使得11A C ∥平面1BED FB ．存在点F ，使得1B D ∥平面1BED FC ．对于任意的点F ，四边形1BED F 均为平行四边形 D ．对于任意的点F ，三棱锥11F BB D -的体积均不变 【答案】B 【解析】 【分析】对于A ，根据线面平行的判定判断即可；对于B ，可知1B D 与平面1BED F 一定相交，从而可知不正确；对于C ，由面面平行的性质可判断；对于D ，由体积公式可判断. 【详解】对于A ，当F 为1AA 的中点时，则E 也为1CC 的中点，11EF AC ∴∥，EF ⊂平面1BED F ， 11A C ⊄平面1BED F ，11A C ∴∥平面1BED F ，故A 为真命题；对于B ，因为1BD ⊂平面1BED F ，由正方体性质知1B D 与1BD 相交于一点，所以1B D ∥平面1BED F 不可能，故B 为假命题；对于C ，由面面平行的性质，可知11//,//BF ED BE FD ，因此四边形1BED F 一定为平行四边形，故C 是真命题；对于D ，1AA ∥平面11BB D ，所以点F 到平面11BB D 的距离为定值，∴三棱锥11F BB D -的体积为定值，故D 是真命题. 故选：B.7．（2022·云南师大附中高三阶段练习（理））如图，在矩形ABCD 中，2,2AB BC ==，E 为BC 中点，把ABE △和CDE △分别沿,AE DE 折起，使点B 与点C 重合于点P ，若三棱锥P ADE -的四个顶点都在球O○………………内………………○………………装………………○………………订………………○………………线………………○…………○………………外………………○………………装………………○………………订………………○………………线………………○………… 学校：______________姓名：_____________班级：_______________考号：______________________的球面上，则球O 的表面积为（ ）A ．3πB ．4πC ．5πD ．9π【答案】C 【解析】 【分析】根据给定条件，推导可得,,PE PA PD 两两垂直，再补形成长方体，求出长方体的体对角线即可计算作答. 【详解】依题意，,PE PA PE PD ⊥⊥，PA PD P =，,PA PD ⊂平面PAD ，则PE ⊥平面PAD ， 又2,2PA PD AD ===，即有222PA PD AD +=，则PA PD ⊥，因此可将三棱锥P ADE -补形成以,,PE PA PD 为相邻三条棱的长方体，若三棱锥P ADE -的四个顶点都在球O 的球面上，则该长方体的各顶点亦在球O 的球面上， 设球O 的半径为R ，则该长方体的体对角线长为2R ，即22225R PE PA PD ++所以球O 的表面积为224(2)5S R R πππ===. 故选：C8．（2022·河南·模拟预测（理））已知球面被平面所截得的部分叫做球冠，垂直于截面的直径被截得的一段叫做球冠的高，若球的半径是R ，球冠的高是h ，则球冠的面积为2πRh ．某机械零件的结构是在一个圆台的底部嵌入一颗小球，其正视图和侧视图均如图所示，已知圆台的任意母线均与小球的表面相切，则小球突出圆台部分的球冠面积为（ ）A ．25πB ．253πC 253D ．1003π 【答案】D 【解析】【分析】由已知条件分别求出球冠的R ,h ，再根据球冠的面积公式2Rh π求值即可. 【详解】依题意，60AB =,253HI = 因为ABC ∆为等边三角形， 所以303CI =所以30325353CH == 因为16DF CH AB CI ==， 所以10DF =， 所以152r DH DF ===， 在CDG ∆中，30DCG ∠=， 所以60DGH ∠=， 所以在DGH ∆中，103R DG ==，53GH = 所以53h EH R GH ==-=， 所以10353100=223S Rh πππ==， 故选：D.二、多项选择题：（本题共4小题，每小题5分，共20分。

教辅：新课标版数学（理）高三总复习：第八章立体几何单元测试卷>第八章单元测试卷一、选择题(本大题共12小题，每小题5分，共60分．每小题中只有一项符合题目要求) 1．设a，b是两条不同的直线，α，β是两个不同的平面，则下列命题错误的是() A．若a⊥α，b∥α，则a⊥b B．若a⊥α，b∥a，b⊂β，则α⊥βC．若a⊥α，b⊥β，α∥β，则a∥b D．若a∥α，a∥β，则α∥β答案 D 解析由题意可得A，B，C选项显然正确，对于选项D：当α，β相交，且a与α，β的交线平行时，有a∥α，a∥β，但此时α与β不平行．故选D. 2．如图所示，在正方体ABCD－A1B1C1D1中，M，N分别是BC1，CD1的中点，则下列说法错误的是() A．MN与CC1垂直B．MN与AC垂直C．MN与BD平行D．MN 与A1B1平行答案 D 解析连接C1D，BD.∵N是D1C的中点，∴N是C1D的中点，∴MN∥BD.又∵CC1⊥BD，∴CC1⊥MN，故A，C正确．∵AC⊥BD，MN∥BD，∴MN⊥AC，故B正确，故选D. 3．用与球心距离为1的平面去截球，所得的截面面积为π，则球的体积为() A. B. C．8π D. 答案 B 解析S圆＝πr2＝1⇒r＝1，而截面圆圆心与球心的距离d＝1，∴球的半径为R ＝＝. ∴V＝πR3＝，故选B. 4．某个长方体被一个平面所截，得到几何体的三视图如图所示，则这个几何体的体积为() A．4 B．2 C. D．8 答案 D 解析由三视图可知，该几何体如图所示，其底面为正方形，正方形的边长为2.HD＝3，BF＝1，将相同的两个几何体放在一起，构成一个高为4的长方体，所以该几何体的体积为×2×2×4＝8. 5.如图所示，正四棱锥P－ABCD的底面积为3，体积为，E为侧棱PC的中点，则PA与BE所成的角为() A. B. C. D. 答案 C 解析连接AC，BD交于点O，连接OE，易得OE∥PA. ∴所求角为∠BEO. 由所给条件易得OB＝，OE＝PA＝，BE＝. ∴cos ∠OEB＝，∴∠OEB＝60°，选C. 6．直三棱柱ABC－A1B1C1的直观图及三视图如下图所示，D为AC的中点，则下列命题是假命题的是() A．AB1∥平面BDC1 B．A1C⊥平面BDC1 C．直三棱柱的体积V＝4 D．直三棱柱的外接球的表面积为4π答案 D 解析由三视图可知，直三棱柱ABC－A1B1C1的侧面B1C1CB是边长为2的正方形，底面ABC是等腰直角三角形，AB⊥BC，AB＝BC＝2.连接B1C交BC1于点O，连接AB1，OD.在△CAB1中，O，D分别是B1C，AC的中点，∴OD∥AB1，∴AB1∥平面BDC1.故A正确．直三棱柱ABC－A1B1C1中，AA1⊥平面ABC，∴AA1⊥BD.又AB ＝BC＝2，D为AC的中点，∴BD⊥AC，∴BD⊥平面AA1C1C. ∴BD⊥A1C.又A1B1⊥B1C1，A1B1⊥B1B，∴A1B1⊥平面B1C1CB，∴A1B1⊥BC1. ∵BC1⊥B1C，且A1B1∩B1C＝B1，∴BC1⊥平面A1B1C. ∴BC1⊥A1C，∴A1C⊥平面BDC1. 故B正确．V＝S△ABC ×C1C＝×2×2×2＝4，∴C正确．此直三棱柱的外接球的半径为，其表面积为12π，D错误．故选D. 7．在平面四边形ABCD中，AD ＝AB＝，CD＝CB＝，且AD⊥AB，现将△ABD沿着对角线BD翻折成△A′BD，则在△A′BD折起至转到平面BCD内的过程中，直线A′C与平面BCD所成的最大角的正切值为() A．1 B. C. D. 答案 C 解析如图所示，OA＝1，OC＝2.当A′C与圆相切时，直线A′C与平面BCD所成的角最大，最大角为30°，其正切值为.故选C. 8．一个圆锥被过顶点的平面截去了较小的一部分，余下的几何体的三视图如图，则该几何体的表面积为() A.＋＋＋1 B．2＋3π＋＋1 C.＋＋ D.＋＋＋1 答案 A 解析还原为直观图如图所示，圆锥的高为2，底面半径为，圆锥的母线长为，故该几何体的表面积为S＝×2×＋×2π×××＋π×()2×＋×2×1＝＋＋＋1. 9．二面角的棱上有A，B两点，直线AC，BD分别在这个二面角的两个半平面内，且都垂直于AB.已知AB＝4，AC＝6，BD＝8，CD＝2，则该二面角的大小为() A．150°B．45°C．60°D．120°答案 C 解析由条件，知·＝0，·＝0，＝＋＋. ∴||2＝||2＋||2＋||2＋2·＋2·＋2·＝62＋42＋82＋2×6×8cos〈，〉＝(2)2.∴cos〈，〉＝－，〈，〉＝120°，∴二面角的大小为60°，故选C. 10．已知某个几何体的三视图如图(主视图的弧线是半圆)，根据图中标出的数据，这个几何体的体积是() A．288＋36πB．60πC．288＋72πD．288＋18π答案 A 解析将几何体的三视图转化为直观图此几何体下面为长方体上面为半圆柱，根据三视图所标数据，可得V长方体＝6×8×6＝288，V半圆柱＝×32×π×8＝36π. ∴此几何体的体积为V＝288＋36π. 11．在正方体ABCD－A1B1C1D1中，E是棱BB1中点，G是DD1中点，F是BC上一点且FB＝BC，则GB与EF所成的角为() A．30°B．120°C．60°D．90°答案 D 解析方法一：连D1E，D1F，解三角形D1EF即可．方法二：如图建立直角坐标系D－xyz，设DA＝1，由已知条件，得G(0,0，)，B(1,1,0)，E(1,1，)，F(，1,0)，＝(1,1，－)，＝(－，0，－)．cos 〈，〉＝＝0，则⊥.故选D. 12．已知正方体ABCD－A1B1C1D1棱长为1，点P在线段BD1上，当∠APC最大时，三棱锥P－ABC的体积为() A. B. C. D. 答案 B 解析以B为坐标原点，BA为x 轴，BC为y轴，BB1为z轴建立空间直角坐标系，设＝λ，可得P(λ，λ，λ)，再由cos∠APC＝可求得当λ＝时，∠APC最大，故VP－ABC＝××1×1×＝. 二、填空题(本大题共4小题，每小题5分，共20分，把答案填在题中横线上) 13．已知四个命题：①若直线l∥平面α，则直线l的垂线必平行于平面α；②若直线l与平面α相交，则有且只有一个平面经过直线l与平面α垂直；③若一个三棱锥每两个相邻侧面所成的角都相等，则这个三棱锥是正三棱锥；④若四棱柱的任意两条对角线相交且互相平分，则这个四棱柱为平行六面体．其中正确的命题是________．答案④解析④正确，如右图，A1C与B1D互相平分，则四边形A1B1CD是平行四边形，同理四边形ABC1D1是平行四边形，则A1B1綊AB綊CD，因此四边形ABCD是平行四边形，进而可得这个四棱柱为平行六面体．14．(2013·江苏)如图所示，在三棱柱A1B1C1－ABC中，D，E，F分别是AB，AC，AA1的中点，设三棱锥F－ADE的体积为V1，三棱柱A1B1C1－ABC的体积为V2，则V1∶V2＝________. 答案1∶24 解析由题意可知点F到面ABC的距离与点A1到面ABC的距离之比为1∶2，S△ADE∶S△ABC＝1∶4. 因此V1∶V2＝＝1∶24. 15．已知正三棱锥P－ABC，点P，A，B，C都在半径为的球面上，若PA，PB，PC两两相互垂直，则球心到截面ABC的距离为________．答案解析正三棱锥P－ABC可看作由正方体PADC－BEFG截得，如图所示，PF为三棱锥P－ABC的外接球的直径，且PF⊥平面ABC. 设正方体棱长为a，则3a2＝12，a＝2，AB ＝AC＝BC＝2. S△ABC＝×2×2×＝2. 由VP－ABC＝VB－PAC，得·h·S△ABC＝××2×2×2，所以h＝，因此球心到平面ABC的距离为. 16.如图所示是一几何体的平面展开图，其中ABCD为正方形，E，F，分别为PA，PD的中点，在此几何体中，给出下面四个结论：①直线BE与直线CF异面；②直线BE与直线AF异面；③直线EF∥平面PBC；④平面BCE⊥平面PAD. 其中正确的有______个．答案 2 解析将几何体展开图拼成几何体(如图)，因为E，F分别为PA，PD 的中点，所以EF∥AD∥BC，即直线BE与CF共面，①错；因为B∉平面PAD，E∈平面PAD，E∉AF，所以BE与AF是异面直线，②正确；因为EF∥AD∥BC，EF⊄平面PBC，BC⊂平面PBC，所以EF∥平面PBC，③正确；平面PAD与平面BCE不一定垂直，④错．三、解答题(本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤) 17．(本小题满分10分)右图为一简单组合体，其底面ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD＝AD＝2EC＝2. (1)请画出该几何体的三视图；(2)求四棱锥B－CEPD的体积．答案(1)略(2)2 解析(1)该组合体的三视图如右图所示．(2)因为PD⊥平面ABCD，PD⊂平面PDCE，所以平面PDCE⊥平面ABCD. 因为四边形ABCD为正方形，所以BC⊥CD，且BC＝DC＝AD＝2. 又因为平面PDCE∩平面ABCD＝CD，BC⊂平面ABCD，所以BC⊥平面PDCE. 因为PD ⊥平面ABCD，DC⊂平面ABCD，所以PD⊥DC. 又因为EC∥PD，PD＝2，EC＝1，所以四边形PDCE为一个直角梯形，其面积S梯形PDCE＝(PD＋EC)×DC＝×3×2＝3. 所以四棱锥B－CEPD的体积VB－CEPD＝S梯形PDCE×BC＝×3×2＝2. 18．(本小题满分12分)如图所示，在四棱锥P－ABCD中，底面ABCD为平行四边形，∠ADC＝45°，AD＝AC＝1，O为AC的中点，PO⊥平面ABCD，PO＝2，M为PD的中点．(1)证明：PB∥平面ACM；(2)证明：AD⊥平面PAC；(3)求直线AM与平面ABCD所成角的正切值．答案(1)略(2)略(3) 解析(1)连接BD，MO，在平行四边形ABCD中，因为O 为AC的中点，所以O为BD的中点．又M为PD的中点，所以PB∥MO.因为PB⊄平面ACM，MO⊂平面ACM，所以PB∥平面ACM.(2)因为∠ADC＝45°，且AD＝AC＝1，所以∠DAC＝90°，即AD⊥AC.又PO⊥平面ABCD，AD⊂平面ABCD，所以PO⊥AD.而AC∩PO＝O，所以AD⊥平面PAC. (3)取DO中点N，连接MN，AN.因为M为PD的中点，所以MN∥PO，且MN＝PO＝1.由PO⊥平面ABCD，得MN⊥平面ABCD，所以∠MAN是直线AM与平面ABCD所成的角．在Rt△DAO中，AD＝1，AO＝，所以DO＝.从而AN＝DO＝.在Rt△ANM中，tan∠MAN＝＝＝，即直线AM与平面ABCD所成角的正切值为. 19．(本小题满分12分)如图所示，在四棱锥P－ABCD中，PA⊥平面ABCD，四边形ABCD为正方形，AB＝4，PA＝3，A点在PD上的射影为G点，E点在AB上，平面PEC⊥平面PCD. (1)求证：AG∥平面PEC；(2)求AE的长；(3)求二面角E－PC－A的正弦值．答案(1)略(2)(3) 解析(1)证明：∵PA⊥平面ABCD，∴PA⊥CD. 又∵CD⊥AD，PA∩AD ＝A，∴CD⊥平面PAD.∴CD⊥AG. 又PD⊥AG，∴AG⊥平面PCD. 作EF⊥PC于点F，连接GF，∵平面PEC⊥平面PCD，∴EF⊥平面PCD.∴EF∥AG. 又AG⊄平面PEC，EF⊂平面PEC，∴AG∥平面PEC. (2)解：由(1)知A，E，F，G四点共面，又AE∥CD，AE⊄平面PCD，CD⊂平面PCD，∴AE∥平面PCD. 又∵平面AEFG∩平面PCD＝GF，∴AE∥GF. 又由(1)知EF∥AG，∴四边形AEFG为平行四边形，∴AE＝GF. ∵PA＝3，AD＝4，∴PD＝5，AG＝. 又PA2＝PG·PD，∴PG＝. 又＝，∴GF＝＝，∴AE＝. (3)解：过E作EO⊥AC于点O，连接OF，易知EO⊥平面PAC，又EF⊥PC，∴OF⊥PC. ∴∠EFO即为二面角E－PC－A的平面角．EO＝AE·sin45°＝×＝，又EF＝AG＝，∴sin∠EFO＝＝×＝. 20．(本小题满分12分)如图所示，△BCD与△MCD都是边长为2的正三角形，平面MCD ⊥平面BCD，AB⊥平面BCD，AB＝2. (1)求证：AB∥平面MCD；(2)求平面ACM与平面BCD所成二面角的正弦值．答案(1)略(2) 解析(1)证明：取CD中点O，因为△MCD为正三角形，所以MO⊥CD. 由于平面MCD⊥平面BCD，所以MO⊥平面BCD. 又因为AB⊥平面BCD，所以AB∥MO.又AB⊄平面MCD，MO⊂平面MCD，所以AB∥平面MCD. (2)连接OB，则OB⊥CD，又MO ⊥平面BCD. 取O为原点，直线OC，BO，OM为x轴，y轴，z 轴，建立空间直角坐标系如图所示．OB＝OM＝，则各点坐标分别为C(1,0,0)，M(0,0，)，B(0，－，0)，A(0，－，2)．＝(－1,0，)，＝(－1，－，2)．设平面ACM的法向量为n1＝(x，y，z)，由得解得x＝z，y＝z，取z＝1，得n1＝(，1,1)．又平面BCD的法向量为n2＝(0,0,1)，所以cos〈n1，n2〉＝＝. 设所求二面角为θ，则sin θ＝. 21．(本小题满分12分) 圆锥PO如图①所示，图②是它的正(主)视图．已知圆O的直径为AB，C是圆周上异于A，B的一点，D为AC的中点．(1)求该圆锥的侧面积S；(2)求证：平面PAC⊥平面POD；(3)若∠CAB＝60°，在三棱锥A－PBC中，求点A到平面PBC的距离．答案(1)π(2)略(3) 解析(1)由圆锥的正视图可知，圆锥的高h＝，底面半径r＝1，所以其母线长为l＝，所以圆锥的侧面积S＝l·2πr＝××2π×1＝π. (2)证明：因为AB是圆O的直径，所以AC⊥BC.又因为O，D分别为AB，AC的中点，所以OD∥BC，所以OD⊥AC. 因为PO⊥平面ABC，所以AC⊥PO. 因为PO∩OD ＝O，PO，OD⊂平面POD，所以AC⊥平面POD. 因为AC⊂平面PAC，所以平面PAC⊥平面POD. (3)因为∠CAB＝60°，AB＝2，所以BC＝，AC＝1.所以S△ABC＝. 又因为PO＝，OC＝OB＝1，所以S△PBC＝. 设A到平面PBC的距离为h，由于VP－ABC＝V A－PBC，得S△ABC·PO＝S△PBC·h，解得h＝. 22．(本小题满分12分)如图所示，正三棱柱ABC－A1B1C1的底面边长是2，侧棱长是，D是AC的中点．(1)求证：B1C∥平面A1BD；(2)求二面角A1－BD－A的大小；(3)在线段AA1上是否存在一点E，使得平面B1C1E⊥平面A1BD？若存在，求出AE的长；若不存在，说明理由．答案(1)略(2)(3)存在且AE＝解析(1)如图①所示，连接AB1交A1B于点M，连接B1C，DM. 因为三棱柱ABC－A1B1C1是正三棱柱，所以四边形AA1B1B是矩形，所以M为AB1的中点．因为D是AC的中点，所以MD是三角形AB1C 的中位线，所以MD∥B1C. 因为MD⊂平面A1BD，B1C⊄平面A1BD，所以B1C∥平面A1BD. (2)作CO⊥AB于点O，所以CO⊥平面ABB1A1，所以在正三棱柱ABC－A1B1C1中建立如图②所示的空间直角坐标系O－xyz. 因为AB＝2，AA1＝，D是AC的中点，所以A(1,0,0)，B(－1,0,0)，C(0,0，)，A1(1，，0)．所以D(，0，)，＝(，0，)，＝(2，，0)．设n＝(x，y，z)是平面A1BD的法向量，所以即令x ＝－，则y＝2，z＝3. 所以n＝(－，2,3)是平面A1BD的一个法向量．由题意可知＝(0，，0)是平面ABD的一个法向量，所以cos〈n，〉＝＝.所以二面角A1－BD－A的大小为. (3)设E(1，y,0)，则＝(1，y －，－)，＝(－1,0，－)．设平面B1C1E的法向量n1＝(x1，y1，z1)，所以即令z1＝－，则x1＝3，y1＝，所以n1＝(3，，－)．又n1·n ＝0，即－3＋－3＝0，解得y＝. 所以存在点E，使得平面B1C1E⊥平面A1BD且AE＝.。

一、选择题1．(2017·湖南省衡阳八中、长郡中学、岳阳十一中等十三校高考一模数学7试题)直线y ＝b a x ＋3与双曲线x 2a 2－y 2b2＝1的交点个数是 ( A )A ．1B ．2C ．1或2D ．0因为直线y ＝ba x ＋3与双曲线的渐近线y ＝b ax 平行，所以它与双曲线只有1个交点． 2．(2016·福州质检)抛物线C 的顶点为原点，焦点在x 轴上，直线x －y ＝0与抛物线C 交于A ，B 两点，若P (1,1)为线段AB 的中点，则抛物线C 的方程为 ( B )A ．y ＝2x 2B ．y 2＝2x C ．x 2＝2yD ．y 2＝－2x设A (x 1，y 1)，B (x 2，y 2)，抛物线方程为y2＝2px ，则⎩⎪⎨⎪⎧y 21＝2px 1，y 22＝2px 2，两式相减可得2p＝y 1－y 2x 1－x 2×(y 1＋y 2)＝k AB ×2＝2，即可得p ＝1，∴ 抛物线C 的方程为y 2＝2x ，故选B ． 3．(2016·厦门期末)过双曲线C ：x 24－y 29＝1的左焦点作倾斜角为π6的直线l ，则直线l与双曲线C 的交点情况是 ( D )A ．没有交点B ．只有一个交点C ．有两个交点且都在左支上D ．有两个交点分别在左、右两支上直线l 的方程为y ＝33(x ＋13)，代入C ：x 24－y 29＝1整理，得23x 2－813x －160＝0，Δ＝(－813)2＋4×23×160>0，所以直线l 与双曲线C 有两个交点，由一元二次方程根与系数的关系得两个交点横坐标符号不同，故两个交点分别在左、右支上．4．(2016·舟山模拟)已知椭圆C 的方程为x 216＋y 2m 2＝1(m >0)，如果直线y ＝22x 与椭圆的一个交点M 在x 轴上的射影恰好是椭圆的右焦点F ，则m 的值为 ( B )A ．2B ．2 2C ．8D ．2 3根据已知条件得c ＝16－m 2，则点(16－m 2，2216－m 2)在椭圆x 216＋y 2m 2＝1(m >0)上，∴16－m 216＋16－m22m2＝1，可得m ＝22，故选B ．5．(2016·雅安月考)抛物线y 2＝4x 的焦点为F ，准线为l ，经过F 且斜率为3的直线与抛物线在x 轴上方的部分相交于点A ，AK ⊥l ，垂足为K ，则△AKF 的面积是 ( C )A ．4B ．3 3C ．4 3D ．8∵y 2＝4x ，∴F (1,0)，l ：x ＝－1，过焦点F 且斜率为3的直线l 1：y ＝3(x －1)，与y 2＝4x 联立，解得A (3,23)，∴AK ＝4，∴S △AKF ＝12×4×23＝43，故选C ．6．(2017·江西省抚州市临川二中期中数学试题)已知椭圆：x 24＋y 23＝1，直线l ：y ＝x＋57，椭圆上任意点P ，则点P 到直线l 的距离的最大值 ( A )A ．314B ．27C ．37D ．214利用椭圆的参数方程，设出点P 的坐标，再由点到直线的距离及辅助角公式，再由正弦函数的性质，即可求出P 到直线l 最大值．解：因为P 是椭圆x 24＋y 23＝1上任意点，可设P (2cos θ，3sin θ)，其中θ∈ 先设出直线方程，再联立直线方程与抛物线方程整理可得A ，B 的横坐标与直线的斜率之间的关系式，结合弦AB 恰好是以P 为中点，以及中点坐标公式即可求出直线的斜率，进而求出直线方程．解：设A (x 1，y 1)，B (x 2，y 2)，弦AB 所在直线方程为：y －1＝k (x －2) 即y ＝kx ＋1－2k联立⎩⎪⎨⎪⎧y ＝kx ＋1－2k y 2＝4x 整理得k 2x 2＋x ＋(1－2k )2＝0. 所以有x 1＋x 2＝－2k－2k －4k2∵弦AB 恰好是以P 为中点， ∴－2k －2k －4k2＝4 解得k ＝2.所以直线方程为 y ＝2x －3，即2x －y －3＝0. 故答案为：2x －y －3＝0.本题主要考查直线与圆锥曲线的综合问题．解决本题的关键在于利用中点坐标公式以及韦达定理得到关于直线的斜率的等式．8．(2016·上海静安一模)已知椭圆C ：x 22＋y 24＝1，过椭圆C 上一点P (1，2)作倾斜角互补的两条直线PA 、PB ，分别交椭圆C 于A 、B 两点．则直线AB 设A (x 1，y 1)，B (x 2，y 2)，同时设PA 的方程为y －2＝k (x －1)，代入椭圆方程化简得(k 2＋2)x 2－2k (k －2)x ＋k 2－22k －2＝0，显然1和x 1是这个方程的两解．因此x 1＝k 2－22k －2k 2＋2，y 1＝－2k 2－4k ＋22k 2＋2.由一k 代替x 1，y 1中的k ，得x 2＝k 2＋22k －2k 2＋2，y 2＝－2k 2＋4k ＋22k 2＋2，所以y 2－y 1x 2－x 1＝ 2. 三、解答题9．(2016·山西模拟)已知椭圆C 的中心在原点，焦点在x 轴上，焦距为2，离心率为12.(1)求随圆C 的方程；(2)设直线l 经过点M (0,1)，且与椭圆C 交于A ，B 两点，若AM →＝2MB →，求直线l 的方程．(1)设椭圆方程为x 2a 2＋y 2b 2＝1(a >b >0)，因为c ＝1，c a ＝12，所以a ＝2，b ＝3，所以椭圆方程为x 24＋y 23＝1.(2)由题意得直线l 的斜率存在，设直线l 的方程为y ＝kx ＋1，联立方程⎩⎪⎨⎪⎧y ＝kx ＋1，x 24＋y23＝1，得(3＋4k 2)x 2＋8kx －8＝0，且Δ>0. 设A (x 1，y 1)，B (x 2，y 2)，由AM →＝2MB →， 得x 1＝－2x 2， 又⎩⎪⎨⎪⎧x 1＋x 2＝－8k3＋4k 2，x 1·x 2＝－83＋4k2，所以⎩⎪⎨⎪⎧－x 2＝－8k3＋4k 2，－2x 22＝－83＋4k2，消去x 2得(8k 3＋4k )2＝43＋4k ，解得k 2＝14，k ＝±12，所以直线l 的方程为y ＝±12x ＋1，即x －2y ＋2＝0或x ＋2y －2＝0.10．(2016·江苏)如图，在平面直角坐标系xOy 中，已知直线l ：x －y －2＝0，抛物线C ：y 2＝2px (p >0).(1)若直线l 过抛物线C 的焦点，求抛物线C 的方程； (2)已知抛物线C 上存在关于直线l 对称的相异两点P 和Q . ①求证：线段PQ 的中点坐标为(2－p ，－p )； ②求p 的取值范围．(1)抛物线C ：y 2＝2px (p >0)的焦点为(p2，0)，由点(p2，0)在直线l ：x －y －2＝0上，得p2－0－2＝0，即p ＝4. 所以抛物线C 的方程为y 2＝8x .(2)设P (x 1，y 1)，Q (x 2，y 2)，线段PQ 的中点M (x 0，y 0)． 因为点P 和Q 关于直线l 对称，所以直线l 垂直平分线段PQ ， 于是直线PQ 的斜率为－1，则可设其方程为y ＝－x ＋b .①由⎩⎪⎨⎪⎧y 2＝2px ，y ＝－x ＋b消去x 得y 2＋2py －2pb ＝0.(*)因为P 和Q 是抛物线C 上的相异两点，所以y 1≠y 2， 从而Δ＝(2p )2－4×(－2pb )>0，化简得p ＋2b >0.方程(*)的两根为y 1,2＝－p ±p 2＋2pb ， 从而y 0＝y 1＋y 22＝－p .因为M (x 0，y 0)在直线l 上，所以x 0＝2－p . 因此，线段PQ 的中点坐标为(2－p ，－p )． ②因为M (2－p ，－p )在直线y ＝－x ＋b 上， 所以－p ＝－(2－p )＋b ，即b ＝2－2p .由①知p ＋2b >0，于是p ＋2(2－2p )>0，所以p <43.因此，p 的取值范围是(0，43)．1．(2016·丽水一模)斜率为1的直线l 与椭圆x 24＋y 2＝1相交于A 、B 两点，则|AB |的最大值为 ( C )A ．2B ．455C ．4105D ．8105设A 、B 两点的坐标分别为(x 1，y 1)，(x 2，y 2)，直线l 的方程为y ＝x ＋t ，由⎩⎪⎨⎪⎧x 2＋4y 2＝4，y ＝x ＋t消去y ，得5x 2＋8tx ＋4(t 2－1)＝0.则x 1＋x 2＝－85t ，x 1x 2＝t 2－5.∴|AB |＝1＋k 2|x 1－x 2| ＝1＋k 2·x 1＋x 22－4x 1x 2＝2·－85t 2－4×t 2－5＝425·5－t 2， 当t ＝0时，|AB |max ＝4105.2．(2016·浦东新区模拟)已知x 1，x 2是关于x 的方程x 2＋mx －(2m ＋1)＝0的两个实数根，则经过两点A (x 1，x 21)，B (x 2，x 22)的直线与椭圆x 216＋y 24＝1公共点的个数是 ( A )A ．2B ．1C ．0D ．不确定方法一：∵x 1，x 2是关于x 的方程x 2＋mx －(2m ＋1)＝0的两个实数根，∴x 1＋x 2＝－m ，x 1·x 2＝－(2m ＋1)，且x 21＋mx 1－(2m ＋1)＝0，x 22＋mx 2－(2m ＋1)＝0.又∵k AB ＝x 21－x 22x 1－x 2＝(x 1＋x 2)＝－m ，直线AB 的方程为：y －x 21＝－m (x －x 1)，即y ＋mx 1－(2m ＋1)＝－m (x －x 1)，即y －(2m ＋1)＝－mx ，即(x －2)m ＋(y －1)＝0，故直线AB 恒为(2,1)点． 又由(2,1)点恒在椭圆内部，故直线与椭圆x 216＋y 24＝1公共点的个数是2个，故选A ．方法二：当m ＝0时，方程x 2＋mx －(2m ＋1)＝0可化为：x 2－1＝0，故x 1＝－1，x 2＝1， 故A ，B 两点的坐标为(－1,1)，(1,1)，此时A ，B 两点均在椭圆x 216＋y 24＝1内部，故直线AB 与椭圆x 216＋y 24＝1有2个公共点，故选A ．3．(2016·大连双基测试)过抛物线y 2＝2px (p >0)焦点F 的直线l 与抛物线交于B ，C 两点，l 与抛物线准线交于点A ，且|AF |＝6，AF →＝2FB →，则|BC | ( A )A ．92B ．6C ．132D ．8不妨设直线l 的倾斜角为θ，其中0<θ<π2，点B (x 1，y 1)，C (x 2，y 2)，则点B 在x轴的上方．过点B 作该抛物线的准线的垂线，垂足为B 1，于是有|BF |＝|BB 1|＝3，|AF ||AB |p|BB 1|，由此得p ＝2，抛物线方程是y 2＝4x ，焦点F (1,0)，cos θ＝p |AF |＝13，∴k ＝tan θ＝22，∴BC ：y ＝22(x －1)，由⎩⎨⎧y ＝22x －y 2＝4x得2x 2－5x ＋2＝0，∴x 1＋x 2＝52，∴|BC |＝x 1＋x 2＋p ＝52＋2＝92，故选A ．4．设双曲线x 24－y 23＝1的左、右焦点分别为F 1，F 2，过F 1的直线l 交双曲线的左支于A ，B 两点，则|BF 2|＋|AF 2|的最小值为_11__.由题意可得|AF 2|－|AF 1|＝2a ＝4， |BF 2|－|BF 1|＝2a ＝4，两式相加得|AF 2|＋|BF 2|－|AB |＝8，所以|AF 2|＋|BF 2|＝8＋|AB |≥8＋2b 2a ＝8＋62＝11，当且仅当AB ⊥x 轴时取等号， 所以|BF 2|＋|AF 2|的最小值为11.5．(2016·肇庆模拟)已知双曲线C 的两个焦点坐标分别为F 1(－2,0)，F 2(2,0)，双曲线C 上一点P 到F 1，F 2距离差的绝对值等于2.(1)求双曲线C 的标准方程；(2)经过点M (2,1)作直线l 交双曲线C 的右支于A ，B 两点，且M 为AB 的中点，求直线l 的方程；(3)已知定点G (1,2)，点D 是双曲线C 右支上的动点，求|DF 1|＋|DG |的最小值． (1)依题意，得双曲线C 的实半轴长a ＝1，半焦距c ＝2，所以其虚半轴长b ＝c 2－a 2＝ 3.又其焦点在x 轴上，所以双曲线C 的标准方程为x 2－y 23＝1.(2)设A ，B 的坐标分别为(x 1，y 1)，(x 2，y 2)，⎩⎪⎨⎪⎧3x 21－y 21＝3，3x 22－y 22＝3，两式相减，得3(x 1－x 2)(x 1＋x 2)－(y 1－y 2)(y 1＋y 2)＝0.因为M (2,1)为AB 的中点，所以⎩⎪⎨⎪⎧x 1＋x 2＝4，y 1＋y 2＝2，所以12(x 1－x 2)－2(y 1－y 2)＝0， 即k AB ＝y 1－y 2x 1－x 2＝6. 故AB 所在直线l 的方程为y －1＝6(x －2)， 即6x －y －11＝0.(3)由已知，得|DF 1|－|DF 2|＝2， 即|DF 1|＝|DF 2|＋2，所以|DF 1|＋|DG |＝|DF 2|＋|DG |＋2≥|GF 2|＋2， 当且仅当G ，D ，F 2三点共线时取等号． 因为|GF 2|＝－2＋22＝5，所以|DF 2|＋|DG |＋2≥|GF 2|＋2＝5＋2. 故|DF 1|＋|DG |的最小值为5＋2.。

第一章测评B(高考体验卷)(时间:90分钟满分:100分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2013安徽高考)在下列命题中,不是公理的是( )A.平行于同一个平面的两个平面相互平行B.过不在同一条直线上的三点,有且只有一个平面C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线解析:由立体几何基本知识知,B选项为公理2,C选项为公理1,D选项为公理3,A选项不是公理.答案:A2.(2013课标全国高考Ⅱ)已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则( )A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l解析:因为m⊥α,l⊥m,l⊄α,所以l∥α.同理可得l∥β.又因为m,n为异面直线,所以α与β相交,且l平行于它们的交线.故选D.答案:D3.(2013山东高考)一个四棱锥的侧棱长都相等,底面是正方形,其主视图如下图所示,则该四棱锥侧面积和体积分别是( )A.4,8B.4C.4(+1),D.8,8解析:由主视图数据可知正四棱锥的底面是边长为2的正方形,高也是2,如图:由图可知PO=2,OE=1,所以PE=,所以V=×4×2=,S=4×2×=4.答案:B4.(2013浙江高考)设m,n是两条不同的直线,α,β是两个不同的平面( )A.若m∥α,n∥α,则m∥nB.若m∥α,m∥β,则α∥βC.若m∥n,m⊥α,则n⊥αD.若m∥α,α⊥β,则m⊥β解析:A选项中直线m,n可能平行,也可能相交或异面,直线m,n的关系是任意的;B选项中,α与β也可能相交,此时直线m平行于α,β的交线;D选项中,m也可能平行于β.故选C.答案:C5.(2013浙江高考)已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )A.108cm3B.100cm3C.92cm3D.84cm3解析:由三视图可知,该几何体是如图所示长方体去掉一个三棱锥,故几何体的体积是6×3×6-×3×42=100(cm3).故选B.答案:B6.(2014吉林高三质检)如图所示是一个几何体的三视图,则该几何体的体积为( )A.16+2πB.8+2πC.16+πD.8+π解析:由图可知该几何体是由两个相同的半圆柱与一个长方体拼接而成,因此V=1×2×4+π×12×2=8+2π,故选B.答案:B7.(2013课标全国高考Ⅰ)某几何体的三视图如图所示,则该几何体的体积为( )A.16+8πB.8+8πC.16+16πD.8+16π解析:由三视图可知该几何体为半圆柱上放一个长方体,由图中数据可知圆柱底面半径r=2,长为4,在长方体中,长为4,宽为2,高为2,所以几何体的体积为πr2×4×+4×2×2=8π+16.故选A.答案:A8.(2013广东高考)某四棱台的三视图如图所示,则该四棱台的体积是( ).A.4B.C.D.6解析:方法一:由三视图可知,原四棱台的直观图如图所示,其中上、下底面分别是边长为1,2的正方形,且DD1⊥面ABCD,上底面面积S1=12=1,下底面面积S2=22=4.又因为DD1=2,所以V台=(S1++S2)h=(1++4)×2=.方法二:由四棱台的三视图,可知原四棱台的直观图如图所示.在四棱台ABCD-A1B1C1D1中,四边形ABCD与四边形A1B1C1D1都为正方形,AB=2,A1B1=1,且D1D⊥平面ABCD,D1D=2.分别延长四棱台各个侧棱交于点O,设OD1=x,因为△OD1C1∽△ODC,所以,即,解得x=2.=V棱锥O-ABCD-=×2×2×4-×1×1×2=.答案:B9.(2014东北四市高三联考)已知三棱锥S-ABC的四个顶点都在半径为1的球面上,底面ABC是等边三角形,SA=SB=SC,且平面ABC过球心,则三棱锥S-ABC的体积是( )A. B. C. D.解析:由已知可得底面等边三角形ABC外接圆的半径为1,设等边三角形ABC的边长为a,则有a=1,解得a=,故V棱锥S-ABC=×()2×1=,故选C.答案:C10.(2013课标全国高考Ⅰ)如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为( ).A. cm3B. cm3C. cm3D. cm3解析:设球半径为R,由题可知R,R-2,正方体棱长一半可构成直角三角形,即△OBA为直角三角形,如图.BC=2,BA=4,OB=R-2,OA=R,由R2=(R-2)2+42,得R=5,所以球的体积为π×53=π(cm3),故选A.答案:A二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中的横线上)11.(2013辽宁高考)某几何体的三视图如图所示,则该几何体的体积是.解析:由三视图可知该几何体是一个底面半径为2的圆柱体,中间挖去一个底面棱长为2的正四棱柱,故体积为π·22·4-2×2×4=16π-16.答案:16π-1612.(2013天津高考)已知一个正方体的所有顶点在一个球面上.若球的体积为,则正方体的棱长为.解析:由题意知V球=πR3=,R=.设正方体的棱长为a,则=2R,a=,所以正方体的棱长为.答案:13.(2013福建高考)已知某一多面体内接于球构成一个简单组合体,如果该组合体的主视图、左视图、俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是.解析:由题意知正方体内接于球,球的直径2r=,所以r=,故该球的表面积为S球=4πr2=4π×3=12π.答案:12π14.(2013江苏高考)如图,在三棱柱A1B1C1-ABC中,D,E,F分别是AB,AC,AA1的中点,设三棱锥F-ADE 的体积为V1,三棱柱A1B1C1-ABC的体积为V2,则V1∶V2=.解析:由题意可知点F到面ABC的距离与点A1到面ABC的距离之比为1∶2,S△ADE∶S△ABC=1∶4.因此V1∶V2==1∶24.答案:1∶2415.(2013课标全国Ⅰ高考)已知H是球O的直径AB上一点,AH∶HB=1∶2,AB⊥平面α,H为垂足,α截球O所得截面的面积为π,则球O的表面积为.解析:如图,设球O的半径为R,则AH=,OH=.又因为π·EH2=π,所以EH=1.因为在Rt△OEH中,R2=+12,所以R2=.所以S球=4πR2=.答案:π三、解答题(本大题共4小题,共25分.解答时应写出文字说明、证明过程或演算步骤)16.(6分)(2013课标全国Ⅱ高考)如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.(1)证明:BC1∥平面A1CD;(2)设AA1=AC=CB=2,AB=2,求三棱锥C-A1DE的体积.解:(1)连接AC1交A1C于点F,则F为AC1中点.又D是AB中点,连接DF,则BC1∥DF.因为DF⊂平面A1CD,BC1⊄平面A1CD,所以BC1∥平面A1CD.(2)因为ABC-A1B1C1是直三棱柱,所以AA1⊥CD.由已知AC=CB,D为AB的中点,所以CD⊥AB.又AA1∩AB=A,于是CD⊥平面ABB1A1.由AA1=AC=CB=2,AB=2得∠ACB=90°,CD=,A1D=,DE=,A1E=3,故A1D2+DE2=A1E2,即DE⊥A1D.所以=1.17.(6分)(2013辽宁高考)如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.(1)求证:BC⊥平面PAC;(2)设Q为PA的中点,G为△AOC的重心,求证:QG∥平面PBC.解:(1)由AB是圆O的直径,得AC⊥BC.由PA⊥平面ABC,BC⊂平面ABC,得PA⊥BC.又PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,所以BC⊥平面PAC.(2)连OG并延长交AC于M,连接QM,QO,由G为△AOC的重心,得M为AC中点.由Q为PA中点,得QM∥PC.又O为AB中点,得OM∥BC.因为QM∩MO=M,QM⊂平面QMO,MO⊂平面QMO,BC∩PC=C,BC⊂平面PBC,PC⊂平面PBC,所以平面QMO∥平面PBC.因为QG⊂平面QMO,所以QG∥平面PBC.18.(6分)(2013山东高考)如图,四棱锥P-ABCD中,AB⊥AC,AB⊥PA,AB∥CD,AB=2CD,E,F,G,M,N分别为PB,AB,BC,PD,PC的中点.(1)求证:CE∥平面PAD;(2)求证:平面EFG⊥平面EMN.解:(1)证法一:取PA的中点H,连接EH,DH.因为E为PB的中点,所以EH∥AB,EH=AB.又AB∥CD,CD=AB,所以EH∥CD,EH=CD.因此四边形DCEH是平行四边形,所以CE∥DH.又DH⊂平面PAD,CE⊄平面PAD,因此CE∥平面PAD.证法二:连接CF.因为F为AB的中点,所以AF=AB.又CD=AB,所以AF=CD.又AF∥CD,所以四边形AFCD为平行四边形.因此CF∥AD.又CF⊄平面PAD,所以CF∥平面PAD.因为E,F分别为PB,AB的中点,所以EF∥PA.又EF⊄平面PAD,所以EF∥平面PAD.因为CF∩EF=F,故平面CEF∥平面PAD.又CE⊂平面CEF,所以CE∥平面PAD.(2)证明:因为E,F分别为PB,AB的中点,所以EF∥PA.又AB⊥PA,所以AB⊥EF.同理可证AB⊥FG.又EF∩FG=F,EF⊂平面EFG,FG⊂平面EFG, 因此AB⊥平面EFG.又M,N分别为PD,PC的中点,所以MN∥CD.又AB∥CD,所以MN∥AB.因此MN⊥平面EFG.又MN⊂平面EMN,所以平面EFG⊥平面EMN.19.(7分)(2013湖南高考)如图所示,在直棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=,AA1=3,D是BC的中点,点E在棱BB1上运动.(1)证明:AD⊥C1E;(2)当异面直线AC,C1E所成的角为60°时,求三棱锥C1-A1B1E的体积.解:(1)证明:因为AB=AC,D是BC的中点,所以AD⊥BC.①又在直三棱柱ABC-A1B1C1中,BB1⊥平面ABC,而AD⊂平面ABC,所以AD⊥BB1.②由①,②得AD⊥平面BB1C1C.由点E在棱BB1上运动,得C1E⊂平面BB1C1C,所以AD⊥C1E.(2)因为AC∥A1C1,所以∠A1C1E是异面直线AC,C1E所成的角,由题设,∠A1C1E=60°,因为∠B1A1C1=∠BAC=90°,所以A1C1⊥A1B1,又AA1⊥A1C1,从而A1C1⊥平面A1ABB1,于是A1C1⊥A1E.故C1E==2,又B1C1==2,所以B1E==2,从而×A1C1=×2×.。

高中数学新课标人教B版必修二第一章《立体几何初步》单元测试4文试题山东省新人教B版2012届高三单元测试4必修2第一章《立体几何初步》(本卷共150分，考试时间120分钟)一、选择题(本大题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的)1(下列命题中，正确的是( )A(经过不同的三点有且只有一个平面B(分别在两个平面内的两条直线一定是异面直线C(垂直于同一个平面的两条直线是平行直线D(垂直于同一个平面的两个平面平行解析:选C.A中，可能有无数个平面，B中，两条直线还可能平行，相交，D 中，两个平面可能相交(2(有一个几何体的三视图及其尺寸如图(单位:cm)，则该几何体的表面积及体积为( )2,32,3A(24π cm12π cm B(15π cm12π cm 2,3C(24π cm36π cm D(以上都不正确解析:选A.由三视图知该几何体为一个圆锥，其底面半径为3 cm，母线长为5 cm，高为4 cm，求表面积时不要漏掉底面积(3(若正四棱锥的侧面是正三角形，则它的高与底面边长之比为( ) A(1?2B(2?1C(1?2 D.2?1331222解析:选C.设正四棱锥底边长为a，则斜高为a，高h,a,a,a 2222 2?高与底边长之比为a?a,1?2. 24(如果圆锥的侧面展开图是半圆，那么这个圆锥的顶角(圆锥轴截面中两条母线的夹角)是( )A(30? B(45?C(60? D(90?解析:选C.本题主要考查圆锥侧面展开图的有关性质及侧面展开图中心角公式(设圆锥r1底面半径为r，母线长为l，依条件则有2πr,πl，如图所示，?,，即?ASO,30?， 2l?圆锥顶角为60?.5(已知圆锥的底面半径为R，高为3R，在它的所有内接圆柱中，全面积的最大值是( )922A(2πR B.πR 48522C.πR D.πR 322解析:选B.如图所示，设圆柱底面半径为r，则其高为3R,3r，全面积S,2πr，2πr(3R39392222,3r),6πRr,4πr,,4π(r,R)，πR，故当r,R时全面积有最大值πR. 44446(在正四面体P,ABC中，D、E、F分别是AB、BC、CA的中点，下面四个结论中不成立的是( )A(BC?面PDFB(DF?面PAEC(面?面 PDEABCD(面PAE?面ABC解析:选C.因为BC?DF，所以BC?面PDF，即A正确;由中点有BC?PE，BC?AE，所以BC?平面PAE，所以DF?平面PAE，即B正确;由BC?平面PAE可得平面PAE?平面ABC，即D正确(7(在纬度为α的纬线圈上有A，B两点，这两点间的纬线圈上的弧长为πRcosα，其中R为地球半径，则这两点间的球面距离是( )ππ,,,,,2α,αA. B. RR,,,,22,,,,C((π,2α)R D((π,α)R解析:选C.由题意易求得球心角为π,2α，所以球面距离为(π,2α)R. 8(正方体的外接球与内切球的球面面积分别为S和S则( ) 12A(,2 B(,3 SSSS1212C(,4 D(,23 SSSS1212解析:选B.不妨设正方体的棱长为1，则外接球直径为正方体的体对角线长为3，而内S312切球直径为1，所以,(),3，所以S,3S. 12S129(棱锥被平行于底面的平面所截，当截面分别平分棱锥的侧棱、侧面积、体积时，相应的截面面积分别为S、S、S，则( ) 123A(S<S<S B(S<S<S 123321C(S<S<S D(S<S<S 213132解析:选A.设底面积为S，由截面性质可知(S212,()?S,S; 1141SS21,?S,S; 2122SS213( ),?,. SS313S34可知S<S<S，故选A. 12310(平行六面体ABCD,ABCD的所有棱长都相等，且?AAB,?AAD,?BAD,60?，则111111对角面BBDD是( ) 11A(平行四边形 B(菱形C(矩形 D(正方形解析:选D.AA在面ABCD内的射影在底面的一条对角线上，?AC?BD， 1?AA?BD，?BB?BD. 11又??BAD,60?，?BD,AB,BB， 1?BBDD是正方形( 11上、下底面是正方形，各侧面均为全等的等腰梯形)的上、下底面的11(一个正四棱台(边长分别为a，b，高为h，且侧面积等于两底面积之和，则下列关系正确的是( )11111A.,， B., habha，b111111C.,， D.,， abhbahb,aa，b2222解析:选A.S,4× h，×a，b， ,侧22b,a222222即4[h，(]?(a，b),(a，b)， )2化简得h(a，b),ab，111?,，. hab12. 如图所示，三棱锥P,ABC的高PO,8，AC,BC,3，?ACB,30?，M、N分别在BC 和PO上，且CM,x，PN,2x(x?[0,3])，下列四个图象大致描绘了三棱锥N,AMC的体积V与x的变化关系，其中正确的是( )11112解析:选A.,?,(×3×sin30?)?(8,2),,(,2)，2，?[0,3]，VSNOxxxx?AMC3322故选A.二、填空题(本大题共4小题，请把答案填在题中横线上)613(若一个底面边长为，侧棱长为6的正六棱柱的所有顶点都在一个球面上，则此球2的体积为________(解析:球的直径等于正六棱柱的体对角线的长(设球的半径为R，由已知可得2R,644π2233，6,23，R,3.所以球的体积为πR,×(3),43π. 233答案:43π14(一根细金属丝下端挂着一个半径为1 cm的金属球，将它浸没在底面半径为2 cm的圆柱形容器内的水中，现将金属丝向上提升，当金属球全部被提出水面时，容器内的水面下降的高度是________cm.4π解析:由题意知，金属球的体积等于下降的水的体积，设水面下降h cm，则有,312π×2×h，解得h,. 31答案: 315(如果规定:x,y，y,z，则x,z叫做x、y、z关于等量关系具有传递性，那么空间三直线a、b、c关于相交、垂直、平行、异面、共面这五种关系具有传递性的是________( 答案:平行16(点M是线段AB的中点，若点A、B到平面α的距离分别为4 cm和6 cm，则点M到平面α的距离为________(解析:(1)如图(1)，当点A、B在平面α的同侧时，分别过点A、B、M作平面α的垂线AA′、BB′、MH，垂足分别为A′、B′、H，则线段A A′、BB′、MH的长分别为点A、B、MAA′，BB′4，6到平面α的距离(由题设知AA′,4 cm，BB′,6 cm.因此MH,,,5(cm)( 22(2)如图(2)，当点、在平面α的异侧时，设交平面α于点， ABABO?AA′?BB′,4?6，?AO?OB,4?6.又?M为AB的中点，?MH?AA′,1?4，即MH,1(cm)(故点M到平面α的距离为5 cm或1 cm.答案:5 cm或1 cm三、解答题(本大题共6小题，解答时应写出必要的文字说明、证明过程或演算步骤) 17(已知正方体ABCD,ABCD中，E，F分别为DC，CB的中点，AC?BD,P，AC?EF1111111111,.求证: Q(1)D，B，E，F四点共面;(2)若AC交平面BDEF于R点，则P，Q，R三点共线( 1证明:如图所示((1)连接BD.?E，F分别为DC，CB的中点，?EF?BD， 11111111又?BD?BD， 11?EF?BD，?EF与BD共面，?E，F，B，D四点共面((2)?AC?BD,P，?P?平面AACC?平面BDEF.同理，Q?平面AACC?平面BDEF. 1111?AC?平面DBFE,R， 1?R?平面AACC?平面BDEF， 11?P，Q，R三点共线(18(一球内切于圆锥，已知球和圆锥的底面半径分别为r，R，求圆锥的体积( 解:如图，设圆锥的高AD,h，AOOE由???，可得,， AOEACDACCD2h,rrrR2即,，解得h,， 2222R,rR，Rh4rRπ2π2?所以圆锥的体积为V,Rh,. 223R,r19(在正方体ABCD,ABCD中，E、F分别是BB、CD的中点，设AA,2，求三棱锥F,111111AED的体积( 11解:如图，连接AE，容易证明AE?DF. 1又?AD?AE， 11?AE?平面AFD. 11?AD?AD，AD?平面ABCD， 1111设平面AFD?平面ABCD,FG， 11则AD?FG且G为AB的中点， 11?AE?平面AGFD，AE?AG， 111设垂足为点H，则EH即为点E到平面AFD的距离， 1123?AA,2，?AE,5，AH,，?EH,. 1551又?S,S,5， ?11?11AFDAGFD213?V,,×5×,1， 11FAED35故三棱锥F,AED的体积为1. 11220. 如图?ABC中，AC,BC,AB，四边形ABED是边长为a的正方形，平面ABED?平面2ABC，若G、F分别是EC、BD的中点((1)求证:?平面; GFABC(2)求证:平面EBC?平面ACD; (3)求几何体ADEBC的体积V. 解:(1)证明:如图，取BE的中点H，连接HF，GH.?G，F分别是EC和BD的中点， ?HG?BC，HF?DE.又?四边形ADEB为正方形， ?DE?AB，从而HF?AB.?HF?平面ABC，HG?平面ABC. ?平面HGF?平面ABC.?GF?平面ABC.(2)证明:?ADEB为正方形，?EB?AB.又?平面ABED?平面ABC， ?BE?平面ABC.?BE?AC. 222又?CA，CB,AB，?AC?BC. ?AC?平面BCE.从而平面EBC?平面ACD. (3)取AB的中点N，连接CN，?AC,BC，11?CN?AB，且CN,AB,a. 22又平面ABED?平面ABC，?CN?平面ABED.?C,ABED是四棱锥，111123?V,S?CN,a?a,a. C,ABEDABED332621(如图是一个直三棱柱(以ABC为底面)被一平面所截得到的几何体，截面为ABC.已知111AB,BC,1，?ABC,90?，AA,4，BB,2，CC,3.设点O是AB的中点，求证:OC?平1111111111面ABC. 111证明:作OD?AA交AB于点D，连接CD，则OD?BB?CC. 111111因为O是AB的中点，所以OD1,(AA，BB),3,CC， 1112则四边形ODCC是平行四边形，因此有OC?CD.因为CD?平面CBA且OC?平面CBA，111111111?平面. 所以OCABC11122(如图所示的三个图中，上面的是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图在下面画出(单位:cm)((1)按照画三视图的要求画出该多面体的俯视图; (2)按照给出的尺寸，求该多面体的体积;(3)在所给直观图中连接BC′，求证:BC′?面EFG. 解:(1)如图所示((2)所求多面体体积V,V,V 长方体正三棱锥112843,4×4×6,×(×2×2)×2,(cm)( 323(3)证明:如图，在长方体ABC D,A′B′C′D′中，连接AD′，则AD′?BC′.因为E，G分别为AA′，A′D′的中点，所以AD′?EG，从而EG?BC′.又BC′?平面EFG，所以BC′?面EFG.。

2016-2017学年高中数学 第一章 立体几何初步单元测验 新人教B版必修2．各个面都是三角形的几何体是三棱锥．以三角形的一条边所在直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫．棱锥的侧棱长与底面多边形的边长相等，则该棱锥可能是正六棱锥．圆锥的顶点与底在圆周上的任意一点的连线都是母线倍，底面半径缩小为原来的，底面面积为S ，则V ＝13hS ，新圆锥的高为∴V′＝13×2h×S 4＝12V.4．如图，已知正方体ABCD －A 1B 1C 1D 1，E 是DD 1的中点，F 是BB 1的中点，设过点C 1，E ，F 三点的平面为α，则正方体被平面α所截的截面的形状为( )A ．菱形B ．矩形C ．梯形D ．五边形 答案：A解析：设正方体棱长为a ，连接AE ，C 1F 易发现AE∥C 1F ，所以平面α经过点A ，所以截面是四边形AEC 1F ，根据勾股定理易求得AE ＝EC 1＝C 1F ＝AF ＝52a ，所以截面为菱形．5．如图所示是一个正方体表面的一种展开图，图中的四条线段AB 、CD 、EF 和GH 在原正方体中不在同一平面内的有________对．( )A ．1B ．2C ．3D ．4答案：C解析：将展开图恢复为正方体，如图所示，则有AB 与CD ，AB 与GH ，EF 与GH. 6．一个画家有14个边长为1 m 的正方体，他在地面上把它摆成如图所示的形式，然后，他把露出的表面都染上颜色，那么被染上颜色的面积为( )A ．21 m 2B ．24 m 2C ．33 m 2D ．37 m 2 答案：C解析：上表面面积为3×3＝9(m 2)侧面面积为3×4＋2×4＋1×4＝24(m 2)故被染上颜色的面积为33 m 2.7．如图，在三棱锥P －ABC 中，PA⊥平面ABC ，AB⊥BC，PA ＝AB ，D 为PB 的中点，则下列推断不正确的是( )A ．BC⊥平面PAB所示的几何体，那么此几何体的全面积为( )2)a22)a2，所以：x＝22a.2 2a＋2×⎝⎛⎭⎪⎫22a2＝2a2＋2a2＝(两个相同的正四棱锥组成如图所示的几何体，可放在棱长为与正方体的某一个平面平行，且各顶点均在正方体的面上，则这样的几何体体本题可以转化为一个正方形可以有多少个内接正方形，显然有无穷多个．⊥BC1，A1C1⊥A1B1，小题，每小题5分，共201B1C1D1中，M、N的平面与棱CD交于Q，则，DQ＝2，∴PQ＝214．如图，半径为2的半球内有一个内接正六棱锥P －ABCDEF ，则此正六棱锥的侧面积是________．答案：67解析：显然正六棱锥P －ABCDEF 的底面的外接圆是球的一个大圆，由已知，可得大圆的半径为 2.易得其内接正六边形的边长为 2.又正六棱锥P －ABCDEF 的高为2，则斜高为22＋32＝7，所以该正六棱锥的侧面积为6×12×2×7＝67.15．对于四面体ABCD ，下列命题正确的是________．(写出所有正确命题的编号)． ①相对棱AB 与CD 所在的直线是异面直线；②由顶点A 作四面体的高，其垂足是△BCD 三条高线的交点；③若分别作△ABC 和△ABD 的边AB 上的高，则这两条高的垂足重合； ④任何三个面的面积之和都大于第四个面的面积；⑤分别作三组相对棱中点的连线，所得的三条线段相交于一点． 答案：①④⑤ 解析：本题考查空间几何体的线线关系，以及空间想象能力．如图所示，四面体ABCD 中，AB 与CD 是异面直线，故①正确；当四面体ABCD 中，对棱AB 与CD 不垂直时，由顶点A 作四面体的高，其垂足不是△BCD 三条高线的交点，故②不正确；若分别作△ABC 和△ABD 的边AB 上的高，则这两条高的垂足不一定重合，故③不正确； 如图，过顶点A 作AO⊥面BCD ，O 为垂足，连结OB 、OC 、OD ，则S △ABC >S △BOC ，S △ACD >S △COD ，S △ABD >S △BOD ，∴S △ABC ＋S △ACD ＋S △ABD >S △BOC ＋S △COD ＋S △BOD ＝S △BCD ， 故④正确．如图四面体ABCD 中取AB 、CD 、AD 、BC 的中点分别为E 、F 、M 、N ，连线EF 、MN ，则EF 、MN 分别为▱EMFN 的对角线，∴EF、MN 相交于点O ，且O 为EF 、MN 的中点，取AC 、BD 的中点分别为R 、H ，图中的三个直角三角形是一个体积为20 cm的几何体的三视图，由三视图可知，棱锥的三条长分别为5,6，h的侧棱两两垂直，＝4.小题，共70分，解答应写出文字说明、证明过程或演算步骤．已知底面为正方形的四棱锥P－ABCD，如图(1)所示，PC⊥面)视图和侧(左)视图，它们是腰长为4 cm的全等的等腰直角三角形．所给的正视图、侧视图，画出相应的俯视图，并求出该俯视图的面积；该四棱锥的俯视图为内含一条对角线，边长为4 cm的正方形，俯视图如下图所PC2＋CD2＝42＋42＝32＝4 2.AD⊥PD，PD2＋AD2＝22＋42＝4 3如图，在侧棱垂直于底面ABC的三棱柱ABC－A1不同于点C)，且AD⊥DE，F是B1C1的中点．BCC1B1；ABC，又AD⊂平面ABC，所以CC1⊥AD.平面BCC1B1，CC1∩DE＝E，所以AD⊥平面.，所以A1F∥平面ADE.是圆柱的母线，O′是上底面的圆心，△BCDCD的中点．，O′A，OO′，∵AB是母线，EFG.到平面PCE的距离．中点，连接ME、MF.为平行四边形．，∠PDA＝45°，∵PF＝FD，∴AF⊥PD，又∵PA⊥平面PCD.，∵平面PCE⊥平面17.，使得平面APC1⊥平面，在△ABC中，ACC1，过P作PF⊥AC而两平行线PF、BD所确定的平面即为两相交直线的交点，PF∥BD，P∈DD1知，P也是DD中点时，ACC1.中点时，面APC1⊥面ACC1.。

（全国通用版）2018-2019高中数学第一章立体几何初步检测B 新人教B 版必修2编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（全国通用版）2018-2019高中数学第一章立体几何初步检测B 新人教B版必修2）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（全国通用版）2018-2019高中数学第一章立体几何初步检测B 新人教B版必修2的全部内容。

第一章立体几何初步检测（B）（时间：90分钟满分:120分）一、选择题（本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的）1若直线l不平行于平面α，且l⊄α，则(）A.α内的所有直线与l异面B。

α内不存在与l平行的直线C.α内存在唯一的直线与l平行D。

α内的直线与l都相交解析:依题意，直线l∩α=A（如图),α内的直线若经过点A,则与直线l相交；若不经过点A,则与直线l是异面直线,故选B.答案：B2某几何体的三视图如图,则该几何体的体积为()A。

16+8πB.8+8πC.16+16πD。

8+16π解析：该几何体为一个半圆柱与一个长方体组成的一个组合体.V半圆柱=π×22×4=8π,V长方体=4×2×2=16.所以所求体积为16+8π.故选A.答案:A3某几何体的三视图如图,则该几何体的表面积为（)A。

180 B.200 C。

220 D。

240解析：由三视图知该几何体是底面为等腰梯形的直棱柱,如图，S上=2×10=20,S下=8×10=80，S前=S后=10×5=50,S左=S右=（2+8)×4=20，所以S表=S上+S下+S前+S后+S左+S右=240,故选D。