轴的直径大小计算方法

轴得设计、计算、校核以转轴为例,轴得强度计算得步骤为:一、轴得强度计算1、按扭转强度条件初步估算轴得直径机器得运动简图确定后,各轴传递得P与n为已知,在轴得结构具体化之前,只能计算出轴所传递得扭矩,而所受得弯矩就是未知得。

这时只能按扭矩初步估算轴得直径,作为轴受转矩作用段最细处得直径dmin,一般就是轴端直径。

根据扭转强度条件确定得最小直径为:(mm)式中:P为轴所传递得功率(KW)n为轴得转速(r/min)Ao为计算系数,查表3若计算得轴段有键槽,则会削弱轴得强度,此时应将计算所得得直径适当增大,若有一个键槽,将d min增大5％,若同一剖面有两个键槽,则增大10％。

以dmin为基础,考虑轴上零件得装拆、定位、轴得加工、整体布局、作出轴得结构设计。

在轴得结构具体化之后进行以下计算。

2、按弯扭合成强度计算轴得直径l)绘出轴得结构图2)绘出轴得空间受力图3)绘出轴得水平面得弯矩图4)绘出轴得垂直面得弯矩图5)绘出轴得合成弯矩图6)绘出轴得扭矩图7)绘出轴得计算弯矩图8)按第三强度理论计算当量弯矩:式中:α为将扭矩折合为当量弯矩得折合系数,按扭切应力得循环特性取值:a)扭切应力理论上为静应力时,取α=0、3。

b)考虑到运转不均匀、振动、启动、停车等影响因素,假定为脉动循环应力,取α=0、59。

c)对于经常正、反转得轴,把扭剪应力视为对称循环应力,取α=1(因为在弯矩作用下,转轴产生得弯曲应力属于对称循环应力)。

9)校核危险断面得当量弯曲应力(计算应力):式中:W为抗扭截面摸量(mm3),查表4。

为对称循环变应力时轴得许用弯曲应力,查表1。

如计算应力超出许用值,应增大轴危险断面得直径。

如计算应力比许用值小很多,一般不改小轴得直径。

因为轴得直径还受结构因素得影响。

一般得转轴,强度计算到此为止。

对于重要得转轴还应按疲劳强度进行精确校核。

此外,对于瞬时过载很大或应力循环不对称性较为严重得轴,还应按峰尖载荷校核其静强度,以免产生过量得塑性变形。

轴的设计计算2）根据轴向定位的要求确定轴的各段直径和长度如上图 从左到右依次为1d 2d 3d 4d 5d 6d 7d 与大带轮配合的轴 mm d 381= mm d d d 08.4408.63808.02112=+=⨯+= 取mm d 452= mm d d 4523=≥ 且此处为基孔制配合（其中孔为轴承内孔） 取mm d 503=mm d d 5034=≥ 取mm d 554= mmd d d 8.638.85508.02445=+=⨯+=取mm d 645=mm d d d 5885008.02336=+=⨯+= mm d d 5037== mm l 831=mm l 502252=⨯=∆++=s b l 3由于使用的轴承为深沟球轴承6010（GB/T276-1993）查《机械设计手册》P64表6-1得b=16mm主动轴如左图的装配方案mm d 381=mm d 452=mm d 503=mm d 554=mm d 645=mm d 586=对于从动轴：1）拟定轴上零件的装配方案现选用如图所示的装配方案从动轴如左图所示的装配方案mm mm h b 1422⨯=⨯，键槽用键槽铣刀加工，长为80mm ，选择齿轮轴毂与轴的配合为67k H ；同样半联轴器与轴的连接，选用平键为mm mm mm l h b 901118⨯⨯=⨯⨯，半联轴器与轴的配合为67k H 。

滚动轴承与轴的周向定位是通过过渡配合来保证的，此处选轴的直径尺寸公差为m64）确定轴上圆角和倒角尺寸 参考《机械设计》教材P365表15-2 mm d 601= mm d 757= 取轴端倒角为0452⨯，各轴肩处的圆角半径见轴的俯视图上标注(3) 按弯扭合成应力校核轴的强度 1)主动轴的强度校核圆周力 1t F =112000d T =2000×255.86/93=5502.37N 径向力1r F =1t F tan α=5502.37×tan20°=5502.37×0.36=1980.85N 由于为直齿圆柱齿轮，轴向力1a F =0带传动作用在轴上的压力齿轮轴毂与轴的配合为67k H半联轴器与轴的配合为67k H 。

轴的标准直径轴是机械传动中常用的零部件，其标准直径是指在制造和使用过程中所遵循的直径标准。

轴的标准直径对于机械传动的正常运转和使用寿命具有非常重要的作用。

本文将从轴的标准直径的定义、计算方法、影响因素等方面进行详细介绍。

一、轴的标准直径的定义。

轴的标准直径是指在制造和使用过程中所遵循的直径标准。

通常情况下，轴的标准直径是根据轴的承载能力、转速、工作环境等因素来确定的。

在实际应用中，轴的标准直径需要满足一定的强度、刚度和耐磨性等要求，以确保机械传动的正常运转。

二、轴的标准直径的计算方法。

1. 根据承载能力计算，轴的标准直径可以根据轴的承载能力来计算。

一般情况下，轴的承载能力与轴的直径成正比，因此可以根据轴的承载能力和工作条件来确定轴的标准直径。

2. 根据转速计算，轴的标准直径也可以根据轴的转速来计算。

转速较高的轴需要具有更大的刚度和强度，因此其标准直径也会相应增大。

3. 根据工作环境计算，工作环境对轴的磨损和疲劳寿命有着重要影响，因此在确定轴的标准直径时需要考虑工作环境的影响因素，以确保轴具有足够的耐磨性和疲劳寿命。

三、轴的标准直径的影响因素。

1. 轴的承载能力，轴的承载能力是确定轴的标准直径的重要因素之一。

一般情况下，承载能力越大，轴的标准直径也会越大。

2. 轴的转速，转速较高的轴需要具有更大的刚度和强度，因此其标准直径也会相应增大。

3. 工作环境，工作环境对轴的磨损和疲劳寿命有着重要影响，因此在确定轴的标准直径时需要考虑工作环境的影响因素。

四、总结。

轴的标准直径是机械传动中非常重要的参数，其合理选择对于机械传动的正常运转和使用寿命具有重要作用。

通过本文的介绍，相信大家对于轴的标准直径有了更加深入的了解，希望能够在实际应用中加以充分考虑，确保机械传动的安全可靠运行。

轴的设计计算【一】能力目标1.了解轴的功用、分类、常用材料及热处理。

2.能合理地进行轴的结构设计。

【二】知识目标1.了解轴的分类，掌握轴结构设计。

2.掌握轴的强度计算方法。

3.了解轴的疲劳强度计算和振动。

【三】教学的重点与难点重点：轴的结构设计难点：弯扭合成法计算轴的强度【四】教学方法与手段采用多媒体教学（加动画演示），结合教具，提高学生的学习兴趣。

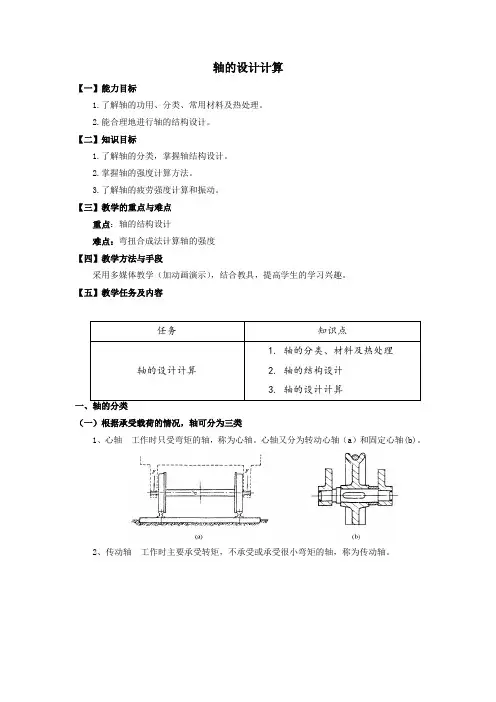
【五】教学任务及内容任务 知识点轴的设计计算 1. 轴的分类、材料及热处理2. 轴的结构设计3. 轴的设计计算一、轴的分类（一）根据承受载荷的情况，轴可分为三类1、心轴 工作时只受弯矩的轴，称为心轴。

心轴又分为转动心轴（a ）和固定心轴(b)。

2、传动轴 工作时主要承受转矩，不承受或承受很小弯矩的轴，称为传动轴。

3、转轴工作时既承受弯矩又承受转矩的轴，称为转轴。

（二）按轴线形状分：1、直轴（1）光轴作传动轴（应力集中小）（2）阶梯轴优点：1）便于轴上零件定位；2）便于实现等强度2、曲轴另外还有空心轴（机床主轴）和钢丝软轴（挠性轴）——它可将运动灵活地传到狭窄的空间位置。

如牙铝的传动轴。

二、轴的结构设计轴的结构设计就是确定轴的外形和全部结构尺寸。

但轴的结构设计原则上应满足如下要求：1)轴上零件有准确的位置和可靠的相对固定；2)良好的制造和安装工艺性；3)形状、尺寸应有利于减少应力集中；4）尺寸要求。

（一）轴上零件的定位和固定轴上零件的定位是为了保证传动件在轴上有准确的安装位置；固定则是为了保证轴上零件在运转中保持原位不变。

作为轴的具体结构，既起定位作用又起固定作用。

1、轴上零件的轴向定位和固定：轴肩、轴环、套筒、圆螺母和止退垫圈、弹性挡圈、螺钉锁紧挡圈、轴端挡圈以及圆锥面和轴端挡圈等。

2、轴上零件的周向固定：销、键、花键、过盈配合和成形联接等，其中以键和花键联接应用最广。

（二）轴的结构工艺性轴的结构形状和尺寸应尽量满足加工、装配和维修的要求。

为此，常采用以下措施：1、当某一轴段需车制螺纹或磨削加工时，应留有退刀槽或砂轮越程槽。

传动轴匹配计算公式传动轴的匹配计算是传动装置设计中的重要环节之一、正确的匹配计算可以有效地保证传动装置的正常运转，并确保传动系统具有较长的寿命和较高的工作效率。

在进行传动轴的匹配计算时，需要考虑传动系统的工作条件、传动装置的功率和转速等因素。

下面将介绍传动轴匹配计算的公式和计算步骤。

一、额定转矩的计算公式额定转矩是指传动装置在最大负载条件下所承受的转矩。

根据传动装置的工作条件和所需的工作性能，可以通过以下公式来计算传动轴的额定转矩：T=(P×60)/(2×π×n)其中，T为传动轴的额定转矩，P为传动装置的功率，n为传动装置的转速。

二、传动轴直径的计算公式在传动轴匹配计算中，确定传动轴的直径是非常重要的一步。

传动轴的直径可以根据以下公式来计算：d=k×(16×T/τ)^(1/3)其中，d为传动轴的直径，k为传动轴的系数，T为传动轴的额定转矩，τ为传动轴的弯曲应力。

三、传动轴校核的计算公式在匹配计算过程中，需要对传动轴进行校核，以确保传动轴的强度满足设计要求。

传动轴的校核可以通过以下公式来计算：σ=(32×T)/(π×d^3)其中，σ为传动轴的应力，T为传动轴的额定转矩，d为传动轴的直径。

以上公式是传动轴匹配计算中常用的公式，通过这些公式可以得出传动轴的合适直径和满足设计要求的强度。

在进行匹配计算时，还需要根据具体的工作条件和实际情况进行调整和修正，以确保传动装置的正常运转和较高的工作效率。

总之，传动轴匹配计算是传动装置设计中非常重要的一环，通过合理的公式和计算可以得出满足设计要求的传动轴直径和强度。

但在实际工程中，还需要根据具体情况进行调整和修正，以确保传动装置的可靠性和稳定性。

空心轴的设计计算公式
空心轴是一种常见的机械零件，其设计需要考虑多个因素，包括轴的材料、直径、长度、载荷等。

在设计空心轴时，需要使用一些计算公式来确定其尺寸和性能。

我们需要确定空心轴的最大扭矩。

扭矩是轴所能承受的力矩，通常用牛顿米（N·m）或英尺磅（ft·lb）表示。

最大扭矩的计算公式为：Tmax = (π/16) * σy * d^3
其中，Tmax为最大扭矩，σy为轴材料的屈服强度，d为轴的直径。

这个公式假设轴是圆形的，且材料的应力分布是均匀的。

接下来，我们需要计算空心轴的弯曲应力。

弯曲应力是轴在受到弯曲力矩时所产生的应力，通常用帕斯卡（Pa）表示。

弯曲应力的计算公式为：
σb = (M * y) / I
其中，σb为弯曲应力，M为弯曲力矩，y为轴的截面形心距，I为轴的截面惯性矩。

这个公式假设轴是直线的，且材料的应力分布是均匀的。

我们需要计算空心轴的转动惯量。

转动惯量是轴在旋转时所具有的惯性，通常用千克·米^2（kg·m^2）表示。

转动惯量的计算公式为：
I = (π/64) * (d^4 - d1^4)
其中，d为轴的外径，d1为轴的内径。

这个公式假设轴的截面是圆环形的。

设计空心轴需要考虑多个因素，包括最大扭矩、弯曲应力和转动惯量等。

通过使用上述计算公式，可以确定空心轴的尺寸和性能，从而满足机械系统的要求。

轴的设计1、轴的机构设计 (1) 轴的设计计算① 轴的直径的确定(Ⅰ轴) 按扭转强度条件计算： 3npA do ≥ 其中：首选45号钢进行设计，查表A O =120,P=10.56 ,n=486.7r/min 于是d 1≥33.47取d 1=34m②作用在齿轮上的力F t =112d T =31033.7723.2072⨯⨯=5.34⨯103N （其中：T 1为Ⅰ轴受到的转矩，d 1为齿轮1的直径）F r =F t βcos tan n a ⨯=2⨯103N （其中：αn 为齿轮的压力角，β为螺旋角）F a =F t ·tan β=1342N同理可求得Ⅱ轴、Ⅲ轴的直径和轴上齿轮的受力： Ⅱ轴 d 2≥42.4 mm 取d 2=45 mm 轴上齿轮的受力：F t =2700 N 、F r = 1023 N 、 F a =780 NⅢ轴 d 3≥63.7 mm 取d 3=65 mm 轴上齿轮的受力：F t =8340 N 、F r =3100 N 、 F a =1800 N (2) 校核轴上轴承的受力和轴承的寿命 Ⅰ轴1、求轴承受到的径向载荷F r1和F r2将轴系部件受到的空间力系分解为铅垂面和水平面的两个力系，如下图所示根据图示力的分析可知道：由图（b ）得F r1v =5.1905.6625.661+⨯-⨯d Fa Fr =5.1905.6625.678145.661007.13+⨯-⨯⨯=170N F r2v =F r -F r1v =1070-170=900NF r1H =5.1905.665.66+F t =7.29⨯102F r2H =F r -F r1H =2820-729=2091F r1=2211Hr F F v r +=22900170+=748.6 NF r2=2222H r v r F F +=222091729+=2276.5 N 2 求两轴承的计算轴向力F a1和F a2对于70000AC 型轴承，按表13-7轴承的派生轴向力为F d =0.68⨯F r (5-8)F d1=0.68×F r1=0.68×748.6=509.6 N F d2=0.68×F r2=0.68×2276.5=1547.99 N 根据轴向力和轴承的安装方向分析可知，轴承2压紧：∴ F a1=F d1=509.6 NF a2=F a +F d1=1323 N3 求轴承的当量动载荷 11r a F F =6.7486.509=0.68=e(5-9)22r a F F =5.22761323=0.58<e 由表13-5分别进行查表或插值计算得径向载荷系数和轴向载荷系数为： 对与轴承1： X 1=1 ; Y 1=0 对轴承2： X 2=1 ; Y 2=0 因轴承运转中有轻微的冲击载荷，按照表13-6，f p =1.0～1.2则 P 1=f p(X 1F r1+Y 1F a1)=1.1×(1×748.6+0×2362)=823.46(5-10)P 2=f p (X 2F r2+Y 2F a22)=1.1×(1×2276.5+0)=2504.15 (5-11) 4 计算轴承的寿命L h =ε⎪⎪⎭⎫⎝⎛266010P C n =72060106⨯⨯315.250423500⎪⎭⎫ ⎝⎛=19131 h<28800 h(5-12)寿命不能满足工作要求，所以应选择中载系列，选用型号为7307AC,在次进行验证：L h ’=72060106⨯⨯398.259732800⎪⎭⎫ ⎝⎛=420839 h>28800 h(5-13)满足工作寿命的要求，所以轴承选用7307AC 系列。

轴的设计和计算需要考虑到以下因素：
1. 轴的材料及其特性，如弹性模量、屈服强度、硬度、疲劳极限等；
2. 轴的几何形状，如直径、长度、转角等；
3. 轴所承受的载荷类型、大小和方向，如弯曲载荷、剪切载荷、轴向载荷等；
4. 轴所处的工作环境，如温度、湿度、腐蚀等因素的影响。

轴的计算公式主要有以下几个：
1. 轴的直径计算公式：d=K*P^(1/3)，其中d为轴的直径，K为系数，P为功率。

2. 轴的弯曲应力计算公式：σ=M*y/I，其中σ为弯曲应力，M为弯矩，y为轴截面上的距离，I为轴截面的惯性矩。

3. 轴的扭转应力计算公式：τ=T*r/J，其中τ为扭转应力，T为扭矩，r为轴半径，J为极限扭转惯性矩。

4. 轴的疲劳强度计算公式：S=Kf*S0，其中S为轴的疲劳强度，Kf为系数，S0为基本疲劳强度。

以上公式仅为轴的设计和计算中的一部分，实际应用中需要根据具体情况进行综合考虑和计算。

轴最小直径计算公式
1轴最小直径的计算公式
轴最小直径是工程制造中常见的概念，是指轴的最小实际外径，它可用于估算机械装配件的尺寸、容量和强度。

轴最小直径的计算公式是轴心轴的最小外径的计算公式，可以根据实际情况调整。

轴最小直径的计算公式是：dD=d1+d2+dT，其中，dD是轴的最小外径；d1是轴类型的额定尺寸，这取决于轴类型，如空心轴，非空心轴等；d2是细节因素的加入，主要包括接触到轴的螺母的夹持压力，以及轴上接头和任何精度要求；dT是一个补偿量，可以考虑表面处理、机械安装或填充润滑脂等因素影响。

一般情况下，轴最小直径越大，轴承容量就越大，轴承强度也越高。

因此，工程制造中，求取轴最小直径的计算公式是非常重要的，可以确定机械装配件的实际尺寸、容量和强度。