光学透镜成像公式推导(稻谷书屋)

口诀法──喜欢口诀辅助记忆的同学可选用此法凸透镜成像规律可用简要归纳成下面几句话：一倍焦距分虚实，（即物体放在凸透镜的焦点处，不能成像；当物距小于焦距时，成虚像；物距大于焦距时，成实像，也就是说，焦点是凸透镜成虚像或实像的分界点）二倍焦距定大小。

（是说物距大于1倍焦距而小于2倍焦距时，成倒立、放大的实像；物距大于2倍焦距时，成倒立、缩小的实像；在物距小于1倍焦距时，成正立、放大的虚像。

即2倍焦距处是成放大实像或缩小实像的分界点）实像总是异侧倒，（即成实像时，总是像、物异侧，像相对于物是倒立的）虚像总是同侧正。

（即成虚像时，总是像、物同侧，像相对于物是正立的）作图法是利用几何光学中的三条特殊光线来推导透镜成像规律的方法。

三条特殊光线如图2分别是：①是通过凸透镜光心的光线传播方向不改变；②是跟主光轴平行的入射光线，通过凸透镜后要经过焦点；③是过焦点的入射光线，通过凸透镜后沿与主光轴平行的方向射出。

选用其中的两条通过凸透镜的光线就可以作出凸透镜所成的像。

凸透镜成像情况作图如图4。

（说明：凸透镜在此图中用两端带箭头的竖直线段来表示）1．当u<f时，凸透镜成正立、放大的虚像，如图中A1所成的像A1′这是放大镜的原理。

此时v>u。

2．当u=f时，物体射出去的光线经过凸透镜后平行射出，此时凸透镜不成像，如图中A2所射出的光不能会聚成像。

这是成实像和成虚像的分界点。

3。

当f<u<2f时，凸透镜成倒立、放大的实像，如图中A3所成的像A3′，这是投影仪、幻灯机的原理。

此时v>2f。

4．当u=2f时，凸透镜成倒立、等大的实像，如图中A4所成的像A4′，这是成放大或缩小实像的分界点。

此时v=u=2f。

5．u>2f时，凸透镜成倒立、缩小的实像，如图中A5所成的像A5′，这是照相机的原理。

此时f<v<2f。

U>2F时,在光屏上可得到倒立,缩小的实像U=2F时,在光屏上可得到倒立,等大的实像F<u<2F时,在光屏上可得到倒立,放大的实像U<F时,可透过凸透镜看到正立,放大的虚像u是物距v是像距f是焦距物距像距像的大小像的正倒和虚实应用例子u>2f f<v<2f 缩小倒立的实像照相机u2f v=2f 等大倒立的实像f<u<2f v>2f 放大倒立的实像幻灯机投影仪u=f 不成像（呈平行光射出）！！u<f v>u 放大正立的虚像放大镜。

物理学一直是人类探究宇宙规律的重要科目之一。

在初中物理第一册中，透镜成像是一个重要的知识点。

掌握透镜成像方法和相关公式，对于理解光学、科学研究甚至日常生活都有一定帮助。

本文将针对初中物理第一册教案，介绍透镜成像的方法和相关公式。

一、透镜成像的类型透镜成像分为实像和虚像两种。

实像是物体的像能够投影在屏幕上，亦即在远离透镜的地方形成的像。

虚像则是物体放置在一个透镜的近处，像出现在透镜背面的地方。

二、透镜的相关公式透镜成像的公式有以下三种：1.聚焦距离公式聚焦距离f是透镜最重要的参数之一。

它指的是在垂直于透镜轴线的位置上，物体被聚焦所需要的距离。

针对透镜而言，聚焦距离是一个恒定值。

对于一个透镜，要计算出聚焦距离公式，可以使用以下公式：1/f=1/u+1/v其中，u是物体距离透镜的距离，而v是像距离透镜的距离。

2.放大倍率公式放大倍率指的是物体和像之间的大小比例。

对于放大倍率的计算，使用以下公式：m(h/h')=v/u其中，h表示物体的高度，h'表示像的高度。

v和u的意义同上。

3.倒立像的特征公式对于一个倒立像而言，使用以下公式：h'/h= -v/u其中，符号负号表示像是倒置的。

三、透镜成像的方法计算透镜成像方法有以下步骤：1.确定光线的方向针对一组物体和透镜，计算出透镜弧形上和轴线与此物体相交的两个点。

在这两个点上，绘制出两条与轴线平行的光线。

2.交点计算计算出两条光线在透镜处的交点，该点即为像的位置。

3.计算像的性质根据像的位置和性质，计算出透镜成像的性质，例如像的大小、方向和正反。

四、结论透镜成像方法和相关公式是初中物理中的一个重要知识点。

掌握透镜弧形上和轴线与此物体相交的两个点的方法，能够帮助学生快速地确定透镜成像的方向和光线的走向。

同时，透镜成像的三个公式能够方便计算物体与像之间的大小比例，让学生更好地理解透镜成像。

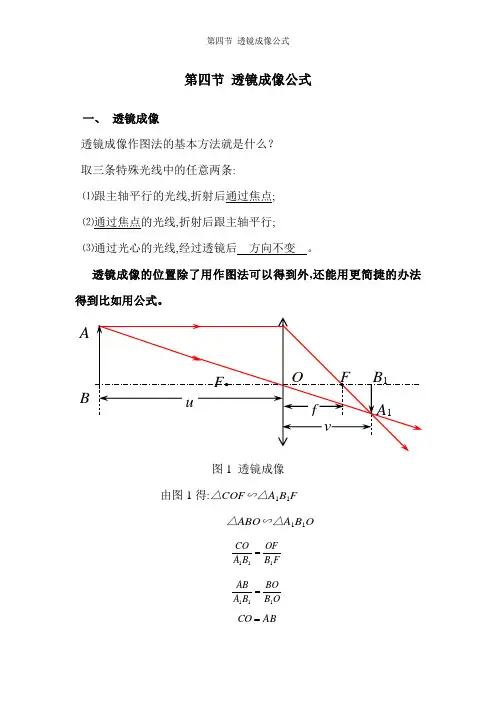
第四节 透镜成像公式一、 透镜成像透镜成像作图法的基本方法就是什么？取三条特殊光线中的任意两条:⑴跟主轴平行的光线,折射后通过焦点;⑵通过焦点的光线,折射后跟主轴平行;⑶通过光心的光线,经过透镜后 方向不变 。

透镜成像的位置除了用作图法可以得到外,还能用更简捷的办法得到比如用公式。

图1 透镜成像由图1得:△COF ∽△A 1B 1F △ABO ∽△A 1B 1OFB OF B A CO 111= OB BO B A AB 111= AB CO =OF=f , B 1F = v －f , BO=u , B 1O=v由 OB BO F B OF 11=得:即:整理得: ——此公式为透镜成像公式⏹ 凸透镜:u , f 总取正值;⏹ u>f 时,v 为正值,像物异侧,实像⏹ u<f 时,v 为负值,像物同侧,虚像二、凹透镜公式⏹ 可以证明,以上公式完全适用于凹透镜,但需注意,焦距应取负值(虚焦点)。

⏹ 由 可知v 为负,这表示凹透镜总成虚像。

注意:其它均为负,在计算题中往往被忽视。

三、放大率定义:像长跟物长的比ABB A 11叫做像的放大率。

因为△ABO ∽△A 1B 1O:所以u v AB B A m ==11 m>1,表示成放大的像,m<1,表示成缩小的像。

注意:实像v 取正,虚像v 取负。

根据 得: vu f v f =-uv fu fv =+f v u 111=+fv u 111=+fv u 111=+⏹ 当u →∞时,u －f ≈ u , v ≈ f 、意义:太阳射来的平行光经凸透镜折射后再焦点会聚。

⏹ 当u >2f 时, u －f > f , v<u , m= u v <1、 意义:成倒立、缩小的实像,如照相机。

⏹ 当u =2f 时, u-f= f , v=u , m=uv =1、意义:成倒立的与物体等大小的实像。

⏹ 当f<u<2f 时,u －f< f , v>u , m=u v >1、意义:成倒立、 放大的实像,如幻灯机。

凸透镜、凹透镜成像原理与公式透镜分凸透镜和凹透镜两种⼀、凸透镜成像规律：物体放在焦点之外，在凸透镜另⼀侧成倒⽴的实像，实像有缩⼩、等⼤、放⼤三种。

物距越⼩，像距越⼤，实像越⼤。

物体放在焦点之内，在凸透镜同⼀侧成正⽴放⼤的虚像。

物距越⼤，像距越⼤，虚像越⼤。

⼀）凸透镜成像规律顺⼝溜：1. ⼆倍焦距以外，倒⽴缩⼩实像；⼀倍焦距到⼆倍焦距，倒⽴放⼤实像；⼀倍焦距以内，正⽴放⼤虚像；成实像物和像在凸透镜异侧，成虚像在凸透镜同侧2. ⼀倍焦距分虚实两倍焦距分⼤⼩物近像远像变⼤物远像近像变⼩三）为了研究各种猜想，⼈们经常⽤光具座进⾏试验。

蜡烛，凸透镜，光屏应尽量保持在同⼀条直线上。

利⽤透镜的特殊光线作透镜成像光路：（1）、物体处于2倍焦距以外（2）、物体处于2倍焦距和1倍焦距之间（3）、物体处于焦点以内（4）、凹透镜成像光路四）实验研究凸透镜的成像规律是：当物距在⼀倍焦距以内时，得到正⽴、放⼤的虚像；在⼀倍焦距到⼆倍焦距之间时得到倒⽴、放⼤的实像；在⼆倍焦距以外时，得到倒⽴、缩⼩的实像。

透镜成像满⾜透镜成像公式：1/u(物距)+1/v（像距）=1/f（透镜焦距）⼆、凹透镜成像规律：只能⽣成缩⼩的正⽴的虚像。

成虚像时，若是放⼤定是凸透镜⽣成的，缩⼩的⼀定是凹透镜⽣成的。

⽆论是什么透镜⽣成的虚像⼀定是正⽴的，⽣成的实像⼀定是倒⽴的。

⼀）凹透镜成像规律公式1/u+1/v=1/f(u为物距，v为相距，f为焦距，与凸透镜⼀样）凹透镜成的像与物体、焦距的关系⼆）对于薄凹透镜：当物体为实物时，成正⽴、缩⼩的虚像，像和物在透镜的同侧；当物体为虚物，凹透镜到虚物的距离为⼀倍焦距以内时，成正⽴、放⼤的实像，像与物在透镜的同侧；当物体为虚物，凹透镜到虚物的距离为⼀倍焦距时，成像于⽆穷远；当物体为虚物，凹透镜到虚物的距离为⼀倍焦距以外两倍焦距以内时，成倒⽴、放⼤的虚像，像与物在透镜的异侧；当物体为虚物，凹透镜到虚物的距离为两倍焦距时，成与物体同样⼤⼩的虚像，像与物在透镜的异侧；当物体为虚物，凹透镜到虚物的距离为两倍焦距以外时，成倒⽴、缩⼩的虚像，像与物在透镜的异侧。

光学透镜成像公式推导光学透镜的成像公式是描述光线经过透镜后形成的像的公式。

推导成像公式的基本原理是根据光线在透镜上的折射规律、物距、像距及焦距之间的关系。

首先，我们需要定义一些基本概念。

-物距（u）：指的是物体与透镜之间的距离，可以是实物或者虚物，以正数表示实物的物距，以负数表示虚物的物距。

-像距（v）：指的是像与透镜之间的距离，以正数表示实像的像距，以负数表示虚像的像距。

-焦距（f）：指的是透镜的焦点与透镜之间的距离。

在光线经过透镜时，根据折射定律可以得到以下关系：\[\frac {sin\theta_1}{sin\theta_2} = \frac {n_2}{n_1}\]其中，\[\theta_1\] 是入射角，\[\theta_2\] 是折射角，\[\ n_1\] 是透镜外的介质折射率，\[\ n_2\] 是透镜的折射率。

根据几何光学的规则，我们可以得到下图所示的光线通过透镜的示意图：我们假设光线经过透镜后的入射角是\[\alpha_1\]，出射角是\[\alpha_2\]。

根据几何规律，我们可以得到以下关系：\[\theta_1 = \alpha_1\]\[\theta_2 = \alpha_2\]根据几何光学的成像原理，入射光线与出射光线在透镜的焦点处相交，可以得到以下几何关系：\[\frac {h_1}{u} = \frac {h_2}{v} = \frac {h_1+h_2}{f}\]其中，\[\h_1\]是物体的高度，\[\h_2\]是像的高度。

然后，我们可以推导出物距和像距之间的关系。

根据相似三角形关系，我们可以得到：\[\frac {h_1}{u} = \frac {h_2}{v}\]将上述两个等式结合起来，得到：\[\frac {h_1}{u} = \frac {h_1+h_2}{f} = \frac {h_2}{v}\]通过简单的等式转换和代数运算，我们可以得到成像公式：\[\frac {1}{f} = \frac {1}{v} - \frac {1}{u}\]其中，\[\u\]是物距，\[\v\]是像距，\[\f\]是焦距。

透镜成像公式的推导与应用一、透镜成像公式透镜成像公式是描述透镜成像规律的重要公式，其表达式为：[ = - ]其中，( f )表示透镜的焦距，( v )表示像距，( u )表示物距。

二、透镜成像规律1.物距与像距的关系根据透镜成像公式，物距与像距的关系可以分为以下三种情况：（1）物距大于二倍焦距：( u > 2f )，成倒立、缩小的实像，应用于照相机和摄像头。

（2）物距等于二倍焦距：( u = 2f )，成倒立、等大的实像，此时像距( v = 2f )。

（3）物距小于二倍焦距：( u < 2f )，成倒立、放大的实像，应用于投影仪和幻灯机。

2.焦距与成像性质的关系（1）焦距越大：成像距离越远，成像越大。

（2）焦距越小：成像距离越近，成像越小。

三、透镜成像应用1.照相机和摄像头：利用物距大于二倍焦距的原理，成倒立、缩小的实像，广泛应用于摄影和监控领域。

2.投影仪和幻灯机：利用物距小于二倍焦距的原理，成倒立、放大的实像，用于教学演示和商务汇报。

3.放大镜：利用物距小于焦距的原理，成正立、放大的虚像，用于观察细小物体。

4.望远镜和显微镜：利用透镜组的设计，实现对远处或微小物体的放大观察。

5.眼睛的成像原理：人眼相当于一个复杂的透镜系统，通过调整晶状体的焦距，使物体在视网膜上形成清晰的倒立实像。

透镜成像公式是光学基础知识的重要组成部分，掌握透镜成像规律和应用，有助于我们更好地理解光学现象，并广泛应用于日常生活和科技领域。

习题及方法：1.习题：一个凸透镜的焦距是20cm，物体放在距凸透镜30cm处，求像的性质和大小。

方法：由题意知，物距( u = 30cm )，焦距( f = 20cm )，因为( u > 2f )，所以成倒立、缩小的实像。

根据透镜成像公式，可以求出像距( v )：[ = - ][ = - ][ = + ][ v = 60cm ]因为像距( v )大于二倍焦距，所以像的大小小于物体的大小。

凸透镜成像公式推导在物理光学中，凸透镜成像是一个重要的概念。

凸透镜是一种光学元件，能够将通过它的光线聚焦或发散。

为了描述凸透镜成像的过程，我们需要推导出凸透镜的成像公式。

首先，让我们定义一些术语。

我们将凸透镜的中心线称为主光轴，记为OA。

凸透镜的中心称为光心，记为O，而凸透镜的焦点则分为前焦点和后焦点，分别记为F和F'。

凸透镜的焦距是指从光心到焦点的距离，记为f。

假设一个物体被放置在凸透镜的一侧，距离物体的高度为h，而物体到凸透镜的距离为u。

在成像过程中，存在一个成像点，我们将其距离光心的高度记为h'，距离凸透镜的距离记为v。

根据物体和像的几何关系，我们可以得到以下公式：(1) 1/f = 1/v - 1/u这是凸透镜薄透镜公式的一般形式，其中f表示凸透镜的焦距，v表示像的位置，u表示物的位置。

为了推导具体的凸透镜成像公式，我们需要根据光线的传播规律来进行分析。

根据光线在凸透镜上的折射规律，我们可以得到以下两个关系式：(2) h/u = h'/v(3) h'/h = v/u将式(3)代入式(2)，可得到：h/u = v/u => h = v从而我们可以推导出以下凸透镜成像公式：(4) 1/f = 1/v - 1/u利用这个成像公式，我们可以计算出物体、像的位置和大小。

特别地，当物体位于无穷远处时，即u→∞，我们可以得到以下成像公式：(5) 1/f = 1/v这个公式称为“物体在无穷远处成像的公式”，它表示平行光线通过凸透镜后会聚于焦点。

另外，如果我们将v的正负值分别代入公式(4)和(5)中，可以得出以下结论：- 当物体位于焦点之前，即u < f，成像距离v为正，物像关系为实像。

- 当物体位于焦点之后，即u > f，成像距离v为负，物像关系为虚像。

- 当物体位于焦点上，即u = f，无成像，光线通过透镜后保持平行。

通过以上的推导，我们可以得出凸透镜成像公式及其应用。

透镜光屏成像规律
透镜光屏成像规律是指透过透镜的光线经透镜折射后，在光屏上形成的图像规律。

根据透镜成像规律，可以得出以下两个重要规律：
1. 物距和像距关系：
假设物体距离透镜的距离是p，物体的高度是h，像距离透镜的距离是q，像的高度是h'。

根据透镜成像规律，物距和像距以及焦距的关系可以表示为：
1/p + 1/q = 1/f
其中，f为透镜的焦距。

该公式也被称为薄透镜成像公式。

2. 放大率：
放大率（m）是指图像的高度与物体高度之间的比值。

通过透镜成像规律，可以得到放大率的表达式：
m = -q/p
放大率的负号表示图像的方向与物体的方向相反。

透镜成像规律还可以根据光线的入射角和折射角之间的关系，推导出许多其他的规律，例如透镜成像的畸变规律、倒立成像规律等。

这些规律对于理解和描述透镜光屏成像非常重要。

凸透镜的成像公式的两种证明方法1.几何光学的证明方法：几何光学的证明方法是基于物距、像距、焦距之间的几何关系推导出凸透镜的成像公式。

（1）设物体距离凸透镜的距离为u，像距离为v，焦距为f。

（2）根据凸透镜的焦距定义，得到1/f=1/v-1/u。

（3）将方程整理为一个以u为自变量、v为因变量的二次方程：1/v=(1/f)+(1/u)。

（4）根据几何光学的基本原理，当光线从上方射入凸透镜时，经过折射后会汇聚于焦点，因此可以得到物距与像距之间的关系：u+v=f。

（5）将(4)式中的v代入(3)式，得到u + f = fu/v。

（6）进一步整理，得到(u + f)v = fu。

（7）根据几何光学的基本原理，当物体在光轴上时，物体与像一定在同一高度，因此可以得到(u+v)=2f。

（8）将(7)式代入(6)式，得到2fv = fu。

（9）两边除以fu，得到2fv/fu = 1（10）进一步化简，得到v/u=1/2，即v=u/2（11）将v代入(4)式，得到u+u/2=f。

（12）化简得到u=2f。

（13）将u代入(4)式，得到v=2f。

（14）综上所述，根据几何光学的证明方法，可以得到凸透镜的成像公式为1/v+1/u=1/f。

2.光线追迹法的证明方法：光线追迹法是基于光线从物体射入凸透镜后经折射而成像的原理，通过追踪光线来推导出凸透镜的成像公式。

（1）根据凸透镜的焦距定义，使光线射入凸透镜的方向与光轴平行时，光线经过凸透镜后会聚于焦点。

（2）设物体距离凸透镜的距离为u，用一条平行于光轴的光线射入凸透镜，经过折射后与焦距相交于像距离为v的位置。

（3）根据几何关系，可以得到直角三角形的相似关系：u/f=v/(v–f)。

（4）将(3)式整理，得到v = uf/(u – f)。

（5）将(4)式进一步整理，得到1/v=(1/f)–(1/u)。

（6）根据光线追迹法的原理，凹透镜的成像同样可以使用该方法证明，推导出的成像公式为1/v–1/u=1/f。