8.2 理想气体的压强和温度
- 格式:ppt
- 大小:550.00 KB
- 文档页数:23

标准情况下温度和压强在物理学中,温度和压强是描述物质状态的重要物理量。
它们对于描述物质的性质和行为起着至关重要的作用。
本文将对标准情况下温度和压强进行详细的介绍和分析。
首先,我们来了解一下温度。
温度是描述物质热运动状态的物理量,通常用摄氏度(℃)或者开尔文(K)来表示。
在标准情况下,即标准大气压下,温度为0摄氏度,相应的绝对温度为273.15开尔文。
温度的变化会直接影响物质的热运动状态,当温度升高时,分子的热运动加剧,物质的体积也会相应膨胀。
因此,温度是描述物质热力学性质的重要参数。
接下来,我们来讨论一下压强。
压强是描述单位面积上受到的力的大小,通常用帕斯卡(Pa)来表示。
在标准情况下,即标准大气压下,压强为101325帕斯卡。
压强的变化会直接影响物质的密度和形态,当压强增大时,物质的密度也会相应增大,形态也会发生变化。
因此,压强是描述物质力学性质的重要参数。
温度和压强是密切相关的物理量,它们之间存在着一定的关系。
根据理想气体状态方程PV=nRT,温度和压强是成正比的关系。
当温度升高时,压强也会相应增大;当温度降低时,压强也会相应减小。
这种关系是由理想气体的性质所决定的,而在实际的物质中,这种关系可能会受到一定的影响。
除了理想气体状态方程中的关系外,温度和压强还存在着其他的相互影响。
比如,在热力学系统中,温度的升高会导致分子热运动加剧,从而使得分子之间的相互作用增强,这会导致压强的增大。
而在固体和液体中,温度的升高也会导致分子热运动加剧,从而使得物质的体积膨胀,这同样会导致压强的增大。
因此,温度和压强之间存在着复杂而微妙的相互关系。
综上所述,温度和压强是描述物质状态的重要物理量,它们之间存在着密切的关系。
在标准情况下,温度为0摄氏度,压强为101325帕斯卡,它们之间存在着一定的正比关系。
然而,在实际的物质中,温度和压强之间的关系可能会受到一定的影响,需要根据具体的情况进行具体分析。
希望本文能够对读者对温度和压强有所帮助,谢谢阅读!。

温度和压力的变化
温度和压力之间存在一定的关系。
在理想气体状态下,温度和压强成正比关系,温度越高,压强越大,反之亦然。
在实际的气体状态下,温度和压力的关系会受到气体分子之间的相互作用和气体分子的热运动的影响。
具体来说,温度和压力的变化有以下规律:
1.当温度升高时,气体的压强通常也会增大。
这是因为气体分子的热运动速度加快,相互碰撞的频率增加,导致气体分子对容器壁的撞击力增大,从而压强增大。
2.当温度降低时,气体的压强通常会减小。
这是因为气体分子的热运动速度减慢,相互碰撞的频率减少,导致气体分子对容器壁的撞击力减小,从而压强减小。
3.当气体的压强增大时,气体的温度也可能会升高。
这是因为气体分子之间的相互作用加强,导致气体分子的热运动速度加快,从而温度升高。
4.当气体的压强减小时,气体的温度也可能会降低。
这是因为气体分子之间的相互作用减弱,导致气体分子的热运动速度减慢,从而温度降低。
需要注意的是,温度和压力的变化并不是简单的线性关系,而是受到多种因素的影响。
例如,气体的体积、物质的种类、气体的状态等都会对温度和压力的变化产生影响。
因此,在实际的气体状态分析中,需要综合考虑各种因素来准确描述温度和压力之间的关系。


理想气体的压强与温度
根据理想气体状态方程,理想气体的压强与温度之间存在以下关系:P * V = n * R * T
其中,P为气体的压强,V为气体的体积,n为气体的物质的量,R
为气体常数,T为气体的绝对温度。
由上述方程可以推导出,理想气体的压强与温度成正比关系,即当
温度升高时,压强也会增加;当温度降低时,压强也会减小。
这是因
为温度的增加会使气体内分子的平均动能增加,分子运动更加剧烈,
从而增加碰撞力,导致气体的压强增加。
需要注意的是,上述关系在气体的体积和物质的量不发生变化的条
件下成立。
同时,上述关系只适用于符合理想气体状态的气体,即低压、高温下气体分子之间几乎没有相互作用,可以近似看作质点。
对
于高压或低温下的气体,分子之间的相互作用不能忽略,此时可能需
要考虑气体的比较复杂的状态方程。

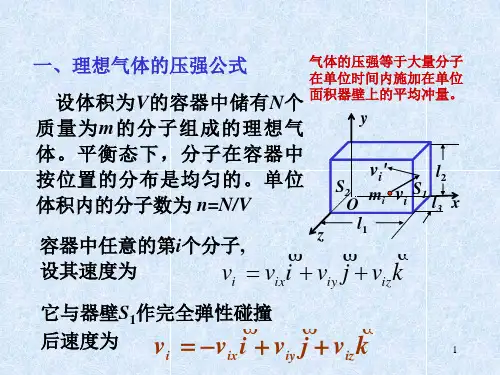

一、理想气体的压强公式1.压强的产生气体作用于器壁的压力是气体中大量分子对器壁不断碰撞的综合效果。
由于是大量分子对器壁的碰撞,就使得器壁受到一个持续的、均匀的压力的作用。
压强即为单位面积上作用器壁上的平均冲力。
2.气体压强公式的简单推导假设有一个边长为x ,y ,z 的长方形容器,其中含有N 个同类理想气体分子,每个分子质量均为m 。
在平衡状态下,长方形容器各个面的压强应当是相等的。
现在我们来推导作用在与x 轴垂直的面1A 的压强。
以第i 个分子为研究对象。
设在某一时刻其速度为k v j v i v v iz iy ix i ++=,它与器壁碰撞必受到器壁的作用力。
在此力的作用下,i 分子在x 轴上(以x 轴为研究对象,取标量式)的动量由ix mv 变为ix mv -。
根据动量定理,i 分子在x 轴上所受的冲量等于该分子在该坐标轴上的动量的增量,即:ixix ix i mv mv mv t f 2-==∆--i 分子对器壁的碰撞是间歇的,它从A 1面弹回,飞向A 2面与A 2面碰撞,又回到A 1面再作碰撞。
i 分子与A 1面碰撞两次,在x 轴上运动的距离为2x ,所需的时间为2x/v ix ,于是在单位时间内,i 分子作用在A 1面的次数是v ix /2x ,单位时间内i 分子作用在A 1面的冲力为x mv v x mv ix ix ix 2)/2(2-=-,这也就是容器壁对i 分子的平均冲力,由牛顿第三定律知道,i 分子施于器壁的冲力为xmv f ix i 2=N 个气体分子施于器壁的总冲力为上述单个分子给予器壁的冲力的总和(同类气体分子的质量相等),即)....(22221∑∑+++==xv v v m f F Nx x x i x 给上式右边上下同乘以N 得222221)....(x Nx x x i x v xNm N v v v x Nm f F ∑∑=+++==根据压强的定义,(1A 面的面积S=yZ ),则 22x x x x v nm v xyzNm yz F P === 其中n=N/V 为单位体积内的分子数,称为分子数密度。

压强体积温度的关系
压强体积温度的关系是热力学中的基本概念之一,它描述了在一定温度下,压强和体积之间的变化关系。
这个关系可以用理想气体状态方程来描述,即PV=nRT,其中P表示压强,V表示体积,n表示摩尔数,R表示气体常数,T表示温度。
1. 压强和体积的关系
在一定温度下,当压强增加时,体积会减小;当压强减小时,体积会增大。
这个关系可以用波义尔定律来描述,即在一定温度下,气体的压强与体积成反比例关系,即PV=常数。
2. 压强和温度的关系
在一定体积下,当温度升高时,压强会增加;当温度降低时,压强会减小。
这个关系可以用查理定律来描述,即在一定体积下,气体的压强与温度成正比例关系,即P/T=常数。
3. 体积和温度的关系
在一定压强下,当温度升高时,体积会增大;当温度降低时,体积会减小。
这个关系可以用盖-吕萨克定律来描述,即在一定压强下,气体的体积与温度成正比
例关系,即V/T=常数。
总之,压强体积温度的关系是气体热力学中的基本概念,它们之间的变化关系可以用理想气体状态方程、波义尔定律、查理定律和盖-吕萨克定律来描述。
这些关系在工业、科学研究和日常生活中都有广泛应用。

一定质量的气体在体积不变的情况下压强与温度的关系式一定质量的气体在体积不变的情况下,压强与温度的关系式是理想气体状态方程的一部分。
理想气体状态方程是描述理想气体行为的方程,它包括了气体的压力、体积和温度之间的关系。
根据理想气体状态方程,一定质量的气体在体积不变的情况下,压强与温度的关系式可以用数学公式表示为P1/T1=P2/T2,其中P1和T1分别是气体的初始压强和温度,P2和T2分别是气体的最终压强和温度。
在深入探讨这一关系式之前,让我们先简单了解一下理想气体状态方程的基本原理。
理想气体状态方程可以表示为PV=nRT,其中P代表气体的压力,V代表气体的体积,n代表气体的物质量,R代表气体常数,T代表气体的温度。
这个方程描述了理想气体的状态,即在一定质量下的理想气体,在体积不变的情况下,压力与温度成正比。
了解了理想气体状态方程的基本原理,我们可以开始探讨一定质量的气体在体积不变的情况下,压强与温度的关系式P1/T1=P2/T2了。
这个关系式实际上是描述了玻义-马利约定律,也被称为查理定律。
根据该定律,如果一定质量的气体在体积不变的情况下,其压力与温度成正比。
这意味着,当温度升高时,气体的压力也会升高;当温度下降时,气体的压力也会下降。
具体来说,如果一定质量的气体在体积不变的情况下,将其温度从初始温度T1升高到最终温度T2,那么根据查理定律,其压力也会从初始压力P1升高到最终压力P2。
这种线性关系使得一定质量的气体在体积不变的情况下,压强与温度的关系式成为了一条直线。
这一关系式的数学表示P1/T1=P2/T2清晰地展现了气体压强与温度之间的简单而直接的关系。
除了数学表达之外,我们可以通过一些实际的例子来更直观地理解一定质量的气体在体积不变的情况下,压强与温度的关系式。
假设我们有一定质量的气体,它在一个封闭的容器中,容器的体积保持不变。
当我们向容器中加热时,气体的温度会上升,根据查理定律,气体的压力也会增加。


化学试题气体压力与温度关系的计算在化学学科中,气体的性质与行为一直是研究的重要内容之一。
而气体的压力与温度之间的关系也是化学试题中常见的考点。
本文将介绍气体压力与温度的关系以及计算方法。
一、理想气体状态方程在研究气体压力与温度之间的关系之前,我们首先需要了解理想气体状态方程。
理想气体状态方程可以用以下数学公式表示:PV = nRT其中,P代表气体的压力,V代表气体的体积,n代表气体的物质的量,R代表气体常数,T代表气体的温度。
理想气体状态方程可以描述气体在不同温度和压力下的状态,不过需要注意的是,该方程只适用于理想气体,即分子之间无相互作用力的气体。
二、气体压力与温度的关系根据理想气体状态方程,我们可以得出气体压力与温度的关系。
当其他条件恒定时,气体压力与温度成正比,即当温度上升时,气体压力也会增加;反之,当温度下降时,气体压力会减小。
这是由于温度的增加会导致气体分子更加活跃,分子运动速度增加,与容器壁撞击的频率增加,从而增加了气体分子对容器壁的压力。
相反,温度的降低会导致分子运动速度减慢,压力也会相应减小。
三、气体压力与温度的计算方法在实际问题中,我们需要通过给定的气体量、体积和温度等条件,来计算气体的压力。
以下是几种常见的计算方法:1. 气体量固定时的计算方法:当气体量n固定时,可以运用理想气体状态方程来计算气体压力与温度之间的关系。
例如,已知气体的物质的量为2摩尔,体积为5升,温度为300K,我们可以通过理想气体状态方程进行计算:P = (nRT) / V= (2 mol * 8.314 J/(mol*K) * 300 K) / 5 L≈ 997.68 Pa2. 气体质量固定时的计算方法:当气体的质量m固定时,我们可以通过将气体的质量与物质的量之间的关系代入理想气体状态方程来进行计算。
例如,已知气体的质量为10克,体积为2升,温度为273K,我们可以通过以下步骤进行计算:首先,计算气体的物质的量n:n = m / M= 10 g / (摩尔质量)在此例中,假设气体为氢气,其摩尔质量为2 g/mol。