16.理想气体物态方程、压强和温度公式

热学公式1.3.1物态方程：（1.1）1.3.2体积膨胀系数、压缩系数、压强系数：(1.3)(1.4)(1.5)1.3.3理想气体（压强趋于零的极限状态下的气体/能严格满足理想气体物态方程的气体）物态方程：pV=vRT (1.7)1.3.4混合理想去气体物态方程：(1.9)1.4.3温标：T(p)=(其中不变) （1.10）(1.11)=(体积不变) （1.12）(体积不变) （1.13）1.5.1物质由大数分子组成：(1.14)法拉第常量F=分子热运动：（1.15）1.6.1理想气体微观模型：洛喜密脱常量(1.16)1.6.2单位时间内在单位面积器壁上平均分子数(1.18) (1.19)1.6.3理想气体压强公式：(1.20)(1.21)P=P=(1.23)K=(1.24)1.6.4温度的微观意义：(1.25)气体分子的平均根速度：=(1.26) 1.7.1分子间互作用势能曲线：d(1.29)或F=(1.30)令r时=0 则(1.31) 1.7.2分子碰撞有效直径、固体分子热震动、固体热膨胀：d=分子碰撞有效直径（1.31）1.7.3范德瓦尔斯方程：p=(1.33) （1.34）方程为：(1.43)2.2.2等概率性与概率的基本性质:(2.1)2.2.3平均值及其运算法则：(2.2)n（2.3）2.3.2麦克斯韦速率分布：f(v)dv=4(2.13)三种速率：（1）平均速率：==(2.14)(2)平均根速度：(2.15)(3)最概然速率(2.16)三种速率的比：(2.17) 2.4.1速度空间：f((2.20)2.4.2麦克斯韦速度分布：(2.26) 2.6.1等温大气压强公式：p(z)=p(0)) (2.61)2.7.1理想气体热容：C=(2.75)2.7.3能量均分定理：(2.81)3.1.1牛顿粘性定律:f=3.2.1菲克定律(3.10)3.3.1傅力叶定律：(3.14)热流密度：(3.15)3.8.1气体黏性系数导出：=(3.62)3.8.2气体的导热系数：K=(3.67)气体的扩散系数：D=(3.69)4.2.2体积膨胀功：W=（对外界系统所做的总功）（4.3）理想气体在几种可逆过程中功的计算：(1)等温过程:W=(2)等压过程:W=(3)等体过程:W=04.3.2内能定理：（4.12）热力学第一定律一般表达式：无限小过程第一定律表达式：dU=dQ+dW准静态过程第一定律表达式：dU=dQ4.4.1定体热熔：(4,19) (4.20)4.4.2定压热熔与焓：H=U+pV (4.22)4.5.1理想气体内能：(4.33) 4.5.2理想气体的等体、等压、等温过程：（1）等体过程：(4.39)（2）等压过程：Q(4.40)（3）等温过程：(4.42)4.5.3一般绝热过程准静态绝热过程：理想气体绝热过程中功及温度变化：4.5.6多方过程方程：(4.68)多方过程热熔：4.6.1热机效率的定义：=（4.81）(4.82) (4.83) 4.6.2卡诺热机的效率：（4.90）4.7.1制冷系数：（4.99）卡诺制冷剂效率：（4.100）5.3.1克劳休斯等式：=05.3.2熵和熵的计算：TdS=（5.23）熵的微分表达式以熵来表示热熔(5.25)(5.26)理想气体的熵：(5.29)5.3.7热力学第二定律表达式：热力学基本方程：热学习题课(2007.4.18) Ⅰ教学基本要求气体动理论及热力学1.了解气体分子热运动的图象。

气体状态方程温度压力与体积的关系气体状态方程是描述气体性质的基本定律之一，它表明气体的温度、压力和体积之间存在着一定的关系。

这个关系被称为气体状态方程，可以用来描述气体的物理变化和行为。

在本文中，我们将详细讨论气体状态方程中温度、压力和体积之间的关系及其应用。

1. 气体状态方程的基本表达式气体状态方程的基本表达式可以通过对理想气体的研究得出。

理想气体状态方程可以表示为：PV = nRT其中，P表示气体的压力，V表示气体的体积，n表示气体的物质的量，R为气体常数，T表示气体的温度（以绝对温度来表示，单位为开尔文）。

2. 温度与压力、体积的关系根据气体状态方程，当压力和体积固定时，气体的温度与两者呈正比关系。

换言之，如果压力和体积不变，温度升高则气体会膨胀，温度降低则气体会收缩。

这个关系被称为热膨胀原理，它在日常生活和工业生产中具有重要的应用，如温度计和压力调节装置等。

3. 温度与体积的关系当气体的压力和物质的量都保持不变时，根据气体状态方程可以推导出温度和体积呈正比的关系。

换言之，如果压力和物质的量不变，温度升高则体积会增大，温度降低则体积会减小。

这个关系被称为热膨胀原理的逆过程，它也具有重要的应用，如气体瓶中的压力调节和容器的温度控制等。

4. 温度、压力和体积的综合关系根据气体状态方程，当温度、压力和体积同时改变时，它们之间的关系可以通过变量的改变来确定。

例如，当温度和压力增加时，体积会相应地增加或减少，具体的变化取决于其他条件的影响。

这个综合关系是气体状态方程研究的重点之一，用于解释气体的复杂变化和相互作用。

总结：气体状态方程温度、压力和体积之间有着密切的关系。

温度和压力、体积呈正比，温度升高则体积会增大；但温度和体积呈反比，温度升高则体积会减小。

当温度、压力和体积同时改变时，它们之间的关系可以通过气体状态方程的基本表达式进行推导和计算。

了解气体状态方程的温度、压力和体积的关系对于深入理解气体的性质和应用具有重要意义。

1、热力学第零定律在不受外界影响的条件下，两个热力学系统同时与第三个热力学系统处于热平衡，则两个热力学系统也必定处于热平衡。

2、在宏观上，温度是决定一系统是否与其它系统处于热平衡的物理量。

一切互为热平衡的系统都具有相同的温度值。

开氏温标 理想气体定律：P tr 为气体温度计在水的三相点时的压强。

热力学温度与摄氏温度的关系： t = T- 273.15物态或状态方程 1、玻意耳定律P V = C (当T 不变) 2、盖吕萨克定律V = V 0（1 + αV t ） (P 不变) 气体膨胀系数αV 3、查理定律P = P 0（ 1 + αP t ） (V 不变) 气体压强系数 αP①该三条定律近似地适用于所有气体，只要温度不太低，则气体愈稀薄（低压气体），以上三式就能愈准确地描述气体状态的变化；②在气体无限稀薄的极限下，所有气体的αV 、αP 趋于共同的极限α ，其数值约为1/273。

αV =αP = 1/T 0=1/273 理想气体物态方程 1、同一成份（A ）同一状态之间关系（门捷列夫-克拉珀龙方程）PV = ν RT =(M/M mol )RT γ为混合气体的总摩尔数γ1+γ2 （B ）同一系统不同平衡态之间关系： P 1V 1 / T 1 = P 2V 2 / T 2 2、道尔顿分压定律混合气体总压强等于各种组分的分压强之和。

P = P 1+P 2+……+P n3、几种成份：P = P 1 + P 2 + ...... + P n = ( ν1 + ν2 + ......+ νn )RT/ VR = 8.31 J mol -1 K -1称为普适气体常量。

阿伏伽德罗常数：N A = 6.02× 10 23 mol -1理想气体的微观模型无外场时，分子在各处出现的概率相同 N 个分子给予器壁的压强n ：分子数密度分子热运动平均平动动能 压强公式：trX XK X T 16.273)(=0()PV T P Rγ=()273.16limtr P trP T P K P →=⋅单位时间内碰在单位面积器壁上平均分子数理想气体物态方程的另一种形式k = R/N A = 1.38×10-23 J K -1温度的微观意义 温度是平衡态系统的微观粒子热运动程度强弱的量度。

物理知识点气体的压强和温度的关系气体是物理学中重要的研究对象之一。

在研究气体性质的过程中，人们发现气体的压强与温度之间存在一定的关系。

本文将介绍气体的压强和温度的关系，并探讨其相关的知识点。

一、理想气体状态方程理想气体状态方程是描述气体行为的重要公式。

根据理想气体状态方程，气体的压强与温度有一定的关联。

理想气体状态方程的表达式为：PV = nRT其中，P表示气体的压强，V表示气体的体积，n表示气体的物质的量，R为气体常数，T表示气体的温度。

二、压强和温度的关系根据理想气体状态方程可以得出，气体的压强与温度成正比，即温度升高时，气体的压强也随之增加；温度降低时，气体的压强也减少。

这是因为温度的升高会增加气体分子的动能，使分子运动更加剧烈，撞击容器壁的频率增加，从而增加了气体分子对容器壁施加的压力，进而增加了气体的压强。

三、温度的单位在物理学中，温度的单位有多种，常见的有摄氏度（℃）和开尔文（K）。

摄氏度是常用的温度单位，与开尔文之间有简单的转换关系：T(℃) = T(K) - 273.15在理想气体状态方程中，温度应使用开尔文表示，因为开尔文温标的零点是绝对零度，与分子的平均动能密切相关。

四、实际气体与理想气体需要注意的是，理想气体状态方程是在一定条件下对气体行为的近似描述。

在实际气体中，一些因素如分子间的相互作用、分子体积等会对气体的性质产生一定的影响。

当气体压力较高、温度较低时，理想气体状态方程对气体行为的描述就不太准确了，此时需要考虑气体的真实性质，并运用其他气体方程进行描述。

五、应用案例1. 汽车轮胎充气时，气体的压强与温度的关系对安全驾驶非常重要。

在高温天气下，汽车轮胎内气体受热膨胀，压强升高，如果不适当减少气体压力，轮胎可能会爆胎。

因此，驾驶员应定期检查轮胎气压，确保在安全范围内。

2. 工业生产中，气体的压强和温度关系也常被应用于化学反应器的控制。

在某些高温反应中，控制反应器内气体的温度可以调节反应速率和产物的选择性，从而提高产量和质量。

1.理想气体物态方程：pV=NkT 变形1：Pv=νRT （R=N A k）变形2：P=nkT （n=N/V为分子数密度）2．理想气体压强公式：P=（1/3）nmv^2 变形：P=2/3nεk (εk分子平均平动动能)3理想气体平均平动动能与温度关系：1/2mv^2=εk=3/2kT4方均根速率： Vrms=(3kT/m)^(1/2)= (3Rt/M)^(1/2)5自由度：单i=3 双刚=5 双非=7 三以上刚=6 ε =i1/2kT6理想气体内能：E=N A i1/2kT =i/2RT7三种统计速率：1）最概然速率V p=(2kT/m)^(1/2)= (2RT/M)^(1/2) 2）平均速率v =(8kT/πm)^(1/2) 3）4 8分子平均碰撞次数：Z，分子连续两次碰撞间的路程均值叫做平均自由程λλ=v/ Z Z =1.41πd ^2 vn 9准静态过程中体积变化做功：ΔW=PΔV=(Sv1v2)pdV10.摩尔定体热容：C v,m=dQ/dT dE=：C v,m* dT11热机效率：η=W/Q1 =(Q1-Q2)/Q1 =1-Q1/Q2 (Q1为吸热量 Q2为热源吸收量)12等体过程中V为常量，即dW=0 dQ=dE 吸收热量全部转化为内能13转动定理：M=Jα常见转动惯量1）中心轴细棒：ml^2 /12 2）圆柱体：mR^2 / 2 3)薄圆环J=mR24)端点轴细棒：J=ml2/14平行轴定理：J=J C+md215电容器电能：W=1/2 QU=1/2 CU216 电场能量密度：w=1/2εΕ217.磁场能量：W=1/2 LI2 密度w=W/V=B2/2μ19.毕奥撒法尔定律：dB=(μ0/4π)*(Idlsinθ/r^2)= (μ0/4π)*(Idl e r/r^2)20.运动电荷磁场：B=(μ0/4π)*(qvr/r^3)21.无限长直导线B=μ0I/2πr022.库伦定律 F=（1/4πε0）（q1q2/r^2）e r23圆形载流导线轴线上一点 B=(μ0/2)(R2I/(R2+x2)3/2) x>>R B=μ0IR2/2x3A-B 等温膨胀内能不变对外做功W1=从T1高温处吸热Q1W1=Q1=vRTT1ln(V2/V1)B-C 绝热膨胀对外做功等于气体减少的内能W2=vCv，m（T1-T2）C-D 等温压缩：外界对气体做功等于气体给低温热源的热量W3=Q2= vRTT2ln(V4/V3)。

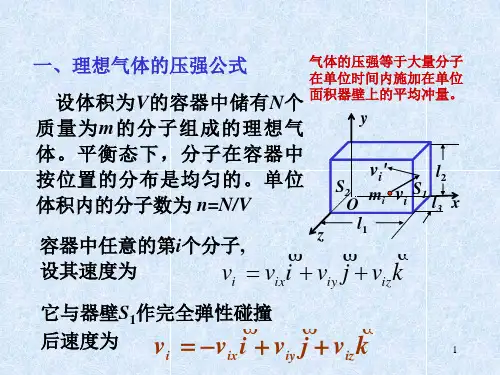
内容提要一、平衡态 理想气体物态方程 1.气体的物态参量气体的体积、压强和温度三个物理量称为气体的物态参量.在国际单位制中，体积的单位是立方米，符号为3m 。

压强的单位是帕[斯卡]，符号为Pa ，760m m Hg Pa 101.013 atm 15=⨯=。

热力学温度的单位是开［尔文］，符号为K ，273.15T t =+。

2. 理想气体物态方程：mpV RT M=二、理想气体的压强公式 温度的微观本质 1.热动平衡的统计规律（1）分子按位置的分布是均匀的：d d N Nn V V== （2）各方向运动概率均等：0x y z ===v v v ；222213x y z ===v v v v 2.理想气体压强的微观公式：2kt 12 33p mn n ε==v3.理想气体物态方程：p nkT =4.理想气体分子的平均平动动能与温度的关系：2kt 013 22m kT ε==v 三、能量均分定理和理想气体的内能1.刚性分子自由度2.能量均分定理气体处于平衡态时，分子任何一个自由度的平均能量都相等，均为12kT ，这就是能量按自由度均分定理。

3.理想气体的内能：2m iE RT M =四、麦克斯韦气体速率分布定律 1.麦氏分布函数：1d ()d Nf N =v v物理意义：气体在温度为T的平衡状态下，速率在v附近单位速率区间的分子数占总数的百分比。

2.三种统计速率（1）最概然速率：p==v（2）平均速率：==v（3==习题精选一、选择题1.对于一定质量的理想气体，以下说法正确的是( )A、如果体积减小，气体分子在单位时间内作用于器壁单位面积的总冲量一定增大B、如果压强增大，气体分子在单位时间内作用于器壁单位面积的总冲量一定增大C、如果温度不变，气体分子在单位时间内作用于器壁单位面积的总冲量一定不变D、如果密度不变，气体分子在单位时间内作用于器壁单位面积的总冲量一定不变2.关于温度的意义，下列说法正确的是 ( )（１）气体的温度是分子平均平动动能的量度（２）气体的温度是大量气体分子热运动的集体表现，具有统计意义（３）温度的高低反映物质内部分子运动剧烈程度的不同（４）从微观上看，气体的温度表示每个气体分子的冷热程度A、（1）、（2）、（4）B、（1）、（2）、（3）C、（2）、（3）、（4）D、（1）、（2）3.如图12-1所示，一气室被可以左右移动的隔板分成相等的两部分，一边装氧气，另一边装氢气，两种气体的质量相同、温度一样。

理想气体的物态方程理想气体的物态方程：1、定义：理想气体模型是以克朗F={PV=RT}热力学方程为基础，把真实气体的volume、pressure、temperature之间的变化关系简化成一个简单二次函数而形成。

这个函数就是理想气体物态方程，也称为理想状态方程。

2、特征：（1）气体表现出一种像玻璃球一样的球形性质，可以与此同时显示出球形的压强。

（2）气体的压强随它的容积的变化而变化，且容积变化量越大，那么其对应的压强变化量也越大。

（3）温度不变时，气体的压强与其容积呈正比。

（4）温度不变时，气体的容积与温度之间没有关系。

3、公式：理想气体物态方程为：PV=nRT其中：P=气体的压强，（单位：Pa）V=气体的体积，（单位：m³）n=气体的物质的量（单位：kg）R=理想气体常数，（单位：J/K）T=气体的温度，（单位：K）4、物态方程的类型：（1）通用物态方程：PV=nRT（2）非通用物态方程：PV^γ=aRT其中γ<1，γ为状态方程的绝热比率；a为某种特定物态方程中的绝热常数。

（3）同行物态方程：PV=B其中B为状态方程的固定常数，PV恒定。

5、物态方程的应用：（1）理想气体的定压过程：指的是在定压条件下，理想气体的体积V 随温度T变化的过程，根据PV=nRT，有V/T = constant = nRT/P，即定压过程的物态方程为V/T=nR/P。

（2）理想气体的定容过程：指的是在定容条件下，理想气体的压强P 随温度T变化的过程，根据PV=nRT，有P/T = constant = nRT/V，即定容过程的物态方程为P/T=nR/V。

热力学理想气体三个状态方程热力学理想气体三个状态方程1. 引言热力学理想气体三个状态方程是描述气体行为的重要方程，它包括了爱因斯坦、克劳修斯和麦克斯韦三位著名物理学家的工作成果。

理想气体的状态方程可以描述气体的物态、热态和力学性质，对于工程、化工、材料等领域有着重要的意义。

在本文中，我们将深入探讨理想气体三个状态方程的内容，并对其进行全面的评估和分析。

2. 理想气体的状态方程理想气体的状态方程包括了压强、温度、体积和气体的物质量之间的关系。

理想气体的三个状态方程分别为爱因斯坦方程、克劳修斯方程和麦克斯韦方程。

这三个方程分别为：2.1 爱因斯坦方程爱因斯坦方程描述了理想气体在恒定体积下压强和温度的关系。

其数学表达式为：\[PV = RT\]式中，\(P\)代表气体的压强，\(V\)代表气体的体积，\(T\)代表气体的温度，\(R\)代表气体常数。

爱因斯坦方程揭示了在恒定体积下，理想气体的压强和温度成正比的关系。

这为气体的热力学性质提供了重要的理论基础。

2.2 克劳修斯方程克劳修斯方程描述了理想气体在恒定压强下体积和温度的关系。

其数学表达式为：\[V/T = \text{常数}\]式中，\(P\)代表气体的压强，\(V\)代表气体的体积，\(T\)代表气体的温度。

克劳修斯方程表明了在恒定压强下，理想气体的体积和温度成反比的关系。

这为气体的物态转化提供了重要的理论依据。

2.3 麦克斯韦方程麦克斯韦方程描述了理想气体在等温条件下压强和体积的关系。

其数学表达式为：\[P \cdot V = \text{常数}\]式中，\(P\)代表气体的压强，\(V\)代表气体的体积，\(T\)代表气体的温度。

麦克斯韦方程揭示了在等温条件下，理想气体的压强和体积成反比的关系。

这为气体的压缩、膨胀等过程提供了重要的理论基础。

3. 对理想气体三个状态方程的评估理想气体三个状态方程为我们提供了理解气体热力学行为的重要工具。

这些方程从不同的角度刻画了理想气体的物态、热态和力学性质，为工程应用提供了重要的理论基础。

大物知识点整理第一章︰质点运动学1质点运动的描述位置矢量︰从所指定的坐标原点指向质点所在位置的有向线段。

运动方程︰位移︰从质点初始时刻位置指向终点时刻位置的有向线段 速度︰表示物体运动的快慢。

瞬时速率等于瞬时速度的大小 2圆周运动角加速度α=Δω / Δt 角速度ω=Φ/t=2π/T=2πf 线速度V=s/t=2πR/T， ω×r=V 切向加速度沿切向方向法向加速度 指向圆心加速度kz j y i x r+＋＝222zy x r ++=例题1 已知质点的运动方程x＝2t,y＝2-t^2,则t=1时质点的位置矢量是（）加速度是（），第一秒到第二秒质点的位移是（），平均速度是（）。

（详细答案在力学小测中）注意：速度≠速率平时作业：P36 1.6 1.11 1.13 1.16 (1.19建议看一下)第二章：牛顿定律1、牛顿第一定律： 1任何物体都具有一种保持其原有运动状态不变的性质。

2力是改变物体运动状态的原因。

2、牛顿第二定律：F=ma3、牛顿第三定律：作用力与反作用力总是同时存在，同时消失，分别作用在两个不同的物体上，性质相同。

4、非惯性系和惯性力非惯性系：相对于惯性系做加速运动的参考系。

惯性力：大小等于物体质量与非惯性系加速度的乘积，方向与非惯性加速度的方向相反，即F=-ma例题：P51 2.1 静摩擦力不能直接运算。

2.2 对力的考察比较全面，类似题目P64 2.1 2.2 2.62.3运用了微积分，这种题目在考试中会重点考察，在以后章节中都会用到，类似P66 2.13该章节对惯性力涉及较少，相关题目有P57 2.8 P65 2.7(该题书中的答案是错的，请注意，到时我会把正确答案给你们。

)P67 2.17.第三章 动量守恒定律与能量守恒定律1动量P=mv2冲量 其方向是动量增量的方向。

Fdt=dP3动量守恒定律P=C （常量）条件：系统所受合外力为零。

若系统所受合外力不为零，但沿某一方向合力为零时，则系统沿该方向动量守恒。

气体的压强与温度关系气体是一种物质状态，其粒子间距离很大，彼此之间只有微弱的相互作用力。

当气体处于一个封闭的容器中时，气体分子会不断地与容器壁碰撞，并产生一定的压强。

气体的压强与温度有着密切的关系，这一关系可以由理想气体状态方程来描述。

理想气体状态方程表达了一个理想气体的状态，其形式为PV = nRT。

其中，P表示气体的压强，V表示气体所占容积，n为气体的物质量，R为气体常数，T表示气体的温度。

这个方程说明了气体的压强与温度成正比关系。

根据理想气体状态方程的形式，可以推导出气体的压强与温度关系式。

以下是根据理想气体状态方程推导出的气体的压强与温度关系式：P1 / T1 = P2 / T2其中，P1和T1分别为初始状态下气体的压强和温度，P2和T2分别为最终状态下气体的压强和温度。

这个关系式表明了气体的压强与温度成正比关系。

当温度升高时，气体的分子动能增加，碰撞容器壁的频率和冲击力增大，从而导致气体的压强增加。

反之，当温度下降时，气体分子动能减小，碰撞容器壁的频率和冲击力减小，导致气体的压强下降。

实际气体在高压和低温条件下无法符合理想气体状态方程，因此需要引入修正因子来考虑实际气体的非理想性。

修正因子通常表示为Z，当Z等于1时，气体可以近似看作理想气体，当Z不等于1时，气体呈现出非理想性。

在实际气体中，Z的值通常会随着温度和压强的变化而变化。

气体的压强与温度关系在实际应用中有重要的意义。

例如，在工业生产中，高温高压气体常用于驱动设备和进行化学反应。

了解气体的压强与温度关系，可以帮助我们合理控制温度和压强，确保设备和反应的正常运行。

总之，气体的压强与温度呈正比关系。

理解气体的压强与温度关系对于工业生产和科学研究具有重要意义。

通过研究和实践，我们能够更好地利用和控制气体的性质，为各个领域的发展做出贡献。

热力学中的理想气体热力学是研究热能与功以及它们与物质的关系的学科。

在热力学中，理想气体是一个重要的概念，它在很多领域都有广泛的应用。

本文将介绍理想气体的基本特性和应用，以及理想气体状态方程和热力学过程的研究。

一、理想气体的特性理想气体是热力学研究中经常使用的一个模型，它有以下几个基本特性：1. 分子无相互作用：理想气体的分子之间几乎没有相互作用力，它们之间只存在碰撞。

分子间的相互作用力可以被忽略不计。

2. 分子数量无限：理想气体的分子数量非常大，可以近似认为是无限大，从而可以应用统计物理学的方法进行分析。

3. 分子质量无限小：理想气体的分子质量非常小，可以认为是零。

这种假设使得理想气体的分子在碰撞时无能量损失。

4. 完全弹性碰撞：理想气体的分子之间碰撞是完全弹性碰撞，即碰撞前后分子的动能守恒。

二、理想气体状态方程理想气体状态方程是描述理想气体物态变化的方程式，以压强P、体积V、温度T为变量，可以表示为以下三种形式：1. 爱尔金方程：P V = n R T，其中P为气体的压强，V为气体的体积，n为气体的摩尔数，R为气体常数，T为气体的温度。

2. 克拉珀龙方程：P V^γ = C，其中γ为气体的绝热指数，C为常数。

绝热过程是指在无热量交换的情况下，气体发生的压强和体积变化。

3. 波义耳－马略特定律：P/T = C，其中P为气体的压强，T为气体的温度，C为常数。

这个定律说明，在恒定摩尔数的情况下，气体的压强与温度成正比。

根据不同的条件和问题，可以选择不同的理想气体状态方程进行研究和计算。

三、理想气体的热力学过程在热力学中，理想气体的热力学过程是指气体在不同温度和压力下发生的变化。

常见的热力学过程包括等温过程、等压过程、等容过程和绝热过程。

1. 等温过程：在等温过程中，气体的温度保持不变，即T = 常数。

根据爱尔金方程，可以得到PV = 常数。

在等温过程中，气体的压强和体积成反比。

2. 等压过程：在等压过程中，气体的压强保持不变，即P = 常数。