下载文档原格式
2.11 有理数的乘方1．(－3) 4表示 ( )A ．4个(－3)相乘的积B ．－3乘4的积C ．3个(－4)相乘的积D ．4个(－3)相加的和2．若x =2，则318x 的值是 ( ) A ．12B ．1C ．4D ．8 3．下列对于a n 的读法：①a 的n 次幂；②n 个a 相乘；③a 的n 次方；④n 个a 相加；⑤以a 为底，n 为指数．其中正确的有 ( )A ．1种B ．2种C ．3种D ．4种4．若0<x <1，则x ，x 2，x 3的大小关系是 ( )A ．x <x 2<x 3B ． x 2<x 3<xC ． x 3 <x 2< xD ．x < x 3< x 25．下列各组数：①－52与(－5) 2；②(－3) 3与－33；③－(－0．3) 5与0．35；④0100与0200； ⑤(－1) 3与(－1) 2．其中相等的有 ( )A ．1组B ．2组C ．3组D ．4组6．a 为有理数，则下列说法中，正确的是 ( )A ．a >0B ．a 2－1>0C ．a 2+1>0D ．a 3+1>07．若有理数a >b ，则a 2和b 2的大小关系是 ( )A ．a 2>b 2B ．a 2<b 2C ．a 2≥b 2D ．不能确定8．若2(2)30a b -++=，则2009()a b +的值是 ( ) A ．0 B ．1 C ．－1 D ．20099．(－2) 3读作____________，－23读作__________________．10．计算：(－5) 4=__________；－54=__________；323⎛⎫- ⎪⎝⎭=__________． 11．把(－4．8)×(－4．8)×(－4．8)×(－4．8)写成乘方运算的形式是__________．12．现规定一种运算“*”：a *b =a b ，如3*2=32=9，则12*3=____________． 13．计算：(1)(－3) 3； (2)－0．12； (3)327⎛⎫ ⎪⎝⎭； (4)225； (5)－(－2) 2； (6)35-．14．计算：(1)3293⎛⎫-⨯ ⎪⎝⎭；(2)－23÷(－3) 2；(3)()()32111414⎛⎫-⨯-÷- ⎪⎝⎭；(4)(－2) 2－(－3) 3+42－(－5) 2．15．计算： (1)3112⎛⎫- ⎪⎝⎭；(2)－32×(－2)2；(3)222233⎛⎫⎛⎫⨯- ⎪ ⎪⎝⎭⎝⎭；(4)(－2) 2－(－1) 2；(5)(－1)2007－(－1) 2008+(－1) 2009； (6)233228----+．16．计算：31=________，32=_________，32=_________，34=_________，35=_______，36=_________……根据上面的计算结果，你能知道32009的个位数字是多少吗?参考答案1．A 2．B 3．D 4．A 5．C 6．C 7．D 8．C9．负2的3次方 负的2的3次方10．625 －625 －827 11．(－4．8) 412．1813．(1)－27 (2)－0．01 (3)8343 (4)45 (5)－4 (6)125 14．(1)－83 (2)－89 (3)14(4)22 15．(1)－278 (2)－36 (3)1681(4)3 (5) －1 (6)11 16．3 9 27 81 243 729 32009的个位数字是3。
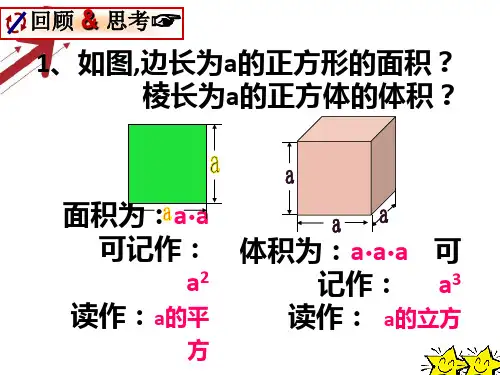
有理数的乘方1．乘方的意义(1)乘方的定义求n个相同因数a 的积的运算叫做乘方，乘方的结果叫做幂．如图，a 叫做底数，n 叫做指数，a n 读作：a 的n 次幂(a 的n 次方)． 乘方是一种特殊的乘法运算(因数相同)，幂是乘方运算的结果；乘方的底数是相同因数，指数是相同因数的个数．(2)乘方的意义a n 表示n 个a 相乘．即a n ＝n aa a a a ⨯⨯⨯⋯⨯个.如：(－2)3＝(－2)×(－2)×(－2)表示3个(－2)相乘．释疑点 (－a )n 与－a n 的区别①(－a )n 表示n 个－a 相乘，底数是－a ，指数是n ，读作：－a 的n 次方；②－a n 表示n 个a 乘积的相反数，底数是a ，指数是n ，读作：a 的n 次方的相反数．如：(－3)3底数是－3，指数是3，读作负3的3次方，表示3个(－3)相乘．(－3)3＝(－3)×(－3)×(－3)＝－27.－33底数是3，指数是3，读作3的3次方的相反数．－33＝－(3×3×3)＝－27.(3)乘方的书写①一个数可以看成这个数本身的一次方．如5就是51，通常指数1省略不写．②负数或分数做底数时，应用括号把负数或分数括起来，再在其右上角写指数，指数应写小一点．如(－1)2不能写成－12，⎝⎛⎭⎫322不能写成322. 【例1】 填空：(1)式子(－1.2)10表示__________，其中底数是__________，指数是__________．(2)120137111777⎛⎫- ⎪⎝⎭⎛⎫⎛⎫⎛⎫-⨯-⨯⋯⨯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭个写成乘方的形式是__________，读作__________． 解析：(1)乘方表示几个相同因数的积，相同的因数是底数，指数即相同因数的个数；(2)把n 个相同因数的积写成乘方的形式，相同因数写成底数，本题中⎝⎛⎭⎫－17是底数，相同因数的个数2 013写成指数．答案：(1)10个－1.2相乘 －1.2 10(2)⎝⎛⎭⎫－17 2 013 负17的2 013次幂⎝⎛⎭⎫或负17的2 013次方 2．乘方运算的符号法则乘方运算的符号法则乘方运算就是根据乘方的意义把它转化为乘法进行计算．如：33＝3×3×3＝27. ①正数的任何次幂都是正数；②负数的奇次幂是负数；③负数的偶次幂是正数；④0的奇次幂、偶次幂都是0.任何一个有理数的偶次幂都是非负数，即a 2n ≥0(n 为正整数)；若用n 表示正整数，则2n 表示偶数，而用(2n ＋1)表示奇数，则(－1)2n ＝1，(－1)2n ＋1＝－1.【例2】 下列说法不正确的是( )．A ．(－2)2 013是负数B ．－4200是正数C ．0的任何次幂(指数不为0)都等于它本身D ．－1的38次幂等于它的相反数解析：－4200表示4的200次方的相反数，是负数，故B 错误．答案：B3．有理数乘方的运算乘方运算的方法如下：与有理数的加、减、乘、除四种运算一样，有理数的乘方也是一种运算，其运算的方法是：①确定幂的符号；②进行乘法的运算．析规律 对于乘方的理解①乘方是一种运算，是特殊的乘法(因数相同的乘法运算)，幂是乘方运算的结果． ②因为a n 表示n 个a 相乘，所以可以利用有理数的乘法进行乘方运算，即将乘方转化成乘法运算．4．绝对值与乘方非负性的综合运用(1)平方、立方及平方的非负性在a n 中，若n ＝2，则为a 2，读作a 的2次幂，也读作a 的平方；当n ＝3时，a 3可读作a 的3次方，也可读作a 的立方．平方、立方是乘方中最常见的．①根据乘方与乘法的关系可知：正数的平方是正数，负数的平方也是正数，0的平方等于0.也就是任何一个有理数的平方都是非负数．②平方等于它本身的数：0,1；立方等于它本身的数：0,1，－1.(2)绝对值的非负性任何一个数的绝对值都是非负数，即|a |≥0.(3)非负数的性质性质：若几个非负数的和等于0，则这几个非负数都等于0.比如：若|a |＋b 2＝0，则a ＝0，且b ＝0.__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________【例3】 计算：(1)(－2)4；(2)－34；(3)⎝⎛⎭⎫453；(4)⎝⎛⎭⎫－1232；(5)－472；(6)(－1)2 014. 分析：根据乘方的意义和符号法则求解．(1)(－2)4表示4个(－2)相乘；(2)－34表示34的相反数；(3)⎝⎛⎭⎫453表示3个45相乘；(4)⎝⎛⎭⎫－1232表示2个⎝⎛⎭⎫－53相乘；(5)－472表示4除以7的2次方的相反数；(6)(－1)2 014表示2 014个(－1)相乘．解：(1)(－2)4＝(－2)×(－2)×(－2)×(－2)＝16；(2)－34＝－(3×3×3×3)＝－81；(3)⎝⎛⎭⎫453＝45×45×45＝64125； (4)⎝⎛⎭⎫－1232＝⎝⎛⎭⎫－53×⎝⎛⎭⎫－53＝259； (5)－472＝－47×7＝－449； (6)(－1)2 014＝()()()()20141111--⨯-⨯⋯⨯-个＝1.【例4－1】 下列说法正确的有( )．①负数的平方是负数；②正数的平方是正数；③平方是它本身的数是0和1；④1的立方等于它本身；⑤－1的平方等于它的倒数；⑥任何一个有理数的平方都是非负数．A ．3个B ．4个C ．5个D ．2个解析：① × 乘方是特殊的乘法运算，两数相乘，同号得正，异号得负，故①，②都为正数② √ ③ √ 0的平方等于0,1的平方等于1④ √ 1的立方是1⑤ × －1的平方是1，－1的倒数是－1，所以不相等⑥ √ 0的平方是0，正数和负数的平方都是正数答案：B【例4－2】 若x ，y 为有理数，且(5－x )4＋|y ＋5|＝0，则⎝⎛⎭⎫x y 2 013的值为( )．A ．1B ．－1C ．2D ．－2解析：因为(5－x )4和|y ＋5|都是非负数，且(5－x )4＋|y ＋5|＝0，所以由非负数的性质得(5－x )4＝0，|y ＋5|＝0，即5－x ＝0，y ＋5＝0.解得x ＝5，y ＝－5.所以⎝⎛⎭⎫x y 2 013＝⎝ ⎛⎭⎪⎫5－5 2 013＝(－1)2 013＝－1.故选B. 答案：B5．有理数乘方规律探究及应用(1)有理数乘方规律探究①观察给出的一组数字或式子，分析所包含的乘方运算，结合连续偶数、连续奇数等知识，探究其中的规律．②根据其规律，按要求进行计算或解答．(2)乘方的应用生活中乘方的应用主要是裂变和对折．①裂变：将某一物体一分二、二分四、四分八、八分十六……像这样以倍增的速度发生变化就是裂变．裂变规律：裂变一次即原来的数量乘21，裂变两次乘22，裂变三次乘23，…，裂变n 次乘2n .②对折：一张纸对折，对折次数与纸的层数、折痕数、单层纸占整张纸的面积比例之间次数 1 2 3 … n层数 2 4 8 … 2n折痕数 1 3 7 … 2n －1单面占 的比例12 14 18 … 12n 【例5－1】 (只有数码0和1)，它们两者之间可以互相换算，如将(101)2，(1011)2换算成十进制数应为：(101)2＝1×22＋0×21＋1×20＝4＋0＋1＝5；(1011)2＝1×23＋0×22＋1×21＋1×20＝11.按此方式，将二进制(1001)2换算成十进制数的结果是__________．(说明：20＝1)解析：从例子中可以看出，把二进制数转换成十进制数要通过乘方运算．二进制数的进率是2，右边第一位数字0或1就是十进制中的0或1，右边第二数位代表21，右边第三位代表22，右边第四位代表23，依此类推，相加即可转化为十进制数．所以(1001)2＝1×23＋0×22＋0×21＋1×20＝8＋0＋0＋1＝9.答案：9【例5－2】 面积是128平方分米的一张纸片，第一次剪去一半，第二次剪去剩下的一半，第三次再将剩下的一半剪去，…，如此下去，剪完第6次后剩下的面积还有多少平方分米？分析：解：128×⎝⎛⎭⎫126＝128×164＝2(平方分米)． 答：剪完第6次后剩下的面积还有2平方分米．。
2.11 有理数的乘方1．有理数乘方的概念(1)乘方的意义：一般地，n 个相同的因数a 相乘：，记作a n ，即＝a n ，这种求几个相同因数的积的运算，叫做乘方，乘方的结果叫做幂．在a n 中，a 叫做底数，n 叫做指数，a n 读作a 的n 次方(或a 的n 次幂)．(2)乘方的表示方法(3)学习乘方的意义，需要注意的几个方面：①注意乘方的双重含义乘方指的是求几个相同因数的积的运算，其结果叫做幂．由此不难发现，乘方具有双重含义：一是乘方表示一种运算；二是乘方表示一种特殊的乘法运算的结果．如25中，25可以看成一种运算，表示有5个2相乘，即25＝2×2×2×2×2，这时，25应读作2的五次方；另一方面，25又可看成5个2相乘的结果，即2×2×2×2×2＝25，这时25却读作2的5次幂；②注意乘方底数的书写格式乘方的书写一定要规范，不然会引起误会．当底数是负数或分数时，一定要记住添上括号，以体现底数是负数或分数的整体性．如(－3)×(－3)×(－3)×(－3)应记作(－3)4，不能记作－34.(－3)4与－34表示的意义和结果完全不同．前者表示4个－3相乘，结果为81；后者为4个3相乘的积的相反数，结果为－81.再如54×54×54×54×54×54应记作⎝⎛⎭⎫546，不能记作564； ③一个数可以看成这个数本身的一次方，如3就是31，a 就是a 1，只是指数1通常省略不写；④a n 与－a n 的区别：ⅰ.a n 表示n 个a 相乘，底数是a ，指数是n ，读作：a 的n 次方．ⅱ.－a n 表示n 个a 乘积的相反数，底数是a ，指数是n ，读作：a 的n 次方的相反数．如：(－3)3底数是－3，指数是3，读作－3的3次方，表示3个－3相乘，(－3)3＝(－3)×(－3)×(－3)＝－27.－33底数是3，指数是3，读作3的3次方的相反数．－33＝－(3×3×3)＝－27.所以(－3)3与－33的结果虽然都是－27，但表示的含义并不同． ⑤注意乘方运算的转化．计算乘方运算的结果时，应将乘方运算转化为乘法运算来完成．如计算(－5)3时，应将它转化为计算(－5)×(－5)×(－5)的积；再如计算⎝⎛⎭⎫124时，应将它转化为计算12×12×12×12的积． 【例1】 把下列各式写成乘方的形式，并指出底数，指数各是什么？(1)(－8.3)×(－8.3)×(－8.3)×(－8.3)×(－8.3)；(2)25×25×25×25； (3)a ×a ×a ×…×a (2 011个a )．分析：以上三题都是相同因数相乘，可用乘方的形式表示，相同因数为底数，相同因数的个数为指数，指数写在右上角．解：(1)(－8.3)×(－8.3)×(－8.3)×(－8.3)×(－8.3)＝(－8.3)5；(2)25×25×25×25＝⎝⎛⎭⎫254； (3)a ×a ×a ×…×a (2 011个a )＝a 2 011.警误区 书写乘方的注意事项 当底数是负数或分数时，写成乘方的形式时，底数一定要加上括号，如(1)，(2)两题．2．乘方运算的符号法则(1)有理数乘方的符号法则：①正数的任何次幂是正数；②负数的偶次幂是正数，奇次幂是负数；③0的任何次幂等于0；1的任何次幂等于1.(2)根据乘方的符号法则和乘方运算的转化，关于乘方有如下几个性质：①0的任何正整数次幂都是0；互为相反数的偶次幂相等；互为相反数的奇次幂互为相反数．如0n ＝0(n 是正整数)；(－4)6＝46；(－4)3＝－43.②进行乘方运算时与其他运算一样，先要确定符号，再计算出绝对值，同时还应注意(－a )2n ＝a 2n ，(－a )2n ＋1＝－a 2n ＋1(n 是正整数)，由乘方的法则我们还知道：a 2n ≥0，即任何有理数的偶次幂是非负数．谈重点 决定乘方结果的符号的因素 有理数乘方结果的符号取决于：一底数的符号，二指数的奇偶．【例2】 利用有理数乘方运算的符号法则计算：(1)(－3)2；(2)1.53；(3)⎝⎛⎭⎫－434；(4)(－1)11； (5)(－1)2；(6)(－1)2n ；(7)(－1)2n －1.分析：根据有理数乘方的符号法则：(2)正数的任何次幂都是正数，(1)(3)(5)(6)是负数的偶次幂，结果为正；(4)(7)是负数的奇次幂，结果为负．解：(1)(－3)2＝3×3＝9；(2)1.53＝1.5×1.5×1.5＝3.375；(3)⎝⎛⎭⎫－434＝43×43×43×43＝25681； (4)(－1)11＝－1；(5)(－1)2＝1；(6)(－1)2n ＝1；(7)(－1)2n －1＝－1.3．有理数乘方的运算有理数乘方运算的思路：确定幂的符号；确定幂的绝对值．有理数的乘方是一种特殊的乘法运算——因数相同的乘法运算，幂是乘方运算的结果． 因此有理数的乘方运算可以转化为乘法来运算，先根据有理数乘方的符号法则确定幂的符号，再根据乘方的意义把乘方转化为乘法，来运算幂的绝对值，最后得出幂的结果．例如计算(－5)3，先确定幂的符号为“－”号，再计算53＝125，即(－5)3＝－125；再如，计算(－2)×32时，先算32＝9，再算(－2)×9＝－18.正确理解有理数乘方的意义是进行乘方运算的前提，千万不能把底数与指数直接相乘． 在进行有理数的乘方运算时要辨别清楚底数和指数，以及符号问题，避免出错．【例3－1】 计算：(1)－33；(2)(－2)2；(3)(－3×2)3；(4)－(－2)3.分析：运算时，先确定符号，再计算乘方．(1)负号在幂的前面，结果是负数；(2)负数的偶次幂，结果是正数；(3)先计算底数－3×2＝－6，再计算(－6)3；(4)先计算(－2)3，其结果是负数，再加上前面的负号，最后结果是正数．解：(1)－33＝－(3×3×3)＝－27；(2)(－2)2＝4；(3)(－3×2)3＝(－6)3＝－216；(4)－(－2)3＝－(－8)＝8.警误区勿把底数乘指数在进行乘方运算时，一定要避免出现把底数与指数直接相乘的运算错误．如－33＝－(3×3)＝－9，这是由于没有理解乘方的意义导致的．【例3－2】计算(－0.25)10×412的值．分析：直接求(－0.25)10和412比较麻烦，但仔细观察可以发现(－0.25)10＝0.2510，表示10个0.25相乘，而412表示12个4相乘，这就提醒我们利用乘法的交换律和结合律，比较容易求出结果．解：(－0.25)10×412＝(0.25)10×412＝[(0.25)10×410]×42＝(0.25×4)10×42＝1×16＝16.4.有理数乘方运算的应用有理数的乘方运算在现实生活中有广泛的应用，给生活中经常出现的大数的读写带来了极大的方便．现代高科技技术离不开数学技术，数学也是一门神奇的艺术，它那神奇的力量常常让人感到意外和惊奇！比如，一层楼高约3米，一张纸的厚度只有0.1毫米，0.1毫米与3米相比几乎可以忽略不计，如果我们将纸对折、再对折，如此这样对折20次后，其厚度将比30层楼房还要高，这就是有理数乘方的神奇魔力，在现实生活中有着很广泛的应用．数学是一门规律性很强的学科，只要掌握了它的规律，很多问题都可以迎刃而解了，乘方的规律也不例外．同学们要认真思考，仔细观察找到有理数乘方应用的规律．【例4】“兰州拉面”在学校门口开了一个连锁店，今天开张，做拉面的张师傅站在门口进行广告宣传，当众拉起了拉面．他精湛的拉面技术赢得了围观顾客的阵阵喝彩，吃面的人更是络绎不绝．张师傅先是用一根直径约13厘米的粗面条，把两头捏起来拉长，然后再把两头捏起来拉长，不断地这样，张师傅共拉了10次，在他手里出现了一根根直径约0.1毫米的细面条．算一算：张师傅拉10次共拉出了多少根细面条？若拉n次呢？(请把探索的结果填入下表中)分析：第一次拉出2＝2根，第二次拉出2＝4根，第三次拉出2＝8根，所以第n次拉出2n根．解：拉面的根数与拉面的次数n有关系，拉面的根数＝2n.面条根数248163264...2 (2)5．与乘方相关的探究题探究题是近几年中考中的亮点，渗透多个知识点，形式多样．解题时，一般遵循从特殊到一般的探究思路，先准确计算几个特例的结果，再通过对这些结果的分析、归纳得到一个较一般的结论，最后再应用这个结论解决问题．由于乘方是一种新运算，它是一种特殊的乘法，特殊在因数相同，是同学们新接触的运算，所以解决问题时要注意，当底数是分数或负数时，写成幂时底数要加括号．与有理数的乘方有关的探究题主要有以下几种：(1)个位数字是几，在中考中经常涉及到，例如3n 的个位数字是3,9,7,1,3,9,7,1，…依次循环；(2)拉面的条数、折纸的张数、握手的次数、绳子的长度、细胞分裂的个数等，都利用2n 或⎝⎛⎭⎫12n 求解．【例5－1】 有一张厚度是0.1毫米的纸，将它对折1次后，厚度为2×0.1毫米．(1)对折2次后，厚度为多少毫米？(2)对折20次后，厚度为多少毫米？ 分析：此题的关键是将纸的层数化为幂的形式，找出对应关系．根据问题容易得到当对折两次后厚度为4×0.1＝22×0.1毫米，对折3次后厚度变为8×0.1＝23×0.1毫米，对折4次是16×0.1＝24×0.1毫米，对折5次是32×0.1＝25×0.1毫米，……，从中探寻规律，解答问题．解：(1)0.1×22＝0.4(毫米)．(2)(220×0.1)毫米．【例5－2】 1米长的小棒，第1次截去一半，第2次截去剩下的一半，如此截下去，第7次后剩下的小棒有多少米长？分析：此题的关键是找出每次截完后，剩下的小棒占整根棒的比例与所截次数之间的关系．解：第7次后剩下的小棒有⎝⎛⎭⎫127×1＝1128(米)．。
