Bode图绘制例题

控制系统的开环频率特性目的：掌握开环Bode 图的绘制根据Bode 图确定最小相位系统的传递函数 重点：开环Bode 图的绘制、根据Bode 图确定最小相位系统的传递函数1 开环伯德图手工作图的一般步骤：1）将开环传递函数表示为时间常数表达形式，计算各个典型环节的交接频率2）求20lgK 的值，并明确积分环节的个数ν 3）通过（1,20lgK ）绘制斜率为-20vdB/dec 低频段 4）随着频率增加，每遇到一个典型环节的交接频率，就改变一次斜率最小相位系统定义： 递函数的零点、极点全部位于S 左半平面，同时又无纯滞后环节的系统称为最小相位系统。

否则就是非最小相位系统。

对数幅频特性与相频特性之间存在确定的对应关系。

对于一个最小相位系统，我们若知道了其幅频特性，它的相频特性也就唯一地确定了。

也就是说：只要知道其幅频特性，就能写出此最小相位系统所对应的传递函数，而无需再画出相频特性。

非最小相位系统高频时相角迟后大，起动性能差，响应缓慢。

对响应要求快的系统，不宜采用非最小相位元件。

2 典型环节的伯德图绘制曲线在MA TLAB 中实现，利用下述的程序段：num=[b2 b1 b0]; den=[1 a2 a1 a0]; H=tf(num,den); bode(H) margin(H) hold on2.1 比例环节传递函数：()G s K = 频率特性：()G j K ω=对数幅频特性：()20lg L j K ω= 对数相频特性：()0ϕω=程序段：num=[0 10]; den=[0 1]; H=tf(num,den); bode(H)margin(H) holdon结论：放大环节的对数幅频特性是一条幅值为20lgK 分贝，且平行于横轴的直线，相频特性是一条和横轴重合的直线。

K>1时，20lgK>0dB ；K<1时，20lgK<0dB 。

2.2 惯性环节（低通滤波特性）传递函数：1()1G s sτ=+频率特性：()()()j G j A e ϕωωω=对数幅频特性：21()20lg 1()L ωτω=+对数相频特性：()arctan ϕωτω=-绘制1()10.1G s s=+的Bode 图程序段：num=[0 1]; den=[0.1 1];H=tf(num,den); bode(H) margin(H) holdon结论：惯性环节的对数幅频特性可以用在1ωτ= 处相交于0分贝的两条渐近直线来近似表示：当1ωτ时，是一条0分贝的直线； 当1ωτ时，是一条斜率为-20dB/dec 的直线。

《自动控制原理》复习参考资料一、基本知识11、反馈控制又称偏差控制，其控制作用是通过输入量和反馈量的差值进行的。

2、闭环控制系统又称为反馈控制系统。

3、在经典控制理论中主要采用的数学模型是微分方程、传递函数、结构框图和信号流图。

4、自动控制系统按输入量的变化规律可分为恒值控制系统、随动控制系统和程序控制系统。

5、对自动控制系统的基本要求可以概括为三个方面，即：稳定性、快速性和准确性。

6、控制系统的数学模型，取决于系统结构和参数, 和外作用及初始条件无关。

7、两个传递函数分别为G1(s)和G2(s)的环节，以并联方式连接，其等效传递函数为G1(s)+G2(s)，以串联方式连接，其等效传递函数为G1(s)*G2(s)。

8、系统前向通道传递函数为G（s），其正反馈的传递函数为H（s），则其闭环传递函数为G（s）/(1- G（s）H（s）)。

9、单位负反馈系统的前向通道传递函数为G（s），则闭环传递函数为G（s）/(1+ G（s）)。

10、典型二阶系统中，ξ=0.707时，称该系统处于二阶工程最佳状态，此时超调量为4.3%。

11、使用劳斯判据判断系统稳定性，劳斯表中第一列数据全部为正数，则系统稳定。

12、线性系统稳定的充要条件是所有闭环特征方程的根的实部均为负，即都分布在S平面的左平面。

13、随动系统的稳态误差主要来源于给定信号，恒值系统的稳态误差主要来源于扰动信号。

14、对于有稳态误差的系统，在前向通道中串联比例积分环节，系统误差将变为零。

15、系统稳态误差分为给定稳态误差和扰动稳态误差两种。

16、对于一个有稳态误差的系统，增大系统增益则稳态误差将减小。

17、对于典型二阶系统，惯性时间常数T 愈大则系统的快速性愈差。

18、使用频域分析法，穿越频率越大，则对应时域指标t s 越小，即快速性越好19最小相位系统是指S 右半平面不存在系统的开环极点及开环零点。

20、按照校正装置在系统中的不同位置，系统校正可分为串联校正、反馈校正、 补偿校正和复合校正四种。

《自动控制原理》复习参考资料一、基本知识11、反馈控制又称偏差控制，其控制作用是通过输入量与反馈量的差值进行的。

2、闭环控制系统又称为反馈控制系统。

3、在经典控制理论中主要采用的数学模型是微分方程、传递函数、结构框图和信号流图。

4、自动控制系统按输入量的变化规律可分为恒值控制系统、随动控制系统与程序控制系统。

5、对自动控制系统的基本要求可以概括为三个方面，即：稳定性、快速性和准确性。

6、控制系统的数学模型，取决于系统结构和参数, 与外作用及初始条件无关。

7、两个传递函数分别为G1(s)与G2(s)的环节，以并联方式连接，其等效传递函数为G1(s)+G2(s)，以串联方式连接，其等效传递函数为G1(s)*G2(s)。

8、系统前向通道传递函数为G（s），其正反馈的传递函数为H（s），则其闭环传递函数为G（s）/(1- G（s）H（s）)。

9、单位负反馈系统的前向通道传递函数为G（s），则闭环传递函数为G（s）/(1+ G（s）)。

10、典型二阶系统中，ξ=0.707时，称该系统处于二阶工程最佳状态，此时超调量为4.3%。

11、应用劳斯判据判断系统稳定性，劳斯表中第一列数据全部为正数，则系统稳定。

12、线性系统稳定的充要条件是所有闭环特征方程的根的实部均为负，即都分布在S平面的左平面。

13、随动系统的稳态误差主要来源于给定信号，恒值系统的稳态误差主要来源于扰动信号。

14、对于有稳态误差的系统，在前向通道中串联比例积分环节，系统误差将变为零。

15、系统稳态误差分为给定稳态误差和扰动稳态误差两种。

16、对于一个有稳态误差的系统，增大系统增益则稳态误差将减小。

17、对于典型二阶系统，惯性时间常数T 愈大则系统的快速性愈差。

18、应用频域分析法，穿越频率越大，则对应时域指标t s 越小，即快速性越好19最小相位系统是指S 右半平面不存在系统的开环极点及开环零点。

20、按照校正装置在系统中的不同位置，系统校正可分为串联校正、反馈校正、 补偿校正与复合校正四种。

实验七 控制系统的Bode 图一 实验目的1．利用计算机作出控制系统的Bode 图2．观察记录控制系统得开环频率特性；3．控制系统得开环频率特性分析；二、实验步骤1．开机执行程序C ：＼matlab ＼bin ＼matlab.exe (或用鼠标双击图标)进人MATLAB 命令窗口;2．相关MATLAB 函数Bode(num,den)Bode(num,den,w) %w 极为频率变量ω[mag,phase,w]= Bode(num,den) %mag-相位，phase-幅角给定系统开环传递函数G 0(s) 多项式模型，作系统bode 图。

其计算公式为。

)()()(0s den s num s G = 式中， num 为开环传递函数G 0(s)的分子多项式系数向量，den 为开环传递函数G 0(s)的分母多项式系数向量。

函数格式1：给定num 、den 作波得图，角频率向量w 的范围自动设定。

函数格式2：角频率向量w 的范围可以由人工给定。

(w 为对数等分，由对数等分函数logsspacpce()完成．例如w ＝logspace(-1，1，100)。

函数格式3：返回变量格式。

计算所得的幅值mag 、相角Phase 及角频率w 返回至MA TLAB 命令窗口，不作图。

更详细的命令说明，可键入“help bode ”在线帮助查阅。

例如，系统的开环传递函数10210)()()(20++==s s s den s num s G 作图程序为：（分两次输入）num=[10];den=[1 2 10];bode(num,den); ％得到bode 图9-6 bode 图，注意横标。

再输入以下语句w=logspace(-1,1,32); ％执行后得到bode 图9-7 bode 图，注意横标。

bode(num,den,w);比较图9-6、图9-7的横坐标命令（人工定标）w ＝logspace(d1，d2，n) 将变量w 作对数等分。

实验三系统Bode图及Nyquist曲线的绘制1．实验的目的和要求1）加深了解系统及元件频率特性的物理概念；2）进一步加深对Bode图及Nyquist曲线的了解；3）熟练掌握用Matlab分析系统频率特性的方法。

2．实验内容1）系统的模拟电路原理图及系统的结构方框图分别如图5-1、5-2所示。

图5-1 系统的模拟电路原理图图5-2 系统的结构方框图2）绘制系统的Bode图及Nyquist曲线，并分析K对Bode图及Nyquist曲线的影响。

3．需用的仪器计算机、Matlab6.5编程软件4．实验步骤1）计算系统的开环传递函数；2）取R2=500K，绘制系统开环Bode图及Nyquist曲线；3）K取不同值，实验分析K对开环幅相曲线及Bode图的影响。

5．教学方式讲授与指导相结合6．实验报告要求1)、计算开环传函G k(s)=10s ×10.1s+1×K =10K0.1s2+s2）、取R2=500K，绘制Bode图和Nyquist图⑴、Simulink指令块Bode图:Nyquist图:3)、K取不同值，对开环幅相曲线及Bode图的影响⑴、K取不同值，对开环幅相曲线的影响程序：》y1=tf([50],[0.1,1,0]);y2=tf([100],[0.1,1,0]);y3=tf([200],[0.1,1,0]);nyquist(y1);set(findobj('Color','b'),'LineWidth',3)hold on;nyquist(y2);nyquist(y3);set(findobj('Color','r'),'LineWidth',6);grid;legend('k=5响应曲线','K=10响应曲线','K=20响应曲线'); title('李山 1206074118');图形：分析,φ(jw)=arctan(10w)得出，K的改变不会影响角度的由公式A(w)=|G(jw)|=10k0.01w4+w2变化，只会影响幅值。

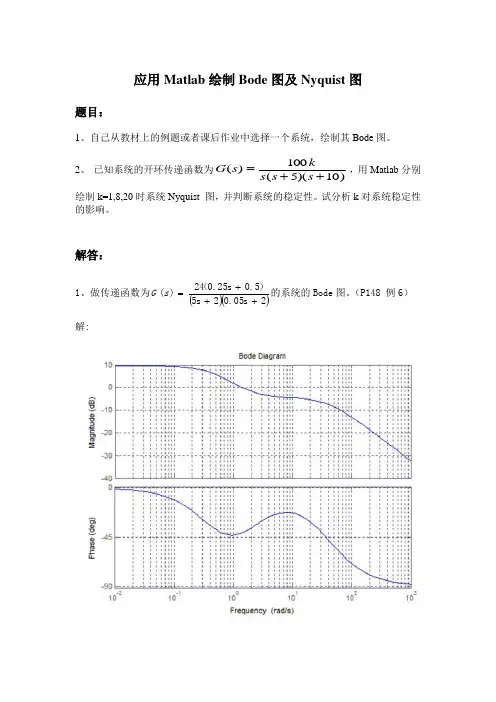
典型环节的B o d e图-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN控制系统的开环频率特性目的：掌握开环Bode图的绘制根据Bode图确定最小相位系统的传递函数重点：开环Bode图的绘制、根据Bode图确定最小相位系统的传递函数1 开环伯德图手工作图的一般步骤：1）将开环传递函数表示为时间常数表达形式，计算各个典型环节的交接频率2）求20lgK的值，并明确积分环节的个数ν3）通过（1,20lgK）绘制斜率为-20vdB/dec低频段4）随着频率增加，每遇到一个典型环节的交接频率，就改变一次斜率最小相位系统定义：递函数的零点、极点全部位于S 左半平面，同时又无纯滞后环节的系统称为最小相位系统。

否则就是非最小相位系统。

对数幅频特性与相频特性之间存在确定的对应关系。

对于一个最小相位系统，我们若知道了其幅频特性，它的相频特性也就唯一地确定了。

也就是说：只要知道其幅频特性，就能写出此最小相位系统所对应的传递函数，而无需再画出相频特性。

非最小相位系统高频时相角迟后大，起动性能差，响应缓慢。

对响应要求快的系统，不宜采用非最小相位元件。

2 典型环节的伯德图绘制曲线在MATLAB中实现，利用下述的程序段：num=[b2 b1 b0];den=[1 a2 a1 a0];H=tf(num,den);bode(H)margin(H)hold on比例环节传递函数：()G s K=频率特性：()G j Kω=对数幅频特性：()20lgL j Kω=对数相频特性：()0ϕω=程序段：num=[0 10]; den=[0 1]; H=tf(num,den);bode(H)margin(H) hold on结论：放大环节的对数幅频特性是一条幅值为20lgK分贝，且平行于横轴的直线，相频特性是一条和横轴重合的直线。

K>1时，20lgK>0dB；K<1时，20lgK<0dB。

Matlab中Bode图的绘制技巧我们经常会遇到使用Matlab画伯德图的情况，可能我们我们都知道bode这个函数是用来画bode图的，这个函数是Matlab内部提供的一个函数，我们可以很方便的用它来画伯德图，但是对于初学者来说，可能用起来就没有那么方便了。

譬如我们要画出下面这个传递函数的伯德图：1.576e010 s^2H(s)=------------------------------------------------------------------------------------------s^4 + 1.775e005 s^3 + 1.579e010 s^2 + 2.804e012 s + 2.494e014(这是一个用butter函数产生的2阶的，频率范围为[20 20K]HZ的带通滤波器。

)我们可以用下面的语句：num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den);bode(H)这样，我们就可以得到以下的伯德图：可能我们会对这个图很不满意，第一，它的横坐标是rad/s，而我们一般希望横坐标是HZ；第二，横坐标的范围让我们看起来很不爽；第三，网格没有打开（这点当然我们可以通过在后面加上grid on解决）。

下面，我们来看看如何定制我们自己的伯德图风格：在命令窗口中输入：bodeoptions我们可以看到以下内容：ans =Title: [1x1 struct]XLabel: [1x1 struct]YLabel: [1x1 struct]TickLabel: [1x1 struct]Grid: 'off'XLim: {[1 10]}XLimMode: {'auto'}YLim: {[1 10]}YLimMode: {'auto'}IOGrouping: 'none'InputLabels: [1x1 struct]OutputLabels: [1x1 struct]InputVisible: {'on'}OutputVisible: {'on'}FreqUnits: 'rad/sec'FreqScale: 'log'MagUnits: 'dB'MagScale: 'linear'MagVisible: 'on'MagLowerLimMode: 'auto'MagLowerLim: 0PhaseUnits: 'deg'PhaseVisible: 'on'PhaseWrapping: 'off'PhaseMatching: 'off'PhaseMatchingFreq: 0PhaseMatchingValue: 0我们可以通过修改上面的每一项修改伯德图的风格，比如我们使用下面的语句画我们的伯德图：P=bodeoptions;P.Grid='on';P.XLim={[10 40000]};P.XLimMode={'manual'};P.FreqUnits='HZ';num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den);bode(H,P)这时，我们将会看到以下的伯德图：上面这张图相对就比较好了，它的横坐标单位是HZ，范围是[10 40K]HZ，而且打开了网格，便于我们观察-3DB处的频率值。