Matlab中Bode图的绘制技巧
- 格式:doc
- 大小:115.50 KB
- 文档页数:5

matlab画幅频响应和相频响应
要使用MATLAB绘制系统的幅频响应和相频响应,可以按照以下步骤进行:
1. 定义系统传递函数或频率响应函数。
假设你有一个系统的传递函数H(s),可以使用MATLAB的`tf`函数定义传递函数。
例如,假设传递函数为H(s) = (s+1)/(s^2+2s+3),可以使用以下代码定义传递函数:
matlab
num = [1 1];
den = [1 2 3];
H = tf(num, den);
2. 绘制幅频响应。
使用MATLAB的`bode`函数可以绘制系统的幅频响应曲线。
以下代码演示如何绘制幅频响应曲线:
matlab
bode(H);
这将绘制出系统的幅频响应曲线,并显示频率范围和幅度值。
3. 绘制相频响应。
使用MATLAB的`bode`函数的输出参数可以获取系统的相频响应数据。
以下代码演示如何获取相频响应数据并绘制相频响应曲线:
matlab
[mag, phase, wout] = bode(H);
semilogx(wout, squeeze(phase));
这将绘制出系统的相频响应曲线,并显示频率范围和相位值。
以上是基本的步骤,你可以根据实际需求和系统的特点进行相应的修改和调整。

红河学院工学院实验报告单
《机械工程控制基础》Matlab 仿真实验报告单
课程名称:
姓名:
日期:
成绩:
年级专业: 学号: 实验场地:
实验序号: 4
实验名称:控制系统Bode 图的Matlab 实验
一、实验内容。
已知控制系统开环传递函数,绘制开环传递函数Bode 图,。
1000()(1)(2)(5)
K G s s s s =
+++ 二、实验目的。
1、熟悉Matlab 操作
2、掌握Matlab 中,绘制传递函数的Bode 图。
三、相关Matlab 仿真程序。
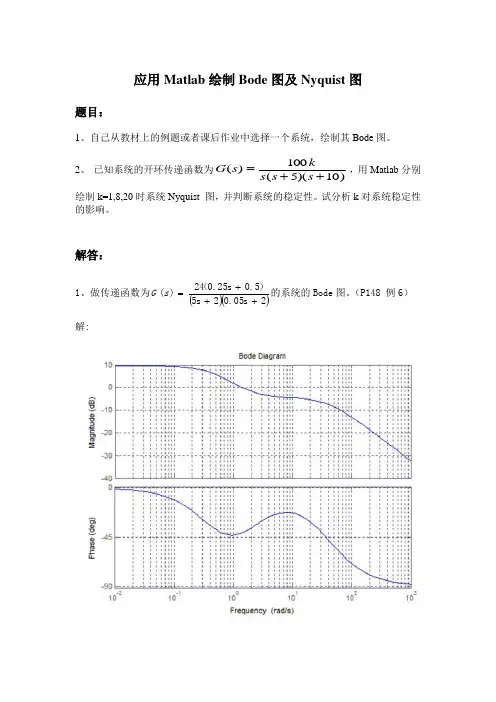
已知控制系统开环传递函数,绘制开环传递函数Bode 图。
1000()(1)(2)(5)
K G s s s s =+++
相关程序:
clear
num=1000;
den=conv([1 1],conv([1 2],[1 5]));
GKs=tf(num,den)
w=logspace(-2,3,100);
bode(GKs,w);
grid on
margin(GKs)
四、相关Matlab仿真图形。
五、判断系统稳定性,并说明理由。
幅值裕度的值为-18dB
相位裕度的值为-44.4deg
剪切频率 4.12rad/sec
相位穿越频率9.51rad/sec
从图形中可以看出来,剪切频率大于相位穿越频率,又因为其开环传递是最小相位系统,所以其闭环系统不稳定。
另一方面,幅值裕度和相位裕度都为负值,也证明其闭环系统不稳定。
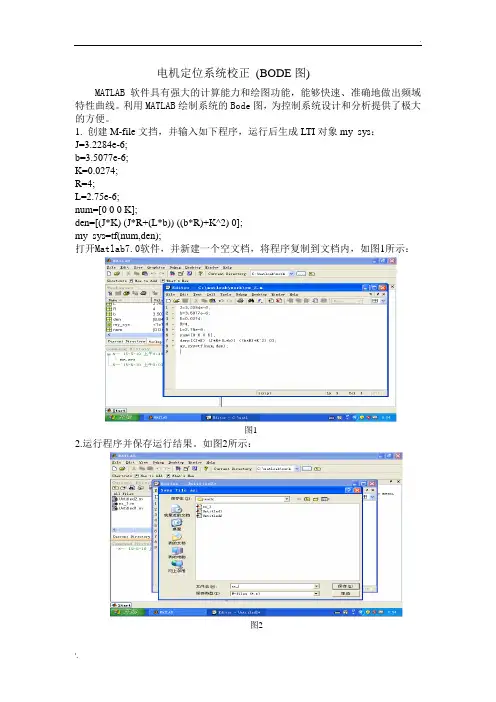
电机定位系统校正(BODE图)MATLAB软件具有强大的计算能力和绘图功能,能够快速、准确地做出频域特性曲线。
利用MATLAB绘制系统的Bode图,为控制系统设计和分析提供了极大的方便。
1. 创建M-file文挡,并输入如下程序,运行后生成LTI对象my_sys:J=3.2284e-6;b=3.5077e-6;K=0.0274;R=4;L=2.75e-6;num=[0 0 0 K];den=[(J*K) (J*R+(L*b)) ((b*R)+K^2) 0];my_sys=tf(num,den);打开Matlab7.0软件,并新建一个空文档,将程序复制到文档内,如图1所示:图12.运行程序并保存运行结果。
如图2所示:图23.打开Start-Toolboxes—Control System—SISO Design Tool。
启动SISO Design,如图3所示图34.将my_sys程序导入到SISO Design Tool中,如图4所示图45.在View菜单中,关闭根轨迹显示,只显示开环的Bode图。
如图5所示图56. 加积分环节;加零点(60角频率)将各个参数进行积分:空白处右键—Add Pole/Zero—Integrator。
如图6所示:图67.在magnitude曲线加零点,然后Analysis菜单下Response to Step Command 指令。
如图7所示:图78.在管理反馈界面中,只显示闭环的r与y的关系—LT1 Viewer For SISO Design Tool界面空白处右键—Systems—Closed Loop :r to u (green),如图8所示:图89.添加零点和极点,如图8所示,并移动极点、零点和线的位置,调整LT1 Viewer For SISO Design Tool窗口中函数图像的变化直到符合Bode图,如图9所示:图910.用鼠标上下移动观察阶越响应的超调量变化,满足校正要求。



用Matlab/Simulink画波特图Bode图在Matlab中,大多时候,我们都是用M语言,输入系统的传递函数后,用bode函数绘制bode图对系统进行频率分析,这样做,本人觉得效率远不如Simulink建模高。
如何在Matlab/Simulink中画bode图,以前也在网上查过些资料,没看到太多有用的参考。
今天做助教课的仿真,又要画电机控制中电流环的bode图,模型已经建好,step response也很容易看出来,可这bode图怎么也出不来,又不愿意用m语言写出传递函数再画。
baidu和google了好一阵,几乎没有一个帖子说的清清楚楚的,经过一番摸索,终于掌握了Simulink里画bode图的方法。
.其实,Simulink里画bode图,非常的easy,也很方便。
写此文的目的是希望对那些常用Simulink进行仿真希望画bode图又不愿用M语言的新手有所帮助。
以下均是以Matlab R2008a为例。
首先,在simulink里建好model。
如图1,这里需要注意的是,输入和输出要用input port和output port,这样以后画bode图的时候,系统就会知道是这两个变量之间的关系。
图1 建好model其次,选择线性分析。
Tools->Control Design ->Linear Analysis。
如图2。
图2 选择Linear Ansysis将出现如图3所示的Control and Estimation Tools Manager窗口。
图3 Control and Estimation Tools Manager窗口第三步,激动人心的时刻到了,哈哈。
如果你是按照前面的步骤来的,那么这时候,你就应该可以直接画出bode图,在窗口的下方,将“Plot linear analysis result in a ”前面的方框打上勾,已打的就不用管了,再在后面的下拉框里选择“bode response plot”,即画output port和input port之间的bode图,再点击“Linearize Model”按钮,就OK了。

在MATLAB中,使用Bode图来分析系统的频率响应时,指数函数可能用于描述频率的幂次。
Bode图是一种图表示方法,用于显示系统的频率响应特性,包括幅频特性和相频特性。
在MATLAB中绘制Bode图时,可以使用bode函数来计算并绘制系统的频率响应。
该函数可以绘制幅频图和相频图,其中幅频图显示了系统在不同频率下的增益或幅度,而相频图显示了系统在不同频率下的相位延迟。
在描述频率响应时,可以使用指数函数来表示增益或相位的变化。
例如,可以使用形如A * exp(-alpha *
w)的指数函数来描述频率响应的幅度,其中A是常数,alpha是衰减系数,w是角频率。
类似地,可以使用形如phase_shift + alpha * w的指数函数来描述相位延迟。
在MATLAB中,可以使用exp函数来计算指数函数。
例如,要计算exp(-alpha * w),可以使用以下代码:matlab复制代码
w = 0:0.01:10; % 生成频率向量
alpha = 1; % 衰减系数
A = 1; % 常数
y = A * exp(-alpha * w); % 计算幅值
类似地,可以使用以下代码计算相位延迟:
matlab复制代码
phase_shift = 0; % 相位偏移量
y = phase_shift + alpha * w; % 计算相位延迟
然后,可以使用bode函数将计算得到的幅值或相位绘制成Bode图:
matlab复制代码bode(y); % 绘制Bode图
请注意,以上代码仅为示例,实际使用时需要根据具体的应用场景和需求进行修改和调整。

matlab中bode的用法-回复Matlab中的bode函数是用于绘制系统的频率响应曲线的工具。
在信号处理和控制系统设计中,频率响应是一个重要的概念,它描述了系统对不同频率输入信号的响应程度。
bode函数提供了针对线性时不变系统和连续时间系统进行频率响应分析的功能。
在本文中,我们将一步一步回答以下问题,以帮助读者了解如何使用Matlab中的bode函数:1. 什么是频率响应?2. bode函数的基本语法是什么?3. 如何创建传输函数?4. 如何绘制频率响应曲线?5. 如何在频率响应曲线中增加标记和注释?6. 如何通过bode函数获取频率响应数据?接下来,我们将详细解答这些问题。
1. 什么是频率响应?频率响应是描述系统对不同频率输入信号的输出响应的一种方法。
它通常用于分析控制系统的稳定性和性能。
频率响应可以通过传输函数来表示,传输函数是描述系统输入和输出之间关系的一种数学表达式。
2. bode函数的基本语法是什么?bode函数的基本语法如下:[bode_mag, bode_phase, w] = bode(sys)其中,sys是输入传输函数,bode_mag是频率响应的幅值(也称为增益),bode_phase是频率响应的相位,w是频率响应的频率。
bode_mag、bode_phase和w是由bode函数返回的输出参数。
3. 如何创建传输函数?在Matlab中,我们可以使用tf函数来创建传输函数。
tf函数的基本语法如下:sys = tf(num, den)其中,num是传输函数的分子多项式的系数,den是传输函数的分母多项式的系数。
例如,创建一个传输函数为G(s) = (s+1)/(s^2+4s+3)的示例代码如下:num = [1 1];den = [1 4 3];sys = tf(num, den);4. 如何绘制频率响应曲线?在创建好传输函数后,可以使用bode函数来绘制频率响应曲线。
以下代码演示了如何使用bode函数来绘制传输函数sys的频率响应曲线:bode(sys)运行以上代码后,Matlab将自动绘制出频率响应的幅值和相位曲线。
Matlab中Bode图的绘制技巧我们经常会遇到使用Matlab画伯德图的情况,可能我们我们都知道bode这个函数是用来画bode 图的,这个函数是Matlab内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
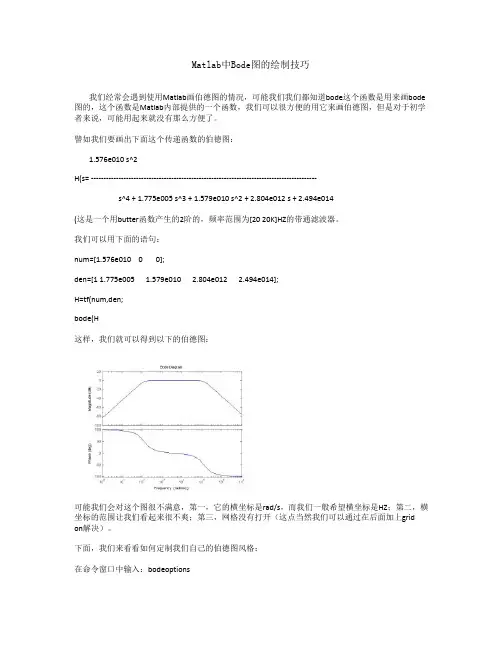
譬如我们要画出下面这个传递函数的伯德图:1.576e010 s^2H(s= ------------------------------------------------------------------------------------------s^4 + 1.775e005 s^3 + 1.579e010 s^2 + 2.804e012 s + 2.494e014(这是一个用butter函数产生的2阶的,频率范围为[20 20K]HZ的带通滤波器。
我们可以用下面的语句:num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den;bode(H这样,我们就可以得到以下的伯德图:可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on解决)。
下面,我们来看看如何定制我们自己的伯德图风格:在命令窗口中输入:bodeoptions我们可以看到以下内容:ans =Title: [1x1 struct] XLabel: [1x1 struct] YLabel: [1x1 struct] TickLabel: [1x1 struct] Grid: 'off'XLim: {[1 10]} XLimMode: {'auto'} YLim: {[1 10]} YLimMode: {'auto'} IOGrouping: 'none' InputLabels: [1x1 struct] OutputLabels: [1x1 struct] InputVisible: {'on'} OutputVisible: {'on'} FreqUnits: 'rad/sec' FreqScale: 'log' MagUnits: 'dB' MagScale: 'linear' MagVisible: 'on' MagLowerLimMode: 'auto' MagLowerLim: 0 PhaseUnits: 'deg' PhaseVisible: 'on' PhaseWrapping: 'off'PhaseMatching: 'off'PhaseMatchingFreq: 0PhaseMatchingValue: 0我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图:P=bodeoptions;P.Grid='on';P.XLim={[10 40000]};P.XLimMode={'manual'};P.FreqUnits='HZ';num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den;bode(H,P这时,我们将会看到以下的伯德图:上面这张图相对就比较好了,它的横坐标单位是HZ,范围是[1040K]HZ,而且打开了网格,便于我们观察-3DB处的频率值。
Matlab中Bode图的绘制技巧我们经常会遇到使用Matlab画伯德图的情况,可能我们我们都知道bode这个函数是用来画bode图的,这个函数是Matlab内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
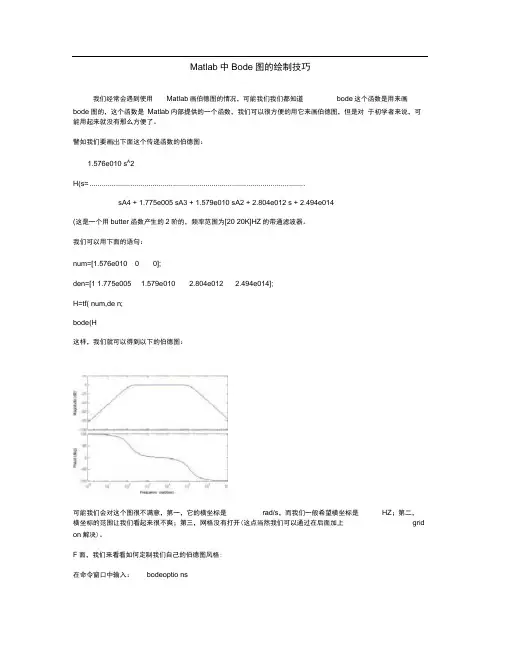
譬如我们要画岀下面这个传递函数的伯德图:1.576e010 s A2H(s= ..........................................................................................................sA4 + 1.775e005 sA3 + 1.579e010 sA2 + 2.804e012 s + 2.494e014(这是一个用butter函数产生的2阶的,频率范围为[20 20K]HZ的带通滤波器。
我们可以用下面的语句:num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf( num,de n;bode(H这样,我们就可以得到以下的伯德图:可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on解决)。
F面,我们来看看如何定制我们自己的伯德图风格:在命令窗口中输入:bodeoptio ns我们可以看到以下内容:ans =Title: [1x1 struct] XLabel: [1x1 struct] YLabel: [1x1 struct] TickLabel: [1x1 struct] Grid: 'off' XLim: {[1 10]} XLimMode: {'auto'} YLim: {[1 10]} YLimMode: {'auto'} IOGrouping: 'none' InputLabels: [1x1 struct] OutputLabels: [1x1 struct] InputVisible: {'on'} OutputVisible: {'on'} FreqUnits: 'rad/sec' FreqScale: 'log' MagUnits: 'dB' MagScale: 'linear' MagVisible: 'on' MagLowerLimMode: 'auto' MagLowerLim: 0 PhaseUnits: 'deg' PhaseVisible: 'on' PhaseWrapping: 'off'是这样的,运行命令 ctrlpref ,出现控制系统工具箱的设置页面, Units 改为Hz 就好了PhaseMatchi ng: 'off'PhaseMatchi ngFreq: 0PhaseMatchi ngValue: 0我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图: P=bodeopti ons;P.Grid='o n';P.XLim={[10 40000]};P.XLimMode={'ma nual'};P.Freq Un its='HZ';num=[1.576e010 00]; den=[1 1.775e0051.579e0102.804e012 2.494e014];H=tf( num,de n;bode(H,P这时,我们将会看到以下的伯德图:上面这张图相对就比较好了,它的横坐标单位是HZ ,范围是[10 40K]HZ ,而且打开了网格,便于我们观察-3DB 处的频率值。
matlab伯德函数用法在MATLAB中,伯德图(Bode plot)是一种用于分析线性时不变系统频率响应的方法。
它显示了系统的幅度和相位随频率变化的特性。
要使用MATLAB绘制伯德图,您可以使用`bode`函数。
以下是使用`bode`函数绘制伯德图的基本步骤:1. 定义系统对象:首先,您需要定义一个描述系统的对象。
这通常是通过定义系统的传递函数、差分方程或状态方程来实现的。
例如,假设您有一个传递函数H(s) = 10/(s^2 + 2s + 5),您可以将其表示为MATLAB的`tf`对象:```matlabnum = [1];den = [1 2 5];sys = tf(num, den);```2. 绘制伯德图:使用`bode`函数绘制伯德图。
例如:```matlabbode(sys);```这将绘制出系统的幅度和相位响应随频率变化的曲线。
默认情况下,`bode`函数将绘制出从0到10倍于系统最高频率的频率范围的响应。
3. 自定义频率范围:如果您想在特定的频率范围内绘制伯德图,可以使用`bode`函数的频率参数来指定频率范围。
例如,要绘制从0到1000 Hz的频率响应,可以这样做:```matlabbode(sys, 0:1000);```4. 添加标题和标签:为了使图形更易于理解,您可能希望添加标题和标签。
使用MATLAB的图形处理功能(如`title`, `xlabel`, `ylabel`等)来添加这些元素。
例如:```matlabtitle('Bode Plot of the System');xlabel('Frequency (Hz)');ylabel('Magnitude and Phase Response');```5. 显示图形:最后,使用`grid on`命令添加网格线,然后使用`drawnow`命令更新图形窗口以显示结果。
bodeplot函数
Bodeplot函数是Matlab中用来画频率响应曲线的一个函数,可以将一个系统的频率响应曲线画出来,这样一来就可以清晰的看出系统的特性和各种参数对系统的影响。
bodeplot函数的用法如下:
bodeplot (num,den,w)
参数 num 和 den 是一个系统的传递函数的分子和分母多项式的系数;w 是一个对应输入信号的频率向量。
如果用示波器查看系统,可以把示波器频率设置为w,然后把输出信号连接到示波器上,看到的曲线就是系统的频率响应曲线。
bodeplot函数的使用可以很方便的查看系统的频率响应曲线,而不必使用示波器查看,节省了大量的时间。
- 1 -。
Matlab波特图绘制在Matlab中,大多时候,我们都是用M语言,输入系统的传递函数后,用bode函数绘制bode图对系统进行频率分析,这样做,本人觉得效率远不如Simulink建模高。
如何在Matlab/Simulink中画bode图,以前也在网上查过些资料,没看到太多有用的参考。
今天做助教课的仿真,又要画电机控制中电流环的bode图,模型已经建好,step response也很容易看出来,可这bode图怎么也出不来,又不愿意用m语言写出传递函数再画。
baidu和google 了好一阵,几乎没有一个帖子说的清清楚楚的,经过一番摸索,终于掌握了Simulink里画bode图的方法。
.其实,Simulink里画bode图,非常的easy,也很方便。
写此文的目的是希望对那些常用Simulink进行仿真希望画bode图又不愿用M语言的新手有所帮助。
以下均是以Matlab R2008a为例。
首先,在simulink里建好model。
如图1,这里需要注意的是,输入和输出要用input port 和output port,这样以后画bode图的时候,系统就会知道是这两个变量之间的关系。
其次,选择线性分析。
Tools->Control Design ->Linear Analysis。
如图2。
将出现如图3所示的Control and Estimation Tools Manager窗口。
第三步,激动人心的时刻到了,哈哈。
如果你是按照前面的步骤来的,那么这时候,你就应该可以直接画出bode图,在窗口的下方,将“Plot linear analysis result in a ”前面的方框打上勾,已打的就不用管了,再在后面的下拉框里选择“bode response plot”,即画output port和input port之间的bode图,再点击“Linearize Model”按钮,就OK了。
其实除了bode图,还可以画其他很多响应曲线,比如step response、impulse response和Nyquist图等等,只需选择相应的step response plot,inpulse response plot或者Nyquist plot等等。
M A T L A B中b o d e图绘制技巧(精)-标准化文件发布号:(9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KIIMatlab中Bode图的绘制技巧学术收藏 2010-06-04 21:21:48 阅读54 评论0 字号:大中小订阅我们经常会遇到使用Matlab画伯德图的情况,可能我们我们都知道bode这个函数是用来画bode图的,这个函数是Matlab内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
譬如我们要画出下面这个传递函数的伯德图:1.576e010 s^2H(s= ------------------------------------------------------------------------------------------s^4 + 1.775e005 s^3 + 1.579e010 s^2 + 2.804e012 s + 2.494e014(这是一个用butter函数产生的2阶的,频率范围为[20 20K]HZ的带通滤波器。
我们可以用下面的语句:num=[1.576e010 0 0];den=[11.775e005 1.579e0102.804e012 2.494e014];H=tf(num,den;bode(H这样,我们就可以得到以下的伯德图:可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on解决)。
下面,我们来看看如何定制我们自己的伯德图风格:在命令窗口中输入:bodeoptions我们可以看到以下内容:ans =Title: [1x1 struct]XLabel: [1x1 struct]YLabel: [1x1 struct]TickLabel: [1x1 struct]Grid: 'off'XLim: {[1 10]}XLimMode: {'auto'}YLim: {[1 10]}YLimMode: {'auto'}IOGrouping: 'none'InputLabels: [1x1 struct]OutputLabels: [1x1 struct]InputVisible: {'on'}OutputVisible: {'on'}FreqUnits: 'rad/sec'FreqScale: 'log'MagUnits: 'dB'MagScale: 'linear'MagVisible: 'on'MagLowerLimMode: 'auto'MagLowerLim: 0PhaseUnits: 'deg'PhaseVisible: 'on'PhaseWrapping: 'off'PhaseMatching: 'off'PhaseMatchingFreq: 0PhaseMatchingValue: 0我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图:P=bodeoptions;P.Grid='on';P.XLim={[10 40000]};P.XLimMode={'manual'};P.FreqUnits='HZ';num=[1.576e010 0 0];den=[11.775e005 1.579e0102.804e012 2.494e014];H=tf(num,den;bode(H,P这时,我们将会看到以下的伯德图:上面这张图相对就比较好了,它的横坐标单位是HZ,范围是[10 40K]HZ,而且打开了网格,便于我们观察-3DB处的频率值。
Matlab中Bode图的绘制技巧
用simulink提供的linmod()或者linmod2()两个函数,从连续系统中提取线性模型,两个函数命令执行后都可以得到一个[a,b,c,d]表达的状态空间模型。
利用bode(sys)或者bode(a,b,c,d)函数绘制系统的对数幅频和相频特性曲线。
1) 修正原来的simulink模型,使其输入用inport表示,输出用outport表示。
这些端口在6.1版中分别位于sources和sinks组。
2)编写m文件内容为:
[A,B,C,D]=linmod(‘untitled1’) % untitled1’为系统的动态模型或simulink文件名。
[num,den]=ss2tf(A,B,C,D); %转换成传递函数模型
printsys(num,den,’s’); %显示系统的传递函数模型
sys=ss(A,B,C,D);
bode(sys); %即可绘制系统的开环系统bode图
bode(A,B,C,D); %也可以采用此语句代替上面紫色语句
3)、直接在命令窗执行m文件。
Matlab中Bode图的绘制技巧
我们经常会遇到使用Matlab画伯德图的情况,可能我们我们都知道bode这个函数是用来画bode图的,这个函数是Matlab内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
譬如我们要画出下面这个传递函数的伯德图:
s^2
H(s)=
------------------------------------------------------------------------------------------
s^4 + s^3 + s^2 + s +
(这是一个用butter函数产生的2阶的,频率范围为[20 20K]HZ的带通滤波器。
)
我们可以用下面的语句:
num=[ 0 0];
den=[1 ];
H=tf(num,den);
bode(H)
这样,我们就可以得到以下的伯德图:
v1.0 可编辑可修改
可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on解决)。
下面,我们来看看如何定制我们自己的伯德图风格:
在命令窗口中输入:bodeoptions
我们可以看到以下内容:
ans =
Title: [1x1 struct]
XLabel: [1x1 struct]
YLabel: [1x1 struct]
TickLabel: [1x1 struct]
Grid: 'off'
XLim: {[1 10]}
XLimMode: {'auto'}
YLim: {[1 10]}
YLimMode: {'auto'}
IOGrouping: 'none'
InputLabels: [1x1 struct]
OutputLabels: [1x1 struct]
InputVisible: {'on'}
OutputVisible: {'on'}
FreqUnits: 'rad/sec'
FreqScale: 'log'
MagUnits: 'dB'
MagScale: 'linear'
MagVisible: 'on'
MagLowerLimMode: 'auto'
MagLowerLim: 0
PhaseUnits: 'deg'
PhaseVisible: 'on'
PhaseWrapping: 'off'
PhaseMatching: 'off'
PhaseMatchingFreq: 0
PhaseMatchingValue: 0
我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图:P=bodeoptions;
='on';
={[10 40000]};
={'manual'};
='HZ';
num=[ 0 0];
den=[1 ];
H=tf(num,den);
bode(H,P)
这时,我们将会看到以下的伯德图:
上面这张图相对就比较好了,它的横坐标单位是HZ,范围是[10 40K]HZ,而且打开了网格,便于我们观察-3DB处的频率值。
当然,你也可以改变bodeoptions中的其它参数,做出符合你的风格的伯德图。
R = abs(Z)
theta = angle(Z)。