用matlab画bode图
- 格式:pdf
- 大小:183.28 KB
- 文档页数:3

关于一阶二阶传递函数的伯德图一阶惯性系统的通式为:将式子两边同时除以a0得令00a K b =为系统静态灵敏度; 01a a =τ为系统时间常数; 则有)()()1(s KX s Y s =+τ故有 )1()()()(+==s K s X s Y s H τ 以液柱式温度计为例,传递函数为 )1(1)()()(+==s s X s Y s H τ可得频率响应函数)1j (1)(+=τωs H )()()(001t x b t y a dtt dy a =+)()()(0001t x a b t y dt t dy a a =+可得传递函数的幅频与相频特性 2)1(1)()(τωωω+==j H Aωτωωϕarctan )()(-=∠=j H 在MATLAB 上输入程序(此时令1=τ)num=[1];den=[1,1];figuresys=tf(num,den);bode(sys);grid on可得bode 图二阶惯性系统的通式为:将式子两边同时除以a 0得令00a K b =为系统静态灵敏度; 20n a a =ω为系统无阻尼固有频率;1012a a a =ξ为系统阻尼器 传递函数为12)()()(22++==n ns s K s X s Y s H ωξω可得传递函数的幅频与相频特性 2222)(4)1(1)()(2n n K j H A ωωξωωωω+-==)()()()(001222t x b t y a dtt dy a dt t y d a =++)()()()(00012202t x a b t y dt t dy a a dt t y d a a =++2212arctan )()(n n j H ωωωωξωωϕ--=∠= 例如传递函数12)()()(2++==s s s X s Y s H在MATLAB 上输入程序 num=[2];den=[1,1,1]; figuresys=tf(num,den); bode(sys);grid on 可得bode 图。

初始条件:G(s)=75600试用频率法设计串联超前——滞后s s+10s+()(60)校正装置输入速度为时1rad/s,稳态误差不大于1/126rad。
(2)相角裕度不小于γ>,截止频率为20rad/s。
(3)放大器的增益不变。
30ο要求完成的主要任务:1、用Matlab画出开环系统的波特图和奈奎斯特图,并用奈奎斯特判据分析系统的稳定性。
2、校正前后系统输出性能的比较。
3、求出开环系统的截至频率、相角裕度和幅值裕度。
时间安排:12.29~31 明确设计任务,建立系统模型1.1 绘制波特图和奈奎斯特图,判断稳定性1.2~3 计算频域性能指标,撰写课程设计报告指导教师签名:年月日系主任(或责任教师)签名:年月日摘要当系统设计要求满足的性能指标属频域特征量时,通常采用频域校正方法。
在开环系统频率特性基础上,以满足稳态误差、开环系统截止频率和相角裕度等要求为出发点时,可采用串联校正的方法。
在此次课程设计中,主要用到超前校正、滞后校正两种不同的方法分别对直流电动机进行校正设计,以达到设计要求并改善性能的目的。
在设计过程中,首先根据两种不同校正方法的原理将时域性能指标要求转化到频域来分析计算,并得出传递函数,再用matlab仿真软件进行仿真验证,分别绘出串联超前网络和滞后网络校正前后的伯德图、根轨迹图、阶跃响应曲线、斜坡响应曲线,对曲线逐一对比,从不同角度进行分析,以此得出超前校正和滞后校正的动态性能及静态性能的变化,总结超前网络及滞后网络的作用。
对比总结超前网络滞后网络的不同特点。
在生产实践中,需要需要选择最佳校正方案。
关键字:校正动态性能静态性能 matlab仿目录1 校正前装置的特性 (1)1.1校正前系统电路图 (1)1.2设计校正超前滞后装置 (1)2 校正装置前后的比较 (4)2.1利用MATLAB作出系统校正前与校正后的单位阶跃响应曲线 (4)2.2绘制系统校正前与校正后的根轨迹图 (4)3系统前后幅值裕量、相位裕量的比较 (7)3.1画Bode图 (7)3.2计算校正前系统的幅值裕量,相位裕量,幅值穿越频率 (7)3.3计算校正后系统的幅值裕量,相位裕量,复制穿越频率 (8)4 参考文献 (10)滞后-超前校正装置的设计1 校正前装置的特性1.1 校正前系统电路图设输入为单位阶跃函数,则电路图如图1:G(s)= 75600()()s s+10s+60图11.2 设计串联校正超前——滞后装置因为系统的传递函数是典型环节的乘积形式,所以将传递函数化成表达式为G(s)=126/(s*(0.1s+1)*(0.0167s+1))用MATLAB写出传递函数,指令代码如下所示:>> z=[];>> p=[0,-10,-60];>> k=126*10*60;>> s1=zpk(z,p,k);Zero/pole/gain:75600---------------s (s+10) (s+60)用MATLAB画出校正前的系统的Bode图>> bode(s1)>> grid on>> title('系统校正前的Bode图')曲线如图2所示:图2由图可以查出未校正前的剪切频率w,c w=32.5;c相角裕量γ=180-90-arctan(w /10)-arctan(c w /60)=-11.34c表明未校正系统不稳定。

《自动控制原理》实践报告实验三系统频率特性曲线的绘制及系统分析熟悉利用计算机绘制系统伯德图、乃奎斯特曲线的方法,并利用所绘制图形分析系统性能。
一、实验目的1.熟练掌握使用MATLAB软件绘制Bode图及Nyquist曲线的方法;2.进一步加深对Bode图及Nyquist曲线的了解;3.利用所绘制Bode图及Nyquist曲线分析系统性能。
二、主要实验设备及仪器实验设备:每人一台计算机奔腾系列以上计算机,配置硬盘≥2G,内存≥64M。
实验软件:WINDOWS操作系统(WINDOWS XP 或WINDOWS 2000),并安装MATLAB 语言编程环境。
三、实验内容已知系统开环传递函数分别为如下形式, (1))2)(5(50)(++=s s s G (2))15)(5(250)(++=s s s s G(3)210()(21)s G s s s s +=++ (4))12.0)(12(8)(++=s s s s G (5)23221()0.21s s G s s s s ++=+++ (6))]105.0)125.0)[(12()15.0(4)(2++++=s s s s s s G 1.绘制其Nyquist 曲线和Bode 图,记录或拷贝所绘制系统的各种图形; 1、 程序代码: num=[50];den=conv([1 5],[1 2]); bode(num,den)num=[50];den=conv([1 5],[1 2]); nyquist(num,den)-80-60-40-20020M a g n i t u d e (d B)10-210-110101102103-180-135-90-450P h a s e (d e g )Bode DiagramFrequency (rad/sec)-1012345-4-3-2-11234Nyquist DiagramReal AxisI m a g i n a r y A x i s2、 程序代码: num=[250];den=conv(conv([1 0],[1 5]),[1 15]); bode(num,den)num=[250];den=conv(conv([1 0],[1 5]),[1 15]);-150-100-5050M a g n i t u d e (d B )10-110101102103-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)nyquist(num,den)3、 程序代码: num=[1 10];den=conv([1 0],[2 1 1]); bode(num,den)-150-100-50050100M a g n i t u d e (d B)10-210-110101102103-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)-1-0.9-0.8-0.7-0.6-0.5-0.4-0.3-0.2-0.10-15-10-551015System: sys Real: -0.132Imag: -0.0124Frequency (rad/sec): -10.3Nyquist DiagramReal AxisI m a g i n a r y A x i snum=[1 10];den=conv([1 0],[2 1 1]); nyquist(num,den)-25-20-15-10-5-200-150-100-5050100150200Nyquist DiagramReal AxisI m a g i n a r y A x i s-100-5050100M a g n i t u d e (d B )10-210-110101102-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)4、 程序代码: num=[8];den=conv(conv([1 0],[2 1]),[0.2 1]); bode(num,den)-18-16-14-12-10-8-6-4-20-250-200-150-100-50050100150200250Nyquist DiagramReal AxisI m a g i n a r y A x i snum=[8];den=conv(conv([1 0],[2 1]),[0.2 1]); nyquist(num,den)5、 程序代码: num=[1 2 1]; den=[1 0.2 1 1]; bode(num,den)num=[1 2 1];den=[1 0.2 1 1]; nyquist(num,den)-40-30-20-10010M a g n i t u d e (d B )10-210-110101102-360-270-180-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)-2.5-2-1.5-1-0.500.51 1.5-3-2-1123Nyquist DiagramReal AxisI m a g i n a r y A x i s-100-5050100M a g n i t u d e (d B )10-210-110101102-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)6、 num=[2 4];den=conv(conv([1 0],[2 1]),[0.015625 0.05 1]); bode(num,den)num=[2 4];den=conv(conv([1 0],[2 1]),[0.015625 0.05 1]); nyquist(num,den)2.利用所绘制出的Nyquist 曲线及Bode 图对系统的性能进行分析:(1)利用以上任意一种方法绘制的图形判断系统的稳定性; 由Nyquist 曲线判断系统的稳定性,Z=P-2N 。



matlab中bode的用法Bode's Usage in MATLABBode plot is a graphical representation that depicts the frequency response of a system. This plot consists of two parts: magnitude response and phase response. MATLAB provides a powerful function called "bode" to generate Bode plots and analyze the frequency characteristics of a system. In this article, I will explain the usage of the "bode" function in MATLAB.The syntax of the "bode" function in MATLAB is as follows:[magnitude, phase, frequency] = bode(sys)Here, "sys" represents the transfer function or state-space model of the system under consideration. Upon execution, the "bode" function returns three outputs: magnitude, phase, and frequency.The "magnitude" output represents the magnitude response of the system and is usually plotted in decibels (dB). It indicates how the system amplifies or attenuates different frequencies. Positive values indicate amplification, while negative values indicate attenuation.The "phase" output represents the phase response of the system and is plotted in degrees. It shows the phase shift introduced by the system for each frequency. Positive values indicate a phase lead, while negative values indicate a phase lag.The "frequency" output represents the frequency axis corresponding to the magnitude and phase responses. It is usually plotted in logarithmic scale.To generate a Bode plot using the "bode" function, we need to define the system in MATLAB first. This can be accomplished by creating a transfer function or state-space model using the appropriate MATLAB functions.For example, let's consider a simple transfer function:sys = tf([1],[1 2 1])To generate the Bode plot of this system, we can use the following code:[magnitude, phase, frequency] = bode(sys)After executing this code, the magnitude, phase, and frequency responses will be stored in the variables "magnitude," "phase," and "frequency," respectively.To visualize the Bode plot, we can use the "semilogx" function to plot the magnitude response and the "semilogx" or "semilogy" function to plot the phase response. Additionally, we can use the "grid" function to add gridlines for better readability.Here's an example code snippet to plot and visualize the Bode plot:semilogx(frequency, 20*log10(magnitude))grid onxlabel('Frequency')ylabel('Magnitude (dB)')title('Bode Plot - Magnitude Response')figuresemilogx(frequency, phase)grid onxlabel('Frequency')ylabel('Phase (degrees)')title('Bode Plot - Phase Response')By executing the above code, two separate figures will be displayed showing the magnitude and phase responses of the system, respectively.In conclusion, the "bode" function in MATLAB is a useful tool for generating Bode plots and analyzing the frequency characteristics of a system. By providing the transfer function or state-space model of the system, the function calculates and returns the magnitude, phase, and frequency responses, allowing us to visualize and study the behavior of the system at different frequencies.。


题 目: 用MATLAB 进行控制系统的滞后-超前校正设计。
初始条件:已知一单位反馈系统的开环传递函数是)2)(1()(++=s s s Ks G要求系统的静态速度误差系数110-=S K v , 45=γ。
要求完成的主要任务: (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、MATLAB 作出满足初始条件的最小K 值的系统伯德图,计算系统的幅值裕量和相位裕量。
2、前向通路中插入一相位滞后-超前校正,确定校正网络的传递函数。
3、用MATLAB 画出未校正和已校正系统的根轨迹。
4、课程设计说明书中要求写清楚计算分析的过程,列出MATLAB 程序和MATLAB 输出。
说明书的格式按照教务处标准书写。
时间安排:指导教师签名: 年 月 日 系主任(或责任教师)签名: 年 月用MATLAB 进行控制系统的滞后-超前校正设计1滞后—超前设计目的和原理1.1滞后—超前设计的目的对控制系统进行的校正,就是在了解系统已知特性与参数的情况和系统的全部性能指标的,满足系统要求的设计,对系统进行优化设计,使其符合系统所要求的性能指标。
按校正装置在系统中的连接方式,控制校正方式可分为串联校正、反馈校正、前馈校正和复合校正四种。
设计方法主要有综合法和分析法。
滞后—超前校正建有滞后和超前校正的优点,及已校正系统响应速度较快,超调量较小,机制高频噪声的性能也较好。
当校正系统不稳定,且要求校正后系统的响应速度、相较于都和稳态精度较高时,以采用串联滞后—超前校正为宜。
其基本原理是利用滞后—超前网络的超前部分来增大系统的相角裕度,同时利用滞后部分来改善系统的稳态性能。
1.2滞后—超前校正设计原理无源滞后—超前校正RC 网络电路图1图1 无源滞后—超前RC 网络其传递函数为:222112122112211211122)(1)1)(1(211111)(SC R C R S C R C R C R S C R S C R SC S SC S S R R R C R G c ++++++=++++=(1) 此处令Ta=R1C1,Tb=R2C2,Tab=R1C2,令试(1)的分母二项式有两个不相等的负实根,则试(1)可以写为:)T 1)(1()1)(1()(21S S T S T T S G b a C ++++=(2)使(1)、(2)两试相进行比较,可得: ab b a T T T T T ++=+21b a T T T T =21设 a T >1T ,α121==b a T T T T 其中α>1,则有: a T T α=1,αbT T =2,于是无源滞后—超前网络的传递函数最后可以表示为:)1)(1()1)(1()(ααsT s T s T s T s G b a b a c ++++=(3), 试)1/()1(s T s T a a α++为网络的滞后部分,)/1/()1(αs T s T b b ++为网络滞后 分。

实验七 控制系统的Bode 图一 实验目的1.利用计算机作出控制系统的Bode 图2.观察记录控制系统得开环频率特性;3.控制系统得开环频率特性分析;二、实验步骤1.开机执行程序C :\matlab \bin \matlab.exe (或用鼠标双击图标)进人MATLAB 命令窗口;2.相关MATLAB 函数Bode(num,den)Bode(num,den,w) %w 极为频率变量ω[mag,phase,w]= Bode(num,den) %mag-相位,phase-幅角给定系统开环传递函数G 0(s) 多项式模型,作系统bode 图。
其计算公式为。
)()()(0s den s num s G = 式中, num 为开环传递函数G 0(s)的分子多项式系数向量,den 为开环传递函数G 0(s)的分母多项式系数向量。
函数格式1:给定num 、den 作波得图,角频率向量w 的范围自动设定。
函数格式2:角频率向量w 的范围可以由人工给定。
(w 为对数等分,由对数等分函数logsspacpce()完成.例如w =logspace(-1,1,100)。
函数格式3:返回变量格式。
计算所得的幅值mag 、相角Phase 及角频率w 返回至MA TLAB 命令窗口,不作图。
更详细的命令说明,可键入“help bode ”在线帮助查阅。
例如,系统的开环传递函数10210)()()(20++==s s s den s num s G 作图程序为:(分两次输入)num=[10];den=[1 2 10];bode(num,den); %得到bode 图9-6 bode 图,注意横标。
再输入以下语句w=logspace(-1,1,32); %执行后得到bode 图9-7 bode 图,注意横标。
bode(num,den,w);比较图9-6、图9-7的横坐标命令(人工定标)w =logspace(d1,d2,n) 将变量w 作对数等分。
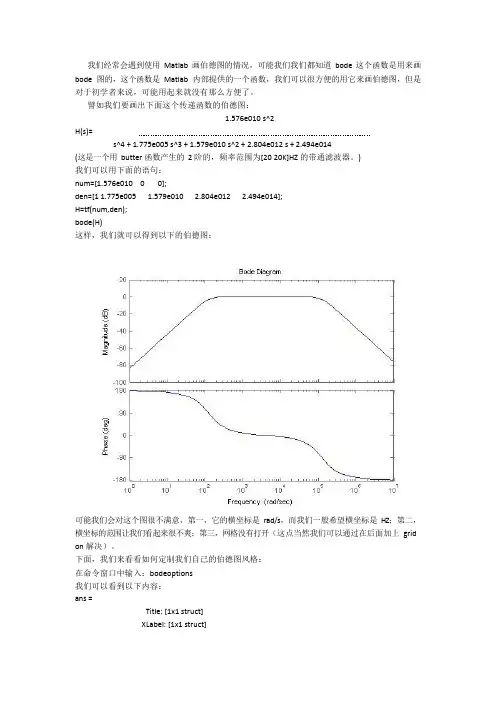
我们经常会遇到使用Matlab 画伯德图的情况,可能我们我们都知道bode 这个函数是用来画bode 图的,这个函数是Matlab 内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
譬如我们要画出下面这个传递函数的伯德图:1.576e010 s^2H(s)=s^4 + 1.775e005 s^3 + 1.579e010 s^2 + 2.804e012 s + 2.494e014(这是一个用butter 函数产生的2 阶的,频率范围为[20 20K]HZ 的带通滤波器。
)我们可以用下面的语句:num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den);bode(H)这样,我们就可以得到以下的伯德图:可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on 解决)。
下面,我们来看看如何定制我们自己的伯德图风格:在命令窗口中输入:bodeoptions我们可以看到以下内容:ans =Title: [1x1 struct]XLabel: [1x1 struct]YLabel: [1x1 struct]TickLabel: [1x1 struct]Grid: 'off'XLim: {[1 10]}XLimMode: {'auto'}YLim: {[1 10]}YLimMode: {'auto'}IOGrouping: 'none'InputLabels: [1x1 struct]OutputLabels: [1x1 struct]InputVisible: {'on'}OutputVisible: {'on'}FreqUnits: 'rad/sec'FreqScale: 'log'MagUnits: 'dB'MagScale: 'linear'MagVisible: 'on'MagLowerLimMode: 'auto'MagLowerLim: 0PhaseUnits: 'deg'PhaseVisible: 'on'PhaseWrapping: 'off'PhaseMatching: 'off'PhaseMatchingFreq: 0PhaseMatchingValue: 0我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图:P=bodeoptions;P.Grid='on';P.XLim={[10 40000]};P.XLimMode={'manual'};P.FreqUnits='HZ';num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den);bode(H,P)这时,我们将会看到以下的伯德图:上面这张图相对就比较好了,它的横坐标单位是HZ,范围是[10 40K]HZ,而且打开了网格,便于我们观察-3DB 处的频率值。
Matlab中Bode图的绘制技巧我们经常会遇到使用Matlab画伯德图的情况,可能我们我们都知道bode这个函数是用来画bode 图的,这个函数是Matlab内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
譬如我们要画出下面这个传递函数的伯德图:1.576e010 s^2H(s= ------------------------------------------------------------------------------------------s^4 + 1.775e005 s^3 + 1.579e010 s^2 + 2.804e012 s + 2.494e014(这是一个用butter函数产生的2阶的,频率范围为[20 20K]HZ的带通滤波器。
我们可以用下面的语句:num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den;bode(H这样,我们就可以得到以下的伯德图:可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on解决)。
下面,我们来看看如何定制我们自己的伯德图风格:在命令窗口中输入:bodeoptions我们可以看到以下内容:ans =Title: [1x1 struct] XLabel: [1x1 struct] YLabel: [1x1 struct] TickLabel: [1x1 struct] Grid: 'off'XLim: {[1 10]} XLimMode: {'auto'} YLim: {[1 10]} YLimMode: {'auto'} IOGrouping: 'none' InputLabels: [1x1 struct] OutputLabels: [1x1 struct] InputVisible: {'on'} OutputVisible: {'on'} FreqUnits: 'rad/sec' FreqScale: 'log' MagUnits: 'dB' MagScale: 'linear' MagVisible: 'on' MagLowerLimMode: 'auto' MagLowerLim: 0 PhaseUnits: 'deg' PhaseVisible: 'on' PhaseWrapping: 'off'PhaseMatching: 'off'PhaseMatchingFreq: 0PhaseMatchingValue: 0我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图:P=bodeoptions;P.Grid='on';P.XLim={[10 40000]};P.XLimMode={'manual'};P.FreqUnits='HZ';num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den;bode(H,P这时,我们将会看到以下的伯德图:上面这张图相对就比较好了,它的横坐标单位是HZ,范围是[1040K]HZ,而且打开了网格,便于我们观察-3DB处的频率值。
Matlab中Bode图的绘制技巧我们经常会遇到使用Matlab画伯德图的情况,可能我们我们都知道bode这个函数是用来画bode图的,这个函数是Matlab内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
譬如我们要画岀下面这个传递函数的伯德图:1.576e010 s A2H(s= ..........................................................................................................sA4 + 1.775e005 sA3 + 1.579e010 sA2 + 2.804e012 s + 2.494e014(这是一个用butter函数产生的2阶的,频率范围为[20 20K]HZ的带通滤波器。
我们可以用下面的语句:num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf( num,de n;bode(H这样,我们就可以得到以下的伯德图:可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on解决)。
F面,我们来看看如何定制我们自己的伯德图风格:在命令窗口中输入:bodeoptio ns我们可以看到以下内容:ans =Title: [1x1 struct] XLabel: [1x1 struct] YLabel: [1x1 struct] TickLabel: [1x1 struct] Grid: 'off' XLim: {[1 10]} XLimMode: {'auto'} YLim: {[1 10]} YLimMode: {'auto'} IOGrouping: 'none' InputLabels: [1x1 struct] OutputLabels: [1x1 struct] InputVisible: {'on'} OutputVisible: {'on'} FreqUnits: 'rad/sec' FreqScale: 'log' MagUnits: 'dB' MagScale: 'linear' MagVisible: 'on' MagLowerLimMode: 'auto' MagLowerLim: 0 PhaseUnits: 'deg' PhaseVisible: 'on' PhaseWrapping: 'off'是这样的,运行命令 ctrlpref ,出现控制系统工具箱的设置页面, Units 改为Hz 就好了PhaseMatchi ng: 'off'PhaseMatchi ngFreq: 0PhaseMatchi ngValue: 0我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图: P=bodeopti ons;P.Grid='o n';P.XLim={[10 40000]};P.XLimMode={'ma nual'};P.Freq Un its='HZ';num=[1.576e010 00]; den=[1 1.775e0051.579e0102.804e012 2.494e014];H=tf( num,de n;bode(H,P这时,我们将会看到以下的伯德图:上面这张图相对就比较好了,它的横坐标单位是HZ ,范围是[10 40K]HZ ,而且打开了网格,便于我们观察-3DB 处的频率值。
一、概述在控制系统工程中,频率响应是系统性能分析的重要手段之一。
Bode 图是频率响应的常用图示方法之一,它能够直观地展现系统的幅频特性和相频特性。
在MATLAB中,我们可以利用bode函数来绘制系统的Bode图,对系统的频率响应进行分析和评估。
二、bode函数的基本语法MATLAB中bode函数的基本语法如下:[bode_mag, bode_phase, w] = bode(sys)其中,sys表示系统的传递函数模型或状态空间模型;bode_mag和bode_phase分别表示系统的幅频特性和相频特性;w表示频率范围。
三、bode函数的使用方法1. 导入系统模型在使用bode函数之前,首先需要导入系统的传递函数模型或状态空间模型。
对于传递函数模型G(s),可以使用以下命令进行导入:sys = tf([1],[1 2 1])2. 绘制Bode图一旦导入了系统模型,就可以利用bode函数来绘制系统的Bode图。
使用以下命令可以实现:[bode_mag, bode_phase, w] = bode(sys)3. 显示Bode图绘制Bode图之后,可以使用以下命令来显示幅频特性和相频特性:figuresubplot(2,1,1)semilogx(w,20*log10(bode_mag))grid onxlabel('Frequency (rad/s)')ylabel('Magnitude (dB)')title('Bode Magnitude Plot')subplot(2,1,2)semilogx(w,bode_phase)grid onxlabel('Frequency (rad/s)')ylabel('Phase (deg)')title('Bode Phase Plot')四、实例演示下面我们以一个具体的系统为例,演示bode函数的使用方法。
Matlab中Bode图的绘制技巧
用simulink提供的linmod()或者linmod2()两个函数,从连续系统中提取线性模型,两个函数命令执行后都可以得到一个[a,b,c,d]表达的状态空间模型。
利用bode(sys)或者bode(a,b,c,d)函数绘制系统的对数幅频和相频特性曲线。
1) 修正原来的simulink模型,使其输入用inport表示,输出用outport表示。
这些端口在6.1版中分别位于sources和sinks组。
2)编写m文件内容为:
[A,B,C,D]=linmod(‘untitled1’) % untitled1’为系统的动态模型或simulink文件名。
[num,den]=ss2tf(A,B,C,D); %转换成传递函数模型
printsys(num,den,’s’); %显示系统的传递函数模型
sys=ss(A,B,C,D);
bode(sys); %即可绘制系统的开环系统bode图
bode(A,B,C,D); %也可以采用此语句代替上面紫色语句
3)、直接在命令窗执行m文件。