实验四 一元线性回归分析
- 格式:doc
- 大小:54.00 KB
- 文档页数:1

1、实验过程和结果记录:(1)实验数据(2)人均可支配收入与人均消费性支出散点图(3)数据分析步骤4、(5)最终实验结果2、人均可支配收入为12千元时的人均消费性支出和置信度为95%的预测区间计算步骤: (1)一元线性回归方程为Y=0.72717+0.6741420X(2)将0X =12带入样本回归方程可得0Y 的预测值=0.72717+0.674142*12=8.816874千元(3)0e S =千元 结论:因此,当城镇居民家庭的人均可支配收入为12千元时,人均消费性支出地点预测为8.816874千元;置信度为95%的预测区间为(8.816874-1.96*0.0542千元,8.816874+1.96*0.0542千元) 即(8.71千元,8.92千元)六、实验结果及分析1、实验结果:当城镇居民家庭的人均可支配收入为12千元时,人均消费性支出地点预测为8.816874千元;置信度为95%的预测区间为(8.816874-1.96*0.0542千元,8.816874+1.96*0.0542千元) 即(8.71千元,8.92千元)2、实验分析(1)相关系数:相关系数R 实际上是判定系数的平方根,相关系数R 从另一个角度说明了回归直线的拟合优度。
|R|越接近1,表明回归直线对观测数据的拟合程度就越高。
R=0.999592,接近于1,所以人均可支配收入和人均消费支出相关程度高。
(2)判定系数:该指标测度了回归直线对观测数据的拟合程度。
若所有观测点,落在直线上,残差平方和RSS=0,则R^2=1,拟合是完全的;0≤R^2≦1。
R^2越接近1,表明回归平方和占总平方和的比例越大,回归直线与各观测点越接近,用X 的变化来解释Y 值的部分就越多,回归直线的拟合度就越好;反之,R^2越接近0,回归直线的拟合度就越差。
所以,判定系数R^2=0.999185,表示所观测到的我国城镇居民家庭人均消费支出的值与其均值的偏差平方和中有99.92%可以通过人均可支配收入来解释。

实验四地理数据回归分析一、实验目的1. 掌握地理数据线性相关的度量方法;2. 掌握地理数据的一元线性回归分析的方法和步骤;3. 掌握地理数据一元非线性回归分析的方法和步骤;4. 掌握地理数据多元线性回归分析的方法和步骤。
二、仪器设备(及耗材)1. 给定的地理数据2. 电子计算机3. Excel软件4.DPS统计软件三、简述原理地理相关分析是应用相关分析法来研究各地理要素间的相互关系和联系强度,以相关系数和等级相关系数作为衡量两个变量线性相关的指标。
地理系统各要素间的关系,可通过观测获得一定的数据,并利用回归分析方法,以回归方程的形式表达各要素间的数量关系,进一步可利用建立的回归方程对地理系统中的因变量进行预测、延长、插补或控制等。
根据变量关系的类型,回归分析可分为一元线性、一元非线性及多元线性等。
四、实验步骤1. 计算给定的地理数据中两要素之间的相关系数及等级相关系数;2. 利用一元线性回归分析方法对给定的地理数据进行回归分析;3. 利用一元非线性回归分析方法对给定的地理数据进行回归分析;4. 利用多元线性回归分析方法对给定的地理数据进行回归分析。
五、结果及分析通过实验进行地理要素的相关分析及回归分析,完成如下内容:1.附录1的地理要素的线性相关系数及等级相关系数,并对相关系数进行显著性检验;2. 附录2的地理要素的一元线性回归分析参数一览表(回归直线斜率、截距、判定系数、剩余标准差、回归平方和、剩余平方和、F-检验相关参数及结果);3.附录2的地理要素的原始数据散点及一元线性回归直线图;4. 附录3的地理要素的一元非线性回归分析参数一览表(回归曲线的相应参数、相关指数、剩余标准差、回归平方和、剩余平方和);5. 附录3的地理要素的原始数据散点及一元非线性曲线图;6. 附录4的地理要素的多元线性回归分析参数一览表(方程常数项、各变量系数、判定系数、剩余标准差、回归平方和、剩余平方和、F-检验相关参数及结果)。

一、线性回归分析若是自变数与依变数都是一个,且Y 和X 呈线性关系,这就称为一元线性回归。
例如,以X 表示小麦每667m 2有效穗数,Y 表示小麦每667m 2的产量,有效穗数即属于自变数,产量即属于依变数。
在这种情形下,可求出产量依有效穗数而变更的线性回归方程。
在另一种情形下,两类变数是平行关系很难分出哪个是自变数,哪个是依变数。
例如,大豆脂肪含量与蛋白质含量的关系,依照需要确信求脂肪含量依蛋白质含量而变更的回归方程,或求蛋白质含量依脂肪含量而变更的回归方程。
回归分析要解决的问题要紧有四个方面:一是依如实验观看值成立适当的回归方程;二是查验回归方程是不是适用,或对回归方程中的回归系数的进行估量;三是对未知参数进行假设考试;四是利用成立起的方程进行预测和操纵。
(一)成立线性回归方程用来归纳两类变数互变关系的线性方程称为线性回归方程。
若是两个变数在散点图上呈线性,其数量关系可能用一个线性方程来表示。
这一方程的通式为:上式叫做y 依x 的直线回归。
其中x 是自变数,y ˆ是依变数y 的估量值,a 是x =0时的y ˆ值,即回归直线在y 轴上的截距,称为回归截距,b 是x 每增加一个单位时,y 将平均地增加(b >0时)或减少(b <0时) b 个单位数,称为回归系数或斜率(regression coefficient or slope )。
要使 能够最好地代表Y 和X 在数量上的互变关系,依照最小平方式原理,必需使将Q 看成两个变数a 与b 的函数,应该选择a 与b ,使Q 取得最小值,必需求Q 对a ,b 的一阶偏导数,且令其等于零,即得:()()⎩⎨⎧∑=∑+∑∑=∑+212xyx b x a yx b an ()()∑∑=--=-=nn Q bx a y yy Q 1min212ˆbx a y +=ˆ()1.7ˆbx a y+=由上述(1)解得:将()代入(2),那么得:()的分子 是x 的离均差与y 的离均差乘积总和,简称乘积和(sum of products ),可记为SP ,分母是x 的离均差平方和,也可记为SS x 。

线性回归分析实验报告实验报告:线性回归分析一、引言线性回归是一种基本的统计分析方法,用于研究自变量与因变量之间的线性关系。
此实验旨在通过一个实际案例对线性回归进行分析,并解释如何使用该方法进行预测和解释。
二、实验方法1.数据收集:从电商网站收集了一份销售量与广告费用的数据集,其中包括了十个月的数据。
该数据集包括两个变量:广告费用(自变量)和销售量(因变量)。
2.数据处理:首先对数据进行清洗,包括处理缺失值和异常值等。
然后进行数据转换,对广告费用进行对数转换,以适应线性回归的假设。
3.构建模型:使用线性回归模型,将广告费用作为自变量,销售量作为因变量,构建一个简单的线性回归模型。
模型的公式为:销售量=β0+β1*广告费用+ε,其中β0和β1是回归系数,ε是误差项。
4.模型评估:通过计算回归系数的置信区间和检验假设以评估模型的拟合程度和相关性。
此外,还使用残差分析来检验模型的合理性和独立性。
5.模型预测:根据模型的回归系数和新的广告费用数据,预测销售量。
三、实验结果1.数据描述:首先对数据进行描述性统计。
数据集的平均广告费用为1000元,标准差为200元。
平均销售量为1000件,标准差为150件。
广告费用和销售量之间的相关系数为0.8,说明两者存在一定的正相关关系。
2. 模型拟合:通过拟合线性回归模型,得到回归系数的估计值。
估计值的标准误差很小,R-square值为0.64,说明模型可以解释63%的销售量变异。
3.置信区间和假设检验:通过计算回归系数的置信区间,发现β1的置信区间不包含零,说明广告费用对销售量有显著影响。
假设检验结果也支持这一结论。
4.残差分析:通过残差分析,发现残差的分布基本符合正态性假设,没有明显的模式或趋势。
这表明模型的合理性和独立性。
四、结论与讨论通过线性回归分析,我们得出以下结论:1.广告费用对销售量有显著影响,且为正相关关系。
随着广告费用的增加,销售量也呈现增加的趋势。
2.线性回归模型可以解释63%的销售量变异,说明模型的拟合程度较好。

一.实验目的与要求(一)目的实验一: EXCEL的数据整理与显示1. 了解EXCEL的基本命令与操作、熟悉EXCEL数据输入、输出与编辑方法;2. 熟悉EXCEL用于预处理的基本菜单操作与命令;3. 熟悉EXCEL用于整理与显示的基本菜单操作与命令。
实验二: EXCEL的数据特征描述、抽样推断熟悉EXCEL用于数据描述统计、抽样推断实验三: 时间序列分析掌握EXCEL用于移动平均、线性趋势分析的基本菜单操作与命令。
实验四: 一元线性回归分析掌握EXCEL用于相关与回归分析的基本操作与命令。
(二)要求1.按要求认真完成实验任务中规定的所有练习;2.实验结束后要撰写格式规范的实验报告, 正文统一用小四号字, 必须有页码;3、实验报告中的图表制作要规范, 图表必须有名称和序号;4、实验结果分析既要简明扼要, 又要能说明问题。
二、实验任务实验一根据下面的数据。
1.1用Excel制作一张组距式次数分布表, 并绘制一张条形图(或柱状图), 反映工人加工零件的人数分布情况。
从某企业中按随即抽样的原则抽出50名工人, 以了解该企业工人生产状况(日加工零件数):117 108 110 112 137 122 131 118 134 114 124 125 123127 120 129 117 126 123 128 139 122 133 119 124 107133 134 113 115 117 126 127 120 139 130 122 123 123128 122 118 118 127 124 125 108 112 135 5091.2整理成频数分布表, 并绘制直方图。
1.3 假设日加工零件数大于等于130为优秀。
实验二百货公司6月份各天的销售额数据如下(单位:万元)257 276 297 252 238 310 240 236 265 278271 292 261 281 301 274 267 280 291 258272 284 268 303 273 263 322 249 269295(1)计算该百货公司日销售额的均值、众数、中位数;(2)计算该百货公司日销售额的极差、标准差;(3)计算日销售额分布的偏态系数和峰度系数。


一、前言作为一名经济专业的学生,我对经济学有着浓厚的兴趣。
为了更好地理解经济学的理论和实践,我参加了经济实验课程。
通过一系列的经济实验,我对经济学有了更深刻的认识,以下是我对经济实验的心得体会。
二、实验过程回顾1. 实验一:一元回归分析在这次实验中,我们学习了如何运用一元回归分析来研究两个变量之间的关系。
通过收集数据、建立模型、估计参数、检验模型等步骤,我们得出了两个变量之间的相关关系。
这次实验让我明白了经济学研究中数据分析和模型建立的重要性。
2. 实验二:经济仿真实验在这个实验中,我们模拟了一个包含政府、企业、消费者等主体的经济环境。
通过调整政策、制定战略、分析市场变化等环节,我们了解了宏观经济政策对企业经营的影响。
这次实验让我感受到了经济学在实际生活中的应用,以及政策制定者面临的挑战。
3. 实验三:实验经济学实验在实验经济学实验中,我们模拟了一个沙盘经济环境,通过扮演不同角色,进行市场交易、政策制定等活动。
这次实验让我明白了市场经济中的竞争与合作,以及供求关系对价格的影响。
4. 实验四:EViews计量经济学实验在这个实验中,我们运用EViews软件进行了简单线性回归分析,研究了国内生产总值对财政收入的影响。
通过数据收集、模型设定、参数估计、模型检验等步骤,我们得出了结论。
这次实验让我掌握了计量经济学的基本方法,以及如何运用软件进行数据分析。
三、心得体会1. 理论与实践相结合通过经济实验,我深刻体会到理论与实践相结合的重要性。
理论知识为我们提供了分析问题的框架,而实验则让我们在实际操作中运用这些知识,从而更好地理解经济学原理。
2. 数据分析能力提升经济实验要求我们收集、整理、分析数据,这对我们的数据分析能力提出了挑战。
通过实验,我学会了如何运用统计软件进行数据处理,提高了自己的数据分析能力。
3. 团队合作精神经济实验往往需要团队合作完成,这让我明白了团队合作的重要性。
在实验过程中,我们分工合作,共同解决问题,这让我学会了与他人沟通、协作,培养了团队精神。
⼀元线性回归实验报告实验⼀⼀元线性回归⼀实验⽬的:掌握⼀元线性回归的估计与应⽤,熟悉EViews的基本操作。
⼆实验要求:应⽤教材P61第12题做⼀元线性回归分析并做预测。
三实验原理:普通最⼩⼆乘法。
四预备知识:最⼩⼆乘法的原理、t检验、拟合优度检验、点预测和区间预测。
五实验内容:第2章练习12下表是中国2007年各地区税收Y和国内⽣产总值GDP的统计资料。
单位:亿元(1)作出散点图,建⽴税收随国内⽣产总值GDP变化的⼀元线性回归⽅程,并解释斜率的经济意义;(2)对所建⽴的回归⽅程进⾏检验;(3)若2008年某地区国内⽣产总值为8500亿元,求该地区税收收⼊的预测值及预测区间。
六实验步骤1.建⽴⼯作⽂件并录⼊数据:(1)双击桌⾯快速启动图标,启动Microsoft Office Excel, 如图1,将题⽬的数据输⼊到excel表格中并保存。
(2)双击桌⾯快速启动图标,启动EViews6程序。
(3)点击File/New/ Workfile…,弹出Workfile Create对话框。
在WorkfileCreate对话框左侧Workfile structure type栏中选择Unstructured/Undated 选项,在右侧Data Range中填⼊样本个数31.在右下⽅输⼊Workfile的名称P53.如图2所⽰。
图 1 图 2(4)下⾯录⼊数据,点击File/Import/Read Text-Lotus-Excel...选中第(1)步保存的excel表格,弹出Excel Spreadsheet Import对话框,在Upper-left data cell栏输⼊数据的起始单元格B2,在Excel 5+sheet name栏中输⼊数据所在的⼯作表sheet1,在Names for series or Number if named in file栏中输⼊变量名Y GDP,如图3所⽰,点击OK,得到如图4所⽰界⾯。
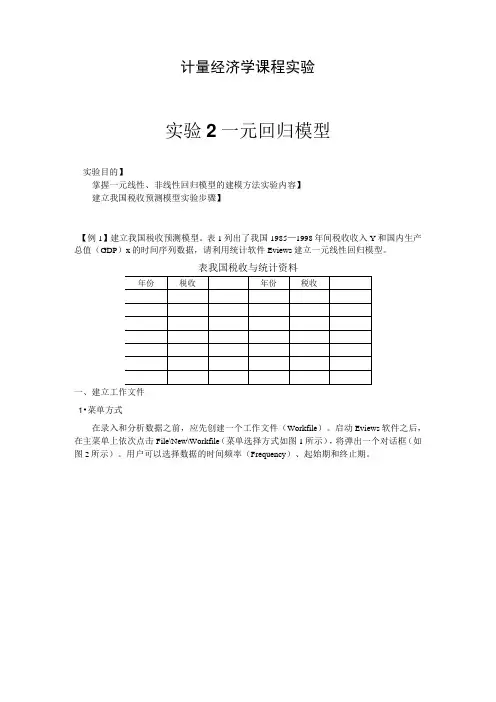
计量经济学课程实验实验2一元回归模型实验目的】掌握一元线性、非线性回归模型的建模方法实验内容】建立我国税收预测模型实验步骤】【例1】建立我国税收预测模型。
表1列出了我国1985—1998年间税收收入Y和国内生产总值(GDP)x的时间序列数据,请利用统计软件Eviews建立一元线性回归模型。
表我国税收与统计资料一、建立工作文件1•菜单方式在录入和分析数据之前,应先创建一个工作文件(Workfile)。
启动Eviews软件之后,在主菜单上依次点击File\New\Workfile(菜单选择方式如图1所示),将弹出一个对话框(如图2所示)。
用户可以选择数据的时间频率(Frequency)、起始期和终止期。
图1Eviews 菜单方式创建工作文件示意图IorkfileRangeWorkfilefrequency: <+AnnualSemi-annual〉Quarterly 〉Monthly〉WeeklyDailv[5davweeks] Dailv[7davweeks] Undatedorirregular本例中选择时嚙频率为 和9示)。
然后点击OK ,在Eviews 件的主显示窗口将显示相应 期85 3所View I Frocs I Objects阳化|tch|呂toi~e|lUeteGem~|S2豳fflffl回giTiupdlre sidTorkfile :SHUISHDU-(c:\ev±evs3\shu±shou.vf1)|""|~|"-Range:19851998Filter:DefaultEq:None Sample:19851998y图3Eviews 工作文件窗口一个新建的工作文件窗口内只有2个对象(Object ),分别为c (系数向量)和residAnnual ( )在起始栏和终止栏的工差)。
它们当前的取值分别是0和NA(空值)。
可以通过鼠标左键双击对象名打开该对象查看其数据,也可以用相同的方法查看工作文件窗口中其它对象的数值。

一元线性回归分析研究实验报告一元线性回归分析研究实验报告一、引言一元线性回归分析是一种基本的统计学方法,用于研究一个因变量和一个自变量之间的线性关系。
本实验旨在通过一元线性回归模型,探讨两个变量之间的关系,并对所得数据进行统计分析和解读。
二、实验目的本实验的主要目的是:1.学习和掌握一元线性回归分析的基本原理和方法;2.分析两个变量之间的线性关系;3.对所得数据进行统计推断,为后续研究提供参考。
三、实验原理一元线性回归分析是一种基于最小二乘法的统计方法,通过拟合一条直线来描述两个变量之间的线性关系。
该直线通过使实际数据点和拟合直线之间的残差平方和最小化来获得。
在数学模型中,假设因变量y和自变量x之间的关系可以用一条直线表示,即y = β0 + β1x + ε。
其中,β0和β1是模型的参数,ε是误差项。
四、实验步骤1.数据收集:收集包含两个变量的数据集,确保数据的准确性和可靠性;2.数据预处理:对数据进行清洗、整理和标准化;3.绘制散点图:通过散点图观察两个变量之间的趋势和关系;4.模型建立:使用最小二乘法拟合一元线性回归模型,计算模型的参数;5.模型评估:通过统计指标(如R2、p值等)对模型进行评估;6.误差分析:分析误差项ε,了解模型的可靠性和预测能力;7.结果解释:根据统计指标和误差分析结果,对所得数据进行解释和解读。
五、实验结果假设我们收集到的数据集如下:经过数据预处理和散点图绘制,我们发现因变量y和自变量x之间存在明显的线性关系。
以下是使用最小二乘法拟合的回归模型:y = 1.2 + 0.8x模型的R2值为0.91,说明该模型能够解释因变量y的91%的变异。
此外,p 值小于0.05,说明我们可以在95%的置信水平下认为该模型是显著的。
误差项ε的方差为0.4,说明模型的预测误差为0.4。
这表明模型具有一定的可靠性和预测能力。
六、实验总结通过本实验,我们掌握了一元线性回归分析的基本原理和方法,并对两个变量之间的关系进行了探讨。
一元线性回归在公司加班制度中的应用院(系):专业班级:学号姓名:指导老师:成绩:完成时间:一元线性回归在公司加班制度中的应用一、实验目的掌握一元线性回归分析的基本思想和操作,可以读懂分析结果,并写出回归程,对回归程进行差分析、显著性检验等的各种统计检验二、实验环境SPSS21.0 windows10.0三、实验题目一家保险公司十分关心其总公司营业部加班的程度,决定认真调查一下现状。
经10时间,收集了每加班数据和签发的新保单数目,x为每签发的新保单数目,y为每加班时间(小时),数据如表所示y 3.5 1.0 4.0 2.0 1.0 3.0 4.5 1.5 3.0 5.01.画散点图。
2.x与y之间大致呈线性关系?3.用最小二乘法估计求出回归程。
4.求出回归标准误差σ∧。
5.给出0β∧与1β∧的置信度95%的区间估计。
6.计算x与y的决定系数。
7.对回归程作差分析。
8.作回归系数1β∧的显著性检验。
9.作回归系数的显著性检验。
10.对回归程做残差图并作相应的分析。
x=,需要的加班时间是多少?11.该公司预测下一签发新保单0100012.给出0y的置信度为95%的精确预测区间。
E y的置信度为95%的区间估计。
13.给出()0四、实验过程及分析1.画散点图如图是以每加班时间为纵坐标,每签发的新保单为横坐标绘制的散点图,从图中可以看出,数据均匀分布在对角线的两侧,说明x和y之间线性关系良好。
2.最小二乘估计求回归程用SPSS 求得回归程的系数01,ββ分别为0.118,0.004,故我们可以写出其回归程如下:0.1180.004y x =+3.求回归标准误差σ∧ANOVA a模型 平和 自由度均 F 显著性1回归 16.682 1 16.682 72.396.000b残差 1.843 8 .230总计18.5259a. 因变量:yb. 预测变量:(常量), x由差分析表可以得到回归标准误差:SSE=1.843 故回归标准误差:2=2SSEn σ∧-,2σ∧=0.48。
计量经济学实验指导书《计量经济学》实验指导书⼭东经济学院统计与数学学院2006年11⽉6⽇⽬录实验⼀、⼀元线性回归模型 (3)实验⽬的实验内容简介实验步骤实验⼆、多元线性回归模型 (6)实验⽬的实验内容简介实验步骤实验三、异⽅差 (9)实验⽬的实验内容简介实验步骤实验四、⾃相关性 (14)实验⽬的实验内容简介实验步骤实验五、多重共线性 (18)实验⽬的实验内容简介实验步骤实验⼀、⼀元线性回归模型【实验⽬的】掌握⼀元线性回归模型的估计⽅法。
【实验内容】根据表1-1案例,建⽴⼀元回归模型。
表1-1 我国各地区2003年FDI和GDP的数据项⽬2003年FDI(万美元)2003GDP(亿元)项⽬2003年FDI(万美元)2003GDP(亿元)北京2191263663.10河南539037048.59天津1534732447.66湖北1568865401.71河北964057098.56湖南1018354638.73⼭西213612456.59⼴东78229413625.87内蒙88542150.41⼴西418562735.13辽宁2824106002.54海南42125670.93吉林190592522.62重庆260832250.56⿊龙江321804430.00四川412315456.32上海5468496250.81贵州45211356.11江苏105636512460.83云南83842465.29浙江4980559395.00陕西331902398.58安徽367203972.38⽢肃23421304.60福建2599035232.17青海2522390.21江西1612022830.46宁夏1743385.34⼭东60161712435.93新疆15341877.61【实验步骤】⼀、模型设定1.菜单⽅式建⽴⼀个新的⼯作⽂件,表1-1的数据分别命名为GDP和FDI。
建⽴⼀个数组,包含GDP和FDI两个序列。
一元线性回归分析实验报告.doc一、实验目的本实验旨在通过一元线性回归模型,探讨两个变量之间的关系,即一个变量是否随着另一个变量的变化而呈现线性变化。
通过实际数据进行分析,理解一元线性回归模型的应用及其局限性。
二、实验原理一元线性回归是一种基本的回归分析方法,用于研究两个连续变量之间的关系。
其基本假设是:因变量与自变量之间存在一种线性关系,即因变量的变化可以由自变量的变化来解释。
一元线性回归的数学模型可以表示为:Y = aX + b,其中Y是因变量,X是自变量,a是回归系数,b是截距。
三、实验步骤1.数据收集:收集包含两个变量的数据集,用于建立一元线性回归模型。
2.数据预处理:对数据进行清洗、整理和标准化,确保数据的质量和准确性。
3.绘制散点图:通过散点图观察因变量和自变量之间的关系,初步判断是否为线性关系。
4.建立模型:使用最小二乘法估计回归系数和截距,建立一元线性回归模型。
5.模型评估:通过统计指标(如R²、p值等)对模型进行评估,判断模型的拟合程度和显著性。
6.模型应用:根据实际问题和数据特征,对模型进行解释和应用。
四、实验结果与分析1.数据收集与预处理:我们收集了一个关于工资与工作经验的数据集,其中工资为因变量Y,工作经验为自变量X。
经过数据清洗和标准化处理,得到了50个样本点。
2.散点图绘制:绘制了工资与工作经验的散点图,发现样本点大致呈线性分布,说明工资随着工作经验的变化呈现出一种线性趋势。
3.模型建立:使用最小二乘法估计回归系数和截距,得到一元线性回归模型:Y = 50X + 2000。
其中,a=50表示工作经验每增加1年,工资平均增加50元;b=2000表示当工作经验为0时,工资为2000元。
4.模型评估:通过计算R²值和p值,对模型进行评估。
在本例中,R²值为0.85,说明模型对数据的拟合程度较高;p值为0.01,说明自变量对因变量的影响是显著的。
一元线性回归模型的参数估计实验报告一、实验目的通过实验了解一元线性回归模型,理解线性回归模型的原理,掌握回归系数的计算方法和用途,并运用Excel对一组数据进行一元线性回归分析,并解释拟合结果。
二、实验原理1.一元线性回归模型一元线性回归模型是指只有一个自变量和一个因变量之间存在线性关系,数学为:`Y = β0 + β1X + ε`其中,Y表示因变量的数值,X表示自变量的数值,β0和β1分别是系数,ε表示误差项。
系数是待求的,误差项是不可观测和无法准确计算的。
2.回归系数的计算方法回归系数通常使用最小二乘法进行计算,最小二乘法是一种通过最小化误差平方和来拟合数据的方法。
具体计算方法如下:(1)计算X的平均值和Y的平均值;(2)计算X和Y的样本标准差;(3)计算X和Y的协方差以及相关系数;(4)计算回归系数β1和截距β0;三、实验步骤1.导入实验数据将实验数据导入Excel,并进行清理。
2.绘制散点图在Excel中绘制散点图,判断是否存在线性关系。
3.计算相关系数通过Excel的相关系数函数计算出X和Y的相关系数。
通过Excel的回归分析函数计算出回归方程。
5.分析结果分析回归方程的拟合程度以及回归系数的意义。
四、实验结果1.数据准备通过Excel的回归分析函数,计算出回归系数为β0=1.1145,β1=2.5085,回归方程为`Y=1.1145+2.5085X`,如下图所示:(1)拟合程度:相关系数为0.870492,说明自变量和因变量之间存在一定的线性关系,回归方程的拟合程度较好。
(2)回归系数的意义:截距为1.1145,表示当自变量为0时,因变量的值为1.1145;回归系数为2.5085,表示自变量增加1个单位,因变量会增加2.5085个单位。
线性回归分析实验报告实验报告:线性回归分析一、引言线性回归是一种常用的统计分析方法,用于建立自变量与因变量之间的线性关系模型。
它可以通过对已知数据的分析,预测未知数据的数值。
本实验旨在通过应用线性回归分析方法,探究自变量和因变量之间的线性关系,并使用该模型进行预测。
二、实验方法1. 数据收集:收集相关的自变量和因变量的数据,确保数据的准确性和完整性。
2. 数据处理:对收集到的数据进行清洗和整理,确保数据的可用性。
3. 模型建立:选择合适的线性回归模型,建立自变量和因变量之间的线性关系模型。
4. 模型训练:将数据集分为训练集和测试集,使用训练集对模型进行训练。
5. 模型评估:使用测试集对训练好的模型进行评估,计算模型的拟合度和预测准确度。
6. 预测分析:使用训练好的模型对未知数据进行预测,分析预测结果的可靠性和合理性。
三、实验结果1. 数据收集和处理:我们收集了100个样本数据,包括自变量X和因变量Y。
通过数据清洗和整理,我们得到了可用的数据集。
2. 模型建立:我们选择了简单线性回归模型,即Y = aX + b,其中a为斜率,b为截距。
3. 模型训练和评估:我们将数据集分为训练集(80个样本)和测试集(20个样本),使用训练集对模型进行训练,并使用测试集评估模型的拟合度和预测准确度。
4. 预测分析:使用训练好的模型对未知数据进行预测,分析预测结果的可靠性和合理性。
四、实验讨论1. 模型拟合度:通过计算模型的拟合度(如R方值),可以评估模型对训练数据的拟合程度。
拟合度越高,说明模型对数据的解释能力越强。
2. 预测准确度:通过计算模型对测试数据的预测准确度,可以评估模型的预测能力。
预测准确度越高,说明模型对未知数据的预测能力越强。
3. 模型可靠性:通过对多个不同样本集进行训练和评估,可以评估模型的可靠性。
如果模型在不同样本集上的表现一致,说明模型具有较高的可靠性。
五、实验结论通过本实验,我们建立了一种简单线性回归模型,成功实现了对自变量和因变量之间的线性关系进行分析和预测。
实验四 一元线性回归分析
1.棉花红铃虫第一代产卵高峰日百株卵量x (粒)与百株累计卵量y (粒)的8组观测数据如下表:
棉花红铃虫第一代卵量的观测数据
(2)如果令200=x ,试求此点的预测值及置信水平05.0=α的置信区间.
2.炼钢厂出钢时所用的盛钢水的钢包,在使用过程中由于钢液及炉渣耐火材料的浸蚀,其容积不断增大.经试验得钢包的容积Y 与相应使用的次数X 的数据如下表:
钢包浸蚀数据
(1) 绘制Y 对X 的散点图,从图能否看出Y 与X 的函数关系)(x f y =?
(2) 假定Y 与X 的函数关系为①双曲线:
x
b
a y +=1,②幂函数:x
b a y +=,③对数函数:x b a y log +=,④负指数函数:x b
ae y =,试作变量变换化非线性回归为线
性,并用REG 过程建立回归方程.
(3) 比较以上四种函数关系,找出最佳的拟合曲线.。