当前位置：文档之家 › 机械振动的能量与合成共26页

机械振动的能量与合成共26页

  • 格式：ppt
  • 大小：2.53 MB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

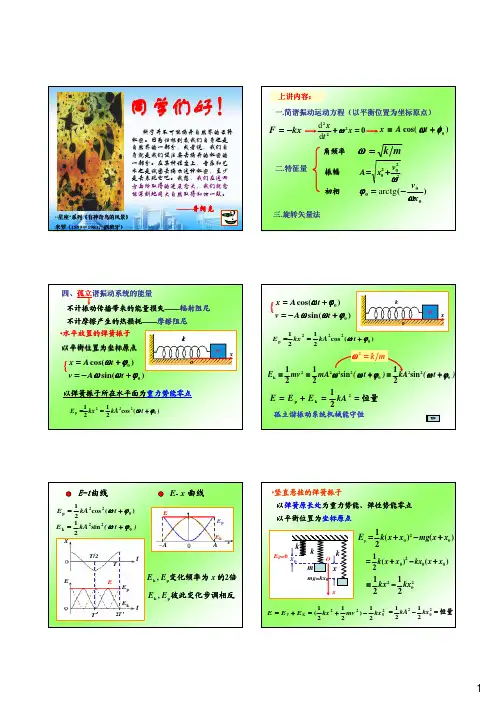
能量与振动合成

能量与振动合成

两边对时间求导： 两边对时间求导：
a= d2 x = −ω 2 x → ω → T = 2π ω dt 2
1 1 1 1 v Ek = mv 2 + Jω ′ 2 = mv2 + J 2 2 2 2 R
滑轮转动角速度
2
教材 P12 [例 [例5]
1 1 E p = kx 2 + E p滑轮 = kx 2 + c 2 2
上讲内容： 上讲内容： 一.简谐振动运动方程（ 简谐振动运动方程（以平衡位置为坐标原点） 以平衡位置为坐标原点）
F = − kx
d2 x +ω 2x = 0 dt 2
角频率
x = A cos( ω t + φ 0 )
ω = k m
ω2 v ϕ 0 = arctg ( − 0 ) ωx0
2 A = x0 + 2 v0
本节要求
掌握： 掌握：同一直线上同频率 一直线上同频率谐振动的合成 同频率谐振动的合成 了解： 了解： 1.同一直线上 1.同一直线上不同频率 同一直线上不同频率的谐振动的合成 不同频率的谐振动的合成 ，“拍” 2.频谱分析 2.频谱分析 3.互相垂直的谐振动合成 互相垂直的谐振动合成（ 互相垂直的谐振动合成（物理实验课） 物理实验课）
A1
A2
O
x
A2
3
讨论2 讨论2： 多个同一直线上, 多个同一直线上,同频率谐振动的合成
——多边形法则
An
A = A1 + A2 + ⋅ ⋅ ⋅ + An
特例： 特例：
例： 教材 P19 [例 [例1] 同一直线上 n 个同频率谐振动， 个同频率谐振动，其振幅相等而 初相依次相差一个恒量， 初相依次相差一个恒量，求合振动。 求合振动。

机械简谐振动的运动学与能量

机械简谐振动的运动学与能量

机械简谐振动的运动学与能量引言机械简谐振动是物理学中重要的概念之一，它在很多领域都有广泛的应用。

本文将介绍机械简谐振动的运动学和能量方面的内容。

首先，我们将对机械简谐振动的定义进行说明，接着讨论它的运动学表达式，最后深入探讨与机械简谐振动相关的能量变化。

机械简谐振动的定义机械简谐振动是指在无外力作用的情况下，质点围绕平衡位置做线性回复的振动。

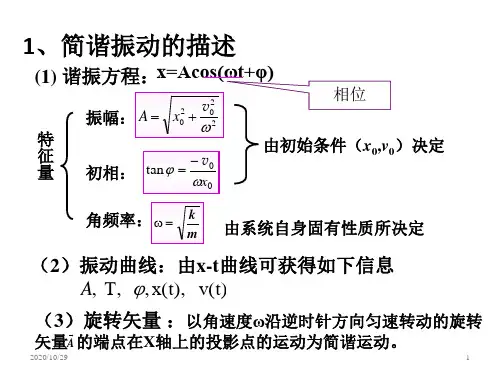
简谐振动的运动规律可以用如下的数学表达式表示：$$x(t) = A \\cdot \\sin(\\omega t +\\varphi)$$其中，x(t)表示质点在时间t时的位移，A是振幅，$\\omega$是角频率，$\\varphi$是相位常数。

机械简谐振动的运动学机械简谐振动的运动学研究主要关注质点的位移、速度和加速度随时间的变化规律。

1.位移：如前文所述，机械简谐振动的位移可以用上述的数学表达式表示。

位移随时间的变化是一个正弦曲线，振幅A决定了曲线的最大值，相位常数$\\varphi$则决定了曲线在时间轴上的平移。

2.速度：速度是位移对时间的导数，可以通过对位移函数求一阶导数得到：$$v(t) = A\\omega \\cdot \\cos(\\omega t + \\varphi)$$速度也是一个正弦曲线，它的幅值$A\\omega$是振幅和角频率的乘积，相位常数$\\varphi$则决定了曲线在时间轴上的平移。

3.加速度：加速度是速度对时间的导数，可以通过对速度函数求一阶导数得到：$$a(t) = -A\\omega^2 \\cdot \\sin(\\omega t + \\varphi)$$加速度也是一个正弦曲线，它的幅值$-A\\omega^2$是振幅和角频率的平方的乘积，相位常数$\\varphi$则决定了曲线在时间轴上的平移。

机械简谐振动的运动学分析可以帮助我们了解振动物体在不同时刻的位移、速度和加速度情况，从而更好地描述和预测振动过程。

机械简谐振动的能量在机械简谐振动中，质点的能量会随着时间的变化而发生变化。

振动的能量和合成

振动的能量和合成
x=9.810-2cos(10t+3/2) m
1 g 2 2 l
固有频率
1.6Hz
对同一谐振动取不同的计时起点不同，但、A不变。
2020/10/29
12
§9-4 简谐运动的能量特征 • 1）简谐振动的动能： 以水平的弹簧振子为例
k
m x
ox
设在任一时刻t，振子位移为x，速度为v，则其动能Ek
E 1 kA2 2
Ep
1 2
k A2
cos2 t
t Ek
1 2
m 2 A2
sin2 t
2020/10/29
16
讨论 简谐运动能量特征：
E
Ek
Ep
1 mv2 2
1 kx2 2
1 kA2 2
力学谐振系统中的振动势能
Ep
1 kx2 2
Ep一定是弹性势能吗？
答：不一定
弹性势能 水平放置的弹簧振子
振动势能 E p
2
A1
1
A1 cos1 A2 cos2 A c os
x(t) Acos(t )
A2 sin 2
A1 sin 1
X
A A12 A22 2A1A2 cos(2 1)
arctg A1 sin 1 A2 sin 2
A1 cos1 A2 cos 2
2020/10/29
23
振幅A与相差 有关。特别是
1、简谐振动的描述
(1) 谐振方程：x=Acos(ωt+φ)
相位
特
振幅： A
x02
v02
2
征 量
初相：
tan v0 x0
由初始条件（x0,v0）决定
角频率： k

大学物理机械振动简谐运动能量

大学物理机械振动简谐运动能量
16.1.5 简谐振动的能量
第16章 机械振动
16.1.5 简谐振动的能量
1
16.1.5 简谐振动的能量
第16章 机械振动
以弹簧振子为例
振子质量m，弹性系数k，振动角频率 k/m
Fkx xAcos(t) vAsin(t)
E k1 2m v21 2m 2A 2si2( n t )
E p1 2k2x1 2k2 A co 2( st)
E p=T 1T 01 2k A 2c o s2td t1 4k A 21 4m A 2 2
结论：简谐运动的动能与势能在一个周期内的 平均值相等，它们都等于总能量的一半。
6
16.1.5 简谐振动的能量
第16章 机械振动
应用：
忽略阻力，作 简谐运动的系统只 有动能和势能，且 机械能守恒，有
d
8
16.1.5 简谐振动的能量
第16章 机械振动
例：质量为 0.10kg 的物体，以振幅1.0102m
作简谐运动，其最大加速度为 4.0ms2，求：
（1）振动的周期； （2）通过平衡位置的动能； （3）总能量； （4）物体在何处其动能和势能相等？
解：（1） amaxA2
T 2π 0.314s
a max A
2
k m
EEkEp1 2kA 2A2（振幅的动力学意义）
线性回复力是保守力，作简谐运动的系统机械能守恒。
2
16.1.5 简谐振动的能量
第16章 机械振动
x,v
简谐运动能量图
ห้องสมุดไป่ตู้
xt 0
o
t xA co ts
T vt v A si n t
能量
o T T 3T T 42 4

机械振动的能量与合成

机械振动的能量与合成

简谐运动的能量与振幅的平方成正比
二、应用
•振幅
1 2
mv
2 0
1 2
kx02
1 2
kA2
•简谐运动方程
d2 x m v dt 2 k xv 0
d2 x dt 2
k m
x
0
d
dt
Ek Ep
0
例题、用机械能守恒定律求弹簧振子的
运动方程。
令 2＝ k
m
解：弹簧振子在振动过程中，机械能守恒
机械振动的能量与合成
• 简谐运动的能量 • 简谐运动的合成 • 阻尼振动、受迫振动、共振
复习题
1．什么是简谐运动？简谐运动 有何特征？如何证明一个物体是 否作简谐运动？ 2．描述简谐运动的特征量有哪 些？它们是如何计算的？ 3．什么是旋转矢量？它有何作 用？ 4．什么是单摆？什么是复摆？
9－5 简谐运动的能量
2 0
2
t
欠阻尼
阻力使周期增大
由初始条件决定A和初相位 0 ,设
t 0, x (0) x0 , v t0 v0
即有： x0 Acos v0 A sin A cos
A
x02
(v0
x0 2
)2
tg0
v0 x0 x0
情况2：过阻尼
2
2 0
x(t) C1e(
2
2 0
)
t
C e(
2
A2 sin 2
2k
A A1 A2
A1 sin 1 情况2
x (2k 1)
A A1 A2
A A12 A22 2A1 A2 cos(2 1 ) 情况3：一般情况
tg A1 sin1 A2 sin2 A1 cos1 A2 cos2

大学物理机械振动课件

大学物理机械振动课件

03 阻尼振动
阻尼振动的定义与特点
定义
阻尼振动是指振动系统受到阻力 作用，使得振动能量逐渐减少的
振动过程。
特点
随着时间的推移，振幅逐渐减小， 频率逐渐降低，直至振动停止。
阻尼力
阻尼振动过程中，系统受到的阻力 称为阻尼力，它与振动速度成正比， 方向与振动速度方向相反。
阻尼振动的描述方法
微分方程
阻尼振动的运动方程通常表示为二阶常微分方程，形式为 `m * d²x/dt² + c * dx/dt + k * x = 0`，其中 m、c、k 分别为质量、
振动压路机
利用共振原理来提高压实效果。
振动输送机
利用共振来输送物料，提高输送效率。
受迫振动与共振的能量转换
能量转换过程
外界周期性力对系统做正 功，系统动能增加；阻尼 使系统能量耗散，系统势 能减小。
转换关系
在振动过程中，外界对系 统的总能量输入等于系统 动能和势能的变化之和。
影响因素
阻尼系数、驱动力频率、 物体固有频率等。
能量耗散途径
阻尼振动的能量耗散途径 主要包括与周围介质之间 的摩擦、空气阻力、内部 摩擦等。
能量耗散的意义
阻尼振动的能量耗散有助 于减小系统振幅，避免因 过大振幅导致的结构破坏 或噪声污染等问题。
04 受迫振动与共振
受迫振动的定义与特点
定义：在外来周期性力的持 续作用下，物体发生的振动
称为受迫振动。
确定各简谐振动的振幅、相位差和频 率，在复平面内绘制振动相量，通过 旋转和位移操作找到合成振动的相量 表示。
振动合成的能量法
描述
能量法是通过分析各简谐振动的能量分布和转化，来研究振 动合成过程中的能量传递和平衡。

机械振动的能量与合成


x( t ) A0e
cos( t )
2 0 2
2 时，其解为： 0
A cos( p t )
三、共振
1、共振的概念
当强迫力的频率为某一值时，稳定受迫振 动的位移振幅出现最大值的现象，叫做位 移共振，简称共振。
2、共振角频率和共振振幅
A ＝ p
动力学方程：
阻尼 系数
d x dx m 2 C kx dt dt
2
k m
2 0
C 2m
d x dx 2 2 0 x 0 dt 2 dt
2
固有频 率
3、讨论
x(t )
•情况1：欠阻尼
2 02 x(t ) Ae t cos(t )
dv
k 2x
1
dx
0
x A cost
9－6
简谐运动的合成
一、两个同方向同频率简谐运动的合成
质点——两个同频率且在同一条直线上的简谐运动
x2 A2 cos t 2
合振动
x1 A1 cos t 1
令
A sin A1 sin 1 A2 sin 2 A cos A1 cos 1 A2 cos 2
x A1 cos( t 1 ) y A2 cos( t 2 )
合振动的轨迹方程为
x y 2 xy 2 1 sin2 2 1 2 cos 2 A1 A2 A1 A2
是个椭圆方程，具体形状由相位差决定。
2
2
讨论1
2 1 0
d Ek E p 0 dt
例题、用机械能守恒定律求弹簧振子的

机械振动的合成

A 斜率 2 A 1
y
x
质点离开平衡位置的位移
S = x + y = A + A cos(ωt +ϕ)
2 2 2 1 2 2
18
利用旋转矢量合成
∆ϕ = 0
y
2 1
y
1
8 7 6
4
2
3
4
3 7 6
4
8
x
5
5 3
2 1
5 6 7
x
19
8
x2 y2 x y 2 + 2 −2 cos(ϕ2 −ϕ1 ) = sin (ϕ2 −ϕ1 ) 2 A A A A 1 2 1 2
x1 (t ) = A cos(ω1t + ϕ ) x2 (t ) = A cos(ω 2t + ϕ )
利用三角函数关系式： 利用三角函数关系式：
cos α + cos β = 2 cos
合成振动表达式：
α−β
2
⋅ cos
α+β
2
x(t ) = A cos(ω1t + ϕ ) + A cos(ω 2t + ϕ ) (ω 2 − ω1 )t (ω 2 + ω1 )t
A=
2 A12 + A2 + 2 A1 A2 cos(ϕ 2 − ϕ 1 )
x
x
若两分振动同相位： 若两分振动同相位：
o ϕ A
o
T
ϕ = ϕ 2 = ϕ1 + 2 k π
x = ( A1 + A2 ) cos( ω t + ϕ )
A ω
A 2
1
t
合振动振幅最大， 合振动振幅最大， 两分振动相互加强。 两分振动相互加强。

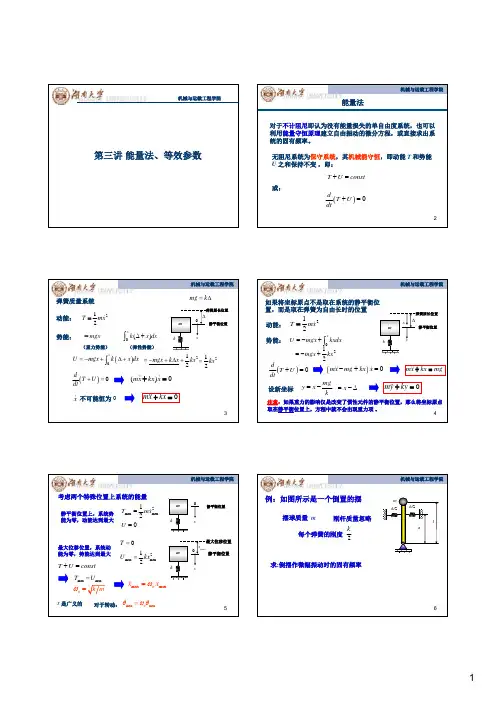
机械振动3能量法


Tmax U max ,
max n max
x
利用能量法求解固有频率时，对于系统的动能的计算只 考虑了惯性元件的动能，而忽略不计弹性元件的质量所具有 的动能，因此算出的固有频率是实际值的上限。这种简化方 法在许多场合中都能满足要求，但有些工程问题中，弹性元 件本身的质量因占系统总质量相当大的比例而不能忽略，否 则算出的固有频率明显偏高。
k mt m
弹簧的动能:
Tt 1 2 mt x 弹簧等效质量 mt 2
系统最大动能：
1 1 2 1 2 2 max mt x max max (m mt ) x mx 2 2 2 2 系统最大势能： U max 1 kxmax 2 Tmax
、 x 分别取最大值时： 当x
解法1：
广义坐标 动能 势能 平衡位置1
m k/2
零平衡位置1
解法2：
平衡位置2
m k/2 k/2 l

k/2 l

1 2 1 2 2 T I ml 2 2
a
11 2 U 2 k a mgl 1 cos 22 1 ka 2 2 2mgl sin 2 2 2
机械与运载工程学院
机械与运载工程学院
考虑两个特殊位置上系统的能量
静平衡位置上，系统势 能为零，动能达到最大
1 2 max Tmax mx 2 U 0
T 0 U max 1 2 kxmax 2
m
0
例：如图所示是一个倒置的摆
静平衡位置
m k/2 k/2 l a
k
x
摆球质量 m
刚杆质量忽略
每个弹簧的刚度
0 k mt m x
m k2

振动能量 振动合成


五、两个垂直方向不同频率简谐运动的合成 五、两个垂直方向不同频率简谐运动的合成
合成运动不是周期性的运动。下面就两种情况讨论
情况1：两个分振动的频率相差很小
ν 2 −ν1 ≈ 0 视为同频率的合成：两个振动的相位差缓
θ
l
2、运动方程
F = − mg sin θ ≈ − mgθ
2
T
（摆角小于5°)
2
d x dθ = m 2 = ml 2 dt dt
F
v mg
dθ − mgθ = ml 2 dt
2
2
d θ g + θ =0 2 dt l
2
g g 单摆的圆频率 ω = ω= l l l 1 1 频率 ν = ＝ 周期 T ＝2π T 2π g
2π (3) ωt + ϕ = 3
O
ω
t=0.5s 0.12m
ωt + ϕ =
x
π
6
ϕ
A
t=0
3π 5 3π 2π ′+ϕ = ωt ) /ω = s Δt = ( − 2 6 2 3
v
5π ϕ = − (或 ) 3 3
π
单摆——数学摆 单摆——数学摆 1、概念
单摆是一个理想化的振动系统： 它是由一根无弹性的轻绳挂一 个摆锤构成。
| A1 − A 2 |< A < | A1 + A 2 |
v A2
三、同方向、不同频率谐振动的合成 设两个初相相同，振幅、频率不同的简谐振动 t=0时合振动振幅最大，为A=A1+A2; 设ω2>ω1,则A2矢量比A1旋转更快，经历 时间 t1 =
x1 = A1 cos ω1t x2 = A2 cos ω 2t
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人，越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智，自知者明。胜人者有力，自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利
机械振动的能量与合成
16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以后的事， 只想现 在的事 。现在 有成就 ，以后 才能更 辉煌。
18、敢于向黑暗宣战的人，心里必须 充满光 明。 19、学习的关键--重复。
20、懦弱的人只会裹足不前，莽撞 人只能 引为烧 身，只 有真正 勇敢的 人才能 所向披 靡。