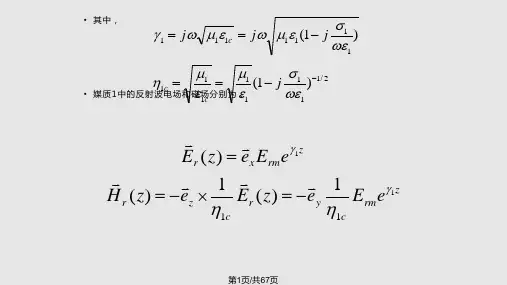当前位置：文档之家 › 电磁场理论基础 第6章PPT课件

电磁场理论基础 第6章PPT课件

  • 格式：ppt
  • 大小：1.61 MB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

6电磁场与电磁波图文图文课件.2节

6电磁场与电磁波图文图文课件.2节


4. 导电媒质中的平面波
导电媒质中电、磁场和坡印廷矢量的表达式为
Ex E0eze jz
Hy
1
~
E0eze jze j0
Sav
1 2
Re
E
H*
az
E0 2
2~
e-2z
c os 0
结论
导电媒质中的均匀平面波仍然是TEM波。 在导电媒质中的波是一个衰减的行波。电场和磁场的振幅 随距离按指数规律衰减，衰减的快慢取决于 ，称为衰减 常数，它表示场强在单位距离上的衰减，单位是Np/m。
~ k
~ j
因此电磁波的相速 不再是个常数，它 不仅取决于媒质参 数，还与信号的频
1
1
2
1
2
1
2
率有关。
1

1 2
1
2
1
2
复波阻抗 ~
~
~ e j0
结论
电磁波的相速随着频率的变化而变化的现象称为色散。因 此，导电媒质为色散媒质(dispersive medium)。 由于 、 都随着频率的变化而变化，当信号在导电媒质 中传播时，不同频率的波有不同的衰减和相移。 对于模拟信号来说，带宽为 的信号在前进过程中其波 形将一直变化，当信号到达目的地时发生了畸变，这将会 引起信号的失真； 对于数字信号来说，由于频率越高衰减越大，使到达接收 点的数字信号脉冲展宽，因此，要降低误码必然要降低信 号的传输速率，这必影响数字通信的带宽和容量。
结论
表示在传播过程中相位的变化，称为相位常数。 和
从不同的侧面反映场在传播过程中的变化，称为 传
播常数。
k~
电场与磁场不同相，
彼此间存在一个
固定的相位差!
电磁场理论 PPT课件

电磁场理论 PPT课件

• 9. 1822年，法国科学家安培提出了安培定律，将奥斯特的发 现上升为理论。 • 10. 1825年，德国科学家欧姆得出了第一个电路定律：欧姆 定律。
• 11. 1831年，英国实验物理学家法拉第发现了电磁感应定律 。 并设计了世界上第一台感应发电机。
• 12、1840年，英国科学家焦耳提出了焦耳定律，揭示了电磁 现象的能量特性。
三、电磁理论发展简史
电、磁现象是人类和大自然之间最重要的往来现象，也是 最早被科学家们关心和研究的物理现象，其中贡献最大的有富 兰克林、伏特、法拉第等科学家。 19世纪以前，电、磁现象作为两个独立的物理现 象，没有 发现电与磁的联系。
1.电现象最早的记载：公元前 600年左右（摩擦起电） 2. 1745年，荷兰莱顿大学教授马森布罗克制成了莱顿瓶，可以 将电荷储存起来，供电学实验使用，为电学研究打下了基础。 3. 1752年7月，美国著名的科学家、文学家、政治家富兰克林 的风筝试验，证实了闪电是放电现象，从此拉开了人们研究 电学的序幕。
• 13、1848年 ，德国科学家基尔霍夫提出了基尔霍夫电路理论， 使电路理论趋于完善。
• 奥斯特的电生磁和法拉第的磁生电奠定了电磁学的基础。
• 14、电磁学理论的完成者---英国的物理学家麦克斯韦 （1831~1879）。麦克斯韦深入研究并探讨了电与磁之间发 生作用的问题，发展了场的概念。在法拉第实验的基础上， 总结了宏观电磁现象的规律，引进位移电流的概念,并预言 了电磁波的存在 。这个概念的核心思想是：变化着的电场 能产生磁场；与变化着的磁场产生电场相对应。在此基础上 提出了一套偏微分方程来表达电磁现象的基本规律，称为麦 克斯韦方程组，是经典电磁学的基本方程---用最完美的数学 形式表达了宏观电磁学的全部内容 。 • 麦克斯韦从理论上预言了电磁波的存在。
《电磁场的基本理论》PPT课件

《电磁场的基本理论》PPT课件


安培
安培
10
例.半径为R=0.1m 的两块圆形平板电容器, 两板 间距为d<<R,充电过程某时刻两板之间电场的时 间变化率为 d E 1013V / m s
dt
求：1、此时刻两板间的I位; 2、两板间离中心线r1=0.02m处, r2=0.12m处的
B
E L2
I传 R L1
I传
r1 r2
d 11
q q 0 cos t
i Im sint
19
即电荷，电流都是随时间t按正弦（余弦）规律 变化的，是振荡的。
振荡电流 变化的磁场 变化的电场 变化的电场 发射电磁波
20
LC电路中的电流在自感线圈中产生磁场，电容器上的电荷在电容器
两极板间产生电场。电流和电荷相互交替地周期性变化，因此LC电
路是能产生电磁振荡的一种简单电路。
S
I传 S
D------为电位移的通量。
-
I传
充电时，板间为均匀电场
dD
d(
DS )
d(
ES )
d
S
dSΒιβλιοθήκη dQI传dt
dD I传 dt
I位
dD
dt
I传
6
讨论
（1）位移电流的大小：
I位
dD
dt
S
d
dt
将电容器中的电场随时间变化产生的磁效应， 等效为位移电流产生的。
整个电路中的电流就连续了。 （2）位移电流的方向：即 dD 的方向。
【解】
E L2
(1)因为d<<R,所以板间电场
I传 R L1
I传
均匀,忽略边缘效应。
r1
I位
dD
《电磁场理论》课件

《电磁场理论》课件

《电磁场理论》PPT课件
探索电磁场的奇妙世界。从电磁场的基本概念出发，深入了解麦克斯韦方程 组的原理，并探究电场和磁场的相互作用。
电磁场的基本概念
1 电磁场的定义
介绍电磁场的基本概念和特性，包括电场和磁场的形成和作用。
2 电磁场的方程
了解麦克斯韦方程组，掌握其含义并探索其丰富的物理意义。
3 场强和场线
电场和磁场的相互作用
洛伦兹力
探讨洛伦兹力的作用机制和应用，以及电磁场与带电粒子之间的相互作用。
电磁感应
解释电磁感应的原理和应用，研究磁场变化对电流和电动势的影响。
电磁波的产生和传播
电磁波的产生
深入了解电磁波的产生机制，探究电场和磁场的交 替在空间中的传播特性，包括传播速度、 衰减和反射等现象。
深入了解电磁感应在电动机、变压器等
电磁波的应用
2
设备中的应用原理和工作机制。
探索电磁波在通信、遥感和医学等领域
的广泛应用和前沿技术。
3
磁共振成像
介绍磁共振成像技术的原理和应用，探 究其在医学和科研领域的重要性。
总结和展望
总结电磁场理论的核心概念和主要内容，并展望未来电磁场理论的发展方向和前景。
解释电磁场强度的概念和场线的作用，以及如何分析和表示电磁场的分布情况。
麦克斯韦方程组的介绍
1
高斯定律
详细阐述高斯定律的原理和应用，探讨电场和磁场的产生和分布规律。
2
法拉第定律
深入理解法拉第定律，包括电磁感应的原理、电动势的产生和磁场变化的影响。
3
安培定律
解释安培定律的含义和应用，了解电流和磁场的相互作用及其影响。
电磁场的能量和动量
1 能量守恒定律
探究电磁场能量的来源和 转化，以及能量守恒定律 在电磁场中的应用。
电磁场讲义.ppt

电磁场讲义.ppt


第一章 矢量分析
❖ 场：物理量数值的无穷集合表示一种场。例 温度场 T r,t 与空间 r 、时间 t 有关。
场重要属性：占有空间。
• 静态场：与时间无关.
• 动态场或时变场：与空间和时间有关。
• 标量场：只需用标量函数描绘的场。例：T、t、、。
• 矢量场：需要物理矢量描绘的场。例：力场 F ，流速场 v 。
无线电远距离传播。 1894年 无线电报 1906年 无线电广播 1911年 导航 1916年 无线电话
6 2020/10/6 Jin Jie
前言
1921年 短波通信 1923年 传真 1929年 电视 1933年 微波通信 1935年 雷达 近代：无线电遥测、遥控、卫星通信、光纤通信、移动 通信等。
❖ 学习时抓概念，掌握公式、定理，灵活运用，独立完成习 题；注意总结与归纳。做课堂笔记。
四、参考书
•电磁场理论基础 牛中奇著 电子工业出版社
•电磁场理论基础 陈 重著 北京理工大学
•电磁场与波
冯恩信著 西安交通大学
•电磁场与电磁波 郭辉萍著 西安电子科技大学
•电磁学专题研究 陈秉乾著 高教出版社
•电磁场与电磁波教学指导书 赵家升等著 高教出版社
(直角坐标系)
矢量场强处场线稠密；弱处场线稀疏。 场线上的切线方向代表该处矢量场的方向。
14 2020/10/6 Jin Jie
第一章 矢量分析
1.2 矢量与矢量场的不变特性 （指与坐标系关系）
(1)空间点的曲线坐标与坐标系
空间中任一点与有序数 的曲线坐标。
一一对应，则称
坐标曲线相互正交，且符合右手定则，即
8 2020/10/6 Jin Jie
第一章 矢量分析
电磁场与电磁波_第六章PPT课件

电磁场与电磁波_第六章PPT课件


S1av S2av
第19页/共67页
6.2 均匀平面波对多层分界平面的 垂直入射
• 设有三层不同的无损耗媒质，两个分界面相互平行。媒质1与媒质2的分界面位
于 ,而媒质2厚度为d，与媒质3交界面为 • 电磁波从媒质1垂直入射，在两个分界面都要发生反射和透射
z0
z d • 媒质1与媒质2中都存在沿正z与负z方向传播的行波。媒质3中只存在沿+z方向
第27页/共67页
• 如果取媒质2的本征阻抗为
2 13
• 则：
ef 1
第28页/共67页
• 由此得媒质1和媒质2的分界面的反射数:
1 0
• 表明，只要插入四分之一波长厚度之媒质，且 媒质本征阻抗满足特定关系，则可以消除媒质1 的表面上的反射。
• 这种插入的媒质称为四分之一波长匹配层
第29页/共6r
(z)
ex
[
Eim
e
1
z
Erme1z
]
H• 媒1(质z2)中只有H透射i (波z，)其电场H和r磁(场z分) e 别为：y
1
1c
[ Eim e 1z
Erme1z ]
E2
(z)
Et
(z)
ex
Etme 2z
H2(z)
Ht (z)
ez
1
2c
Et (z)
• 合成波在空间没有移动，只是在原来的位置振动，故称这种波为驻波。
•在
的位置，电场振幅始终为0，故称这些点为电场的波节点
z n • 相对应振幅最大的位置，称为波腹点： 1
1z
n
z
n
2
(n
0,1,2,....)
1z
(2n
第6章交变电磁场课件

第6章交变电磁场课件


t
1 2
E2
1 2
mH
2
s
E2
利用矢量恒等式 ( E H ) H ( E ) E ( H )
E
H
t
1 2
E2
1 2
mH
2
s
E2
在时变场中总电磁能量密度为
于是得
w
we
wm
1E2 2
1 2
mH
2
(E
H
)
w t
p
单位体积损耗的的焦耳热为
p s E2
取体积分，并应用散度定理得
S
EH
20
例题：课本例6.4
一个漏电的圆盘电容器,其漏电导率为s, 介电常数 为, 导磁率为m0, 圆盘面积足够大以致可以忽略边
缘效应. 当电容器所加电压为U=U0cosωt时, 求电容器中任意点的磁场强度H。
解： 由第一方程
JT
H • dl C
sE
S Jd
JT Jd • dS D E
j
1 2
U0I0
sin
耗能
储能
复数形式的坡印廷定理
对于简谐振荡的电磁场 E E0e jkz H H 0e jkz
说明相位变化的方向是+z方向，电磁波能量传播的方向是
+z方 向， 时间因子包含于E0和H0中.
1 2
EH*
• dS
jw
V
1 2
mH
2 0
E02
dV
V
1 2
(s
E2 )dV
填充空气,电压为U=U0sinωt, 距离d 很小, 面 积S 较大，电容器中的电场均匀分布。
证明：流进封闭面的传导电流等于流出封闭面的位移 电流。
2020高中物理竞赛-电磁学篇(电磁场理论)06电磁波的辐射：小电流环—磁偶极子天线 (共12张PP

2020高中物理竞赛-电磁学篇(电磁场理论)06电磁波的辐射：小电流环—磁偶极子天线 (共12张PP


1
I
2 0
π
Re
0
E H
2πr 2sind
320π
4
s
2
2
【例】 设导线的长度为1米，求制作成圆环和电 偶极子天线的辐射电阻。电磁振荡频率为1MHz
电偶极子天线
小圆环天线
Rr
80π 2
L
2
0.88102
Rr
2P
I
2 0
320π
4
s
2
2
2.44 108
计算结果表明，同样频率、同样长度的导线制作
成小电流环天线的辐射阻抗远小于制作电偶极子 天线的辐射阻抗。这说明小电流环天线辐射电磁 波的能力远小于电偶极子天线。其原因何在？
4 小电流环与磁偶极子等效
在静态电磁场中，恒定小电流环可用磁偶极子等 效。在时变电磁场中，置于坐标原点的磁偶极子
m eˆ zm 的磁矢势〔参考（6-1-12)式〕为：
Ar, , jk0
电磁场理论
Electromagnetic Theory 2020高中物理竞赛 （电磁学篇）
6.3 小电流环—磁偶极子天线
1 小电流环天线结构
电流环上通有随时间谐变的电流，电流的振幅为 恒量，数学上可表示为：
如果电流环半径很小，考虑到是随位置变化的，将
其在球坐标系中表示，即
J r eˆ I0 z a
jk
r
1
1 jkr
1kLeabharlann 2Er E 0E
0 0
I0k 2ssin
4πr
e jkr
1
1
jk
r
近场区电磁场
kr 1,exp jkr 1
H
r
第6章狭义相对论(完全版1)PPT课件

第6章狭义相对论(完全版1)PPT课件


*
9
a´ = a
经典力学认为,物体的质量与运动无关，于是有 Fm 'am aF
S
S
这就是说, 力学规律(牛顿运动定律)对一切惯性 系来说,都具有相同的形式;或者说, 在研究力学规 律时，一切惯性系都是等价的。力学规律(牛顿运 动定律)在伽利略变换下的这种不变性，叫做力学 相对性原理，或伽利略相对性原理。
绝对空间的传统观点。
飞行，宇船0.8c），那么飞船上测得的长度为
0.6米！！
大家对牛顿经典力学比较熟悉，牛顿经典力学适用
于宏观、低速运动。就是包括航天科技的科学试验也服
从牛顿力学。尽管火箭速度很大，但用经典力学去研究
不会出现偏差。因为火箭的速度和光速比较，还是太小
太小。
*
5
我们来看看牛顿的经典时空观：
1 时间间隔与参考系无关 所有的惯性参考系中对两事件的时间间隔测量
结果相同。时间的长短与参考系无关。 时间间隔是绝对的。
2 空间的长短与参考系无关 所有的惯性参考系中对两事件的空间间隔测量
结果相同。空间间隔的长短与参考系无关。
空间间隔是绝对的。
*
6
3 同时性与参考系无关 如果在一个惯性参照系下看，某两个事件
同时发生；在另一个惯性系下，该二事件仍然
同时发生。 同时性是绝对的。
第6 章
狭义相对论
Einstein (1879—1955)
(special relativity)
(6)
*
1
相对论和量子理论是20世纪物理学的两个最伟 大的科学发现。我们首先介绍相对论，再讨论量子 论。
爱因斯坦的相对论分为狭义相对论和广义相对 论。前者分析时空的相对性,建立高速运动力学方 程;后者论述弯曲时空和引力理论。
电磁场理论第6章：平面波汇总

电磁场理论第6章：平面波汇总


电场强度矢量的两个分量的瞬时值为
Ex Exm cos(t kz x ) Ey Eym cos(t kz y )
(6-41)
第6章 平面电磁波
6.3.2 平面电磁波的极化形式
周晓为于2015修订
1. 线极化
设Ex和Ey同相，即φx=φy=φ0。为了讨论方便，在空间任取一固 定点z=0，则式(6-41)变为
2E
1 u2
2E t 2
0
2H
1 u2
2H t 2
0
式中
u 1/
第6章 平面电磁波
周晓为于2015修订
均匀平面电磁波指电磁场值仅沿传播方向发生变 化,在垂直于传播方向的平面上其值不变。现选传播方 向为Ｚ轴，如图所示均匀平面电磁波沿+z方向传播。
图 6-1 均匀平面电磁波的传播
第6章 平面电磁波
无激励源、无界的导电媒质中麦克斯韦方程组为
J E
H E jE E jH
H 0 E 0
(7-22a)
第6章 平面电磁波
周晓为于2015修订
式(7-22a)可以写为
H
j
j
E
j cE
其中：
c
j
1
j
经推导可得如下波动方程：
其中γ2=ω2μεc
2E 2E 0 2H 2H 0
匀平面电磁波的相关参数可以近似为
, ,
2
第6章 平面电磁波
周晓为于2015修订
（2）良导体中。有关表达式可以用泰勒级数简化并近似表达为
2
, p
2 , 2
2
c
(1 j) 2
e
j
4
高频率电磁波传入良导体后，由于良导体的电导率一般在107
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ຫໍສະໝຸດ ]可见2 t2
Ex(t)R
2 et2
(Exejt
)R
e[2Exejt]
t
Ex(t)jEx
这就是说, Ex(t)对时间t的微分运算可化为对复振幅 E x 乘以jω的 代数运算。这正是采用复数表示的一个方便之处。
8
第六章 时变电磁场和平面电磁波 设时谐电场E(t)除了分量Ex(t)外, 还有分量Ey(t)和Ez(t) 。将这3
(1)求磁场强度瞬时值H(t); (2)求电场强度瞬时值E(t)。
15
第六章 时变电磁场和平面电磁波 ［解］ （1）
H(t)Reyˆ0[.0e1j(100/3)zej25190t]
yˆ0.01co1s1 0[0t(100/3)z] (A/m)
16
第六章 时变电磁场和平面电磁波
（2）由 H j0E 知
10
第六章 时变电磁场和平面电磁波 由表2-1中式(b)、 (c)、 (d)分别得
H J j D D v
B 0
其复数形式为
Jjv
11
第六章 时变电磁场和平面电磁波
6.2.2 复数形式的本构关系和边界条件
在简单媒质中, 电磁场复矢量的关系为
D E
B H
J E
利用这些关系后, 复麦氏方程组(6-12)化为
第六章 时变电磁场和平面电磁波
§6.3 复坡印廷矢量和复坡印廷定理
6.3.1 复坡印廷矢量
由复数公式(6-5a)知,
E(t)ReE[ejt]1[Eejt E*ejt] 2
第六章 时变电磁场和平面电磁波
第六章 时变电磁场和平面电磁波
§6.1 时谐电磁场的复数表示 §6.2 复数形式麦克斯韦方程组 §6.3 复坡印廷矢量和复坡印廷定理 §6.4 理想介质中的平面波 §6.5 导电媒质中的平面波 §6.6 等离子体中的平面坡 §6.7 电磁波的色散和群速 §6.8 电磁波的极化
个分量都用复数表示, 则有
E (t)x ˆE xcot sx( )y ˆE ycot sy( ) z ˆE zcot sz( )
Rx ˆe E xe [jz( y ˆE yejy z ˆE zejz)ej t]
于是 E(t)E xˆExejz yˆEyejyzˆEzejz xˆE xyˆE yzˆE z
a'aa*, a"aa*
2
2j
a 2 aa *, ( a *)* a
(6-5a)
(a b)* a * b*
( ab ) * a * b *
a b
*
a* b*
5
第六章 时变电磁场和平面电磁波
6.1.2 复矢量
设时谐电磁场电场强度矢量E(t)的一个坐标分量为Ex(t), 它的
一般表达式为
1
第六章 时变电磁场和平面电磁波
总体概述
标题添加
点击此处输入相 关文本内容
点击此处输入 相关文本内容
标题添加
点击此处输入相 关文本内容
点击此处输入 相关文本内容
2
第六章 时变电磁场和平面电磁波
§6.1 时谐电磁场的复数表示
6.1.1 复数
复数a定义为
a a ' j" a |a |e ja |a |(c a o jss a i)n
E x(t)E xco t s(x)
6
图6-1 时谐函数Ex(t)
第六章 时变电磁场和平面电磁波
与交流电路中的处理相似, 可将Ex(t)写作:
E x (t) R E x e e j t][,E x E x e jx
式中, Re［ ］表示对括号中的量取实部。不过在习惯上, 为了简化, Re［(·)ejωt］这一符号一般都不重复列出。这样
Ex(t)(等 效 )E 于 xExejz
复数 E x 称为复振幅, 又称为相量。Ex(t) 是时间t的函数, E x 不再是t的函数而只是空间坐标的函数。Ex(t)是实数, 而 E x 是复数,
但只要取其实部便可得出Ex(t)。并有
7
第六章 时变电磁场和平面电磁波
t
Ex(t)Ret
(Exejt)Rej[Exejt
E(t)ReE e[jt]
9
第六章 时变电磁场和平面电磁波
§6.2 复数形式麦克斯韦方程组
6.2.1 复数形式麦克斯韦方程组
对表2-1麦克斯韦方程组的式(a)今有
RE e e j t][ Rje B ej[ t]
式中▽是对空间坐标的微分算子, 它和取实部符号Re可以调换次 序。从而得
EjB
a b (a ' b ') j(a " b " )
ab | a | | b | e j(a )
a | a | e j(a )
b |b|
4
第六章 时变电磁场和平面电磁波
a的共轭复数定义为
a * a ' j" a |a |e ja |a |(c a o jsa s i)n
容易证明,
式中j是虚数 , j 1 ; a′是a的实部, a″是a的虚部, 即
a' Rea[] | a| cosa a"Ima[] | a| sina
3
第六章 时变电磁场和平面电磁波
|a|称为a的模或绝对值, 又称为a的辐角, 并有
a a'2a"2 0
设复数b为 则
aArgaarcat"g a'
bb'jb "|b|ej
nˆ ( E 1 E 2 ) 0 nˆ ( H 1 H 2 ) J s nˆ ( D 1 D 2 ) s nˆ ( B 1 B 2 ) 0
14
第六章 时变电磁场和平面电磁波 例6.1 在自由空间某点存在频率为5 GHz的时谐电磁场, 其磁
场强度复矢量为
H y ˆ0.0e1 j(10/03)z (A/m )
E jH H J jE
E v
H 0
12
第六章 时变电磁场和平面电磁波
非齐次复矢量波动方程:
Ek2E j J
H k2H J
式中
k
在无源区, J =0, 上述方程化为齐次复矢量波动方程:
2E k2E 0 2H k2H 0
13
第六章 时变电磁场和平面电磁波
对有限区域求解波动方程时, 需要利用边界条件。边界条件 的复数形式与瞬时形式相同, 只是各物理量不是瞬时值而是复数 值:
E j H
0
xˆ
yˆ
zˆ
j
1010 1 109 x
y
z
36
0
0.01e j(100 /3)z 0
xˆ1.2e j(100 /3)z
E(t)Rx ˆe 1.2 [ej(1 e ] 0 /3 0)z j110 0t x ˆ1.2co1s10 0 [t(10 /0 3)z] (V/m 17 )