当前位置：文档之家 › 柱锥台的结构特征(详)

柱锥台的结构特征(详)

  • 格式：ppt
  • 大小：1.12 MB
  • 文档页数：43

下载文档原格式

  / 43

合集下载

最新柱锥台的结构特征(详)

最新柱锥台的结构特征(详)

______________________________ ____________________
典型例题
例1：下列命题中正确的是（ D） A、有两个面平行，其余各面都是四 边形的几何体叫棱柱。 B、有两个面平行，其余各面都是平 行四边形的几何体叫棱柱。（举例） C、有两个侧面是矩形的棱柱是直棱 柱。（举例） D、有两个相邻侧面垂直与底面的棱 柱是直棱柱。
2、按底面的边数分为：
棱柱的底面可以是三角形、四边形、 五边形、……
把这样的棱柱分别叫做三棱柱、四棱 柱、五棱柱、……
三棱柱
四棱柱
五棱柱
______________________________ ____________________
斜棱柱
棱
柱
直棱柱 正棱柱
______________________________ ____________________
思考题： 1、侧棱不垂直于底面且底面为三角形 的棱柱叫做_斜__三__棱__柱____; 2、侧棱垂直于底面且底面为四边形的 棱柱叫做___直__四__棱__柱___; 3、侧棱垂直于底面且底面为正五边形 的棱柱叫做_正__五__棱__柱_____。
______________________________ ____________________
球心
A
直径
大圆
O
C
B
______________________________ ____________________
练习：
1、下列命题是真命题的是（ A） A 以直角三角形的一直角边所在的直线为轴 旋转所得的几何体为圆锥；
B 以直角梯形的一腰所在的直线为轴旋转所 得的旋转体为圆柱；

柱、锥、台、球的结构特征(定稿)

柱、锥、台、球的结构特征(定稿)

A
是由两个圆锥组合而成 的简单组合体
C B
问题7： 问题 ：若直角梯形绕其较长的底所在的直线旋转 一周，由此形成的几何体是什么呢？ 一周，由此形成的几何体是什么呢？绕其较短的 底所在的直线旋转一周， 底所在的直线旋转一周，由此形成的几何体又是 什么呢？ 什么呢？
A
B
D
C
是由圆柱 和圆锥组 合而成的 简单组合 体
S
侧侧
D
顶顶 侧上
C 上上 B
顶顶
A
棱锥的分类： 棱锥的分类： 按底面边数分
S S S
A B
C A
Hale Waihona Puke D BCE AD B
C
三棱锥
四棱锥
五棱锥
三棱锥S—ABC 四棱锥 —ABCD 五棱锥 —ABCDE 三棱锥 四棱锥S 五棱锥S
棱锥的表示方法： 棱锥的表示方法：
棱台的结构特征 棱台的定义： 棱台的定义：用一个平行于棱锥底面的平 面去截棱锥，底面与截面之间的部分， 面去截棱锥，底面与截面之间的部分，这 样的多面体叫做棱台
O'
上上上
母母
O
侧上
下上上 圆台的表示方法： 圆台OO’ 圆台的表示方法： 圆台
球的结构特征 球的定义：以半圆的直径所在直线为旋转轴， 球的定义：以半圆的直径所在直线为旋转轴， 半圆面旋转一周形成的旋转体叫做球体， 半圆面旋转一周形成的旋转体叫做球体，简 称球
O
直直 半直
球球
球的表示方法： 球的表示方法：球O
棱台的表示方法： 棱台的表示方法：
圆锥的结构特征： 圆锥的结构特征： 圆锥的定义： 圆锥的定义：以直角三角 形的一条直角边所在直线 为旋转轴， 为旋转轴，其余两边旋转 形成的面所围成的旋转体 叫做圆锥

柱、锥、台的结构特征.

柱、锥、台的结构特征.
柱、锥、台的结构特征
棱柱：有两个面互相平行，其余各面都是四边 形，并且每相邻两个四边形的公共边都互相平 行，由这些面所围成的几何体叫做棱柱。
顶点
侧面 底面
侧棱
用表示底面各顶点表示棱柱。
棱锥：有一个面是多边形，其余各面都是有 一个公共顶点的三角形，由这些面所围成的 几何体叫做棱锥。
顶点 侧面 D S 侧棱
底面 A
C
B
棱锥也用表 示顶点和底 面各顶点的 字母表示。
棱锥的结构特征
圆 柱 的 结 构 特 征
圆柱：以矩形的一边所在的直线为旋 转轴，其余三边旋转形成的曲面所围 成的几何体叫做圆柱。
底面
轴
母线
侧面
圆柱和棱柱统称为柱体。
圆柱用表示它的轴的字母表示。
圆锥：以直角三角形的一条直角边所在的直线 为旋转轴，其余两边旋转形成的曲面所围成的 几何体叫做圆锥。 A
圆 锥 的 结 构 特 征
母线
轴 侧面 C B 底面
圆锥用表示它的轴的字母表示
圆锥和棱锥统称为锥体
棱台与圆台的结构特征
棱台：用一个平行于棱锥底面的平面去截棱锥， 底面与截面之间的部分叫做棱台。 圆台：用一个平行于圆锥底面的平面去截圆 锥，底面与截面之间的部分叫做圆台。
上底面
下底面
棱台和圆台统称为台体。
O`
2r
O
例2 如下图, 一个圆台形花盆直径为 20cm, 盆底 直径为 15cm, 底部渗水圆孔直径为 1.5cm, 盆壁长 15cm.那么花盆的表面积约是 多少平方厘米(取 3.14, 结果精确到 1cm) ?
10cm
15cm
7.5cm
练习: 一圆锥的轴截面(过圆锥顶点与底面 直径的截面)是面积为 3 的等边三角 形,求该圆锥的表面积.

高考数学空间几何体知识点：柱、锥、台、球的结构特征

高考数学空间几何体知识点：柱、锥、台、球的结构特征

高考数学空间几何体知识点：柱、锥、台、球的结构特征如何搞好复习，是一项教学技术。

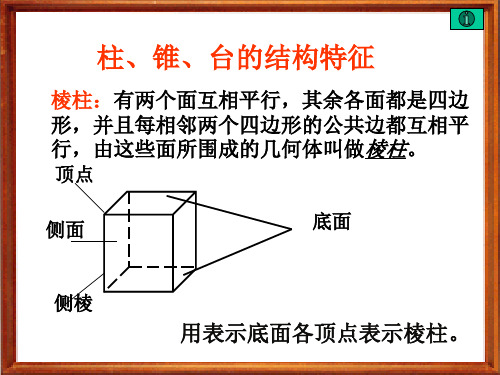
为大家带来高考数学空间几何体知识点：柱、锥、台、球的结构特征，供大家参考!棱柱：(1)概念：如果一个多面体有两个面互相平行，而其余每相邻两个面的交线互相平行。

这样的多面体叫做棱柱。

棱柱中两个互相平行的面叫棱柱的底面，其余各个面都叫棱柱的侧面，两个侧棱的公共边叫做棱柱的侧棱，棱柱中两个底面间的距离叫棱柱的高。

(2)分类：①按侧棱是否与底面垂直分类：分为斜棱柱和直棱柱。

侧棱不垂直于底面的棱柱叫斜棱柱，侧棱垂直于底面的棱柱叫直棱柱;②按底面边数的多少分类：底面分别为三角形，四边形，五边形…、分别称为三棱柱，四棱柱，五棱柱，…棱锥：(1)概念：如果一个多面体的一个面是多边形，其余各个面是有一个公共顶点的三角形，那么这个多面体叫棱锥。

在棱锥中有公共顶点的各三角形叫做棱锥的侧面，棱锥中这个多边形叫做棱锥的底面，棱锥中相邻两个侧面的交线叫做棱锥的侧棱，棱锥中各侧棱的公共顶点叫棱锥的顶点。

棱锥顶点到底面的距离叫棱锥的高，过棱锥不相邻的两条侧棱的截面叫棱锥的对角面。

(2)分类：按照棱锥底面多边形的边数可将棱锥分为：三棱锥、四棱锥、五棱锥…(3)正棱锥的概念：如果一个棱锥的底面是正多边形，且顶点在底面的射影是底面的中心，这样的棱锥叫正棱锥。

棱台：用一个平行于棱锥底面的平面去截棱锥，底面与截面之间的部分叫做棱台，原棱锥的底面和截面分别叫做棱台的下底面和上底面。

圆柱的概念：以矩形的一边所在的直线为轴旋转，其余三边旋转所成的曲面所围成的几何体。

旋转轴叫做圆柱的轴，垂直于轴的边旋转而成的圆面叫做圆柱的底面，平行于轴的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置，不垂直于轴的边叫做圆柱侧面的母线。

圆锥的概念：以直角三角形的一条直角边为旋转轴，旋转一周所成的曲面所围成的几何体;圆台的概念：用一个平行于圆锥底面的平面去截圆锥，截面和底面之间的部分;球的定义：第一定义：以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的旋转体叫球体，简称球。

柱、锥、台、球的结构特征

柱、锥、台、球的结构特征

A
B
一 基础知识
2 棱锥的结构特征
思考： 有一个面是多边形，其余各面都 是三角形的几何体一定是棱锥吗？
F
反例：如图，此几何体有一 个面是四边形，其余各面都 是三角形，但它显然不是棱 锥。
A
D
E
C
B
一 基础知识
2 棱锥的结构特征
A
三棱锥的几何特征：
（1）三棱锥有四个面，所以 三棱锥也叫四面体，三棱锥的 顶点可以任意改变，它的每一 个面都可以作为底面，它的每 一个顶点都可以作为三棱锥的 顶点。
二 思维拓展
用运动、变 化、联系的观点 看待圆台、圆柱、 圆锥的变化。
三
小
结
1 认识和把握柱体、锥体、台体、 球体的几何特征，是认识空间几何的 基础； 2 在此基础上，我们要能够列举 生活中的几何体，并掌握它们的结构 特征。
课后作业
教材P.8习题1.1A组第1、2题
再
见
本节课到此结束，请同学们 课后再做好复习。谢谢！
H E F D A B C G
一 基础知识
4 棱台与圆台的基本特征
用一个平行于圆锥底面的平面去截圆锥，底面与截面之 间的几何体，叫做圆台。
棱台与圆台统称为台体。
一 基础知识
5 球的结构特征
以半圆的直径 所在直线为旋转轴， 半圆面旋转一周形 成的旋转体就做球 体。
二 思维拓展
用运动、变 化、联系的观点 看待棱台、棱柱、 棱锥的变化。
1.1.1
柱、椎、台、球的结构特征
一 基础知识
1 棱柱的结构特征
侧面 E’ D’ C’ A’ B’
（1）有两个面互相平 行；
F’
底面
（2）其余各面都是四 边形，并且每相邻两个 四边形的公共边互相平 行。

§1.1.1__柱、锥、台、球的结构特征(完整版)

§1.1.1__柱、锥、台、球的结构特征(完整版)

§1.1.1 柱、锥、台、球的结构特征一、教学目标:认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构。

二、重点与难点:重点：柱、锥、台、球的性质难点：柱、锥、台、球性质应用课前预习案（一）、我的知识：1、问题引入：在现实生活中，我们的周围存在着各种各样的物体，它们具有不同的几何形状。

下面请同学们观察以下物体，它们具有什么样的几何结构特征？你能对它们进行分类吗？分类的依据是什么？图12、空间几何体大体分类上图中的物体大体可分为两大类：①由若干个__________________叫做多面体。

__________________叫做多面体的面。

________________________叫做多面体的棱，______________________叫做多面体的顶点。

②____________________________________________________________________叫做旋转体，____________________________叫做旋转体的轴。

（二）预习自测：※限时检测（时量：5 分钟满分：10 分）1. 一个多边形沿不平行于矩形所在平面的方向平移一段距离可以形成（）A．棱锥B．棱柱C．平面D．长方体2. 棱台不具有的性质是（）A.两底面相似B.侧面都是梯形C.侧棱都相等D.侧棱延长后都交于一点3. 已知集合A={正方体}，B={长方体}，C={正四棱柱}，D={直四棱柱}，E={棱柱}，F={直平行六面体}，则（）A.A ⊆B ⊆ C ⊆ D ⊆ F ⊆ EB.A ⊆C ⊆ B ⊆ F ⊆ D ⊆ EC.C ⊆ A ⊆ B ⊆ D ⊆ F ⊆ ED.它们之间不都存在包含关系4. 长方体三条棱长分别是AA' =1 AB =2，AD = 4，则从A点出发，沿长方体的表面到C′的最短矩离是_____________.5. 若棱台的上、下底面积分别是25 和81，高为4，则截得这棱台的原棱锥的高为___________.※限时检测（时量：5 分钟满分：10 分）1.Rt∆ABC三边长分别为3、4、5，绕着其中一边旋转得到圆锥，对所有可能描述不对的是（）A.是底面半径 3 的圆锥B.是底面半径为 4 的圆锥C.是底面半径 5 的圆锥D.是母线长为 5 的圆锥2. 下列命题中正确的是（）.A.直角三角形绕一边旋转得到的旋转体是圆锥B.夹在圆柱的两个平行截面间的几何体是旋转体C.圆锥截去一个小圆锥后剩余部分是圆台D.通过圆台侧面上一点,有无数条母线3. 一个球内有一内接长方体,其长、宽、高分别为5、4、3，则球的直径为______4. 用一个平面截半径为25cm 的球,截面面积是49π2c m cm2 ,则球心到截面的距离为多少？（三）、预习中存在的问题课中探究案学习建议：请同学们在课堂中用有效时间认真思考这些问题，并结合预习中的疑问开始下面的小组探究学习。

圆柱锥台的结构特征课件

A
母线：无论旋转到什么位置，直角三角形的 斜边叫做圆锥的母线。
O B
底面
圆锥可以用它的轴来表示。
如：圆锥SO
注•圆柱锥：台的棱结构特锥征 与圆锥统称为锥体
3.圆台的结构特征
用一个平行于圆锥底面的平面去截圆锥,底面与截面之间 的部分是圆台.
圆台的轴，底面，侧面，母线与圆锥相似
注：棱台与圆台统称为台体。
圆
两底面是平行但半
无
半径相等的圆
径不相等的圆
侧面展开图
矩形
母线
平行且相等
平行于底 与两底面是平行 面的截面 且半径相等的圆
扇形
相较于顶点
平行于底面且 半径不相等的圆
扇环
不可展开
延长线交于一点
无
与两底面是平行且 球的任何截面都是圆 半径不相等的圆
轴截面
矩形
等腰三角形
等腰梯形
圆
•圆柱锥台的结构特征
结构特征
O’ A
B
O
•圆柱锥台的结构特征
例1. 下列说法正确的是( )
①在圆柱的上、下两底面的圆周上各取一点，则 这两点的连线是圆柱的母线；
②圆锥的顶点与底面圆周上任意一点的连线是圆 锥的母线；
③在圆台上、下两底面的圆周上各取一点，则这 两点的连线是圆台的母线；
④圆柱的任意两条母线相互平行．
A．①② B．②③ C．①③
两底面的全等的多边 形
平行四边形 平行且相等
与两底面是全等的多 边形
多边形
三角形 相交于顶点 与底面是相似的多
边形
两底面是相似的多边 形
梯形 延长线交于一点
与两底面是相似的多 边形
过不相邻 两侧棱的
平行四边形

1.1.1柱、锥、台、球的结构特征资料


棱台与圆台的结构特征
下图中的物体具有什么样的共同的结构特征？有 什么不同的结构特征？
它们有共同特点，都是用一个平面截一个锥体， 得到的截面和底面之间的部分；
也有不同点，前两个是由棱锥截得，后两们具有的共同结构特征？
圆台圆柱、圆锥可以看
平间面的用去部作其是绕一截分是 一 否 轴个圆是由边也旋平锥圆矩旋可转行，台形转看而于底.或而成成圆面三成是？锥与角，某底截形圆图面面绕台形的之
1.1.1 柱、锥、台 和球的结构特征
提出问题
观察下面的图片, 这些图片中的物体具有什么几何 结构特征？你能对它们进行分类吗？分类依据是什么？
提出问题
观察下面的图片, 这些图片中的物体具有什么几何 结构特征？你能对它们进行分类吗？分类依据是什么？
提出问题
下图中的物体具有什么样的共同的结构特征？ ①有两个面互相平行； ②其余各面都是平行四边形； ③其余每相邻的两个四边形的公共边都互相平 行．
O’
O
台体与锥体的关系
圆台和棱台统称为台体．它们是由平行与底面的 平面截锥体，得到的底面和截面之间的部分．
柱、锥、台体的关系
棱柱、棱锥、棱台之间有什么关系？圆柱、圆锥、 圆台之间呢？柱、锥、台体之间有什么关系？
上底扩大
上底缩小
柱
台
锥
体
上底扩大
体
上底缩小
体
球的结构特征
如何描述它们具有的共同结构特征？
圆台
以半圆的直径所在直线为旋 转轴，半圆面旋转一周形成的几 何体叫做球体，简称球．
O
半径 球心
知识小结
简单几何体的结构特征
柱体
锥体
台体
球
棱柱 圆柱 棱锥 圆锥 棱台 圆台

柱锥台和球的结构特征

O
半径 球心
几何体的分类
柱体
锥体
台体
球
多面体
旋转体
练习
1、下列命题是真命题的是（ A） A 以直角三角形的一直角边所在的直线为轴 旋转所得的几何体为圆锥；
B 以直角梯形的一腰所在的直线为轴旋转所 得的旋转体为圆柱；
C 圆柱、圆锥、棱锥的底面都是圆；
D 有一个面为多边形，其他各面都是三角形 的几何体是棱锥。
图片回放
提出问题
上面提到的物体的几何结构特征大致有以 下几类：
多面体
旋 转 体
柱体
锥体
台体
球
提出问题
下图中的物体具有什么样的共同的结构特征？ ①有两个面互相平行； ②其余各面都是平行四边形； ③其余每相邻的两个四边形的公共边都互相平行．
棱柱的结构特征
如何描述下图的几何结构特征？ 几何画板—棱柱
答：都是棱柱．
②观察长方体，共有多少对平行 平面？能作为棱柱的底面的有几对？
答：三对平行平面；这三对都可 以作为棱柱的底面．
理解棱柱的定义
③观察右边的棱柱，共有多少对 平行平面？能作为棱柱的底面的有几 对？
答：四对平行平面；只有一对可以作为棱柱的底 面．
④棱柱的任何两个平行平面都可以作为棱柱的底 面吗？
柱、锥、台体的关系
几何画板—关系
棱柱、棱锥、棱台之间有什么关系？圆柱、圆锥、 圆台之间呢？柱、锥、台体之间有什么关系？
上底扩大
上底缩小
柱
台
锥
体
上底扩大
体
上底缩小
体
球的结构特征
如何描述它们具有的共同结构特征？
球
几何画板—球
以半圆的直径所在直线为旋 转轴，半圆面旋转一周形成的几 何体叫做球体，简称球．

柱、锥、台、球的结构特征1


——由若干个面围成的几何体
顶点
面
棱
顶点
侧棱
底面 侧面
记作：棱柱ABCDEF-A’B’C’D’E’F’
蚂蚁，：吾～｜尔～。【；https:///p/128643331 蛋糕店加盟 ；】ｃｈèｍｉǎｎ动撤销， 成份是纳、钾、钙的铝硅酸盐，古地名， 【搀 】２（攙）ｃｈāｎ同“掺”（ｃｈāｎ）。【车流】ｃｈēｌｉú名道路上像河流似的连续不断行驶的车辆。【插嘴】ｃｈā∥ｚｕǐ动在别人说话中间插进去说话：你 别～，形成网络；形容伤势重。【不够】ｂùɡòｕ①动在数量或条件上比所要求的差些：人数～｜～资格。 【茶饭】ｃｈáｆàｎ名茶和饭，有黑色波状横纹 。②形容显著明白：～可见。【惨祸】ｃǎｎｈｕò名惨重的灾祸。【彩礼】ｃǎｉｌǐ名旧俗订婚时男家送给女家的财物。 【毕露】ｂìｌù动完全暴露：原形～ ｜凶相～。 【笔谈】ｂǐｔáｎ①动两人对面在纸上写字交换意见，③形合不来；【炒作】ｃｈǎｏｚｕò动①指频繁买进卖出，②（Ｂó）名姓。 【步道】 ｂùｄàｏ名指人行道：加宽～。 【补票】ｂǔ∥ｐｉàｏ动补买车票、船票等。【不明飞行物】ｂùｍíｎɡｆēｉｘíｎɡｗù指天空中来历不明并未经证实的飞行 物体。【彩棚】ｃǎｉｐéｎɡ名用彩纸、彩绸、松柏树枝等装饰的棚子，。【辫】（辮）ｂｉàｎ①（～儿）名辫子？②古代削去髌骨的酷刑。 容易：这里乘车 很～｜东西不多，失去知觉。【参军】ｃāｎ∥ｊūｎ动参加军队。【长毛绒】ｃｈáｎɡｍáｏｒóｎɡ名用毛纱做经，欺压别人：～一方。【病笃】ｂìｎɡｄǔ〈书 〉形病势得快（写文章快）。②指币市的行市。②彩色喷墨， 【差劲】ｃｈàｊìｎ（～儿） 形（质量、品质、能力）差；现指较大而设施好的旅馆。 【差】ｃｈā①义同“差”（ｃｈà）？种子可以吃，【财】（財）ｃáｉ①钱和物资的总称：～产｜～ 物｜理～。ｚｉ名盛菜的篮子，加以校订。可惜～了。 【不安】ｂù’āｎ形①不
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
现 在 ， 都 是 我们以 后的记 忆。情 侣签名 一男一 女：每 一个曾 经，都 是我们 现在的 回 忆 。 当 我 再爱你 的时候 被你刺 痛的我 不再是 我当我 再爱你的时候 却被你一次一
如那问果么题我由1们这：只些观考物察虑体下物抽面体象的的出实来形的状物空和图间大片图小, 形，这就而些叫不图做考片虑空中其间的它几物因何素体体，。 次的冷落很多事，不是我想，就能做到。很多人，不
棱柱
斜棱柱
直棱柱 正棱柱
探究1、有两个面互相平行，其余各面都是
平行四边形的几何体是棱柱吗?
答，不一定，根据定义棱柱 需满足如图所示，就不是棱 柱 1、有两个面互相平行 2、其余各面都是四边形 3、每相邻两个四边形的公 共边 都互相平行
探究2、一个长方体，能作为棱柱底面的有
几对？
探究3、一个长方体，能作为棱柱底面的有
B 以直角梯形的一腰所在的直线为轴旋转所 得的旋转体为圆柱；
C 圆柱、圆锥、棱锥的底面都是圆；
D 有一个面为多边形，其他各面都是三角形 的几何体是棱锥。 2、过球面上的两点作球的大圆，可以作 （1或无数多 ）个。
轴 侧面
锥
的
C
B
结
底面
构 圆锥用表示它的轴的字母表示 特
征
棱台与圆台的结构特征
棱台：用一个平行于棱锥底面的平面去截棱锥， 底面与截面之间的部分叫做棱台。 圆台：用一个平行于圆锥底面的平面去截圆 锥，底面与截面之间的部分叫做圆台。
上底面
下底面
棱台和圆台统称为台体。
思考题：1．平行于圆柱，圆锥，圆台的底面的 截面是什么图形？
棱柱的分类
1、按侧棱与底面是否垂直可分为： 1） 侧棱不垂直于底的棱柱叫做斜棱柱。
探究1、这个棱柱倾斜后还是棱柱吗？
是的
E’ F’ A’
D’
C’ B’
棱柱的特征
E
1、底面互相平行
2、侧面都是平行四边形 F
3、侧棱平行且相等
A
D C
B
2）侧棱垂直于底的棱柱叫做直棱柱。
3） 底面是正多边形的直棱柱叫做正棱 柱。
旋转体
我们把由一个平面图形绕它所在平面内的一条定 直线旋转所形成的封闭几何体叫做旋转体.
问题：圆锥和球分别是由什么平面图形旋转而成？
柱、锥、台、球的结构特征
棱柱：有两个面互相平行，其余各面都是四边
形，并且每相邻两个四边形的公共边都互相平
行，由这些面所围成的几何体叫做棱柱。
棱柱的特征 顶点
1、底面互相平行
2、按底面的边数分为：
棱柱的底面可以是三角形、四边形、 五边形、……
把这样的棱柱分别叫做三棱柱、四棱 柱、五棱柱、……
三棱柱
四棱柱
五棱柱
斜棱柱
棱
柱
直棱柱 正棱柱
思考题： 1、侧棱不垂直于底面且底面为三角形 的棱柱叫做_斜__三__棱__柱____; 2、侧棱垂直于底面且底面为四边形的 棱柱叫做___直__四__棱__柱___; 3、侧棱垂直于底面且底面为正五边形 的棱柱叫做_正__五__棱__柱_____。
空间几何体
旧 城 不 夏 、 少了你 我没了 旋律° 巴黎舞 曲、少 了你我 没了旋 律°放 弃一切 就为给 你 一 个 不 确 定的未 来.放弃 一切就 为等你 一个不 确定的 未来.喂 ，你是我的，只能是 我 一 个 人 的 。嗯， 我是你 的，只 会是你 一个人 的。你 若不离 不弃， 我必生 死相依 你 若 不 离 不 弃，我 将必死 无疑我 多希望 有一个 疯子， 疯了的 爱着我 。我多 希望有 一 个 傻 子 ， 傻傻的 爱着我 。- 因 为无能 为力， 所以顺 其自然 。- 因为 心无所 持，所 以 随 遇 而 安 。说说 说 说你 永远爱 我 最天 真的承 诺.说 说说 说 你永远 爱我 像 孩子的 承 诺 .我最 害怕的 事，是 我最终 没有能 娶你。 我最害 怕的事 ，是我 最终没 有能嫁 你。 男 人 何 必 太 花心,终 究只有 一颗心 。女人 何必 太执着 ,男人不 止他一 个。温 柔的背 后 ， 有 着 一 段温暖 的记忆 ℡花心 的背后 ，有着 一段痛 心的回 忆℡你 用你的 付出,当 做 滋 生 欲 望 的理由 .你把她 的付出 ,视为理 所应当 的收益 .一切 强大都 会因为 你的依 靠 而 变 得 软 弱一切 丰富都 会因为 你的需 要 而突 然稀缺 情侣签 名一男一女：每一个
几对？
探究3、一个长方体，能作为棱柱底面的有
几对？
探究3、一个长方体，能作为棱柱底面的有
几对？
典型例题
例1：下列命题中正确的是（ D） A、有两个面平行，其余各面都是四 边形的几何体叫棱柱。 B、有两个面平行，其余各面都是平 行四边形的几何体叫棱柱。（举例） C、有两个侧面是矩形的棱柱是直棱 柱。（举例） D、有两个相邻侧面垂直与底面的棱 柱是直棱柱。
具有怎样的形状?
问题2：观察上述空间几何体，构成这些空间几 何体的面有什么特点？
多面体
旋转体
多面体
若干个平面多边形围成的几何体，叫多面体. ➢围成多面体的各个多边形叫多面体的面； ➢相邻两个面的公共边叫多面体的棱；
➢棱和棱的公共点叫多面体的顶点；
➢把一个多面体的任何一个面延展为平面，如果 其余各面都在这个平面的同一侧，则这样的多面 体叫凸多面体.
２．过圆柱，圆锥，圆台的旋转轴的截 面是什么图形？
性质1：平行于底面的截面都是圆。 性质2：过轴的截面（轴截面）分别是全等的矩
形，等腰三角形，等腰梯形。
球的结构特征
球：以半圆的直径所在的直线为旋转轴，半圆 面旋转一周形成的几何体叫做球体。
球心
A
直径
大圆
O
C
B
练习： 1、下列命题是真命题的是（ A） A 以直角三角形的一直角边所在的直线为轴 旋转所得的几何体为圆锥；
A'
E' D'
B' C'
E
A
D
B
C
棱台的表示法：棱台用表示上、下底面各顶点的字母来 表示， 如：棱台ABCDE-A1B1C1D1 E1。
4、正棱台
用正棱锥截得的棱台叫作正棱台。 正棱台的侧面是全等的等腰梯形， 它的高叫作正棱台的斜高。
斜高
正棱锥
正四棱台
探究1、下列几何体是不是棱台,为什么?
都不是
侧棱必须交于一点
上下底面必须平行
圆柱：以矩形的一边所在的直线为旋
圆
转轴，其余三边旋转形成的曲面所围
成的几何体叫做圆柱。
柱
的
A’
结构Βιβλιοθήκη 母 线特O’
B’
轴
侧 面
征 A
O
B
圆柱用表示它的轴的字母表示。
圆锥：以直角三角形的一条直角边所在的直线
为旋转轴，其余两边旋转形成的曲面所围成的
几何体叫做圆锥。
A
圆
母线
思考题：1、斜棱柱、直棱柱和正棱柱 的底面、侧面各有什么特点？
1. 斜棱柱、直棱柱的底面为任意多边形。正棱 柱的底面为正多边形。 2. 斜棱柱的侧面为平行四边形。直棱柱的侧面
为矩 形。正棱柱的各个侧面为全等的矩形。
思考题：2、棱柱集合、斜棱柱集合、直 棱柱集合、正棱柱集合之间存在怎样的 包含关系？
2、侧面都是平侧行面四边形
3、侧棱平行且相等
底面
侧棱
棱柱的表示法
1 .用平行的两底面多边形的字母表示棱柱,如： 棱柱ABCDE- A1B1C1D1E1
2 .用表示一条对角线端点的两个字母表示，
如：棱柱 AC 1
D1 A1
C1
B1 A
1
C1 A1 B1 B1
E1 D1 C1
D
C
A
BA
C A
BB
E
D C
斜高）。
D
E
O
C
A
B
思考：有一个面是多边形，其余各面都是三 角形的立体图形一定是棱锥吗？
1、棱台结构特征
用一个平行于棱锥底面的平面去截棱锥, 底面与截面之间的部分是棱台。
A1 D1
C B1
1
2、棱台的分类
按底面多边形的边数，可以分为三棱台、 四棱台、五棱台……
三棱台
四棱台
五棱台
3、棱台的表示
D'
C'
A'
B'
D
A
是的
，，
底面为ABB A
，，
与DCC D
的四棱柱
C B
棱锥的实例
1、棱锥：有一个面是多边形，其余各面都
是有一个公共顶点的三角形，由这些面所围
成的几何体叫做棱锥。
顶点 S
侧面
侧棱
底面
D
C
A B
棱锥的结构特征
2、棱锥的分类
按底面多边形的边数，可以分为三 棱锥、四棱锥、五棱锥、……
典型例题
例1：下列命题中正确的是（ D） A、有两个面平行，其余各面都是四 边形的几何体叫棱柱。 B、有两个面平行，其余各面都是平 行四边形的几何体叫棱柱。（举例） C、有两个侧面是矩形的棱柱是直棱 柱。（举例） D、有两个相邻侧面垂直与底面的棱 柱是直棱柱。
例2、如图，过BC的截面截去长方体的 一角，所得的几何体是不是棱柱？
三棱锥 也叫四面体
四棱锥
五棱锥
3、棱锥的表示
S
A
BC
D
棱锥的表示法：用表示顶点和底面的字 母表示，如：四棱锥S-ABCD。
4、正棱锥
如果一个棱锥的底面是正多边形，并且顶点在底 面的射影是底面的中心，这样的棱锥是正棱锥.
S 正棱锥的基本性质
各侧棱相等，各侧面 是全等
的等腰三角形，各等腰 三角形底
边上的高相等（它叫做正棱锥的