农大理论力学与材料力学作业第二套答案

理论力学规范化 练习册 答案
2008.12
精选课件
1
静力学
精选课件
2
精选课件
3
精选课件
4
精选课件
5
精选课件
6
精选课件
7
精选课件
8
精选课件
9
精选课件
ቤተ መጻሕፍቲ ባይዱ10
精选课件
11
精选课件
12
精选课件
13
精选课件
14
精选课件
15
精选课件
16
精选课件
17
精选课件
18
运动学
精选课件
19
精选课件
20
精选课件
21
精选课件
22
精选课件
23
精选课件
24
精选课件
25
精选课件
26
精选课件
27
精选课件
28
精选课件
29
精选课件
30
精选课件
31
精选课件
32
精选课件
33
动力学
精选课件
34
精选课件
35
精选课件
36
精选课件
37
精选课件
38
精选课件
39
精选课件
40
精选课件
41
精选课件
42
精选课件
43
精选课件
44
精选课件
45
精选课件
46
精选课件
47
精选课件
48
精选课件
49
精选课件
50
精选课件
51
精选课件
52
精选课件

理论力学第二版习题答案理论力学第二版习题答案理论力学是力学的基础学科，它研究物体在力的作用下的运动规律。

对于学习理论力学的学生来说，做习题是非常重要的一部分，通过做习题可以巩固理论知识，提高解题能力。

本文将为大家提供理论力学第二版习题的答案，希望对广大学生有所帮助。

第一章：牛顿力学的基本概念和基本定律1. 问题：一个质点从速度为v0的位置自由下落，求它下落的时间。

答案：根据自由下落的运动学公式，下落的时间t可以通过以下公式计算：t =√(2h/g)，其中h为下落的高度，g为重力加速度。

由于自由下落是垂直向下的，所以h可以表示为h = (1/2)gt^2。

将h代入上述公式，可得t = √(2h/g) =√(2(1/2)gt^2/g) = √t^2 = t。

2. 问题：一个质点在水平方向上以初速度v0做匀速直线运动，求它在时间t内所走的距离。

答案：由于匀速直线运动的速度保持不变，所以在时间t内，质点所走的距离s 可以通过以下公式计算：s = v0t。

第二章：质点的运动方程1. 问题：一个质点在x轴上做直线运动，其运动方程为x = 2t^2 + 3t + 1，求其速度和加速度。

答案：质点的速度可以通过对运动方程求导得到：v = dx/dt = 4t + 3。

质点的加速度可以通过对速度求导得到：a = dv/dt = 4。

2. 问题：一个质点在y轴上做直线运动，其运动方程为y = 3t^3 + 2t^2 + t，求其速度和加速度。

答案：质点的速度可以通过对运动方程求导得到：v = dy/dt = 9t^2 + 4t + 1。

质点的加速度可以通过对速度求导得到：a = dv/dt = 18t + 4。

第三章：质点系和刚体的运动1. 问题：一个质点系由两个质点组成，质点1质量为m1，质点2质量为m2，它们之间通过一根质量可忽略不计的绳子连接，求质点系的重心位置。

答案：质点系的重心位置可以通过以下公式计算：x = (m1x1 + m2x2)/(m1 + m2)，其中x1和x2分别为质点1和质点2的位置坐标。

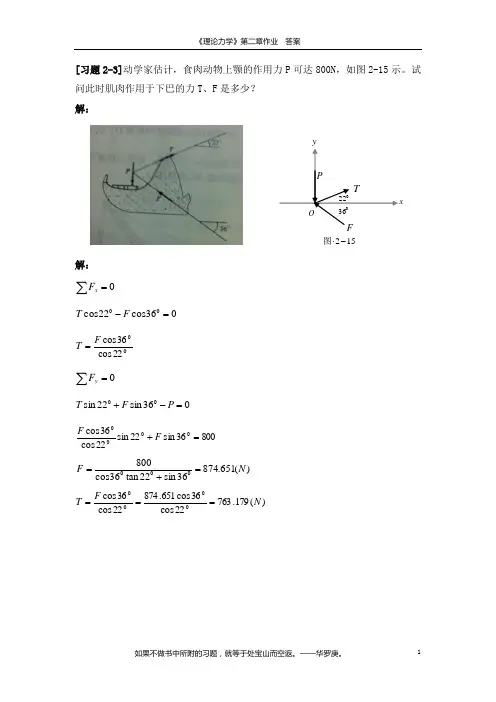
xyPTF22036O152-⋅图[习题2-3]动学家估计，食肉动物上颚的作用力P 可达800N ，如图2-15示。

试问此时肌肉作用于下巴的力T 、F 是多少？ 解：解：0=∑xF036cos 22cos 00=-F T22cos 36cos F T =0=∑yF036sin 22sin 00=-+P F T 80036sin 22sin 22cos 36cos 000=+F F )(651.87436sin 22tan 36cos 80000N F =+=)(179.76322cos 36cos 651.87422cos 36cos 000N F T ===182-⋅图B[习题2-6] 三铰拱受铅垂力P F 作用，如图2-18所示。

如拱的重量不计，求A 、B 处支座反力。

解：0=∑x F0cos 45cos 0=-θB A R RB A R l l l R 22)23()2(222+=B A R R 10121=B A R R 51=0=∑yF0sin 45sin 0=-+P B A F R R θP B A F R l l l R =++22)23()2(2321P B A F R R =+10321的受力图轮A P B B F R R =+⨯1035121P B F R =104P P B F F R 791.0410≈=31623.0101)23()2(2cos 22≈=+=l l l θ0565.71≈θ P P P A F P F R 354.04241051≈=⨯=方向如图所示。

[习题2-10] 如图2-22所示，一履带式起重机，起吊重量kN F P 100=，在图示位置平衡。

如不计吊臂AB 自重及滑轮半径和摩擦，求吊臂AB 及揽绳AC 所受的力。

解：轮A 的受力图如图所示。

0=∑x F030cos 20cos 45cos 000=--P AC AB F T R的受力图轮A 603.869397.07071.0=-AC AB T R AC AB T R 3289.1476.122+=0=∑yF030sin 20sin 45sin 000=---P P AC AB F F T R010*******.07071.0=---AC AB T R 1503420.07071.0=-AC AB T R1503420.0)3289.1476.122(7071.0=-+⨯AC AC T T 1503420.09397.06023.86=-+AC AC T T 3977.635977.0=AC T )(069.106kN T AC ≈)(432.263069.1063289.1476.1223289.1476.122kN T R AC AB =⨯+=+=解法二：用如图所示的坐标系。

理论力学第二版习题答案理论力学是物理学中研究物体运动规律的基础学科，它包括经典力学、相对论力学和量子力学等。

在经典力学中，牛顿运动定律是核心内容，而理论力学则进一步发展了这些定律，提供了更深入的分析和理解。

第二版的理论力学教材通常会包含更丰富的习题和更详尽的解答，以帮助学生更好地掌握力学的基本概念和方法。

习题1：牛顿运动定律的应用题目：一个质量为m的物体在水平面上受到一个恒定的力F作用，求物体的加速度。

解答：根据牛顿第二定律，力F等于物体质量m与加速度a的乘积，即F=ma。

因此，物体的加速度a等于力F除以质量m，即a=F/m。

习题2：动能和势能的计算题目：一个质量为m的物体从高度h自由落体，求落地时的动能。

解答：物体在自由落体过程中，重力势能转化为动能。

落地时的动能E_k等于重力势能的减少量，即E_k=mgh。

习题3：圆周运动的动力学分析题目：一个质量为m的物体以角速度ω在半径为R的圆周上做匀速圆周运动，求物体所受的向心力。

解答：匀速圆周运动的向心力F_c由公式F_c=mω^2R给出，其中m是物体的质量，ω是角速度，R是圆周的半径。

习题4：简谐振动的周期计算题目：一个质量为m的弹簧振子，弹簧的劲度系数为k，求其振动周期。

解答：简谐振动的周期T可以通过公式T=2π√(m/k)计算，其中m是振子的质量，k是弹簧的劲度系数。

习题5：刚体转动的动力学分析题目：一个均匀分布质量的刚体，其转动惯量为I，角速度为ω，求其转动动能。

解答：刚体的转动动能E_r可以通过公式E_r=0.5Iω^2计算，其中I是转动惯量，ω是角速度。

习题6：相对论效应的讨论题目：一个质量为m的物体以接近光速的速度v运动，求其相对论质量。

解答：在相对论中，物体的相对论质量m_r可以通过洛伦兹变换公式m_r=m/√(1-v^2/c^2)计算，其中m是静止质量，v是物体速度，c是光速。

习题7：量子力学的初步介绍题目：简述量子力学与经典力学的主要区别。

材料力学习题第二章答案材料力学习题第二章答案材料力学是工程力学的重要分支，主要研究物质在外力作用下的变形和破坏规律。

在学习材料力学的过程中，习题是不可或缺的一部分。

通过解答习题，可以巩固理论知识，提高问题解决能力。

本文将针对材料力学习题第二章进行解答，并探讨其中的一些重要概念和原理。

第一题：一根长为L，截面积为A的均匀杆件，两端分别受到大小相等、方向相反的拉力F。

求该杆件的伸长量。

解答：根据胡克定律，杆件的伸长量与拉力成正比。

设伸长量为ΔL，则有ΔL = FL/EA，其中E为杨氏模量。

根据题意，两个拉力的大小相等，方向相反，因此合力为零。

根据牛顿第三定律，合力为零时，杆件处于力的平衡状态，即ΔL = 0。

因此，该杆件的伸长量为零。

第二题：一根长为L，截面积为A的均匀杆件，受到大小为F的拉力，使其产生弹性变形。

求该杆件的应变能。

解答：应变能是指物体在外力作用下所储存的能量。

对于弹性杆件，应变能可以通过应力-应变关系来计算。

设杆件的应变为ε，则有ε = σ/E，其中σ为杆件的应力。

应变能的计算公式为U = (1/2)σεV，其中V为杆件的体积。

将应力-应变关系代入，可得U = (1/2)σ^2V/E。

根据题意，杆件受到大小为F的拉力，应力为F/A，体积为AL，因此应变能为U = (1/2)(F^2/A^2)(AL)/E。

第三题：一根长为L，截面积为A的均匀杆件，受到大小为F的拉力，使其产生塑性变形。

求该杆件的塑性应变。

解答：塑性变形是指杆件在超过弹性极限后，无法恢复原状的变形。

对于塑性材料，应力-应变关系是非线性的。

设杆件的塑性应变为εp，则有εp = σp/E，其中σp为杆件的塑性应力。

根据题意，杆件受到大小为F的拉力，应力为F/A。

塑性应力通常大于弹性极限，因此可以将塑性应力近似为弹性极限σy，其中σy 为屈服强度。

由此可得塑性应变为εp = σy/E。

通过以上习题的解答，我们可以看到材料力学中一些重要的概念和原理的应用。

理论力学第二版习题集答案理论力学是物理学的基础课程之一，它研究物体在力的作用下的运动规律。

对于理论力学的学习，习题是非常重要的一部分，通过解答习题可以加深对理论知识的理解和应用能力的提升。

本文将为读者提供《理论力学第二版》习题集的答案，帮助读者更好地掌握理论力学的知识。

第一章：牛顿力学1. 一个质点以速度v沿着x轴正方向运动，它受到一个与速度方向垂直的恒力F。

求质点的运动轨迹。

答：由于质点受到的力与速度方向垂直，所以质点的速度大小保持不变。

根据牛顿第二定律，质点受到的力与速度方向垂直，所以质点的加速度与速度方向垂直。

因此，质点的运动轨迹是一个圆。

圆心位于速度方向的反方向上，圆的半径为质点的速度大小除以加速度的大小。

2. 一个质点以速度v在半径为R的圆周上运动，它受到一个与速度方向垂直的恒力F。

求质点的加速度大小。

答：由于质点受到的力与速度方向垂直，所以质点的速度大小保持不变。

根据牛顿第二定律，质点受到的力与速度方向垂直，所以质点的加速度与速度方向垂直。

因此，质点的加速度大小等于质点的速度大小除以运动半径。

第二章：拉格朗日力学1. 一个质点在一个势能为V(r)的保守力场中运动，其中r为质点到力场中心的距离。

求质点的运动方程。

答：根据拉格朗日方程，质点的运动方程可以通过势能函数V(r)求导得到。

运动方程为m(d²r/dt²) = -dV/dr，其中m为质点的质量。

通过求解这个微分方程，可以得到质点的运动方程。

2. 一个质点在一个势能为V(x)的保守力场中运动，其中x为质点的位移。

求质点的运动方程。

答：同样地，根据拉格朗日方程，质点的运动方程可以通过势能函数V(x)求导得到。

运动方程为m(d²x/dt²) = -dV/dx，其中m为质点的质量。

通过求解这个微分方程，可以得到质点的运动方程。

第三章：哈密顿力学1. 一个质点在一个势能为V(q)的保守力场中运动，其中q为广义坐标。

显然，B’C’段内的切应力分布和BC段的切应力分布相对于z 轴对称，方向相同，因此切应力的合力必大小相等，方向 相同，（题12.8图（c））
材料力学（II ）Mechanics of Materials 上海电力学院
材料力学（II ）Mechanics of Materials 上海电力学院
cc截面与B截面之间的面积（题12.8图（b））对z轴 的面矩为
b1 0
τ1δ1dξ
=
ξ F b1 Sy b1 −ξ
0
2Iz
δ1dξ
= FSyb13δ1
12Iz
根据合力矩定理，合力对一点之矩，等于其分力对同一点之
矩的代数和，可以证明
为 和 F S y
F S1
F S2
的合力。如
对B点取矩，水平方向剪应力的合力和剪力对B点之矩为零，
故有
FS y e = FS1 h
从上上式求得弯曲中心位置
⎤ ⎥ ⎦
=
24 bh2
Fl
=
24 × 6 × 103 × 1.25 75 × 10 −3 × 150 2 × 10 −6
Pa
= 107 M P a (拉 )
材料力学（II ）Mechanics of Materials 上海电力学院
B点的坐标为
yOB
=
h 3
zOB
=
−
b 3
带入广义弯曲应力公式，得
的壁厚 δ为常量，且壁厚及开口切缝都很小。
解: 如图（b）所示。开口处B面与bb截面间的面积 对在z轴的面距为
S
* z
=
(ξ δ
)ξ
2
=
δξ 2
2
⎛ ⎜⎝
0

一．选择题（8个）1. 图示矩形截面直杆，右端固定，左端在杆的对称平面内作用有集中力偶，数值为M 。

关于固定端处横截面A －A 上的内力分布，有四种答案，根据弹性体的特点，试分析哪一种答案比较合理。

( C )2. 图示直杆ACB 在两端A 、B 处固定。

关于其两端的约束力有四种答案。

试分析哪一种答案最合理。

( D)3.平衡微分方程中的正负号由哪些因素所确定？简支梁受力及Ox 坐标取向如图所示。

试分析下列平衡微分方程中哪一个是正确的。

( D) （A ）)(d d Q x q x F =；Q d d F xM=； （B ）)(d d Q x q x F -=，Q d d F xM-=； （C ）)(d d Q x q x F -=，Q d d F xM=； （D ）)(d d Qx q xF =，Q d d F xM-=。

4.若要在已知力系上加上或减去一组平衡力系，而不改变原力系的作用效果，则它们所作用的对象必需是( C )(A) 同一个刚体系统； (B) 同一个变形体；(C) 同一个刚体，原力系为任何力系；(D) 同一个刚体，且原力系是一个平衡力系。

5.图示机构，以整体为对象，以下所列的平衡方程中，哪一个是正确的( C )(A) ∑m O (F) = - m + P ⋅b = 0(B) ∑m O (F) = - m + N A ⋅b/cos θ + N D ⋅L = 0 (C) ∑m O (F) = - m + P ⋅b + N D ⋅L = 0(D) ∑m O (F) = - m + P ⋅b + N A ⋅ b/cos θ + N D ⋅L = 0B PO DCθm A Lb6.图示均质圆轮绕通过其圆心的水平轴转动，轮上绕一细绳，绳的右端挂一重为P 的重物，左端有一重量也是P 的小孩，图(a)的小孩站在地面上，拉动细绳使重物上升；图(b)的小孩离地在绳上爬动而使重物上升。

问以下的几种说法中，哪一个是正确的？( B )(A) 两种情况，其整个系统（指小孩、圆轮和重物一起）对转轴的动量矩都守恒。

理论力学（郝桐生）第一章习题1-1．画出下列指定物体的受力图。

解：习题1-2．画出下列各物系中指定物体的受力图。

解：习题1-3．画出下列各物系中指定物体的受力图。

解：第二章习题2-1．铆接薄钢板在孔心A、B和C处受三力作用如图，已知P1=100N沿铅垂方向，P2=50N沿AB方向，P3=50N沿水平方向；求该力系的合成结果。

解：属平面汇交力系；合力大小和方向：习题2-2．图示简支梁受集中荷载P=20kN，求图示两种情况下支座A、B的约束反力。

解：(1)研究AB，受力分析：画力三角形：相似关系：几何关系：约束反力：(2) 研究AB，受力分析：画力三角形：相似关系：几何关系：约束反力：习题2-3．电机重P=5kN放在水平梁AB的中央，梁的A端以铰链固定，B端以撑杆BC支持。

求撑杆BC所受的力。

解：(1)研究整体，受力分析：(2) 画力三角形：(3) 求BC受力习题2-4．简易起重机用钢丝绳吊起重量G=2kN的重物，不计杆件自重、磨擦及滑轮大小，A、B、C三处简化为铰链连接；求杆AB和AC所受的力。

解：(1) 研究铰A，受力分析（AC、AB是二力杆，不计滑轮大小）：建立直角坐标Axy，列平衡方程：解平衡方程：AB杆受拉，BC杆受压。

(2) 研究铰A，受力分析（AC、AB是二力杆，不计滑轮大小）：建立直角坐标Axy，列平衡方程：解平衡方程：AB杆实际受力方向与假设相反，为受压；BC杆受压。

习题2-5．三铰门式刚架受集中荷载P作用，不计架重；求图示两种情况下支座A、B的约束反力。

解：(1) 研究整体，受力分析（AC是二力杆）；画力三角形：求约束反力：(2) 研究整体，受力分析（BC是二力杆）；画力三角形：几何关系：求约束反力：习题2-6．四根绳索AC、CB、CE、ED连接如图，其中B、D两端固定在支架上，A端系在重物上，人在E点向下施力P，若P=400N，α=4o，求所能吊起的重量G。

解：(1) 研究铰E，受力分析，画力三角形：由图知：(2) 研究铰C，受力分析，画力三角形：由图知：习题2-7．夹具中所用的两种连杆增力机构如图所示，书籍推力P作用于A点，夹紧平衡时杆AB与水平线的夹角为；求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。

农大理论力学与材料力学作业第二套答案理论力学与材料力学第2套您已经通过该套作业,请参看正确答案1、正应力公式σ＝N/A的应有条件是（）A.材料服从胡克定律B.弹性范围内加载C.N的作用线通过截面形心且垂直于截面D.ABC三条件同时具备参考答案：C2、拉压杆变形公式的应用条件是（）A.弹性范围加载，在长度L内轴力为常量B.材料服从胡克定律并在弹性范围内加载C.只要在长度L内轴力为常量D.BC两条件同时具备参考答案：D3、关于低碳钢试样拉伸至屈服时，有如下结论（）A.应力和塑性变形很快增加，因而认为材料失效B.应力和塑性变形虽然很快增加，单不意味着材料的失效C.应力不增加塑性变形很快增加，因而认为材料失效D.应力不增加塑性变形很快增加，但不意味着材料失效参考答案：C4、仁兴材料冷作硬化之后，材料的力学性能发生下列的变化（）A.屈服强度提高，弹性模量降低B.屈服强度提高，韧性降低C.屈服强度不变，弹性模量不变D.屈服强度不变，韧性不变参考答案：B5、低碳钢加载-卸载-加载途径有以下四种，如图2-1（）图 2-1A.OAB-BC-COABB.OAB-BAO-ODBC.OAB-BAO-ODBD.OAB-BD-DB参考答案：D6、图2-2所示结构中，各段杆的横截面面积均为A，材料的拉压许用应力均为[σ],可以算得其许可载荷[P]=3A[σ]/2。

现将BC段杆改名为中空的，横截面面积减小为A/2,这时结构的许可载荷[P]等于（）图 2-2A. A[σ]B.3A[σ]C. A[σ]/2D.3A[σ]/2参考答案：A7、关于弹性体受力后某一方向的应力与应变关系，有如下论述（）A.有应力一定有有应变，有应变不一定有应力B.有应力不一定有有应变，有应变不一定有应力C. 有应力不一定有有应变，有应变一定有应力D. 有应力一定有有应变，有应变一定有应力参考答案：B8、材料的三个弹性常数之间的关系，G=E/[2(1+ν)]成立的条件是（）A.各向同性材料，应力不大于比例极限B.各向同性材料，应力大小无限制C.任意材料，应力不大于比例极限D.任意材料，应力大小无限制参考答案：A9、杆纯弯曲时，截面保持平面，在下列那种情况下是正确的（）A.直杆，弹性范围B.直杆，弹性和塑性范围C.直杆和曲杆，弹性范围D.直杆和曲杆、塑性范围参考答案：D10、弯曲变形时截面保持平面导致正应变沿截面高度方向线性分布，只有在下列那种情况下才是正确的（）A.直杆，弹性范围B.直杆，弹性和塑性范围C.直杆和曲杆，弹性范围D.直杆和曲杆、塑性范围参考答案：B11、由正应变沿截面高度线性分布导致正应力沿截面高度方向线性分布，只有在下列那种情况下才是正确的（）A.直杆，弹性范围B.直杆，弹性和塑性范围C.直杆和曲杆，弹性范围D.直杆和曲杆、塑性范围参考答案：A12、根据弯曲正应力的分析过程，中性轴通过截面形心的条件是（）A.轴力为零，正应力沿截面高度线性分布B.轴力为零C.正应力沿截面高度线性分布D.轴力为零，弹性范围参考答案：A13、下列关于纯弯曲应力和变形公式的适用条件，那些是正确的（）A.平面弯曲，弹性范围B.弹性范围C.仅适用于对称弯曲和弹性范围D.所有平面弯曲参考答案：A14、关于平面弯曲，对称弯曲和非对称弯曲之间的关系，有下列论述（）A.只有对称弯曲才可能是平面弯曲B.对称弯曲和非对称弯曲都可能是平面弯曲，也可能是斜弯曲C.对称弯曲必为平面弯曲，非对称弯曲不一定是平面弯曲D.对称弯曲一定是平面弯曲，非对称弯曲必为非平面弯曲参考答案：C15、承受相同弯矩的三根直梁，其截面组成方式分别如图(a)、(b)、(c)所示。

P u \:PN1PD[ u TO 0$ FRV FRV PD[PD[u M 00]PN1 $ VLQ VLQ PD[PD[u M 00\PN1PD[PD[ u uu u \\]]$:0:0V 03D \$%PO\¸¸¹·¨¨©§ ¸¸¹·¨¨©§]\\]\],T ,T (O Z Z Z¸¸¹·¨¨©§u u ¸¸¹·¨¨©§u u u uuPuu uu uuPPhPPhPP%]]:0PD[PD[V \\:0PD[PD[VPD[\%\%%Z Z Z Z &%]&$]&$&%\&\&\%O (,O)(,O )O Z Z u uTPu u u u u K Z ,]]u u u u u u u u u u u u u \%Z P u Pu u u u uE Z ,\\\$%]%(,O )ZPu u u u u u u)PD[]0u:03D PN1PD[ uV =\U\³³1GG$$)$$VV³³GG$$$\($\(UU³³GG$$$\,$\,,(,(U³³GG$$$\($\(@>@>QQQQ[\\E(\K[\E(&&\[\[K$E[$[K EQ&&\$(\$(\$($(N1)*3DZ(UV\(]³³GG$$$\($\(UU]6]]6(6(@>@>uuuuuuuu KKKPP³³³³G G G G $$$$,(,($\($\($\$\0UUU VV¦6 6 \)\)0$,\\PPH$DVLQ U $6]$WDD D VLQ VLQ VLQ 6 6 6UW )W U $U $)W ,6)DD VLQ U H |$TD$DD D D D D FRV VLQ FRV VLQ UH\PPP\PD[uuuu uG G 0:0VVHH$VV))%VVV$)&&VVVVVVV$)$)$)&&$)%V V ¦ D)D )D )0%$FRVV X D V $)VV VFRV V V D V $)FRVV V V V)))) V V D V V V)X)PPPP'GVVVXuuuu³G7G WUWUPN1@>VVKXuuu³G'7'G WUWUXV777VVVVVVU5UUU75UU³³WWUUWUUWUW75UW75UV::EFWFVGVLQGTG M UU$\666:GGGGGU UUUUGGGGGGU UUUUUVEK EK ::03DVV PPu u \\\F W V\\\66: uPP @ > u u \P N1 V V X u u u :0VPPPP KE 03DVVD$X X0O T O )00%$XD OD O T D O )%X XD OD O T D O D O TDE(GO)(GO)G (O )($O )9LLL ¦u[G [)991DFO[T[[0dd³³O O[[0[[0(,9(,O TO TO T(,[TO[T[(,OO@>@GG>³³($O )[[0[[0(,9OO@G G >1DEHV %$[$&³³ HH HH H H V@>''''HDOO[$$&$&$&»»»¼º«««¬ªD%OO%%Y[$\$$%$%$%$%''H[$\$D D%''F$DD(,)O)9$\FG($O)(,O)9ww'O)OT)T+$')GGG(,D 0\0[[D[0D (,09D D0%%%G GHH HE9$'¿¾½¯®­³³9³³w wOO[[TO[TO [[TO[TO (,)9)$'(,TO$%%³³w wO O ))$\O )\O )(,[[)(,)9GG$' )))9 w wGG$TGG%TGG @>³³w w O O $\)\(,[[T[[TO)(,)9%,$%$%D&0&³³ O O \\)\\)(,9G G^ H ³G @ >O &[[O 0)O )`G @> [)O [O 0)O &³E@GG >DD[D)D \)\(,)9(,)D&T &&T &0FG@>GG^³³³ DDD [[D )\)D [)[`G @ >G G 9 $%'³³³w w D D D [[D )\)D [)[(,)9G@ >G G ^³³ DD\\))D [)[G G ³ DD )D )>G @[[+ $%'S9$%'$$$FFTw w$%0$%$%09T³³SG VLQ FRV G FRV VLQ TT T T T T )5*,5)5(,5S*,)5$%DDTTT VLQ $%TFRV($O )($O )9$&$&$%$%$))))$&$%+$'($)D )9)$%D'%9D%E³³ O O '[[T[;[(,[[[TO ;(,G G ' (,;O O T O ;(,O TO ;(,O;)O O [);O [0 w w ³³ O O $[O )O O [);O (,[[;[O )(, G @G 'O )O O );O (,O O ;O )O (,);)$)D 0$)D 0%I))D;;;E;³TO ;O;EE;;;³D[T[(,9;;9FED N1 N1 ;N1 N1 ;PN1 D ;0%PN1TE E ;D ;0&TD TDTDTD 016$%&TGO[[;[0ddwwww[0[;wwwwdd[7;7O[;[7O[;)[[;[0ddwwww;0[;O[;7O;7O;[7ddwwww³³@GG> O O[[;)[[;[[[;(,'³O3[O O;*,G(,*, SSO;O)O;(,*,O;)O;O;³G FRV VLQ VLQ T T T T (,)5 (,)5(,)5G VLQ $0$50)5(,TT T³E>FRVFRV TT T5;)50 @G@>(,)5 @(,)5G VLQFRVFRV T T T T '55)5(,;$\³FRV FRVFRVT T T (,)5TT T T G FRV VLQVLQ$;³G FRV T T T 5)5(,;$³(,)5FFRV T w w 5)³G FRV FRV T T T(,)5(,)5G VLQ FRV TT T '55)5(,;$\³G FRV TT T 5)5(,;$(,)5GVLQVLQ dd w w T T T T 55))5)5055T³³5$\55)5(,[[)[(,G VLQ VLQ T T T (,)5(,)5(,)5G FRV VLQ T T T '55)5(,;$[³G VLQGTT T³(,)5(,)5(,)5HG VLQ VLQ T T T '55)5(,$]³³³SGFRV FRV G FRV T TT T T *,)5(,)5@`^@w w w w ;7;0\³ $$$G @ VLQ FRV > T T '555(,;$[G VLQ VLQ T T T MT 5)5(,$³PPG *3D('O )7)O [7 w w³³ O O '(,[O )O (,[[)[(,G G '³³ OO[O )O *,[[)[SGG S S*,)O (,)O *,)O O O O (,)u u u uu u u uu u u u u u u u)*['[GG G G G G '' '*&*%*$*G 'G G 'G G 'G ' '*&*%*$*GGG GG 'O($O($)9L LL %%[DEO [OO [TO [0d dEO [[[0d d³O$[(,[0[0 GT ³ G O [(,T[[(,O [TO O O G @ > ³ (,TO (,TO(,TOFD$EO [[[0d d[O O [[[0O [Od d³O&[(,[0[0 GG ³ H G O [(,[[O 0³ O O [(,[O 0[O 0 H H G(,O 0(,O 0(,O 0 H H HFO [O[[0d dGD$O [T[[0d dO[O O [TO T[[0d dEO[[[0d dO[O O[O [[[0d d³G@>OO[(,O[O[TOT[(,TOP Pd d[[[[[0($F(,D$E%$ '&F&' & ' E) ) 1³³ DD [(,[)[[(,[)[G G (,)DF%&''EFGD'&)[[0+' '@G G > ³³ DD [D [D )[[)D (, (,)DG[0[0'T ³³³ D D D[[D )[)D [)[(, @G G G >(,)D&%)D [0&&F&%[0%$[0 [7EO[7 &&³ O[O TO *,S GS*,TO (,TOFVLQFRVT T T 5G VLQFRVFRV T T T T 55)5(,!S (,)5³FRV 5G )5(,$TTF))[[05[d dVLQ T T )50(,)5³³SG VLQ FRV G FRV VLQ TT T T T T T )5*,)5(,$ S*,)5(,)5$T$$G$DK$KO [0d d TE(,)O Z Z$%EF。

二、 杆件受力如图所示，计算 BC 段的轴力时分离体的最佳取法是（ ）
【A】
【B】
【C】
【D】 解：正确答案为【D】； 【A】 分离体上不能带有支座，因为支座处的支反力要影响分离体的平衡（如下图所示），
因此必须将支座去除，用相应的支反力取而代之； 【B】 用截面法计算轴力时，不要在集中力作用点上取截面，因为此处的受力比较复杂，
为了保险起见，建议大家用 的公式来计算线应变。从这个公式可以看出，当材料相同的时， E
线应变的变化规律与正应力的变化规律相同，正应力发生变化的截面上，线应变也将发生变化。
三、图示立柱由横截面面积分别为 A 和 2A 的 AB 和 BC 段组成，已知材料的容重为 ，弹性模量为 E，则
解：正确答案为【A】。 [B]问题出在分子上的 3，在用胡克定律计算变形时分子上要用轴力，而不能用杆件上作用的外力。 [C]这是一个常见的错误，很多同学会仿照对变形进行分段累加的算法来计算线应变，要注意变形有累 加意义，即一段杆件的总的变形量等于每个分段变形量的代数和；但是线应变指的是在一个很小的范围 内杆件的变形程度，可以简单地将线应变理解成是属于某个截面的。当一段杆件受力均匀时，这段杆件 各个横截面上的线应变都是相等的，你可以笼统地说这段杆件的线应变是多少，但是当两段杆件的轴力 不同时，只能说两段杆件的线应变个各是多少，而不能把两段杆件的线应变加起来。不要说是两段杆件 的线应变，即便是把两个截面不同的线应变加起来都没有任何力学意义。就像汽车在公路上行驶，在第 一段上是一个速度，在第二段上是另一个速度，显然把这两个速度加起来是没有什么意义的。 [D]当两段杆件的变形程度不同时，不能像本选项那样将两段杆件连在一起，一次性计算线应变，必须 是各算各的。
在材料力学中采用“突变”的形式来处理。在这种处理方式下，这个截面上的轴力 是不确定的，在材料力学中绘制出来的集中力作用截面附近的轴力图，如下图所示， 此时只需要求出集中力作用截面左右两条线代表的轴力值即可，因此，应该在集中 力作用截面的左右两侧取计算截面。，而不要把计算截面取在集中力的作用截面上。

材料力学第二版课后答案1. 弹性力学。

1.1. 什么是材料的弹性？材料的弹性是指材料在受力后能够恢复原状的性质。

当外力作用于材料上时，材料会发生形变，但在去除外力后，材料会恢复到原来的形状和尺寸。

1.2. 什么是胡克定律？胡克定律是描述弹性体在弹性变形时，应力和应变之间的关系。

它可以用数学公式表示为，σ = Eε，其中σ表示应力，E表示弹性模量，ε表示应变。

1.3. 什么是杨氏模量？杨氏模量是描述材料抗拉伸性能的指标，它表示单位面积内的拉应力增加一个单位的长度时，材料的伸长量。

杨氏模量的计算公式为，E = σ/ε。

2. 塑性力学。

2.1. 什么是材料的塑性？材料的塑性是指材料在受力后会发生永久性变形的性质。

当外力作用于材料上时，材料会发生塑性变形，去除外力后，材料无法完全恢复原状。

2.2. 什么是屈服点？屈服点是材料在受力过程中，应力-应变曲线上的一个特殊点，表示材料从弹性变形进入塑性变形的临界点。

在屈服点之后，材料会发生永久性变形。

2.3. 什么是材料的硬度？材料的硬度是指材料抵抗外力压入的能力。

硬度测试可以用来评价材料的耐磨性、耐压性等性能，常用的硬度测试方法包括洛氏硬度、巴氏硬度等。

3. 断裂力学。

3.1. 什么是断裂韧性？断裂韧性是材料抵抗断裂的能力。

它是指材料在受到外力作用时，能够吸收大量的能量而不发生断裂的能力。

3.2. 什么是脆性断裂？脆性断裂是材料在受力过程中，发生迅速、不可逆的断裂现象。

脆性断裂的特点是断裂前往往不伴随明显的塑性变形。

3.3. 什么是韧性断裂？韧性断裂是材料在受力过程中，发生缓慢、可逆的断裂现象。

韧性断裂的特点是断裂前伴随明显的塑性变形，能够吸收大量的能量。

4. 疲劳力学。

4.1. 什么是疲劳寿命？疲劳寿命是指材料在受到交变应力作用下，经过一定次数的循环载荷后发生疲劳断裂的次数。

4.2. 什么是疲劳强度？疲劳强度是指材料在受到交变应力作用下，能够承受的最大应力水平，也可以理解为材料的抗疲劳能力。

解 册究対繼*晦矍*曲：/」平衛ii 殳宦廉，交廉”的钓痕力耳欝珊谊寸c 乃向如I 用 b 陌示.収啪杯爺Cy*血平胡那论鬥式⑴* (?)峡立・解紂佔2…已暂 F 兰5 am N .棗与撑祎自虫不计匚求 BC'ffK 内力及铁员 的反力。

解该系统曼力如图(訂， 三力匸交于艰0・苴封訥的力 三角膠如图冷人祥得 屉二5OOON 』仏 二疔000 W2-2在铰链A 、B 处有力F i , F 2作用，如图所示。

该机 F i 与F 2的关系。

2-3铰链4杆机构CABD 的CD 边固定, 构在图示位置平衡，不计杆自重。

求力 30T >◎60°检(b)B解⑴柠点掐坐WAS 力如囲 归所示"H3平祈刖论咼节点瓦腿标歴覺力如国 所小*血丫轉理论得2S -F^ ccs 30fr -f ； cosW ）0 =0^=-^=—^— = 1.553^F 、: - 0.644已扣两伦备車P A ^P L •处于T册状态,杆電不比求I ）若片=丹=巴 角e -?2）若 P A - 300 B = 0血=?ffi 八5两轮受力分别 如图示■对A 辂育SX = 0* F 刚 cEjedO* — F\g oos$ = 0SY 二 0a F sx tin60T - F 屈 sinfl - P A = tj对 B 轮育 SX ■ 0, Fn ooa? - F,\&8^3(/ = 0 IV = 0. F rw sinff 下 F 斶 anJO* - P n =(1) 四牛封程嬴立求AL 爾＜3-30*(2) 把拧-0\F A - 300 M 代入方社，联立解筹P fl = 100 N2-5如图2-10所示，刚架上作用力F 。

试分别计算力F解 M A (F) = -FbcoseM s [F) - -Fb cos0 + FosinB二F(osiii0-bcos0)2-6已知梁AB 上作用1力偶，力偶矩为M ，梁长为I ，梁重不计。

力学第二版习题答案力学是物理学中的一个重要分支，它研究物体在力的作用下的运动规律。

在力学的学习过程中，习题练习是巩固理论知识和提高解题技巧的重要手段。

以下是力学第二版习题的一些参考答案，供同学们参考和学习。

习题1：牛顿运动定律的应用问题：一个质量为m的物体在水平面上受到一个恒定的拉力F，求物体的加速度。

答案：根据牛顿第二运动定律，\[ F = ma \]。

因此，物体的加速度\( a = \frac{F}{m} \)。

习题2：动量守恒定律问题：两个质量分别为m1和m2的物体，以速度v1和v2沿同一直线相向而行，它们相撞后粘在一起。

求碰撞后物体的共同速度v。

答案：根据动量守恒定律，碰撞前后系统的总动量不变。

设碰撞后速度为v，有：\[ m1v1 - m2v2 = (m1 + m2)v \]解得：\[ v = \frac{m1v1 + m2v2}{m1 + m2} \]习题3：能量守恒定律问题：一个质量为m的物体从高度h处自由下落，忽略空气阻力。

求物体落地时的动能。

答案：根据能量守恒定律，物体的势能转化为动能。

物体落地时的动能Ek为：\[ Ek = mgh \]习题4：圆周运动问题：一个物体在水平面上以速度v做匀速圆周运动，半径为r。

求物体所受向心力。

答案：物体做匀速圆周运动时，向心力Fc由下式给出：\[ Fc = \frac{mv^2}{r} \]习题5：简谐振动问题：一个质量为m的弹簧振子，其弹簧常数为k。

求振子的振动周期。

答案：简谐振动的周期T由下式给出：\[ T = 2\pi\sqrt{\frac{m}{k}} \]习题6：刚体的转动问题：一个均匀圆盘，质量为M，半径为R，绕通过其对称轴的轴旋转。

求圆盘的转动惯量。

答案：对于均匀圆盘，其转动惯量I为：\[ I = \frac{1}{2}MR^2 \]习题7：流体力学基础问题：一个不可压缩流体在水平管道中流动，流速为v。

求管道横截面上的压强差。

答案：根据伯努利方程，管道两端的压强差\( \Delta P \)为：\[ \Delta P = \frac{1}{2}\rho v^2 \]其中，\( \rho \)是流体的密度。

材料力学第二版答案材料力学是研究材料的力学性能和行为的学科，它是材料科学与工程中的重要基础学科之一。

材料力学的研究对象是各种材料在受力作用下的变形、断裂和破坏行为，以及其力学性能的表征和评价。

材料力学的发展对于材料的设计、加工、应用和改性具有重要的指导作用，因此在材料科学与工程领域中具有重要的地位。

本文档将针对材料力学第二版中的一些问题进行详细的解答和讨论，希望能够帮助读者更好地理解和掌握材料力学的相关知识。

1. 什么是材料的应力应变关系？材料的应力应变关系是指材料在受力作用下的应力和应变之间的关系。

在弹性阶段，材料的应力应变关系是线性的，可以用胡克定律来描述。

而在材料超过弹性极限后，应力应变关系将变得非线性，材料会发生塑性变形，这时需要考虑材料的屈服点和应力应变曲线的非线性特性。

2. 材料的断裂行为有哪些特点？材料的断裂行为是材料力学研究的重要内容之一。

材料的断裂行为具有脆性和韧性两种不同的特点。

脆性断裂是指材料在受到较大应力作用下会迅速发生断裂，而韧性断裂则是指材料在受到较大应力作用下会出现一定程度的变形和吸能，使得材料具有一定的韧性和延展性。

材料的断裂行为受到材料本身的性质、受力条件和环境因素的影响。

3. 如何评价材料的力学性能？评价材料的力学性能需要考虑材料的强度、韧性、硬度、刚度等多个方面的指标。

强度是指材料抵抗外部力量破坏的能力，韧性是指材料在受力作用下发生变形和吸能的能力，硬度是指材料抵抗表面划伤和穿刺的能力，刚度是指材料抵抗变形的能力。

这些指标综合反映了材料的力学性能，对于材料的选择和设计具有重要的意义。

4. 材料的疲劳行为有哪些特点？材料的疲劳行为是指材料在长期交变应力作用下发生疲劳断裂的现象。

材料的疲劳行为具有很强的随机性和不可预测性，疲劳断裂往往是突然发生的，对于材料的安全性和可靠性具有重要的影响。

因此，研究材料的疲劳行为对于材料的设计和应用具有重要的意义。

总之，材料力学是一个复杂而又重要的学科，它涉及到材料的力学性能和行为，对于材料的设计、加工、应用和改性具有重要的指导作用。

1-1 图示曲线规尺的杆长200OA AB ==mm ，而50CD DE AC AE ====mm 。

如果OA 绕O 轴转动的规律是5/t πϕ=，初始时0t =，求尺上D 点的运动方程和轨迹。

解：A 点运动已知，欲求D 点运动，可从D 点相对A 点的几何出发求解。

以,,(,,,,)i i x y i A B C D E =分别表示各点的,x y 坐标。

由OA AB =，CD DE AC AE ===可知：运动过程中ACDE 始终为一个平行四边形，从而：D A x x =，2A D C y y y += OA 绕O 轴转动，转角5tπϕ=∴cos 200cos5A t x OA π=ϕ=，sin 200sin 5A t y OA π=ϕ= s i n ()s i n 150s i n 5C ty O CO A A C π=ϕ=-ϕ= ∴ 200cos 5D A t x x π==(mm)， D C 2100sin 5A ty y y π=-=(m m)得到D 点的运动方程为：22221200100D Dx y +=1-2 图示AB 杆长为l ，绕B 点按t ϕω=的规律转动。

与杆连接的滑块按sin s a b t ω=+的规律沿水平线作简谐振动，其中a 、b 、ω为常数，求A 点的轨迹。

解： 点A 的运动为滑块B 与杆AB 二者运动的合成。

在oxy 坐标中，t 时刻x x l y l A B A =+=sin ,cos ϕϕ代入 x s a b B ==+sin ϕ，可得A 的轨迹为122=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+-l y l b a x A A1-3 半径为r 的半圆形凸轮以等速0v 在水平面上滑动，如图所示，求当︒=30θ瞬时顶杆上升的速度大小与加速度大小（杆与凸轮的接触点为M ）。

解：由已知条件可得M 点的坐标为0=x ，22002022)(tv t rv t v r r y -=--=，则y 方向上的速度和加速度分别为：202y rv t =（1）22002200220022002022/)(2tv t rv tv t rv t v r v t v t rv v y------= （2）当30=θ时，r t v r 230=-，即r t v )231(0-=代入（1）式和（2）式，可以得到x0303|v y == θ，r r y 20308|-== θ1-4 半径为R 的圆弧与AB 墙相切，在圆心O 处有一光源，点M 从切点C 处开始以等速度0υ沿圆弧运动，如图所示，求M 点在墙上影子'M 的速度大小与加速度大小。