2017二年级学而思秋季数学超常班讲义第五讲

随堂测 3 >
如图，△ABC 中，∠BAC 的平分线交 BC 于点 D，AB = AC +CD，∠C = 80◦，那么 ∠B 的度数
是
◦．
随堂测 4 >
如图，△ABC 是边长为 3 的等边三角形，△BDC 是等腰三角形，且 ∠BDC = 120◦．以 D 为
顶点作一个 60◦ 角，使其两边分别交 AB 于点 M，交 AC 于点 N，连接 MN，则 △AMN 的周
（1）如图 1，当 ∠MAN 绕点 A 旋转到 BM = DN 时，有 BM + DN = MN．当 ∠MAN 绕点 A 旋转 到 BM ̸= DN 时，如图 2，请问图 1 中的结论是否还成立？如果成立，请给予证明，如果不成 立，请说明理由．
（2）当 ∠MAN 绕点 A 旋转到如图 3 的位置时，线段 BM、DN 和 MN 之间有怎样的数量关系？请 写出你的猜想，并证明．
3
模块 2 倍长中线
5
模块 3 截长补短
8
第 2 讲 全等辅助线（二）
12
模块 1 角平分线相关的辅助线
13
模块 2 “半角”模型
16
第 3 讲 全等三角形综合提高
22
模块 1 全等三角形辅助线综合
24
第 4 讲 轴对称综合
28
模块 1 等腰三角形的综合证明
29
模块 2 等腰三角形与动态问题
B. 2 < AD < 14 D. 无法确定
融会贯通
如图，AD 是 △ABC 的 BC 边上的中线，AB = 7，AD = 5，则 AC 的取值范围为
．
6
初二 | 数学 | 菁英班
例 3 ★★★☆ 如图，在 △ABC 中，AD 为 BC 边上的中线，E 为 AC 边上的一点，BE 交 AD 于点 F，已知 AE = EF．求证：AC = BF．

一年级寒假班第一讲突破加减竖式第二讲巧填算符初步第三讲剪拼图形第四讲图文代换第五讲巧移物体第六讲左右脑开发3（逻辑推理）第七讲期末测评二年级寒假班第一讲认识倍第二讲带余除法初步第三讲有趣的自然数串第四讲分割图像第五讲枚举法的妙用第六讲鸡兔同笼初步第七讲期末测评三年级寒假班第一讲角度初识第二讲速算与巧算之四则运算第三讲字母表示数第四讲和差倍第五讲倒退与图示第六讲方阵三年级春季班第一讲巧填算符第二讲小数的认识第三讲平行四边形与梯形第四讲年龄问题第五讲带余除法初步第六讲简单统计第七讲图形计数初步第八讲组合中的点线关系第九讲等差数列初步第十讲页码问题第十一讲标数法第十二讲简易方程第十三讲简易方程应用第十四讲路程速度与时间第十五讲期末测评四年级暑假班第一讲简单抽屉原理第二讲奇数和偶数第三讲二次相遇问题第四讲应用题：假设法和还原法（鸡兔同笼，还原问题，方阵综合应用）第五讲应用题：图示法和对应法（年龄，盈亏，平均数综合）第六讲图形计数进阶第八讲四边形中的基本图形第九讲体育比赛中的数学第十讲期末测评四年级秋季班第一讲定义新运算第二讲体育比赛中的数学问题第三讲图形计数进阶第四讲多位数计算第五讲等积变型第六讲一半模型第七讲最值问题初步第八讲数阵图初步—从幻方谈起第九讲平均数进阶第十讲破译乘除法竖式第十一讲方程和方程组第十二讲方程组解应用题第十三讲环形跑道第十四讲火车过桥第十五讲期末测评四年级寒假班第一讲小数巧算第二讲格点与割补第三讲数表从日历谈起第四讲第五种运算（乘方的认识，运算性质，平方差认识）第五讲质数合数初步第六讲包含与排除第七讲期末测评四年级春季班第一讲等积变形第二讲整数与数列第三讲统筹和最优化第四讲加乘原理进阶第五讲最值问题进阶第六讲抽屉原理初步第七讲流水行船第八讲方程与方程组第九讲一半模型第十讲相遇与追及综合第十一讲平移、选择和对称第十二讲破译横式（奇偶分析，枚举试算）第十三讲进位制初步第十四讲数阵图进阶第十五讲期末测评五年级暑假班第一讲分数乘除第二讲分数加减第三讲棋盘中的数学第四讲枚举法进阶第五讲排列组合初步第六讲质数合数进阶（因数个数、因数个数的正反应用）第七讲列方程组解应用题第八讲牛吃草第九讲数阵图综合第十讲比和比例第十一讲比例模型第十二讲分组和配对（高斯求和，分组和配对思想）第十三讲容斥原理第十四讲必胜策略第十五讲期末测评五年级秋假班第一讲因数和倍数初步第二讲循环小数第三讲鸟头模型第四讲分数应用题第五讲电梯和发车第六讲神奇的9第七讲蝴蝶模型第八讲排列组合进阶第九讲工程问题初步第十讲几何计数进阶第十一讲数字谜中的最值第十二讲燕尾模型第十三讲定义新运算进阶第十四讲方程法解行程第十五讲期末测评五年级寒假班第一讲长方体正方体第二讲数表—从杨辉三角谈起第三讲比例应用题第四讲时钟问题第五讲圆与扇形初步第六讲因数倍数进阶第七讲期末测评五年级春季班第一讲勾股定理第二讲分数四则混合运算第三讲带余除法进阶第四讲同余第五讲不定方程第六讲浓度问题第七讲圆与扇形进阶（弓，镰刀，谷子形，环形）第八讲完全平方数第九讲比较和估算第十讲比例法解行程第十一讲位值原理第十二讲立体图形和空间想象第十三讲概率初识第十四讲从反面情况考虑（几何，数论，计数中的反面情况考虑）第十五讲期末测评六年级暑假班第一讲分数列项第二讲归纳和递推（找规律计数，斐波那契数列，汉诺塔）第三讲切片与染色第四讲韩信点兵第五讲应用题综合选讲（和差、年龄、盈亏、鸡兔、牛吃草）第六讲整数列项与通项归纳第七讲弦图第八讲逻辑推理综合第九讲数论中的组合（最值与计数）第十讲特殊图形（正六边形正十二边形的特征与性质）第十一讲从整体考虑（由换元发引出整体打包思想）第十二讲多次相遇和追及第十三讲应用题综合（分百、比例）第十四讲最值问题综合（最值定理、构造中的最值）第十五讲期末测评六年级秋假班第一讲数形结合（平方和公式、立方和公式、代数公式的几何表示）第二讲圆柱和圆锥第三讲复合图形分拆（模型复习、添加辅助线技巧）第四讲经济问题第五讲数论中的规律第六讲旋转与轨迹（圆柱和圆锥的旋转，圆中的滚动扫过面积）第七讲算两次（方程思想；综合其他模块，行程和计数）第八讲从极端考虑（几何、数论、行程中的极端思想）第九讲数字谜中的计数第十讲工程问题进阶第十一讲变速问题第十二讲进位制进阶第十三讲应用题综合三（复习经济、工程、浓度，方程思想）第十四讲抽屉原理进阶第十五讲期末测评六年级寒假班第一讲计算问题综合选讲（一）第二讲图形问题综合选讲（一）第三讲整数问题综合选讲（一）第四讲组合问题综合选讲第五讲应用题问题综合选讲第六讲行程问题综合选讲第七讲期末测评六年级春季班第一讲计算问题综合选讲（二）第二讲图形问题综合选讲（二）第三讲整数问题综合选讲（二）第四讲计算问题综合选讲（三）第五讲图形问题综合选讲（三）第六讲整数问题综合选讲（三）第七讲计数数问题综合选讲第八讲小升初代数衔接第九讲小升初几何衔接第十讲小升初分班模拟考。

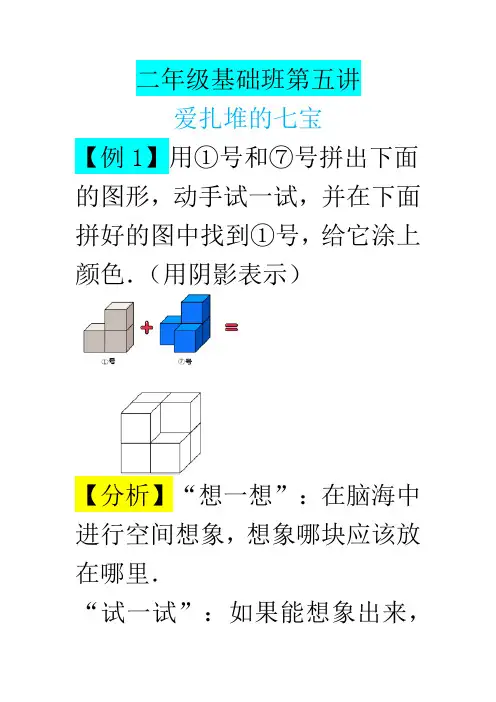
二年级基础班第五讲爱扎堆的七宝【例1】用①号和⑦号拼出下面的图形，动手试一试，并在下面拼好的图中找到①号，给它涂上颜色．（用阴影表示）【分析】“想一想”：在脑海中进行空间想象，想象哪块应该放在哪里．“试一试”：如果能想象出来，可以实际动手操作验证一下．当无法想象出来的时候，可以进行动手操作．我们已经学习了“知道位置两拼”和“知道粘贴面两拼”，本活动是知道拼好的样子去两拼，和前面的方法一样，可以先将其中的一个摆在桌子上，比如先将⑦号放在桌子上，再将①号和⑦号拼在一起，观察拼成的图形是什么样子，是否和题中所给图形相同，或者拼好的图形经过旋转、翻转以后，是否和题中所给图形相同．“记一记”：把我们尝试出来的结果记录下来，并总结方法．可以利用“找图形法”帮助分析图形，在题目所给的图形中，找到①号，标注出来，如果①号在上面一层，那么剩下的不可能是⑦号；如果①号在下面一层，那么剩下的可能是⑦号；如果①号在左面一层，那么剩下的可能是⑦号；如果①号在右面一层，那么剩下的不可能是⑦号；如果①号在前面一层，那么剩下的不可能是⑦号；如果①号在后面一层，那么剩下的可能是⑦号．再在所有可能的情况里确定①号和⑦号的具体位置，将①号画出来．要求学生至少能找到一种可能，并画出来，程度好的班，可以要求学生找出尽可能多的情况．通过尝试，答案如下：【例2】用①号和⑥号拼出下面的图形，动手试一试，并在下面拼好的图中找到①号，给它涂上颜色．（用阴影表示）【分析】用①号和⑥号拼出下面的图形，动手试一试，并在下面拼好的图中找到①号，给它涂上颜色．（用阴影表示）“想一想”：在脑海中进行空间想象，想象哪块应该放在哪里．“试一试”：如果能想象出来，可以实际动手操作验证一下．当无法想象出来的时候，可以进行动手操作．我们已经学习了“知道位置两拼”和“知道粘贴面两拼”，本例题是知道拼好的样子去两拼，和前面的方法一样，可以先将其中的一个摆在桌子上，比如先将⑥号放在桌子上，再将①号和⑥号拼在一起，观察拼成的图形是什么样子，是否和题中所给图形相同，或者拼好的图形经过旋转、翻转以后，是否和题中所给图形相同．“记一记”：把我们尝试出来的结果记录下来，并总结方法．可以利用“找图形法”帮助分析图形，在题目所给的图形中，找到①号，标注出来，如果①号在上面一层，那么剩下的不可能是⑥号；如果①号在下面一层，那么剩下的可能是⑥号；如果①号在左面一层，那么剩下的不可能是⑥号；如果①号在右面一层，那么剩下的可能是⑥号；如果①号在前面一层，那么剩下的不可能是⑥号；如果①号在后面一层，那么剩下的可能是⑥号．再在所有可能的情况里确定①号和⑥号的具体位置，将①号画出来．要求学生至少能找到一种可能，并画出来，程度好的班，可以要求学生找出尽可能多的情况．通过尝试，答案如下：（答案不唯一）【例3】①号和③号拼在一起会变成什么样的图形呢？请你动手试一试．下面的A、B、C、D 都是由①号和③号拼成的，请你把它们的①号都涂上颜色．（用阴影表示）【分析】“想一想”：在脑海中进行空间想象，想象①号和③号拼在一起，会变成什么样子．“试一试”：如果能想象出来，可以实际动手操作验证一下．当无法想象出来的时候，可以进行动手操作．和前面的方法一样，可以先将其中的一个摆在桌子上，比如先将③号放在桌子上，再将①号和③号拼在一起，观察拼成的图形是什么样子，是否和选项中所给图形相同，或者拼好的图形经过旋转、翻转以后，是否和选项中所给图形相同．“记一记”：把我们尝试出来的结果记录下来，并总结方法．可以利用“找图形法”帮助排除选项，在选项中，找到③号，本题可以从和①号相比特殊的③号入手，③号要在能放下3块的地方，那么A选项中，③号可以在右面横着，剩下的部分正好是①号，A选项正确，在选项中画出①号；B选项中，③号可以在下面横着，剩下的部分正好是①号，B选项正确，在选项中画出①号；C选项中，③号可以在前面横着，剩下的部分正好是①号，C选项正确，在选项中画出①号；D选项中，③号可以在后面横着，剩下的部分正好是①号，D选项正确，在选项中画出①号．要求学生至少可以判断出选项是否符合题意，程度好的班，可以要求学生自己动手操作，尽量多的拼出和选项不同的情况．通过尝试，答案如下：（答案不唯一）【例4】④号和⑦号拼在一起会变成什么样的图形呢？请你动手试一试．下面的A、B、C、D都是由④号和⑦号拼成的，请你把它们的④号都涂上颜色．（用阴影表示）【分析】“想一想”：在脑海中进行空间想象，想象⑦号和④号拼在一起，会变成什么样子．“试一试”：如果能想象出来，可以实际动手操作验证一下．当无法想象出来的时候，可以进行动手操作．和前面的方法一样，可以先将其中的一个摆在桌子上，比如先将④号放在桌子上，再将⑦号和④号拼在一起，观察拼成的图形是什么样子，是否和选项中所给图形相同，或者拼好的图形经过旋转、翻转以后，是否和选项中所给图形相同．“记一记”：把我们尝试出来的结果记录下来，并总结方法．可以利用“找图形法”帮助排除选项，在选项中，找到④号，本题可以从和⑦号相比特殊的④号入手，④号要在能放下3块的地方，那么A选项中，④号可以在后面横着，剩下的部分正好是⑦号，A选项正确，在选项中画出④号；B选项中，④号可以在后面竖着，剩下的部分正好是⑦号，B选项正确，在选项中画出④号；C选项中，④号可以在后面竖着，剩下的部分正好是⑦号，C选项正确，在选项中画出④号；D选项中，④号可以在后面横着，剩下的部分正好是⑦号，D选项正确，在选项中画出④号．要求学生至少可以判断出选项是否符合题意，程度好的班，可以要求学生自己动手操作，尽量多的拼出和选项不同的情况．通过尝试，答案如下：（答案不唯一）【例5】用③号、⑤号和⑦号拼出下面的床，动手试一试，并在下面拼好的床中找到⑦号，给它涂上颜色．（用阴影表示）【分析】“想一想”：在脑海中进行空间想象，想象哪块应该放在哪里．⑤号和⑦号无论从哪个方向都是两层，只有③号可以平铺在一层，而床头是两层，床板是一层，可以推测③号平铺在床板上，⑤号和⑦号拼出床头．“试一试”：如果能想象出来，可以实际动手操作验证一下．当无法想象出来的时候，可以进行动手操作．可以先将其中的一个摆在桌子上，比如先将③号放在桌子上，再将⑤号和⑦号拼在一起，观察拼成的图形是什么样子，是否和题中所给图形相同，或者拼好的图形经过旋转、翻转以后，是否和题中所给图形相同．“记一记”：把我们尝试出来的结果记录下来，并总结方法．可以利用“找图形法”帮助从结果入手分析图形，在题目所给的图形中，找到⑤号和⑦号，本题中⑤号和⑦号比较特殊，它们不能平铺在一层，总要高出一块，那么可以知道⑤号和⑦号要拼出床头，剩下的用③号补充完整．要求学生一定要动手操作．通过尝试，答案如下：。

分数基本计算与比例初步内容提要：分数比例分数分数的概念把整体平均分成若干份，表示这样的一份或几份的数叫做分数如25表示把整体平均分成5份，占其中的2份分母表示把一个物体平均分成几份，分子是表示取其中的几份注意：分母不能为0分数的种类真分数：分子比分母小的分数，如2 3假分数：分子比分母大的分数，如3 2带分数：把假分数化成整数和真分数加在一起的分数，如32＝1＋2１＝112分数的性质1．分子和分母同时乘以或除以相同的数(0除外)，分数的大小不变如246369＝＝，8421005025＝＝2．约分与通分约分：分子分母同时除以公因数，如425025＝最简分数通分：把多个分数的分母变成一样，如224833412⨯⨯＝＝比较大小333944312⨯⨯＝＝注意：有时通分也可把分子变成一样3．分数的倒数倒数：乘积为1的两个数互为倒数分数：分子与分母的位置互换注意：0没有倒数分数和小数互化分数化小数：分子除以分母小数化分数：小数点后有1位数，2位数，3位数…，分母分别为10，100，1000…分子就是小数点后的数注意要化成最简分数如2250.4 5÷＝＝0.012＝123 1000250＝分数的运算1．加减法同分母加减法：分母不变，分子相加减，结果化为最简分数异分母加减法：先通分，变为分母相同的分数，分子再相加减如：347888＋＝23342761 917153153153 +=+=2．乘除法乘法：分子乘分子，分母乘分母如3312311 88882243⨯4⨯4=⨯====1⨯133123 8884010 443⨯4⨯=⨯===55⨯5除法：除以一个数等于乘以这个数的倒数如33121 888242 343⨯4÷=⨯===43⨯3注意：分数的乘除法运算过程中可以先约分分数的四则混合运算的规律与整数一样特殊的约分连锁约分 整体约分连锁约分：4433221⨯⨯⨯=122⨯33⨯44⨯1=整体约分：3333123123246369123(123)13526103915135(123)⨯⨯⨯⨯+⨯⨯+⨯⨯⨯⨯⨯++⨯⨯+⨯⨯+⨯⨯⨯⨯⨯++＝＝33(123)⨯++13⨯335(123)⨯⨯++25＝我们来看看分数的乘除法 计算下列各式：28157549⨯＝__________；315711÷＝__________。

二年级数学培优讲义第一讲有序地思虑问题（一）例题：二年级数学培优讲义像这样和是88的倒序数共有多少对？7718把4二年级数学培优讲义把10分拆成三个不同的自然数相加的形式（0除外）；共有多少种不同的分拆方式？用数字卡片3、4、6；能够构成多少个不同的三位数？把1、2、3、4、5、6、7、8这八个数均匀分红两组；使每组的四个数相加的和相等；这样的分法有几种？练习：1.下边算式中的○和□；各有多少种不同的填法？（1）20（2）3○-1○+1□□52两个两位数相加的和是191；像这样的两位数加两位数和等于191的算式一共有多少对？把19分拆成不大于9的三个不同的数相加（0除外）；有多少中不同的分拆方式？十位上的数大于个位上的数的两位数有多少个？将1、2、3、4、5、6这六个数分别填在以下图中的圆圈里；使每条线上的三个数的和相等；共有多少种不同的填法？6.从1——9这九个数中选两个数相加和等于11；有多少种不同的方法？1/16我们把12和21这样的两个数叫做倒序数.像这样的和在100之内的倒序数有多少对？第二讲有序地思虑问题（二）例题：把5个梨放在三个相同的盘子里；同意有的盘子空着不放；共有多少种不同的放法？展览馆前方有4级台阶；假如规定一步只好走一级或两级台阶；这个台阶共有多少种不同的上法？君华家到学校有两条路；学校到公园有三条路；见以下图.君华家经过学校到公园共有多少种走法呢？甲君华家乙公园学校丙有一架天平易1克、2克、5克的砝码各1个；砝码只好放在天平右侧的盘上；用这3个砝码在天平上能称几种不同重量的物体？从1枚5分硬币；3枚2分硬币；6枚1分硬币中；要取出6分钱来；有多少种不同的方法？有五盏灯的价格分别是7元、5元、4元、3元和2元；3个灯架的价格分别是8元、6元和3元.假如一盏灯配一个灯架；一共能够配成多少种不同价格的灯具？练习：把4个苹果放到两个相同的抽屉里；有多少种不同的放法？把6个苹果放到三个相同的盘子里；有多少种不同的放法？1.把6块糖分红若干份；每份放1块或2块.共有多少种放法？2/16乒乓手中有四张5角的邮票和三张1元的邮票.请你帮他算一算；用这些邮票能够构成多少种不同的邮资？妈妈从家到单位上班；要经过电影院.从家到电影院有两条路；从电影院到单位有四条路；妈妈从家经电影院到单位上班有多少种不同的走法？第三讲绘图解鸡兔同笼问题例题：鸡、兔装在同一笼子里；共有10个头；28条腿.笼里有几个鸡？几个兔？一只蜻蜓6条腿；一只蜘蛛8条腿；蜻蜓和蜘蛛共有10只；68条腿.蜻蜓和蜘蛛各有多少只？一辆自行车有2个轮子；一辆三轮车有3个轮子；车棚里有自行车和三轮车共8辆；20个轮子.自行车和三轮车各有多少辆？名女同学站成一排；每隔2名女同学插3名男同学.共有多少名男同学插队？1.练习：孔雀和长颈鹿共有30只；腿96条.孔雀和长颈鹿各有多少只？蛐蛐和蜘蛛共有12只；腿82条.蛐蛐和蜘蛛各有几个？鸡、兔同笼；共有14个头；38条腿.有几个鸡？几个兔？3/16泊车场停有大汽车和小汽车共14辆；共有72个轮子.已知大汽车有6个轮子；小汽车有4个轮子.大、小汽车各有多少辆？5.一队猎手和一队狗；二队并成一队走；共有36个头；94条腿.有多少个猎手、多少条狗？第四讲智巧问题（一）例题：三个人同时吃3个西红柿；用3分钟吃完.100个人同时吃100个西红柿需要100分钟才能吃完；对吗？有18个人要到河的对岸去.河畔只有一条小船；船上每次只好载4个人.小船起码要载几次才能让18个人所有过河？3.大勺子能装油350克；小勺子能装油250克.你能用这两把勺子往桶里倒入450克油吗？爸爸买回不到20个鸡蛋；3个3个地数多1个；4个4个地数也多1个.爸爸买了多少个鸡蛋？5.老师率领32名学生去郊游；见一家冷饮店规定：喝完汽水后；每4个空瓶子能够换1瓶汽水.老师身上的钱只够买24瓶汽水；为了让每个学生都喝上汽水；又不给学生增添负担；他该怎么办？4/16练习：有两对母女一同到市场上去买鸡.回家时；每人手里都拿着一只鸡.想想；他们起码买了几个鸡？有一堆沙子；两个砝码；一个重9克；一个重5克.你能用这两个砝码称出22克的沙子吗？谈谈你的方法.李老师和同学们做游戏.王英在一旁把李老师和男、女同学的人数加起来；聪聪把男生和女生人数乘起来；与王英的得数相同.你知道最罕有几个人做游戏吗？个人以相同的速度从甲地到乙地需要2个小时；那么6个人以相同的速度一同从甲地到乙地需要几个小时？第五讲数的读写例题：用两个4和两个0构成一个四位数.当零不读出来时；这个数是多少？当只读一个零时；这个数是多少？里有一个0；但读660时；这个0不读出来.请你用两个6和两个0构成一个四位数；使这个四位数只读一个零.最大的两位数与最小的三位数相差多少？最小的四位数与最大的四位数相差多少？用0、2、7、5、8这五个数字构成最大的五位数和最小的五位数；它们各是多少？用2、3、4、5这四个数字；能够构成多少个不同的四位数？将它们依据从小到大的次序摆列；第20个数是多少？3.有这样一个算式：23+32=55；我们把23和32这样的两个数叫做倒序数.像这类和在100之内的倒序数有多少对？5/16练习：用两个2和两个0构成一个四位数.当零都不读出来时；这个数是多少？当只读一个零时；这个数是多少？用三个1和两个0构成一个五位数.当零都不读出来时；这个数是多少？当只读一个零时；这个数是多少？当读两个零时；这个数是多少？将以下各数按从小到大的次序摆列起来.356 635 365 536 653将以下各数按从大到小的次序摆列起来.4560、5460、6540、5640、5406用7、3、5构成三位数；你能写出多少个？都写出来（个、十、百位上的数不相同）.这些三位数的和是多少？最大的三位数与最小的三位数的差是多少？6.一个5、一个7和两个0构成只读一个0的最大的四位数是（）.7.从8、6、4、0这四个数中；选三个数构成三位数；最大是（）；最小是（）.用2、3、4、5、6、7这六个数构成两个三位数；使它们的差最小；应当如何组数？第六讲认识时间例题：四名同学50米赛跑的成绩是：明显12秒；立立14秒；梅梅10秒；伟伟11秒.问谁跑得最快？察看以下图时钟所表示的时辰；看看有什么规律；再往返答以下问题.图④时钟所表示的时辰是多少？请你在图④上标出来.3.图③所表示的时辰是多少？请你在图③上标出来.弟弟下学后从5时30分开始造作业；5时50分做完后又接着做自然学具；向来做到6时30分.弟弟造作业和做自然学具各用了多少时间？一共用了几个小时？6/16王平家的钟每到半小时敲1下；1时敲1下；2时敲2下12时敲12下.有一天；王平在家看一本故事书；听到钟敲了1下；他仰头看钟正好是1时；他把这本书看完时；听到钟正好敲了4下.他一共听到钟敲了多少下？蜗牛从9厘米深的碗底往上爬；每爬3厘米要用3分钟；而后停2分钟.问蜗牛从碗底爬到碗口要用多长时间？练习：王老师上午7时30分到学校上班；11时30分下班.王老师上午在学校多长时间？一只蜗牛从20厘米深的沟底往上爬.每爬4厘米要用2分钟；而后停1分钟.蜗牛从沟底爬到沟沿上要用多长时间？小玲家的钟停了.电台2时报时；奶奶跟电台对时；因为年迈眼花；把时针与分针调颠倒了.小玲下学回家时见钟才2时整；大吃一惊.请你帮小玲想想；正确的时间是多少？李新清晨6时30分起床；张英清晨6时45分起床.他俩谁起得早？早多少分钟？小飞家的闹钟逢整点报时；有几时就敲响几下.一天；当小飞开始做模型时闹钟正好报时；当模型做好后闹钟又报时.从开始到结束；闹钟共响了9下.小飞的模型共做了几小时？孔健30秒钟能写8个字；问他1分钟能写多少个字？9分钟能写多少个字？第七讲智巧问题（二）例题：个人吃菜；每人1个饭碗；两个人1个菜碗；3个人1个汤碗.一共需要几个碗？有一部电视连续剧共有15集；要在5天内播完；并且每日播放的集数各不相同；应如何播放？王华有一些卡片.假如他的卡片数加上3；再减去4；而后除以5；再乘以6得王华有卡片多少张？4.某池塘中的睡莲所掩盖的面积；每日扩大一倍；20天恰巧遮遮住整个水池.若只遮遮住水池的一半需要多少天？7/16练习：小朋友吃饭；每一个人一个饭碗；2个人一个菜碗；3个人一个汤碗；一共需要11个碗.请你算一算；终究有多少个小朋友吃饭？2.每日将25颗珠子排成数目不等的五堆；每堆颗数恰巧都是单数.你知道每堆各有多少颗？有48个同学参加三项体育活动.已知参加每项活动的人数不相同；但都有一个数字“6”.参加三项体育活动的各有多少人？一个数加上6；乘以6；减去6；除以6；其结果仍是6.这个数是多少？做一道加法题时；小刚把个位上的6看作0；把十位上的5看作3；结果和是63.正确的答案是多少？6.做一道减法题时；小粗心把被减数个位上的0看作8；又把十位上的2看作3；结果得数是92.正确的答案是多少？有一栽种物；每日长高一倍；20天正好长到20厘米.它长大5厘米需要多少天？第八讲应用题（一）例题：小朋友们排成两队.李老师把第一队的4个小朋友调到第二队；两队的人数正好相同多.本来第一队比第二队多几个小朋友？1.有两筐苹果；甲筐有9个苹果；假如从甲筐取出2个放入乙筐；那么两筐苹果相同多.乙筐本来有多少个苹果？8/16晓军本来比王平多8本书；晓军给了王平5本书后；谁的书多？多几本？张明和小亮各有36块积木；张明送给小亮几块后；小亮就比张明多12块.张明此刻有几块积木？爸爸买了两袋苹果；甲袋中有苹果86个；乙袋中有苹果32个.每次从甲袋中取出3个放到乙袋里；要拿几次才能使两袋里苹果的个数相等？练习：每日有16根小棒；芳芳有6根小棒.每日拿几根小棒给芳芳后；两人的小棒根数相同多？有两盘糖；从第一盘糖里拿4粒放入第二盘后；两盘的粒数相等.已知第二盘本来有9粒糖；第一盘本来有几粒糖？3.丁丁有两个书架；第一个书架上的书比第二个书架上的书多40本.假如从第二个书架上拿4本书放到第一个书架；那么第一个书架比第二个书架的书多几本？黄强把自己的4张画片送给张华后；两人画片的张数相同多.黄强本来比张华多几张画片？有两箱水果；从第一箱中取出3个放入第二箱后；第一箱比第二箱还多1个.本来两箱水果相差几个？第九讲应用题（二）例题：把一根长20厘米的绳索剪成5厘米长的短绳；需要剪几次？1.小朋友排队；12个人排成一行；相邻两个人之间的距离是2米.从第一个小朋友9/16到最后一个小朋友之间的距离是多少米？3.一条道路长200米.绿化工人们在道路的两旁每隔5米栽一棵树；一共要栽多少棵树？圆形花园的周长是54米；在它的边上每隔3米栽一棵树；一共要栽多少棵树？在一条长1200米的道路两边每隔40米插一杆红旗.在相邻的2杆红旗之间又补插1杆绿旗.这条道路两边一共插了多少杆旗？有一个正方形的水池；要在它的周围栽上树.假如每边栽5棵；一共要栽多少棵树？练习：有一条长15米的水泥路；在路的两旁每隔3米放一盆花；一共放了多少盆花？把一根长6米的电线；剪了两次；使每段长度相同；每段长多少米？一根绳索长18米；把它剪成3米长的小段；能够剪成几段？一根木材长10米；要把它锯成2米长的小段.每锯一次要用4分钟；一共要用多少分钟？学校舞台的宽是16米；在它的前方每隔2米放一盆花；重新到尾共要放多少盆花？第十讲应用题（三）例题：10/161.王老师出了两组数学题给数学兴趣小组的20名同学做；做对第一组题的有18名同学；做对第二题的有16名同学.两组题都做对的有多少名同学？个解放军叔叔排成一队报数.从左侧报起小王报10；从右侧报起小张报12.从小王开始往左数；数到小张为止一共有几个解放军叔叔？个小朋友排成一队；从左侧数起小红排第2个；小军排在小红后边第4个.从右往左数小军排第几个？二（一）班的同学参加课外活动；有24人参加美术班；有28人参加体育班；此中有8人两个班都参加.二（一）班共有多少人？少儿园王老师将8张手帕用夹子夹在绳索上晾晒；每1张手帕的两边；一定用夹子夹住；同一个夹子夹住相邻的2张手帕.王老师一共用多少个夹子？练习：少儿园阿姨将洗好的毛巾用夹子夹在绳索上晾晒.每张毛巾的两边都用夹子夹住；同一个夹子能够夹住相邻的两张毛巾；这样一共用了10个夹子.绳索上晾了多少张毛巾？2.小朋友们做操；正好排成一个方形队伍；以前、后、左、右数；冬冬都排第6个.这一排共有多少个小朋友？学校鼓号队的同学在训练时站成了一个“+”队型；指挥的同学恰巧站在“+”字队型的中间.以前、后、左、右数；指挥的同学都是第8个.学校鼓号队有多少名同学？盏彩灯串成一串；从左侧数起第15盏是红灯；从右侧数起这盏红灯排第几？个小朋友排队去观光；均匀分红2队.小华排在第一队；她的前方有3人；她的后边有几人？11/164.第十一讲速算与巧算例题：1.计算（1）63+18+19（2）28+28+282.计算（1）45 –18+19（2）45+18 –193.计算（1）23+20+19+22+18+21（2）102+100+99+101+98计算29+29+29计算7+7+7+7计算（1）984-（84+67）（2）143+（57–29）练习：计算（1）95 –140+105+240 （2）354+120 –154+80 （3）258+49-158+51 （4）75+638 –438+25计算.（1）9+99+999+1999+4 （2）998+98+8+6（3）1997+997+97+9 （4）995+95+5995+20计算.（1）9+98+997+1+2+3（2）99 –1+98 –2+97 –3+96 –4（3）1999+199+19+9计算.12/16（1）1+2+3+4+5+1+2+3+4+5+1+2+3+4+5+6（2）6+24+18+54+36+60+42（3）97+87+77+67+57+47+37+27+17+7减8加3；再减8加3；；这样连续做多少次其结果为2 0？6.请将下边算式中的一个加号改为减号；使等式建立.1+1+23+4+5+67+8+97.把198拆成两个两位数的和；有几种拆法？请写出来.第十二讲列表试试法例题：老大、老二、老三兄弟三人年纪的和是32.老大的年纪比老二大3岁；并且老大的年纪是老三的2倍.兄弟三人各多少岁？甲、乙二人年纪之和是99岁.甲比乙大9岁；并且甲的年纪的两个数字相互互换地点后恰巧是乙的年纪.甲、乙各多少岁？元钱均匀分给几个人.正在分钱时；有一个人走开了；因此此刻每人多分了1元钱.此刻有多少人？小王、小张和小李本来是街坊；此后他们分别当了医生、教师和战士.只知道：小李比战士年龄大；小王和教师不同岁；教师比小张年龄小.他们中谁是医生；谁是教师；谁是战士？练习：个人吃100个馒头；大人一人吃2个；儿童两人吃1个；恰巧吃完.大人、儿童各多少人？13/16元币和5元币共45张；共计350元.10元币多少张？5元币多少张？3.学校五年级3个班举行乒乓球混淆双打竞赛；每班各出男、女生1名；男生有甲、乙、丙；女生有A、B、C.规定：同班的男女生不可以配对.第一盘：甲和A对丙和B；第二盘：丙和C对甲和与乙同班的女生.甲的同班女生是谁？第十三讲年龄问题例题：弟弟今年8岁；姐姐13岁；10年此后；姐姐比弟弟大几岁？小林今年10岁；他比爸爸小25岁；5年前爸爸是多少岁？姐姐今年12岁；姐姐3年前的年龄与妹妹2年后的年龄相等.妹妹今年多少岁？今年弟弟8岁；哥哥14岁.当两个人的年龄的和是40岁时；应当是几年此后的事？1.冬冬、大春、小李三人的年龄和是32岁；冬冬年龄比大春大3岁；冬冬的年龄是小李的2倍.三人的年龄各是几岁？小红今年6岁；爸爸30岁；爸爸的年龄是小红的5倍.几年此后；爸爸的年龄正好是小红的4倍？14/16练习：年前爸爸26岁；宝宝刚出生.今年宝宝多少岁了？珍珍今年8岁；爸爸的年龄是珍珍的4倍.4年前；爸爸的年龄和珍珍相差多少岁？妹妹今年6岁；哥哥今年8岁.哥哥15岁时；妹妹多少岁？欢欢今年12岁；每日4年后的年龄和欢欢今年的年龄相等.每日今年多少岁？爸爸今年32岁；儿子4岁.当父子俩的年龄的和是50岁时；应当是多少年后的事？第十四讲逆序推理法例题：老师想了一个数；对他的学生说：“一个数加上9；再取和的一半是5.”他叫学生们把这个数算出来.你会算吗？小亮拿着1包糖；遇到好朋友A；把他的糖分给了A一半；过一会儿有遇到了好朋友B；把他剩下的糖的一半分给了B；此后又遇到了好朋友C；他把手中所剩下的糖的一半又分给了C；这时他自己手里只有一块糖了.在没有遇到A以前；小亮那包糖有几块？3.农妇卖蛋；第一次卖掉蓝中鸡蛋的一半又1个；第二次又卖掉剩下的一半又1个；这时蓝中还剩1个.本来蓝中有几个蛋？小鸭、小羊、小兔、小牛共有60棵青菜.假如小鸭的青菜棵数扩大5倍；小羊的青菜棵数减去1；小兔的青菜棵数加上4；小牛的青菜棵数减少一半；这样它们的青菜棵数就相等了.小鸭、小羊、小兔、小牛本来各有多少棵青菜？练习：15/161.一个数加上100；乘以100；减去100；除以100；结果仍是100. 这个数是多少？16/16。

截图扫码，领 取课程资料
例3
每隔一段时间就会有一款新的手表生产完成，请你来算一算吧！
截图扫码，领 取课程资料
例3
每隔一段时间就会有一款新的手表生产完成，请你来算一算吧！
截图扫码，领 取课程资料
例4
突然，钟表厂传来一个坏消息：一颗美丽的水晶凭空消失了。莉莉快速转 动大脑，提议查看监控，找出罪魁祸首。
莉莉家的神秘手表
时间的应用
截图扫码，领 取课程资料
前言
莉莉回到家中，发现爸爸正埋 头修理一块古老的手表，手表的表 盘上有一圈漂亮的水晶，只可惜少 了一颗。
爸爸认真地修好手表后，告诉 莉莉这可是来自钟表之国——瑞士 的古老手表。
截图扫码，领 取课程资料
例1
钟面上有时针、分针和12个数。 短而粗的是时针，长而细的是分针。 钟面上把一个圈平均分成12个大格，每个大格又分成相等的5小格。 这样，钟面上一圈共有60个相等的小格。 时针从数字1走到数字2，走这样的1大格时间是1时。分针走1小格 的时间是1分，分针从数字1走到数字2，走这样的一大格就是5分。 分针走一圈是60分，时针走一圈是12时。
本讲总结
截截图图扫扫码码，，领领 取取课课程程资资料料
按要求把（ ）填写完整。
截图扫码，领 取课程资料
按要求把（ ）填写完整。
截图扫码，领 取课程资料
下节课见！
截图扫码，领 取课程资料
截图扫码，领 取课程资料
例1
截图扫码，领 取课程资料
ቤተ መጻሕፍቲ ባይዱ 例2
爸爸的话让莉莉、许多和阿丘对瑞士的钟表产生了兴趣。他们决定 利用永恒之书去瑞士一探究竟。
截图扫码，领 取课程资料
例2
请把下面的钟表和对应的时间连起来吧。

枚举组数1．用6、7、8、9四个数可以组成许多个没有重复数字的4位数，把它们从小到大排列起来，9768排在第（）个。

2．用数字1、2、3、4组成各位数字都不相同的两位数，并按从小到大的顺序排列，第10个数比第7个数大（）3．智慧爷爷今年已经有一百多岁了，如果把他的年龄的各位数字相加，和是9，如果把各位数字相乘，积等于16，那么今年智慧爷爷（）岁。

有一个四位数，它的各位数字和为9，积为24，那么组成这个数的四个数字中，奇数是（）。

横式数字谜4．“小朋友真厉害”这六个汉字分别表示1、2、3、4、6、7这6个数字，根据下面的算式，可以得到小=（），朋=（），友=（），真=（），厉=（），害=（）小+友+真=9小+朋=8友—真=4厉—害=小5．“万事如意”这四个汉字分别表示一个10以内不同的双数，根据下面的算式可以得到万=（），事=（），如=（），意=（）万—事如+意=9万—事如—意=1意—（万—事）如=3日历中的数学6．牛牛暑假跟着爸妈去海南旅游，他们一起连续玩了4天，这4天的日期数相加的和是70（不含月份），那么他们是从（）日玩到（）日的。

7．2015年1月和2月是寒假，乐乐寒假在奶奶家连续住了5天，这5天的日期数相加的和是67（不含月份），那么乐乐从（）月（）日开始住在奶奶家。

8．牛牛同学在某月的日历上圈出2 2个数（如图），正方形方框内的4个数的和是28，那么A=（），B=（），C=（），D=（）。

9．西西同学在日历上圈出5个数，呈十字框型（如图），他们的和是65，则正中间的C=（）10．某月有5个星期日，这5个星期日的日期之和为80（不含月份），则这个月中第一个星期日的日期数是（）。

11．某年的6月有4个星期一和5个星期日，那么这月的第一天是星期（）12．某年的10月有4个星期日和5个星期一，那么这个月的第一天是星期（）和差倍问题1.小林在课桌上摆了一排棋子，数一数，黑、白棋子共有56颗，其中白棋子的颗数正好是黑棋子的6倍，黑白棋子各有多少颗？2.果园里一共种有34棵桃树和杏树，其中桃树的颗数比杏树的3倍多6棵，两种树各种了多少棵？3.两筐水果共重50千克，其中第一筐比第二筐的2倍少13千克，请问两筐水果各重多少千克？4.甲、乙两桶共有油168千克，从甲桶倒出27千克后，甲桶剩下的油是乙桶的两倍，求甲乙两桶原来各有油多少千克？5.一个长方形，周长是30厘米，长是宽的2倍，求这个长方形的长和宽各是多少厘米？6.一个数除以另一个数，商是10，这两个数的和再加上商，和是87，被除数是（），除数是（）。

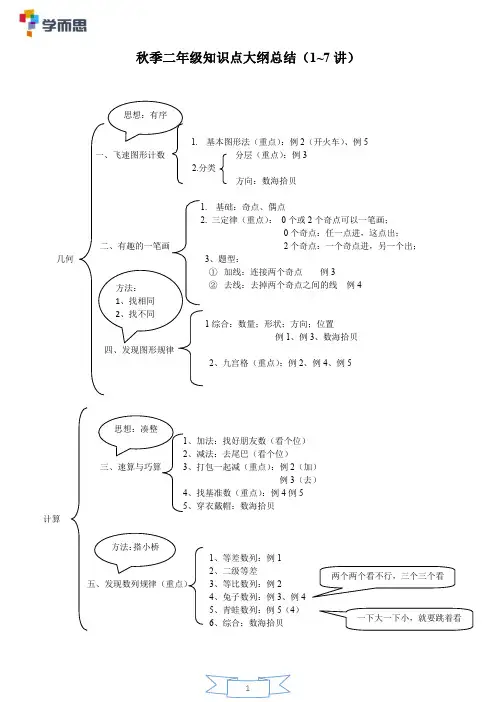
秋季二年级知识点大纲总结（1~7讲）基本图形法（重点）：例2（开火车）、例5分层（重点）：例3方向：数海拾贝基础：奇点、偶点 三定律（重点）： 0个或2个奇点可以一笔画； 0个奇点：任一点进，这点出；2个奇点：一个奇点进，另一个出；几何 3、题型：① 加线：连接两个奇点 例3② 去线：去掉两个奇点之间的线 例4 1综合：数量；形状；方向；位置例1、例3、数海拾贝 2、九宫格（重点）：例2、例4、例5 、加法：找好朋友数（看个位） 、减法：去尾巴（看个位）、打包一起减（重点）：例2（加）例3（去）、找基准数（重点）：例4例5 、穿衣戴帽：数海拾贝计算 1、等差数列：例1 2、二级等差五、发现数列规律（重点） 3、等比数列：例24、兔子数列：例3、例45、青蛙数列：例5（4）6、综合：数海拾贝1、两端都种（重点）：棵数=段数+1例1（1）、例2、例4、数海拾贝、2、两端不种：棵数=段数-1例1（2）、3、一端种：棵数=段数例1（3）4、环形：棵数=段数例1（4）、例3、例5一、烙饼（重点）：画图（例1）注意：保证锅的空间都要利用二、做家务：先判断事情顺序、再找可以同时进行的事组合：七、合理安排注意：在题目中画出关键句（例2、例3）三、过河（例4、例5）四、合理安排（数海拾贝、尖子班挑战）（重点）方法：使等待时间最短，让最快的先做。

第一讲飞速图形计数【例题巩固】【例1】数一数，下图中共有多少条线段？【例题分析】方法：开火车①，②，③；3个①②，②③；2个①②③；1个共：3+2+1=6（个）答：一共有6条线段。

【例2】数一数，图（1）中共有多少个锐角？图（2）中共有多少个三角形？【例题分析】方法：开火车4+3+2+1=10（个）5+4+3+2+1=15（个）答：图（1）中共有10个锐角，图（2）共有15个三角形。

【例3】数一数下图中共有多少个长方形？【例题分析】方法：分层法上层：3+2+1=6（个）下层：3+2+1=6（个）合：3+2+1=6（个）共：6×3=18（个）答：图中共有18个长方形。

速算与巧算1． 计算集中营．【答案】⑴358；⑵98；⑶54；⑷251；⑸179．2． 加减一长串，分组更简便．【答案】⑴5；⑵8；⑶5；⑷38．3． 看谁算得快！【答案】⑴7749⨯=；⑵3030900⨯=；⑶1010432190⨯-+++=（）． 4． 等差数列来求和．⑴1+2+3+4+5+6+7+6+5+4+3+2+1⑵1+2+3+4+…+29+30+29+…+4+3+2+1⑶1+2+3+4+5+6+7+8+9+10+9+8+7+6+5⑴20-19+18-17+16-15+14-13+12-11⑵1-2+3-4+5-6+7-8+9-10+11-12+13-14+15⑶（22+24+26+28+20）-（21+23+25+27+19)⑷38+37-36-35+34+33-32-31+30+29-28-27+26⑴26+75+174+25+58⑵198-56-44⑶137-（46+37）⑷38+39+41+43+44+46⑸31+29+32+33+26+28【答案】⑴7749⨯=；⑵422102130+⨯÷=（）；⑶54082180+⨯÷=（）．5． 在下面的□中填上5个连续的数，使等式成立．【答案】67891040++++=．6． 下面的题你会算吗？【答案】135959799++++++L 20003692730------L1995021005022500=+⨯÷=⨯÷=（）或50502500=⨯=20003692730200033010220001651835=-+++++=-+⨯÷=-=L （）（） ⑴1+3+5+L +95+97+99⑵2000-3-6-9-L -27-30⑴1+3+5+7+9+11+13⑵4+6+8+10+12+14+16+18+20+22⑶5+10+15+20+25+30+35+40【答案】想要把一个西瓜切成9块，我们可以在西瓜上横着切2刀，再竖着切2刀，切成一个“井”字形，这样周围有8块，中间1块，正好9块．这样切成9块的西瓜，吃完后有没有10块西瓜皮呢？只要再想一想，就可以发现，正中间的那一块上下都有瓜皮，把瓜吃完后，这一块有2块瓜皮，不是正有10块瓜皮吗． 豆豆家里来了四位客人，爸爸买了一个大西瓜回来招待客人．但爸爸要求豆豆只许切4刀，切完必须给爷爷、奶奶、爸爸、妈妈、豆豆和四位客人每人一块，而且吃完西瓜后必须有10块瓜皮．请你帮豆豆想一想，该怎样切才合适?。

蜗牛爬井第六讲【例题分析】第6天；可以先考虑特殊的最后一天，蚂蚁爬5米刚好爬到井口，不再滑下，那么它在前几天一共向上移动了205-=15米；它每天爬上5米，又滑下2米，相当于每天只移动了52-=3米，之前爬了153÷=5天，所以第51+=6天爬到井口．一只蚂蚁从一口20米深的枯井底部往上爬，它每天往上爬5米后，就会滑下2米，像这样爬，这只蚂蚁第几天刚好爬到井口？【例题分析】第7天；水缸打水和蜗牛爬井一样，可以先考虑最后一天，这天早上工作人员刚好第一次将水缸装满，那么在此之前水缸里一共有水295-=24桶．每天打回5桶水，又用掉1桶水，则相当于每天往缸里增加51-=4桶水，需要244÷=6天，则第61+=7天第一次把水缸装满．有一口空水缸，需要29桶水才能刚好装满．工作人员每天早上会打回5桶水倒入缸中，傍晚又会用掉缸里1桶水，那么工作人员第几天才能第一次让水缸装满水？【例题分析】第6天；先考虑最后一天，水缸刚好第一次装满，那么在此之前水缸里一共有水216-=15桶．每天倒入6桶水，又用掉3桶水，则相当于每天往缸里增加63-=3桶水，需要153÷=5天，则第51+=6天才能第一次将水缸装满．【例题分析】32米；树懒每天向上爬6米，晚上滑下2米，每天树懒只向上移动了62-=4米．树懒第8天才到顶端，那么前7天共移动了47⨯=28米，再加上第8天的4米，树一共高284+=32米．树懒爬树，它从树底端开始，每天白天向上爬6米，晚上睡觉时滑下2米，第8天爬了4米后终于爬到了树顶端．请问这棵树高多少米？一个空水缸装满水需要21桶，婷婷每天早上向缸里倒入6桶水，晚上又用掉缸里3桶水，婷婷第几天才能第一次将水缸装满？【例题分析】31个；洋洋每次装5个桃子，又吃掉1个，相当于每次只装了514-=个桃子，7次后一共装了7428⨯=个桃子，最后又装3个桃子筐就满了．那么这个筐装满能装28331+=个桃子．【例题分析】18米；小猴爬的最高的位置，是第8次往上爬，还没有滑下来时的位置．小猴每次向上爬4米，然后滑下2米，相当于每次只向上移动了422-=米，第7次时爬到了2714⨯=米的位置，第8次时再往上爬4米到了最高位置，即14418+=米．【例题分析】6米；小丑第8天爬了4米爬到了树顶， 说明前817-=天小丑共向上移动了25421-=米，每天移动了2173÷=米．每次滑下3米，那么每次向上爬336+=米．一个小丑从一棵25米高的树底往上爬，每次向上爬若干米，接着又滑下3米，第8次爬了4米爬到树顶，那么小丑每次向上爬了几米呢？小猴爬竹杆，每次先向上爬4米，接着滑下2米．小猴从竹杆底端开始，共爬了8次，那么小猴最高时爬到了多少米高的位置？洋洋往一个空筐里装桃子，她每次往筐里装5个桃子，然后偷吃掉1个，像这样，第8次装了3个就把筐装满了，那么这个筐装满能装多少个桃子？【例题分析】4米；小蜗牛第6天爬了5米到井口，也就说明前5天一共向上移动了1055-=米，每天移动了551÷=米． 每天白天向上爬5米，则每天夜里会滑下514-=米．【例题分析】42桶；梦梦每天白天打回6桶水，晚上又用掉2桶，相当于每天水缸会增加624-=桶水，30624-=桶，2446÷=天，即第7天打6桶水时，水缸刚好第一次装满．此时梦梦一共打了6742⨯=桶水．一个空水缸，装满需要30桶水，梦梦每天白天会打回6桶水倒入水缸，晚上又会用掉水缸里的2桶水，那么到水缸刚好第一次装满时，梦梦一共打了多少桶水呢？一个空水缸，装满需要33桶水，洋洋每天白天会打回7桶水倒入水缸，晚上又会用掉水缸里的几桶水，第七天洋洋打回3桶水后水缸刚好第一次装满，那么洋洋每天晚上用掉了几桶水呢？小蜗牛从10米深的井底往上爬，每天白天向上爬5米，每天夜里又滑下若干米，第6天爬了5米爬到井口，那么小蜗牛每天夜里滑下了几米呢？【例题分析】64步；舞者先前进4步再后退2步，这样跳一次实际只向前移动了422-=步，24420-= 步，20210÷=次，即第11次时前进4步刚好跳到了另一头．前10次每一次跳了426+=步，这个人一共跳了610464⨯+=步．一位舞者沿一条直线前进4步，接着后退2步，像这样从舞台的一头跳到另一头．舞台的两头相距24步，这个人一共跳了多少步？。

秋季二年级知识点大纲总结（1~7讲）基本图形法（重点）：例2（开火车）、例5分层（重点）：例3方向：数海拾贝基础：奇点、偶点 三定律（重点）： 0个或2个奇点可以一笔画； 0个奇点：任一点进，这点出；2个奇点：一个奇点进，另一个出；几何 3、题型：① 加线：连接两个奇点 例3② 去线：去掉两个奇点之间的线 例4 1综合：数量；形状；方向；位置例1、例3、数海拾贝 2、九宫格（重点）：例2、例4、例5 、加法：找好朋友数（看个位） 、减法：去尾巴（看个位）、打包一起减（重点）：例2（加）例3（去）、找基准数（重点）：例4例5 、穿衣戴帽：数海拾贝计算 1、等差数列：例1 2、二级等差五、发现数列规律（重点） 3、等比数列：例24、兔子数列：例3、例45、青蛙数列：例5（4）6、综合：数海拾贝1、两端都种（重点）：棵数=段数+1例1（1）、例2、例4、数海拾贝、2、两端不种：棵数=段数-1例1（2）、3、一端种：棵数=段数例1（3）4、环形：棵数=段数例1（4）、例3、例5一、烙饼（重点）：画图（例1）注意：保证锅的空间都要利用二、做家务：先判断事情顺序、再找可以同时进行的事组合：七、合理安排注意：在题目中画出关键句（例2、例3）三、过河（例4、例5）四、合理安排（数海拾贝、尖子班挑战）（重点）方法：使等待时间最短，让最快的先做。

第一讲飞速图形计数【例题巩固】【例1】数一数，下图中共有多少条线段？【例题分析】方法：开火车①，②，③；3个①②，②③；2个①②③；1个共：3+2+1=6（个）答：一共有6条线段。

【例2】数一数，图（1）中共有多少个锐角？图（2）中共有多少个三角形？【例题分析】方法：开火车4+3+2+1=10（个）5+4+3+2+1=15（个）答：图（1）中共有10个锐角，图（2）共有15个三角形。

【例3】数一数下图中共有多少个长方形？【例题分析】方法：分层法上层：3+2+1=6（个）下层：3+2+1=6（个）合：3+2+1=6（个）共：6×3=18（个）答：图中共有18个长方形。

1初一秋季·第5讲·基础-提高班·教师版生活水平提高了满分晋级阶梯漫画释义5找规律、程序运算 和定义新运算代数式3级 找规律、程序运算 和定义新运算代数式2级整体思想求值代数式1级整式的概念及加减运算2初一秋季·第5讲·基础-提高班·教师版题型切片（六个） 对应题目题型目标 数列的规律 例1；练习1 数表的规律 例2；练习2 图形的规律 例3；练习3 算式的规律 例4；练习4 程序运算例5、例6：练习5 定义新运算 例7；练习6找规律解题思维过程：从简单、局部或特殊情况入手，经过提炼、归纳和猜想，探索规律，获得结论.有时候还需要通过类比联想才能找到隐含条件.一般有下列几个类型：⑴一列数的规律：把握常见几类数的排列规律及每个数与排列序号n 之间的关系.⑵一列等式的规律：用含有字母的代数式总结规律，注意此代数式与序号n 之间的关系. ⑶图形（图表）规律：观察前几个图形，确定每个图形中图形的个数或图形总数与序号n 之间的关系.⑷图形变换的规律：找准循环周期内图形变换的特点，然后用图形变换总次数除以一个循环变换周期，进而观察商和余数.⑸数形结合的规律：观察前n 项（一般前3项）及利用题中的已知条件，归纳猜想一般性结论.常见的数列规律：⑴ 1，3，5，7，9，… ，21n -（n 为正整数）． ⑵ 2，4，6，8，10，…，2n （n 为正整数）． ⑶ 2，4，8，16，32，…，2n （n 为正整数）． ⑷ 2，5，10，17，26，…，21n +（n 为正整数）． ⑸0, 3, 8, 15， 24，…，21n - （n 为正整数）． ⑹ 2， 6， 12， 20，…， (1)n n +（n 为正整数）． ⑺x -，x +，x -，x +，x -，x +，…，(1)n x -（n 为正整数）．⑻x +，x -，x +，x -，x +，x -，…，1(1)n x +-（n 为正整数）． ⑼特殊数列：①斐波那契数列：1，1，2，3，5，8，13，…，从第三个数开始每一个数等于与它相邻的前两个数的和.②三角形数：1,3,6,10,15,21，…，(1)2n n +.【例1】 ⑴ 观察下列一组数：12，34，56，78，…，它们是按一定规律排列的．那么这一组数 的第k 个数是 ．（k 为正整数）数列的规律思路导航题型切片3初一秋季·第5讲·基础-提高班·教师版⑵瑞士中学教师巴尔末成功地从光谱数据95，1612，2521，3632，…中得到巴尔末公式，从而打开了光谱奥妙的大门．请你按这种规律写出第八个数据是 ．⑶找规律，并按规律填上第五个数:357924816--，，，， ，第n 个数为： . （n 为正整数）⑷有一列数12-，25，310-，417，…，那么第7个数是 ．第n 个数为 . （n 为正整数）（5）一组按规律排列的式子：2b a -，52b a ，83b a -，114b a，…（0ab ≠），其中第7个式子是 ，第n 个式子是 .（n 为正整数）【解析】 ⑴ 212k k -； （2） 10096， ⑶1132-，21(1)2n n n +-；⑷ 750-，2(1)1nn n -+ ；（5）207b a -，31(1)n n nb a --．【例2】 ⑴将杨辉三角中的每一个数都换成分数，得到一个如图所示的分数三角形，称为莱布尼茨三角形，若用有序数对(),m n 表示第m 行，从左到右第n 个数，如()4,3表示分数112.那么()9,2表示的分数是 . 1112211136311114121241111152030205（2） 正整数按图的规律排列. 请写出第20行第21列的数字: ．数表的规律4初一秋季·第5讲·基础-提高班·教师版⑶按一定的规律排列成的数表如图所示.①当“X”型框中间数字为15时，框中五个数的和为 .当“X”型框中间数字为-57时，框中五个数的和为 .②如果设“X”型框中间的数为a ，请用含a 的代数式表示“X”型框中五个数的和； ③若将“X”型框上下左右移动，所框住的五个数之和能等于－285吗？若能，请求出这-13 -5 7 -9 11 -13 15 -17 19 -21 23 -25 27 -29 31 -33 35 -37 39 -41 43 -45 47 -49 51 -53 55 -57 59 -61 63 -65 67 -69 71 ………………【解析】 ⑴172⑵ 420；观察可得规律： 第一行第二列的数：212=⨯；第二行第三列的数：623=⨯； 第三行第四列的数：1234=⨯； ……第n 行第1n +列的数：(1)n n +故可得第20行第21列的数为：2021420⨯=.（3）①-45，171 ②-3a ③不能，中间数字应该为95，但是95却在最后一列第一行 第二行 第三行 第四行 第五行 第一列第二列 第三列 第四列 第五列 1 2 5 10 17 ... 4 3 6 11 18 ... 9 8 7 12 19 ... 16 15 14 13 20 (25)232221………5初一秋季·第5讲·基础-提高班·教师版【例3】 ⑴ 下图是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，第3个图案由 个基础图形组成，……，第n （n 是正整数）个 图案由 个基础图形组成．⑵观察下列图形：它们是按照一定规律排列的，依照此规律，第9个图形中共有个★，第n 个图形有 个★.⑶ 图1是一个三角形，分别连接这个三角形三边的中点得到图2，再分别连接图2中间小三角形三边的中点，得到图3．图3图2图1① 图2有 个三角形；图3有 个三角形；② 按上面的方法继续下去，第n 个图形中有多少个三角形？⑷如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n 个图形需要黑色棋子的个数是 ．【解析】 ⑴ 10，31n +； ⑵；28,3n+1；⑶ ①5，9．② 43n -． ⑷(2)n n +或22n n +或2(1)1n +-；算式的规律图形的规律第1个图形 第2个图形 第3个图形 第4个图形6初一秋季·第5讲·基础-提高班·教师版【例4】 观察下列等式：①23a a +=；②65a a +=；③127a a+=；④209a a +=…；则根据此规律第6个等式为 ，第n 个等式为 ．【解析】 1342=+aa ； 122+=++n a n n a .一般的以计算机程序为背景的新型求值题，解这类题的关键是弄清计算机程序与数学表达式之间的关系．【例5】 ⑴ 如下图，输入23x =-，则输出值y 是 ．y=-x +4(x >1)y=x +4(x ≤1)输出 y输入 x⑵ 如下图所示是计算机程序计算，若开始输入1x =-，则最后输出的结果是 .YES NO输出结果<-5计算1+x -2x 2输入x 的值⑶ 如图所示的运算程序中，若开始输入的x 值为48，我们发现第1次输出的结果为24， 第2次输出的结果为12，……，第2013次输出的结果为 ．x +3x 2x 为奇数x 为偶数输出输入x⑷ 按下面的程序计算，若开始输入的值x 为正整数，最后输出的结果为853，试求出满足条件的x 的所有值.程序运算思路导航7初一秋季·第5讲·基础-提高班·教师版>800输出结果是否将值赋给x ，再次运算计算4x +1的值输入x【解析】 ⑴5-；此程序为选择式，因91x =-≤，故4945y x =+=-+=-.⑵ 9-；经过第一次程序运算得2-，因为25->-，需要返回循环；经第二次运算得9-，因为95-<-，此程序结束，故输出结果为9-. ⑶ 6．（提示：利用循环，多进行几次运算．）⑷ 由题意：()85314213>0-÷=，()2131453>0-÷=，()531413>0-÷=，()13143>0-÷=，()1314>02-÷=∴只有213，53，13，3符合题意．（也可用方程思想理解：∵ x 为正整数， ∴ 415x +≥. 当41853x +=时，213x =. 当41213x +=时，53x =. 当4153x +=时，13x =. 当4113x +=时，3x =.综上所述，213x =或53x =或13x =或3x =）.【例6】 阅读右面的框图并回答下列问题： （1）若A 为785，则E=_____________；（2）按框图流程，取不同的三位数A ，所得E 的值都相同吗？如果相同，请说明理由；如果不同，请求出E 的所有可能的值；（3）将框图中的第一步变为“任意写一个个位数字不为0的三位数A ，它的百位数字减去个位数字所得的差大于．．2．”，其余的步骤不变，请猜想E 的值是否为定值？并对你猜想的结论加以证明． 【解析】 ⑴E =1089； ⑵ E 的值都相同．理由如下：设A =100a+10b +c 且a －c =2，则B =100c +10b + a ．∴C =A －B =(100a +10b +c )－(100c +10b + a )=99a －99c =99(a －c )=99×2=198． ∴D =891．∴E =C +D =198+891=1089． (3) E =1089．8初一秋季·第5讲·基础-提高班·教师版证法1：设A =100a +10b +c 且a －c >2，则B =100c +10b + a ．∴C =A －B =(100a +10b +c )－(100c +10b + a )=100(a －c )+(c －a )=100(a －c －1)+10×9+(10+c －a ) ． ∴D =100(10+c －a ) +10×9+ (a －c －1) ．∴E =C +D =[100(a －c －1)+10×9+(10+c －a )]+[ 100(10+c －a ) +10×9+ (a －c －1)]=1089．定义新运算⑴基本思路：严格按照新定义的运算规则，把已知的数代入，转化为加减乘除的运算，然后按照基本运算过程、运算律进行运算.⑵注意事项：①新的运算不一定符合运算律，特别注意运算顺序. ②每个新定义的运算符号只能在本题中使用.【例7】 ⑴现定义两种新运算∆∇、，对于任意两个整数a 、b ，都有：1a b a b ∆=+-， 1b a b a ∇=-.试求：(∆∆∇(34)21)的值.⑵ 用“×”定义新运算：对于任意a b ，，都有a ×b 2a b =-． 例如，4×27479=-=，那么5×3= ； 当m 为有理数时，m ×（1-×2）= ．⑶ 对于正整数a ，b ，c ，d ，规定a b ad bc c d=-，若1134bd <<，则b d += ．⑷ 定义：a 是不为1的有理数，我们把11a -称为a 的差倒数．．．．如：2的差倒数是1112=--，1-的差倒数是()11112=--．已知113a =-， ① 2a 是1a 的差倒数，则2a = ； ② 3a 是2a 的差倒数，则3a = ；③ 4a 是3a 的差倒数，则4a = ，…，依此类推，则2009a = ．【解析】 ⑴ 6；⑵ 22，21m +；⑶由题意得42bd -=，故2bd =，又b d ，为正整数，所以3b d +=.定义新运算思路导航9初一秋季·第5讲·基础-提高班·教师版⑷ ①34；② 4；③ 13-；34. 【点评】 一个值得注意的问题是：定义一个新运算，这个新运算常常不满足加法、乘法所满足的运算律，因此在没有确定新运算是否具有这些性质之前，不能运用这些运算律来解题．【选讲题】【例8】 （1）右图为手的示意图，在各个手指间标记字母A B C D ，，，．请你按图中箭头所指方向（即A B C D C B A B →→→→→→→C →→…的方式）从A 开始数连续的正整数1234，，，，…，当数到12时，对应的字母是_______；当字母C 第201次出现时，恰好数到的数是 ；当字母C 第21n +次出现时（n 为正整数），恰好数到的数是 （用含n 的代数式表示）．【解析】 B ，603，63n + . （2）数1234,,,,a a a a 满足下列条件：10a =，211a a =-+ ,322a a =-+,433a a =-+,则2013a 的值为 .【解析】 1006(3)如图，将一张正方形纸片，剪成四个大小形状一样的小正方形，然后将其中的一个小正方形再按同样的方法剪成四个小正方形，再将其中的一个小正方形剪成四个小正方形，如此循环进行下去：⑴ 填表：⑵ 如果剪了100次，共剪出多少个小正方形？ ⑶ 如果剪n 次，共剪出多少个小正方形？【解析】 ⑴ 如表．剪的次数1 23 4 5 正方形个数 47101316⑵ 如果剪了100次，共剪出11003301+⨯=个小正方形； ⑶ 如果剪n 次，共剪出13n +个小正方形.剪的次数1 2 3 4 5 正方形个数 4 710 初一秋季·第5讲·基础-提高班·教师版训练1. 下面是一组按规律排列的数：1，2，4，8，16，……，第2002个数应该是（ ）A ．20022B ．200221-C ．20012D ．以上答案均不对【解析】 C.训练2. 根据右图所示的程序计算变量y 的值，若输入自变量x 的值为32，则输出的结果是 ．（汇文中学期中） 【解析】 72-.训练3. 读一读：式子“12345100++++++”表示1开始的100个连续自然数的和．由于上述式子比较长，书写也不方便，为了简便起见，我们可以将“12345100++++++”表示为1001n n =∑，这里“∑”是求和符号．例如：1357999++++++，即从1开始的100以内的连续奇数的和，可表示为50121n n =-∑（）； 又如333333333312345678910+++++++++可表示为1031n n =∑．通过对以上材料的阅读，请解答下列问题．⑴ 246810100++++++（即从2开始的100以内的连续偶数的和）用求和符号可表示为 ． ⑵ 计算5211n n =-=∑（） ．（填写最后的计算结果）（北大附中期中）【解析】 ⑴ 5012n n =∑；⑵ 50,52222221(1(11(21(31(41(5150n n=-=-----=∑))+)+)+)+)训练4. 在某种特制的计算器有一个按键★★★，它代表运算2a b a b++-．例如：输入顺序 1，★★★，2-，ENTER=屏幕显示()1***2-2上述操作即是求()()12122+-+--的值，运算结果为2．回答下面的问题：y=-x -2(1<x ≤2)y=x 2(-1≤x ≤1)y=x -2(-2≤x <-1)输出y 的值输入x 的值11初一秋季·第5讲·基础-提高班·教师版⑴ 小明的输入顺序为5-，★★★，7，ENTER=，运算结果是 ．⑵ 小杰的输入顺序为100101，★★★，165-，ENTER=，★★★，1101-，ENTER=，★★★，6665-，ENTER=，★★★，101100，ENTER=，运算结果是 ．⑶ 若在20112012-，20102011-，20092010-，……，12-，0，12，……，20092010，20102011这些数中，任意选取两个作为a 、b 的值，进行★★★运算，则所有的运算结果中最大的值是 ．（一零一期中）【解析】 ⑴ 7⑵6665⑶ 2011201212 初一秋季·第5讲·基础-提高班·教师版数列的规律【练习1】 ⑴ 观察一列有规律的数：4，8，16，32，…，它的第2007个数是（ ）A ．20072B ．200721-C ．20082D ．20062⑵ 观察下列单项式，2x ，25x -，341017x x -，，……根据你发现的规律写出第5个式子是 ，第8个式子是 ，第n 个式子是 ．（n 为正整数）【解析】 ⑴ C ． ⑵ 582665x x -， ，12(1)(1)n n n x +-+.数表的规律【练习2】 下面是由自然数排成的数表，分为A ，B ，C 三列，按这个规律，1999在第 列。

二年级超常班第五讲爱扎堆的七宝【例1】用①号和⑦号拼出下面的图形，动手试一试，并在下面拼好的图中找到①号，给它涂上颜色．（用阴影表示）【分析】“想一想”：在脑海中进行空间想象，想象哪块应该放在哪里．“试一试”：如果能想象出来，可以实际动手操作验证一下．当无法想象出来的时候，可以进行动手操作．我们已经学习了“知道位置两拼”和“知道粘贴面两拼”，本活动是知道拼好的样子去两拼，和前面的方法一样，可以先将其中的一个摆在桌子上，比如先将⑦号放在桌子上，再将①号和⑦号拼在一起，观察拼成的图形是什么样子，是否和题中所给图形相同，或者拼好的图形经过旋转、翻转以后，是否和题中所给图形相同．“记一记”：把我们尝试出来的结果记录下来，并总结方法．可以利用“找图形法”帮助分析图形，在题目所给的图形中，找到①号，标注出来，如果①号在上面一层，那么剩下的不可能是⑦号；如果①号在下面一层，那么剩下的可能是⑦号；如果①号在左面一层，那么剩下的可能是⑦号；如果①号在右面一层，那么剩下的不可能是⑦号；如果①号在前面一层，那么剩下的不可能是⑦号；如果①号在后面一层，那么剩下的可能是⑦号．再在所有可能的情况里确定①号和⑦号的具体位置，将①号画出来．要求学生至少能找到一种可能，并画出来，程度好的班，可以要求学生找出尽可能多的情况．通过尝试，答案如下：【例2】用①号和⑥号拼出下面的图形，动手试一试，并在下面拼好的图中找到①号，给它涂上颜色．（用阴影表示）【分析】用①号和⑥号拼出下面的图形，动手试一试，并在下面拼好的图中找到①号，给它涂上颜色．（用阴影表示）“想一想”：在脑海中进行空间想象，想象哪块应该放在哪里．“试一试”：如果能想象出来，可以实际动手操作验证一下．当无法想象出来的时候，可以进行动手操作．我们已经学习了“知道位置两拼”和“知道粘贴面两拼”，本例题是知道拼好的样子去两拼，和前面的方法一样，可以先将其中的一个摆在桌子上，比如先将⑥号放在桌子上，再将①号和⑥号拼在一起，观察拼成的图形是什么样子，是否和题中所给图形相同，或者拼好的图形经过旋转、翻转以后，是否和题中所给图形相同．“记一记”：把我们尝试出来的结果记录下来，并总结方法．可以利用“找图形法”帮助分析图形，在题目所给的图形中，找到①号，标注出来，如果①号在上面一层，那么剩下的不可能是⑥号；如果①号在下面一层，那么剩下的可能是⑥号；如果①号在左面一层，那么剩下的不可能是⑥号；如果①号在右面一层，那么剩下的可能是⑥号；如果①号在前面一层，那么剩下的不可能是⑥号；如果①号在后面一层，那么剩下的可能是⑥号．再在所有可能的情况里确定①号和⑥号的具体位置，将①号画出来．要求学生至少能找到一种可能，并画出来，程度好的班，可以要求学生找出尽可能多的情况．通过尝试，答案如下：（答案不唯一）【例3】①号和③号拼在一起会变成什么样的图形呢？请你动手试一试．下面的A、B、C、D 都是由①号和③号拼成的，请你把它们的①号都涂上颜色．（用阴影表示）【分析】“想一想”：在脑海中进行空间想象，想象①号和③号拼在一起，会变成什么样子．“试一试”：如果能想象出来，可以实际动手操作验证一下．当无法想象出来的时候，可以进行动手操作．和前面的方法一样，可以先将其中的一个摆在桌子上，比如先将③号放在桌子上，再将①号和③号拼在一起，观察拼成的图形是什么样子，是否和选项中所给图形相同，或者拼好的图形经过旋转、翻转以后，是否和选项中所给图形相同．“记一记”：把我们尝试出来的结果记录下来，并总结方法．可以利用“找图形法”帮助排除选项，在选项中，找到③号，本题可以从和①号相比特殊的③号入手，③号要在能放下3块的地方，那么A选项中，③号可以在右面横着，剩下的部分正好是①号，A选项正确，在选项中画出①号；B选项中，③号可以在下面横着，剩下的部分正好是①号，B选项正确，在选项中画出①号；C选项中，③号可以在前面横着，剩下的部分正好是①号，C选项正确，在选项中画出①号；D选项中，③号可以在后面横着，剩下的部分正好是①号，D选项正确，在选项中画出①号．要求学生至少可以判断出选项是否符合题意，程度好的班，可以要求学生自己动手操作，尽量多的拼出和选项不同的情况．通过尝试，答案如下：（答案不唯一）【例4】④号和⑦号拼在一起会变成什么样的图形呢？请你动手试一试．下面的A、B、C、D都是由④号和⑦号拼成的，请你把它们的④号都涂上颜色．（用阴影表示）【分析】“想一想”：在脑海中进行空间想象，想象⑦号和④号拼在一起，会变成什么样子．“试一试”：如果能想象出来，可以实际动手操作验证一下．当无法想象出来的时候，可以进行动手操作．和前面的方法一样，可以先将其中的一个摆在桌子上，比如先将④号放在桌子上，再将⑦号和④号拼在一起，观察拼成的图形是什么样子，是否和选项中所给图形相同，或者拼好的图形经过旋转、翻转以后，是否和选项中所给图形相同．“记一记”：把我们尝试出来的结果记录下来，并总结方法．可以利用“找图形法”帮助排除选项，在选项中，找到④号，本题可以从和⑦号相比特殊的④号入手，④号要在能放下3块的地方，那么A选项中，④号可以在后面横着，剩下的部分正好是⑦号，A选项正确，在选项中画出④号；B选项中，④号可以在后面竖着，剩下的部分正好是⑦号，B选项正确，在选项中画出④号；C选项中，④号可以在后面竖着，剩下的部分正好是⑦号，C选项正确，在选项中画出④号；D选项中，④号可以在后面横着，剩下的部分正好是⑦号，D选项正确，在选项中画出④号．要求学生至少可以判断出选项是否符合题意，程度好的班，可以要求学生自己动手操作，尽量多的拼出和选项不同的情况．通过尝试，答案如下：（答案不唯一）【例5】用③号、⑤号和⑦号拼出下面的床，动手试一试，并在下面拼好的床中找到⑦号，给它涂上颜色．（用阴影表示）【分析】“想一想”：在脑海中进行空间想象，想象哪块应该放在哪里．⑤号和⑦号无论从哪个方向都是两层，只有③号可以平铺在一层，而床头是两层，床板是一层，可以推测③号平铺在床板上，⑤号和⑦号拼出床头．“试一试”：如果能想象出来，可以实际动手操作验证一下．当无法想象出来的时候，可以进行动手操作．可以先将其中的一个摆在桌子上，比如先将③号放在桌子上，再将⑤号和⑦号拼在一起，观察拼成的图形是什么样子，是否和题中所给图形相同，或者拼好的图形经过旋转、翻转以后，是否和题中所给图形相同．“记一记”：把我们尝试出来的结果记录下来，并总结方法．可以利用“找图形法”帮助从结果入手分析图形，在题目所给的图形中，找到⑤号和⑦号，本题中⑤号和⑦号比较特殊，它们不能平铺在一层，总要高出一块，那么可以知道⑤号和⑦号要拼出床头，剩下的用③号补充完整．要求学生一定要动手操作．通过尝试，答案如下：【超常挑战】1.用①号、②号、③号和④号拼出下面的墙角，动手试一试，并在下面拼好的墙角中找到②号，给它涂上颜色．（用阴影表示）2.用②号、④号、⑤号和⑦号拼出下面的楼梯，动手试一试，并在下面拼好的楼梯中找到⑦号，给它涂上颜色．（用阴影表示）3.用①号、②号、④号和⑤号拼出下面的坦克，动手试一试，并在下面拼好的坦克中找到④号，给它涂上颜色．（用阴影表示）4.有3个和图1相同的图形．把3个图形组合到一起，可以组成各种形状．从①到⑥的6个图形中，找出能够用3个图1的图形组合起来构成的图形，并用○表示，不能组成的，请用×表示．（2009年第1届日本算术奥林匹克预赛试题）【分析】1.用①号、②号、③号和④号拼出下面的墙角，动手试一试，并在下面拼好的墙角中找到②号，给它涂上颜色．（用阴影表示）答案如下：（答案不唯一）2.“想一想”：在脑海中进行空间想象，想象哪块应该放在哪里．“试一试”：如果能想象出来，可以实际动手操作验证一下．当无法想象出来的时候，可以进行动手操作．可以先将其中的一个摆在桌子上，比如先将②号放在桌子上，再将④号、⑤号和⑦号拼在一起，观察拼成的图形是什么样子，是否和题中所给图形相同，或者拼好的图形经过旋转、翻转以后，是否和题中所给图形相同．“记一记”：把我们尝试出来的结果记录下来，并总结方法．可以利用“找图形法”帮助从结果入手分析图形，可以从楼梯的顶端开始拼，能放在顶端的只有④号或⑦号，如果将⑦号放在顶端，那么剩下的三块不能拼出剩下的楼梯．那么顶端就是④号竖着放，剩下的用②号、⑤号和⑦号补充完整．要求学生一定要动手操作．通过尝试，答案如下：3.答案如下：（答案不唯一）4.①○；②○；③○；④×；⑤×；⑥×．显而易见，①、②、③都可以分成3个图1的图形，④、⑤、⑥最多可以分出两个图1的图形．在④中，面前的两个小正方体都只能和中间的小正方体组合，所以不行；在⑤中，高出去的两个小正方体无法组成图①的图形，所以不行；在⑥中，最左和最右的两个小正方体都只有一种组合方法，这样剩下中间一列三个小正方体，所以不行．。

二年级超常班第二讲藏在宝石里的数【例1】找出下面数列的规律，在“()”里填上适当的数．⑴1，2，4，8，（），（），64，128．⑵2，6，18，( ) ，( ) ，486，1458．⑶1，10，100，1000，( ) ，( ) ，1000000，10000000．【分析】这是一组等比数列，通过这个题的学习老师引导学生认识什么是等比数列．⑴⑵⑶这三个数列每组数列每相邻两个数之间相乘的数都是一样的，这样的数列是等比数列．【例2】找出下面数列的规律，在“( )”里填上适当的数．⑴1，1，2，8，（），1024．⑵1，1，3，27，( ) ，59049．【分析】这是一组二级等比数列，通过这个题的学习老师引导学生认识什么是二级等比数列．⑴⑵【例3】找出下面数列的规律，在“()”里填上适当的数．⑴1，2，2，4，8，( )，256．⑵2，3，6，18，（），1944．【分析】⑴从第三个数开始，每一项是前两项的积，故（）里应是；后一个数应该是．⑵从第三个数开始，每一项是前两项的积，故（）里应是；后一个数应该是【例4】根据前几幅图的规律，在下列各图中填出问号处的数．【分析】每个图中数的排列是有规律的，具体分析如下：⑴左数第一个数加第二个数再减去第三个数，就得到第四个数．如13+14-15=12，17+18-19=16，那么第三个图中“？”处就应该是：20+21-22=19．⑵这个图中三个数的规律是：三个角上的数相加等于中间的数．如5+6+7=18，8+9+10=27那么第三个图中“？”处就应该是：11+12+13=36.⑶每个三角形上面的数与左边的数相加再减去右边的数恰好等于三角形内的数．如22+23-20=25，37+38-25=50，所以“？”处应填41+42-23=60．【例5】根据规律，填出所缺的数．【分析】这个数表的每一行的第一个数组成了一个自然数列．第二行中后一个数比前一个数多2，第三行中从第二个数起，每个数比前一个数多3，第四行中每个数比前一个数多4，第五行中每个数应该比前一个数多5，所以第五行第4个数是15+5=20．第六行第4个数是18+6=24．【超常挑战】1.在下面数表中，第10 行的第3 个数是几（从左往右数）？2.在下面数表中，第10 行的第3 个数是几（从左往右数）？3.观察下面的数列，找出其中的规律，并根据规律，在括号中填上合适的数．⑴1，4，9，（），64，169，441．⑵1，2，6，16，44，（），328．4.根据前几幅图的规律，在下列各图中填出问号处的数．【分析】1.观察可知在图形中第1行有1个数，第2行有2个数，第3行有3个数，…，第9行有9个数，前9行一共有1+2+3+4+5+6+7+8+9=45个数，所以第9行的最后一个数为45，那么第10行为：46，47，48，49，…这样就可以得出第10行的第3个数应该是48．2.观察发现，奇数行的数从左往右写，偶数行的数从右往左写，第10 行最左端第一个数为55，所以第10 行的数从左往右是：55，54，53，从左往右数第三个数为53．3.⑴第一个数是，第二个数是，第三个数是，第五个数是第六个数是，第七个数是，这个数列中每个数都是兔子数列中的数自己乘自己，因此第四个数应该是．⑵从第三个数开始都是前两个数和的2倍．4.每个图中数的排列是有规律的，具体分析如下：⑴左数第一个数乘第二个数再减去第三个数，就得到第四个数．如，，那么第三个图中“？”处就应该是：．⑵这个图中三个数的规律是：左边两个数相乘减去3就等于右边的数．如，，那么第三个图中“？”处就应该是：⑶每个三角形上面的数与左边的数相乘再减去右边的数恰好等于三角形内的数．如，，所以“？”处应填．。

二年级超常班第四讲
从24点玩儿起
【例1】在下面式子中适当的地方添上括号使等式成立．
36－12－10＝34
7×5－3＝14
20－5÷5＋8＝11
【分析】
【例2】将“＋,－,×,÷”分别填入下面的○里，使等式成立．
【分析】
【例3】将“＋,－,×,÷”填入合适的“○”里，使下面的等式成立．
【分析】
【例4】将“＋,－,×,÷，( )”填入合适的地方，使下面的等式成立．
【分析】
【例5】在下面每两个数字之间
填上“＋”或“－”，使等式成立．
【分析】
【超常挑战】1.将“＋,－,×,÷，( )”填入合适的地方，使下面的等式成立．
2.将“＋,－,×,÷，( )”填入
合适的地方，使下面的等式成立．
3.将“＋,－,×,÷，( )”填入合适的地方，使下面的等式成立．
4.在合适的地方填上“＋或－”，使等式成立．（位置相邻的两个数字可以组成一个数）
【分析】1.
2.
3.
4.。

学而思二年级数学植树的问题学而思二年数学直的，再区分：两端都种，段数 =的数量 -1两端都不种，段数=的数量 +1一端种，一端不种，段数 =的数量如果是封形的，段数等于的数量.学而思二年数学带余数的除法被除数除数 =商⋯⋯ .余数被除数 =商除数+余数除数 =（被除数—余数）商=（被除数—余数）除数余数，最大除数减去1，就可以知道余数一共有多少种可能性.如果不整除，余数最小是1，最大是除数— 1.例题一箱苹果不到 40个， 4个 4个地数还多 2个， 5个 5个地数还多 1个，这箱苹果有个.枚举法中的乘数原理一件事情，如果需要两个步骤完成，第一个步骤有 a 个选择，第二个步骤，有 b 个选择，那么完成这件事情，一共有a排队题目排队题目，最重要的是画图.其次，区分是第几个，还是前面后或者后面有几个.注意，小米和小兰之间相差 3 个人，如果没有明确，可能是小米在前，也可能是小兰在前，要分两种情况分别考虑的 .周期问题（普通周期，数列周期，日期周期）一定需要先写出周期的排序.没有余数，也就余数为0，就是周期的最后一个.对于日期来说，区分第10 天，和再过10 天.过河过桥问题过河问题，如果一只船只能坐两个人，那么一定是速度最快的人来回.过桥问题，最多只有两个人可以同时通过，并且要送一件东西回来的话，如果是 4 个人的话，甲乙丙丁，用的时间是丁 >丙 >乙 >甲，第一次甲乙一起过第二次甲回来第三次丁丙一起过第四次乙回来第五次甲乙一起过烙饼问题如果一次可以同时烙两个饼，时间 =烙饼的数量烙一面饼的时间（注意，是烙一面饼的时间） .如何表示饼的正面和反面？搭配问题乘法公式，以及通过枚举法解决组数问题组数的问题，可以通过乘法公式解决，先确定位置，比如千位，百位，十位，个位.例题：3,5,6,7 可以组成多少个没有重复数字的偶数？2,4,5,7 可以可以组成多少个没有重复数字的偶数？拆数问题把一个整数拆成几个不同的数的和，可以用枚举法解决.5级的台阶，只能爬一个或者两个台阶，一共有几种不同的方法？可乐，薯条，汉堡三种食物，一天只能选一种，连续两天不能重复，小麦决定第一天吃汉堡，第五天吃汉堡， 5 天内一共有几种不同的吃法？加减法巧算分组的方法，分成几组，在每组中，计算简单.例子：100+99-98-97+96+95-94-93+⋯⋯ .+4+3-2-1凑整法179-99168-101234+20597+96+95+86+87+88金字塔数列等差数列求和末项 =首项 +（项数 -1）项数 =（末项 -首项）公差+1首项 =末项 -（项数 -1）公差 =（末项 -首项）（项数-1）等差数列之和 =（首项 +末项）2如果是奇数项，可以用下面这个公式：等差数列之和 =中间项组合图形求周长关键是凑成规则的长方形或者正方形.鸡兔同笼和倍问题，和差问题两种方法，线段法以及前后表格法.前后表格法，需要假设未知数，尽量假设一个未知数.要搞清楚，前后表格法中，总计这个数，有没有发生变化.如果发生变化了，能否求出变化后的总计的数字 .前后表格法如下：前后甲乙合计逆向思维，流程图画法例题一只小猴子特别喜欢吃桃子，有一天，他摘了一堆桃子，每天都吃掉这堆桃子的一半又10个，这样吃了三天，还剩 10个 .请问这堆桃子最初有多少个？找规律，数列与图形规律移多补少的问题用前后表格法，抓住总和不变这个关键.重要的数学方法表达关系法例题艾迪在小动物的带领下来到猛兽小区门前门上印着一个谜语：一数真离奇，自己加自己，自己减自己，自己乘自己，自己除自己，得数在一起，相加三十六，猜猜它是几？例题艾迪帮警察抓住坏蛋之后，警察决定送艾迪回家，在路上艾迪想去商店买些礼物送给薇儿．他发现商店里 1 辆玩具车等于 2 个书包加上 1 个音乐盒的价格， 1 个书包等于 3 个音乐盒的价格， 1 个音乐盒等于 4 根铅笔的价格，那么 1 辆玩具车相当于____▲ ____根铅笔的价格．尝试法尝试法的举例子例题有一列数，第一个数是4，第二个数是第一个数乘以 3 的个位数，以此类推，那么第40个数是多少？例题，沙漏是一种计时工具，图中的沙漏里所有沙子从一边到另一边用的时间为 1 分钟，可以来计一分钟的时间，下次再用来计时的时候翻过来即可．小红拿它开始计时的时候沙子都在 B 中，小红用它计了 3 分钟，小明又用它计了 10 分钟，然后小乐又用它计了 5 分钟，当小乐用完时，沙子在_________中（ A 或 B）尝试法，例题黑板上写着2、4、 6、 8、10、 12、14、 16、18 共 9 个数，老师每次任意擦掉两个数，并把它们的和写到黑板上．那么，当黑板上只剩下一个数时，这个数是_________例题将数字 1～9 分别填入下面的□中，每个□中填一个数字（不能重复，其中9已填好），使得算式成立．例题，某学校进行乒乓球比赛，进行的是淘汰赛（输者淘汰，胜者晋级）.一共有 64名参赛队员，请问一共需要多少场比赛才能确定冠军.枚举法中，非常重要的是分类讨论.比如， 3,4,5,6 可以组成多少个没有重复数字的整数？枚举法中，有个非常重要的概念是位置，位置可以是没有区别的，也可能是有区别的 .比如， 10 个铅笔放入 3 个相同的文具盒中，每个文具盒至少要放入一个铅笔 .这个位置就是相同的 .比如，妈妈给小麦 7 个苹果，要求每天至少吃 2 个，并且必须 3 天吃完，有多少钟不同的吃饭 .3,4,5,6 可以组成多少个没有重复数字的四位数？这个题目中，位置是什么？例题，艾迪决定再买些苹果给小动物吃，他发现商店里卖的苹果都是5 个一袋或3 个一袋的，只能一袋一袋卖．已知 5 个一袋的价格是 20 元，3 个一袋的价格是 15 元，要给车上的 26 位小动物每位发一个苹果，最少要花 ____▲____元．文氏图中的公式A 表示属于 A 的有多少，B 表示属于 B 的有多少， AB 表示既属于 A，又属于 B 的是多少 .A 和B 总共多少 =A+B-AB上面的公式行恒等形，可以得到既属于 A，又属于 B 的 AB 等于什么 . AB= A+B- A 和 B 总共多少一笔画的问题①凡是由偶点组成的连通图，一定可以一笔画成；画时可以任一偶点为起点，最后一定能以这个点为终点画完此图.②凡是只有两个奇点（其余均为偶点）的连通图，一定可以一笔画成；画时必须以一个奇点为起点，另一个奇点为终点.③其他情况的图，都不能一笔画成.数线段的问题首先要分成不同的直.其次，数直上有几个点，比如一条直有 5 个点，那么条直上一共有1+2+3+4 条段 .公式：如果一条直有n 个点，那么，条直上有1+2+3+ ⋯⋯ ..+(n-1) 条段 .数角的，和段是同的公式.一个萝卜一个坑的题目两两握手的问题一共 n 个人，两两握手一次，不能握手两次，一共有1+2+3+ ⋯ ..(n-1) 次手 .杀手数独和正常数独等量替换（每空 6 分，共 12 分）下面的式子中，相同的汉字代表相同的数，不同的汉字代表不同的数，请你根据式子判断，“数” =________，“学” =________．数+学+5=20学+学=数对应法解题芳芳在看一本数学书，如果她第一天读 6 页，以后每一天都比前一天多读9 页，结果到最后一天时，还剩 40 页没有读完；如果她第一天读24 页，以后每一天也比前一天多读9 页，结果比上一种情况少用一天，但也还剩10 页没有读完．那么，这本数学书共有多少页．染色问题从最下一层开始数，画出每层的平面图 .注意，与地上相接的一层，只是一个面没有涂到，不要乘以 2.其余的两个面相接，需要乘以 2.鸡兔同笼的问题11/11。

二年级数学思维秋季班方法讲义：第一讲《比谁眼力好》姓名方法点播：小朋友，如果给你一组图形，其中有一个图形与其他图形的特征不一样，你能很快辨认出来吗？或者先画了几幅图，要你接着画下去你会画吗？这就要比谁的眼力好了。

我们可以从图形的形状、位置、大小、方向等方面观察、比较。

要学会这种本领，小朋友一定要认真观察，根据前后几个图形的排列，找出变化的规律，才能推算出下面该画什么图形。

【典型例题】【例1】下面一组图中，有一个是不同的，你能找出它吗？练习1：（1）下面一组图，其中有一个是不同的，你能找出来吗？（2）你能把与其他不同的找出来吗？【例2】根据规律接着画。

练习2:（1）按顺序仔细观察图，第三幅“？”处该怎么填？（2）按顺序仔细观察，在“？”处填图。

【例3】在方框里填上适当的字母。

练习3：（1）按规律在空格里画上图形。

（2）接着画。

【例4】请你根据前三个图形的变化规律，画出第四个图形来。

练习4：（1）接下去该怎样画？（2）仔细观察图，在第四幅中应画什么图形？第十幅图应画什么图形？【例5】接着应该怎样画？请画在空格里。

练习5:（1）仔细观察，第四幅图应画什么图形？（2）仔细观察，想一想第三幅图应该怎样填？【课后巩固】1、找出与其他图形不同的那组图。

2、接着画。

3、在空格里填上适当的图形。

4、请你根据前三个图形的变化规律，画出第四个图形来。

5、想一想，第四幅图该怎么填？★家长签字：二年级数学思维秋季班方法讲义：第二讲《按规律填数》姓名方法点播：我们经常会看到按一定规律排列起来的一列数，如果要接在一列数后面再写几个数，就要仔细观察这列数中已经出现的几个数之间有什么规律，找准了规律，就能按规律接下去填数了。

按规律填数不是很容易就填对的，要运用数的顺序和加、减、乘、除法的知识，通过仔细观察，根据同组数排列的顺序和前后、上下之间的相互关系，才能找出数与数间的排列规律。

【典型例题】【例1】按规律填数。

(1) 1, 3, 5, 7, 9, ( ), ( ), 15, 17(2) 1, 2, 4, 8， ( )练习1：（1）20, 18, 16, 14, ( ), ( ), 8, 6, 4（2）1, 7, 13, 19, ( ), ( ), 37, 43(3) 40, 35, 30, 25, ( ), ( ), 10, 5(4) 16, 8, 4, 2, ( )【例2】仔细观察，找规律填数。