学而思超常班二年级寒假班作业及答案第七讲

学而思选拔考试答案(二年级数学)一、基础题（80分）1.（共20分）计算(1)23+65=88(2)51+12=63(3)11+36=47(4)50-11=39(5)12-8=4(6)44-22=22(7)8+19=27(8)43+10=53(9)27+39=66(10)12+33=45(11)47-19=28(12)87-25=62(13)40-23=17(14)6×9=54(15)7×3=21(16)5×7=35(17)8×4=32(18)56÷7=8(19)25÷5=5(20)16÷4=42.（10分）在一条笔直的马路一侧种着很多小树苗；其中梧桐树的左边有12棵树；梧桐树的右边有10棵树；那么马路这一侧总共有________棵树．【解析】考查的排队问题；不仅要将左右相加；还得将梧桐树本身加进去；12+10+1=23（棵）．【答案】23．3.（10分）小丽在出门前想挑一套自己喜欢的衣服；她一共有2件不同的上衣；3条不同的裤子；请问小丽一共可以搭配出________套不一样的衣服．【解析】衣服的搭配问题；将三件上衣记为A、B、C；两条裤子记为①、②；那么可以是A①、A②、B①、B②、C①、C②；一共有六种不同的搭配．【答案】6．4.（共10分）在一根拉直的绳子上剪3刀；可以把这根绳子分成________段；要剪成10段；剪________刀．【解析】考查间隔问题．剪1刀；分成了两段；剪2刀；分成了三段；那么剪3刀；分成了4段；总结一下规律；段数比刀数多1；所以要剪成10段；只需要剪9刀．【答案】4；9．5.（共10分）找规律填数：（1）31；35；39；43；47；________；________．（2）5；7；10；14；19；________；________．（3）2；40；5；35；8；30；11；25；________；________．（4）5；8；13；21；34；________；________．（5）______；_____．【解析】考查数列和图形的规律．（1）从第二个数开始；每个数都比前面一个数大4；所以接下来应该是51；55．（2）第二个数比第一个数大2；第三个数比第二个数大3；第四个数比第三个数大4；所以这是一个二次等差；接下来应该是25；32．（3）这是一个双重数列；一个隔一个的去看才会发现规律；2；5；8；11……和40；35；30；25……，分别是两个等差数列；因此接下来应该是14；20．（4）这是一个兔子数列；从第三个数开始；每个数都等于前两个数的和；所以接下来应该是55；89．（5）考查图形的规律；都是箭头；只不过方向不一样；上右下左依次出现．【答案】（1）51；55．（2）25；32．（3）14；20．（4）55；89．（5）6.（共10分）哥哥和弟弟各带了一些钱；弟弟带了4元；去买牛奶的时候发现：哥哥如果给弟弟2元钱；他们俩的钱就刚好能够各买一瓶牛奶；那么牛奶一瓶________元钱；哥哥比弟弟多带了________元钱．【解析】考查加减法应用；根据“哥哥如果给弟弟两元钱；他们俩的钱就刚好能够各买一瓶牛奶”可以得出哥哥比弟弟多4元；所以哥哥带了8元；给两元给弟弟刚好可以买一瓶牛奶；说明一瓶牛奶8-2=6（元）．【答案】6；4．7.（共10分）数一数．有________个方块有________个三角形【解析】考查图形计数.第一个立体图形可以将最上面的三个正方体翻到第二层；此时一共两层；每层10个；共20个；第二个数三角形；可以分层去数；上面一层有1+2+3=6个；下面一层没有三角形；两层合起来有1+2+3=6个；所以共有6+6=12个．【答案】20；12．二、拓展题（60分）8.（12分）小明和小亮比赛爬楼梯；小明从一楼爬到四楼用了12分钟；小亮从一楼爬到七楼用了18分钟；那么________爬楼的速度比较快(填“小明”或“小亮”）．【解析】考查间隔问题中的爬楼梯；小明一楼到四楼总共爬了3层；用时12分钟；所以每一层用12÷3=4分钟；小亮一楼到七楼总共爬了6层；用时18分钟；所以每一层用18÷6=3分钟；所以小亮的爬楼速度比较快．【答案】小亮．9.（12分）巧算．（1）45+67+145-57=________（2）200-23-46-14-17=________【解析】考查巧算能力；凑整．【答案】（1）原式=45+145+67-57=190+10=200．（2）原式=200-（23+17+46+14）=200-100=100．10.（12分）下面的式子中；不同的汉字代表不同的数；请你根据式子判断；“数”=________；“学”=________．数+学+5=20学+学=数【解析】考查图文算式．由第二个式子可以知道“数”和“学”的等量关系；将这个等量关系代入到第一个式子中可以得到：“学”+“学”+“学”+5=20；所以3个“学”=15；“学”=5；所以“数”=5+5=10．【答案】10；5．11.（12分）熊大有12根玉米；他如果给熊二2根；他们俩就有一样多的玉米了；请问：熊二原来有________根玉米．【解析】考查加减法的应用；根据“他如果给熊二两根；他们俩就有一样多的玉米了”可以得到熊大比熊二多4根；所以熊二原来有12-4=8（根）．【答案】8．12.（12分）小林生日的时候带了一盒巧克力和小伙伴们分享；乐乐先吃了这些巧克力的一半；明明又吃了剩下巧克力的一半；萍萍吃了3颗；最后还剩下3颗；那么小林总共带了________颗巧克力．【解析】考查的是还原问题．可以画一个图帮助理解【答案】（3+3）×2×2=24（颗）．三、挑战题（60分）13.（15分）下面的式子中；A、B分别代表了不同的数字；请你根据下式判断A=_________；B=_________；AB表示的两位数是_________．【解析】考查竖式谜.通过尾数判断；可以得知B+B的尾数应该是8；所以B=4或9；若B=4；那么A+A+A=13；无解；若B=9；那么A+A+A=12；所以A=4；那么AB表示的两位数是49．【答案】4；9；49．14.（15分）艾迪去商店买书；买完总共要付38元；他带了一张20元；3张10元；4张5元；10张1元；那么艾迪有________种不同的付钱方法．【解析】考查付钱方法；枚举．【答案】9种．20元10元5元1元11131108103310280313030802330228014815.（15分）王平、宋丹、韩涛三个人都是少先队员的干部；一个是大队长；一个是中队长；一个是小队长．一次数学测验中；这三个人的成绩是：(1)韩涛比大队长的成绩好；(2)王平和中队长的成绩不相同；(3)中队长比宋丹的成绩差．请你根据这几个人的成绩判断：_________是大队长．【解析】考查逻辑推理；由（2）和（3）可知；中队长既不是王平也不是宋丹；所以中队长是韩涛；由（1）和（3）可知大队长和宋丹不是一个人；所以大队长只能是王平．【答案】王平．16.（15分）沙漏是一种计时工具；图中的沙漏里所有沙子从一边到另一边用的时间为1分钟；可以来计一分钟的时间；下次再用来计时的时候翻过来即可．小红拿它开始计时的时候沙子都在B中；小红用它计了3分钟；小明又用它计了10分钟；然后小乐又用它计了5分钟；当小乐用完时；沙子在________中（填A或B）【解析】考查奇偶数的应用；总共用来计时3+10+5=18（分钟）；18是一个偶数；所以沙子应该还在B中．【答案】B．。

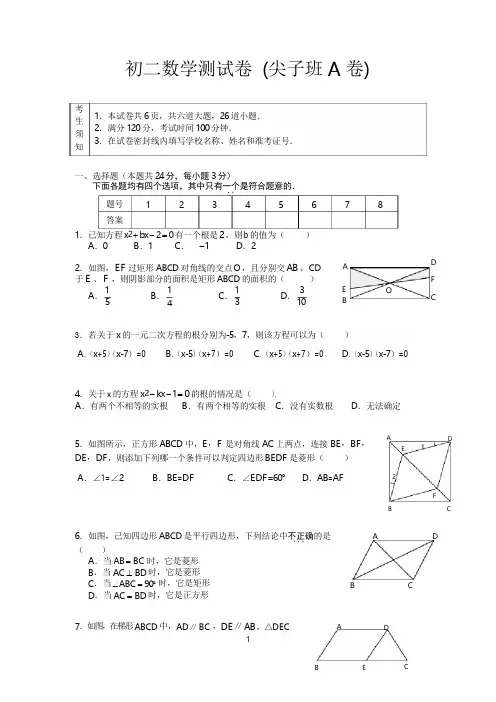
．．A ．B ．C ．D ．4 6．如图，已知四边形 ABCD 是平行四边形，下列结论中不正确的是考 生 须 知初二数学测试卷 (尖子班 A 卷)1．本试卷共 6 页，共六道大题，26 道小题． 2．满分 120 分，考试时间 100 分钟．3．在试卷密封线内填写学校名称、姓名和准考证号．一、选择题（本题共 24 分，每小题 3 分）下面各题均有四个选项，其中只有一个是符合题意的．题号 1 2 3 4 5 6 7 8答案1．已知方程 x 2 + b x - 2 = 0 有一个根是 2 ，则 b 的值为（）A ．0B ．1C ． -1D ．22．如图， EF 过矩形 ABCD 对角线的交点 O ，且分别交 AB 、 CD 于 E 、 F ，则阴影部分的面积是矩形 ABCD 的面积的（ ）1 1 1 3 5 3 10AEBODFC3．若关于 x 的一元二次方程的根分别为-5，7，则该方程可以为（）A ．（x +5）（x-7）=0B ．（x-5）（x +7）=0C ．（x +5）（x +7）=0D ．（x-5）（x-7）=04．关于 x 的方程 x 2 - kx - 1 = 0 的根的情况是（ ）．A ．有两个不相等的实根B ．有两个相等的实根C ．没有实数根D ．无法确定5．如图所示，正方形 ABCD 中，E ，F 是对角线 AC 上两点，连接 BE ，BF ， DE ，DF ，则添加下列哪一个条件可以判定四边形 BEDF 是菱形（ ）AE1DA ．∠1=∠2B ．BE =DFC ．∠EDF =60°D ．AB =AF2FB C．．． （ ）A ．当 AB = BC 时，它是菱形 B ．当 AC ⊥ BD 时，它是菱形 C ．当 ∠ABC = 90︒ 时，它是矩形 D ．当 AC = BD 时，它是正方形7．如图，在梯形 ABCD 中，AD ∥ BC ，DE ∥ AB ，△DECA DB CA D的周长为10cm，BE=4cm，则该梯形的周长为cm．A．25B．23C．21D．18A8．如图，菱形ABCD中，∠B=60︒，AB=2，E、F分别是BC、CD的中点，连接AE、EF、AF，则△AEF的周长为（）B DA．3B．23C．33D．6ECF二、填空题（本题共12分，每小题3分）题号9101112答案9．已知关于x的一元二次方程ax2+b x+c=0(a≠0)有一个根为-1，则b-c-a=．10.如图所示，正方形ABCD和正方形OEFG的边长均为5，O为正方形ABCD的中心，则图中重叠部分的面积是．D C GOF11．一元二次方程x2-3x+2=0的两个实数根都是等腰△ABC的边长，则这个等腰三角形的周长是．A BE y12．如图，菱形ABCD的边长为2，∠ABC=45︒，则点D的坐标为_________.A DO(B)C x三、解答题（本题共16分，每小题4分）13．用直接开方法解方程：(x-1)2=(4-2x)214．用配方法解方程：x2-4x-1=015．用公式法解方程：2x2-8x+3=016．用因式分解法解方程：(x-5)2+2(5-x)=(5-x)x四、解答题（本题共30分，每小题5分）AD17.若关于 x 的一元二次方程 x 2 + 4x + 2k = 0 有两个实数根，求 k 的取值范围及 k 的非负整数 值.18. 如图，矩形 ABCD 中，点 E 是 BC 上一点，AE ＝AD ，DF ⊥AE 于 F ，连接 DE ．求证：DF ＝DC ． A DFB19.如图，菱形 ABCD 的对角线 AC 与 BD 相交于点 O ，点 E 、F 分别为边AB 、AD 的中点，连接 OE 、OF ．求证：四边形 AEOF 是菱形．BE CAE FOD20 在正方形 ABCD 中，AC 为对角线，E 为 AC 上一点，连接 EB 、 △ED ．⑴求证： BEC ≌△DEC ；⑵延长 BE 交 AD 于 F ，当∠BED =120° 时，求∠EFD 的度数．EF CBC21.如图，在梯形 ABCD 中， AD ∥ B C ， AB ⊥ AC ， ∠B = 45o ， AD = 2 ，BC = 4 2 ，求 DC 的长．A DBC22.已知关于 x 的一元二次方程 x 2 + 2 (k - 1)x + k 2 - 1 = 0 有两个不相等的实数根..⑴求实数k的取值范围；⑵0可能成为方程的一个根吗？若是，请求出它的另一个根；若不是，请说明理由五、解答题（本题共18分，每小题9分）23.如图所示，有两种形状不同的直角三角形纸片各两块，其中一种纸片的两直角边长都为3，另一种纸片的两条直角边长分别为1和3．图1、图2、图3是三张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1．⑴请用三种方法（拼出的两个图形只要不全等就认为是不同的拼法）将图中所给四块直角三角形纸片拼成平行四边形（非矩形），每种方法要把图中所给的四块直角三角形纸片全部用上，互不重叠且不留空隙，并把你所拼得的图形按实际大小画在图1、图2、图3的方格纸上（要求：所画图形各顶点必须与方格纸中的小正方形顶点重合；并要保留四块直角三角形纸片的拼接痕迹）；⑵三种方法所拼得的平行四边形的面积和周长是否是定值？若是定值，请直接写出这个定值；若不是定值，请直接写出三种方法所拼得的平行四边形的面积和周长各是多少．33331133图1图2图324．已知一次函数的图象经过点A（2，1），B（-1，-3）．（1）求此一次函数的解析式；（2）求此一次函数的图象与x轴、y轴的交点坐标；（3）求此一次函数的图象与两坐标轴所围成的三角形面积．x = ， x = 3∴ x = ， x =2 2六、附加题（每题 10 分，共 20 分）25．已知 a > 0，b > a + c ，判断关于 x 的一元二次方程 ax 2 + b x + c = 0 的根的情况.26．如图， B F 平行于正方形 ABCD 的对角线 AC ，点 E 在 BF 上，且 AE = AC ，CF ∥ AE ，求 ∠BCF 的度数.FDCEAB参考答案及评分标准一、选择题（本题共 24 分，每小题 3 分）题号答案1C2B3A4A5B 6D7D8C二、填空题（本题共 12 分，每小题 3 分）题号 9 10答案 0 254115(2 +122 ， 2)三、解答题（本题共 16 分，每小题 4 分） 13. x - 1 = 4 - 2 x 或 x - 1 = 2 x - 451 32 14. x 2 - 4x + 4 - 4 - 1 = 0(x - 2 )2 = 5x - 2 =± 5 x = 2 ± 5x = 2 + 5 ， x = 2 - 51215.a = 2 ，b = -8 ，c = 3 ．∆ = b 2 - 4ac = (-8)2 - 4 ⨯ 2 ⨯ 3 = 40∴ x = -b ± b 2 - 4ac 8 ± 40=2a 2 ⨯ 24 + 10 4 - 101 2 16.(x - 5)2 - 2 (x - 5) + (x - 5) x = 0 (x - 5)(x - 5 - 2 + x ) = 0 (x - 5)(2x - 7 ) = 0∴AE=1x-5=0或2x-7=0x=5，x= 127 2四、解答题（本题共30分，每小题5分）17∵关于x的一元二次方程x2+4x+2k=0有两个实数根，∴∆=42-4⨯1⨯2k=16-8k≥0解得k≤2∴k的非负整数值为0,1,218.证明：方法1：Q AD=AE∴∠ADE=∠FEDA D又AD∥BCB FE C∴∠ADE=∠DEC∴∠DEC=∠DEF 又DF⊥DE∴△DEF≌△DEC∴DF=DE方法2：S△ADE =12AD⨯CD=12AE⨯FD∵AD=AE∴CD=FD19.证明：∵点E、F分别为AB、AD的中点A12AB，AF=2AD E F又∵四边形ABCD是菱形∴AB=AD，∴AE=AF，又∵菱形ABCD的对角线AC与BD相交于点O ∴O为BD的中点，∴OE、OF是△A BD的中位线B O DC∴ AE = EC = BC = 2 2 ．∴OE ∥AD ，OF ∥AB∴四边形 AEOF 是平行四边形∵AE =AF四边形 AEOF 是菱形AFD20. ⑴证明：∵四边形 ABCD 是正方形∴BC ＝CD ，∠ECB ＝∠ECD ＝45°又 EC ＝EC∴△ABE ≌△ADE△⑵∵ ABE ≌△ADEEB C∴∠BEC ＝∠DEC ＝ 1 2∠BED∵∠BED ＝120°∴∠BEC ＝60°＝∠AEF∴∠EFD ＝60°+45°＝105°21. 解法一：如图 1，分别过点 A ，D 作 AE ⊥ BC 于点 E ，DF ⊥ BC 于点 F ．∴ AE ∥ D F ．A D又 AD ∥ B C ，∴四边形 AEFD 是矩形．∴ EF = AD = 2 ．Q AB ⊥ AC ， ∠B = 45o ， BC = 4 2 ， BC∴ AB = AC ．12∴ DF = AE = 2 2 ，CF = EC - EF = 2 BA DE F 图 1C在 △Rt DFC 中， ∠DFC = 90o ，∴ DC = DF 2 + CF 2 = (2 2) 2 + ( 2) 2 = 10 ．解法二：如图 2，过点 D 作 DF ∥ AB ，分别交 AC ，BC 于点 E ，F ．∵ AB ⊥ AC ，∴ ∠AED = ∠BAC = 90o ．AD∵ AD ∥BC ，E24. (1)根据一次函数解析式的特点，可得出方程组 ⎨， -k + b = -3⎪⎪ 3解得 ⎨ ，则得到 y = x - ⎪b = - 5所以与 x 轴的交点坐标为 ,0 ⎪ ，与 y 轴的交点坐标 0, - ⎪⎩x - 中，令 x = 0 ，解得： y = - ，则函数与 y 轴的交点是 0, - ⎪ x - 中，令 y = 0 ，解得 x =∴ ∠DAE = 180o - ∠B - ∠BAC = 45o ． 在 △Rt ABC 中， ∠BAC = 90o ， ∠B = 45o ， BC = 4 2 ，∴ AC = AB = 4 2 ⨯2= 42 在 △Rt ADE 中， ∠AED = 90o ， ∠DAE = 45o ， AD = 2 ， ∴ DE = AE = 1 ．∴ CE = AC - AE = 3． 在 △Rt DEC 中， ∠CED = 90o ，∴ DC = DE 2 + CE 2 = 12 + 32 = 10 ．22. ⑴ b 2 - 4ac = 4(k -1)2 - 4(k 2 -1)= -8k + 8∵ 方程有两个不相等的实根，∴ -8k + 8 > 0 ∴ k < 1⑵ 当 x = 0 时， k 2 -1 = 0 ， k = ±1 ∵ k < 1 ∴ k = -1当 k = -1 时，方程为 x 2 - 4x = 0 x = 0，x = 412∴ 0 是方程的一个根，另一个根为 4.五、解答题（本题共 18 分，每小题 9 分）23.如下图：面积均为 12，周长分别为： 8 + 2 10 ； 8 + 6 2 ； 2 10 + 6 2⎧2k + b = 1 ⎩⎧4 k = 4 53 3 ⎪3 （2）根据一次函数的解析式 y =4 x -5 ，得到当 y = 0, x = 5 ; 当 x = 0, y = - 53 34 3 ⎛5 ⎫ ⎛ 5 ⎫ ⎝ 4 ⎭ ⎝3 ⎭（3）在 y = 4 5 5 ⎛ 5 ⎫ 3 3 3 ⎝ 3 ⎭在 y = 4 5 5 3 3 4；因此一次函数的图像与两坐标轴所围城的三角形面积是： ⨯ ⨯ =∴ CH = OB = AC ，CH = CF ，又 ∠CHF = 90︒1 5 5 252 3 4 24六、附加题（每题 10 分，共 20 分） 25.⑴当 c > 0 时， a > 0 ， b > a + c ，从而 b 2 > (a + c )2 ， b 2 - 4ac - (a - c )2 > 0 ，b 2 - 4ac > (a - c )2 ≥0 ，即 ∆ > 0⑵ 当 c = 0 时，由 a > 0 ， b > a + c = a ，得 b > 0 ， ∆ > 0⑶ 当 c < 0 时，由 a > 0 ，得 ac < 0 ， ∆ = b 2 - 4ac > 0 . 综上可知，方程总有两个不等实根.26.如图，连接 BD 交 AC 于 O ，过 C 作 CH ⊥ BF 于点 H ， 可证 OBHC 为正方形，1 2又可知 AEFC 为菱形，DCF12∴ ∠F = 30︒ ， ∠HCF = 60︒ OA BEH ∴ ∠BCF = 45︒+ 60︒ = 105︒。

学而思选拔考试答案(二年级数学)一、基础题（80分）1.（共20分）计算(1)23+65=88(2)51+12=63(3)11+36=47(4)50-11=39(5)12-8=4(6)44-22=22(7)8+19=27(8)43+10=53(9)27+39=66(10)12+33=45(11)47-19=28(12)87-25=62(13)40-23=17(14)6×9=54(15)7×3=21(16)5×7=35(17)8×4=32(18)56÷7=8(19)25÷5=5(20)16÷4=42.（10分）在一条笔直的马路一侧种着很多小树苗，其中梧桐树的左边有12棵树，梧桐树的右边有10棵树，那么马路这一侧总共有________棵树．【解析】考查的排队问题，不仅要将左右相加，还得将梧桐树本身加进去，12+10+1=23（棵）．【答案】23．3.（10分）小丽在出门前想挑一套自己喜欢的衣服，她一共有2件不同的上衣，3条不同的裤子，请问小丽一共可以搭配出________套不一样的衣服．【解析】衣服的搭配问题，将三件上衣记为A、B、C，两条裤子记为①、②，那么可以是A①、A②、B①、B②、C①、C②，一共有六种不同的搭配．【答案】6．4.（共10分）在一根拉直的绳子上剪3刀，可以把这根绳子分成________段；要剪成10段，剪________刀．【解析】考查间隔问题．剪1刀，分成了两段；剪2刀，分成了三段；那么剪3刀，分成了4段，总结一下规律，段数比刀数多1，所以要剪成10段，只需要剪9刀．【答案】4；9．5.（共10分）找规律填数：（1）31，35，39，43，47，________，________．（2）5，7，10，14，19，________，________．（3）2，40，5，35，8，30，11，25，________，________．（4）5，8，13，21，34，________，________．（5）______，_____．【解析】考查数列和图形的规律．（1）从第二个数开始，每个数都比前面一个数大4，所以接下来应该是51，55．（2）第二个数比第一个数大2，第三个数比第二个数大3，第四个数比第三个数大4，所以这是一个二次等差，接下来应该是25，32．（3）这是一个双重数列，一个隔一个的去看才会发现规律，2，5，8，11……和40，35，30，25……,分别是两个等差数列，因此接下来应该是14，20．（4）这是一个兔子数列，从第三个数开始，每个数都等于前两个数的和，所以接下来应该是55，89．（5）考查图形的规律，都是箭头，只不过方向不一样，上右下左依次出现．【答案】（1）51，55．（2）25，32．（3）14，20．（4）55，89．（5）6.（共10分）哥哥和弟弟各带了一些钱，弟弟带了4元，去买牛奶的时候发现：哥哥如果给弟弟2元钱，他们俩的钱就刚好能够各买一瓶牛奶，那么牛奶一瓶________元钱，哥哥比弟弟多带了________元钱．【解析】考查加减法应用，根据“哥哥如果给弟弟两元钱，他们俩的钱就刚好能够各买一瓶牛奶”可以得出哥哥比弟弟多4元，所以哥哥带了8元，给两元给弟弟刚好可以买一瓶牛奶，说明一瓶牛奶8-2=6（元）．【答案】6；4．7.（共10分）数一数．有________个方块有________个三角形【解析】考查图形计数.第一个立体图形可以将最上面的三个正方体翻到第二层，此时一共两层，每层10个，共20个；第二个数三角形，可以分层去数，上面一层有1+2+3=6个，下面一层没有三角形，两层合起来有1+2+3=6个，所以共有6+6=12个．【答案】20；12．二、拓展题（60分）8.（12分）小明和小亮比赛爬楼梯，小明从一楼爬到四楼用了12分钟，小亮从一楼爬到七楼用了18分钟，那么________爬楼的速度比较快(填“小明”或“小亮”)．【解析】考查间隔问题中的爬楼梯，小明一楼到四楼总共爬了3层，用时12分钟，所以每一层用12÷3=4分钟，小亮一楼到七楼总共爬了6层，用时18分钟，所以每一层用18÷6=3分钟，所以小亮的爬楼速度比较快．【答案】小亮．9.（12分）巧算．（1）45+67+145-57=________（2）200-23-46-14-17=________【解析】考查巧算能力，凑整．【答案】（1）原式=45+145+67-57=190+10=200．（2）原式=200-（23+17+46+14）=200-100=100．10.（12分）下面的式子中，不同的汉字代表不同的数，请你根据式子判断，“数”=________，“学”=________．数+学+5=20学+学=数【解析】考查图文算式．由第二个式子可以知道“数”和“学”的等量关系，将这个等量关系代入到第一个式子中可以得到：“学”+“学”+“学”+5=20，所以3个“学”=15，“学”=5，所以“数”=5+5=10．【答案】10；5．11.（12分）熊大有12根玉米，他如果给熊二2根，他们俩就有一样多的玉米了，请问：熊二原来有________根玉米．【解析】考查加减法的应用，根据“他如果给熊二两根，他们俩就有一样多的玉米了”可以得到熊大比熊二多4根，所以熊二原来有12-4=8（根）．【答案】8．12.（12分）小林生日的时候带了一盒巧克力和小伙伴们分享，乐乐先吃了这些巧克力的一半，明明又吃了剩下巧克力的一半，萍萍吃了3颗，最后还剩下3颗，那么小林总共带了________颗巧克力．【解析】考查的是还原问题．可以画一个图帮助理解【答案】（3+3）×2×2=24（颗）．三、挑战题（60分）13.（15分）下面的式子中，A、B分别代表了不同的数字，请你根据下式判断A=_________，B=_________，AB表示的两位数是_________．【解析】考查竖式谜.通过尾数判断，可以得知B+B的尾数应该是8，所以B=4或9，若B=4，那么A+A+A=13，无解；若B=9，那么A+A+A=12，所以A=4，那么AB表示的两位数是49．【答案】4；9；49．14.（15分）艾迪去商店买书，买完总共要付38元，他带了一张20元，3张10元，4张5元，10张1元，那么艾迪有________种不同的付钱方法．【解析】考查付钱方法，枚举．【答案】9种．20元10元5元1元11131108103310280313030802330228014815.（15分）王平、宋丹、韩涛三个人都是少先队员的干部，一个是大队长，一个是中队长，一个是小队长．一次数学测验中，这三个人的成绩是：(1)韩涛比大队长的成绩好，(2)王平和中队长的成绩不相同，(3)中队长比宋丹的成绩差．请你根据这几个人的成绩判断：_________是大队长．【解析】考查逻辑推理，由（2）和（3）可知，中队长既不是王平也不是宋丹，所以中队长是韩涛，由（1）和（3）可知大队长和宋丹不是一个人，所以大队长只能是王平．【答案】王平．16.（15分）沙漏是一种计时工具，图中的沙漏里所有沙子从一边到另一边用的时间为1分钟，可以来计一分钟的时间，下次再用来计时的时候翻过来即可．小红拿它开始计时的时候沙子都在B中，小红用它计了3分钟，小明又用它计了10分钟，然后小乐又用它计了5分钟，当小乐用完时，沙子在________中（填A或B）【解析】考查奇偶数的应用，总共用来计时3+10+5=18（分钟），18是一个偶数，所以沙子应该还在B中．【答案】B．。

学而思09年寒假二年级数学入学测试题各位家长和同学：45分钟完成，共12道题，一定要独立完成！试卷说明：答案完全正确的得分，多解、漏解、错解都不得分.1．小红把一个薄饼切三刀，最多能切（）块．妈妈把一块豆腐要切成8块，最少能切（）刀．2．数一数．（）条线段（）个正方形（）个三角形（）个长方形3．找出下列各数列的规律，按其规律在( )内填上合适的数⑴1，1，2，3，5，8，（），21，……⑵56，51，46，41，36，（），26，……⑶4，8，16，（），64，（），256，……⑷0，75，5，70，10，65，（），（），……4．下图是一个公园的平面图．要使游客走遍每条路而不重复，出入口应分别设在（）点与（）点．I HGFE DCBA5．画一画．⑴ 把12个圆片放到下图中的8个空白方格里，怎样放才能使每边的圆片加起来都是5个？画一画．⑵ 下图中7只小动物被围在一个圆圈里，请画3条直线，把它们全部隔开．6．观察下面的图，你知道小鸡、小鸭、小兔各重多少千克吗？7．小马虎在做两位数加法时，由于粗心，把一个加数个位上的3看成了8，把十位上的4看成了7，结果得到的答案是90．那么，正确的答案应该是（）.8．有6位小朋友在一起吃饭，每人一个饭碗，2人一个菜碗，3人一个汤碗，请你算一算他们一共用了多少个碗？9．学校有一条长50米的走道，计划在道路两旁栽树．每隔5米栽一棵，（两端都栽），那么共需多少棵树苗？10．小毛的妈妈买了一台录音机500元，接着又以540元卖掉了．接着她又以550元的价钱买了回来，随后又以580元的价钱卖掉了．请问：小毛的妈妈一共赚了多少钱呢？11．小明和奶奶一起爬楼，小明到达3楼时，奶奶才爬到2楼．奶奶到达4楼时，小明已到了几楼？12．大象、老虎、猴子三只动物的年龄中，大象和老虎共90岁，大象和猴子共70岁，老虎和猴子共40岁，请你算一算，三只动物各多少岁？。

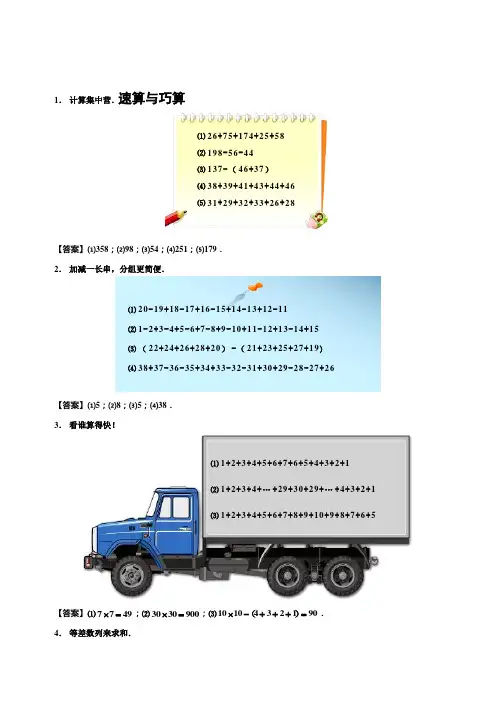
速算与巧算1． 计算集中营．【答案】⑴358；⑵98；⑶54；⑷251；⑸179．2． 加减一长串，分组更简便．【答案】⑴5；⑵8；⑶5；⑷38．3． 看谁算得快！【答案】⑴7749⨯=；⑵3030900⨯=；⑶1010432190⨯-+++=（）． 4． 等差数列来求和．⑴1+2+3+4+5+6+7+6+5+4+3+2+1⑵1+2+3+4+…+29+30+29+…+4+3+2+1⑶1+2+3+4+5+6+7+8+9+10+9+8+7+6+5⑴20-19+18-17+16-15+14-13+12-11⑵1-2+3-4+5-6+7-8+9-10+11-12+13-14+15⑶（22+24+26+28+20）-（21+23+25+27+19)⑷38+37-36-35+34+33-32-31+30+29-28-27+26⑴26+75+174+25+58⑵198-56-44⑶137-（46+37）⑷38+39+41+43+44+46⑸31+29+32+33+26+28【答案】⑴7749⨯=；⑵422102130+⨯÷=（）；⑶54082180+⨯÷=（）．5． 在下面的□中填上5个连续的数，使等式成立．【答案】67891040++++=．6． 下面的题你会算吗？【答案】135959799++++++L 20003692730------L1995021005022500=+⨯÷=⨯÷=（）或50502500=⨯=20003692730200033010220001651835=-+++++=-+⨯÷=-=L （）（） ⑴1+3+5+L +95+97+99⑵2000-3-6-9-L -27-30⑴1+3+5+7+9+11+13⑵4+6+8+10+12+14+16+18+20+22⑶5+10+15+20+25+30+35+40【答案】想要把一个西瓜切成9块，我们可以在西瓜上横着切2刀，再竖着切2刀，切成一个“井”字形，这样周围有8块，中间1块，正好9块．这样切成9块的西瓜，吃完后有没有10块西瓜皮呢？只要再想一想，就可以发现，正中间的那一块上下都有瓜皮，把瓜吃完后，这一块有2块瓜皮，不是正有10块瓜皮吗． 豆豆家里来了四位客人，爸爸买了一个大西瓜回来招待客人．但爸爸要求豆豆只许切4刀，切完必须给爷爷、奶奶、爸爸、妈妈、豆豆和四位客人每人一块，而且吃完西瓜后必须有10块瓜皮．请你帮豆豆想一想，该怎样切才合适?。

1.鸡兔同笼共有14个头，38条腿，有几只鸡？几只兔？【答案】有5只兔子和9只鸡．2.蛐蛐和蜘蛛共八只，腿54条，蛐蛐和蜘蛛各几只？【答案】有3只蜘蛛和5只蛐蛐．3.三轮货车和小轿车共有9辆，一共有30个轮子，三轮货车和小轿车各几辆？【答案】6辆三轮车，3辆小轿车．4. 王强和李明都想买一本《趣味数学》，但王强的钱少2元5角，李明的钱少3元1角．如果两个人的钱合在一起就刚够买这本书．问一本《趣味数学》多少钱？王强和李明各有多少钱？【答案】一本书的书价是： 2元5角+3元1角=5元6角．王强有3元1角，李明有2元5角．5.小白兔挑了一筐萝卜去卖，这筐萝卜连筐共重30千克．上午卖出萝卜的一半，下午卖出剩下的一半，这时连筐还重12千克．原来这筐萝卜重多少千克？【答案】30123424-÷⨯=（）（千克），原来这筐萝卜重24千克．6.小初、小美、小英三个人分糖块．小美比小英多3块，小初比小美多2块．已知糖块总数是50块，那么每人各分到多少块？【答案】依题意画图，可以先画小英，见上图中①，再画小美，它比小英多3块，见上图中②，接着再画小初，它又比小美多2块，见上图中③，至此，图已画完，下面借助此图进行分析推理．由图可见，小初比小英多325+=块，由图还可以看出，503542（）(块)就是小英糖数的3倍，所以小英的一份是：-+=÷=(块)；42314由此可求出小美的一份是14317+=(块)；小初的一份是17219+=(块)．池塘里的浮萍池塘里的浮萍每天面积长大一倍，10天就能长满整个池塘．那么请问，浮萍长满半个池塘需要多少天呢？【答案】需要9天就可以长满半个池塘．（注：文档可能无法思考全面，请浏览后下载，供参考。

可复制、编制，期待你的好评与关注）。

蜗牛爬井第六讲【例题分析】第6天；可以先考虑特殊的最后一天，蚂蚁爬5米刚好爬到井口，不再滑下，那么它在前几天一共向上移动了205-=15米；它每天爬上5米，又滑下2米，相当于每天只移动了52-=3米，之前爬了153÷=5天，所以第51+=6天爬到井口．一只蚂蚁从一口20米深的枯井底部往上爬，它每天往上爬5米后，就会滑下2米，像这样爬，这只蚂蚁第几天刚好爬到井口？【例题分析】第7天；水缸打水和蜗牛爬井一样，可以先考虑最后一天，这天早上工作人员刚好第一次将水缸装满，那么在此之前水缸里一共有水295-=24桶．每天打回5桶水，又用掉1桶水，则相当于每天往缸里增加51-=4桶水，需要244÷=6天，则第61+=7天第一次把水缸装满．有一口空水缸，需要29桶水才能刚好装满．工作人员每天早上会打回5桶水倒入缸中，傍晚又会用掉缸里1桶水，那么工作人员第几天才能第一次让水缸装满水？【例题分析】第6天；先考虑最后一天，水缸刚好第一次装满，那么在此之前水缸里一共有水216-=15桶．每天倒入6桶水，又用掉3桶水，则相当于每天往缸里增加63-=3桶水，需要153÷=5天，则第51+=6天才能第一次将水缸装满．【例题分析】32米；树懒每天向上爬6米，晚上滑下2米，每天树懒只向上移动了62-=4米．树懒第8天才到顶端，那么前7天共移动了47⨯=28米，再加上第8天的4米，树一共高284+=32米．树懒爬树，它从树底端开始，每天白天向上爬6米，晚上睡觉时滑下2米，第8天爬了4米后终于爬到了树顶端．请问这棵树高多少米？一个空水缸装满水需要21桶，婷婷每天早上向缸里倒入6桶水，晚上又用掉缸里3桶水，婷婷第几天才能第一次将水缸装满？【例题分析】31个；洋洋每次装5个桃子，又吃掉1个，相当于每次只装了514-=个桃子，7次后一共装了7428⨯=个桃子，最后又装3个桃子筐就满了．那么这个筐装满能装28331+=个桃子．【例题分析】18米；小猴爬的最高的位置，是第8次往上爬，还没有滑下来时的位置．小猴每次向上爬4米，然后滑下2米，相当于每次只向上移动了422-=米，第7次时爬到了2714⨯=米的位置，第8次时再往上爬4米到了最高位置，即14418+=米．【例题分析】6米；小丑第8天爬了4米爬到了树顶， 说明前817-=天小丑共向上移动了25421-=米，每天移动了2173÷=米．每次滑下3米，那么每次向上爬336+=米．一个小丑从一棵25米高的树底往上爬，每次向上爬若干米，接着又滑下3米，第8次爬了4米爬到树顶，那么小丑每次向上爬了几米呢？小猴爬竹杆，每次先向上爬4米，接着滑下2米．小猴从竹杆底端开始，共爬了8次，那么小猴最高时爬到了多少米高的位置？洋洋往一个空筐里装桃子，她每次往筐里装5个桃子，然后偷吃掉1个，像这样，第8次装了3个就把筐装满了，那么这个筐装满能装多少个桃子？【例题分析】4米；小蜗牛第6天爬了5米到井口，也就说明前5天一共向上移动了1055-=米，每天移动了551÷=米． 每天白天向上爬5米，则每天夜里会滑下514-=米．【例题分析】42桶；梦梦每天白天打回6桶水，晚上又用掉2桶，相当于每天水缸会增加624-=桶水，30624-=桶，2446÷=天，即第7天打6桶水时，水缸刚好第一次装满．此时梦梦一共打了6742⨯=桶水．一个空水缸，装满需要30桶水，梦梦每天白天会打回6桶水倒入水缸，晚上又会用掉水缸里的2桶水，那么到水缸刚好第一次装满时，梦梦一共打了多少桶水呢？一个空水缸，装满需要33桶水，洋洋每天白天会打回7桶水倒入水缸，晚上又会用掉水缸里的几桶水，第七天洋洋打回3桶水后水缸刚好第一次装满，那么洋洋每天晚上用掉了几桶水呢？小蜗牛从10米深的井底往上爬，每天白天向上爬5米，每天夜里又滑下若干米，第6天爬了5米爬到井口，那么小蜗牛每天夜里滑下了几米呢？【例题分析】64步；舞者先前进4步再后退2步，这样跳一次实际只向前移动了422-=步，24420-= 步，20210÷=次，即第11次时前进4步刚好跳到了另一头．前10次每一次跳了426+=步，这个人一共跳了610464⨯+=步．一位舞者沿一条直线前进4步，接着后退2步，像这样从舞台的一头跳到另一头．舞台的两头相距24步，这个人一共跳了多少步？。

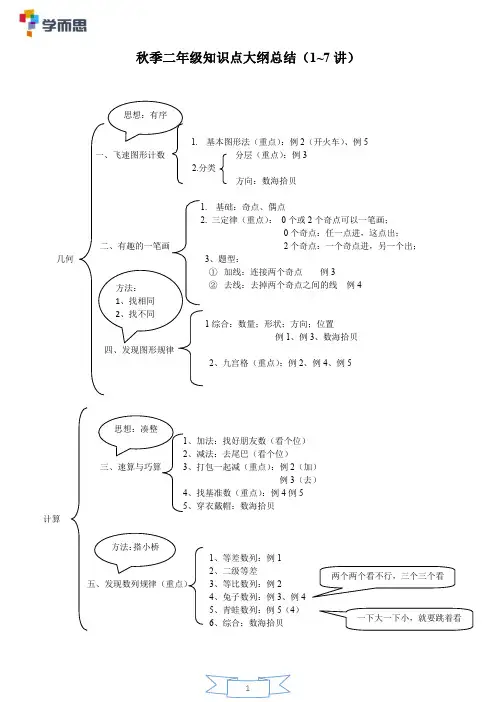
秋季二年级知识点大纲总结（1~7讲）基本图形法（重点）：例2（开火车）、例5分层（重点）：例3方向：数海拾贝基础：奇点、偶点 三定律（重点）： 0个或2个奇点可以一笔画； 0个奇点：任一点进，这点出；2个奇点：一个奇点进，另一个出；几何 3、题型：① 加线：连接两个奇点 例3② 去线：去掉两个奇点之间的线 例4 1综合：数量；形状；方向；位置例1、例3、数海拾贝 2、九宫格（重点）：例2、例4、例5 、加法：找好朋友数（看个位） 、减法：去尾巴（看个位）、打包一起减（重点）：例2（加）例3（去）、找基准数（重点）：例4例5 、穿衣戴帽：数海拾贝计算 1、等差数列：例1 2、二级等差五、发现数列规律（重点） 3、等比数列：例24、兔子数列：例3、例45、青蛙数列：例5（4）6、综合：数海拾贝1、两端都种（重点）：棵数=段数+1例1（1）、例2、例4、数海拾贝、2、两端不种：棵数=段数-1例1（2）、3、一端种：棵数=段数例1（3）4、环形：棵数=段数例1（4）、例3、例5一、烙饼（重点）：画图（例1）注意：保证锅的空间都要利用二、做家务：先判断事情顺序、再找可以同时进行的事组合：七、合理安排注意：在题目中画出关键句（例2、例3）三、过河（例4、例5）四、合理安排（数海拾贝、尖子班挑战）（重点）方法：使等待时间最短，让最快的先做。

第一讲飞速图形计数【例题巩固】【例1】数一数，下图中共有多少条线段？【例题分析】方法：开火车①，②，③；3个①②，②③；2个①②③；1个共：3+2+1=6（个）答：一共有6条线段。

【例2】数一数，图（1）中共有多少个锐角？图（2）中共有多少个三角形？【例题分析】方法：开火车4+3+2+1=10（个）5+4+3+2+1=15（个）答：图（1）中共有10个锐角，图（2）共有15个三角形。

【例3】数一数下图中共有多少个长方形？【例题分析】方法：分层法上层：3+2+1=6（个）下层：3+2+1=6（个）合：3+2+1=6（个）共：6×3=18（个）答：图中共有18个长方形。

学而思二年级数学思维训练
1、数量关系题
题目：有一堆糖果，如果每盒装3个，那么会剩下2个；如果每盒装5个，那么会剩下3个。

请问这堆糖果一共有多少个？
答案：根据题目，我们可以列出两个方程式：
3x+2=糖果总数
5x+3=糖果总数
解方程得x=1，所以糖果总数为3×1+2=5。

2、计算题
题目：计算10-3×2÷5-1的值。

答案：按照运算顺序，先算乘除，再算加减。

3、10-3×2÷5-1=10-6÷5-1=10- 2-1= 8。

4、图形识别题
题目：下面的图形中，哪些是三角形？哪些是圆形？哪些是正方形？
答案：根据图形的形状，我们可以识别出哪些是三角形、圆形和正方形。

三角形：（1）（3）（5）
圆形：（2）（4）
正方形：（6）
5、逻辑推理题
题目：如果你面前有一个盒子，盒子里有红、蓝、绿三种颜色的球。

已知红球有2个，蓝球有3个，绿球有4个。

请问盒子里的球一共有多少个？
答案：根据题目，我们可以得知盒子里的球的总数为：2（红）+3（蓝）+4（绿）=9。

6、应用题
题目：小明和小红一共有40个彩色铅笔，如果小明有16个，小红有多少个彩色铅笔？
答案：根据题目，我们可以得知小明和小红一共有的彩色铅笔数量为40个。

已知小明有16个，因此小红有的彩色铅笔数量为：40-16=24个。

学而思二年级数学植树的问题学而思二年数学直的，再区分：两端都种，段数 =的数量 -1两端都不种，段数=的数量 +1一端种，一端不种，段数 =的数量如果是封形的，段数等于的数量.学而思二年数学带余数的除法被除数除数 =商⋯⋯ .余数被除数 =商除数+余数除数 =（被除数—余数）商=（被除数—余数）除数余数，最大除数减去1，就可以知道余数一共有多少种可能性.如果不整除，余数最小是1，最大是除数— 1.例题一箱苹果不到 40个， 4个 4个地数还多 2个， 5个 5个地数还多 1个，这箱苹果有个.枚举法中的乘数原理一件事情，如果需要两个步骤完成，第一个步骤有 a 个选择，第二个步骤，有 b 个选择，那么完成这件事情，一共有a排队题目排队题目，最重要的是画图.其次，区分是第几个，还是前面后或者后面有几个.注意，小米和小兰之间相差 3 个人，如果没有明确，可能是小米在前，也可能是小兰在前，要分两种情况分别考虑的 .周期问题（普通周期，数列周期，日期周期）一定需要先写出周期的排序.没有余数，也就余数为0，就是周期的最后一个.对于日期来说，区分第10 天，和再过10 天.过河过桥问题过河问题，如果一只船只能坐两个人，那么一定是速度最快的人来回.过桥问题，最多只有两个人可以同时通过，并且要送一件东西回来的话，如果是 4 个人的话，甲乙丙丁，用的时间是丁 >丙 >乙 >甲，第一次甲乙一起过第二次甲回来第三次丁丙一起过第四次乙回来第五次甲乙一起过烙饼问题如果一次可以同时烙两个饼，时间 =烙饼的数量烙一面饼的时间（注意，是烙一面饼的时间） .如何表示饼的正面和反面？搭配问题乘法公式，以及通过枚举法解决组数问题组数的问题，可以通过乘法公式解决，先确定位置，比如千位，百位，十位，个位.例题：3,5,6,7 可以组成多少个没有重复数字的偶数？2,4,5,7 可以可以组成多少个没有重复数字的偶数？拆数问题把一个整数拆成几个不同的数的和，可以用枚举法解决.5级的台阶，只能爬一个或者两个台阶，一共有几种不同的方法？可乐，薯条，汉堡三种食物，一天只能选一种，连续两天不能重复，小麦决定第一天吃汉堡，第五天吃汉堡， 5 天内一共有几种不同的吃法？加减法巧算分组的方法，分成几组，在每组中，计算简单.例子：100+99-98-97+96+95-94-93+⋯⋯ .+4+3-2-1凑整法179-99168-101234+20597+96+95+86+87+88金字塔数列等差数列求和末项 =首项 +（项数 -1）项数 =（末项 -首项）公差+1首项 =末项 -（项数 -1）公差 =（末项 -首项）（项数-1）等差数列之和 =（首项 +末项）2如果是奇数项，可以用下面这个公式：等差数列之和 =中间项组合图形求周长关键是凑成规则的长方形或者正方形.鸡兔同笼和倍问题，和差问题两种方法，线段法以及前后表格法.前后表格法，需要假设未知数，尽量假设一个未知数.要搞清楚，前后表格法中，总计这个数，有没有发生变化.如果发生变化了，能否求出变化后的总计的数字 .前后表格法如下：前后甲乙合计逆向思维，流程图画法例题一只小猴子特别喜欢吃桃子，有一天，他摘了一堆桃子，每天都吃掉这堆桃子的一半又10个，这样吃了三天，还剩 10个 .请问这堆桃子最初有多少个？找规律，数列与图形规律移多补少的问题用前后表格法，抓住总和不变这个关键.重要的数学方法表达关系法例题艾迪在小动物的带领下来到猛兽小区门前门上印着一个谜语：一数真离奇，自己加自己，自己减自己，自己乘自己，自己除自己，得数在一起，相加三十六，猜猜它是几？例题艾迪帮警察抓住坏蛋之后，警察决定送艾迪回家，在路上艾迪想去商店买些礼物送给薇儿．他发现商店里 1 辆玩具车等于 2 个书包加上 1 个音乐盒的价格， 1 个书包等于 3 个音乐盒的价格， 1 个音乐盒等于 4 根铅笔的价格，那么 1 辆玩具车相当于____▲ ____根铅笔的价格．尝试法尝试法的举例子例题有一列数，第一个数是4，第二个数是第一个数乘以 3 的个位数，以此类推，那么第40个数是多少？例题，沙漏是一种计时工具，图中的沙漏里所有沙子从一边到另一边用的时间为 1 分钟，可以来计一分钟的时间，下次再用来计时的时候翻过来即可．小红拿它开始计时的时候沙子都在 B 中，小红用它计了 3 分钟，小明又用它计了 10 分钟，然后小乐又用它计了 5 分钟，当小乐用完时，沙子在_________中（ A 或 B）尝试法，例题黑板上写着2、4、 6、 8、10、 12、14、 16、18 共 9 个数，老师每次任意擦掉两个数，并把它们的和写到黑板上．那么，当黑板上只剩下一个数时，这个数是_________例题将数字 1～9 分别填入下面的□中，每个□中填一个数字（不能重复，其中9已填好），使得算式成立．例题，某学校进行乒乓球比赛，进行的是淘汰赛（输者淘汰，胜者晋级）.一共有 64名参赛队员，请问一共需要多少场比赛才能确定冠军.枚举法中，非常重要的是分类讨论.比如， 3,4,5,6 可以组成多少个没有重复数字的整数？枚举法中，有个非常重要的概念是位置，位置可以是没有区别的，也可能是有区别的 .比如， 10 个铅笔放入 3 个相同的文具盒中，每个文具盒至少要放入一个铅笔 .这个位置就是相同的 .比如，妈妈给小麦 7 个苹果，要求每天至少吃 2 个，并且必须 3 天吃完，有多少钟不同的吃饭 .3,4,5,6 可以组成多少个没有重复数字的四位数？这个题目中，位置是什么？例题，艾迪决定再买些苹果给小动物吃，他发现商店里卖的苹果都是5 个一袋或3 个一袋的，只能一袋一袋卖．已知 5 个一袋的价格是 20 元，3 个一袋的价格是 15 元，要给车上的 26 位小动物每位发一个苹果，最少要花 ____▲____元．文氏图中的公式A 表示属于 A 的有多少，B 表示属于 B 的有多少， AB 表示既属于 A，又属于 B 的是多少 .A 和B 总共多少 =A+B-AB上面的公式行恒等形，可以得到既属于 A，又属于 B 的 AB 等于什么 . AB= A+B- A 和 B 总共多少一笔画的问题①凡是由偶点组成的连通图，一定可以一笔画成；画时可以任一偶点为起点，最后一定能以这个点为终点画完此图.②凡是只有两个奇点（其余均为偶点）的连通图，一定可以一笔画成；画时必须以一个奇点为起点，另一个奇点为终点.③其他情况的图，都不能一笔画成.数线段的问题首先要分成不同的直.其次，数直上有几个点，比如一条直有 5 个点，那么条直上一共有1+2+3+4 条段 .公式：如果一条直有n 个点，那么，条直上有1+2+3+ ⋯⋯ ..+(n-1) 条段 .数角的，和段是同的公式.一个萝卜一个坑的题目两两握手的问题一共 n 个人，两两握手一次，不能握手两次，一共有1+2+3+ ⋯ ..(n-1) 次手 .杀手数独和正常数独等量替换（每空 6 分，共 12 分）下面的式子中，相同的汉字代表相同的数，不同的汉字代表不同的数，请你根据式子判断，“数” =________，“学” =________．数+学+5=20学+学=数对应法解题芳芳在看一本数学书，如果她第一天读 6 页，以后每一天都比前一天多读9 页，结果到最后一天时，还剩 40 页没有读完；如果她第一天读24 页，以后每一天也比前一天多读9 页，结果比上一种情况少用一天，但也还剩10 页没有读完．那么，这本数学书共有多少页．染色问题从最下一层开始数，画出每层的平面图 .注意，与地上相接的一层，只是一个面没有涂到，不要乘以 2.其余的两个面相接，需要乘以 2.鸡兔同笼的问题11/11。

二年级奥数寒假班讲义第一节倒过来算--XXX框框法【知识要点】同学们在玩迷宫游戏时，往往会发现，根据要求从里面往外找出路，经常会走入死路，如果反过来思考，从外面的出口往里走，却能很快走到里面的出发点。

数学中有些问题的解答，就像走迷宫一样，需要我们从所求问题出发，倒着想，回到已知条件，这种倒着想的方法，叫做倒推法。

今天我们一起探究邦德框框法的妙处！【课前热身】23＋□=30□－42=15□×3=24□÷4=5【典型例题】例1一个数加上8，再减去2，结果等于8，求这个数是多少？例2某数加上3，乘以5，再减去8，等于12，则这个数是多少？例3一根铁管，第一次截去2米，第二次截去剩下的一半，还剩下5米，这根铁管原有多少米？1二年级数学A例4XXX从学校回家，坐地铁走了全程的一半，坐汽车走了剩下的路程的一半，这时离她家还有2千米，学校到XXX家有多少千米？【经典回顾】例5（1）2、5、3、5、4、5、（）、（）（2）11、4、8、4、5、4、（）、（）（3）1、2、3、5、8、13、（）（4）2、5、6、9、10、13、14、( )、( )（5）1、2、3、2、3、4、3、4、5、( )、( )、( )（6）1、2、4、8、（）（7）6、1、8、3、10、5、12、7、（）、（）；2二年级数学A【小试矛头】1．一个数减去2，再乘以4，结果是24，求这个数？2．一个数加上5，再减去8，成效是12，求这个数？3．一个数除以5，加上6，再减去2，成效是8，求这个数是多少？4．一个数加上2，乘以4，减去4，再除以4，末了成效还是4，求这个数？5．有一盘桃子，猴哥哥取走了10个，猴妹妹取了剩下的一半，这时还剩下4个桃子，问原有桃子多少个？6．有甲、乙、丙三个鸡笼，如果从甲笼取6只小鸡到乙笼，又从乙笼取5只小鸡到丙笼，再从丙笼取4只小鸡到甲笼，这时三个鸡笼里的小鸡都是12只。

求三个鸡笼原各有多少只小鸡？3二年级数学A【大显身手】1．一个数加上7，再乘以2，结果是18，求这个数？2．一个数减去2，乘以3，加上4，除以5后等于2，求这个数？3．一根绳子用去7米，再用去余下的一半，还剩9米，这根绳子原有多长？4．妈妈去商店购物，第一次用去所带钱的一半，第二次又用去了余下的一半，这时妈妈还剩下30元，妈妈原有多少钱？★5．甲、乙、丙三堆砂子，第一次从甲堆取出5千克给乙堆，第二次从乙堆取出10千克给丙堆，第三次从丙堆取出6千克给甲堆，这时三堆砂子都是48千克。

PDF合并工具-未注册版PDF合并工具-未注册版PDF合并工具-未注册版数一数和算一算12动手操作问题2有趣的乘法2有趣的除法12【例2】(★★★)张由完成这张方格纸是由一些大小完全一样的小正方形组成的。

我想沿格子线剪成形状相同且大小相等的两块分给我的两个儿子你们能找出几种不同的方法呢？两个儿子，你们能找出几种不同的方法呢？下面是我搭的积木。

从不同的角度来观察下面哪几幅图是我有可能看到的？配餐要求：每份饭含一个荤菜和一个素菜，外加一份饮料。

请你们试试看有多少种不同的配餐方法？1们分配一下有几种乘车情况？车库里停放着一些三轮车和自行车。

我刚刚擦洗完12个车轮子。

你们猜一猜我擦洗的可能是什么车？各擦洗了几辆？猜猜我擦洗的能是什么车各擦洗辆【例1】★★看图回答,一个足球是40元，一个皮球是( )元钱。

比一比，1只鸭和1只鸡，谁重一些？【拓展】★★★★【例4】★★★请问：1串葡萄重多少克？【例5】★★★★1只袋鼠的重量相当于多少只小鸡的重量？【例6】★★★★★在下图中的“？”处放上几个小，才能使天平保持左右平衡？【拓展】★★★★★(“学而思杯”试题)如图所示，两个天平是平衡的。

现在知道每个的重量是50克，那么一个●的重量是_____克。

图形的等积变换【预备知识】什么是图形的等积变换？有一张纸被分成大小相等的个方格请你沿着方格纸有一张纸，被分成大小相等的16个方格。

请你沿着方格纸的边把这张纸剪成两部分，使得这两部分正好可以拼成一个正方形。

该怎样剪拼呢？中间空白是空的个形怎样剪拼(中间)有张被成相等请着张有一张纸，被分成大小相等的16个方格。

请你沿着方格纸的边把这张纸剪成两部分，使得这两部分正好可以拼成一个正方形。

该怎样剪拼呢？(中间空白是空的)下图是由18个小正方形组成的图形，请你把它分成6个形状大小完全相同的图形。

将下图分割成大小、形状相同的三块，使每块都包含一个小圆圈。

在下面的方格中有4个圆圈，请你把方格分成形状大小完全一样的4块，使每部分都有1个圆圈(圆圈的位置相同)。

启用前★绝密2017年第七届南京学而思综合能力䈀ᯣ数学（二年级）考试时间：60分钟满分：200分考生须知：请将所有的答案写在答题纸．．．对应位置上一、基础过关（每题8分，共40分）1.计算：（1）1＋4＋7＋10＋13＋16＋19= ▲．（2）96－（56＋19）= ▲．2.春天到啦，薇儿要出去郊游，她想要选择一条裙子和一双鞋子．薇儿一共有三条裙子，两双鞋子．薇儿一共有▲种不同的搭配方法．3.武西要看一本书，第一天看了这本书的一半，第二天看了剩下部分的一半，第三天看了8页，还剩5页没有看完，这本书一共有▲页．4.悟空招来他的猴子猴孙，4只小猴分一组，分了4组还剩3只小猴．聪明的小朋友，算一算，悟空招来了▲只小猴子．5.图中有红桃3，方片6和梅花10，请你再摆上一张黑桃牌，让黑色牌的点数之和是红色牌点数之和的2倍，你会放上黑桃▲．红桃3 方片6 梅花10 黑桃？二、思维训练（每题10分，共50分）6.25个小朋友排队，从左往右数艾迪是第12个，从右往左数薇儿是第9个，艾迪和薇儿之间有▲个小朋友．7.下面的线条图形中，只有一幅图可以一笔画出，这幅图是▲．（请填入A、B、C或D）A B C D8.4月1日是愚人节，今年的愚人节是星期六．现在有写着数字4、1、6的三张卡片，则共可以组成▲个不同的三位数．（6可以旋转变成9）9.一只鸡有1个头2条腿，一只兔子有1个头4条腿．如果笼子里的鸡和兔子共有10个头和26条腿，那么鸡有▲只，兔有▲只．10.艾迪寒假的时候去海边度假，穿着当地特色的衣服，拍了照片．现在我们一起来数一数，照片里一共．．可以数出▲个三角形．三、 思维拓展（每题10分，共50分）11. X 别动队队员找到个藏宝屋，发现藏宝屋的门锁是一个密码锁（如下图所示），其中的数是按照一定规律排列的，请按照你找到的规律，将正确的数填入空格内，这个数是 ▲ ．12. 我国的农历用“鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪”这十二种动物按顺序轮流代表各年的年号．例如，第一年如果是鼠年，那第二年就是牛年，第三年就是虎年，……如果从某年往后数的第1年是鸡年，那么第120年是 ▲ 年．13. 乘乘用四个相同的长方形和一个小正方形组成一个大正方形，每个长方形的周长为10厘米，大正方形的周长为 ▲ 厘米．14. 艾迪排在一个十字形队伍的正中间，这个队伍一共有27人，横排人数是竖排人数的 3 倍，那么横排有 ▲ 人．15. 薇儿一共有22张积分卡，平均分给了一些小朋友，最后还剩4张无法继续分，那么小朋友的人数有 ▲ 种可能．四ǃ挑战（每题12分，共60分）16. 有一个如图所示形状的花坛，艾迪要绕着这个花坛摆花盆，每隔2米摆一盆，一共要摆 ▲ 盆花．（图中单位均为米）17. 将1、2、3、4、5、6这6个数字分别填入下面的“” 中，使得下面的一句话成立．其中有一个中的数字已经填好．这句话是这样的：玲玲非常喜欢做《计算天天练》，每做完一页需要18分钟，玲玲从开始做，做完一页后正好是．18. 在空格中填入数字1-4，使得每行、每列和每个粗线框内数字都不重复．格里的小数表示这个格的上下左右四个格中有多少个比它大的数字．图中B 代表的数是 ▲ ．64101019.有4张卡片，每张卡片上各写着一个互不相同的数字．博士首先将这4张卡片发给大毛、二毛、三毛和四毛四个小朋友，然后收回来再分别发给四人各一张，如此一共发了3次．如果把3次收到的卡片上的数字相加，大毛的和是0，二毛的和是3，三毛的和是11，四毛的和是16．请问这四张卡片上最大的数字是▲．20.下图给出了用火柴棍摆数字0～9 的方法．（1）现有9根火柴棍，要求全用完，则能摆出最小．．的两位数是▲．（2）现有20根火柴棍，要求全用完，则能摆出最小．．的数是▲．2017年第七届南京学而思综合能力诊断（答题纸）数学(二年级)总分：200分考试时间：2017年4月4日8:30 - 9:30准考证号（请用2B铅笔填涂下方的考号）姓名17请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效启用前★绝密2017年第七届南京学而思综合能力诊断数学（二年级）考试时间：60分钟满分：200分考生须知：请将所有的答案写在答题纸．．．对应位置上一、 基础过关（每题8分，共40分） 1. 计算：（1）1＋4＋7＋10＋13＋16＋19= ▲ ． （2）96－（56＋19）= ▲ ．【解析】（1）等差数列求和，个数为奇数，和=中间数×个数，10×7=70 （2）去括号，96－56－19=21 【答案】70；212. 春天到啦，薇儿要出去郊游，她想要选择一条裙子和一双鞋子．薇儿一共有三条裙子，两双鞋子．仔细想一想，薇儿一共有 ▲ 种搭配方法． 【解析】三条裙子可分别标记为A 、B 、C ，两双鞋子可分别标记为1、2．所有搭配为：A 1、A 2、B 1、B 2、C 1、C 2，共6种． 【答案】63. 武西要看一本书，第一天看了这本书的一半，第二天看了剩下部分的一半，第三天看了8页，还剩5页没有看完，这本书一共有 ▲ 页． 【解析】逆向思考，画流程图【答案】524. 悟空招来他的猴子猴孙，4只小猴分一组，分了4组还剩3只小猴．聪明的小朋友，算一算，悟空招来了 ▲ 只小猴子．()()()5132652822−→−−→−−→−÷÷－【解析】4×4＋3=19（只）．【答案】195.图中有红桃3，方片6和梅花10，请你再摆上一张黑桃牌，让黑色牌的点数之和是红色牌点数之和的2倍，你会放上黑桃▲．【解析】红色扑克牌点数和为3＋6=9，那么黑色扑克牌点数和为9×2=18，还需放上的黑桃牌点数为18－10=8．【答案】8二、思维训练（每题10分，共50分）6.25个小朋友排队，从左边数起艾迪是第12个，从右边数起薇儿是第9个，艾迪和薇儿之间有▲个小朋友．【解析】排队问题．25－9－12=4（人）．【答案】47.下面的线条图形中，只有一幅图可以一笔画出，这幅图是▲．（请填入A、B、C或D）A B C D【解析】一笔画问题，数奇点个数，0个或2个奇点可以一笔画．A、B、C、D 分别有4个、4个、4个、2个奇点，D可以一笔画．【答案】D8.4月1日是愚人节，今年的愚人节是星期六．现在有写着数字4、1、6的三张卡片，问：共可以组成▲个不同的三位数．（6可以旋转变成9）【解析】因为数字6的卡片可以倒过来当作数字9．当卡片为4、1、6时，可以组成：416、461、146、164、641、614，6种．当卡片为4、1、9时，可以组成：419、491、149、194、941、914，6种．所以，一共有6+6=12（种）．【答案】129.一只鸡有1个头2条腿，一只兔子有1个头4条腿．如果笼子里的鸡和兔子共有10个头和26条腿，那么鸡有▲只，兔有▲只．【解析】假设法．假设全是鸡，2×10=20（条），26－20=6（条），4－2=2（条），6÷2=3（只）兔，10－3=7（只）鸡．【答案】7；310.艾迪寒假的时候去海边度假，穿着当地特色的衣服，拍了照片．现在我们一起来数一数，照片里一共．．可以数出▲个三角形．【解析】最上面帽子有2个小三角形和1个大三角形，帽子下面有5个小三角形，身体有2个小三角形和1个大三角形，脚有2个小三角形．2＋1＋5＋2＋1＋2=13（个）【答案】13三、思维拓展（每题10分，共50分）11.X别动队队员找到个藏宝屋，发现藏宝屋的门锁是一个密码锁（如下图所示），其中的数是按照一定规律排列的，请按照你找到的规律，将正确的数填入空格内，这个数是 ▲ ．【解析】从1开始按照方向在图中依次填上连续的奇数【答案】1312. 我国的农历用“鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪”这十二种动物按顺序轮流代表各年的年号．例如，第一年如果是鼠年，那第二年就是牛年，第三年就是虎年，……如果从某年往后数的第1年是鸡年，那么第120年是 ▲ 年．【解析】周期：鸡、狗、猪、鼠、牛、虎、兔、龙、蛇、马、羊、猴；周期是12．120÷12=10（组），没有余数，就是周期中的最后一个，猴． 【答案】猴13. 乘乘用四个相同的长方形和一个小正方形组成一个大正方形，每个长方形的周长为10厘米，大正方形的周长为 ▲ 厘米．【解析】大正方形的边长等于长方形的长+宽，长方形的长+宽是10÷2=5（厘米），大正方形的周长是5×4=20（厘米）． 【答案】2014. 艾迪排在一个十字形队伍的正中间，这个队伍一共有23人，横排人数是竖排人数的2倍，那么横排有 ▲ 人．【解析】排队问题，和倍问题．正中间的艾迪既在横排，又在竖排，所以横排人数+竖排人数为27+1=28（人）；竖排有：28÷（3+1）=7（人），横排有：7×3=21（人）． 【答案】2115. 薇儿一共有22张积分卡，平均分给了一些小朋友，最后还剩4张，那么小朋友的人数有 ▲ 种可能．【解析】22÷（人数）=（每人分的张数）……4，除数比余数大，人数可能是6人、9人、18人，有3种可能． 【答案】3四、 挑战（每题12分，共60分）16. 有一个如图所示形状的花坛，艾迪要绕着这个花坛摆花盆，每隔2米摆一盆，一共要摆 ▲ 盆花．（图中单位均为米）【解析】通过平移，花坛周长是长为20米，宽为10＋6=16（米）的长方形周长，周长为（20＋16）×2=72（米），隔2米摆一盆，共摆72÷2=36（盆）． 【答案】3664101066420101017. 将1、2、3、4、5、6这6个数字分别填入下面的“” 中，使得下面的一句话成立.其中有一个中的数字已经填好.这句话是这样的：玲玲非常喜欢做《计算天天练》，每做完一页需要18分钟，玲玲从开始做，做完一页后正好是．【解析】每个数字填一次，从2点多开始做，做完3点多．做一页需要18分钟，要满足条件，2：56到3：14． 【答案】2；5；6；1；418. 空格中填入数字1-4，使得每行、每列和每个粗线框内数字都不重复．格里的小数表示这个格上下左右四个格中有多少个比它大的数字．图中B 代表的数是 ▲ ．【答案】219. 有4张卡片，每张卡片上各写着一个互不相同的数字．博士首先将这4张卡片发给大毛、二毛、三毛和四毛四个小朋友，然后收回来再分别发给四人各一张，如此一共发了3次．如果把3次收到的卡片上的数字相加，大毛的和是0，二毛的和是3，三毛的和是11，四毛的和是16．请问这四张卡片上最大的数字是 ▲ ．【解析】大毛3次的和是0，大毛每次拿到的都是0；二毛3次的和是1，二毛每次拿到的都是1；三毛、四毛3次的和都不能被3整除，说明三毛、四毛另外两张卡片都拿到过，都是另外两张卡片各拿一次，剩余一次三毛拿了其中小的一张，四毛拿了其中大的一张．三毛的和比四毛的和小5，说明另外两张相差5．满足三毛和是11，四毛和是16，另两张为2，7．【答案】720.下图给出了用火柴棍摆数字0～9 的方法．（1）现有9根火柴棍，要求全用完，则能摆出最小．．的两位数是▲．（2）现有20根火柴棍，要求全用完，则能摆出最小．．的数是▲．【解析】（1）摆0~9分别要用6、2、5、5、4、5、6、3、7、6根火柴棍．要使两位数最小，十位最小为1，用去2根火柴棍，剩下7根只能摆出8，最小为18．（2）要使数最小，数位越少，数越小．用火柴棍摆出两位数最多用2×7=14（根），摆出三位数最多用3×7=21（根）．20根火柴棍摆出最小的数为三位数，并且一定要用14根组成2个8，剩余6根要使数最小，摆成6，最小为688．【答案】18；688。

一笔画游戏第七讲下列图形能一笔画成吗？如果可以，在图形下面的方框里画上√，如果不可以，在图形下面的方框里画上╳．【例题分析】在这些图形中可以一笔画出的是：①、②、④；不可以一笔画出的是：③．一个图形是否能一笔画成跟这些点有什么关系？⑴从一点出发的线的条数是偶数（双数），这点称为偶点（双数点）．⑵从一点出发的线的条数是奇数（单数），这点称为奇点（单数点）．观察此题的每个图：①有2个奇点，能一笔画成；②有0个奇点，能一笔画成；③有4个奇点，不能一笔画成；④有2个奇点，能一笔画成．最后总结出：有0个或2个奇点的连通图能够一笔画成，否则不能一笔画成．下列图形能一笔画成吗？为什么？如果可以，在图形下面的方框里画上√，如果不可以，在图形下面的方框里画上╳．【例题分析】①、②、③可以，④不可以．①有2个奇点，②有0个奇点，③有2个奇点，所以①、②、③可以一笔画．④有4个奇点，所以④不能一笔画．下列图形能一笔画成吗？如果可以，在图形下面的方框里画上√，如果不可以，在图形下面的方框里画上╳．【例题分析】①③⑤可以；②④不可以．①有0个奇点；③有2个奇点；⑤有0个奇点；所以①③⑤可以一笔画．②有4个奇点；④有6个奇点；所以②④不能一笔画．【例题分析】⑴ 图①中有4个点是奇点，所以不能一笔画成，要想使这个图形能一笔画成，可以添加一条线段，使这个图形的奇点变成2个．如下图（答案不唯一）：⑵图②因为有4个点是奇点，所以不能一笔画成，要想使这个图形能一笔画成，可以添加一条线段，使这个图形的奇点变成2个．如下图（答案不唯一）：⑶图③中有4个点是奇点，所以不能一笔画成，要想使这个图形一笔画成，可以添加一条线段，使这个图形的奇点变成2个．如下图：下面的图形都不能一笔画成，请你分别在各图中添上一条线段，使它能一笔画成．【例题分析】上图一共有6个奇点，只添一条线段无法变成2个奇点，至少需要添上2条线段．如下图（答案不唯一）：下面的图形都不能一笔画成，请你在各个图中分别去掉一条线，使它能一笔画成，在去掉的线上打╳．下面的图形不能一笔画成，至少添上几条线段才能使它一笔画成？试着添一添．【例题分析】⑴图①中有4个点是奇点，所以不能一笔画成，要想使这个图形能一笔画成，就要使这个图形的奇点变成2个．如下图（答案不唯一）：⑵图②和图①相似，因为有4个点是奇点，所以不能一笔画成，要想使这个图形能一笔画成，就要使这个图形的奇点变成2个．如下图（答案不唯一）：⑶图③中有4个点是奇点，所以不能一笔画成，要想使这个图形一笔画成，就要使这个图形的奇点变成2个．如下图（答案不唯一）：下面的图形不能一笔画成，请你去掉一条线，使它能一笔画成，在去掉的线上打╳．【例题分析】图中有4个点是奇点，所以不能一笔画成，要想使这个图形能一笔画成，就要使这个图形的奇点变成2个．如下图（答案不唯一）：（ ）→（ ）→（ ）→（ ）→（ ）→（ ）→（ ）→（ ）→（ ）→（ ）→（ ）→（ ）→（ ）→（ ）【例题分析】出入口应设在A 、C 两个奇点处．A →B →C →I →A →H →G →I →E →G →F →E →D →C （路线不唯一）． 本题实际上是这个图以哪两点为起点和终点一笔画出的问题，观察上图可以发现仅有两个奇点： A 点与C 点．因此，出入口应设在A 、C 两个奇点处．下图是一个小区街道的平面图．要不重复地走遍每条街道，出入口应设在哪里？请你再设计一条不重复走遍每条街道的行走路线，用字母和箭头表示出来．下图是乡间的小河，上面建有九座桥，你能从其中一个村子出发一次不重复地走遍所有的桥吗？ (每座桥最多只准走一次，陆地上可以重复地走)【例题分析】可以，丁→丙→丁→甲→丁→乙→丙→乙→甲→乙.（路线不唯一）首先将实物图转化成点线图，所有的村庄都转化成点，所有的桥都转化成线（如下图），图中有2个奇点，所以可以一笔画，也就存在一条路线，能够不重复地走遍所有的桥．我国著名数学家陈景润所著《数学趣谈》一书中，有这样一道题：在法国的首都巴黎有一条河，河中有两个小岛，那里的人们建了15座桥把两个小岛和河岸连接起来，如下图所示．那么，从任一岸出发，不重复地走遍所有的桥到达另一岸，能做到吗？【例题分析】能．将实物图转化成点线图，如下图，图中有2个奇点，可以一笔画，也就是说可以从任一岸出发，不重复地走遍所有的桥到达另一岸．如图是一个超市的平面图，超市共有A、B、C、D、E、F六个门，简乐想一次走遍所有通道而又不走重复路线，请你帮他设计一种进出方法．【例题分析】把每一条通道看作是边，通道的交点看作是点(每个门处即为一个点)，可得下图，这样问题就转化为能否从某点出发将图一笔画的问题．观察可知，如上右图中只有两个奇点(点C和点D)，根据一笔画原理可得：将点C和点D分别作为起点和终点，可将右图一笔画出．即简乐从C门(或D门)进超市，一次走遍所有通道后从D门(或C门)出超市，其行进路线为：C→D→E→O→C→B→E→F→A→B→O→D（路线不唯一）．下图是某展览厅的平面图，它由五个展室组成，任意两个展室之间都有门相通，整个展览厅还有一个入口和一个出口，问游人能否一次不重复地穿过所有的门，并且从入口进，从出口出？【例题分析】把每个展室看作一个点，整个展厅的外部也看作一个点，两室之间有门相通，可以看作两点之间有线相连．这样，展厅的平面图就转化成图②，一个实际问题也就转化为这个图能否一笔画成的问题了，即能否从A出发，一笔画完此图，最后再回到A．图②中，所有的点都是偶点，因此，一定可以以A作为起点和终点而一笔画完此图．即游人可以从入口进，一次不重复地穿过所有的门，最后从出口出来．下面仅给出一种参观路线：A→E→B→C→E→F→C→D→F→A．。