结构设计-圆形柱-轴力弯矩相关曲线及计算

任意截面 P-M 曲线绘制原理及其 在强度验算中的应用
郭 磊，徐常泽
（山东省交通规划设计院，山东 济南 250031）
摘要：《公路钢筋混凝土及预应力混凝土桥涵设计规范 （JTG 3362-2018）》 中关于偏压构件承载能力的计算仅适用
矩形、T 型等规则截面。本文根据 《混凝土结构设计规范 （GB 50010-20100）》 附录 E 相关内容讨论异性桥墩的偏
压构件验算方法，并据此提出任意截面 P-M 曲线的绘制原理及其在强度验算中的应用。
关键词：P-M 曲线；承载能力；应力；应变
中图分类号：U443.15
文献标识码：A
文章编号：1673-6478（2019）02-0098-03
Principle of P-M Curve Drawing of Arbitrary Section and Its Application in Strength Checking
1.2
+Dc+
1 P-M 曲线概述
120 × 80 cm 的 截 面 （如 图 1） 上 下 缘 各 配 置 8 根 直 径 25 的 钢 筋 （HRB400），其 P-M 曲线 （如图 2） 表现为以抗弯承载力为横坐标，以抗 压承载力为纵坐标类似椭圆的形态。截面的抗弯、抗压 （拉） 性能可通过 P-M 曲线直观的描述。与 X 轴的交点为其纯弯承载能力，与 Y 轴交点为其 轴心抗压 （拉） 承载能力。偏心受压构件的承载能力不同于纯弯构件，不 同轴力下的抗弯承载力不同，反之依然。外荷载弯矩 M 及轴力 N，可“简 化”为偏心轴力 N 及其偏心距 e0 （M/N），故曲线也可理解为不同偏心距 下偏压构件的承载力能力。
考虑到本文最后要与规范算法对比，故仍以开 篇所举矩形截面为例计算曲线中的某一极限状态 （受压区高度为 802.41 mm），计算简图如图 5。

计算底层中柱截面处组合的弯矩和轴力设计值底层中柱截面的弯矩和轴力设计值计算方法在建筑结构中，柱是承受建筑物重力和水平荷载的重要承载构件。

在底层中柱截面处，由于所承受的荷载较大，因此需要计算柱截面的弯矩和轴力设计值，以保证柱的安全稳定运行。

1、弯矩设计值的计算弯矩设计值的计算需要先确定柱的荷载情况。

一般情况下，底层中柱同时承受垂直荷载和水平荷载。

因此，需要将荷载分解为垂直荷载和水平荷载两个方向。

首先，需要对底层中柱进行截面分析，确定其截面尺寸和受力情况。

随后，可以根据受力情况确定柱截面处的应力状态，进而计算柱截面内沿周向和轴向的应力。

在确定柱截面内的应力后，可以计算出沿周向的弯矩设计值。

对于底层中柱，其弯矩设计值较大，需要特别注意。

弯矩设计值的计算公式为：M = σZ*(bh^2/6 - (bh-2a)*(h-2a)^2/6)其中，M为弯矩设计值，σZ为柱截面内沿轴向的应力，b和h分别为柱截面的宽度和高度，a为柱截面的边角半径。

2、轴力设计值的计算轴力设计值的计算同样需要考虑底层中柱所承受的垂直荷载和水平荷载。

在计算轴力设计值时，需要先确定柱截面内的轴向应力。

对于矩形截面的柱，轴向应力可以通过杨氏模量和柱截面的惯性矩计算得出。

其计算公式为：σz = N/A - MyIx/Iz其中，N为轴向荷载，A为柱截面面积，My为弯矩设计值，Ix和Iz分别为柱截面沿x和z轴方向的惯性矩。

通过求解轴向应力，可以计算出底层中柱截面处的轴力设计值。

同样需要注意的是，由于底层中柱所承受的荷载较大，轴力设计值也相对较大。

综上所述，底层中柱截面处的弯矩和轴力设计值计算需要考虑柱截面的几何形态、荷载情况以及受力状态等因素。

在进行相关计算时，需要精确分析柱截面的受力情况并采用合理的计算方法，以确保柱能够安全、稳定地运行。

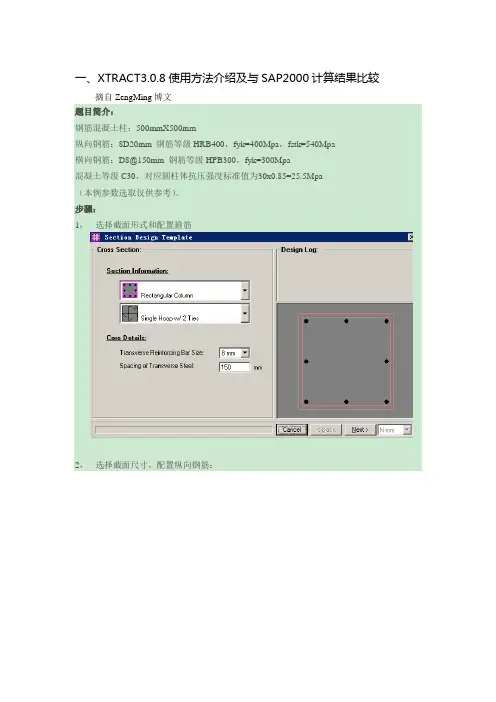
一、XTRACT3.0.8使用方法介绍及与SAP2000计算结果比较-------摘自ZengMing博文题目简介：钢筋混凝土柱：500mmX500mm纵向钢筋：8D20mm钢筋等级HRB400，fyk=400Mpa，fstk=540Mpa横向钢筋：D8@150mm钢筋等级HPB300，fyk=300Mpa混凝土等级C30，对应圆柱体抗压强度标准值为30x0.85=25.5Mpa（本例参数选取仅供参考）。

步骤：1，选择截面形式和配置箍筋2，选择截面尺寸，配置纵向钢筋：3,定义材料本构：非约束混凝土材料：约束混凝土纵向钢筋：4，定义纤维尺寸，生成分析截面5，定义加载工况计算弯矩曲率曲线工况计算轴力-弯矩相关曲线工况定义弯矩2-弯矩3相关曲线工况, 6，运行分析，查看分析结果点击，运行所有的分析，分析结果在界面自动出现。

弯矩-曲率曲线轴力-弯矩相关性曲线弯矩2-弯矩3相关性曲线7，提取分析结果点击，然后选择section1，然后选择M-C工况，选择Section Output。

同理可以绘制出轴力-弯矩相关曲线，在此不再赘述。

在SAP2000截面求解器中编辑此截面，并与之对比。

1，截面信息由上图可知，两种软件在弹性阶段基本重合，在塑性阶段，Xtract计算的弯矩要比SAP2000计算的要大。

二、关于其中强度值选取的讨论1，详细见混规P286页。

立方体抗压强度为C30为例，立方体抗压强度标准值为30MPa，考虑实验的因素，试件混凝土强度为30x0.88=26.4Mpa，转换为棱柱体抗压强度，再折减0.76，即26.4x0.76=20.064Mpa，即表4.1.3-1所示混凝土轴心抗压强度20.1Mpa。

2， Xtract根据ACI规范或软件设计者本意（陆新征老师建议），取圆柱体抗压强度，圆柱体抗压强度为0.79x26.4Mpa=20.856Mpa，这与棱柱体抗压强度20.1Mpa比较接近的，即轴心混凝土轴心抗压强度。

4.1.1在主平面内受弯的实腹构件(考虑腹板屈曲后强度者参见本规范第4.4.1条)，其抗弯强度应按下列规定计算:`(M_x)/(γ_xW_(nx))+(M_y)/(γ_xW_(ny))≤f`（4.1.1）式中M x、M y——同一截面处绕x轴和y轴的弯矩(对工字形截面：x轴为强轴，y轴为弱轴);Wｎｘ、Wｎｙ——对x轴和y轴的净截面模量;γx、γy——截面塑性发展系数;对工字形截面γy=1.20;对箱形截面，γX=Y y=1.05;对其他截面，可按表5.2.1采用;f——钢材的抗弯强度设计值。

当梁受压翼缘的自由外伸宽度与其厚度之比大于13`sqrt(235//f_y)`而不超过15`sqrt(235//f_y)`时，γx=1.0。

f y应取为钢材牌号所指屈服点。

对需要计算疲劳的梁，宜取γx=γy=1.0。

4.1.2在主平面内受弯的实腹构件(考虑腹板屈曲后强度者参见本规范第4.4.1条)，其抗剪强度应按下式计算:`τ=(VS)/(It_w)`(4.1.2)式中V——计算截面沿腹板平面作用的剪力;S——计算剪应力处以上毛截面对中和轴的面积矩;I——毛截面惯性矩;t w——腹板厚度;fv——钢材的抗剪强度设计值。

4.1.3当梁上翼缘受有沿腹板平面作用的集中荷载、且该荷载处又未设置支承加劲肋时，腹板计算高度上边缘的局部承压强度应按下式计算:`σ_c=(varphiF)/(t_wl_z)≤f`(4.1.3-1)式中F——集中荷载，对动力荷载应考虑动力系数;ψ——集中荷载增大系数;对重级.工作制吊车梁ψ=1. 35;对其他梁，ψ=1.0；l z——集中荷载在腹板计算高度上边缘的假定分布长度，按下式计算:l2=a+5h y+2h R ( 4.1.3-2 )a——集中荷载沿梁跨度方向的支承长度，对钢轨上的轮压可取50mm;h y——自梁顶面至腹板计算高度上边缘的距离;h R——轨道的高度，对梁顶无轨道的梁h R=0;f——钢材的抗压强度设计值。

一、XTRACT3.0.8使用方法介绍及与SAP2000计算结果比较-------摘自ZengMing博文题目简介：钢筋混凝土柱：500mmX500mm纵向钢筋：8D20mm钢筋等级HRB400，fyk=400Mpa，fstk=540Mpa横向钢筋：D8@150mm钢筋等级HPB300，fyk=300Mpa混凝土等级C30，对应圆柱体抗压强度标准值为30x0.85=25.5Mpa（本例参数选取仅供参考）。

步骤：1，选择截面形式和配置箍筋2，选择截面尺寸，配置纵向钢筋：3,定义材料本构：非约束混凝土材料：约束混凝土纵向钢筋：4，定义纤维尺寸，生成分析截面5，定义加载工况计算弯矩曲率曲线工况计算轴力-弯矩相关曲线工况定义弯矩2-弯矩3相关曲线工况, 6，运行分析，查看分析结果点击，运行所有的分析，分析结果在界面自动出现。

弯矩-曲率曲线轴力-弯矩相关性曲线弯矩2-弯矩3相关性曲线7，提取分析结果点击，然后选择section1，然后选择M-C工况，选择Section Output。

同理可以绘制出轴力-弯矩相关曲线，在此不再赘述。

在SAP2000截面求解器中编辑此截面，并与之对比。

1，截面信息由上图可知，两种软件在弹性阶段基本重合，在塑性阶段，Xtract计算的弯矩要比SAP2000计算的要大。

二、关于其中强度值选取的讨论1，详细见混规P286页。

立方体抗压强度为C30为例，立方体抗压强度标准值为30MPa，考虑实验的因素，试件混凝土强度为30x0.88=26.4Mpa，转换为棱柱体抗压强度，再折减0.76，即26.4x0.76=20.064Mpa，即表4.1.3-1所示混凝土轴心抗压强度20.1Mpa。

2， Xtract根据ACI规范或软件设计者本意（陆新征老师建议），取圆柱体抗压强度，圆柱体抗压强度为0.79x26.4Mpa=20.856Mpa，这与棱柱体抗压强度20.1Mpa比较接近的，即轴心混凝土轴心抗压强度。

圆钢管混凝土截面轴力弯矩曲率关系实用计算方法下载温馨提示:该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by theeditor.I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!圆钢管混凝土截面轴力、弯矩与曲率关系的实用计算方法一、引言在土木工程领域，圆钢管混凝土结构因其优良的力学性能和良好的抗震性能，被广泛应用。

圆形截面受弯构件单筋、非均匀配筋--弯矩求配筋输入M= N·mm459960000输入半径R= mm400输入混凝土fc= MPa11.9纵筋强度fy= MPa360计算k4=-0.862770108计算q=-0.53288742计算初始值α=0.810734192试算值α=0.8967（取α在初始值附近值使ε绝对值逼近 0.001）计算初始值ε=-0.188773068ε=α+（1/1.4)*sinα-0.5*sin2α-(1/4.2)*sin3α+k4迭代求终值ε=0.000434754受压区扇形角度= °161.406计算受拉侧As= mm22163.351394圆形截面受弯构件单筋、非均匀配筋--配筋求承载弯矩输入M初= N·mm268350000M0=274177846（取输入M初在M0值附近值使ε绝对值逼近 0.001输入半径R= mm300输入混凝土fc= MPa9.6纵筋强度fy= MPa310实配受拉侧As= mm22000计算值α=0.970295917受压区扇形角度= °174.6532651计算H=222.8244499计算ε=0.001869264（当ε绝对值逼近 0.001时，Mu=M初）继续试算268350000圆形截面受弯构件抗剪计算输入V设= N710520 0.7ftbh0=704704输入半径R= mm500输入混凝土ft= MPa 1.43箍筋强度fyv= MPa270计算Asv/S=0.026925926构造Min（Asv/S)= 1.118578设S= mm200计算Asv=223.7156箍筋单肢As1= mm2111.8577778环形截面受弯构件均匀配筋--已知配筋求承载弯矩环形截面受弯构件均匀配筋--已知弯矩求配筋输入外半径r1= mm500输入纵筋rs=r1-as mm470输入外半径r1= mm500输入纵筋rs=r1-as mm450输入内半径r2= mm400环形截面积A=282744输入内半径r2= mm300环形截面积A=502656输入混凝土fc= MPa16.7输入混凝土fc= MPa16.7纵筋强度fy= MPa360纵筋强度fy= MPa360实配纵筋As= mm23600设计弯矩M= Nmm600000000计算值α=0.162776754当α＞0.6667时αt=0输入值α=0.122962应α＜0.4，使ε绝对值接近10000，取值计算αt=0.755834868计算ε=263.4982927受压区扇形角度= °44.26632计算Mu=560441461受压区扇形角度= °58.59963计算As= mm24139.771857圆形截面受弯构件均匀配筋--已知配筋求承载弯矩输入半径r= mm600输入纵筋rs=r-as mm529输入混凝土fc= MPa16.7纵筋强度fy= MPa310实配纵筋As= mm211309.7输入α=0.25126105应α＜0.625，使ε绝对值小于 100，取值在0.21附近计算ε=-7.458550587计算αt=0.7474779受压区扇形角度= °90.45398计算Mu=1700198973圆形截面受弯构件均匀配筋--已知弯矩求配筋输入半径r= mm500输入纵筋rs=r-as mm430输入混凝土fc= MPa14.3圆形截面积A=785400纵筋强度fy= MPa360计算αt=0.682444设计弯矩M= Nmm1361140000输入α=0.283778应α＜0.625，使ε绝对值小于 10000，取值在0.28附近计算ε=7016.033087受压区扇形角度= °102.1601计算As= mm210031.9359910000，取值在0.13附近。

桥台桩以北桥台桩基控制荷载近似考虑125安全系数1一基本资料计算弯距mj34539kn计算轴力nj70937kn混凝土级别r20ra11mpaeh260e04mpa钢筋级别2级钢rg340mpaeg200e05mpa构件直径d08m构件计算长度l0102m钢筋保护层厚度c005m选用钢筋直径18mm二配筋计算dgd2c0682mgdgd0853e0mjnj0487me02531044e00508m经试算得03281080a06575b04541c08621d1757004760n70978kn与nj相接近
=
=
e
= = = =
345.39 KN 709.37 KN 20 # 11 MPa 2.60E+04 MPa Ⅱ 级钢 340 MPa 2.00E+05 0.8 10.2 0.05 18 MPa m m m mm
2
= = = = = =
=D-2c-φ
=Dg/D =Mj/Nj
=
= 1-
= = =
0.682 m 0.853 0.487 m 0.253 1.044 0.508 m 0.328 0.80 0.6575 0.4541 -0.8621 1.7570 0.4760 ％ 709.78 KN 与Nj相接近。 <=1 见规范 （JTJ023－ 85）附录三
圆一、基本资料 计算弯距 计算轴力 混凝土级别 昌化路桥改建工程 桥台桩（以北桥台桩基控制，荷载近似考虑1.25安全系数） 1 Mj Nj R Ra Eh 钢筋级别 Rg Eg 构件直径 D 构件计算长度 l0 钢筋保护层厚度 c 选用钢筋直径 二、配筋计算 Dg g e0 α η η e0 经试算，得 ξ β A B C D μ N
0.1 + 0.143 = 0.3 + e0 d

第 12 期
丁发兴， 等： 圆钢管混凝土截面轴力 － 弯矩 － 曲率关系实用计算方法
· 135·
4 种因 素， 对 于 f s 在 Q235 ～ Q420 、f cu 在 C30 ～ C100 和径厚比 D / t 在 20 ～ 100 之间的实际工程 中应用的圆钢管混凝土， 考虑套箍指标 Φ 和 钢材屈服强度的影响， 拟合得到钢管混凝土压弯 构件截面轴力 － 弯矩相关实用计算公式为 n0 1 N0 2 － · （ 0. 97 － n0 ） N u （ 0. 97 － n0 ）
［ 8］ 、 丁发兴等 在对钢管混凝土纯弯构件截 面进行数值分析的基础上， 建立了钢管混凝土纯 ［ 7］
角为 dθ = 2 π / （ 2 n） = π / n （ 图 1 ） . 2， …， n） ， θ k = kdθ （ k = 1 ， dA sk = （ r c + t / 2 ） tdθ， dA ck = r c 2 cos2 （ θ k － 0. 5dθ） ·dθ. 式中： r c 和 t 分别为混凝土的半径和钢管的壁厚 . 由此可以得到该截月
哈 尔 滨 工 业 大 学 学 报 JOURNAL OF HARBIN INSTITUTE OF TECHNOLOGY
Vol. 41
No. 12
Dec. 2009
圆钢管混凝土截面轴力 － 弯矩 － 曲率 关系实用计算方法
1， 2 丁发兴 ，张 1 1 2 鹏 ，余志武 ，欧进萍
n
N in = 2 ∑ （ σ sk dA sk + σ ck dA ck ） .
k =1
对于压弯构件截面， 故应保证轴力 N in = N0 （ N0 为钢管混凝土压弯构件截面上的外轴力 ） . 具体计算方法为： 在给定截面曲率 的情况 下， 通过调整截面形心应变 ε0 ， 当截面内轴力 N in 等于外轴力 N0 时， 计算得到截面弯矩 M in . 数值计 算得到的典型钢管混凝土压弯构件截面 N0 － M － 关 系 如 图 2 所 示. 图 2 中 轴 压 比 n a = 0. 9 （ n a = N0 / N u ， N u 为圆钢管混凝土轴压短柱的 10 ］ 极限承载力， 按文献［ 计算 ） 时曲线上升段的 可能是采用的核心混凝土轴 刚度不是单调减少， 对称三轴受压应力 － 应变关系中上升段刚度偏低 而引起的.

(1 1Ncr
2
)
Ncr 2
x
2 EA 2EA
1
N
v dv1dv2
dz
N
格构式构件的换算长细比
第5.1.3条：
格构式轴压构件整体稳定计算
规范 计算公式
N f
A
计算方法同实腹式
1. 稳定系数 按(1)钢种、(2)换算长细比λ o、(3)截面分类查表
2. m in m in x , y
框架柱的计算长度
第5.3.4条：单厂阶形柱的计算长度
考虑折减——荷载较大的柱失稳时会受到低荷载柱的支承作用； ——考虑厂房的空间作用； ——对多跨厂房，如刚性屋盖或设屋盖纵向水平支撑――则将柱顶视作不动铰支座。
单阶柱
（1）下段柱的计算长度系数 2 ：
当柱上端和横梁铰接时，按柱上端为自由的单阶柱的数值乘以折减系数（整体作用）
1、受压时保证单构件稳定 2、受拉是保证均匀传力 3、分支距离近，填板刚度大，
可视作实腹截面
轴压构件的抗剪验算
第5.1.6条：
第5.1.7条：
1.此时如按柱剪力验算支撑，不十 分恰当，因为该剪力可视作轴压构 件的偶然剪力。
当撑杆的作用是支撑一系列柱 时，就完全不对了 2.原理：带支撑压杆的挠度增量及 支撑构件的轴向变形，根据变形协 调条件推导其轴力； 3.此支撑力不与其他作用产生的轴 力叠加，而是取较大值； 4.一道支撑架在同一方向所支撑的 柱不宜超过8根。
按 max max ox , y
或 m ax max x , oy
截面分类b，钢号，查表得 min
或 max max ox , oy
格构式轴压构件的分支长细比
第5.1.4条：
1、控制单肢长细比用以保证单肢稳定 2、单肢关于实轴的计算长度与全截面相同 3、单肢关于虚轴的计算长度取决于缀材的间距 第5.1.5条：

HOHAI UNIVERSITY
F kN Q 1 72
M 1 0
F kN Q 2 72
12 3 12 3
4 4
5 6
5 6
M 144 kN m 2
F kN Q 3 72
FAy
FQ (kN) 72
FRB
60
M 16 kN m 3
F 88 kN Q 4
M 80 kN m 4
5 6
FAy
72
FRB
60
剪力图是斜直线； 弯矩图是二次抛物线。
(kN)
+
3.6m
16
—
+
88
80
—
20
M (kN· m)
+
144
+
113.6
25
HOHAI UNIVERSITY
例8 作如图所示联合梁的剪力图和弯矩图。 MC
1
1
2 2
3
3
4
4
解： 1.求支座反力
FRA
FCy
kN M F 40 kN F 240 kN m Cy 80 C RA
梁的分类： 按梁的支承情况，梁有三种基本形式。
静定梁： 可由静力 平衡方程 求出所有 支座反力 的梁。
1.简支梁：一端为固定铰支座，另一端为 可动铰支座的梁。 2.外伸梁：简支但一端或两端具有外伸部 分的梁。
3.悬臂梁：一端固定，另一端为自由的梁。
超静定梁：仅用静力平衡方程不能求出全部支座反力的梁。
28
HOHAI UNIVERSITY
如图 按叠加原理作其弯矩图
Me=1/8ql 2 A
q
B
l

圆形截面基础弯矩计算公式在土木工程中，基础是承受建筑物重量并将其传递到地基的重要结构。

而基础的设计中，弯矩计算是一个关键的步骤，它可以帮助工程师确定基础的尺寸和材料，以确保其能够承受建筑物的重量并保持稳定。

本文将重点介绍圆形截面基础弯矩计算公式，以帮助读者更好地理解基础设计中的重要计算。

圆形截面基础是一种常见的基础形式，它通常用于承受较小的建筑物或结构的重量。

在进行弯矩计算时，我们需要考虑基础的几何形状、材料特性以及受力情况。

对于圆形截面基础，其弯矩计算公式可以通过以下步骤来推导和应用。

首先，我们需要了解圆形截面基础的几何特性。

圆形截面的面积可以通过公式A=πr^2来计算，其中r为圆形截面的半径。

而基础的周长可以通过公式P=2πr来计算。

这些几何参数将在后续的弯矩计算中起到重要作用。

其次，我们需要了解基础所受力的情况。

通常情况下，基础会受到建筑物或结构的垂直荷载以及水平荷载的作用。

在进行弯矩计算时，我们需要将这些荷载转化为力矩，以便于后续的计算。

接下来，我们可以利用基础的几何特性和受力情况来推导圆形截面基础的弯矩计算公式。

对于受到垂直荷载的基础，其弯矩可以通过公式M=σmaxZ来计算，其中σmax为基础的最大应力，Z为基础的抵抗矩阵。

而对于受到水平荷载的基础，其弯矩可以通过公式M=Qe来计算，其中Q为水平荷载的大小，e为基础的偏心距。

最后，我们需要根据实际情况来确定基础的设计参数。

在进行弯矩计算时，我们需要考虑基础的材料特性、土壤的承载能力以及建筑物的重量等因素，以确保基础设计的合理性和安全性。

总的来说，圆形截面基础弯矩计算公式是基础设计中的重要工具，它可以帮助工程师确定基础的尺寸和材料，以确保其能够承受建筑物的重量并保持稳定。

通过了解基础的几何特性、受力情况以及弯矩计算公式，工程师可以更好地进行基础设计，并确保其安全可靠。

希望本文能够帮助读者更好地理解圆形截面基础的弯矩计算方法，从而在实际工程中能够更好地应用和实践。

2 触及问题和疑惑
解答相关问题和疑惑，鼓励学习者进一步探索。
解释构建轴力图的方法和步骤。
荷载变化
讨论不同荷载下轴力图的变化。 解释荷载对轴力图的影响。
绘制技巧
演示绘制轴力图的技巧和方法。
剪力图
实现方法
描述剪力图的实现方法和步骤。
荷载变化影响
分析荷载变化对剪力图的影响和 变化。
制作技巧
展示绘制剪力图制作弯矩图的步骤和方法。
荷载变化影响
探讨荷载变化对弯矩图的影响和 变化。
制作技巧
演示制作弯矩图的技巧和方法。
轴力剪力弯矩图联合使用案例
联合使用概念
讲解轴力剪力弯矩图联合使用的概念和优点。
实现方法
分析轴力剪力弯矩图联合使用的实现方法和步骤。
典型案例
展示一个典型的结构案例，演示轴力剪力弯矩图联合使用的效果。
总结
1 重要性
总结轴力剪力弯矩图的重要性和作用。
轴力剪力弯矩图(课件)
介绍轴力剪力弯矩图课件大纲，包括轴力、剪力和弯矩的基本概念，定义及 作用，材料和结构选择。
概述
基础概念
轴力、剪力和弯矩的详细解 释。
定义与作用
说明轴力剪力弯矩图的定义 及其在结构工程中的重要作 用。
材料和结构
研究选择的材料和结构，以 了解其对轴力剪力弯矩图的 影响。
轴力图
构建方法

框架柱弯矩计算公式在建筑工程中，框架柱是承受垂直载荷的重要承力构件。

在设计框架柱时，需要进行弯矩计算，以确保柱子的安全性能和承受能力。

本文将介绍框架柱弯矩计算公式及其步骤，以帮助读者更好地理解和运用。

框架柱弯矩计算公式框架柱的弯矩计算公式是通过结构力学分析得出的，公式如下：M = Fh * H / 4其中，M表示柱子的弯矩；Fh表示水平荷载；H表示柱子的高度。

框架柱弯矩计算步骤1. 明确计算的参数在计算规划之前，需要明确计算框架柱的高度、截面尺寸、荷载等参数。

只有准确地输入参数才能得出正确的计算结果。

2. 载荷分析进行框架柱弯矩计算的第一步是进行载荷分析。

这涉及到各种计算方法，包括等效荷载法、框架柱荷载分布图法等。

通过载荷分析，可以确定框架柱所受的水平荷载。

3. 确定框架柱的高度在框架柱的弯矩计算中，框架柱的高度是非常重要的参数。

确定柱子的高度的方法是通过结构力学分析，以确定载荷和其他影响因素的作用下，柱子的最大长度。

4. 确定框架柱的截面尺寸框架柱的截面尺寸是指柱子的截面面积和相关属性。

框架柱的截面尺寸应遵循结构力学分析的要求，以确保柱子承受载荷的能力和稳定性。

5. 计算柱子的弯矩框架柱弯矩计算公式是通过结构力学推导出来的，可以通过输入柱子的高度、截面尺寸和荷载等参数来计算柱子的弯矩。

6. 检查计算结果在计算结束后，需要对计算结果进行检查。

检查计算结果的目的是确保计算方法正确、数据准确，并验证计算结果的合理性。

如果发现计算结果错误，则需要重新计算。

总结框架柱弯矩计算公式是设计框架柱的重要计算方法之一，通过输入柱子的高度、截面尺寸和荷载等参数，可以计算柱子的弯矩。

在进行框架柱弯矩计算时，需要根据规范和实际情况进行载荷分析、框架柱高度和截面尺寸的确定、弯矩计算及结果的检查等步骤，以确保柱子的安全性能和承受能力。

混凝土结构设计原理
第七章
一条曲线代表一种配筋 量，越向外，所用的钢筋 越多；
M=0时，N最大；N=0时， M不是最大；界限破坏时， M最大；
无论配筋数量如何变化， 界限破坏时，轴力相同。
混凝土结构设计原理
第七章
N-M相关曲线：
由长细比不同，偏心受压柱分为短柱、长柱和细长柱
短柱：达到承载力极限 状态时弯矩为Nbei,轴向 承载力为Nb 。
长柱：达到承载力极限 状态时弯矩为Nc(ei+af), 轴向承载力为Nc 。
NA
Nb Nbei Nc Ncei
短柱（材料破坏）
B Ncaf C
长柱（材料破坏）
Ne Neei
Neaf
E
细长柱（失稳破坏）
细长柱：达到承载力极 O 限状态时弯矩为Ne(ei+af),
D MBiblioteka 轴向承载力为Ne 。Nb >Nc >Ne

4．地震作用下的轴力和剪力的计算 层 弯 矩 弯矩引起的 数 剪力
8.4m跨 6.0m跨 8.4m跨 6.0m跨
M左
6 5 4 3 2 1 19.34 33.92 64.04 75.81 88.54 80.79
M右
-11.2 8 -16.7 3 -31.7 6 -42.6 5 -46.8 4 -51.7 6
V右
6.58 16.25 22.39 28.64 34.34 30.08
11.4 0 91.27 14.1 0 109.31 16.1 2 95.85 15.7 8
M左
-108.7 7 -109.9 6 -110.2 4 -106.3 9 -103.0 4 -104.4 5
M右
27.1 5 45.9 0 46.8 7 50.5 0 52.8 0 48.2 4
V左
86.30 102.93 103.14 103.95 104.41 103.70
V中左
-101.5 0 -113.2 5 -113.0 8 -112.2 7 -111.8 1 -112.5 2
M右
44.89 45.04 44.80 41.77 44.38 44.49
M左
-35.14 -30.67 -30.83 -31.68 -28.83 -28.75
M右
8.47 12.8 4 13.1 2 14.1 3 14.7 6 13.4 8
V左
27.74 28.78 28.85 29.33 29.18 28.93
M右
6.06 16.7 9 28.5 9 41.3 6 55.5 3 0.00 0
V左
0.99 2.29 5.07 7.39 9.50 0.000
V中左

简述钢筋混凝土纯扭和剪扭构件及扭曲截面承载力及计算...思 考 题8.1 简述钢筋混凝土纯扭和剪扭构件的扭曲截面承载力的计算步骤。

8.2 纵向钢筋与箍筋的配筋强度比ζ的含意是什么？起什么作用？有什么限制？8.3 在钢筋混凝土构件纯扭实验中，有少筋破坏、适筋破坏、超筋破坏和部分超筋破坏，它们各有什么特点？在受扭计算中如何避免少筋破坏和超筋破坏？8.4 在剪扭构件承载力计算中如符合下列条件，说明了什么？000.70.250.8t c c t tV T V T f f bh W bh W 和 8.5 为满足受扭构件受扭承载力计算和构造规定要求，配置受扭纵筋及箍筋应当注意哪些问题？8.6 我国规范受扭承载力计算公式中的t 的物理意义是什么？其表达式表示了什么关系？此表达式的取值考虑了哪些因素？8.7 箍筋在受压构件中有何作用？普通矩形箍筋与螺旋箍筋轴心受压柱的承载力计算有何差别？8.8 螺旋箍筋柱与钢管混凝土柱的受力有何异同？8.9 螺旋箍筋柱不能适用于哪些情况？为什么？8.10 偏心受压正截面破坏形态有几种？破坏特征怎样？与哪些因素有关？偏心距较大时为什么也会产生受压破坏？8.11 偏心受压构件正截面承载力计算与受弯构件正截面承载力计算有何异同？什么情况下，偏心受压构件允许b ξξ>？此时，受拉钢筋的应力如何确定？8.12 如何用偏心距来判别大小偏心受压？这种判别严格吗？8.13 对称配筋矩形截面偏心受压构件，试判别下列情况属于哪一类偏心受压？（1）o c b o i bh af N h e ξη>>同时32.0；（2）o c b o i bh af N h e ξη<<同时32.0。

8.14 试编制程序计算对称配筋矩形截面的u u N M -相关曲线。

8.15 分两种情况编制在压力N 和弯矩M 共同作用下钢筋混凝土截面的受力全过程：（1）给定轴力N ，计算弯矩-曲率（M φ-）关系全曲线；（2）给定偏心距0e ，计算轴力-曲率（N φ-）关系全曲线。