相互独立事件乘积的概率与贝努里概型
- 格式:doc
- 大小:36.50 KB
- 文档页数:2




概率复习重点归纳 一、随机事件与概率 重点难点: 重点:概率的定义与性质,条件概率与概率的乘法公式,事件之间的关系与运算,全概率公式与贝叶斯公式 难点:随机事件的概率,乘法公式、全概率公式、Bayes 公式以及对贝努利概型的事件的概率的计算 常考题型: (1)事件关系与概率的性质 (2)古典概型与几何概型 (3)乘法公式和条件概率公式 (4)全概率公式和Bayes 公式 (5)事件的独立性 (6)贝努利概型 概念辨析1,互不相容(互斥)事件同逆(对立)事件互不相容事件:AB =Φ 逆事件:,A B AB ⋃=Ω=Φ事件互逆指的是非此即彼,即事件之一必定发生;而不相容仅指不能同时发生,但是是可以同时不发生的。
2,独立与互不相容(互斥)对事件A 及B ,若P(A)P(B)>0,且P(AB)=P(A)P(B),则称事件A 及B 互相独立;事件独立同事件互斥是两套不同的概念,不能进行比较;须知独立性针对的是事件概率存在上面的等式关系;而互斥是指事件的不可同时发生,两者之间不存在必然关系。
3、条件概率同乘积概率P(AB)是在样本空间Ω内,事件AB 的概率,而P(A | B)是在试验中增加了新条件B 发生 后的缩减的样本空间B Ω中计算事件A 的概率。
虽然A 、B 都发生,但两者是不同的,一般说来,当A 、B 同时发生时,常用P(AB),而在有包含关系或明确的主从关系时,用P(A | B) .例:袋中有9 个白球1 个红球,作不放回抽样,每次任取一球,取2 次,求:(1)第二次才取到白球的概率;( 2)第一次取到的是白球的条件下,第二次取到白球的概率.问题(1)求的就是一个乘积事件概率的问题,而问题(2)求的就是一个条件概率的问题.4、全概率公式同贝叶斯公式 全概率公式:要求事件A 的概率(通常直接不太好求),将其分成几个比较容易计算的概率之和。
在分析问题的过程中,A 可视为B1∪B2∪B3∪…∪Bn 的子事件,或者把Bi 看成A 发生的原因,A 是结果,而及较易求出,从而可由“因”求出“果”。






学 术 论 坛196科技资讯 SC I EN C E & TE C HN O LO G Y I NF O R MA T IO N贝努里家族在数学与科学上的地位正如巴赫家族在音乐领域的地位一样的显赫。
这个非凡的瑞士家族在三代时间里产生了十余位数学家和物理学家,其中有八位数学家,里面三位是杰出的,他们是雅可布、约翰、丹尼尔。
而贝努里概型就是雅可布.贝努里提出来的。
贝努里概型是一种既简单又非常重要的概型,这种概型是概率论中最早研究的模型之一,也是得到最多研究的模型之一。
在概率论中对概率分布的学习、概率的近似计算有着非常重要的作用。
它在现实生活生产中和在自然科学试验中也有着直接的应用,并在其中发挥着重要的作用,为其解决问题提供了理论支持。
而且,揭示这种简单概型的规律,对于以后研究更复杂的概型有着一定的指导意义和理论支撑。
下面我们就贝努里概型及其应用展开了解。
1 预备知识在许多概率问题中,试验中某事件A是否发生受到的关注较多。
例如,在产品调查中注意的是抽到次品还是抽到正品;在掷硬币时注意的是出现正面还是反面等,在这类问题中试验产生的结果只有两个,即 A 和 A 。
像这样只有两个可能结果的试验成为贝努里试验,投币试验就是最简单的贝努里概型。
在相同的条件下,将同一个试验独立重复进行 n 次,这种随机试验称为重贝努里试验。
现在我们来看看 n 重贝努里试验的定义。
1.1贝努里概型的定义关于 n 重贝努里概型的定义,尽管在各种教材的叙述不尽相同,但都是指满足下列条件的一系列实验:(1) n 次试验时独立的,即每次试验的结果都与其它各次试验的结果无关;(2)每次试验只有两个结果 A 和 A ,且它们出现的概率 ()P A p (01)p ()(1)P A q p q ,在每次试验中是不变的。
则称这种试验为 n 重贝努里( Bernoulli )试验,简称贝努里试验或贝努里概型。
在 n 重贝努里试验中,事件 A 恰好发生 k 次的概率为:(0,1,2,...,)k k n k n C p q k n 例1 (巴拿赫 Banach 火柴盒问题)某人随身带有两盒火柴,吸烟时从任一盒中取一根火柴,经过若干时间后,发现一盒火柴已经用完。
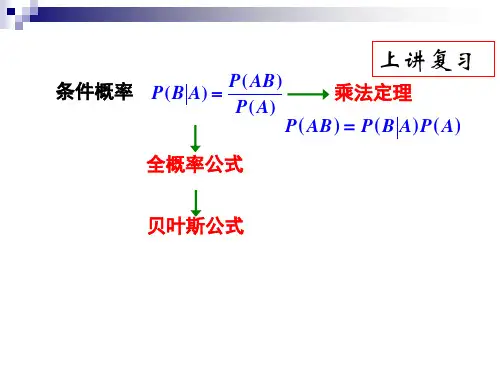
1963.3条件概率及全概率公式教学要求本节要求学生正确理解条件概率的概念及其运算公式, 学会运用概率的乘法定理. 对于全概率公式不但要求能深刻理解其内在含义,而且要求学生会熟练运用此公式去解决实际问题. 要求学生掌握两个事件独立的概念,了解多个事件相互独立的条件.知识点1. 条件概率2. 概率的乘法定理3. 全概率公式4. 两个事件的独立性5. 多个事件的独立性 *6.贝叶斯(Bayes )公式 *7.贝努里(Bernoulli )概型3.3.1 条件概率在实际问题中, 除了要知道事件A 的概率P (A )外, 有时还需要知道在事件B 已发生的条件下,事件A 发生的概率, 这就是我们所要讲的条件概率, 将它记为P (A |B ).我们先通过一个例子来引入条件概率的概念. 掷一颗骰子, 观察其出现点数, 令事件A 表示“出现点数小于4”, 则P (A )=1/2, 如果已知事件B 表示“出现偶数点”, 且B 已发生, 这时只剩下三种可能, 即“2点”,“4点”或“6点”. 从而在B 已发生的条件下, A 发生的概率为P (A |B )=1/3, 注意P (B )=1/2, P (AB )=1/6, 此时有)()()()|(A P B P AB P B A P ≠=. 定义.设A ﹑B 是随机试验E 的二个事件, 且P (B )>0, 则称 )()()|(B P AB P B A P =为事件B 发生条件下事件A 发生的条件概率.不难验证, 条件概率P (A |B )也是一种概率, 它符合概率的三个条件. 由前面的条件概率的定义, 我们可以知道, 计算条件P (A |B )有两种方法: (1)在样本空间Ω的缩减后的样本空间ΩB (事件B 发生时的样本空间)上计算A 发生的(无条件)概率, 就可以得到P (A |B ).(2)样本空间Ω中, 先计算P (AB ) ﹑P (B ), 然后由定义公式求得P (A |B ).197例3.3.1 全年级100名学生中, 有男生(以事件A 表示)80人, 女生20人; 来自北京的(以事件B 表示)有20人, 其中男生12人, 女生8人; 免修英语的(用事件C 表示)40人中有32名男生, 8名女生. 试写出P (A )、P (B )、P (B |A )、 P (A |B ) 、P (AB )、P (C )、P (C |A )、)|(B A P 、P (AC ).解.根据题意有P (A )=80/100=0.8; P (B )=20/100=0.2; P (B |A )=P (AB )/P (A )=12/80=0.15; P (A |B )=P (AB )/P (B )=12/20=0.6 ;P (AB )=12/100=0.12; P (C )=40/100=0.4; P (C |A )=P (AC )/P (A )=32/80=0.4; )|(B A P )()(B P B A P ==15.08012=;P (AC )=32/100=0.32.例3.3.2 8个乒乓球中有5个新的,3个旧的. 第一次比赛时, 同时取出2个, 用完后放回去; 第二次比赛时又取出2个球, 求第一次取到1个新球的条件下, 第二次取到2个新球的概率.解. 设事件A =“第一次取到1个新球”;事件B =“第二次取到2个新球”.由于第一次比赛后, 球被放回去, 因此在A 已发生的条件下, 再取2个球时, 总球数仍为8. 但是, 因第一次比赛所用的一个新球已变成旧球,其新旧比例已变化为: 新球4个, 旧球4个, 所以所求的概率为: 143)|(2824==C C A B P . 由条件概率,我们可以得到概率的乘法定理及两个事件的独立性.3.3.2 概率的乘法定理由前面的条件概率的定义公式,可得到下面的定理.概率的乘法定理. 设A ﹑B 为随机试验E 中的两个事件,且P (B )>0,则有 P (AB )=P (A |B )P (B ).198这个公式称为概率的乘法公式. 同样地,概率的乘法公式还有另一种形式:若P (A )>0, P (AB )=P (B |A )P (A ).例3.3.3. 设在一盒子中装有4个蓝色球和6个红色球, 取球两次, 一次取1个, 取后不放回, 问两次都取到红球的概率是多少? 解. 设事件A =“第一次取到红球”, 事件B =“第二次取到红球” ∵ P (A )=6/10, P (B |A )=5/9,因此 P (AB )=P (B |A )P (A )=1/3.我们还可以将概率的乘法公式推广到3个事件的情形: P (A 1A 2A 3)=P (A 1)P (A 2|A 1)P (A 3|A 1A 2).我们已经学习了条件概率和概率的乘法定理,由此我们可以得到下面的全概率公式.3.3.3 全概率公式前面我们学习了条件概率和概率乘法定理,下面我们介绍一个重要的公式--全概率公式.定理(全概率定理). 如果事件A 1, A 2, …, A n 构成一个完备事件组, 且P (A i )>0,(i =1,2,…,n ). 则对任一事件B , 有 ∑==ni i i A A B P P B P 1)|()()(这个公式称为全概率公式.证明. A 1, A 2,…,A n 是一个完备事件组, 从而A i (i =1,2,…,n )是两两互斥的, 且P (A i )>0, 由于B 被分成n 个部分A i B (i =1,2,…,n )之和, 且A i B (i =1,2,…,n )也是两两互斥的, 于是 B A A B B ni i ni i ∑∑====11.由概率的可加性及概率乘法定理得到:∑∑====ni i ni i B A P B A P B P 11)()()(=∑=ni i i A A P B P 1)()|(.全概率公式应用较广, 它的基本思路是将一个比较复杂的事件分解成若干个较简单且199两两互斥事件的和, 即要找一个完备事件组, 然后利用概率的可加性及概率乘法定理来计算.例3.3.4 设袋中装有5件同样的产品, 其中3件正品, 2件次品, 每次从袋中取1件,无放回地连续取2次, 求第2次取到正品的概率.解. 设事件A 表示“第1次取到正品”, 则A 表示“第1次取到次品”;事件B 表示“第2次取到正品”.事件A A ,构成一个完备事件组, A B BA B +=(即第2次取正品的可能性是与第1次取到正品或次品有关).因A B BA , 互不相容, 则有)()()()(A B P BA P A B BA P B P +=+= )|()()|()(A B P A P A B P A P += =(3/5)×(2/4)+(2/5)×(3/4)=3/5.例3.3.5 某厂有甲﹑乙﹑丙三个车间生产同一种产品,其产量分别占总产量的25%﹑35%﹑40%. 各自的废品率为5%﹑4%﹑2%, 今从总产品中任取一件, 求所取出的产品为废品的概率.解.设A 1=“所取产品为甲车间生产的”; A 2=“所取产品为乙车间生产的”; A 3=“所取产品为丙车间生产的”; B =“所取产品为废品”. 则A i (i =1,2,3)构成一个完备事件组, 且P (A 1)=0.25, P (A 2)=0.35, P (A 3)=0.4, P (B |A 1)=0.05, P (B |A 2)=0.04, P (B |A 3)=0.02, 由全概率公式有∑==31)|()()(i i i A A B P P B P=0.25×0.05+0.35×0.04+0.4×0.02=0.0345.由全概率公式我们可以求出,从总产品中任取一件,其为废品的概率是0.0345;反之,若已知从总产品取出一件,其为废品,反过来求它是甲车间(或乙车间﹑丙车间)生产的可能有多大,即为我们后面要讲的贝叶斯公式.3.3.4 两个事件的独立性前面我们讨论了条件概率P(A|B), 一般说来P(A|B)≠P(A)即事件B的发生对事件A发生的概率是有影响. 但当P(A|B)=P(A), 即B的发生对A发生的概率没有影响,此时即说事件A独立于事件B, 此时由概率乘法定理得到P(AB)=P(A|B)P(B)=P(A)P(B). 由此我们可给出两个事件独立的定义.定义. 设A﹑B是试验E的两个事件, 若有P(AB)=P(A)P(B)则称事件A﹑B为相互独立的事件.由概率乘法定理, 容易得出: 当事件A独立于事件B时, 事件B也独立于事件A, 即独立是一个对称性概念.例如, 从具有次品的一批产品中,有放回的连抽取二次, 每次抽取一件. 这样,事件A(第一次抽得正品)的出现并不影响事件B(第二次抽得正品)的概率, 即事件A与事件B是相互独立的两个事件.定理. 设A﹑B是试验E的两个事件, 且有P(B) >0, 则A与B相互独立的充分必要条件为:P(A|B)=P(A).证明. 必要性. 若A﹑B相互独立,则当P(B)>0时,由概率乘法公 式有:P(B)P(A|B)=P(AB)=P(A)P(B)从而 P(A|B)=P(A).充分性. 若P(A|B)=P(A),由概率乘法公式有:P(AB)=P(B)P(A|B)=P(B)P(A)即A﹑B相互独立.在实际问题中, 往往是通过对问题性质的分析来判断事件间是否独立.例3.3.6 甲﹑乙两人同时射击某一目标.设甲击中目标的概率为0.8,乙击中目标的概率为0.5,求目标被击中的概率.解.设事件A=“甲击中目标”,事件B=“乙击中目标”,事件C=“目标被击中”.从题意可知: C=A+B,且200201P (C )=P (A +B )=P (A )+P (B )-P (AB ).由于甲﹑乙射击是相互独立的, 因此可以认为甲﹑乙互不干扰, 从而A 与B 是相互独立的.P (AB )=P (A )P (B )=0.8×0.5=0.4,所以 P (C )=0.8+0.5-0.4=0.9. 例3.3.7 试证A ﹑B 相互独立与以下每一条件等价:(1)事件A 与B 独立;(2)事件A 与B 独立;(3) 事件A 与B 独立.证明.我们在这里只证由A 和B 相互独立,推出A 与B 独立,对于其它情形,由两个事件独立的对称性,同样可以推出.若A 与B 相互独立,则P (AB )=P (A )P (B ).由概率的性质,得到: )(B A P =P (A -AB )=P (A )-P (AB )=P (A )-P (A )P (B )=P (A )(1-P (B )) =)()(B P A P . 故A 与B 相互独立. 此例的结论,我们可用下表来表示: 表3.3.1表中任意一种情形成立, 都可以推出其它情形成立.由两个事件的独立性的概念,我们可以推出多个事件的独立性.3.3.5 多个事件的独立性前面我们学习了两个事件的独立性的概念﹑定理, 由此我们可以给出三个事件的独立性的概念.定义. 若A ﹑B ﹑C 是随机试验E 中的三个事件, 满足下列条件:(1) P (AB )=P (A )P (B ); (2)P (BC )=P (B )P (C );202(3) P (AC )=P (A )P (C ); (4)P (ABC )=P (A )P (B )P (C )。
贝努里概型伯努利家族在数学与科学上的地位正如巴赫家族在音乐领域的地位一样地显赫。
这个非凡的瑞士家族在三代时间里产生了十余位数学家和物理学家,其中有八位数学家(其中三位是杰出的,他们是雅可布、约翰、丹尼尔),他们又生出了在许多领域里崭露头角的成群后代。
雅可布发明了极坐标,他和他的弟弟约翰是莱布尼茨的朋友,经常书信往来讨论数学问题。
他们对于莱布尼茨发明的微积分方法极为推崇,迅速地接受了莱布尼茨的学说,并且加以发扬光大。
雅可布曾当过洛必达的私人教师,最先提出洛必达法则,是欧拉的老师。
雅可布和约翰两兄弟有时致力于研究同一个问题,但是由于彼此嫉妒和易于激动,这一情况是很遗憾的。
有时两人之间的摩擦爆发成为公开的嫉恨诟骂。
由于解决“最速降线”问题,兄弟两个因为解法的优劣而争论不休,两人之间的口角纷争达数年之久,其所用言辞之粗野很像市井上的对骂而非科学讨论。
这两人之中约翰的脾气似乎更坏,因为多年之后,由于他的二儿子丹尼尔获得了他自己渴望获得的法兰西科学院奖金,约翰竟把他摔出窗外。
n次重复独立试验:(1)相同的条件下重复地做某试验n次;可重复性(2)每次试验结果不受其它各次试验影响;独立性如:掷骰子n重贝努里试验:每次试验结果只有两种可能的n重独立试验1.共进行n次试验;2.各次试验相互独立;3.在每次试验中某事件A或者发生或者不发生;4.在每次试验中事件A出现的概率都是p(0p1)。
n重贝努里试验中事件A恰好发生k(0kn)次的概率为kknkPn(k)Cnp(1p)证明:设Ai={第i次贝努里试验中出现A},B={n重贝努里试验中A出现k次}分步:(1)A在指定的前k次试验中出现,后n-k次中不出现pP(A1...Akk1...n)P(A1)...P(Ak)P(k1)...P(n)pkqnkk(2)事件A可能出现在n次试验中的任何k次,共Cn中情况。
kknk所以Pn(k)Cnpq例1(1)将一个对称的硬币掷2次,求出现:恰好一次正面的概率;(2)将一个对称的硬币掷10次,求出现:恰好4次正面的概率。