二项分布表

目录1 定义▪统计学定义▪医学定义2 概念3 性质4 图形特点5 应用条件6 应用实例定义统计学定义在概率论和统计学中，二项分布是n个独立的是/非试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。

这样的单次成功/失败试验又称为伯努利试验。

实际上，当时，二项分布就是伯努利分布，二项分布是显著性差异的二项试验的基础。

医学定义在医学领域中，有一些随机事件是只具有两种互斥结果的离散型随机事件，称为二项分类变量（dichotomous variable），如对病人治疗结果的有效与无效，某种化验结果的阳性与阴性，接触某传染源的感染与未感染等。

二项分布（binomial distribution）就是对这类只具有两种互斥结果的离散型随机事件的规律性进行描述的一种概率分布。

考虑只有两种可能结果的随机试验，当成功的概率（）是恒定的，且各次试验相互独立，这种试验在统计学上称为伯努利试验（Bernoulli trial）。

如果进行次伯努利试验，取得成功次数为的概率可用下面的二项分布概率公式来描述：P=C(X,n)*π^X*(1-π)^(n-X)二项分布公式式中的n为独立的伯努利试验次数，π为成功的概率，（1-π）为失败的概率，X为在n次伯努里试验中出现成功的次数，表示在n次试验中出现X的各种组合情况，在此称为二项系数（binomial coefficient）。

所以的含义为：含量为n的样本中，恰好有X例阳性数的概率。

概念二项分布（Binomial Distribution），即重复n次的伯努利试验（Bernoulli Experiment），用ξ表示随机试验的结果。

二项分布公式如果事件发生的概率是P,则不发生的概率q=1-p，N次独立重复试验中发生K次的概率是P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k)，其中C(n, k) =n!/(k!(n-k)!)，注意：第二个等号后面的括号里的是上标，表示的是方幂。

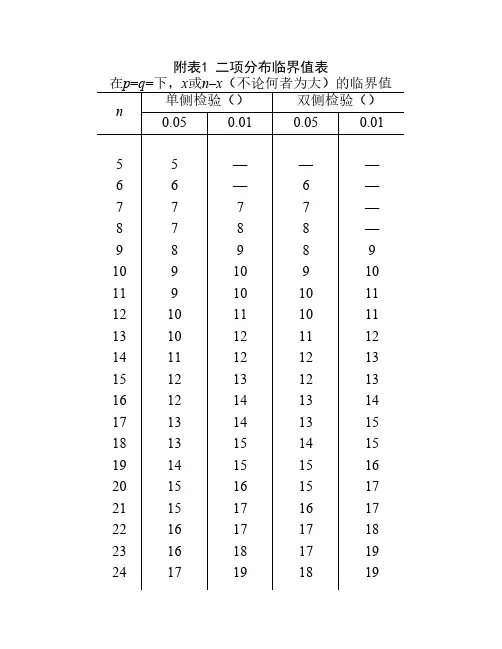
附表1 二项分布临界值表在p=q=下，x或n–x（不论何者为大）的临界值n 单侧检验（）双侧检验（）0.050.010.050.0155———66—6—7777—8788—98989 10910910 119101011 1210111011 1310121112 1411121213 1512131213 1612141314 1713141315 1813151415 1914151516 2015161517 2115171617 2216171718 2316181719 24171918192518191820 2618201920 2719202021 2819212022 2920222122 3020222123附表2 正态分布概率表Z F(Z)Z F(Z)Z F(Z)Z F(Z)0.000.00000.350.27370.700.5161 1.050.7063 0.010.00800.360.28120.710.5223 1.060.7109 0.020.01600.370.28860.720.5285 1.070.7154 0.030.02390.380.29610.730.5346 1.080.7199 0.040.03190.390.30350.740.5407 1.090.72430.050.03990.400.31080.750.5467 1.100.7287 0.060.04780.410.31820.760.5527 1.110.7330 0.070.05580.420.32550.770.5587 1.120.7373 0.080.06380.430.33280.780.5646 1.130.7415 0.090.07170.440.34010.790.5705 1.140.74570.100.07970.450.34730.800.5763 1.150.7499 0.110.08760.460.35450.810.5821 1.160.7540 0.120.09550.470.36160.820.5878 1.170.7580 0.130.10340.480.36880.830.5935 1.180.7620 0.140.11130.490.37590.840.5991 1.190.76600.150.11920.500.38290.850.6047 1.200.7699 0.160.12710.510.38990.860.6102 1.210.7737 0.170.13500.520.39690.870.6157 1.220.7775 0.180.14280.530.40390.880.6211 1.230.7813 0.190.15070.540.41080.890.6265 1.240.78500.200.15850.550.41770.900.6319 1.250.78870.210.16630.560.42450.910.6372 1.260.79230.220.17410.570.43130.920.6424 1.270.79590.230.18190.580.43810.930.6476 1.280.79950.240.18970.590.44480.940.6528 1.290.80300.250.19740.600.45150.950.6579 1.300.80640.260.20510.610.45810.960.6629 1.310.80980.270.21280.620.46470.970.6680 1.320.81320.280.22050.630.47130.980.6729 1.330.81650.290.22820.640.47780.990.6778 1.340.81980.300.23580.650.4843 1.000.6827 1.350.82300.310.24340.660.4907 1.010.6875 1.360.82620.320.25100.670.4971 1.020.6923 1.370.82930.330.25860.680.5035 1.030.6970 1.380.83240.340.26610.690.5098 1.040.7017 1.390.8355附表2（续）Z F(Z)Z F(Z)Z F(Z)Z F(Z)1.400.83851.750.91992.200.97222.900.99621.410.84151.760.92162.220.97362.920.99651.420.84441.770.92332.240.97492.940.99671.430.84731.780.92492.260.97622.960.99691.440.85011.790.92652.280.97742.980.99711.450.85291.800.92812.300.97863.000.99731.460.85571.810.92972.320.97973.200.9986 1.470.85841.820.93122.340.98073.400.9993 1.480.86111.830.93282.360.98173.600.99968 1.490.86381.840.93422.380.98273.800.999861.500.86641.850.93572.400.98364.000.99994 1.510.86901.860.93712.420.98454.500.999994 1.520.87151.870.93852.440.98535.000.999999 1.530.87401.880.93992.460.98611.540.87641.890.94122.480.98691.550.87891.900.94262.500.98761.560.88121.910.94392.520.98831.570.88361.920.94512.540.98891.580.88591.930.94642.560.98951.590.88821.940.94762.580.99011.600.89041.950.94882.600.99071.610.89261.960.95002.620.99121.620.89481.970.95122.640.99171.630.89691.980.95232.660.99221.640.89901.990.95342.680.99261.650.90112.000.95452.700.99311.660.90312.020.95662.720.99351.670.90512.040.95872.740.9939 1.680.90702.060.96062.760.9942 1.690.90902.080.96252.780.99461.700.91092.100.96432.800.9949 1.710.91272.120.96602.820.9952 1.720.91462.140.96762.840.9955 1.730.91642.160.96922.860.9958 1.740.91812.180.97072.880.9960附表3 t分布临界值表单侧双侧=0.10=0.200.050.100.0250.050.010.020.0050.01= 1 3.078 6.31412.70631.82163.6572 1.886 2.920 4.303 6.9659.9253 1.638 2.353 3.182 4.541 5.8414 1.533 2.132 2.776 3.747 4.6045 1.476 2.015 2.571 3.365 4.0326 1.440 1.943 2.447 3.143 3.7077 1.415 1.895 2.365 2.998 3.4998 1.397 1.860 2.306 2.896 2.3559 1.383 1.833 2.262 2.821 3.25010 1.372 1.812 2.228 2.764 3.16911 1.363 1.796 2.201 2.718 3.10612 1.356 1.782 2.179 2.681 3.05513 1.350 1.771 2.160 2.650 3.01214 1.345 1.761 2.145 2.624 2.97715 1.341 1.753 2.131 2.602 2.94716 1.337 1.746 2.120 2.583 2.92117 1.333 1.740 2.110 2.567 2.89818 1.330 1.734 2.101 2.552 2.87819 1.328 1.729 2.093 2.539 2.86120 1.325 1.725 2.086 2.528 2.84521 1.323 1.721 2.080 2.518 2.83122 1.321 1.717 2.074 2.508 2.81923 1.319 1.714 2.069 2.500 2.80724 1.318 1.711 2.064 2.492 2.79725 1.316 1.708 2.060 2.485 2.78726 1.315 1.706 2.056 2.479 2.77927 1.314 1.703 2.052 2.473 2.77128 1.313 1.701 2.048 2.467 2.76329 1.311 1.699 2.045 2.462 2.75630 1.310 1.697 2.042 2.457 2.750 40 1.303 1.684 2.021 2.423 2.704 50 1.299 1.676 2.009 2.403 2.678 60 1.296 1.671 2.000 2.390 2.660 70 1.294 1.667 1.994 2.381 2.648 80 1.292 1.664 1.990 2.374 2.639 90 1.291 1.662 1.987 2.368 2.632 100 1.290 1.660 1.984 2.364 2.626 125 1.288 1.657 1.979 2.357 2.616 150 1.287 1.655 1.976 2.351 2.609 200 1.286 1.653 1.972 2.345 2.6011.282 1.645 1.9602.326 2.576附表4 分布临界值表显著性水平（）0.990.980.950.900.800.700.500.300.200.1010.00020.00060.00390.01580.06420.1480.455 1.074 1.642 2.706 3.841 20.02010.04040.1030.2110.4460.713 1.386 2.403 3.219 4.605 5.991 30.1150.1850.3520.584 1.005 1.424 2.366 3.665 4.642 6.2517.815 40.2970.4290.711 1.064 1.649 2.195 3.357 4.878 5.9897.7799.488 50.5540.752 1.145 1.610 2.343 3.000 4.351 6.0647.2899.23611.070 60.872 1.134 1.635 2.204 3.070 3.828 5.3487.2318.55810.64513.5927 1.239 1.564 2.167 2.833 3.822 4.671 6.3468.3839.80312.01714.0678 1.646 2.032 2.733 3.490 4.594 5.5277.3449.52411.03013.36215.5079 2.088 2.532 3.325 4.168 5.380 6.3938.34310.65612.24214.68416.91910 2.558 3.059 3.940 4.865 6.1797.2679.34211.78113.44215.98718.30711 3.053 3.609 4.575 5.578 6.9898.14810.34112.89914.63117.27519.67512 3.571 4.178 5.226 6.3047.8079.30411.34014.01115.81218.54921.02613 4.107 4.765 5.8927.0428.6349.92612.34015.11916.98519.81222.36214 4.660 5.368 6.5717.7909.46710.82113.33916.22218.15121.06423.68515 5.229 5.9857.2618.54710.30711.72114.33917.32219.31122.30724.99616 5.812 6.6147.9629.31211.15212.62415.33818.41320.46523.54226.29617 6.4087.2558.67210.03512.00213.53116.33819.51121.61524.76927.587 187.0157.9069.39010.86512.85714.44017.33820.60122.76025.98928.869 197.6338.56710.11711.65113.71615.35218.33821.68923.90027.20430.144 208.2609.23710.85112.44314.57816.26619.33722.77525.03828.41231.410 218.8979.91511.59113.24015.44517.18220.33723.85826.17129.61532.671 229.54210.60012.33814.04116.31418.10121.33724.93927.30130.81333.924 2310.19611.29313.09114.84817.18719.02122.33726.01828.42932.00735.172 2410.85611.99213.84815.65918.06219.94323.33727.09629.55333.19636.415 2511.52412.69714.61116.47318.94020.86724.33728.17230.67534.38237.652 2612.19813.40915.37917.29219.82021.79225.33629.24631.79535.56338.885 2712.89714.12516.15118.11420.70322.71926.33630.31932.91236.74140.113 2813.56514.84716.92818.93021.58823.64727.33631.39134.02737.91641.337 2914.25615.57417.70819.76822.47524.57728.33632.46135.13939.08742.5573014.59316.30618.49320.59923.36425.50829.33633.53036.25040.25643.773附表5 F分布临界值表（=0.05）12345681015 1161.4199.5215.7224.6230.2234.0238.9241.9245.9 218.5119.0019.1619.2519.3019.3319.3719.4019.43 310.139.559.289.129.018.948.858.798.70 47.71 6.94 6.59 6.39 6.26 6.16 6.04 5.96 5.865 6.61 5.79 5.41 5.19 5.05 4.95 4.82 4.74 4.626 5.99 5.14 4.76 4.53 4.39 4.28 4.15 4.06 3.947 5.59 4.74 4.35 4.12 3.97 3.87 3.73 3.64 3.518 5.32 4.46 4.07 3.84 3.69 3.58 3.44 3.35 3.229 5.12 4.26 3.86 3.63 3.48 3.37 3.23 3.14 3.0110 4.96 4.10 3.71 3.48 3.33 3.22 3.07 2.98 2.8511 4.84 3.98 3.59 3.36 3.20 3.09 2.95 2.85 2.7212 4.75 3.89 3.49 3.26 3.11 3.00 2.85 2.75 2.6213 4.67 3.81 3.41 3.18 3.03 2.92 2.77 2.67 2.5314 4.60 3.74 3.34 3.11 2.96 2.85 2.70 2.60 2.4615 4.54 3.68 3.29 3.06 2.90 2.79 2.64 2.54 2.4016 4.49 3.63 3.24 3.01 2.85 2.74 2.59 2.49 2.3517 4.45 3.59 3.20 2.96 2.81 2.70 2.55 2.45 2.3118 4.41 3.55 3.16 2.93 2.77 2.66 2.51 2.41 2.2719 4.38 3.52 3.13 2.90 2.74 2.63 2.48 2.38 2.2320 4.35 3.49 3.10 2.87 2.71 2.60 2.45 2.35 2.2021 4.32 3.47 3.07 2.84 2.68 2.57 2.42 2.32 2.1822 4.30 3.44 3.05 2.82 2.66 2.55 2.40 2.30 2.1523 4.28 3.42 3.03 2.80 2.64 2.53 2.37 2.27 2.1324 4.26 3.40 3.01 2.78 2.62 2.51 2.36 2.25 2.1125 4.24 3.39 2.99 2.76 2.60 2.49 2.34 2.24 2.0926 4.23 3.37 2.98 2.74 2.59 2.47 2.32 2.22 2.0727 4.21 3.35 2.96 2.73 2.57 2.46 2.31 2.20 2.0628 4.20 3.34 2.95 2.71 2.56 2.45 2.29 2.19 2.0429 4.18 3.33 2.93 2.70 2.55 2.43 2.28 2.18 2.0330 4.17 3.32 2.92 2.69 2.53 2.42 2.27 2.16 2.01 40 4.08 3.23 2.84 2.61 2.45 2.34 2.18 2.08 1.92 50 4.03 3.18 2.79 2.56 2.40 2.29 2.13 2.03 1.87 60 4.00 3.15 2.76 2.53 2.37 2.25 2.10 1.99 1.84 70 3.98 3.13 2.74 2.50 2.35 2.23 2.07 1.97 1.81 80 3.96 3.11 2.72 2.49 2.33 2.21 2.06 1.95 1.79 90 3.95 3.10 2.71 2.47 2.32 2.20 2.04 1.94 1.78 100 3.94 3.09 2.70 2.46 2.31 2.19 2.03 1.93 1.77 125 3.92 3.07 2.68 2.44 2.29 2.17 2.01 1.91 1.75 150 3.90 3.06 2.66 2.43 2.27 2.16 2.00 1.89 1.73 200 3.89 3.04 2.65 2.42 2.26 2.14 1.98 1.88 1.72∞ 3.84 3.00 2.60 2.37 2.21 2.10 1.94 1.83 1.67附表5（续）12345681015 1405249995403562557645859598160656157 298.5099.0099.1799.2599.3099.3399.3799.4099.43 334.1230.8229.4628.7128.2427.9127.4927.2326.87 421.2018.0016.6915.9815.5215.2114.8014.5514.20 516.2613.2712.0611.3910.9710.6710.2910.059.72 613.7510.929.789.158.758.478.107.877.56 712.259.558.457.857.467.19 6.84 6.62 6.31811.268.657.597.01 6.63 6.37 6.03 5.81 5.52 910.568.02 6.99 6.42 6.06 5.80 5.47 5.26 4.96 1010.047.56 6.55 5.99 5.64 5.39 5.06 4.85 4.56 119.657.21 6.22 5.67 5.32 5.07 4.74 4.54 4.25 129.33 6.93 5.95 5.41 5.06 4.82 4.50 4.30 4.01 139.07 6.70 5.74 5.21 4.86 4.62 4.30 4.10 3.82 148.86 6.51 5.56 5.04 4.69 4.46 4.14 3.94 3.66 158.86 6.36 5.42 4.89 4.56 4.32 4.00 3.80 3.52 168.53 6.23 5.29 4.77 4.44 4.20 3.89 3.69 3.41 178.40 6.11 5.19 4.67 4.34 4.10 3.79 3.59 3.31 188.29 6.01 5.09 4.58 4.25 4.01 3.71 3.51 3.23 198.18 5.93 5.01 4.50 4.17 3.94 3.63 3.43 3.15 208.10 5.85 4.94 4.43 4.10 3.87 3.56 3.37 3.09 218.02 5.78 4.87 4.37 4.04 3.81 3.51 3.31 3.03 227.95 5.72 4.82 4.31 3.99 3.76 3.45 3.26 2.98 237.88 5.66 4.76 4.26 3.94 3.71 3.41 3.21 2.93 247.82 5.61 4.72 4.22 3.90 3.67 3.36 3.17 2.89 257.77 5.57 4.68 4.18 3.85 3.63 3.32 3.13 2.85 267.72 5.53 4.64 1.14 3.82 3.59 3.29 3.09 2.81 277.68 5.49 4.60 4.11 3.78 3.56 3.26 3.06 2.78 287.64 5.45 4.57 4.07 3.75 3.53 3.23 3.03 2.75 297.60 5.42 4.54 4.04 3.73 3.50 3.20 3.00 2.73 307.56 5.39 4.51 4.02 3.70 3.47 3.17 2.98 2.70 407.31 5.18 4.31 3.83 3.51 3.29 2.99 2.80 2.52 507.17 5.06 4.20 3.72 3.41 3.19 2.89 2.70 2.42 607.08 4.98 4.13 3.65 3.34 3.12 2.82 2.63 2.35 707.01 4.92 4.07 3.60 3.29 3.07 2.78 2.59 2.3180 6.96 4.88 4.04 3.56 3.26 3.04 2.74 2.55 2.27 90 6.93 4.85 4.01 3.53 3.23 3.01 2.72 2.52 2.42 100 6.90 4.82 3.98 3.51 3.21 2.99 2.69 2.50 2.22 125 6.84 4.78 3.94 3.47 3.17 2.95 2.66 2.47 2.19 150 6.81 4.75 3.91 3.45 3.14 2.92 2.63 2.44 2.16 200 6.76 4.71 3.88 3.41 3.11 2.89 2.60 2.41 2.13∞ 6.63 4.61 3.78 3.32 3.02 2.80 2.51 2.23 2.04附表6 秩和检验表表中列出了秩和下限及秩和上限的值=0.05=0.025 24311551936263155619 25313562040273175720 26414572243283195821 27416582347293215922 2841859255021042251024 294205102654346186626 210521662850356216728 33615673054367236829 34717683258378256931 357206933633882861033 368226103567399307737 379247739663109337839 3892778417144112571043 3910297943764512288849 310113171046804612328951 44122488528447133581054 4513278954904814389963 461430810579549154191066 47153399661054101644101079 48163691069111551837 4917391010931274101842附表7 游程检验R临界值表表中对应于n1与n2的有两行数值。

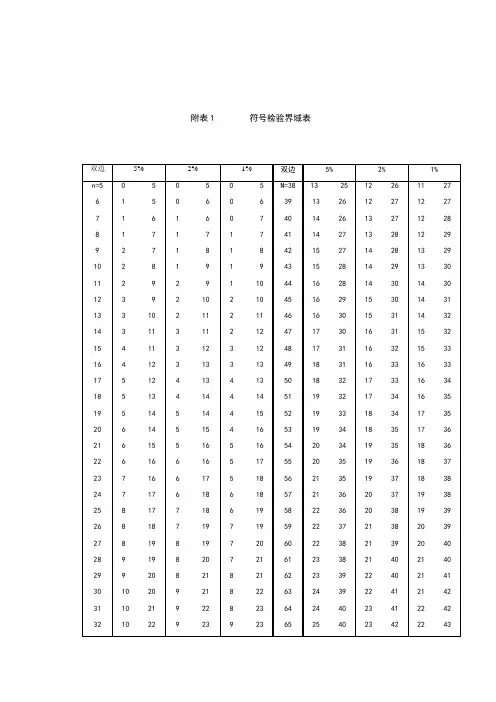
附表1 符号检验界域表附表2 二项分布表()∑=---=≤xk kn k p p k n k n x X P 01)!(!!)(附表3 标准正态分布表[])(1)(21)(22Z z dweZ W ZΦ-=-Φ-Φ-∞-⎰π附表4 威尔科克森带符号的秩和检验临界值（T值）表这里T是最大整数，即P（T≤t/n）≤a累积的单尾概率附表5 秩和检验临界值表括号数值表示样本容量（n1,n2）附表6 曼.怀特尼检验（U的临界值）单尾或双尾单尾或双尾附表7 游程检验的临界值表r下表 (a/2=r上表 (a/2=附表8 关于最长游程检验的临界值表当n1,n2≤25时,W a的值P(W≥W a)≤a Ⅰ a=Ⅱ a=附表9 游程长度平方和检验的临界值表当n=3---15时，使P(W≥W a)≤a的W a的值附表10 X2分布表本表对自由度n的X2分布给出上侧分位数(X2a)表，P(X2n>X2a)=α附表11 Kolmogorov—Smirnov拟合优度检验临界值D n表附表12 Kolmogorov----Smirnov双样本检验中D的分子K D的临界值表(小样本) n1=n2≤30附表12续 Kolmogorov----Smirnov双样本检验中D的临界值表（大样本: n1+n2>35, 双尾检验）附表13 Spearman检验统计量的临界值近似右尾临界值r s*；P(r s>r s*)≤a；n=4--30注意：r s*的相应左尾临界值为-r s*附表14 Kendall检验统计量的临界值当n>60时,T的近似数可以由下式得到：W p≌X p18)52)(1(+-nnn式中X p的值可以从标准正态分布中得到。

上表中只给出肯达尔统计检验量T的数值W p，即T的数值的上界，而下界数可由以下关系式得出：W p=-W p临界域为：T>W p或T<-W p附表15 Kendall协和系数中S的临界值表a=a=附表16 Cruskall---Wallis检验统计量的临界值附表17 上、下游程分布的数目附表18 多重比较的临界值Z。

二项分布概念：二项分布即重复n次独立的伯努利试验。

在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布就是伯努利分布。

该事件发生k次的概率为:P=C(k,n)×p^k×(1-p)^(n-k)，其中C(k,n)表示组合数，即从n个事物中拿出k个的方法数.，p为事件发生的概率，k是发生的次数，其中k=1,2,3...n，Ek=np，方差:Dk=np(1-p)例6-1某种药物治疗某种非传染性疾病的有效率为0.70，无效率为0.30。

今用该药治疗该疾病患者10人，试分别计算这10人中有6人、7人、8人有效的概率(《医学统计学》，第三版，孙振球)。

#源代码例6-1：dbinom(6,10,0.7)#二项分布函数dbinom(7,10,0.7)dbinom(8,10,0.7)#其中dbinom(k,n,p)中，k是发生的次数，10是共次数，p是概率>#源代码例6-1：>dbinom(6,10,0.7)[1]0.2001209>dbinom(7,10,0.7)[1]0.2668279>dbinom(8,10,0.7)[1]0.2334744>#其中dbinom(k,n,p)中，k是发生的次数，10是共次数，p是概率例6-2在对13名输卵管结扎的育龄妇女经壶腹部-壶腹部吻合术后，观察其受孕情况，发现有6人受孕，试据此资料估计该吻合术受孕率的95%可信区间。

#源代码例6-2：binom.test(6,13,p=6/13,conf.level=0.95)>#源代码例6-2：>binom.test(6,13,p=6/13,conf.level=0.95)Exact binomial testdata:6and13number of successes=6, number of trials=13, p-value=1alternative hypothesis:true probability of success is not equal to0.461538595percent confidence interval:0.19223240.7486545sample estimates:probability of success0.4615385例6-3在观测一种药物对某种非传染性疾病的治疗效果时，用该药治疗了此种非传染性疾病患者100人，发现55人有效，试据此估计该药物治疗有效率的95%可信区间。