经典雷达资料-第17章脉冲多普勒(PD)雷达-4
- 格式:doc
- 大小:222.05 KB
- 文档页数:9


脉冲多普勒雷达原理
脉冲多普勒雷达是一种利用脉冲信号来测量目标距离和速度的雷达系统。
它通过发射脉冲信号并接收目标反射的信号来实现目标的探测和跟踪。
脉冲多普勒雷达具有较高的测速精度和抗干扰能力,因此在军事、民用航空等领域得到了广泛的应用。
脉冲多普勒雷达的工作原理主要包括脉冲信号的发射和接收、目标回波信号的处理以及速度测量等几个方面。
首先,当脉冲多普勒雷达工作时,会发射一系列的脉冲信号。
这些脉冲信号会以一定的重复频率被发射出去,然后在空间中传播。
当这些脉冲信号遇到目标时,会被目标反射回来,形成回波信号。
接着,雷达系统会接收这些回波信号,并进行信号处理。
在信号处理过程中,脉冲多普勒雷达会对接收到的回波信号进行时域和频域的分析。
通过时域分析,可以测量目标与雷达之间的距离,即目标的径向距离。
而通过频域分析,可以测量目标的速度。
这是因为目标的运动会导致回波信号的多普勒频移,通过测量多普勒频移的大小,可以计算出目标的速度信息。
除了距离和速度测量外,脉冲多普勒雷达还可以实现目标的探测和跟踪。
当目标被探测到后,雷达系统会不断地追踪目标,并根据目标的运动状态进行预测。
这样可以实现对目标的持续跟踪,从而满足实际应用中对目标监测的需求。
总的来说,脉冲多普勒雷达是一种能够实现目标距离和速度测量的雷达系统。
它通过发射脉冲信号、接收目标回波信号并进行信号处理,实现了对目标的探测和跟踪。
在实际应用中,脉冲多普勒雷达具有较高的测速精度和抗干扰能力,因此在军事、民用航空等领域有着广泛的应用前景。


保护通道保护通道的工作原理是通过比较两个并行接收通道的输出,其中一个与主天线连接,另一个与保护天线连接,以判断接收的信号是来自主波束还是来自副瓣[26]~[28]。
保护通道使用宽波束天线,理想上其天线方向图超过主天线的副瓣。
两个信道的回波在同一个距离单元、同一个多普勒滤波器单元中进行比较。
当在保护接收机中的副瓣回波较大时,副瓣回波被抑制(消除);而主波束回波则通过,因为主通道接收的回波较大。
图17.8是保护通道的方框图。
CFAR电路后(在理想条件下,两个通道是相同的)有3个门限,即主通道门限、保护通道门限及主通道与保护通道信号比门限。
这些门限的检测逻辑如图17.8所示。
由于主通道和保护通道比较而产生的消隐将影响主通道的目标检测性能,因此影响的程度是门限设置的函数。
门限设置是由副瓣杂波引起的虚警与主通道检测性能损耗间的折中。
图17.9是一个不起伏目标回波的例子。
图中,纵坐标是最后输出的检测概率,横坐标是主通道中的信噪比(SNR)。
如图17.10所示中的B2是保护通道SNR与主通道SNR之比。
目标位于主波束时,B2值小;而在副瓣峰值时,B2值则大,约为0dB左右。
在该例中,对主波束中目标而言,由于保护通道的消隐作用,因此检测性能损耗0.5dB。
图17.8双通道副瓣消隐器框图图17.9 采用保护通道的检测概率与信噪比之间的关系曲线图17.10 主天线和保护天线的方向图理想情况下,保护天线方向图增益在除主波束方向外的所有方向上都将超过主天线方向图的增益,从而使雷达通过副瓣检测到的目标数最小。
如果不是那样,则如图17.10所示的保护天线方向图上的副瓣峰点处目标回波将在主信道具有较大的检测概率,这将形成虚警。
检波后STC消隐离散副瓣杂波的第二种方法是采用检波后STC[29]。
其逻辑框图如图17.11所示。
基本上,CFAR的输出数据将在距离上相关(解析)3次。
每个相关器采用M/N准则来计算不图17.11单通道副瓣消隐逻辑框图模糊距离。
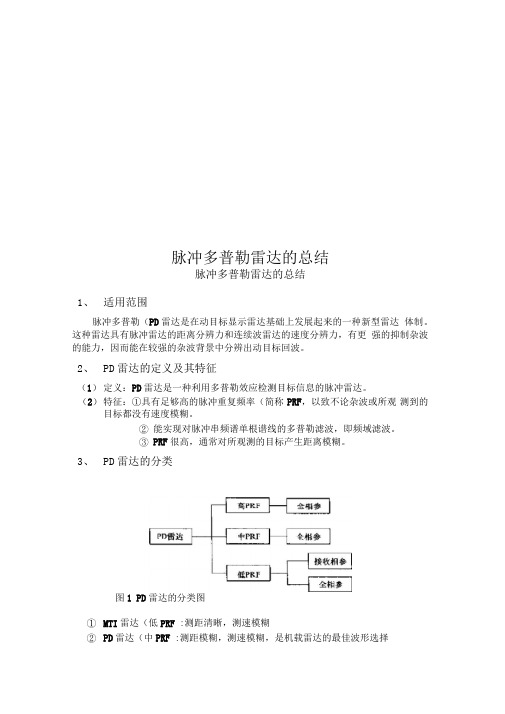
脉冲多普勒雷达的总结脉冲多普勒雷达的总结1、适用范围脉冲多普勒(PD雷达是在动目标显示雷达基础上发展起来的一种新型雷达体制。
这种雷达具有脉冲雷达的距离分辨力和连续波雷达的速度分辨力,有更强的抑制杂波的能力,因而能在较强的杂波背景中分辨出动目标回波。
2、PD雷达的定义及其特征(1)定义:PD雷达是一种利用多普勒效应检测目标信息的脉冲雷达。
(2)特征:①具有足够高的脉冲重复频率(简称PRF,以致不论杂波或所观测到的目标都没有速度模糊。
②能实现对脉冲串频谱单根谱线的多普勒滤波,即频域滤波。
③PRF很高,通常对所观测的目标产生距离模糊。
3、PD雷达的分类图1 PD雷达的分类图①MTI雷达(低PRF :测距清晰,测速模糊②PD雷达(中PRF :测距模糊,测速模糊,是机载雷达的最佳波形选择③PD雷达(高PRF :测距模糊,测速清晰4、机载下视PD雷达的杂波谱分析机载下视PD雷达的地面杂波是由主瓣杂波、旁瓣杂波和高度线杂波所组成f rhtnin >2/ThTT ^ 多普勒中心频率 变化范围 特点主瓣杂波 仏二人僚)=于co 喊 ±2血/入①强度比雷达接收机的噪声强70-90dB ② 与天线主波束的宽度、方向角、载机速度、发射信号波长有 关 旁瓣杂波① 当PDJ 达不运动时,旁瓣杂波与主瓣杂波在频域上相重合; ② 当PDJ 达运动时,旁瓣杂波与主瓣杂波就分布在不同的频域上 高度线杂波/d 宙=90° ① 机载下视PDJ 达做平行于地面的运动 ② 在零多普勒频率处总有一个较强的“杂波" 无杂波区+ 丁 co 引斷 ① 恰当选择雷达信号的PRF 使得其地面杂波既不重叠也不连接 ② 其频谱中不可能有地面杂波,只有接收机内部热噪声的部分5、PRF 的选择(1)高、中、低脉冲重复频率的选择① 机载雷达在没有地杂波背景干扰的仰视情况下,通常采用低 PRF 加脉冲压缩。
② 迎面攻击时高PRF 优于中PRF 尾随时,在低空,中 PRF 优于高PRF ;在 高空,高PRF 优于中PRF③ 交替使用中、高PRF 的方法,或者再加上在下视时采用低 PRF 的方法,并 在低、中PRF 时配合采用脉冲压缩技术,将是在所有工作条件下得到远距离探 测性能的最有效的方法。

脉冲多普勒
《脉冲多普勒》是一项技术,它在距离测量、声波定位及其他方面发挥着重要作用。
它由美国物理学家罗伯特霍金斯发明,该技术是在由他发明的先进技术多普勒雷达基础上发展而来的。
脉冲多普勒是一种采用脉冲波来发射和接收信号的技术。
它可以用来测定物体的距离、速度、方向等信息,并可以在短时间内进行检测。
它主要由发射装置、接收装置和控制系统组成,发射装置由高功率的脉冲放大器和调制器组成,接收装置由接收器、调制器和处理器组成。
控制系统负责控制发射和接收装置,同时还有电源模块和显示模块组成。
脉冲多普勒技术被广泛应用于军事、测绘、搜索和救助等领域。
它可以用来测量和定位物体的距离、速度、方向等信息,同时也可以用于对物体的形状进行计算。
它还可以用来获取物体的不同信息,比如物质组成、温度、压强等。
多普勒雷达技术已经在舰船测绘、海底地形测量、航空和航天领域等领域发挥着重要作用,而脉冲多普勒技术正成为一种新兴技术,可以更快、更精确地探测和定位物体,更有效地进行侦察和救助等活动,极大地提高了我们测绘、搜索、救助等工作的效率。
不过脉冲多普勒技术也存在一定的局限性,并且需要在设备的精度和发射功率方面进行更多的研究。
但是随着科技的发展,脉冲多普勒技术将取得更大的发展,为人类的测绘和搜索提供更多的支持。
- 1 -。
系统损耗下面讨论采用数字信号处理的PD雷达所固有的但不一定是独有的某些损耗。
量化噪声损耗量化噪声损耗是由模/数转换处理过程中所引入的噪声产生的,以及由信号处理电路中有限字长的截断效应产生的[45]。
CFAR损耗这是由检测门限非理想估值与理想的门限相比所造成的。
估计值的波动迫使门限均值高于理想门限值,因而产生了损耗。
多普勒滤波器的跨接损耗由于目标并不总是位于多普勒滤波器的中心,因而造成了多普勒滤波器的跨接损耗。
假设目标多普勒频率在一个滤波器频率范围内是均匀分布的,则可算出该损耗,而且它是FFT 副瓣加权的函数。
幅度加权损耗滤波器副瓣加权使多普勒滤波器的噪声带宽增加,从而导致了幅度加权损耗。
这种损耗可用多普勒滤波器噪声带宽的增量来考虑,而不看做另外的某种损耗。
脉冲压缩失配损耗脉冲压缩失配损耗是由于为了降低时间(距离)副瓣而引入失配产生的。
保护消隐损耗这是由保护通道寄生消隐造成的主信道检测损耗,如图17.9所示。
遮挡和距离波门跨接损耗由于遮挡,因此按式(17.20)给出的距离R0可能是零或最大值之间的任意值,这取决于脉间目标回波的确切位置。
当PRF较高时,会出现许多距离模糊,则扫描间的距离延迟可认为是随机的,且在脉间均匀分布。
在这种情况下,一种近似的性能度量是首先计算从零到脉冲间间隔全部模糊距离的平均检测曲线。
为获得与采用匹配波门接收发射脉冲无跨接时相同的检测概率,遮挡和距离波门跨接损耗等于系统所要求的信噪比提高。
由于检测概率的曲线形状不同,所以损耗取决于所选择的检测概率。
一种粗略的近似是脉间平均信噪比与匹配条件下的信噪比进行比较。
在M 个宽度为的相邻距离波门情况下,这些波门占据了除宽度为的发射脉冲之外的整个脉冲间隔,在信噪比基础上的平均的遮挡和跨接损耗为遮挡和跨接损耗= )1(3+M Y g t ττ= (17.21) 式中,Y 1=(1-R )(2+R ) M =1;Y =(1-R )(1-R +2X )+2+1.75(M -2) M >1, R ≥0.618;Y =(1-R )(1+R +Z )+(Z -R )[Z (Z +X )]+(1-Z )[Z (Z +1)+1]+1+1.75(M -2) M >1, R <0.618;Z =1/(1+X );X =R -1;R =b /;b =第一个波门消隐的宽度;=发射脉冲t 和接收波门g 的宽度;M =相邻波门的数目。
连续可变PRF 测距在单目标跟踪雷达中,距离模糊问题可通过变化PRF 来解决,它使目标回波落于脉冲间周期的中心,可采用0.333~0.5的高占空比。
距离R 可用下式计算f f R R RR -= (17.10) 由于导数测量误差,这种测距方法精度低。
其的优点是目标回波永远不会被发射脉冲遮挡,因此提高了雷达的目标跟踪性能。
缺点是PRF 的谐波分量会以假信号的形式出现在多普勒频带内。
线性载波调频载波的线性频率调制可用于测距,特别是在边搜索边测距的雷达中。
这种使用调制和解调方法来获取目标距离的原理和连续波雷达测距的原理相同,但它发射的仍是脉冲信号。
假设波束扫过目标的驻留时间可分为两个阶段:第一个阶段,雷达不发射调频脉冲,测量目标的多普勒频移;第二个阶段,雷达发射信号的频率以变化率f沿一个方向线性变化。
在至目标的往返期间,本振的频率已经发生变化,因而,目标回波除了有多普勒频移外,还有与距离成正比的频移。
求出这两个阶段中目标回波的频率差∆f ,则目标距离R 可用下式计算,即f f c R2∆= (17.11) 若天线波束宽度内不止有一个目标,则在一个驻留时间内仅有两种频率调制阶段的问题会产生距离幻影。
例如,当两个目标出现在不同多普勒频率时,频率调制期间所观测到的两个频率不能不模糊地和两个无频率调制期间所观测到的两个频率配对。
因此,典型的高PRF 的边搜索边测距应采用三阶段调频方案,即无频率调制阶段、频率上升调制阶段和频率下降调制阶段。
从这3个阶段选择回波求距离,它们应满足的关系为201f f f << (17.12)0212f f f =+ (17.13)式中,f 0,f 1和f 2分别为上述3个阶段的观测频率。
然后,由式(17.11)可得到目标的距离,式中,1012022/)(f f f f f f f ---=∆或或 (17.14) 图17.17是它的一个例子。
观测频率第17章脉冲多普勒(PD)雷达·663·满足式(17.12)的可能的频率组合图17.17 3种斜率频率调制测距举例有两个目标(A和B);频率调制斜率f =24.28MHz/s。
脉冲多普勒雷达总结班级:20090812学号:2009081221姓名:刘玉敬一、PD雷达的基本概念1. 定义:PD雷达是一种利用多普勒效应检测目标信息的脉冲雷达。
2. 特点:①具有足够高的脉冲重复频率,没有速度模糊;②能够实现对脉冲串频谱单根谱线的频域滤波;③由于重复频率很高,通常对所观测的目标产生距离模糊。
3. 分类:高PRF、中PRF、低PRF,前两个为全相参,最后一个可全相参也可接收相参。
低PRF不模糊的距离为:。
中PRF波形是机载PD雷达的最佳波形。
二、PD雷达的杂波多普勒雷达的基本特点之一,是在频域-时域分布相当宽广且相当强的背景杂波中检测出有用的信号。
这种背景杂波通常被称为脉冲多普勒杂波,其杂波频谱是多普勒频率-距离的函数。
1. 机载下视雷达的杂波谱地面杂波分为主瓣杂波区、旁瓣杂波区和高度线杂波区。
孤立目标对雷达发射信号的散射作用所产生的回波信号的多普勒频移,正比于雷达与运动目标之间的径向速度v,所以当雷达平台以地速v R水平移动,地速矢量与地面一小块地杂波之间的夹角为Ψ时,其多普勒频移为(1) 主瓣杂波主波束中心Ψo处对应的多普勒频率为假设天线主波束的宽度为,则主瓣杂波的边缘位置间的最大多普勒频率差值为机载PD雷达的主瓣杂波的强度可以比雷达接收机的噪声强70~90dB,主瓣杂波的多普勒频率fMB也在不断变化,并且变化范围在±2之内。
(2) 旁瓣杂波旁瓣杂波区的多普勒频率范围为,则。
雷达天线的旁瓣波束增益通常要比它的主波束增益低得多。
当PD雷达不运动时,旁瓣杂波与主瓣杂波在频域上重合;当PD雷达运动时,旁瓣杂波与主瓣杂波就分布在不同的频域上。
(3) 高度线杂波通常,把机载下视PD雷达的地面杂波中f d=0位置上的杂波叫做高度线杂波。
在零多普勒频率处总有一个较强的“杂波”。
2. 脉冲重复频率的选择(1) 高脉冲重复频率时的重复频率的选择①使迎面目标谱线不落入旁瓣杂波区中最大多普勒频移为为了在无杂波区检测目标,重复频率应为:即②为了识别迎面和离去的目标的重复频率的选择A. 单边带滤波器对主瓣杂波的频率固定即B. 单边带滤波器对发射频率固定迎面目标的多普勒频移为,离去目标的最低多普勒频移为,最低脉冲重复频率为:。
系统损耗下面讨论采用数字信号处理的PD雷达所固有的但不一定是独有的某些损耗。
量化噪声损耗量化噪声损耗是由模/数转换处理过程中所引入的噪声产生的,以及由信号处理电路中有限字长的截断效应产生的[45]。
CFAR损耗这是由检测门限非理想估值与理想的门限相比所造成的。
估计值的波动迫使门限均值高于理想门限值,因而产生了损耗。
多普勒滤波器的跨接损耗由于目标并不总是位于多普勒滤波器的中心,因而造成了多普勒滤波器的跨接损耗。
假设目标多普勒频率在一个滤波器频率范围内是均匀分布的,则可算出该损耗,而且它是FFT 副瓣加权的函数。
幅度加权损耗滤波器副瓣加权使多普勒滤波器的噪声带宽增加,从而导致了幅度加权损耗。
这种损耗可用多普勒滤波器噪声带宽的增量来考虑,而不看做另外的某种损耗。
脉冲压缩失配损耗脉冲压缩失配损耗是由于为了降低时间(距离)副瓣而引入失配产生的。
保护消隐损耗这是由保护通道寄生消隐造成的主信道检测损耗,如图17.9所示。
遮挡和距离波门跨接损耗由于遮挡,因此按式(17.20)给出的距离R0可能是零或最大值之间的任意值,这取决于脉间目标回波的确切位置。
当PRF较高时,会出现许多距离模糊,则扫描间的距离延迟可认为是随机的,且在脉间均匀分布。
在这种情况下,一种近似的性能度量是首先计算从零到脉冲间间隔全部模糊距离的平均检测曲线。
为获得与采用匹配波门接收发射脉冲无跨接时相同的检测概率,遮挡和距离波门跨接损耗等于系统所要求的信噪比提高。
由于检测概率的曲线形状不同,所以损耗取决于所选择的检测概率。
一种粗略的近似是脉间平均信噪比与匹配条件下的信噪比进行比较。
在M个宽度为τ的相邻距离波门情况下,这些波门占据了除宽度为τ的发射脉冲之外的整个脉冲间隔,在信噪比基础上的平均的遮挡和跨接损耗为第17章 脉冲多普勒(PD )雷达 ·663·遮挡和跨接损耗= )1(3+M Y g t ττ= (17.21) 式中,Y 1=(1-R )(2+R ) M =1;Y =(1-R )(1-R +2X )+2+1.75(M -2) M >1, R ≥0.618;Y =(1-R )(1+R +Z )+(Z -R )[Z (Z +X )]+(1-Z )[Z (Z +1)+1]+1+1.75(M -2) M >1, R <0.618;Z =1/(1+X );X =R -1;R =τb /τ;τb =第一个波门消隐的宽度;τ =发射脉冲τt 和接收波门τg 的宽度;M =相邻波门的数目。
图17.19画出了损耗曲线。
在每个发射脉冲之后的时间τb 内不能接收信号,是由于发射机缓慢关断或收发开关或接收机保护电路恢复时间的原因。
图17.19 在M 个相邻距离波门、相等的发射脉宽和距离波门宽度情况下,遮挡和跨接损耗与接收波门数和消隐宽度的函数关系尽管式(17.21)假设距离波门是相邻的,但波门重叠可降低损耗,其代价是须使用额外的硬件和可能产生更多的距离虚假目标。
虚警概率PD 雷达通常采用多次检测准则来解决距离模糊。
那么在波束扫过目标期间(驻留时间),雷达就须发射多重PRF ,并且只有当雷达不止一次得到门限检测结果时才能输出目标数据。
如果用多普勒滤波器组对每个距离波门进行相参积累处理,且也许后面还有检波后积累器,那么为获得给定虚警报告时间T FR 所要求的在每个距离波门多普勒滤波器中的虚警概率P FA 可近似表示为m T N m n T N P /1FR g d F FA 693.01⎪⎪⎭⎫ ⎝⎛= (17.22)第17章 脉冲多普勒(PD )雷达·664· 式中,N F 为在多普勒通带内可见的独立的多普勒滤波器数(非消隐滤波器数/FFT 加权因子);n 为在驻留时间内观测的次数;m 为通报一个目标所要求的检测次数(如,8重PRF 中3次检测到目标,则m =3,n =8);T d 为多重PRF 的总驻留时间,包括检波后积累时间(如果有的话)和休止时间;⎪⎪⎭⎫ ⎝⎛m n 为二项式系数n !/[m !(n -m )!];N g 为输出不模糊距离间隔内的距离波门数(显示距离/距离波门的宽度);T FR 为虚警报告时间[根据Marcum 的定义,如果虚警概率为0.5,则在虚警报告时间内至少出现一次虚警(参考资料46)]。
式(17.22)适用于输出目标报告不需多普勒相关的情况。
假如同时使用距离相关和多普勒相关,则所要求的P FA 为m m W T N N m n T P /11FR fu g d FA 693.0-⎪⎪⎭⎫ ⎝⎛= (17.23) 式中,N fu 为在不模糊多普勒频域内独立的多普勒滤波器数;W 为用于起始检测之后的相关窗宽度(在滤波器中)。
检测概率第2章介绍的检测概率曲线已推广到包括多次观测检测的准则中,并且在参考资料47中以广义的形式出现,即用gR /R 0来表示该曲线。
其中,因子g 为非相参积累脉冲数和虚警概率的函数。
对相参积累而言,N =1,那么4/1FA )]ln([P g -= (17.24)图17.20画出了不同虚警概率和不同脉冲积累数的g 因子曲线。
图17.20 Swerling 因子g 与P FA 和N 的函数关系曲线(见参考资料47)第17章 脉冲多普勒(PD )雷达 ·665·考虑到参数在很宽变化范围内所取得的Marcum 曲线[46]都非常相似,为了得到广义检测概率曲线,可以使用如图17.21所示的通用Marcum 曲线。
该图是根据参考资料47的通用曲线画出的,不同之处是本图针对不起伏目标。
图中指出,在积累样本数N 在1~100、虚警概率P FA 在10-3~10-8及检测概率在1%~99%的整个范围内,通用曲线的精度均在1dB 以内。
要使用图17.21,首先要从如图17.20所示中求得因子g (P FA , N )的值,然后再用该值将图中的gR /R 0转化为R /R 0或信噪比值。
图17.21 通用Marcum 曲线广义曲线利用通用Marcum 曲线,可求得如图17.22所示的几种检测条件下的检测概率曲线。
它们都针对Swerling I 型目标,即目标幅度在扫描间起伏是不相关的,并且在驻留时间内是固定的。
这些曲线除了起伏损耗外没有包括其他损耗,因此诸如距离波门跨接和遮挡之类的损耗可在计算R 0时计入。
Swerling I 型目标的单次扫描检测曲线可很精确地近似为P P b a FA )]SNR /(1[d += (17.25)第17章 脉冲多普勒(PD )雷达·666· 式中,P d 为单次扫描检测概率;P FA 为虚警概率;SNR 为信噪比= (R 0/R )4。
常数a 和b 可由置换方法求出,首先由如图17.22所示中得到两对P d 和gR /R 0值,然后将gR /R 0换算成SNR ,最后求解联立方程。
图17.22 用于扫描间、Swerling I 型、瑞利起伏目标的归一化的单次扫描检测概率曲线累计检测概率P Ck (K 次扫描中至少有一次发现目标的概率)的定义为:∏--==ki i P P 1d C )](1[1k (17.26)式中,P d (i )为第i 次扫描的检测概率。
在满足1/N 发现准则的条件下,积累可以在多次扫描上进行(扫描次数是可变的),如从P d (i )近似等于零处开始或在规定的扫描次数上进行,则如图17.22所示的单次扫描检测概率曲线可以用来计算出变扫描次数的85%的积累检测概率,如图17.23所示。
∆R 是以固定速度径向飞行目标在相邻扫描间隔内的距离变化量。
受杂波限制的情况上述讨论都假设目标落在多普勒频带中那些受噪声限制的区域(即无杂波区)。
如果目标落在副瓣杂波区,那么测距性能会降低,这是因为与目标抗争的总功率(系统噪声加杂波)增大了的缘故。
但是通过把R 0表示为信号等于副瓣杂波加上系统噪声时的距离,上述讨论也第17章脉冲多普勒(PD)雷达·667·适用于副瓣杂波区[48]~[50]。
由于目标检测区内的杂波发生变化时,门限也随之变化的缘故,故CFAR的损耗也可能更高。
图17.23 用于扫描间、Swerling 型、瑞利起伏目标的广义的85%积累检测概率曲线参考资料1 Skolnik, M. I.: Fifty Years of Radar, Proc. IEEE, vol. 73, pp. 182-197. February 1985.2 Perkins, L. C., H. B. Smith, and D. H. Mooney: The Development of Airborne Pulse Doppler Radar , IEEETrans., vol. AES-20, pp. 290-303, May 1984.3 Clarke, J., D. E. N. Davies, and M. F. Radford: Review of United Kingdom Radar, IEEE Trans., vol. AES-20,pp. 506-520, September 1984.4 Moaveni, M. K.: Corrections to “Radio Interference in Helicopter-Borne Pulse Doppler Radars,”IEEE Trans.,vol. AES-14, p. 688, July 1978.5 Moaveni, M. K.: Radio Interference in Helicopter-Borne Pulse Doppler Radars, IEEE Trans., vol. AES-14, pp.319-328, March 1978.6 Ringel, M. B., D. H. Mooney, and W. H. Long: F-16 Pulse Doppler Radar (AN/APG-66) Performance, IEEETrans., vol. AES-19, pp. 147-158, January 1983.7 Skillman, W. A.: Utilization of the E-3A Radar in Europe, Proc. Mil. Electron. Def. Expo'78, Wiesbaden,Germany, 1978.8 Skillman, W. A.: Microwave Technology, Key to AWACS Success, Proc. IEEE MTT/S, Boston, 1983.9 Clarke, J.: Airborne Early Warning Radar, Proc. IEEE, vol. 73, pp. 312-324, February 1985.10 Doviak, R. J., D. S. Zrnic, and D. S. Sirmans: Doppler Weather Radar, Proc. IEEE, vol. 67, no. 11, pp.1522-1553, 1979.第17章脉冲多普勒(PD)雷达·668·11 Stimson, G. W.: “Introduction to Airborne Radar,”Hughes Aircraft Company, Ei Segundo, Calif., 1983, pt. 7.12 Hovanessian, S. A.: Medium PRF Performance Analysis, IEEE Trans., vol. AES-18, pp. 286-296, May 1982.13 Aronoff, E., and N. M. Greenblatt: Medium PRF Radar Design and Performance, 20th Tri-Service Radar Symp.,1974. Reprinted in Barton, D. K.: "CW and Doppler Radars,"vol. 7, Artech House, Norwood, Mass., 1978, sec.IV-7, pp. 261-276.14 Long, W. H., and K. A. Harriger: Medium PRF for the AN/APG-66 Radar, Proc. IEEE, vol. 73, pp. 301-311,February 1985.15 Goetz, L. P., and J. D. Albright: Airborne Pulse Doppler Radar, IRE Trans., vol. MIL-5, pp. 116-126, April1961. Reprinted in Barton, D. K.: “CW and Doppler Radars,”vol. 7. Artech House, Norwood, Mass., 1978, sec. IV-3, pp. 215-225.16 Skolnik, M. I.: “Introduction to Radar Systems,”2d ed., McGraw-Hill Book Company, New Y ork, 1984, chap. 4.17 Finn, H. M., and R. S. Johnson: Adaptive Detection Mode with Threshold Control as a Function of SpatiallySampled Clutter-Level Estimates, RCA Rev., pp. 414-464, September 1968.18 Steenson, B. O.: Detection Performance of a Mean-Level Threshold, IEEE Trans., vol. AES-4, pp. 529-534,July 1968.19 Rohling, H.: Radar CFAR Thresholding in Clutter and Multiple Target Situations, IEEE Trans., vol. AES-19,pp. 608-621, July 1983.20 Hansen. V. G.: Constant False Alarm Rate Processing in Search Radars, Proc. IEEE Int. Radar Conf., pp.325-332, London, 1973.21 Farrell. J., and R. Taylor: Doppler Radar Clutter, IEEE Trans., vol. ANE-11, pp. 162-172, September 1964.Reprinted in Barton, D. K.: “CW and Doppler Radars,”vol. 7, Artech House, Norwood, Mass., 1978, sec. VI-2, pp. 351-361.22 Helgostam, L., and B. Ronnerstam: Ground Clutter Calculation for Airborne Doppler Radar, IEEE Trans., vol.MIL-9, pp. 294-297, July-October 1965.23 Friedlander, A. L., and L. J. Greenstein: A Generalized Clutter Computation Procedure for Airborne PulseDoppler Radars, IEEE Trans., vol. AES-6, pp. 51-61, January 1970. Reprinted in Barton, D. K.:“CW and Doppler Radars,”vol. 7, Artech House, Norwood, Mass., 1978, sec. VI-3, pp. 363-374.24 Ringel, M. B.: An Advanced Computer Calculation of Ground Clutter in an Airborne Pulse Doppler Radar,NAECON'77 Rec.'pp. 921-928. Reprinted in Barton, D. K.:“CW and Doppler Radars,”vol. 7, Artech House, Norwood, Mass., 1978, sec. VI-4, pp. 375-382.25 Jao, J. K., and W. B. Goggins: Efficient, Closed-Form Computation of Airborne Pulse Doppler Clutter, Proc.IEEE Int. Radar Conf., pp. 17-22, Washington. 1985.26 Harvey, D. H., and T. L. Wood: Designs for Sidelobe Blanking Systems. Proc. IEEE Int. Radar Conf., pp.410-416, Washington, 1980.27 Maisel, L.: Performance of Sidelobe Blanking Systems, IEEE Trans., vol. AES-4, pp. 174-180, March 1968.28 Finn, H. M., R. S. Johnson, and P. Z. Peebles: Fluctuating Target Detection in Clutter Using Sidelobe BlankingLogic, IEEE Trans. V ol. AES-7, pp. 147-159, May 1971.29 Mooney, D. H.: Post Detection STC in a Medium PRF Pulse Doppler Radar, U.S. Patent 690, 754, May 27,1976.第17章脉冲多普勒(PD)雷达·669·30 Skillman, W. A.:“SIGCLUT: Surface and V olumetric Clutter-to-Noise. Jammer and Target Signal-to-NoiseRadar Calculation Software and User's Manual,”Artech House, Norwood, Mass., 1987.31 Ziemer, R. E., and J. A. Ziegler: MTI Improvement Factors for Weighted DFTs , IEEE Trans., vol. AES-16, pp.393-397, May 1980.32 Skillman, W. A.:“Radar Calculations Using the TI-59 Programmable Calculator,”Artech House, Norwood,Mass., 1983, p.308.33 Skillman, W. A.:“Radar Calculations Using Personal Computers,”Artech House, Norwood, Mass., 1984.34 Ward, H. R.: Doppler Processor Rejection of Ambiguous Clutter, IEEE Trans., vol. AES-11, July 1975.Reprinted in Barton, D. K.:“CW and Doppler Radars,”vol. 7, Artech House, Norwood, Mass., 1978, sec. IV-11, pp. 299-301.35 Fletcher, R. H., Jr., and D. W. Burlage: An Initialization Technique for Improved MTI Performance in PhasedArray Radar. Proc. IEEE, vol. 60, pp. 1551-1552, December 1972.36 Skillman, W. A., and D. H. Mooney: Multiple High-PRF Ranging, Proc. IRE Conf. Mil. Electron., PP. 37-40,1961. Reprinted in Barton, D. K.:“CW and Doppler Radars,”vol. 7, Artech House, Norwood, Mass., 1978, sec.IV-1, pp. 205-213.37 Hovanessian, S. A.: An Algorithm for Calculation of Range in Multiple PRF Radar, IEEE Trans., vol. AES-12,pp. 287-289, March 1976.38 Ore, O.:“Number Theory and Its History,”McGraw-Hill Book Company, New York, 1948, pp. 246-249.39 Goetz, L. P., and W. A. Skillman: Master Oscillator Requirements for Coherent Radar Sets, IEEE-NASA Symp.Short Term Frequency Stability, NASA-SP-80, November 1964.40 Raven. R. S.: Requirements for Master Oscillators for Coherent Radar. Proc. IEEE. V ol. 54, pp. 237-243,February 1966. Reprinted in Barton, D. K.: "CW and Doppler Radars," vol.7. Artech House, Norwood, Mass., 1978, sec. V-1, pp. 317-323.41 Gray, M., F. Hutchinson, D. Ridgely, F. Fruge. and D. Cooke: Stability Measurement Problems and Techniquesfor Operational Airborne Pulse Doppler Radar, IEEE Trans., vol. AES-5, pp. 632-637, July 1969.42 Acker, A. E.: Eliminating Transmitted Clutter in Doppler Radar Systems, Microwave J., vol. 18, pp. 47-50,November 1975. Reprinted in Barton, D. K.:“CW and Doppler Radars,”vol.7, Artech House, Norwood, Mass., 1978, sec. V-3, pp. 331-336.43 Black, H. S.:“Modulation Theory,”D. Van Nostrand Company, Princeton, N.J., 1953.p. 265.44 Barton, D. K.:“Radar Systems Analysis,”Prentice-Hall, Englewood Cliffs, N.J., 1964, p. 206.45 Ziemer, R. E., T. Lewis, and L. Guthrie: Degradation Analysis of Pulse Doppler Radars Due to SignalProcessing, NAECON 1977 Rec., pp. 938-945. Reprinted in Barton, D. K.: "CW and Doppler Radars,"vol. 7, Artech House, Norwood, Mass., 1978, sec. IV-12, pp. 303-312.46 Marcum, J. I.: A Statistical Theory of Target Detection by Pulsed Radar, IRE Trans., vol. IT-6, pp. 59-267,April 1960.47 Swerling, P.: Probability of Detection for Fluctuating Targets, IRE Trans., vol. IT-6, pp. 269-308, April 1960.48 Mooney, D., and G. Ralston: Performance in Clutter of Airborne Pulse MTI, CW Doppler and Pulse DopplerRadar, IRE Conv. Rec., vol. 9, pt. 5, pp. 55-62, 1961. Reprinted in Barton, D. K.:“CW and Doppler Radars,”vol. 7, Artech House, Norwood, Mass., 1978, sec. VI-1, pp. 343-350.·670·第17章脉冲多普勒(PD)雷达49 Ringel, M. B.: Detection Range Analysis of an Airborne Medium PRF Radar, IEEE NAECON Rec., Dayton,Ohio, pp. 358-362, 1981.50 Holbourn, P. E., and A. M. Kinghorn: Performance Analysis of Airborne Pulse Doppler Radar, Proc. IEEE Int.Radar Conf., pp. 12-16, Washington, 1985.。