丰富的图形世界测试(基础卷)2020-2021年七年级数学上册尖子生同步培优题(解析版)【北师大版】

2020-2021学年七年级数学上册尖子生同步培优题典【浙教版】专题6.11第6章图形的初步认识单元测试（基础卷）姓名：__________________ 班级：______________ 得分：_________________注意事项：本试卷满分120分，试题共26题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2020•雁塔区校级模拟）如图，是一个几何体的表面展开图，则该几何体中写“英”的面相对面上的字是（）A．“战”B．“疫”C．“情”D．“颂”2．（2020春•肇东市期末）下列几何体中，是棱锥的为（）A．B．C．D．3．（2019秋•凌源市期末）下列四个生产生活现象，可以用公理“两点之间，线段最短”来解释的是（）A．用两个钉子可以把木条钉在墙上B．植树时，只要定出两棵树的位置，就能使同一行树坑在一条直线上C．打靶的时候，眼睛要与枪上的准星、靶心在同一直线上D．为了缩短航程把弯曲的河道改直4．（2020春•哈尔滨月考）若∠A＝38°15′，∠B＝38.15°，则（）A．∠A＞∠B B．∠A＜∠B C．∠A＝∠B D．无法确定5．（2019秋•蚌埠期末）如图，∠AOD＝60°，∠AOB：∠BOC＝1：4，OD平分∠BOC，则∠AOC的度数为（）A．20°B．80°C．100°D．120°6．（2020春•雨花区校级月考）如图，将一副三角板叠在一起使直角顶点重合于点O，（两块三角板可以在同一平面内自由转动），下列结论一定成立的是（）A．∠BOA＞∠DOC B．∠BOA﹣∠DOC＝90°C．∠BOA+∠DOC＝180°D．∠BOC≠∠DOA7．（2020春•老城区校级月考）如图，AC⊥BC，CD⊥AB，下列结论中，正确的结论有（）①线段CD的长度是C点到AB的距离；②线段AC是A点到BC的距离；③AB＞AC＞CD．A．0个B．1个C．2个D．3个8．（2018秋•南京期末）如图，点O是直线EF上一点，且OF平分∠COD，OA⊥OC，OB⊥OD．若OA 平分∠EOB，则图中与∠DOF互补的角有（）A．1个B．2个C．3个D．4个9．（2018秋•临沭县期末）下列结论：①互补且相等的两个角都是90°；②同角的余角相等；③若∠1+∠。

丰富的图形世界1．如图5-1-1所示，组成“陀螺”的几何体有( )A．长方体和圆锥 B．长方形和三角形C．圆和三角形 D．圆柱和圆锥2．(2020独家原创试题)如图5—1—2所示的几何体中，属于柱体的有 ( )A．1个 B．2个 C．3个 D．4个3．在几何图形“线段、圆、圆锥、正方体、角、棱锥”中．属于立体图形的共有个．4．(2020独家原创试题)下列的立体图形中，有4个面的是 ( )A．三棱锥 8．三棱柱 C．四棱锥 D．四棱柱5．如果一个多面体的一个面是多边形，其余各面是有一个公共顶点的三角形，那么这个多面体叫做棱锥．图5-1-3是一个四棱柱和一个六棱锥，它们各有12条棱．下列棱柱中和九棱锥的棱数相等的是 ( ) A．五棱柱 B．六棱柱C．七棱柱 D．八棱柱6．如果一个六棱柱的所有侧棱长之和是48 cm，则它的侧棱长为________cm．7．围成圆柱的面有 ( )A．1个 B．2个 C．3个D．4个8．推导猜测：(1)三棱锥有条棱，四棱锥有条棱，五棱锥有条棱：(2) 棱锥有30条棱；(3)一个棱锥的棱数是l00，则这个棱锥是棱锥．9．如图5一l一4，下列几何体是由几个面围成的?并指出对应的面是曲的还是平的．10．用边长为1的正方形纸板．制成一副七巧板(如图5一1-5①)，将它拼成“小天鹅”图案(如图5—1-5②)，其中阴影部分的面积为 ( )11．已知七巧板的结构如图5-1-6所示．请运用七巧板拼出1～9这九个数中的任意2个数字．说明：七巧板中的七块板可以不用完．拼好后将对应的编号写在拼出的图形中．12．(2020江苏南京高淳期末，2，★☆☆)如图5一l一7，含有曲面的几何体的编号是 ( )A．①② B．①③ C．②③ D．②④13．(2018江苏连云港东海月考，5，★★☆)一个六棱柱模型如图5—1—8所示，底面边长都是5 cm．侧棱长为4cm，这个六棱柱的侧面积是 ( )A．20 cm2 B．60 cm2C．120 cm2 D．240 cm214．(2020江苏无锡宜兴一模，10，★☆☆)若一个棱柱有7个面．则它是棱柱．15．(2019上海南洋模范中学月考，1’，★☆☆)用一个平面去截下列几何体：①正方体；②圆柱；③圆锥；④正三棱柱，得到的截面形状可能为三角形的有___________________(写出所有正确结果的序号)．16．(2019江苏淮安金湖期末．21，★☆☆)如果一个正棱柱一共有l2个顶点，底面边长是侧棱长的一半，并且所有的棱长的和是120 cm，求每条侧棱的长．17．(2019甘肃白银中考，1，★☆☆)下列四个几何体中，是三棱柱的为 ( )18．(2017江苏南京中考，3，★☆☆)不透明的袋子中装有一个几何体模型．两位同学摸该模型并描述它的特征．甲同学：“它有4个面是三角形．”乙同学：“它有8条棱．”该模型的形状对应的立体图形可能是 ( )A．三棱柱 B．四棱柱 C．三棱锥 D．四棱锥19．(2017江苏扬州l中考，5，★-k☆☆)经过圆锥顶点的截面的形状可能是( )20．(2017浙江湖州中考，9．★☆☆)七巧板是我国祖先的一项卓越创造．下列四幅图中有三幅是小明用如图5一1-9所示的七巧板拼成的，则不是小明拼成的那幅图是 ( )21．对于棱柱而言，不同的棱柱由不同的面构成：三棱柱由2个底面，3个侧面，共5个面构成；四棱柱由2个底面，4个侧面，共6个面构成；五棱柱由2个底面。

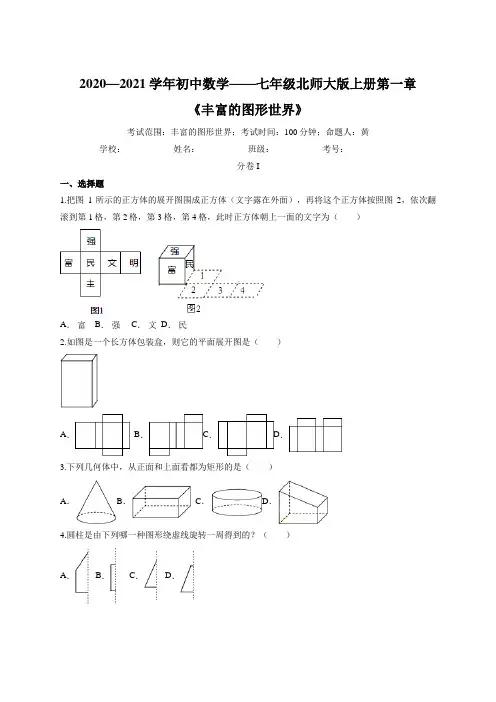
2020—2021学年初中数学——七年级北师大版上册第一章《丰富的图形世界》考试范围：丰富的图形世界；考试时间：100分钟；命题人：黄学校：___________姓名：___________班级：___________考号：___________分卷I一、选择题1.把图1所示的正方体的展开图围成正方体（文字露在外面），再将这个正方体按照图2，依次翻滚到第1格，第2格，第3格，第4格，此时正方体朝上一面的文字为（）A．富 B．强 C．文 D．民2.如图是一个长方体包装盒，则它的平面展开图是（）A． B．C．D．3.下列几何体中，从正面和上面看都为矩形的是（）A．B． C．D．4.圆柱是由下列哪一种图形绕虚线旋转一周得到的？（）A． B． C． D．5.如图1所示，将一个正四棱锥（底面为正方形，四条测棱相等）的其中四条边剪开，得到图2，则被剪开的四条边有可能是（）A．PA，PB，AD，BCB．PD，DC，BC，ABC．PA，AD，PC，BCD．PA，PB，PC，AD6.下列图形不是立体图形的是（）A．球 B．圆柱 C．圆锥 D．圆7.将一个圆围绕它的直径所在的直线旋转180°形成的几何体是（）A．圆锥 B．半球 C．球体 D．圆柱8.如图是一个长方体的表面展开图，6个面上分别标有数字1，2，3，4，5，6（数字都在表表面），与标有数字6的面相对面上的数字是（）A． 3 B． 5 C． 2 D． 19.下列水平放置的几何体中，从上面看是矩形的是（）A．圆柱 B．长方体C．三棱柱 D．圆锥10.埃及金字塔类似于几何体（）A．圆锥 B．圆柱C．棱锥 D．棱柱11.如图是某个几何体从正面看、从左面看、从上面看所得图形，该几何体是（）A．圆锥 B．三棱锥C．圆柱 D．三棱柱12.如图，下列图形全部属于柱体的是（）A． B． C． D．13.圆柱是由长方形绕着它的一边所在直线旋转一周所得到的，那么下图是以下四个图中的哪一个绕着直线旋转一周得到的（）A． B． C． D．14.如图，以下四个图形是由立体图形展开得到的，相应的立体图形的顺次是（）A．正方体、圆柱、圆锥、三棱锥B．正方体、三棱锥、圆柱、圆锥C．正方体、圆柱、三棱柱、圆锥D．三棱锥、圆锥、正方体、圆锥15.汽车的雨刷把玻璃上的雨水刷干净属于的实际应用是（）A．点动成线 B．线动成面C．面动成体 D．以上答案都不对16.李明为好友制作一个（如图）正方体礼品盒，六面上各有一字，连起来就是“预祝中考成功”，其中“预”的对面是“中”，“成”的对面是“功”，则它的平面展开图可能是（）A． B． C． D．17.将如图所示表面带有图案的正方体沿某些棱展开后，得到的图形是（）A． B． C． D．18.下列四个几何体中，从上面看是长方形的是（）A．长方体 B．圆柱 C．球 D．三棱柱19.面与面相交，形成的是（）A．点 B．线 C．面 D．体20.如图的立体图形可由哪个图形绕轴旋转而成（）A． B． C． D．分卷II二、填空题21.机器零件中的六角螺母，圆筒形的易拉罐、足球、火柴盒、铅垂体中，类似于棱柱的物体有，类似于球体的物体有，类似于圆锥的物体有，类似于圆柱的物体有．22.如图，5个边长相等的小正方形拼成一个平面图形，小丽手中还有一个同样的小正方形，她想将它与图中的平面图形拼接在一起，从而可以构成一个正方体的平面展开图，则小丽总共能有__________种拼接方法．23.若一个棱柱的底面是七边形，则它一共有个面．24.根据几何体的特征，填写它们的名称．（1）上下两个底面是大小相同的圆，侧面展开后是长方形．（2）6个面都是长方形．（3）6个面都是正方形．（4）上下底面是形状大小相同的多边形，侧面是长方形．（5）下底面是圆，上方有一个顶点，侧面展开后是扇形．（6）下底面是多边形，上方有一个顶点．（7）圆圆的实体．25.如图，是用若干个小立方块搭成的几何体分别从正面和上面看到的形状图，则搭成这个几何体最少需要个小立方块．26.一个直棱柱有18条棱，则它是一个直棱柱．27.飞机表演的“飞机拉线”用数学知识解释为：．28.如图所示的图形中为柱体的是，其中为圆柱的是，为棱柱的是 .29.笔尖在纸上写字说明；车轮旋转时看起来像个圆面，这说明；一枚硬币在光滑的桌面上快速旋转形成一个球，这说明．30.写出下列物体类似的几何图形：数学课本，笔筒，金字塔，西瓜．31.数学课上，小林同学用n个小立方块搭成一个几何体，从三个方向看到的图形如图所示，则n 的值是．32.如图是某几何体的展开图，那么这个几何体是．三、解答题33.将图中的几何体进行分类，并说明理由．34.有一个小立方块，每一个面上分别写着数字1、2、3、4、5、6，有三个人分别从不同角度观察的结果如图所示，问这个小立方块相对的两个面上的数字分别是多少？35.观察图中的立体图形，分别写出它们的名称．36.将下列几何体与它的名称连接起来．答案解析1.【答案】A【解析】由图1可得，“富”和“文”相对；“强”和“主”相对；“民”和“明”相对；由图2可得，小正方体从图2的位置依次翻到第4格时，“文”在下面，则这时小正方体朝上面的字是“富”，故选A．2.【答案】A【解析】由四棱柱四个侧面和上下两个底面的特征可知，A．可以拼成一个长方体；B，C，D不符合长方体的展开图的特征，故不是长方体的展开图．故选A．3.【答案】B【解析】A．此几何体从正面是等腰三角形，从上面看是圆，故此选项错误；B．此几何体从正面是矩形，从上面看是矩形，故此选项正确；C．此几何体从正面是矩形，从上面看是圆，故此选项错误；D．此几何体从正面是梯形，从上面看是矩形，故此选项错误；故选B．4.【答案】B【解析】圆柱是由长方形绕它的一条边旋转而成的，故选B．5.【答案】A【解析】根据图2中的展开图可知，底面正方形ABCD的左边一个三角形是独立的，据此可知，需剪开图1中的PA、PB，根据正方形右边三个三角形脱离正方形的上下两边可知，需剪开AD、BC，综上，被剪开的四条边可能是：PA、PB、AD、BC，故选A．6.【答案】D【解析】立体图形是指图形的各个面不都在一个平面上，由此可判断出答案．由题意得：只有D选项符合题意．故选D．7.【答案】C【解析】一个圆围绕它的直径所在的直线旋转180°形成的几何体是球体，故选C．8.【答案】C【解析】根据题意和图示可知：“1”的对面是4，“6”的对面是2，“3”的对面是5．故选C．9.【答案】B【解析】A．圆柱从上面看是圆，故此选项错误；B．长方体从上面看是矩形，故此选项正确；C．三棱柱从上面看是三角形，故此选项错误；D．圆锥从上面看是圆，故此选项错误；故选B．10.【答案】C【解析】埃及金字塔底面是多边形，侧面是有公共顶点的三角形，所以是棱锥．故选C．11.【答案】D【解析】根据正面看、从左面看为矩形判断出是柱体，根据从上面看是三角形可判断出这个几何体应该是三棱柱．故选D.12.【答案】C【解析】A．左边的图形属于锥体，故本选项错误；B．上面的图形是圆锥，属于锥体，故本选项错误；C．三个图形都属于柱体，故本选项正确；D．上面的图形不属于柱体，故本选项错误．故选C．13.【答案】A【解析】A．可以通过旋转得到两个圆柱，故本选项正确；B．可以通过旋转得到一个圆柱，一个圆筒，故本选项错误；C．可以通过旋转得到一个圆柱，两个圆筒，故本选项错误；D．可以通过旋转得到三个圆柱，故本选项错误．故选A．14.【答案】C【解析】观察图形，由立体图形及其表面展开图的特点可知相应的立体图形顺次是正方体、圆柱、三棱柱、圆锥．故选C．15.【答案】B【解析】汽车的雨刷实际上是一条线，通过运动把玻璃上的雨水刷干净，所以应是线动成面．故选B．16.【答案】C【解析】正方体的表面展开图，相对的面之间一定相隔一个正方形，A．“预”的对面是“考”，“成”的对面是“祝”，故本选项错误；B．“预”的对面是“功”，“成”的对面是“祝”，故本选项错误；C．“预”的对面是“中”，“成”的对面是“功”，故本选项正确；D．“预”的对面是“中”，“成”的对面是“祝”，故本选项错误．故选C．17.【答案】C【解析】由原正方体知，带图案的三个面相交于一点，而通过折叠后A、B都不符合，且D折叠后图案的位置正好相反，所以能得到的图形是C．故选C．18.【答案】A【解析】A．长方体从上面看是长方形，故此选项正确；B．圆柱从上面看是圆形，故此选项错误；C．球从上面看是圆形，故此选项错误；D．三棱柱从上面看是三角形，故此选项错误；故选A．19.【答案】B【解析】面与面相交，形成的是线．故选B．20.【答案】D【解析】A．此图形绕轴旋转成圆锥，故此选项错误；B．此图形绕轴旋转成圆台，故此选项错误；C．此图形绕轴旋转成球，故此选项错误；D．此图形绕轴旋转成半球，故此选项正确；故选D．21.【答案】火柴盒、六角螺母足球铅垂体易拉罐【解析】棱柱主要特点：上下两个平行的面，侧面是四边形；球体主要特点：一个曲面；圆锥主要特征；两个面，底面是圆，侧面是一个曲面；圆柱主要特征：上下两个全等的平行的圆，侧面是一个曲面．根据以上分析特征故火柴盒六角螺母类似于棱柱；足球类似于球体；铅垂体类似于圆锥；易拉罐似于圆柱．22.【答案】4【解析】如图所示：故小丽总共能有4种拼接方法．故答案为：4．23.【答案】9【解析】一个棱柱的底面是七边形，有7个侧面，两个底面，故答案为：9．24.【答案】（1）圆柱（2）长方体（3）正方体（4）棱柱（5）圆锥（6）棱锥（7）球【解析】根据所给几何体的特征，直接填写它们的名称即可．25.【答案】6【解析】由俯视图易得最底层有5个小立方块，由主视图可得第二层最少有1个小立方块，所以搭成这个几何体最少需要5+1=6个小立方块．故答案为：626.【答案】六【解析】根据一个n直棱柱有3n条棱，进行填空即可．一个直棱柱有18条棱，则它是直六棱柱．27.【答案】点动成线【解析】飞机在空中表演，飞机可看作一个点，则“飞机拉线”用数学知识解释为：点动成线．28.【答案】②③②③【解析】根据柱体是上下一样粗的几何体可得答案；两底面是圆形的柱体是圆柱，底面是多边形的柱体是棱柱．29.【答案】点动成线线动成面面动成体【解析】笔尖在纸上写字说明点动成线；车轮旋转时看起来像个圆面，这说明线动成面；一枚硬币在光滑的桌面上快速旋转形成一个球，这说明面动成体．故答案为：点动成线；线动成面；面动成体．30.【答案】长方体圆柱（或棱柱）四棱锥球【解析】根据实物的形状，可得立体图形．31.【答案】7【解析】易得第一层有4个正方体，第二层有2个正方体，第三层有1个，共有7个．故答案为：7．32.【答案】圆柱【解析】这个几何体是圆柱，故答案为：圆柱33.【答案】解：分类首先要确定标准，可以按组成几何体的面的平或曲来划分，也可以按柱、锥、球来划分．（1）长方体是由平面组成的，属于柱体．（2）三棱柱是由平面组成的，属于柱体．（3）球体是由曲面组成的，属于球体．（4）圆柱是由平面和曲面组成的，属于柱体．（5）圆锥是由曲面与平面组成的，属于锥体．（6）四棱锥是由平面组成的，属于锥体．（7）六棱柱是由平面组成的，属于柱体．若按组成几何体的面的平或曲来划分：（1）（2）（6）（7）是一类，组成它的各面全是平面；（3）（4）（5）是一类，组成它的面至少有一个是曲面，若按柱、锥、球来划分：（1）（2）（4）（7）是一类，即柱体；（5）（6）是一类，即锥体；（3）是球体．【解析】根据分类首先要确定标准，可以按组成几何体的面的平或曲来划分，也可以按柱、锥、球来划分，进而得出答案．34.【答案】解：从3个小立方体上的数可知，与写有数字1的面相邻的面上数字是2，3，4，6，所以数字1面对数字5面，同理，立方体面上数字3对6．故立方体面上数字2对4．【解析】由图一和图二可看出1的相对面是5；再由图二和图三可看出3的相对面是6，从而2的相对面是4．35.【答案】解：从左向右依次是：球、圆锥、正方体、圆柱、长方体．【解析】针对立体图形的特征，直接填写它们的名称即可．36.【答案】解：如图所示：【解析】根据常见立体图形的特征直接连线即可．注意正确区分各个几何体的特征．。

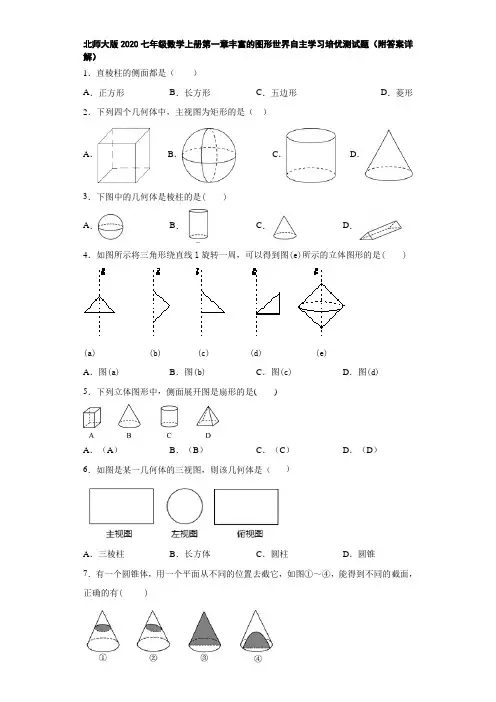
北师大版2020七年级数学上册第一章丰富的图形世界自主学习培优测试题（附答案详解）1．直棱柱的侧面都是（）A．正方形B．长方形C．五边形D．菱形2．下列四个几何体中，主视图为矩形的是（）A．B．C．D．3．下图中的几何体是棱柱的是( )A．B．C．D．4．如图所示将三角形绕直线l旋转一周，可以得到图(e)所示的立体图形的是( )(a) (b) (c) (d) (e)A．图(a)B．图(b)C．图(c)D．图(d)5．下列立体图形中，侧面展开图是扇形的是( )A．（A）B．（B）C．（C）D．（D）6．如图是某一几何体的三视图，则该几何体是（）A．三棱柱B．长方体C．圆柱D．圆锥7．有一个圆锥体，用一个平面从不同的位置去截它，如图①～④，能得到不同的截面，正确的有( )A．1种B．2种C．3种D．4种8．如图是一个由5个相同的正方体组成的立体图形，它的俯视图是（）A．B．C． D．9．如图是一个正方体的表面展开图，则原正方体中与建“字”所在的面相对的面上标的字是___________．10．一个几何体的三视图如图所示，根据所示数据计算这个几何体的侧面积_____．11．若一个几何体的三视图都相同，则这个几何体可以是___________．（填一个即可）12．如图所示是一个包装盒的三视图，则这个包装盒的体积是________．13．小华在一个正方体的六个面上分别写上“x，y，z，1，﹣1，2”字样，表面展开图如图所示，则在该正方体中，相对面的数字相等，则x y=_____．14．如图是一个几何体的三视图（图中尺寸单位：cm），根据图中所示数据计算这个几何体的表面积是．15．如果五棱柱的底面边长都是2 cm，侧棱长都是4 cm，那么它所有棱长的和是________，它的侧面展开图的面积是________．16．某圆柱形的零件，其高为5cm，底面半径为2cm，为防锈需要涂油漆的面积为________2cm．17．一个几何体由几个大小相同的小立方体搭成，从上面观察这个几何体，看到的形状如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，请你画出从正面、左面看到的这个几何体的形状图．18．如图，小华用若干个正方形和长方形准备拼成一个长方体的展开图．拼完后，小华看来看去总觉得所拼图形似乎存在问题．（1）请你帮小华分析一下拼图是否存在问题：若有多余块，则把图中多余部分涂黑；若还缺少，则直接在原图中补全；（2）若图中的正方形边长为3 cm，长方形的长为5 cm，宽为3 cm，请直接写出修正后所折叠而成的长方体的体积是cm3．19．如图所示的几何体是由 5 个相同的正方体搭成的，请分别画出这个几何体的三视图．20．如图是由几个相同的小立方体搭成的几何体的俯视图，小正方形中的数字表示在该位置的小立方体的个数，请画出这个几何体的主视图和左视图．21．如图是几个小立方块所搭几何体的俯视图，小正方形的数字表示该位置小立方块的个数，请画出这个几何体的主视图和左视图．22．如图是由7个完全相同是正方体组成的立体图形，画出从不同方向看该几何体得到的平面图形.23．用小立方体搭成一个几何体，从正面和上面看到该几何体的形状图如图所示，搭建这样的几何体最多要几个小立方体？最少要几个小立方体？并画出最多和最少时从左面看到的形状图．24．如图①是一个正方体，不考虑边长的大小，它的平面展开图为图②，四边形APQC 是截正方体的一个截面．问截面的四条线段AC，CQ，QP，PA分别在展开图的什么位置上？参考答案1．B【解析】【分析】根据棱柱由上下两个底面以及侧面组成；上下两个底面可以是全等的多边形，侧面是四边形；棱长与底面垂直的棱柱叫直棱柱，不垂直的棱柱叫斜棱柱作答．【详解】解：直棱柱不管从哪个侧面看都是长方形．故选B．【点睛】本题考查直棱柱的定义，关键点在于：直棱柱的侧面是长方形，且上下底面是全等的两个多边形．2．C【解析】【分析】根据主视图是从物体正面看，所得到的图形，分别得出四个几何体的主视图，即可解答. 【详解】解：A、正方体的主视图是正方形，不符合题意；B、球的主视图是圆，不符合题意；C、圆柱的主视图是矩形，符合题意；D、圆锥的主视图是三角形，不符合题意.故选C.【点睛】本题考查了简单几何体的三视图.3．D【解析】【分析】根据棱柱的定义逐一进行判断即可得．【详解】A、是球体，不符合题意；B、是圆柱，不符合题意；C、是圆锥，不符合题意；D、是三棱柱，符合题意，故选D.【点睛】本题考查了棱柱，棱柱有两个互相平行的平面，其余各面为平行四边形的多面体，熟练掌握棱柱的定义以及常见几何体的特征是解题的关键.4．B【解析】【分析】根据图e的主视图是一个正方形,被直线l从中间分成两个等腰直角三角形,由此可以判断图e 是由图b绕直线l旋转一周得到.【详解】根据图e的主视图被直线l从中间分成两个等腰直角三角形可得:图e是由图b绕直线l旋转一周得到.故选B.【点睛】本题主要考查面与之间关系,解决本题的关键要熟练掌握面与体之间关系.5．B【解析】【分析】根据各种几何体的展开图进行分析即可.【详解】A.是长方形；B.是扇形；C.是长方形；D.是多边形.故选：B【点睛】本题考核知识点：几何体的展开图.解题关键点：熟悉常见几何体的展开图.6．C【解析】由三视图可知：该几何体为横放的圆柱．故选：A．7．D【解析】根据截面的定义以及特性即可对各选项进行分析,从而得到答案.【详解】如果用平面去截圆锥，平面过圆锥顶点时得到的截面图形是一个三角形；如果不过顶点，且平面与底面平行，那么得到的截面就是一个圆；如果不与底面平行得到的就是一个椭圆或半椭圆．故①②③④均正确．故选：D【点睛】本题考查几何体的截面，关键要理解面与面相交得到线，注意：截面的形状既与被截的几何体有关，还与截面的角度和方向有关．8．C【解析】【分析】根据俯视图的概念可知, 只需找到从上面看所得到的图形即可.【详解】解: 从上面看易得: 有2列小正方形, 第1列有2个正方形, 第2列有2个正方形，故选C. 【点睛】考查下三视图的概念; 主视图、左视图、俯视图是分别从物体正面、左面和上面看所得到的图形;9．棱【解析】分析：正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．详解：正方体的表面展开图中，相对的面一定隔着一个正方形.“设”与“丹”是相对面，“生”与“态”是相对面，“建”与“棱”是相对面。

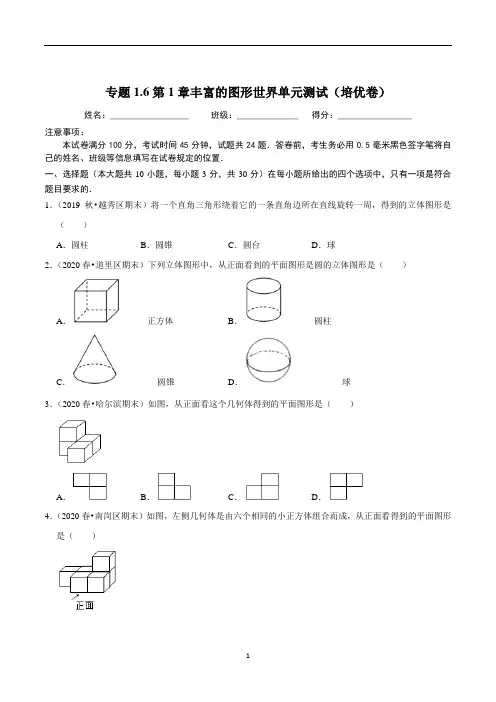
专题1.6第1章丰富的图形世界单元测试（培优卷）姓名：__________________ 班级：______________ 得分：_________________注意事项：本试卷满分100分，考试时间45分钟，试题共24题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2019秋•越秀区期末）将一个直角三角形绕着它的一条直角边所在直线旋转一周，得到的立体图形是（）A．圆柱B．圆锥C．圆台D．球2．（2020春•道里区期末）下列立体图形中，从正面看到的平面图形是圆的立体图形是（）A．正方体B．圆柱C．圆锥D．球3．（2020春•哈尔滨期末）如图，从正面看这个几何体得到的平面图形是（）A．B．C．D．4．（2020春•南岗区期末）如图，左侧几何体是由六个相同的小正方体组合而成，从正面看得到的平面图形是（）A．B．C．D．5．（2019秋•彭水县期末）如图所示的几何体，从上往下看得到的平面图是（）A．B．C．D．6．（2019秋•邗江区校级期末）已知某多面体的平面展开图如图所示，其中是棱锥的有（）A．1个B．2个C．3个D．4个7．（2020春•绥棱县期末）把一支新的圆柱形铅笔削出笔尖，笔尖（圆锥部分）的体积是削去部分的（）A．B．C．D．2倍8．（2019秋•九龙坡区校级期末）把50个同样大小的立方体木块堆砌成如图所示的形状，现在从前、后、左右和上面五个方向朝这堆木块喷漆，则有（）块完全喷不到漆．A．5 B．7 C．17 D．229．（2020春•南岗区期末）下列平面图形中，经过折叠不能围成正方体的是（）A．B．C．D．10．（2019秋•密云区期末）一个正方体的六个面分别标有六个不同的点数，其展开图如图所示，则该正方体可能是（）A．B．C．D．二、填空题（本大题共10小题，每小题3分，共30分）请把答案直接填写在横线上11．（2019秋•崇川区校级期末）如图是一个立体图形的平面展开图，则这个立体图形是．12．（2019秋•青岛期末）如图（1），在边长为acm的正方形纸片的四个角各剪去一个同样大小的正方形，折成一个如图（2）所示的无盖的长方体．设剪去的小正方形的边长为4cm，则这样折成的无盖长方体的容积是cm3．13．（2019秋•渠县期末）如图，是由一些相同的小正方体搭成的几何体从三个方向看到的图形，搭成这个几何体的小正方体的个数是．14．（2019秋•望花区期末）“横看成岭侧成峰，远近高低各不同，不识庐山真面目，只缘身在此山中．”这是宋代诗人苏轼的著名诗句（《题西林壁》）．其“横看成岭侧成峰”中所含的数学道理是．15．（2019秋•三明期末）一个几何体由若干个大小相同的小正方体组成，从正面和从上面看到的形状图如图所示，则这个几何体中小正方体的个数最多是．16．（2019秋•辉县市期末）如图，由十个小正方体组成的几何体中，若每个小正方体的棱长都是2，则该几何体的主视图和左视图的面积之和是．17．（2019秋•李沧区期末）用平面去截球体与圆柱，如果得到的截面形状相同，那么截面的形状是．18．（2019秋•松北区期末）将一根长4米的圆柱体木料锯成2段（2段都是圆柱体），表面积增加60平方分米，这根木料的体积是立方分米．19．（2019秋•郑州期末）一个小立方块的六个面分别标有字母A、B、C、D、E、F，从三个不同方向看到的情形如图所示，其中A、B、C、D、E、F分别代表数字﹣2、﹣1、0、1、2、3，则三个小立方块的下底面所标字母代表的数字的和为．20．（2019秋•市北区期末）如图，是由小立方体组合而成的几何体从正面、左面、上面看到的图形，则至少再加个小立方体该几何体可成为一个正方体．三、解答题（本大题共6小题，共60分．解答时应写出文字说明、证明过程或演算步骤）21．（2019秋•邗江区校级期末）图1所示的三棱柱，高为8cm，底面是一个边长为5cm的等边三角形．（1）这个三棱柱有条棱，有个面；（2）图2框中的图形是该三棱柱的一种表面展开图的一部分，请将它补全（一种即可）；（3）要将该三棱柱的表面沿某些棱剪开，展开成一个平面图形，至少需剪开条棱，需剪开棱的棱长的和的最大值为cm．22．（2019秋•行唐县期末）已知下图为一几何体的三视图．（1）写出这个几何体的名称；（2）画出这个几何体的侧面展开图；（3）若主视图的长为8cm，俯视图中圆的半径为3cm，求这个几何体的表面积和体积？（结果保留π）23．（2019秋•大田县期末）已知下图为从正面、左面、上面看到的一个几何体的形状图．（1）写出这个几何体的名称；（2）若从正面看到的长方形的宽为3cm，从上面看到的正方形的边长为8cm，求这个几何体的表面积．24．（2019秋•唐山期末）如图，是由两个长方体组合而成的一个立体图形的主视图和左视图，根据图中所标尺寸（单位：mm）．（1）直接写出上下两个长方体的长、宽、高分别是多少；（2）求这个立体图形的体积．25．（2019秋•乐清市期中）仓库里有以下四种规格数量足够多的长方形、正方形的铁片（尺寸单位：分米）：从中选5块铁片，焊接成一个无盖的长方体（或正方体）铁盒（不浪费材料），甲型盒是由2块规格①、1块规格②和2块规格③焊接而成的铁盒，乙型盒是容积最小的铁盒．（1）甲型盒的容积为：分米3；乙型盒的容积为：分米3；（直接写出答案）（2）现取两个装满水的乙型盒，再将其内部所有的水都倒入一个水平放置的甲型盒，求甲型盒中水的高度是多少分米？26．（2019秋•城固县期中）一个几何体由大小相同的小立方体搭成，从三个方向看到的几何体的形状图如图所示．（1）求A，B，C，D这4个方格位置上的小立方体的个数；（2）这个几何体是由多少块小立方体组成的？。

第一章丰富的图形世界一、选择题（本大题共14个小题，每题2分，共28分，在每个小题的四个选项中只有一项是符合题目要求的）1．（2020·宁夏回族自治区初一期末）下列不是立体图形的是( )A．球B．圆C．圆柱D．圆锥【答案】B【解析】解：由题意得：只有B选项符合题意．故选B．2．（2020·内蒙古自治区初一期末）下边的立体图形是由哪个平面图形绕轴旋转一周得到的（）A．B．C．D．【答案】A【解析】解：A、直角梯形绕轴旋转一周得到圆台，故本选项符合题意；B、半圆绕轴旋转一周得到球，故本选项不符合题意；C、长方形绕轴旋转一周得到圆柱，故本选项不符合题意；D、直角三角形绕轴旋转一周得到圆锥，故本选项不符合题意．故选：A．3．（2020·河南省初一期末）一个几何体的展开图如图所示，则该几何体的顶点有（）A．10个B．8个C．6个D．4个【答案】C【解析】解：观察图可得，这是个上底面、下底面为三角形，侧面有三个正方形的三棱柱的展开图，则该几何体的顶点有6个．故选C．4．（2018·西安市铁一中学初三其他）下列四张正方形硬纸片，剪去阴影部分后，如果沿虚线折叠，可以围成一个封闭的长方体包装盒的是( )A．B．C．D．【答案】C【解析】A、剪去阴影部分后，组成无盖的正方体，故此选项不合题意；B、剪去阴影部分后，无法组成长方体，故此选项不合题意；C、剪去阴影部分后，能组成长方体，故此选项正确；D、剪去阴影部分后，组成无盖的正方体，故此选项不合题意；故选C．5．（2020·河南省初三二模）由5个大小相同的小正方体拼成的几何体如图所示，则下列说法正确的是（）A．主视图的面积最小B．左视图的面积最小C．俯视图的面积最小D．三个视图的面积相等【答案】B【解析】解：如图，该几何体主视图是由4个小正方形组成，左视图是由3个小正方形组成，俯视图是由4个小正方形组成，三种视图面积最小的是左视图．故选B．6．（2020·广东省深圳市蛇口学校初三期末）如图所示的工件，其俯视图是（）A．B．C．D．【答案】B【解析】试题分析：从上边看是一个同心圆，外圆是实线，內圆是虚线，故选B．7．（2020·内蒙古自治区初一期末）将“守初心担使命”六个字分别写在一个正方体的六个面上，这个正方体的表面展开图如图所示，那么在这个正方体中，和“守”相对的字是（）A．心B．担C．使D．命【答案】B【解析】解：这是一个正方体的平面展开图，共有六个面，其中和“守”相对的字是“担”，故选：B．8．（2020·扬州中学教育集团树人学校初三二模）在下面的四个几何体中，左视图与主视图不相同的几何体是( ) A ． B ． C ． D ．【答案】B【解析】A 、正方体的左视图与主视图都是正方形，故A 选项不合题意；B 、长方体的左视图与主视图都是矩形，但是矩形的长宽不一样，故B 选项与题意相符；C 、球的左视图与主视图都是圆，故C 选项不合题意；D 、圆锥左视图与主视图都是等腰三角形，故D 选项不合题意； 故选B ．9．（2020·北京初一期末）如图所示是某一正方体的表面展开图，则该正方体是（ ） A ． B ． C ． D ．【答案】D 【解析】由正方体的平面展形图可知，实心圆和空心圈在相对面，空心圈与黑色三角形的直角边相邻，实心圆与白色三角形的直角边相邻. 故：D10．（2020·河北省初三期末）一个几何体的三视图如图所示，则该几何体的表面积为（ ） A ．4π B ．3π C ．2π+4 D ．3π+4【答案】D【解析】解：观察该几何体的三视图发现其为半个圆柱，半圆柱的直径为2， 表面积有四个面组成：两个半圆，一个侧面，还有一个正方形. 故其表面积为： 212π1π12223π42⨯⨯⨯+⨯⨯+⨯=+， 故选D.11．（2019·河北省初三一模）如图为一直棱柱，其底面是三边长为5、12、13的直角三角形．若下列选项中的图形均由三个矩形与两个直角三角形组合而成，且其中一个为如图的直棱柱的展开图，则根据图形中标示的边长与直角记号判断，此展开图为何？（ ）A．B．C．D．【答案】D【解析】解：A选项中，展开图下方的直角三角形的斜边长为12，不合题意；B选项中，展开图上下两个直角三角形中的直角边不能与其它棱完全重合，不合题意；C选项中，展开图下方的直角三角形中的直角边不能与其它棱完全重合，不合题意；D选项中，展开图能折叠成一个三棱柱，符合题意；故选：D．12．（2019·福建省初一期中）如图是一个正方体的表面展开图，若折叠成正方体后相对面上的两个数之和都为5，则x＋y＋z的值为()A．0B．4C．10D．30【答案】B【解析】x与10为对面，y与−2为对面，z与3为对面，∴x＝−5，y＝7，z＝2，∴x＋y＋z＝4．故选：B．13．（2020·山东省初三二模）如图，是由几个大小相同的小立方块所搭几何体的俯视图，其中小正方形中的数字表示在该位置的小立方块的个数，则这个几何体的主视图是（）A．B．C．D．【答案】C【解析】由俯视图知该几何体共2列，其中第1列前一排1个正方形、后1排2个正方形，第2列只有前排2个正方形，所以其主视图为：故选C．14．（2019·湖北省思源实验学校初三）有3块积木，每一块的各面都涂上不同的颜色，3块的涂法完全相同．现把它们摆放成不同的位置（如图）,请你根据图形判断涂成绿色一面的对面涂的颜色是( )A．白B．红C．黄D．黑【答案】C【解析】由第一个图可知绿色和白色、黑色相邻，由第二个图可知绿色和蓝色、红色相邻，由已知可得每一块的各面都涂上不同的颜色，3块的涂法完全相同．根据第三个图可知涂成绿色一面的对面涂的颜色是黄色，故答案选C.二、填空题（本题共4个小题；每个小题3分，共12分，把正确答案填在横线上）15．（2020·广东省初三一模）在正方体的截面中，最多可以截出___________ 边形．【答案】六【解析】用平面去截正方体时最多与六个面相交得六边形，最少与三个面相交得三角形，因此最多可以截出六边形，故答案为：六．16．（2019·江西省南昌二中初一期末）如图，某长方体的底面是长为4cm，宽为2cm的长方形，如果从左面看这个长方体时看到的图形面积为6cm2，则这个长方体的体积等于________．【答案】24cm3【解析】解：从左面看这个长方体时看到的图形面积为6cm2，所以长方体的高为3cm；依题意得：长方体的体积=2×3×4=24（cm3）．故答案为24cm3.17．（2019·山东省初三二模）如图，正三棱柱的底面周长为9，截去一个底面周长为3的正三棱柱，所得几何体的俯视图的周长是____．【答案】8【解析】根据从上边看得到的图形是俯视图，可知从上边看是一个梯形：上底是1，下底是3，两腰是2，周长是1+2+2+3=8，故答案为8．18．（2018·江苏省南师附中新城初中初一月考）图(1)是一个水平摆放的小正方体木块，图(2)、(3)是由这样的小正方体木块叠放而成，按照这样的规律继续叠放下去，第六个叠放的图形中，小正方体木块总数应是_____．【答案】66【解析】解：根据题意可得知：图(1)中有1×1＝1个小正方体；图(2)中有1×2+4×1＝6个小正方体；图(3)中有1×3+4×2+4×1＝15个小正方体；以此类推第六个叠放的图形中，小正方体木块总数应是1×6+4×5+4×4+4×3+4×2+4×1＝66个．故答案为66．三、解答题（本题共8道题，19-21每题6分，22-25每题8分，26题10分，满分60分）19．（2020·安徽省初一期末）如图四个几何体分别是三棱柱，四棱柱，五棱柱和六棱柱，三棱柱有5个面，9条棱，6个顶点，观察图形，填写下面的空．（1）四棱柱有个面，条棱，个顶点；（2）六棱柱有个面，条棱，个顶点；（3）由此猜想n棱柱有个面，条棱，个顶点．【答案】（1）6，12，8；（2）8，18，12；（3）（n+2），3n，2n．【解析】解：（1）四棱柱有6个面，12条棱，8个顶点；（2）六棱柱有8个面，18条棱，12个顶点；（3）由此猜想n棱柱有（n+2）个面，3n条棱，2n个顶点．故答案为（1）6，12，8；（2）8，18，12；（3）20．（2017·全国初一单元测试）小明和小彬观察同一个物体，从俯视图看都是一个等腰梯形，但小明所看到的主视图如图（1）所示，小彬看到的主视图如图（2）所示．你知道这是一个什么样的物体？小明和小彬分别是从哪个方向观察它的？【答案】见解析【解析】解：底面为等腰梯形的四棱柱（如图所示）．小明是从前面观察的，而小彬则是从后面观察的（答案不惟一）．21．（2018·辽宁省初一单元测试）如图所示的正方体被竖直截去了一部分，求被截去的那一部分的体积．(棱柱的体积等于底面积乘以高)【答案】5 cm3.【解析】：解：如图所示：根据题意可知被截取的一部分为一个直三棱柱，三棱柱的体积V＝12×(5－4)×(5－3)×5＝5(cm3)．答：被截去的那一部分体积为5 cm3．点睛：本题主要考查的是截几何体，判断出被截取的几何体的形状是解题的关键．22．（2019·甘肃省初一期中）小毅设计了某个产品的包装盒(如图所示)，由于粗心少设计了其中一部分，请你把它补上，使其成为一个两面均有盖的正方体盒子．(1)共有________种添补的方法；(2)任意画出一种成功的设计图．【答案】(1)4；(2)答案不唯一，见解析．【解析】（1）共有4种弥补方法；（2）如图所示：23．（2020·甘肃省初一期末）如图所示，已知直角三角形纸板ABC，直角边AB=4 cm,BC=8 cm.（1）将直角三角形纸板ABC绕三角形的边所在的直线旋转一周，能得到_____种不同的几何体；（2）分别计算绕三角形直角边所在的直线旋转一周，得到几何体的体积.（ 取3）【答案】（1）3；（2）①得到几何体的体积为256cm3或128cm3.【解析】解：（1）3；（2）①当绕三角形直角边AB所在的直线旋转一周时，得到几何体的体积为13×π×82×4=256（cm3）；②当绕三角形直角边BC所在的直线旋转一周时，得到几何体的体积为13×π×42×8=128（cm3）．24．（2018·河南省初一期中）如图所示是长方体的平面展开图．(1)将平面展开图折叠成一个长方体，与字母N重合的点有哪几个？(2)若AG＝CK＝14 cm，FG＝2 cm，LK＝5 cm，则该长方体的表面积和体积分别是多少？【答案】(1)与点N重合的点有H，J两个；(2)146cm2，90cm3．【解析】解：(1)与点N重合的点有H，J两个．(2)∵AG＝CK＝14cm，LK＝5cm，∴CL＝CK－LK＝14－5＝9(cm)，∴长方体的表面积为2×(9×5＋2×5＋2×9)＝146(cm2)，长方体的体积为5×9×2＝90(cm3)．25．（2019·山东省牡丹区二十二中初一月考）仔细观察下面的正四面体、正六面体、正八面体，解决下列问题：⑴填空：①正四面体的顶点数V＝，面数F＝，棱数E＝.②正六面体的顶点数V＝，面数F＝，棱数E＝.③正八面体的顶点数V＝，面数F＝，棱数E＝.⑵若将多面体的顶点数用V表示，面数用F表示，棱数用E表示，则V、F、E之间的数量关系可用一个公式来表示，这就是著名的欧拉公式，请写出欧拉公式：⑶如果一个多面体的棱数为30，顶点数为20，那么它有多少个面？【答案】⑴①4，4，6；②8，6，12；③6，8，12；⑵V+F-E=2;⑶它有12个面.【解析】解：⑴①4，4，6；②8，6，12；③6，8，12；⑵V+F-E=2⑶解：设面数为F，则20+F-30=2解得F=12答：它有12个面.26．（2019·临泽县教育体育和科学技术局初一月考）小明在学习了《展开与折叠》这一课后，明白了很多几何体都能展开成平面图形．于是他在家用剪刀展开了一个长方体纸盒，可是一不小心多剪了一条棱，把纸盒剪成了两部分，即图中的①和②．根据你所学的知识，回答下列问题：（1）小明总共剪开了______条棱．（2）现在小明想将剪断的②重新粘贴到①上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，你认为他应该将剪断的纸条粘贴到①中的什么位置？请你帮助小明在①上补全．（3）小明说：他所剪的所有棱中，最长的一条棱是最短的一条棱的5倍．现在已知这个长方体纸盒的底面是一个正方形，并且这个长方体纸盒所有棱长的和是880cm，求这个长方体纸盒的体积．【答案】（1）8；（2）答案见解析：（3）200000立方厘米【解析】解：（1）小明共剪了8条棱，故答案为8．（2）如图，四种情况．（3）∵长方体纸盒的底面是一个正方形，∴设最短的棱长高为acm，则长与宽相等为5acm，∵长方体纸盒所有棱长的和是880cm，∴4（a+5a+5a）=880，解得a=20cm，∴这个长方体纸盒的体积为：20×100×100=200000cm3．。

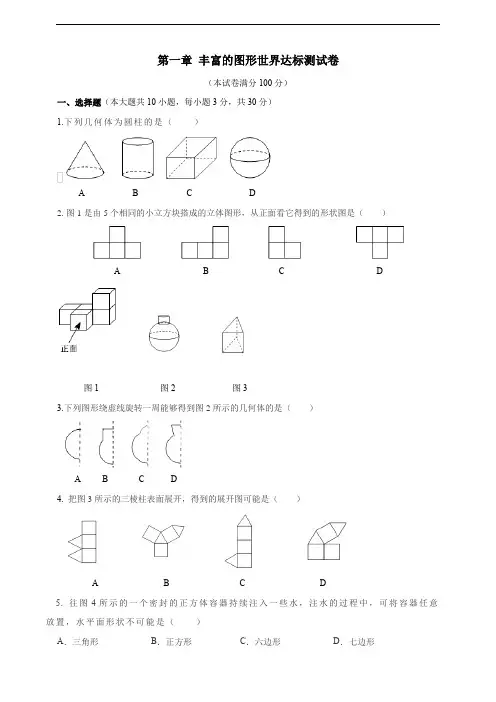
第一章丰富的图形世界达标测试卷（本试卷满分100分）一、选择题（本大题共10小题，每小题3分，共30分）1.下列几何体为圆柱的是（）A B C D2.图1是由5个相同的小立方块搭成的立体图形，从正面看它得到的形状图是（）A B C D图1 图2 图33.下列图形绕虚线旋转一周能够得到图2所示的几何体的是（）A B C D4. 把图3所示的三棱柱表面展开，得到的展开图可能是（）A B C D5. 往图4所示的一个密封的正方体容器持续注入一些水，注水的过程中，可将容器任意放置，水平面形状不可能是（）A．三角形B．正方形C．六边形D．七边形图4 图5 图66. 一个正方体的每个面上都有一个汉字，其展开图如图5所示，那么在该正方体中与“绿”字所在面的相对面上的汉字是（）A．低B．碳C．发D．展7. 图6是由一些大小相同的小立方块搭成的几何体从上面看到的形状图，其中小正方形中的数字表示该位置小立方块的个数，则该几何体从左面看到的形状图是（）A B C D8.下列说法错误的是（）A．若直棱柱的底面边长相等，则它的各个侧面的面积相等B．正九棱柱有9条侧棱，9个侧面，侧面为长方形C．长方体、正方体都是棱柱D．若一个棱柱有12个顶点，则这个棱柱的底面是八边形9. 已知一个不透明的正方体的六个面上分别写着1~6六个数字，如图7是我们能看到的三种情况，请你判断数字4对面上的数字是（）A．6 B．3 C．2 D．1图7图810. 将图8所示的无盖正方体沿①、②、③、④边剪开后展开，则下列展开图的示意图正确的是（）A B C D二、填空题（本大题共6小题，每小题3分，共18分）11. 用一个平面去截一个球，无论怎样切截，截面形状都是_______.12. 粉刷墙壁时，粉刷工人用滚筒在墙上刷过几次后，墙壁马上换上了“新装”，这个现象用数学知识解释为______________.13. 如图9所示的几何体是由________个面围成，面与面相交成________条线，其中直的线有________条，曲线有________条.图9 图1014. 图10是由4个相同的棱长为1的小正方体组成的几何体，则从上面看它的平面图形的面积是______.15. 如图11是一些几何体的展开图，它们的几何体的名称从左到右依次是______________.图11 图1216.一个立体图形由若干个完全相同的小立方块搭成，如图12是分别从正面、左面、上面看这个立体图形得到的形状图．这个立体图形由 _____________个小立方块搭成．三、解答题（本大题共6小题，共52分）17.（6分）如图13所示是一个正六棱柱.（1）填写下表：（2）若该正六棱柱所有侧棱长的和为72 cm，底面的边长为5 cm，求该正六棱柱的所有侧面的面积和.图1318.（8分）如图14，小明同学在制作正方体模型的时候，在方格纸上画出几个小正方形（图中的阴影部分），但是由于疏忽少画了一个，请你给他补画一个，使之可以折叠成正方体，请你把所有的画法都补上，在图上用阴影注明.图14 备用图19.（8分）小明用一个平面去截图15所示的几何体.（1）写出几何体截面形状的名称，①__________，②___________，③___________.（2）除了上述三个截面形状外，还有其他互不相同的截面形状吗? 请分别再写出一个.图1520.（8分）如图16是一张长方形纸片，AB长为4 cm，BC长为6 cm.若将此长方形纸片绕它的一边所在直线旋转一周，（1）得到的几何体是__________；这个现象用数学知识解释为 ______________；（2）若将这个长方形纸片绕它的一边所在直线旋转一周，求形成的几何体的体积．（结果保留π）图16②①③21. （10分）图17是由棱长都为2 cm的6个小立方块搭成的简单几何体．图17（1）请在下面的方格中画出该几何体从三个方向看到的形状图；从正面看从左面看从上面看（2）根据形状图求简单几何体的表面积；（3）如果在这个几何体上再添加一些小立方块，并保持从正面和左面看到的形状图不变，那么最多可以再添加_________个小立方块.22.（12分）现有如图18所示的长方体，长、宽、高分别为4，3，6．图18（1）若将它的表面沿某些棱剪开，展开成一个平面图形，则下列图形中，可能是该长方体的展开图的是 _______．（填序号）（2）图A，B分别是图18所示的长方体的两种表面展开图，求得图A的外围周长为52，请你求出图B的外围周长．（3）图18所示的长方体的表面展开图还有不少，聪明的你能画出一个使外围周长最大的表面展开图吗？请画出这个展开图，并求出它的外围周长．附加题（20分，不计入总分）一个几何体是由若干个棱长为3 cm的小立方块搭成的，从左面、上面看到的几何体的形状图如图所示.（1）该几何体最少由________个小立方块搭成，最多由________个小立方块搭成.（2）当该几何体用最多的小立方块搭成时，将该几何体的形状固定好.①求该几何体的体积；①若将该几何体表面涂上油漆，求所涂的油漆面积.（山西左丁政）第一章丰富的图形世界达标测试卷参考答案答案速览一、1. B 2. C 3. B 4. B 5. D 6. C 7. B 8. D 9. B 10. A二、11. 圆12. 线动成面13. 4 6 4 214. 3 15. 圆锥圆柱16. 9三、解答题见“答案详解”答案详解三、17. 解：（1）填表如下：（2）该正六棱柱的所有侧面的面积的和为（72÷6）×5×6=360（cm2）.18. 解：如图1所示.图119.解：（1）圆长方形梯形（2）有，不唯一，如：还有三角形，椭圆，拱形门，如图2所示.图2几何体顶点数棱数面数正六棱柱___12_____18_______8____三角形拱形门椭圆20. 解：（1）圆柱面动成体（2）分两种情况：①绕AB所在直线旋转一周：V=π×62×4=144π（cm3）；②绕BC所在直线旋转一周：V=π×42×6=96π（cm3）．所以形成的几何体的体积是144π cm3或96π cm3．21. 解：（1）如图3所示.从正面看从左面看从上面看图3（2）简单几何体的表面积为2×（5+3+4）×2×2=96（cm2）.（3）222. 解：（1）①②③（2）图B的外围周长为4×6+4×4+6×3=58.（3）外围周长最大的表面展开图如图4所示，外围周长为8×6+4×4+3×2=70.图4附加题：解：（1）观察图形可知，最少的情形有2+3+1+1+1+1=9（个）小立方块，最多的情形有2+3+3+3+3+1=14（个）小立方块（如图所示）.（2）①该几何体的体积为33×14=378（cm3）.①露在外面的面有2×[6+6+（9+2）]=46（个），所涂的油漆面积为36×9=414（cm2）.。

北师大版七年级上册数学第一章丰富的图形世界含答案一、单选题(共15题，共计45分)1、如图，由3个大小相同的正方体搭成的几何体，其主视图是（）A. B. C. D.2、图1所示的几何体，它的俯视图为图2，则这个几何体的左视图是（）A. B. C. D.3、用平面去截下列几何体，截面的形状不可能是圆的几何体是（）A.球B.圆锥C.圆柱D.正方体4、如图，已知几何体由5个相同的小正方体组成，那么它的主视图是（）A. B. C. D.5、如图是由六个相同的小正方体组成的立方体图形，它的俯视图是（）A. B. C. D.6、下列图形不是正方体的展开图的是（）A. B. C.D.7、将两个长方体如图放置，则所构成的几何体的左视图可能是（）A. B. C. D.8、如图所示的正方体的展开图是（）A. B. C. D.9、如图是一个正方体的表面展开图，则原正方体中与“我”字所在的面相对的面上标的字是（）A.爱B.的C.学D.美10、下列图形中不是正方体的平面展开图的是（）A. B. C. D.11、如图，一个长、宽、高分别为4cm、 3cm、 12cm的长方体盒子能容下的最长木棒长为( )A. cmB.12cmC.13cmD.14cm12、下图是由6个完全相同的小正方体组成的几何体，其俯视图为（）A. B. C. D.13、从图1的正方体上截去一个三棱锥后，得到如图2所示的几何体，则这个几何体的主视图是（）A. B. C. D.14、以下各图均由彼此连接的六个小正方形纸片组成,其中不能折叠成一个正方体的是( )A. B. C. D.15、下列四个立体图形中，它们各自的三视图有两个相同，而另一个不同的是（）A.①②B.②③C.②④D.③④二、填空题(共10题，共计30分)16、在一快递仓库里堆放着若干个相同的正方体快递件，管理员从正面看和从左面看这堆快递如图所示，则这正方体快递件最多有________件.17、如图是某几何体的三视图，根据图中数据，求得该几何体的体积为________．18、如图，是某立体图形的三视图，则这个立体图形的侧面展开图的面积是________．（结果保留π）19、如图是一个小正方体的展开图，把展开图折叠成正方体后，“诚”字的一面相对面上的字是________20、如图，下面两个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色，那么黄色的对面是________．21、如图，长方体的底面边长分别为1cm和3cm，高为6cm．如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要________．22、如图，已知△ABC中BC=3cm，AC=4cm，AB=5cm，将△ABC绕AC旋转一周得到的几何体的侧面积为________．23、如图，直三棱柱ABC﹣A1B1C1的底面为正三角形，且主视图是边长为4的正方形，则此直三棱柱左视图的面积为________24、一个正方体的表面展开图如图所示，把它折叠成正方体后，和“我”字相对的字是________.25、如图是按1：10的比例画出的一个几何体的三视图，则该几何体的侧面积是________.三、解答题(共5题，共计25分)26、已知有一个长为5cm，宽为3cm的长方形，若以这个长方形的一边所在的直线为轴，将它旋转一周，你能求出所得的几何体的表面积吗？27、如图，各图中的阴影图形绕着直线I旋转360°，各能形成怎样的立体图形?28、一次课外活动中，小东用小刀将一个泥塑正方体一刀切下去，请你猜猜看他切下的多面体可能是哪些柱体或锥体？29、如图，将下列图形与对应的图形名称用线连接起来：30、如图是某种几何体的三视图，（1）这个几何体是；（2）若从正面看时，长方形的宽为10m，高为20m，试求此几何体的表面积是多少m2？（结果用π表示）．参考答案一、单选题(共15题，共计45分)1、C2、D3、D4、C5、B6、B7、C8、D9、D10、C12、B13、D14、D15、D二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、27、28、30、。

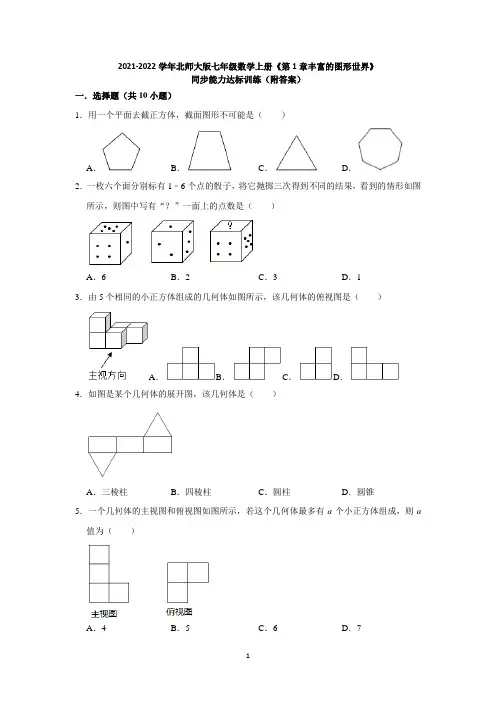
2021-2022学年北师大版七年级数学上册《第1章丰富的图形世界》同步能力达标训练（附答案）一．选择题（共10小题）1．用一个平面去截正方体，截面图形不可能是（）A．B．C．D．2．一枚六个面分别标有1﹣6个点的骰子，将它抛掷三次得到不同的结果，看到的情形如图所示，则图中写有“？”一面上的点数是（）A．6B．2C．3D．13．由5个相同的小正方体组成的几何体如图所示，该几何体的俯视图是（）A．B．C．D．4．如图是某个几何体的展开图，该几何体是（）A．三棱柱B．四棱柱C．圆柱D．圆锥5．一个几何体的主视图和俯视图如图所示，若这个几何体最多有a个小正方体组成，则a 值为（）A．4B．5C．6D．76．下列图形中不能作为正方体的展开图的是（）A．B．C．D．7．一个几何体由大小相同的小立方块搭成，从上面看到的几何体的形状如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，则从正面看到的这个几何体的形状图是（）A．B．C．D．8．如图，粮仓可以近似地看作由圆锥和圆柱组成，其主视图是（）A．B．C．D．9．如图是一个正方体的展开图，把展开图折叠成小正方体后，和“建”字所在面相对的面上的字是（）A．跟B．百C．走D．年10．如图，用一个平面去截正方体，则截面图形是（）A．B．C．D．二．填空题（共7小题）11．一个长方形长为4厘米，宽为2厘米，以它的长边为轴，把长方形转一周后，得到一个体，这个立体图形的体积是立方厘米．（结果中保留π）12．如图，将一个正方体截去一个角变成一个多面体，则这个多面体有个顶点．13．小张外出游玩时买了四盒同样的长方体的礼品（如图），长、宽、高分别为5cm，4cm，3cm，小张想把它们包装成一个大长方体，并使包装表面积最小，则表面积的最小值为cm2．14．如图，是由几个边长为1的小立方体所组成的几何体的俯视图，小正方形中的数字表示在该位置的小正方体的个数，则这个几何体的表面积为．15．如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图，若组成这个几何体的小正方体的块数为n，则n的最小值与最大值的和为．16．已知一个几何体从三个不同方向看到的图形如图所示，则这个几何体是．17．用一个平面从不同的方向去截一个几何体，所截出的面会出现如图所示的三种形式，则该几何体可能是．三．解答题（共4小题）18．如图，是由6个大小相同的小立方体块搭建的几何体，其中每个小正方体的棱长为1厘米．（1）直接写出这个几何体的表面积（包括底部）：；（2）请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图．19．用小立方块搭一个几何体，使它的从正面和从上面看到的这个几何体的形状图如图所示，从上面看到的形状图中的小正方形中的字母表示该位置小立方块的个数，试回答下列问题；（1）x、z各表示多少？（2）y可能是多少？这个几何体最少由几个小立块搭成？最多呢？20．如图，是用塑料薄膜覆盖的蔬菜大棚，长15米，横截面是一个直径2米的半圆．（1）这个大棚的种植面积是多少平方米？（2）覆盖在这个大棚上的塑料薄膜约有多少平方米？（3）大棚内的空间约有多大？21．小明将一个底面为正方形，高为n的无盖纸盒展开，如图（a）所示．（1）请你计算图（a）所示的无盖纸盒的表面展开图的面积S1；（2）将阴影部分剪拼成一个长方形，如图（b）所示，请你计算该长方形的面积S2．（3）比较（1）（2）的结果，你得出什么结论？参考答案一．选择题（共10小题）1．解：正方体有六个面，用平面去截正方体时最多与六个面相交得六边形，最少与三个面相交得三角形．因此不可能是七边形，故选：D．2．解：根据图形可知，与点数1相邻的面的点数有2、3、4、5，∴点数1与6是相对面，对比第一个和第三个图，可知写有“？”的面与点数1是相对面，故写有“？”一面上的点数是6．故选：A．3．解：从上边看第一列是一个小正方形，第二列是两个小正方形且第一个小正方形位于第一层，第三列是一个小正方形，且位于第二层，故B选项符合题意，故选：B．4．解：从展开图可知，该几何体有五个面，两个三角形的底面，三个长方形的侧面，因此该几何体是三棱柱，故选：A．5．解：结合主视图和俯视图可知，左边后排最多有3个，左边前排最多有3个，右边只有一层，且只有1个，所以图中的小正方体最多7块，结合主视图和俯视图可知，左边后排最少有1个，左边前排最多有3个，右边只有一层，且只有1个，所以图中的小正方体最少5块，所以a＝7，故选：D．6．解：正方体展开图的11种情况可分为“1﹣4﹣1型”6种，“2﹣3﹣1型”3种，“2﹣2﹣2型”1种，“3﹣3型”1种，因此选项A符合题意，故选：A．7．解：根据所给出的图形和数字可得：主视图有4列，每列小正方形数目分别为1，2，3，2，则符合题意的是故选：C．8．解：粮仓主视图上部视图为等腰三角形，下部视图为矩形．故选：A．9．解：正方体的表面展开图，相对的面之间一定相隔一个正方形，和“建”字所在面相对的面上的字是“百”．故选：B．10．解：如图所示，截面与正方体的三个面相交，则截面为三角形．故选：A．二．填空题（共7小题）11．解：V＝πr2hV＝π×22×4V＝16π（立方厘米）．答：一个长方形长为4厘米，宽为2厘米，以它的长边为轴，把长方形转一周后，得到一个圆柱体，这个立体图形的体积是16π立方厘米．故答案为：圆柱，16π．12．解：正方体有8个顶点，将这个正方体按照如图所示的方式截去一个角后，所得到的多面体的顶点数为8﹣1+3＝10，故答案为：10．13．解：如图，2×（5×6+5×8+6×8）＝236（cm2）答：2个叠在一起（4×5），然后并起来（5×6），包装表面积最小，表面积的最小值为236cm2．故答案为：236．14．解：这个几何体的主视图有三列，从左到右分别是3，4，1，左视图有三列，从左到右分别是3，4，2，表面积为：（8+9+6）×2＝46，故答案为：46．15．解：根据主视图、俯视图，可以得出最少时、最多时，在俯视图的相应位置上所摆放的个数如下：最少时需要10个，最多时需要16个，因此n＝10+16＝26，故答案为：26．16．解：观察三视图可知，这个几何体是圆锥．故答案为圆锥．17．解：平面平行圆柱底面截圆柱可以得到一个圆；平面竖截不经过圆锥的顶点得到得到图②；平面竖截经过圆锥的顶点得到三角形．故该几何体可能是圆锥．故答案为：圆锥．三．解答题（共4小题）18．解：（1）（5+4+4）×2＝26（cm2），故答案为：26cm2；（2）根据三视图的画法，画出相应的图形如下：19．解：（1）由图可知x＝3，z＝1；（2）y＝1或2；最少由3+2+2+1+1+1+1＝11块搭成；最多由3+2+2+2+1+1+1＝12块搭成．20．解：（1）15×2＝30（m2），答：这个大棚的种植面积是30m2；（2）π×2××15+π×（）2＝16π（m2），答：覆盖的薄膜约有16πm2；（3）π×12×15＝（m3），答：大棚内的空间约有m3．21．解：（1）无盖纸盒的表面展开图的面积S1＝（3m）2﹣4n2＝9m2﹣4n2；（2）长方形的长是：3m+2n，宽是：3m﹣2n，∴长方形的面积S2＝（3m+2n）（3m﹣2n）；（3）由题可得，9m2﹣4n2＝（3m+2n）（3m﹣2n）．。

第一章《丰富的图形世界》检测卷时间:60分钟满分:100分一、选择题(本大题共8小题,每题3分,共24分)1.下列图形中,柱体的个数是()A.1B.2C.3D.42.下列说法正确的是()A.棱柱的每条棱长都相等B.棱柱侧面的形状可能是一个三角形C.长方体的截面形状一定是长方形D.若三棱柱的底面边长相等,则各个侧面的面积相等3.将三角形绕虚线旋转一周,可以得到如图所示的立体图形的是()A B C D4.如图所示的几何体是由7个小立方块堆积而成,某同学画出了从三个方向看到的形状图,在这三个形状图中正确的是()A.①②B.②③C.①③D.①②③5.用一个平面去截棱柱、圆锥、棱锥,相同的截面形状是()A.三角形B.圆C.长方形D.无法确定6.要制作一个正方体模型,且六个面上写着六个数,若相对的两个面上的数的乘积都等于24,则下列展开图中,可行的是()A BC D7.由若干个完全相同的小立方块搭成的一个几何体,这个几何体从左面和上面看到的形状图如图所示,则小立方块的个数不可能是()A.5B.6C.7D.88.如图是由12个棱长为1的小立方块组合而成的几何体,则其从正面、左面和上面所看到的形状图中面积最大的是()A.从正面看到的形状图B.从左面看到的形状图C.从上面看到的形状图D.无法判断二、填空题(本大题共6小题,每题3分,共18分)9.在朱自清的《春》中有描写春雨“像牛毛,像花针,像细丝,密密地斜织着”的语句,这里把雨看成了线,这说明. 10.如图是正方体的表面展开图,“我”字的相对面上的字是.11.用一个平面分别截六棱柱、长方体、圆柱、圆锥,得到的截面不可能为四边形的几何体是.12.若要把一个正方体的表面剪开并展成如图所示的平面图形,则需要剪开条棱.第12题图第13题图13.如图是由一些小立方块搭成的几何体从正面和左面看到的形状图,则搭建该几何体最多需要个小立方块.14.用八个大小相同的小立方块粘成一个大立方体如图1所示,得到的几何体从三个方向看到的形状图如图2所示.若小明从八个小立方块中取走若干个,剩余的小立方块保持原位置不动,并使得到的新几何体从三个方向看到的形状图仍是图2,则他取走的小立方块最多可以是个.图1图2三、解答题(本大题共6小题,共58分)15.(6分)如图所示是一个几何体,画出从正面、左面、上面看到的该几何体的形状图.16.(10分)如图是一个长为4 cm,宽为3 cm的长方形纸片.图1图2(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是,这能说明的事实是;(2)求当此长方形纸片绕长边所在直线旋转一周时(如图1),所形成的几何体的体积;(3)求当此长方形纸片绕短边所在直线旋转一周时(如图2),所形成的几何体的体积.17.(10分)有一种牛奶包装盒及其尺寸如图1所示.为了生产这种包装盒,需要先画出展开图纸样.图1图2(1)如图2所示,给出3种纸样甲、乙、丙,在甲、乙、丙中,正确的是;(2)从已知正确的纸样中选出一种,在图上标注上尺寸;(3)利用你所选的一种纸样,求出包装盒的表面积.18.(10分)设棱锥的顶点数为V,面数为F,棱数为E.(1)观察与发现:如图,三棱锥中,V3= ,F3= ,E3= ;五棱锥中,V5= ,F5= ,E5= .(2)猜想:①十棱锥中,V10= ,F10= ,E10= ;②N棱锥中,V n= ,F n= ,E n= .(用含有n的式子表示)(3)探究:①棱锥的顶点数(V)与面数(F)之间的等量关系:;②棱锥的顶点数(V)、面数(F)、棱数(E)之间的等量关系:.(4)拓展:棱柱的顶点数(V)、面数(F)、棱数(E)之间是否也存在某种等量关系?若存在,试写出相应的等式;若不存在,请说明理由.19.(10分)用小立方块搭一个几何体,使得它从正面和上面看到的形状图如图所示,则搭这个几何体最少要多少个小立方块?并画出此时该几何体从左面看到的形状图(只需画出一种情况即可).20.(12分)在平整的地面上,由若干个完全相同的棱长为10 cm的小立方块堆成一个几何体,如图所示.(1)这个几何体由多少个小立方块组成?请画出从正面、左面、上面看到的这个几何体的形状图.(2)如果在这个几何体的表面(不包括底面)喷上黄色的漆,则在所有的小立方块中,有多少个只有一个面是黄色?有多少个只有两个面是黄色?有多少个只有三个面是黄色?(3)假设现在你手里还有一些相同的小立方块,保持从左面、上面看到的形状图不变,最多可以再添加几个小立方块?这时如果要重新给这个几何体表面(不包括底面)喷上红色的漆,需要喷漆的面积比原几何体增加了还是减少了?增加或减少的面积是多少?第一章综合能力检测卷题号 1 2 3 4 5 6 7 8答案 C D C B A B A A 9.点动成线10.丽11.圆锥12.7 13.16 14.417. (1)甲、丙(2)如图所示,任选其一即可.(3) 288.18. (1)4 4 6 6 6 10(2)①1111 20 ②n+1n+12n(3)①V=F②V+F-E=2(4)存在,相应的等式为V+F-E=2.19.最少需要12个小立方块.此时该几何体从左面看到的形状图如图所示.20. (1) 10个从正面、左面、上面看到的这个几何体的形状图如图所示.(2)略(3)最多可以再添加4个小立方块.400cm21、盛年不重来，一日难再晨。