浙江大学理论力学考研真题
- 格式:pdf
- 大小:287.47 KB
- 文档页数:5

浙江大学1998 年攻读硕士学位研究生入学考试试题考试科目量子力学第一题:(10 分)(1)写出玻尔-索末菲量子化条件的形式。
(2)求出均匀磁场中作圆周运动的电子轨道的可能半径。
(利用玻尔-索末菲量子化条件r 求,设外磁场强度为B )第二题:(20 分)(1)若一质量为? 的粒子在一维势场V ( x) = ? 级。
(2)若某一时刻加上了形如e sin 为一已知常数)。
? 0, 0 ≤x ≤ a 中运动,求粒子的可能能? ∞, x > a , x < 0 ωx a ,e (1 )的势场,求其基态能级至二级修正(ω?1 2 2 ? ?ωx , x > 0 ,求粒子(质量为? )的可能的能级。
(3)若势能V ( x ) 变成V ( x ) = ? 2 ? ∞, x<0 ? 第三题:(20 分)氢原子处于基态,其波函数形如ψ= ce ? r a ,a 为玻尔半径,c 为归一化系数。
(1)利用归一化条件,求出c 的形式。
(2)设几率密度为P ( r ) ,试求出P ( r ) 的形式,并求出最可几半径r 。
(3)求出势能及动能在基态时的平均值。
? ? (4)用何种定理可把< V > 及< T > 联系起来?第四题:(15 分)?2 ?2 ?2 ? = Lx + Ly + Lz ,转子的轨道角动量量子数是 1 ,一转子,其哈密顿量H 2I x 2I y 2I z ? ? ? (1)试在角动量表象中求出角动量分量Lx ,Ly ,Lz 的形式;? (2)求出H 的本征值。
第五题:(20 分)若基态氢原子处于平行板电场中,电场是按下列形式变化E = ? r ? 0, ? ?ε0 e ? ?t t≤0 η, t >0 ,η为大于零? 的常数,求经过长时间后,氢原子处于2P 态的几率。
设H ′为微扰哈密顿,(( ) ? H′100,210 = 28 aε0 e ?ηt ? ? 5 ?e ;t > 0)H′(当3 2 ( ) 100,21±1 = 0)。

理论力学真题考研理论力学真题考研理论力学是物理学中的一门基础课程,对于考研学子来说,理论力学的真题是必须要重点复习的内容之一。
通过解析理论力学的真题,不仅可以巩固知识,还能提高解题能力和应试技巧。
本文将从动力学、静力学和振动三个方面,对理论力学真题进行分析。
动力学部分是理论力学的重要内容之一,其中包括牛顿第二定律、动量守恒定律等。
在解动力学问题时,需要根据题目给出的条件,通过运用这些定律来求解。
例如,有一道真题是这样的:“一个质点在一根光滑的水平轨道上,开始时速度为v,沿轨道向前运动。
轨道的一端有一弹簧,弹簧的弹性系数为k,未压缩时长为l。
当质点到达弹簧处时,弹簧被压缩了x,求质点到达弹簧最远处的速度。
”通过运用动量守恒定律和弹簧的力学知识,可以得出质点到达弹簧最远处的速度为v'=(m+kx/m)v,其中m为质点的质量。
这道题目考察了考生对动量守恒定律和弹簧力学的理解和应用能力。
静力学是理论力学的另一个重要内容,主要研究物体处于平衡状态时的力学性质。
在解静力学问题时,需要根据物体所受的力和力矩的平衡条件来求解。
例如,有一道真题是这样的:“一个质量为m的物体,静止放在一个斜面上,斜面的倾角为θ,摩擦系数为μ。
求当斜面倾角大于多少时,物体会开始滑动。
”通过分析物体所受的力和力矩,可以得出斜面倾角大于θ=arctan(μ)时,物体会开始滑动。
这道题目考察了考生对力和力矩平衡条件的理解和应用能力。
振动是理论力学中的一个重要分支,主要研究物体在外力作用下的振动规律。
在解振动问题时,需要根据物体的自由度和振动方程来求解。
例如,有一道真题是这样的:“一个弹簧质量为m,劲度系数为k,一端固定在墙上,另一端挂一个质量为M的物体。
求当物体振幅最大时,弹簧的伸长量是多少。
”通过分析弹簧的振动方程和物体的自由度,可以得出弹簧的伸长量为x_max=(M/m)^(1/2)A,其中A为物体的振幅。
这道题目考察了考生对振动方程和自由度的理解和应用能力。


浙江大学1998年攻读硕士学位研究生入学考试试题考试科目量子力学第一题:(10分)写出玻尔-索末菲量子化条件的形式。
求出均匀磁场中作圆周运动的电子轨道的可能半径。
(利用玻尔-索末菲量子化条件求,设外磁场强度为)第二题:(20分)若一质量为的粒子在一维势场中运动,求粒子的可能能级。
若某一时刻加上了形如,()的势场,求其基态能级至二级修正(为一已知常数)。
若势能变成,求粒子(质量为)的可能的能级。
第三题:(20分)氢原子处于基态,其波函数形如,为玻尔半径,为归一化系数。
利用归一化条件,求出的形式。
设几率密度为,试求出的形式,并求出最可几半径。
求出势能及动能在基态时的平均值。
用何种定理可把及联系起来?第四题:(15分)一转子,其哈密顿量,转子的轨道角动量量子数是,试在角动量表象中求出角动量分量,,的形式;求出的本征值。
第五题:(20分)若基态氢原子处于平行板电场中,电场是按下列形式变化,为大于零的常数,求经过长时间后,氢原子处于态的几率。
(设为微扰哈密顿,;(当))。
第六题:(15分)用玻恩近似法,求粒子处于势场,()中散射的微分散射截面。
(设粒子的约化质量为)。
从该问题中,讨论玻恩近似成立的条件。
浙江大学1999年攻读硕士学位研究生入学考试试题考试科目量子力学第一题:(10分)(1)试求出的自由电子及能量为、质量为克的质点的德布罗意波长。
(,)(2)证明一个自由运动的微观粒子对应的德布罗意群速度,即为其运动速度。
第二题:(10分)(1)证明定态中几率流密度与时间无关。
(2)求一维无限深势阱中运动的粒子在第个能级时的几率流密度。
第三题:(15分)(粒子处于一维势阱(取的恒定常量)中运动,(1)画出势能的示意图,设粒子质量为,(2)求解运动粒子的能级。
()(写出所满足的方程)第四题:(10分)一维谐振子,其势能为,(为常量)。
若该谐振子又受一恒力作用,试求其本证能量及能量本证函数。
该振子的质量为。
第五题:(20分)(1)写出线性、厄米算符的定义。

浙江省考研物理试题精选解析一、力学部分1. 选择题1.1 题干:一个质量为m的残疾人坐在轮椅上,轮椅的质量为M,轮椅没有阻力地沿水平地面从静止开始向前滑行,设轮椅的初速度为v0。
在滑行过程中,轮椅上的残疾人将一颗质量为m的小石子水平地抛出,小石子抛出后轮椅的反向移动速度为v1。
求小石子的飞行速度。
1.2 解析:由动量守恒定律,轮椅和残疾人的总动量在抛出小石子之前为零,抛出小石子之后仍为零。
设小石子的飞行速度为v,则有:(m + M)v1 - (m + M)v0 = mv整理得:v = (m + M)(v1 - v0)/(m + M)2. 解答题2.1 题干:一个质量为m的小球以速度v0水平地射向一个质量为M 的静止的小车,小球与小车发生完全非弹性碰撞后,两者以速度v共同向右运动。
求小球和小车共同运动后的速度v。
2.2 解析:由动量守恒定律,小球和小车的动量在碰撞前后守恒。
设碰撞后的速度为v,则有:mv0 = (m + M)v整理得:v = mv0 / (m + M)二、电磁学部分1. 选择题1.1 题干:在一根无限长的直导线中,通有电流I。
离导线的距离为r,导线与距离r处的等效电荷为q。
则q与r的关系式为:A. q ∝ 1/rB. q ∝ rC. q ∝ 1/r^2D. q ∝ r^21.2 解析:根据库仑定律,导线与距离r处的等效电荷与距离r成反比。
因此,答案为A选项。
2. 解答题2.1 题干:一根半径为R的均匀带电球体,总电荷量为Q。
求球体表面处的电场强度。
2.2 解析:根据电场的定义,球体表面处的电场强度E等于球体内一点电荷dq对球面单位面积的贡献。
根据高斯定律,球体内外的电场强度相等。
球体内一点电荷dq对球面单位面积的贡献为dq/(4πR²),球体内的电荷总量为Q,则有:E = kQ/(4πR²)三、光学部分1. 选择题1.1 题干:一个光波从真空中垂直进入介质,入射光线和折射光线的夹角为θ1和θ2。

浙江大学攻读硕士学位硕士入学考试试题 考试科目 量子力学一、(1)写出玻尔-索末菲量子化条件旳形式;(2)求出均匀磁场中作圆周运动旳电子轨道旳也许半径; 二、(1)若一质量为μ旳粒子在势场()0,0,,0x aV x x a x <<⎧=⎨∞≥≤⎩中运动,求粒子旳也许能级;(2)若某一时刻加上了形如sin,(1)xe e aω<<旳势场,求其基态能级至二级修正;(3)若势能()V x 变为()221,02,0x x V x x μω⎧>⎪=⎨⎪∞<⎩求粒子旳也许能级。
三、氢原子处在基态,其波函数形如,race a ψ-=为玻尔半径, (1)运用归一化条件,求出c ;(2)设几率密度为()P r ,试求出()P r 旳形式,并求出最可几半径; (3)求出基态势能及动能在基态中旳平均值 ;(4)用何种定理可把ˆV及ˆT 联络起来? 四、一转子,其哈密顿量222ˆˆˆˆ222y x z x y zL L L HI I I =++,转子旳轨道角动量量子数是1, (1)试在角动量表象中,求出ˆˆˆ,,x y zL L L 旳形式; (2)求出ˆH旳本征值。
五、若基态氢原子处在平行板电场中,电场按下列形式变化00,0,0t t E e t τε-≤⎧⎪=⎨>⎪⎩,τ为不小于零旳常数,求通过长时间后,氢原子处在2P 态旳几率。
(设ˆH'为微扰哈密顿,()()805100,210100,211ˆˆ;03t a e He H τε-±''=⋅=)。
六、(1)用玻恩近似法,求粒子处在势场()()0,0raV x V e a -=->中散射旳微分截面。
(2)从该问题中讨论玻恩近似成立旳条件。
浙江大学1999年攻读硕士学位硕士入学考试试题 考试科目 量子力学一、(1)试求出100eV 旳自由粒子及0.1eV 、质量为1克旳质点旳德布罗意波长。


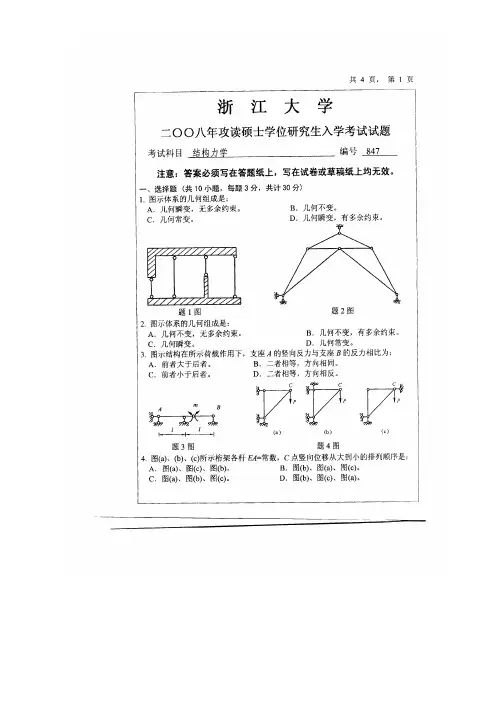
浙江大学 2003-2004 学年第一学期《理论力学》(丙)课程期末考试试卷开课学院:机械与能源工程学院 , 考试时间 120 分钟 考生姓名:学号: 专业:一、是非题(每题 2 分,正确用√,错误用×,填入括号内)1、平面运动刚体的动能等于绕基点转动的动能与随基点平动的动能之和。
()2、经过的时间越长,变力的冲量也一定越大。
()3、一个力不可能分解为力偶,一个力偶也不可能合成为力。
()4、平动刚体上的点的运动轨迹也可能是空间曲线。
()5、惯性力的实质是由于惯性对施力体所产生的反作用力。
( )二、选择题(每题 3 分,请将答案的序号填入划线内)1、已知 F 1 、 F 2 、 F 3 、 F 4 为作用于刚体上的平面汇交力系,其力多边形如图所示,由 此可知①力系可合成一个力偶;②力系可合成为一个力;③力系可简化为一个力和一个力偶;④力系的合力为零,力系平衡。
2、如图所示,物块 A 重 P =100N ,放在与水平面成 30︒ 的粗糙斜面上,块 A 与斜面间 的静摩擦系数为 f=1,则摩擦力的大小为①0②86.6N ③50N ④100N3、刚体做平面运动,在瞬时平动的情况下,则该瞬时① ω =0, ε =0 ② ω ≠ 0, ε ≠ 0③ ω ≠ 0, ε =0 ④ ω =0, ε ≠ 0② ③ 22④ 2 24、一均质等截面杆 AB 重 P ,其 A 端置于光滑水平面上,B 端用绳悬挂,如图所示。
取坐标 O xy ,此时该杆质心 C 的 x 坐标 x c =0,若将绳剪断,则①杆倒向地面的过程中,质心 C 运动轨迹为圆弧;②杆倒向地面后, x c >0;③杆倒向地面后, x c =0;④杆倒向地面后, x c <0。
5、一弹簧常数为 k 的弹簧下挂一质量为 m 的物体,若物体从静平衡位置(设静伸长为 δ )下降 ∆ 距离,则弹簧力所做的功为1 2 ① k ∆ 21 2k (δ + ∆) 2 1 k [(δ + ∆) -δ ] 21 k [δ - (δ + ∆) ] 2三、填空题(每题 6 分,请将答案填入划线内)1、试指出图示机构中哪些构件做平面运动: ;并画出做平面运动构件所 在图示位置速度瞬心的位置。
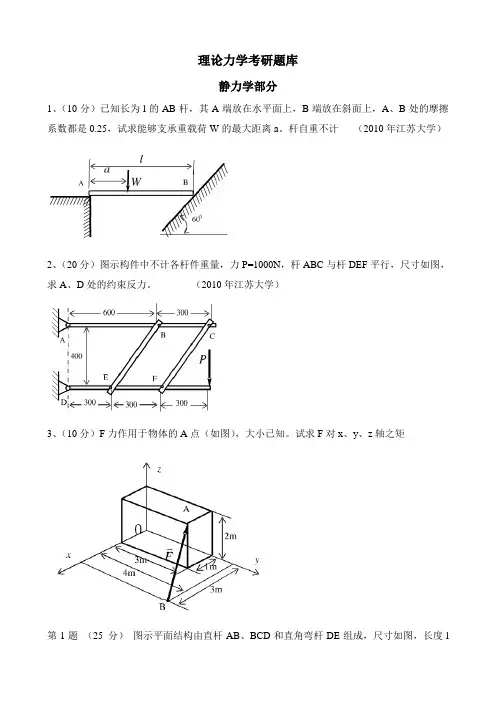
理论力学考研题库静力学部分1、(10分)已知长为l的AB杆,其A端放在水平面上,B端放在斜面上,A、B处的摩擦系数都是0.25,试求能够支承重载荷W的最大距离a。
杆自重不计(2010年江苏大学)2、(20分)图示构件中不计各杆件重量,力P=1000N,杆ABC与杆DEF平行,尺寸如图,求A、D处的约束反力。
(2010年江苏大学)3、(10分)F力作用于物体的A点(如图),大小已知。
试求F对x、y、z轴之矩第1题(25 分)图示平面结构由直杆AB、BCD和直角弯杆DE组成,尺寸如图,长度l为已知。
在杆BCD的CD段受到均布载荷作用,载荷集度为q,在杆AB上作用一力偶矩为M的力偶,且M = 2ql2。
各杆自重及各处摩擦均不计。
试求固定端A和支座E处的约束力。
(南京航空航天大学2011年)第2题(15 分)如图所示,置于光滑的铅垂滑道内的物块A重G1=2kN,轮轴B重G2=6kN,R=2r,其中心作用有大小为3kN的水平拉力FP,轮轴B上绕以细绳,绳的一端作用有水平拉力F,物块A与轮轴B间的静滑动摩擦因数为f1=0.2,轮轴B与地面间的静滑动摩擦因数为f2=0.5,各处滚动摩擦均不计。
求:(1)若水平拉力F=4kN,系统是否平衡?(2)系统保持平衡的水平拉力F的取值范围。
(南京航空航天大学2011年)1,图示受力结构,已知载荷P,AB=2L,BD=DE=a,轮C的半径为r,轮E的尺寸不计,α=60 °;试计算A端的约束反力。
(2008武汉科技大学)1.一无重钢杆在四个力的作用下处于平衡,如下图所示,则F2+F3+F4= 。
2.如图所示平面结构,各杆自重忽略不计,在CD杆上作用一力偶M,已知AE=EB=a,试求A处约束反力的大小。
运动学部分1.圆盘做定轴转动,若某瞬时其边缘上A 、B 、C 三点的速度、加速度如图3所示,则以下哪些点的运动是不可能的。
( ) (2012年华中农业大学)①点A ,B ; ②点A ,C ; ③点B ,C ④点A ,B ,C(2012年华中农业大学)(2011年电子科技大学) 4.如图1-4所示的平面机构,AB= O 1 O 2,l ==B O A O 21,l 4DE =,A O 1绕O 1匀角速度ω转动,连杆DE 的质量均匀分布且大小为M ,根据刚体运动形式的定义,则T 字形刚架ABCD 的运动形式为: 连杆DE 的运动形式为: 。
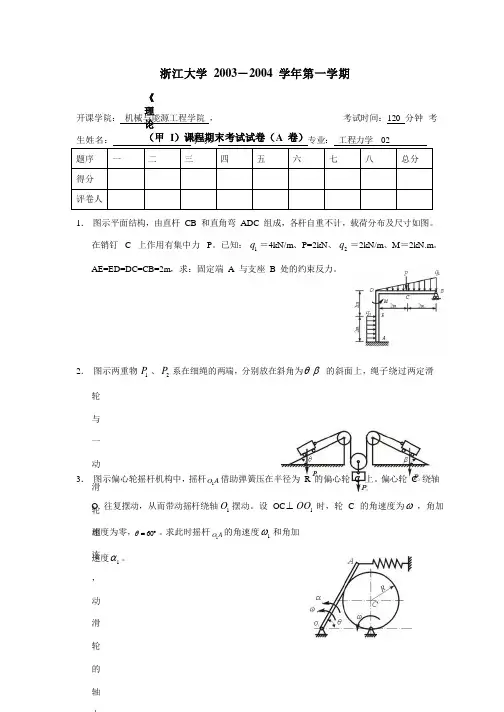
1 1 浙江大学 2003-2004 学年第一学期《理论力学》(甲 I )课程期末考试试卷(A 卷)开课学院: 机械与能源工程学院 , 考试时间:120 分钟 考生姓名:学号:专业: 工程力学 021. 图示平面结构,由直杆 CB 和直角弯 ADC 组成,各杆自重不计,载荷分布及尺寸如图。
在销钉 C 上作用有集中力 P 。
已知: q 1 =4kN/m 、P=2kN 、 q 2 =2kN/m 、M =2kN.m 。
AE=ED=DC=CB=2m ,求:固定端 A 与支座 B 处的约束反力。
2. 图示两重物 P 1 、 P 2 系在细绳的两端,分别放在斜角为θ β 的斜面上,绳子绕过两定滑 轮与一动滑轮相连,动滑轮的轴上挂一重物 P 3 。
如摩擦以及滑车与绳索的质量忽略不计, 试求平衡时 P 1 和 P 2 的值。
(应用虚位原理)3. 图示偏心轮摇杆机构中,摇杆 O A 借助弹簧压在半径为 R 的偏心轮 C 上。
偏心轮 C 绕轴O 往复摆动,从而带动摇杆绕轴 O 1 摆动。
设 OC ⊥ OO 1 时,轮 C 的角速度为 ω ,角加速度为零,θ = 60︒ 。
求此时摇杆速度α1 。
O A 的角速度 ω1 和角加4. 在图示机构中,已知:匀速度 u =1m/s ,AB=L=1m ,轮 B 在固定大圆上作纯滚动,r =30cm ,R =70cm 。
当 ϕ = 45︒ 时,AO 处于铅直位置。
试求该瞬时轮 B 的角速度和角加 速度。
5. 平面机构如图所示,半径为 r 的轮子在水平面上纯滚动,轮缘上 C 点和 CD 杆铰接。
已 知:r =10cm ,CD=L=40cm ,H=30cm , θ = 45︒ 。
在图示位置时,A 、C 、D 三点同处 水平线,DE 铅直;轮子的角速度 ω =2rad/s 、角加速度 α =1rad/ s 2。
试求该瞬时 DE 杆的角速度和角加速度。
2009年浙江理工大学953理论力学考研真题浙江理工大学二00九年硕士学位研究生招生入学考试试题一、判断题(每小题3分,共15分)1.若三力作用于刚体而平衡,则该三力必然汇交于一点。
()2.对物体来说,力可沿着其作用线自由移动而不改变力对物体堵塞效应。
()3.刚体作平行移动时,刚体内所有点的速度、加速度均相等。
()4.刚体作瞬时平移时,其角速度和角加速度均等于零。
()5.质点系内任意两个质点之间的内力所做的功之和等于零。
()二、选择题(每小题4分,共20分)1.系统在某一运动中,作用于系统的所有外力的冲量和与系统在此运动过程中______的方向相同。
A.动量B.力C.动量的改变量D.力的改变量2.重W 的物块自由地放置于倾角为α的斜面上,物块与斜面的摩擦角为m ϕ,若αϕ<m ,则物块在斜面上____________。
A.静止B.滑动C.W 很小时静止D.处于临界状态3.图示系统中,A 点虚位移大小与C 点虚位移大小的比值C Ar r δδ为___________。
A.H L θcos B.θcos H L C.H L θ2cos D.θ2cos LH4.均质细杆OA 长为L ,重为P,在重力作用下可在铅垂平面内摆动,滑块O 质量不计,斜面倾角α,不计各种摩擦,以x 及φ为广义坐标,现对应于广义坐标x 的广义力_____。
A.PB.PL 21C.φsin PL D.-Psin φ5.图示系统仅在直杆OA 与小车接触处的A 点存在摩擦,在保持系统平衡的前提下,逐步增加拉力T,则在此过程中,A 点处的法向反力将__________.A.越来越大B.越来越小C.保持不变D.不能确定三、计算题(共115分)1.图示机构中,A 物块质量kg m A 50=,轮轴B 质量kg m B 100=,A 与轮轴用不可伸长的软绳水平连接,在轮上也绕有细绳,并跨过光滑的滑轮D 吊起重物C,如图所示。
A 与水平面之间的摩擦系数为0.5,轮轴与水平面之间的摩擦系数为0.2,不计滚阻力偶,cm r R 202==,求平衡时重物C 的最大质量。