2007浙江大学硕士研究生入学考试-理论力学试卷

理论力学名校考研真题详解，益星学习网可免费下载题库目录第1章静力学公理和物体的受力分析1.1 重点与难点解析1.2 名校考研真题与期末考试真题详解1.3 名校期末考试真题详解第2章平面会交力系与平面力偶系2.1 重点与难点解析2.2 名校考研真题详解第3章平面任意力系3.1 重点与难点解析3.2 名校考研真题详解3.3 名校期末考试真题详解第4章空间力系4.1 重点与难点解析4.2 名校考研真题详解4.3 名校期末考试真题详解第5章摩擦5.1 重点与难点解析5.2 名校考研真题详解5.3 名校期末考试真题详解第6章点的运动学6.1 重点与难点解析6.2 名校考研真题详解6.3 名校期末考试真题详解第7章刚体的简单运动7.1 重点与难点解析7.2 名校考研真题详解7.3 名校期末考试真题详解第8章点的合成运动8.1 重点与难点解析8.2 名校考研真题详解8.3 名校期末考试真题详解第9章刚体的平面运动9.1 重点与难点解析9.2 名校考研真题详解9.3 名校期末考试真题详解第10章质点动力学的基本方程10.1 重点与难点解析10.2 名校考研真题详解10.3 名校期末考试真题详解第11章动量定理11.1 重点与难点解析11.2 名校考研真题详解11.3 名校期末考试真题详解第12章动量矩定理12.1 重点与难点解析12.2 名校考研真题详解12.3 名校期末考试真题详解第13章动能定理13.1 重点与难点解析13.2 名校考研真题详解13.3 名校期末考试真题详解第14章达朗贝尔原理（动静法）14.1 重点与难点解析14.2 名校考研真题详解14.3 名校期末考试真题详解第15章虚位移原理15.1 重点与难点解析15.2 名校考研真题详解15.3 名校期末考试真题详解第16章非惯性系中的质点动力学16.1 重点与难点解析16.2 名校考研真题详解第17章碰撞17.1 重点与难点解析17.2 名校考研真题详解17.3 名校期末考试真题详解第18章分析力学基础18.1 重点与难点解析18.2 名校考研真题详解18.3 名校期末考试真题详解第19章机械振动基础19.1 重点与难点解析19.2 名校考研真题详解19.3 名校期末考试真题详解附录部分院校考研真题与答案附录1 天津大学2008年《理论力学》考研试题与答案附录2 北京航空航天大学2007年《理论力学》考研试题与答案附录3 北京航空航天大学2009年《力学基础》考研试题与答案附录4 哈尔滨工业大学2007年《理论力学》考研试题与答案附录5 浙江大学2007年《理论力学》考研试题与答案附录6 哈尔滨工程大学2009-2010学年第1学期《理论力学》期末考试试题与答案附录7 重庆大学2005-2006学年《理论力学》期末考试试题与答案附录8 河海大学2003-2004学年第1学期《理论力学》期末考试试题与答案附录9 中国石油大学（华东）2008-2009学年第1学期《理论力学》期末考试试题与答案。

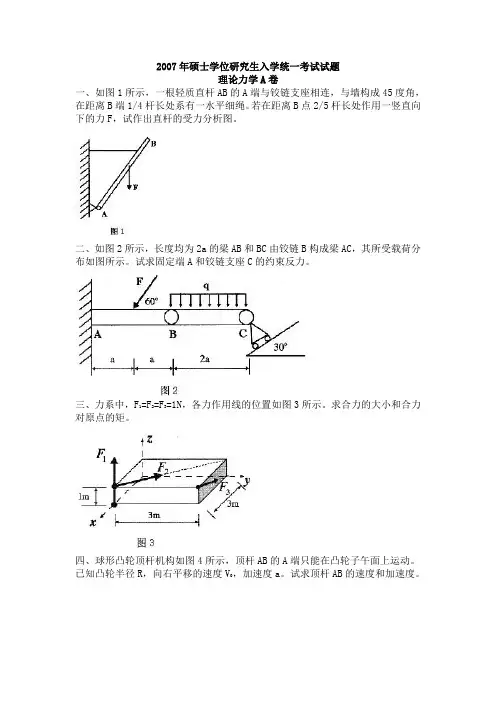
2007年硕士学位研究生入学统一考试试题理论力学A卷一、如图1所示，一根轻质直杆AB的A端与铰链支座相连，与墙构成45度角，在距离B端1/4杆长处系有一水平细绳。

若在距离B点2/5杆长处作用一竖直向下的力F，试作出直杆的受力分析图。

二、如图2所示，长度均为2a的梁AB和BC由铰链B构成梁AC，其所受载荷分布如图所示。

试求固定端A和铰链支座C的约束反力。

三、力系中，F1=F2=F3=1N，各力作用线的位置如图3所示。

求合力的大小和合力对原点的矩。

四、球形凸轮顶杆机构如图4所示，顶杆AB的A端只能在凸轮子午面上运动。

已知凸轮半径R，向右平移的速度V，加速度a。

试求顶杆AB的速度和加速度。

五、如图5所示，一质量为m的物体放在匀速转动的水平转台上，它与转轴的距离为r。

设物体与转台表面的摩擦系数为μ。

当物体不致因转台旋转而滑出时，求水平台的最大转速是多少。

六、图6所示，水平面上放有一质量为M1的均质直三棱柱，在其斜面上又放一质量为M2的均质直三棱柱，质量比为M1:M2=3，两者的尺寸在图中已标注。

设所有摩擦均可忽略，初始时系统静止。

当斜面上的三棱柱下滑到水平面时，质量为M1的三棱柱移动了多少距离。

七、送料机构小车连同矿石的质量为m1，绞轮质量为m2，半径为r，对其转轴的回转半径为r2，轨道的倾角为θ，如图7所示。

在绞轮上作用一不变力矩M将小车提升。

试求小车由静止开始沿轨道上升路程为s时的速度及加速度。

略去摩擦作用及绳索的质量。

八、如图8所示，轮A和B可视为均质圆盘，半径均为r，质量均为m。

绕在二1，并且放在理想光滑的水平面轮上的绳索中间连有物块C，设物块C的质量为m2上。

今在轮B上作用一个不变的力偶M，求轮B与物块C之间那段绳索的张力。

九、均质直杆重为G，长为L，A端为球铰链连接，B端自由，以匀角速度Ω绕铅垂轴AZ转动，如图9所示。

求杆在A端受到铰链的约束力大小。

(应用达朗贝尔原理)图 92007年理论力学A卷参考答案一、答：二、答：1取BC为研究对象进行受力分析，设Nc为C端受到的作用力大小，方cos 30°·2a-2aq·a=0，求得向垂直于斜坡，列出对B点取距的平衡方程Nc。

………密………封………线………以………内………答………题………无………效……图xF 1z y O F 2F 3F 4a a a一、判断题1、全约束反力是摩擦力与法向反力的合力，因此全约束反力的大小为22()R s N N F f F F =+，其与接触处法线间的夹角为摩擦角。

（ ）2、任意两个力都可以合成为一个合力。

（ ）3、空间力对点之矩矢在任意轴上的投影，等于该力对该轴之矩。

（ ）4、平面运动刚体存在速度瞬心的条件是刚体的角速度不为零。

（ ）5、无论刚体作何种运动，也无论向哪一点简化，刚体惯性力系的主矢均为IR C m =-F a 。

其中C a 为质心的加速度，m 为刚体的质量。

（ ）6、若质点的动量守恒，则该质点对任意一定点的动量矩也一定守恒。

（ ）2、填空题（每题3分，共15分）1、如图2-1所示力系，231002F F N ==，4300,2F N a m ==，则此力系向坐标原点O 简化的结果是： ，此力系简化的最终结果是： 。

2、边长为2a cm =的正方形ABCD 在其自身平面内作平面运动。

已知正方形顶点A 、B 的加速度大小分别是22/A a cm s =，242/B a cm s =，方向如图所示。

此时正方形的瞬时角速度ω= ，角加速度ε= ，以及C 点的加速度C a = 。

A B Ca ADa B45图………密………封………线………以………内………答………题………无………效……3、长均为l ，质量均为m 的均质杆OA 、OB 在O 处以光滑铰链相联接。

图示系统的动量P =，质心的速度C v =。

4、半径为r ，质量为m 的均质圆盘A 由杆OA 带动在半径为R 的大圆弧上作纯滚动，设2R r =。

图示瞬时，该圆盘的动量P = ，对轴O 的动量矩O L = ，动能T = 。

5、定轴转动的OAB 杆是由两个质量分别为1m （OA 杆）和2m （AB 杆）的均质细杆焊接而成。

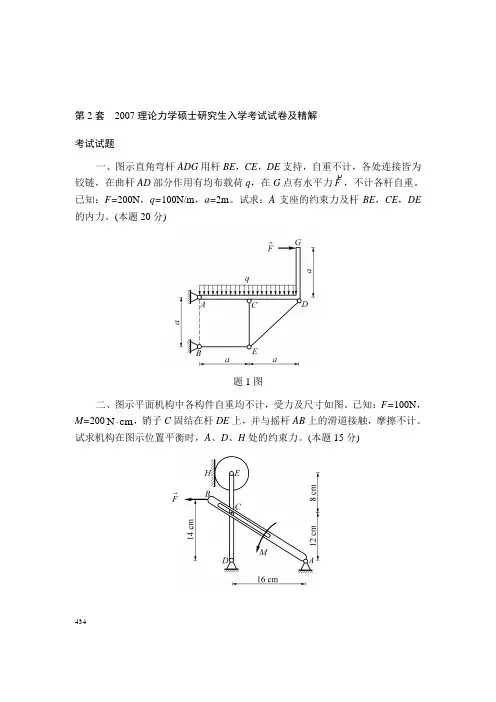
434 第2套 2007理论力学硕士研究生入学考试试卷及精解 考试试题一、图示直角弯杆ADG 用杆BE ，CE ，DE 支持，自重不计，各处连接皆为铰链，在曲杆AD 部分作用有均布载荷q ，在G 点有水平力F，不计各杆自重。

已知：F=200N ，q=100N/m ，a=2m 。

试求：A 支座的约束力及杆BE ，CE ，DE 的内力。

(本题20分)题1图二、图示平面机构中各构件自重均不计，受力及尺寸如图。

已知：F=100N ，M=200cm N ，销子C 固结在杆DE 上，并与摇杆AB 上的滑道接触，摩擦不计。

试求机构在图示位置平衡时，A 、D 、H 处的约束力。

(本题15分)435题2图三、长为l 的OA 杆，A 端恒与三角块B 的斜面接触，并沿倾角︒=30θ的斜面滑动，在图示位置，OA 杆水平。

B 的速度为v 、加速度为a 。

试求此时杆端A 的速度与加速度。

(本题20分)题3图 题4图四、套筒B 沿固定的水平杆滑动，已知：10=OA cm ，210=AB cm 在图示位置（︒=45θ，OA 处于铅垂）时，杆OA 的角速度4=O ωrad/s ，角加速度等于零。

试求：（1）B 点的速度与加速度；（2）杆AB 的角速度与角加速度。

(本题20分)五、一均质板C ，水平地放置在均质圆轮A 和B 上，A 轮和B 轮的半径分别为r 和R ，A 轮作定轴转动，B 轮在水平面上滚动而不滑动，板C 与两轮之间无相对滑动。

已知板C 和轮A 的重量均为P ，轮B 重Q ，在B 轮上作用有常力偶M 。

试求板C 的加速度。

(本题15分)题5图ABABv436 六、 在图示系统中，已知：构架CE 以加速度a =(4/5)g 运动，直角匀质杆ABC 每厘米长度重为1.5N ，l =1.2m ，匀质杆DE 重为225N 。

试用动静法求铰链D 的约束力。

(本题20分)题6图 题7图七、在图示机构中，直角杆EDC 通过杆CB 与杆AB 相连，AB 和CD 均处于水平位置。

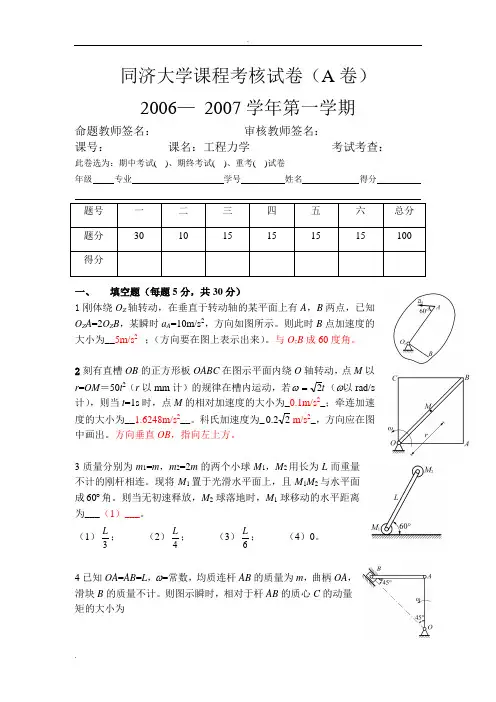
同济大学课程考核试卷（A 卷） 2006— 2007学年第一学期命题教师签名： 审核教师签名：课号： 课名：工程力学 考试考查：此卷选为：期中考试( )、期终考试( )、重考( )试卷年级 专业 学号 姓名 得分一、 填空题（每题5分，共30分）1刚体绕O Z 轴转动，在垂直于转动轴的某平面上有A ，B 两点，已知O Z A =2O Z B ，某瞬时a A =10m/s 2，方向如图所示。

则此时B 点加速度的大小为__5m/s 2 ；（方向要在图上表示出来）。

与O z B 成60度角。

2刻有直槽OB 的正方形板OABC 在图示平面内绕O 轴转动，点M 以r =OM ＝50t 2（r 以mm 计）的规律在槽内运动，若t 2=ω（ω以rad/s 计），则当t =1s 时，点M 的相对加速度的大小为_0.1m/s 2_；牵连加速度的大小为__1.6248m/s 2__。

科氏加速度为_22.0m/s 2_，方向应在图中画出。

方向垂直OB ，指向左上方。

3质量分别为m1=m ，m 2=2m 的两个小球M 1，M 2用长为L 而重量不计的刚杆相连。

现将M 1置于光滑水平面上，且M 1M 2与水平面成︒60角。

则当无初速释放，M 2球落地时，M 1球移动的水平距离为___（1）___。

（1）3L； （2）4L； （3）6L； （4）0。

4已知OA =AB =L ，ω=常数，均质连杆AB 的质量为m ，曲柄OA ，滑块B 的质量不计。

则图示瞬时，相对于杆AB 的质心C 的动量矩的大小为__122ωmL L C =，（顺时针方向）___。

5均质细杆AB 重P ，长L ，置于水平位置，若在绳BC 突然剪断瞬时有角加速度α，则杆上各点惯性力的合力的大小为_g PL 2α，（铅直向上）_，作用点的位置在离A 端_32L_处，并在图中画出该惯性力。

6铅垂悬挂的质量--弹簧系统，其质量为m ，弹簧刚度系数为k ，若坐标原点分别取在弹簧静伸长处和未伸长处，则质点的运动微分方程可分别写成_0=+kx xm _和_mg kx x m =+ _。

浙江大学2007年硕士研究生入学考试试题（高等代数）一：证明；充分性；若该方程组的系数矩阵行列式为1±，故可由克拉默法则可知[]()11Tn n b b b b b ∀= 为整数，方程Ax b =的解均为整数解。

必要性；令Ax b =，由已知可知 对于1,e 存在整数解1β,n e 存在整数解n β所以[][]11n n n A e e E ββ==，若取[]1n B ββ= ，所以1A B =，而,A B 为整数组成的矩阵，从而有1A =±，即该方程组的系数矩阵行列式为1± 二：解：由于21121111211231232222222212341123333111121112212311111111n n n n n n n nn n n n n n n n n n n n n n s s s x x x ss s s x x x x x x x A s s s s x x x x x x x s s s s x x x x x x x ----+------+-⎡⎡⎤⎡⎤⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥==⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥⎣⎦⎣⎦⎣⎤⎥⎥⎥⎥⎥⎥⎦可知()21j i i j nA x x ≤<≤=-∏三：证明：由于00000E A AB E C ABC E B BC E B ---⎡⎤⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦从而()()()()0AB rank ABC rank B rank rank AB rank BC B BC ⎛⎫⎡⎤+=≥+ ⎪⎢⎥⎣⎦⎝⎭四：证明：由于k s <，则必能从12,,,s ξξξ 中必可取()0m >个向量，使它们和12,,,k ηηη 一起构成齐次方程0Ax =的一组基础解系，若m s k <-，则()dim ker A k s k s <+-<这和已知()dim ker A s =矛盾 若m s k >-，则()dim ker A k s k s >+->这和已知()dim ker A s =矛盾 从而m s k =-，从而必能从12,,,s ξξξ 中必可取s k -个向量，使它们和12,,,k ηηη 一起构成齐次方程0Ax =的一组基础解系五：证明：由已知可知，A 的最小多项式()()()23m λλλ--，从而()m λ无重根，即A 可以对角化，由于A 的特征值仅为2和3，而23m n m A -=，从而特征值2的重数为m ，特征值3的重数为n m -，故与A 相似的一个对角矩阵为22020333m n m E E -⎡⎤⎢⎥⎢⎥⎢⎥⎡⎤=⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦六；证明：()1 22,,C D k ⨯∀∈∈ ，由()()()()()()()C D A C D B ACB ADB C D kC A kC B kACB k C ϕϕϕϕϕ+=+=+=+===从而ϕ是V 上的线性变换()2若1λ≠，则,A B 均为可逆矩阵，令()0x ϕ=，则0AxB =，所以0x =，即ϕ是可逆线性变换()3若1λ=，ker ,a b x x c d ϕ⎡⎤∀∈=⎢⎥⎣⎦，根据0x ϕ=可知,a c b d ==，从而12121001ker :,1001k k k k ϕ⎧⎫⎡⎤⎡⎤=+∈⎨⎬⎢⎥⎢⎥⎣⎦⎣⎦⎩⎭ 又对任何a b x c d ⎡⎤=⎢⎥⎣⎦，有 ()()()12111211x a c b d ϕ--⎡⎤⎡⎤=-+-⎢⎥⎢⎥--⎣⎦⎣⎦，从而12121211Im :,1211k k k k ϕ⎧--⎫⎡⎤⎡⎤=+∈⎨⎬⎢⎥⎢⎥--⎣⎦⎣⎦⎩⎭()4当1λ≠时，值域的基即为V 的基，而11122122,,,E E E E 可做为值域的一组基，即可为V 的一组基而()()()()11111221221211122122211112212211111221222222E E E E E E E E E E E E E E E E E E E E ϕλλϕλλϕϕ=+++=----=--++=+--可知，ϕ在这组基下的矩阵为1111212111221λλλλ--⎡⎤⎢⎥--⎢⎥⎢⎥--⎢⎥--⎣⎦当1λ=时，令123412111010,,,12111010εεεε--⎡⎤⎡⎤⎡⎤⎡⎤====⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦，而12,εε为值域的一组基，34,εε为核的一组基，从而12,εε扩充34,εε后可成为V 的一组基，显然可知ϕ在这组基下的矩阵为220042000000000-⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦七：解：由于2222222110001000000110010000λλλλλλλλλλλλλλλλλλλλλλ⎡⎤⎡⎤⎡⎤-+-++⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-→-→-→⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥++⎣⎦⎣⎦⎣⎦⎣⎦从而可知222211λλλλλλλλλλ⎡⎤-+⎢⎥-⎢⎥⎢⎥+⎣⎦的不变因子为21,,λλλ+，初等因子为,,1λλλ+ 八：解()1显然那可知()1234,,,f x x x x222212341213142324348888222222x x x x x x x x x x x x x x x x =+++++--++()2由于A 的特征多项式为()()()395f λλλ=--，从而A 的特征值为9（3重）和5由于()90n E A x -=的基础解系的一组基为：[]11001T ε=-，[]21010Tε=，[]31100Tε=，由于()50n E A x -=的基础解系的一组基为：[]41111Tε=--单位正交化可得100Tα=⎣⎦20Tα=⎣⎦3Tα=⎣⎦411112222T α⎡⎤=--⎢⎥⎣⎦令121002210212662P ⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥-⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦，可知做正交变换TY P X =，就可使()222212341234,,,9995f x x x x y y y y =+++ ()3显然可知A 为正定矩阵，则存在可逆矩阵C ，有T A C C =从而可知(),0T A αααα=≥，且当且仅当0α=时，等号成立(),αβ=()()(),,TTTT T T T A C C C C C C C C A αβαβαββαβαβαβαΩ======k ∀∈()()(),,TT k k A k A k αβαβαβαβ===()()()(),,,TT T A A A αβγαβγαγβγαγβγ+=+=+=+从而(),T A αβαβ=定义了4 上的内积从而该内积下4的一组标准正交基为1100322Tω=-⎢⎣⎦2103636Tω=⎢⎣⎦313Tω=⎣⎦411112222Tω⎤=--⎢⎥⎣⎦()4可取10022000100000021*******1111122222B ⎡⎤⎢⎥⎢⎥⎥⎤⎢⎥⎥⎥-⎢⎥⎥⎢⎥⎢⎥⎥=⎢⎥⎢⎥⎥⎢⎥-⎢⎥⎥⎢⎢⎥⎢⎥⎣⎢⎥⎢⎥--⎢⎥⎢⎥⎣⎦⎣⎦九：证明：假若()f x 为有理数域上的可约多项式，则不妨设存在整系数多项式()(),g x h x 使()()()()()()(),0,0f x g x h x g x h x =∂>∂>，由于()0f x >，从而()f x 无实数根，则()(),g x h x 也无实根，不妨设()()0,0g x h x >>，从而在这n 个不同点1,,n a a ，()(),g x h x 的值均为1，从而()()()(),g x n h x n ∂≥∂≥，否则，()(),g x h x 有个为常数，即()()()()f xg x n ∂=∂=，则()()()11ni i h x g x x a ===+-∏，从而()()()21112n ni i i i f x x a x a ===+-+-∏∏这和已知矛盾，从而假设不成立，从而()f x 在有理数域上不可约。

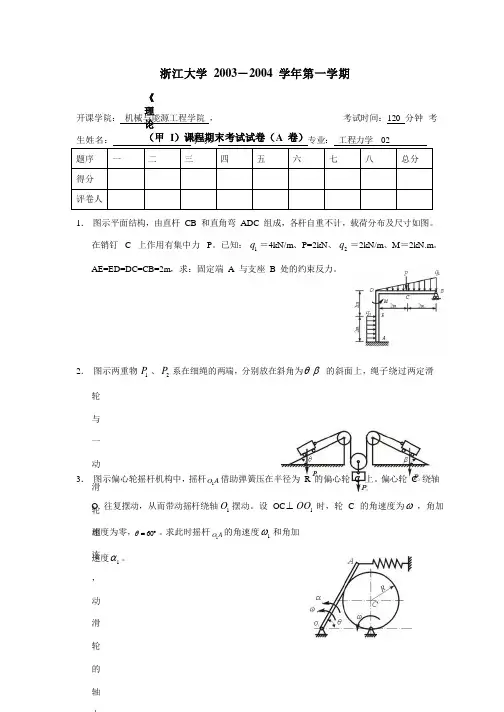
1 1 浙江大学 2003－2004 学年第一学期《理论力学》（甲 I ）课程期末考试试卷（A 卷）开课学院： 机械与能源工程学院 ， 考试时间：120 分钟 考生姓名：学号：专业： 工程力学 021． 图示平面结构，由直杆 CB 和直角弯 ADC 组成，各杆自重不计，载荷分布及尺寸如图。

在销钉 C 上作用有集中力 P 。

已知： q 1 ＝4kN/m 、P=2kN 、 q 2 ＝2kN/m 、M ＝2kN.m 。

AE=ED=DC=CB=2m ，求：固定端 A 与支座 B 处的约束反力。

2． 图示两重物 P 1 、 P 2 系在细绳的两端，分别放在斜角为θ β 的斜面上，绳子绕过两定滑 轮与一动滑轮相连，动滑轮的轴上挂一重物 P 3 。

如摩擦以及滑车与绳索的质量忽略不计， 试求平衡时 P 1 和 P 2 的值。

（应用虚位原理）3． 图示偏心轮摇杆机构中，摇杆 O A 借助弹簧压在半径为 R 的偏心轮 C 上。

偏心轮 C 绕轴O 往复摆动，从而带动摇杆绕轴 O 1 摆动。

设 OC ⊥ OO 1 时，轮 C 的角速度为 ω ，角加速度为零，θ = 60︒ 。

求此时摇杆速度α1 。

O A 的角速度 ω1 和角加4． 在图示机构中，已知：匀速度 u ＝1m/s ，AB=L=1m ，轮 B 在固定大圆上作纯滚动，r ＝30cm ，R ＝70cm 。

当 ϕ = 45︒ 时，AO 处于铅直位置。

试求该瞬时轮 B 的角速度和角加 速度。

5． 平面机构如图所示，半径为 r 的轮子在水平面上纯滚动，轮缘上 C 点和 CD 杆铰接。

已 知：r ＝10cm ，CD=L=40cm ，H=30cm ， θ = 45︒ 。

在图示位置时，A 、C 、D 三点同处 水平线，DE 铅直；轮子的角速度 ω ＝2rad/s 、角加速度 α ＝1rad/ s 2。

试求该瞬时 DE 杆的角速度和角加速度。