当前位置：文档之家 › 平面力系例题教材

平面力系例题教材

  • 格式：ppt
  • 大小：1.72 MB
  • 文档页数：82

下载文档原格式

  / 82

合集下载

第二章 平面力系

第二章 平面力系
第二章
平面力系
§2-1 一般概念
一.力系分类
平面力系（汇交力系、平行力系、一般力系） 空间力系
二.工程实例 在工程地质和工程建筑物中，常遇到
的一些平面力系问题，如：
铁路绗架、水坝、坝基 空间问题一般简化为平面问题处理
W1
W2
1m
§2-2 平面汇交力系的合成与分解
一、二力合成 1、几何法：已知作用在物体上的两个力，F1、F2 ，它们
5.力偶在任意坐标轴上的投影恒等于零.
§2-6 平面力系的合成
一、力的平移定理 作用在物体上的力可以平移到任意点，但必须附加上
一力偶，其矩大小等于此力对新作用点之矩。
M B M B (F ) F d （2 - 10）
二、平面任意力系向已知点简化（如下图）
1、简化方法：
2、简化结果：
主矢 FR Fi 主矩 M O M O (F i) （2 - 11）
P 2 10m
BT T
W1 R
N W2
T
P2
解：可以用解析法和图解法解此题 答案：Ｔ=7500KN，N=21500KN
§2-8 平面一般力系平衡条件和方程式
一、平面任意力系的平衡条件（充要条件）
R0， M00 二、平面任意力系平衡方程式 主矢
必有 主矩
R ( F x)2( F y)20
Fx 0
主矢与简化中心无关，主矩与简化中心有关
三、平面任意力系的合成
1、力和力偶合成一个力 2、合力矩定理：
平面力系的合力，对该平面任一点之矩，等于各分力 对同一点之矩的代数和。
n
M0 R m0(Fi) i1
3、简化结果分析，四种情况有三种结果
§2-7 重心

2平面任意力系简化2-25

2平面任意力系简化2-25
为机床上夹持工件的夹盘，夹盘对工件的约 束就是固定端约束；图2-6c所示为一端镶嵌 在建筑物墙内的门或窗户顶部的雨罩，墙对 于雨罩的约束也属于固定端约束。
固定端对于被约束的构件，在约束处所产生的约束
力，是一种比较复杂的分布力系。在平面问题中，
如果主动力为平面力系，这一颁约束力系也是平面
数、大小和方向）不完全相同，但其所产生的
运动交应却可能是相同的。这时，可以称这些
力系为等效力系。
序
言
为了判断力系是否等效，必须首先确定表示力 系基本特征的最简单、最基本的量——力系基 本特征量。这需要通过力系的简化方能实现。
序言
本章首先在物理学的基础上，对力矩的概念加以 扩展和延伸，同样在物理学的基础上引出力系基 本特征量，然后应用力向一点平移定理和方法对 力秒加以简化，进而导出力系等效定理，并将其
解：根据平面力偶系的简化结果，由式（2-7）得
本例中3个力偶所组成的平面力偶系的合力偶的力 偶矩，等于3个力偶的力偶矩之代数和，即：
图2-4 例题2-2图
Mo Mi
i 1
n
M1 M 2 M 3 F1 h1 F2 h2 F3 h3 0.4m 200 N 1m 600 N 400 N 0.4m 0 sin 30 520 N m
力F1、F2、F3，各力的方向如图2-3a所示，各力
的大小分别F1＝３kN、F2＝4kN、F3＝5kN。试
求：螺钉作用在墙上的力F。
图2-3 例题2-1图
解：要求螺钉用在墙上的力就是要确定作用在 螺钉上所有力的合力。确定合力可以利用力的 平等四边形法则，对力系中的各个力两两合成 。但是，对于力系中力的个数比较多的情形， 这种方法显得很繁琐。而采用合力的投影表达 式（2-6），则比较方便。 为了应用式（2-6），首先需要建立坐标系Oxy ，如图2-3b所示。 先将各力分别向x轴和y轴投影，然后代入式（ 2-6），得：

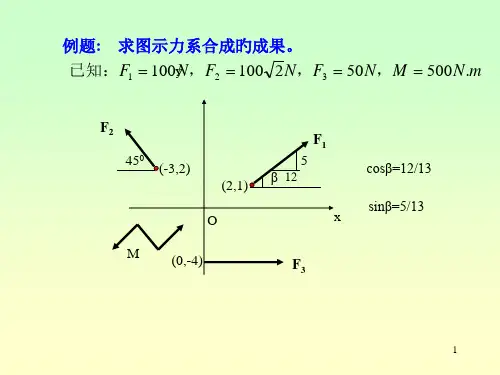
理论力学5平面任意力系

理论力学5平面任意力系

P
1m
q
C
2m
A
2m
B
43
P
1m
q
C
XA
2m
A
YA
2m
XB
B
YB
解: ( 1 ) 取整体为研究对象，画受力图.
44
P
1m
q
C
XA
2m
A
2m
XB
B
YA
MA( F ) = 0
YB
- 4 × 3 × 1.5 - 20 × 3 + 4 YB = 0
YB = 19.5 kN
45
P
1m
q
C
XA
2m
2m
A
FR 0, M O (F ) 0
（一）基本平衡方程
Fx = 0 Fy = 0 Mo ( F ) = 0
（一力矩式）
能解 3 个未知量
16
（二）平面任意力系平衡方程旳其他形式
（1） 二力矩式
MA ( Fi ) = 0 MB ( Fi ) = 0 Fx = 0
投影轴 x 不能与矩心 A 和 B 旳连线垂直.
a
G3 A
C
e G1 L G2
B
NA
b
NB
1、满载时，当重物距离右轨最远时，易右翻。 当起重机平衡 m B( F ) = 0 - G1 ·e - G2 ·L - NA ·b+ G3 ·（a+ b） = 0
NA = [ - G1 ·e - G2 ·L + G3 ·（ a+ b）] / b
33
a
G3 A
XA = 14.14 kN
Fy = 0
YA

2平面任意力系习题

2平面任意力系习题
思考题：P61 3-7
? 平面汇交力系
??? X ? 0 ???? Y ? 0
? 平面一般力系
?
?? ???
MA(F ) X?0
?
0
??? Y ? 0
? 平面力偶系
? Mi ? 0
? 平面平行力系
?
?? ???
MA(F ) Y? 0
?
0
作业
§3-3 物体系的平衡 静定和静不定问题
一、静定和静不定问题 如果一个结构由几个构件组成，当结构平衡时，每个构件也 平衡，所以可分别写出独立的平衡方程数，最多为3n个。 静定：平衡方程数=未知反力数 即所有的未知反力可有平衡方程求出。 超静定：平衡方程数<未知反力数 即平衡方程不能求出全部未知反力，要加补充方程。
F=1KN，滑轮半径r=1m，重物P=2F，CO=OD，求支座E及固定端A
?
的约束力。 解：
B
y
F
OD
1) 取研究对象、取坐标 6 m
2）受力分析 整体、 ABC、 CDE
q
? F (1)
F
? ? FCx FCy
? FAy
? MA FAx
q
z? C
FAx
A ? 3m 3m
FAy M A
?
F
? F (2)
FB
sin600
?a
?
F1
?a 4
?
F2
?sin450
?a 2
?
F2
?cos450
3a ? 0 2
?C
? F2
y F1 45 0
D 30 0 30 0
x
zA
B
FB
?
F1

ll第三章 平面力系

ll第三章 平面力系

第三章 平面力系一、填空题1．力F 作用线向O 点平移时，为不改变它对刚体的作用效果，这时应该 附加一力偶，该力偶的矩等于力F 对O 点的矩。

2．平面任意力系向其作用平面内不同两点简化，所得主矢的关系是相同，所得主矩的关系是力系对新简化中心的主矩等于原力系对原简化中心的主矩加上作用于原简化中心的主矢对新简化中心的矩。

3．平面任意力系平衡方程的二矩式应满足的附加条件是两矩心的连线不垂直于投影轴。

二、选择题1．一平面任意力系向点A 简化后，得到如图3.1所示的主矢和主矩，则该力系的最后合成结果应是（A ）(A ) 作用在点A 左边的一个合力 (B ) 作用在点A 右边的一个合力 (C ) 作用在点A 的一个合力 (D ) 一个合力偶2．在刚体同一平面内A ，B ，C 三点上分别作用1F ，2F ，3F 三个力，并构成封闭三角形，如图3.2所示，此力系是属于什么情况（C ）(A ) 力系平衡 (B ) 力系简化为合力 (C ) 力系可简化为合力偶 (D ) 无法判断3．均质杆长为l ，重为W ，在D 处用一绳将杆吊于光滑槽内，则槽壁在A ，B 处对杆产生的反力A F ，B F 有关系（D ） (A ) A B F F > (B ) A B F F < (C ) 0A B F F ==(D ) 0A B F F =≠ 三、计算题1．试求图3.4中力P 对点O 的矩，已知60a cm =，20b cm =，3r cm =，400P N =。

解：（a ）()4000.6240O M Pa N m ==⨯=⋅P（b ）o 1()sin304000.61202O M P a N m =-⨯=-⨯⨯=-⋅P 图3.2图3.1 图3.3（c ）o o o ()cos20cos204000.03cos2011.3O M P r Pr N m =-⨯=-=-⨯=-⋅P（d）o o 1()sin30cos304000.64000.250.722O M P a P b N m =⨯-⨯=⨯⨯-⨯=⋅P （e）o o 1()cos60sin 604000.64000.2189.32O M P a P b N m =⨯+⨯=⨯⨯+⨯=⋅P2．如图3.5所示，在边长2a m =的正方形平板OABC 的A ，B ，C 三点上作用四个力：13F kN =，25F kN =，36F kN =，44F kN =。

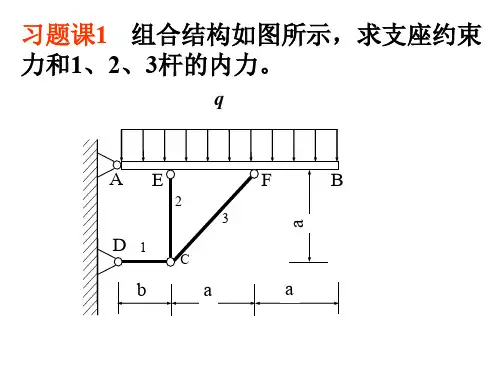
理论力学2—平面力系(习题课)

理论力学2—平面力系(习题课)

FBCx

qa 2
3. 取B销钉为研究对象
Fx 0 :
FBCx FABx 0
FABx

FBCx

qa 2
Fy 0 :
F FBCy FABy 0
FABy F qa
3a a
q
FD M
B
C
aa
A q
F
FABx
B F'BCx
FABy F'BCy
FABx
是AB、BC中点, 求绳EF的张力。
解: 1) 以DC为研究对象, 受
AE
B
力如图。
F
MC (F) 0 :
D C
FDy l
W
l 2

0
FDy

W 2
(1)
FDy FDx D
W
FCy
C
FCx
2) 再以整体为研究对象:
Fy 0 :
FAy FDy 3W 0 (2)
FAy 2.5W
C
求铰链 E 处的所受的力。 解: 1）先以整体为研究对象, 受力如图:
E
l
Fx 0 : FAx 0
Fy 0 : FAy FB P 0

M
A
(F
)

0
:
FBl

P
2 3
l

0
A
B
l P
D
C
解得:
FAy

1 3
P
FB

2 3
P
FAy A
FAx
E FB B
2）下面用不同的方法求铰链 E 的受力。

第二章 平面力系


FR F1 F2 Fn Fi
i 1
n
力FR对刚体的作用与原力系对该刚体的作用等效。所以 称此力为汇交力系的合力。
如力系中各力作用线均沿同一直线，则此力系为共线力系， 它是平面汇交力系的特殊情况。显然力系的合力大小和方向 取决于各分力的代数和，即 n
FR Fi
i 1
24
静力学
例题 1-5
平面力系
合力的大小：
2 Rx 2 Ry
FR F F 171.3 N
合力与轴x，y夹角的方向余弦为：
FRx cos( FR , i ) 0.754 FR
F2
y
F1
60
O
45
30
cos( FR , j )
FRy FR
45
x
F4
0.656
F3
平面力系
Fx Fx1 Fx 2 Fxn Fxi i 1 n Fy Fy1 Fy 2 Fyn Fyi i 1
n
合力矢FR的大小和方向余弦为
FR Fx2 Fy2 ( Fxi ) 2 ( Fyi ) 2
B
D
钢丝绳的另一端绕在铰车D上。 杆AB与BC铰接，并以铰链A，C 与墙连接。如两杆与滑轮的自重
4 .由力三角形图c可得：
I
F
q
FD

J
K
FB
(c)
sin 180 q FB F 750 N sin
11
静力学
例题 1-2
平面力系
水平梁AB中点C作用着力F，其大小等于2 kN，方向与梁
的轴线成60º 角，支承情况如图a 所示，试求固定铰链支座A和活动铰链支座B的约束源自。梁的自重不计。3，

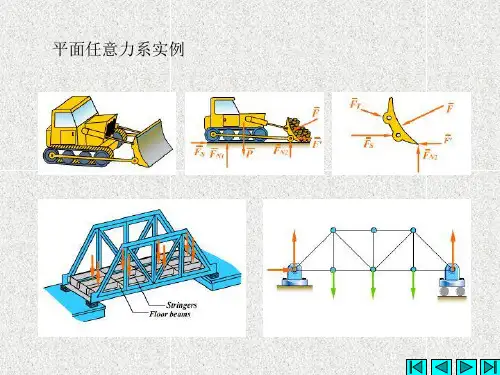
第三章 平面任意力系实例 理论力学Ⅰ第六版 教学课件


解得
F2 8.66kN(拉)
取节点C,画受力图.
Fix 0 F4 cos 300 F1' cos 300 0
解得 F4 10kN(压)
Fiy 0 F3 F1' F4 sin 300 0
解得 F3 10kN(拉)
取节点D,画受力图.
Fix 0 F5 F2' 0
解得 F5 8.66kN(拉)
M B 0 6FAy 3P1 2P2 0
MC 0 FAx AC 3P1 4P2 0
MB
0 0
FT sin 30 6 4P2 3P1 0 6FAy 3P1 2P2 0
（3）
MC 0
FAx AC 3P1 4P2 0
能否从理论上保证三组方程求得的结果相同？
例2-12
已知: P1 10kN, P2 7kN, 各杆长度均为1m;
求: 1,2,3杆受力.
解: 取整体,求支座约束力.
Fix 0 FAx 0
M B 0 2P1 P2 3FAy 0
解得
FAy 9kN
Fiy 0 FAy FBy P1 P2 0
解得
FBy 8kN
用截面法,取桁架左边部分.
Foy F
Mo 0 FA cos R M 0
解得 M FR
例2-7 已知: F=20kN, q=10kN/m, M 20kNm, L=1m;
求: A,B处的约束力. 解: 取CD梁,画受力图.
MC 0
FB sin 60
l ql l F cos 30 2
2l
0
解得 FB=45.77kN
从1，2，3杆处截取左边部分
Fiy 0 F2 MC 0 F1
Fix 0 F3

第三章：平面任意力系

第三章平面任意力系一、要求1、掌握平面任意力系向一点简化的方法。

会应用解析法求主矢和主矩。

熟知平面任意力系简化的结果。

2、深入理解平面任意力系的平衡条件及平衡方程的三种形式。

3、能熟练地计算在平面任意力系作用下物体和物体系的平衡问题。

4、理解简单桁架的简化假设，掌握计算其杆件内力的节点法和截面法。

二、重点、难点1、本章重点：平面任意力系向作用面内任一点的简化，力系的简化结果。

平面任意力系平衡的解析条件，平衡方程的各种形式。

物体及物体系平衡问题的解法。

2、本章难点：主矢与主矩的概念。

物体系的平衡问题。

三、学习指导1、力的平移定理，是力系向一点简化的理论基础。

一个力平移后，它对物体的作用效果发生了改变，要想保持原来力的作用效果，必须附加一个力偶。

2、平面任意力系向一点简化的方法：平面任意力系向一点简化，是依据力的平移定理，将作用在物体上的各力向任一点（称为简化中心）平移，得到作用在简化中心的一个平面汇交力系和平面力偶系（附加力偶系）。

两个力系合在一起与原力系等效。

这样，一个复杂的力系就分解成了两个简单的力系。

然后，分别求平面汇交力系的合力和平面力偶系的合力偶，则原力系由作用在简化中心的一个力和一个力偶所代替，该力的大小和方向等于力系的主矢，该力偶的力偶矩等于力系的主矩。

于是，平面任意力系的简化就成了计算力系的主矢和主矩的问题。

3、主矢和主矩：平面任意力系中，各力的矢量和称为力系的主矢，即平面任意力系中，各力对于简化中心的力矩的代数和称为力系的主矩，即关于主矢和主矩，需要弄清楚以下几点：（1）主矢不是力，主矩不是力偶。

主矢和主矩是描述平面任意力系对物体作用效果的量。

（2）主矢是自由矢量，只有大小和方向，描述平面任意力系使物体平动的作用效果。

平面任意力系的主矩是代数量，只有大小和正负，描述平面任意力系使物体绕点转动的作用效果。

（3）主矢与简化中心的选择无关。

从这个意义上讲，主矢是力系的一个不变量。

主矩与简化中心的选择有关。

平面一般力系习题课


YA
将XA=18.75kN代入（*），得XB=18.75kN
8
[例3]图示结构，水平力P=500N，重物重Q=500N，滑轮H半径r=20cm，不计杆、滑 轮、绳重，求杆CE作用于销钉K的力。
解： （1）以整体为研究对象：
m A ( Fi ) 0, Q( 50 r ) 150 P 100 N E 0 N E 1100N
X i 0, X A 0
Y Yi 0, YA YB YD Q P 0 A 48.33(kN)
13
[*例6]平面构架由杆AB、DE及DB铰接而成。已知重力P，DC=CE=AC=CB=2l；定滑轮半 径为R，动滑轮半径为r，且R=2r=l，θ=450。求A、E支座的约束力及BD杆所受的力。
由 mF ( Fi ) 0
YG 2 Q 1 P 5 0
50510 G Y 50(kN) 2
12
② 研究梁CD mC ( Fi ) 0, YD 6 YG' 1 0 50 YD 8.33(kN ) 6 ③
研究 整体
Y mA ( Fi ) 0, YB 3 YD 12 P 10 Q 6 0 B 100( kN)
① 选坐标、取矩点 ② 列方程为: ③ X i 0, X B 0 解方程得 Yi 0, YB P 0, YB P mB ( Fi ) 0, M B P DE 0
受力图
M B 100011000( Nm)
5
2.
再研究CD杆
① 受力如图 ② ③

YA XA
NE
（2）以HK（带滑轮及重物）为研究对 象：

mD ( Fi ) 0, Tr ( 50 r )Q 50YK 0
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

列平衡方程。
FX 0
FY 0
mA(F) 0
Y L=3
q=2
XA A
C
YA 1
2
B
X
RB
30°
mA(F ) 0 RB cos 30 3 L q 2 (1 1) 0
FX 0
X A RB sin30 0
FY 0
YA q 2 RB cos 30 0
RB 4.23KN X A 2.12KN
dX α
NB
NB AB W sin (d h) W cos AD 0
NB
W
sin
(d
T
h) W cos
Y
AB
AD
5.33KN
hO A
C
NA D
W B
dX α
NB
FX 0 W sin T 0
FY 0
N A NB W cos 0
Y
T
10sin30
T
h
5OKN
AC
NA
10cos 30 5.33 3.W33KN
Y 0
N A NB P qL 0
P’和一力偶m，力P’ 使柱子受轴向“压缩”，
而力偶矩m使柱子发生 “弯曲”。
例4—3 悬臂吊车如图。
横梁AB长l ＝2.5m， 自重P＝1.2kN。拉杆 BC倾斜角α＝30°， 自重不计。电葫芦连
同重物共重量Q=7.5 kN。试求当电葫芦在 图示位置a＝2m时， 拉杆BC的拉力和铰链 A的约束反力。
m
B
L
例4-7 试求题图所示各梁支座的约束反力。设 力的单位为(KN)，力偶矩的单位为(KN.m)， 长度单位为(m)，分布载荷集度为(KN/m)。
解：取梁AB为研究对象、受力与坐标选取 如图所示，列平衡方程。
1
0.1
0.1
0.1
C
A
B 30°
0.8
FX 0 X A 0.8cos 30 0
解:⑴ 以梁AB为研究对象，受力图如图所示。
解:⑴ 以梁AB为研究对象，受力图如图所示。
解:⑴ 以梁AB为研究对象，受力图如图所示。 ⑵ 建立平面一般力系的平衡方程，
皆为正值，表示假定的指向与实际指向相同。 ⑵ 建立平面一般力系的平衡方程，
例4—5 已知小车重W＝10 kN，由钢丝绳牵引
沿斜面匀速向上，钢绳与斜面平行，距斜面
平面力系例题
例4—1 用丝银锥攻螺纹时，若两手作用在 丝锥铰手上的力不均称，右手用力P1=20N， 左手用力P2=15N，方向如图所示，试求作用 在丝锥C点上的R力和使丝锥转动的力偶矩。
C
A
B
P2 20°
240mm P1
P2A P2 P2 P2 P2 P2
mc(p2) C
P2 20°
P1
mc(p1)
Y L=3
q=2
XA A
C
YA 1
2
YA 0.34KN
B
X
RB
30°
例4—8 如图,梁AB为工字钢，长为L，每单位 梁长的重为q(N/m)，起吊重物为P. 求图示位置 支座A, B 对梁的约束反力.
解:作横梁AB的受力图,其中分布力Q=L, 作用在L/2处.
qQ
A
B
P
NA L/3
2L/3
NB
列平衡方程用 一个投影式 一个力矩式
NA D
Bd
X α
NB
再列另一平衡方程校核:
mB(F ) 0
T h W cos DB W sin d N A AB 0
代入所求出的未知量
Y
T
50.4 10cos30 10hsin3A0O 0.8C 3.33 2 0
结果为零,说明 以上计算无误.
NA D
W B
dX α
NB
例4-6 悬臂梁AB上有均匀分布载荷集度q (单位长度上力的大小)，在梁的自由端还受 一集中力 P 和一力偶矩为 m 的力偶作用。 已知梁长AB=L试求固定瑞A处的约束反力。
本题中如写出对A B两点的力矩和对X轴的 投影方程同样可以求解。即:
Y
A
XA
YA l/2
P
a
l
30° B X Q
用A、B、C三点的力矩方程同样也可求解:
Y
A
XA
YA l/2
P
a
l
30° B X Q
Y C
Y
A
XA
YA l/2
P
a
l
30° B X Q
例4—4 一悬臂梁如图所示，A端为固定端约束 (或称插入端约束)，梁上受有一集中力 P 及— 力偶m的作用，m＝Pa。求A端的约束反力。
20°
P1 R
mc(p1)
240
BX P1
m =mp1 + mp1 = -20×0.12 – 15cos20°×0.12
= -4.09 N·m
例4-2图中是车间厂房的柱子，行车的轮子
通过钢轨传到柱子上的力为P，距柱子轴线 的距离为a.试分析这个力对柱子引起什么样 的作用。
P’
解： 根据力的平移
定理，把力P向柱子 的轴线平移，得一力
q
P
A
m
B
L
[解] :取悬臂梁AB为研究对象，画受力图 并取坐标系如图，列平衡方程.
FX 0 X A 0
FY 0 YA q L P 0 YA q L P
mA(F) 0
q
Pቤተ መጻሕፍቲ ባይዱ
XA
MA
A
m L
B
YA
mA(F) 0
L MA qL 2 PL m 0
MA
q
L2 2
PL
m
q
P
A
解 (1)根据题意，选横梁AB为研究对象。
(2)分析力，画受力图。
(3)列平衡方程求未知量.选坐标轴如图所示
Y
T
A
XA
30° B X
YA l/2
P
Q
a
l
Y
A
XA
YA l/2 a
T 30°
P
Q
l
BX
=13.2 KN
XA= 11.43 KN YA = 2.1 KN
计算结果皆为正值，表示假定的指向与实际 指向相同。
mB 0 YA 0.2 1 0.1 0.8sin30 0.1 0
FY 0 RB YA 1 0.8sin30 0
X A 0.96(KN ) YA 0.3KN RB 1.1KN
Y 1
XA
0.1
0.1
0.1
X
C
A YA
B 30°
RB
0.8
解:取梁AB为研究对象，受力和坐标如图
h＝0.4m，小车重心 C 点距斜面 d ＝0.8m，
α＝30°, AD＝
BD＝1m，如图
所示。若不计摩
擦，试求钢丝绳 拉力和地面给车
h A
C
轮的反力。
D
Bd α
解 (1)取小车为研究对象
⑵画受力图并选定
Y
坐标系如图所示。 T
⑶列平衡方程求解: h
O A
C
(取O为矩心)
mo(F) 0
NA D
W B
B
R P1 P124P01 P1 P1 P1
解: 根据力的平移定理，将力P1 P2平移到C点， 得一力 R 和一附加力偶，其矩为mC(p).
R = P1 + P2
mC(p)= mc(p1) +mc(p2)
Y
A
P2
P2
mc(p2) C θ
20°
P1 R
mc(p1)
240
BX P1
Y
A
P2
P2
mc(p2) C θ