标准直齿圆锥齿轮传动的强度计算模板
- 格式:ppt
- 大小:137.07 KB
- 文档页数:4

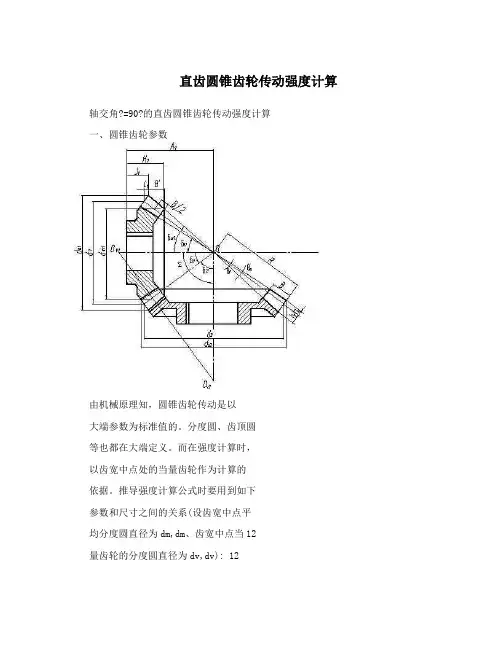
直齿圆锥齿轮传动强度计算轴交角?=90?的直齿圆锥齿轮传动强度计算一、圆锥齿轮参数由机械原理知,圆锥齿轮传动是以大端参数为标准值的。
分度圆、齿顶圆等也都在大端定义。
而在强度计算时,以齿宽中点处的当量齿轮作为计算的依据。
推导强度计算公式时要用到如下参数和尺寸之间的关系(设齿宽中点平均分度圆直径为dm,dm、齿宽中点当12量齿轮的分度圆直径为dv,dv): 12令φ=b/R,称为锥齿轮传动的齿宽系数(通常取φ=0.25-0.35,最常用的值为φ=1/3)于是: RRR二、齿根弯曲疲劳强度计算直齿锥齿轮的弯曲疲劳强度可近似地按平均分度圆处的当量圆柱齿轮进行计算。
因而可直接沿用直齿轮弯曲强度校核公式,得直齿锥齿轮的载荷系数同样为,其中使用系数KA可由表1查取;动载系数Kv 可由图5按低一级的精度线及vm(m/s)查取;齿间载荷分配系数及可取为1;齿向载荷分布系数可按下式计算:= =1.5式中是轴承系数,可从表10中查取Y,Y分别为齿轮系数及应力校正系数,按当量齿数z查表5。
FaSav将:代入校核公式,得设计公式:三、齿面接触疲劳强度计算直齿锥齿轮的齿面接触疲劳强度,仍按平均分度圆处的当量圆柱齿轮计算,工作齿宽即为锥齿轮的齿宽b。
按赫兹公式计算齿面接触疲劳强度时,式中的综合曲率为:将式(l)及代入赫兹公式,并令接触线长度L=b,得:对α=20?的直齿锥齿轮,Z=2.5,于是可得: H上面两式分别为校核式和设计式。
四、曲齿锥齿轮传动简介曲齿锥齿轮传动较之直齿锥齿轮传动具有重合度大、承载能力高、传动效率高、传动平稳、噪音小等优点,因而获得了日益广泛的应用。
曲齿锥齿轮有圆弧齿(简称弧齿,为格里森制齿轮)及长幅外摆线齿(为奥里康制齿轮)等。
格里森制弧齿锥齿轮传动的压力角α取为=20?,平均分度圆处的齿轮螺旋角βm(如右图)取为30?或0?(零度弧齿锥齿轮)。
零度弧齿锥齿轮传动较之直齿锥齿轮传动,平稳性及生产率都高,并因βm=0,轴向力的方向亦不随转矩方向的改变而改变。

齿轮强度计算公式1标准斜齿圆柱齿轮的强度计算一. 齿面接触疲劳强度计算1. 斜齿轮接触方式 !—KF ----------- 12. 计算公式校核式: H Z E Z H - t_u_设计式: bd 1 u3. 参数取值说明1) Z E ---弹性系数2) Z H ---节点区域系数3)…斜齿轮端面重合度4)…螺旋角。
斜齿轮:=8°?25° ;人字齿轮=20 °?35°5)许用应力:[H ]=([ Hl ]+[ H2])/2 1.23[ H2]6)分度圆直径的初步计算在设计式中,K 等与齿轮尺寸参数有关,故需初步估算:a )初取K=K tb )计算 d t d t1c )修正d t二. 齿根弯曲疲劳强度计算1. 轮齿断裂2. 计算公式校核式:设计式:叫3. 参数取值说明1)Y F a 、Y Sa-齿形系数和应力修正系数。
Z v =Z/COS 3 Y Fa 、Y Fa 2)Y …螺旋角系数标准圆锥齿轮传动的强度计算作用:用于传递相交轴之间的运动和动力。
二.几何计算齿轮设计计算简化3 2K t T i u 1 Z E Z H d UH你丫曲 Y Fa Y sadN 2 F3)初步设计计算在设计式中,d )初取K=K te )计算m ntf )修正m n K 等与齿轮尺寸参数有关,故需初步估算: m nt 2中丫曲 Y Fa Y sa2d z 11.锥n1d m/d=(R-°.5b)/R=1-°.5b/R记R=b/R---齿宽系数R=°.25?°.3d m=(1-°.5 R)d2.锥n2V- d224.齿宽中点分度圆直径d1d mA20°A1距3.齿数比:O=Z2/Z1=d2/d1Rtan 2=cot■ _ - K' j5. 齿宽中点模数m n =m (1-0.5 R )三.受力分析大小: F t1 =2T 1/d m1(=F t2)F r1=F t1tan cos F a2)F a1=F t1tan sin 1(=F r2)方向:四. 强度计算1.齿面接触疲劳强度计算K V ---按平均分度圆速度查取K --- K =1 K ---锥齿轮齿向载荷分布系数b )Z E 、Z H 、[ H ]同直齿圆柱齿轮 c ) R =b/R 1/32. 齿根弯曲疲劳强度计算 1)计算公式按齿宽中点当量直齿圆柱齿轮计算、代入大端参数、整理得:2)设数式明a )设计式锥齿轮齿形系数b )Ysa---锥齿轮应力修正系数五.例题(略)第9节齿轮结构一. 齿轮轴(龆(tiao )轮轴)d<1.8d s 二. 实心式da<160三. 腹板式da<500,锻造或铸造四.轮辐式da>400,铸钢或铸铁第10节一.润滑方式1. 人工润滑:用于开式、半开式(速度低)。

标准圆锥齿轮传动的计算参数标准圆锥齿轮传动的计算参数一、引言在机械工程领域中,圆锥齿轮传动广泛应用于各种机械装置中,如汽车变速器、造船机械、起重机械等。
圆锥齿轮传动作为一种重要的动力传递方式,其计算参数的确定对于传动系统的工作性能具有重要影响。
在本文中,我们将探讨标准圆锥齿轮传动的计算参数,以便更好地了解其工作原理和设计方法。
二、标准圆锥齿轮传动的基本概念标准圆锥齿轮传动是由两个相互啮合的圆锥齿轮组成的传动系统,其中一个为主动齿轮,另一个为从动齿轮。
圆锥齿轮传动具有传递大扭矩、平稳传动、传动比变化范围广等特点。
其计算参数主要包括齿数、模数、齿面角、齿顶高、齿根径等。
三、标准圆锥齿轮传动计算参数的深度分析1. 齿数:齿轮的齿数直接影响传动比和传动性能。
在选择齿数时,需要考虑传动的速比和工作环境等因素。
2. 模数:模数是圆锥齿轮传动计算参数中非常重要的一个指标,其大小直接决定着齿轮的尺寸和传动能力。
在确定模数时,需要兼顾传动效率和传动扭矩。
3. 齿面角:齿面角是描述齿轮啮合面上齿廓曲线斜率的参数,其选择直接关系到齿轮的啮合性能和噪声水平。
4. 齿顶高和齿根径:齿顶高和齿根径分别影响齿轮的强度和韧性,其合理选择是保证齿轮传动系统可靠工作的重要保障。
四、标准圆锥齿轮传动计算参数的设计方法1. 确定传动比和速比;2. 选择合适的齿数,考虑齿数的变化范围;3. 根据传动比和齿数确定模数,兼顾传动效率和传动比变化范围;4. 选择合适的齿面角,控制齿轮啮合面的啮合性能和噪声水平;5. 确定齿顶高和齿根径,保证齿轮传动系统的可靠工作。
五、总结与展望通过本文对标准圆锥齿轮传动计算参数的深度分析和设计方法的介绍,我们可以更好地了解圆锥齿轮传动系统的工作原理和设计要点。
在未来的研究中,我们还可以进一步探讨圆锥齿轮传动系统的优化设计和应用实例,以期为相关领域的研究和工程实践提供更多的参考和借鉴。
个人观点:圆锥齿轮传动作为一种重要的动力传递方式,在工程实践中具有广泛的应用前景。



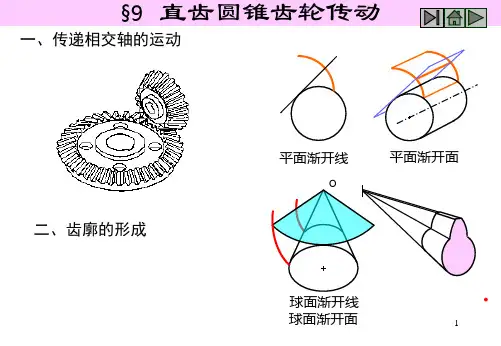
直齿锥齿轮传动设计锥齿轮是圆锥齿轮的简称,它用来实现两相交轴之间的传动,两轴交角S称为轴角,其值可根据传动需要确定,一般多采用90°。
锥齿轮的轮齿排列在截圆锥体上,轮齿由齿轮的大端到小端逐渐收缩变小,如下图所示。
由于这一特点,对应于圆柱齿轮中的各有关”圆柱”在锥齿轮中就变成了"圆锥”,如分度锥、节锥、基锥、齿顶锥等。
锥齿轮的轮齿有直齿、斜齿和曲线齿等形式。
直齿和斜齿锥齿轮设计、制造及安装均较简单,但噪声较大,用于低速传动(<5m/s);曲线齿锥齿轮具有传动平稳、噪声小及承载能力大等特点,用于高速重载的场合。
本节只讨论S=90°的标准直齿锥齿轮传动。
1。
齿廓曲面的形成直齿锥齿轮齿廓曲面的形成与圆柱齿轮类似。
如下图所示,发生平面1与基锥2相切并作纯滚动,该平面上过锥顶点O的任一直线OK的轨迹即为渐开锥面.渐开锥面与以O为球心,以锥长R为半径的球面的交线AK为球面渐开线,它应是锥齿轮的大端齿廓曲线.但球面无法展开成平面,这就给锥齿轮的设计制造带来很多困难。
为此产生一种代替球面渐开线的近似方法。
2。
锥齿轮大端背锥、当量齿轮及当量齿数(1) 背锥和当量齿轮下图为一锥齿轮的轴向半剖面,其中DOAA为分度锥的轴剖面,锥长OA称锥距,用R表示;以锥顶O为圆心,以R为半径的圆应为球面的投影。
若以球面渐开线作锥齿轮的齿廓,则园弧bAc为轮齿球面大端与轴剖面的交线,该球面齿形是不能展开成平面的。
为此,再过A作O1A⊥OA,交齿轮的轴线于点O1.设想以OO1为轴线,以O1A为母线作圆锥面O1AA,该圆锥称为锥齿轮的大端背锥。
显然,该背锥与球面切于锥齿轮大端的分度圆。
由于大端背锥母线1A与锥齿轮的分度锥母线相互垂直,将球面齿形的圆弧bAc投影到背锥上得到线段b’Ac',圆弧bAc与线段b’Ac'非常接近,且锥距R与锥齿轮大端模数m之比值愈大(一般R/m>30),两者就更接近。

齿轮强度计算公式在计算齿轮的强度时,需要考虑以下几个因素:齿轮的材料、齿轮的几何参数、齿轮的载荷等。
下面将详细介绍一些常用的齿轮强度计算公式。
1.根弯曲强度计算:齿轮的根弯曲强度是指齿轮齿根部分在受载条件下的强度。
根据弯曲强度理论,可以得到如下公式:σb=(Ks⋅M)/(Z⋅Y)其中,σb为齿轮的根弯曲应力,Ks是安全系数,M为齿轮的弯矩,Z为齿轮的模数,Y为齿轮的几何弯曲系数。
2.接触疲劳强度计算:接触疲劳强度是指齿轮齿面在接触运动中的承载能力。
根据接触疲劳强度理论,可以得到如下公式:σH=(Z⋅v⋅Kv⋅Kσ)/(b⋅Y)其中,σH为齿轮的接触疲劳应力,v为齿轮的线速度,Kv为速度系数,Kσ为安全系数,b为齿宽,Y为齿轮的几何弯曲系数。
3.齿侧面强度计算:齿侧面强度是指齿轮齿面在受载条件下的强度。
根据齿侧面强度理论,可以得到如下公式:σH=(Ks⋅Mt)/(Z⋅m⋅Y)其中,σH为齿轮的齿侧面应力,Mt为齿轮的扭矩,m为齿数比,Ks为安全系数,Z为齿轮的模数,Y为齿轮的几何弯曲系数。
以上三个公式是常用的齿轮强度计算公式,通过对这些公式的计算,可以得到齿轮在不同工况下的强度情况。
需要注意的是,齿轮的强度计算还需要考虑其他因素,比如表面强度、温度影响等,以得到更准确的结果。
在实际应用中,为了确保齿轮的安全可靠性,通常要选择合适的安全系数,并进行必要的强度验证。
此外,还需要根据实际情况对齿轮的几何参数进行优化,以提高其强度和可靠性。
齿轮的强度计算是齿轮设计中的重要环节,通过合理计算齿轮的强度,可以确保齿轮在使用过程中能够承受合适的载荷,提高齿轮的使用寿命和可靠性。

锥齿轮传动设计计算说明:本程序适用于直齿锥齿轮及 GLEASON 齿制、小齿轮齿数大于或等于 12 的弧齿锥齿轮(包括零度锥齿轮)。
公差数值是按照中点法向模数 1至 10 毫米,中点分度圆直径 400 毫米以下,精度等级 5、6、7、8 级设定的。
弧齿锥齿轮的刀盘直径设定为3.5、6、7.5、9、12、18 英寸。
可进行几何参数计算和承载能力验算(工作条件原动机均匀平稳,从动机中等振动),并可对弧齿锥齿轮加工的可行性(刀盘选择)进行判断。
引用标准:GB11365--89 锥齿轮和准双曲面齿轮精度, GB10062--88 锥齿轮承载能力计算方法主要参考书目:《齿轮手册》上、下册,《机床设计手册》 2 上册,《复杂刀具设计手册》下册注意:本程序有“单变量求解”,应从工具--选项--重新计算中设置反复操作,最多迭代次数10000,最大误差0.0001。
说明:请在兰色框中输入已定或初定数据(黄色框中为判断或参考数据)。
输出数据在最后列表,可单独打印。
左旋小轮齿数Z1大轮齿数Z2大端端面模数m1018法向压力角αn轴交角Σ切向变位系数x s1齿宽参考值b0高度变位系数x h1齿宽实际值b第Ⅰ公差组精度等级全齿高系数x第Ⅱ公差组精度等级工作齿高系数x w第Ⅲ公差组精度等级全齿高h最小法向侧隙种类工作齿高hw法向侧隙公差种类齿数比u小轮基准端面直径极限值小轮基准端面直径大轮基准端面直径极限值大轮基准端面直径最小法向侧隙jn min最大法向侧隙jn max注:如果侧隙不合适,可重新选择最小法向侧隙种类、2—3—合金钢调质, 4—碳钢调质或正火,57—调质钢与1毫米大轮分度圆直径d2155.934516毫米外锥距Ra89.1913389毫米大端端面齿距p27.2157072毫米小轮齿顶高h a111.4178718毫米大轮齿顶高h a2 5.90818554毫米小轮齿根高h f17.64112824毫米大轮齿根高h f213.1508145毫米小轮分度圆锥角δ10.5070985弧度29.0546041度大轮分度圆锥角δ2 1.06369782弧度60.9453959度小轮顶锥角δa10.65348872弧度37.44214535度大轮顶锥角δa2 1.14916034弧度65.84203722度小轮根锥角δf10.42163599弧度24.15796278度大轮根锥角δf20.91730761弧度52.55785465度小轮齿根角γ10.08546251弧度 4.896641315度大轮齿根角γ20.14639021弧度8.387541249度小轮分度圆理论弧齿厚Sa115.9498152毫米大轮分度圆理论弧齿厚Sa211.2658919毫米小轮齿角δt10.12489965弧度7.156222524度大轮齿角δt 20.12422946弧度7.117823623度γ 1 + γ2797.1分0.23311616中点锥距Rm74.1913389内锥距Ri59.1913389D c0*毫米*K111K120K130.25K i115.949815211.26589196.330117910.89449140.766883844.935774035.055323820.321888510.0701730615.674382611.2566459测量小轮齿厚处的锥距L1L89.1913389测量大轮齿厚处的锥距L2L89.1913389110.641757790.09882026小轮大端法向弦齿厚Sx n115.6743826大轮大端法向弦齿厚S xn211.2566459小轮大端法向弦齿高H n112.0596295大轮大端法向弦齿高H n2 6.0070058公差值选取计算:中点法向模数m mn7.20609986中点分度圆直径d m172.0609986d m2中点分度圆弧长之半L m1/2113.193152L m2/2F P145F P24545*±f pt120±f pt22020*齿形相对误差的公差f c111f c21111*切向综合公差F'i158F'i2一齿切向综合公差f'i126f'i2齿圈跳动公差Fr145Fr24545*齿厚 公差Ts180Ts2808080***最小法向侧隙jn min7474齿厚上偏差系数xe747474*****Ess10-25Ess20*齿厚上偏差Ess1-68Ess2齿厚下偏差Esi1-148Esi2制造误差补偿EsΔ125EsΔ22525***最大法向侧隙jn max208最高精度等级7齿坯顶锥母线跳动公差40齿坯基准端面跳动公差250.8937417132323232323232*****轴交角极限偏差±EΣ28.599734628.59973456承载能力验算:当量圆柱齿轮端面参数:小轮齿数Zv111.439589Zv2齿数比u v 3.24分度圆直径d v182.434821d v2当量圆柱齿轮中心距a v174.76182齿顶圆直径d va1101.4301d va1齿宽中点齿顶高h am19.49763961h am2半齿宽高度变位系数x hm10.318x hm2半齿宽切向变位系数x sm10.00345x sm2基圆直径d vb176.1598439αvt0.392699082d vb2端面重合度εvα 1.40825269g vα29.45412216纵向重合度εvβ0总重合度εvγ 1.40825269当量圆柱齿轮法向参数:齿数Zvn111.439589βvb0Zvn2分度圆直径d vn182.434821d vn2齿顶圆直径d van1101.4301d van2基圆直径d vbn176.1598439d vbn2重合度εvαn 1.40825269刀具齿顶高h a07.47993165刀尖圆角半径ρa0名义切向力Fmt6938.56608N使用系数K A 1.5(工作条件原动机均匀平稳,从动机中等振动)m10.01877813m20.060841134m edN0.02804977ya 1.65cv1cv40.9cv50.47cv6动载系数K V 1.0193739亚临界 1.019373899主共振齿向载荷分布系数K Hβ 1.65K Fβ 1.65K Hα0-E162)/(C160*C164K Fα02-E162)/(C160*C164*K Hα0齿间载荷分布系数K Hα 1.40825269K Fα 1.277832999C ZLZ H 2.37841423Z B 1.08632448Z EZ K0.85Z L0.922403034Z V试验齿轮接触疲劳极限ζHmin1500N/mm2注:按合理的制造成本和中等质量考虑。
1. 齿面接触疲劳强度的计算齿面接触疲劳强度的计算中,由于赫兹应力是齿面间应力的主要指标,故把赫兹应力作为齿面接触应力的计算基础,并用来评价接触强度。
齿面接触疲劳强度核算时,根据设计要求可以选择不同的计算公式。
用于总体设计和非重要齿轮计算时,可采用简化计算方法;重要齿轮校核时可采用精确计算方法。
分析计算表明,大、小齿轮的接触应力总是相等的。
齿面最大接触应力一般出现在小轮单对齿啮合区内界点、节点和大轮单对齿啮合区内界点三个特征点之一。
实际使用和实验也证明了这一规律的正确。
因此,在齿面接触疲劳强度的计算中,常采用节点的接触应力分析齿轮的接触强度。
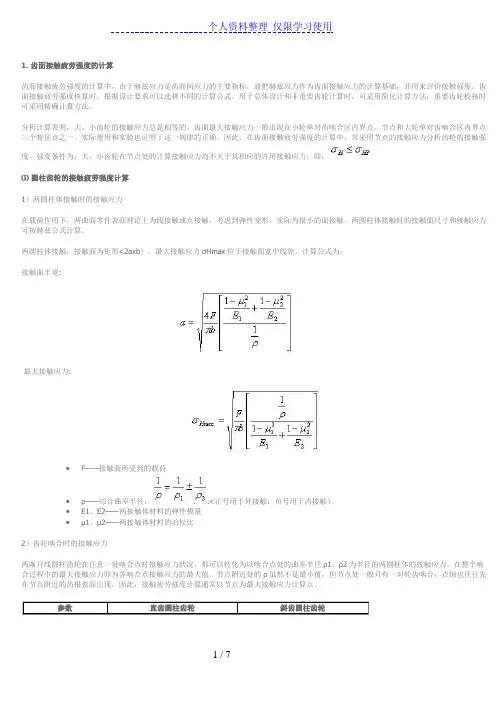
强度条件为:大、小齿轮在节点处的计算接触应力均不大于其相应的许用接触应力,即:⑴圆柱齿轮的接触疲劳强度计算1)两圆柱体接触时的接触应力在载荷作用下,两曲面零件表面理论上为线接触或点接触,考虑到弹性变形,实际为很小的面接触。
两圆柱体接触时的接触面尺寸和接触应力可按赫兹公式计算。
两圆柱体接触,接触面为矩形<2axb),最大接触应力σHmax位于接触面宽中线处。
计算公式为:接触面半宽:最大接触应力:∙F——接触面所受到的载荷∙ρ——综合曲率半径,<正号用于外接触,负号用于内接触)∙E1、E2——两接触体材料的弹性模量∙μ1、μ2——两接触体材料的泊松比2)齿轮啮合时的接触应力两渐开线圆柱齿轮在任意一处啮合点时接触应力状况,都可以转化为以啮合点处的曲率半径ρ1、ρ2为半径的两圆柱体的接触应力。
在整个啮合过程中的最大接触应力即为各啮合点接触应力的最大值。
节点附近处的ρ虽然不是最小值,但节点处一般只有一对轮齿啮合,点蚀也往往先在节点附近的齿根表面出现,因此,接触疲劳强度计算通常以节点为最大接触应力计算点。
,3)圆柱齿轮的接触疲劳强度将节点处的上述参数带入两圆柱体接触应力公式,并考虑各载荷系数的影响,得到:接触疲劳强度的校核公式为:接触疲劳强度的设计公式为:∙KA——使用系数∙KV——动载荷系数∙KHβ——接触强度计算的齿向载荷分布系数∙KHα——接触强度计算的齿间载荷分配系数∙Ft——端面内分度圆上的名义切向力,N;∙T1——端面内分度圆上的名义转矩,N.mm;∙d1——小齿轮分度圆直径,mm;∙ b ——工作齿宽,mm,指一对齿轮中的较小齿宽;∙u ——齿数比;∙ψd——齿宽系数,指齿宽b和小齿轮分度圆直径的比值<ψd=b/d1)。
直齿圆锥齿轮的传动计算产ll设it-时,多T-川这种设计方法-1 17-15农Q;一‘ri F1,'-1 t:和1'1 t:向F没汁的过程4f1lxi 7-1,所示,,l_成三维装13模型后,Invrnnr允许川)、为模型文件(包括之前生成的零件)折定特件如物理I }性.这样可方便存后期对模T1进行下程分析和计算以及仿真等『以图7-I6中的零件—泵盖模眨为例,从图7-17所示的特性长中可扮出In%rnlor己经分析出了模创的质址、休积,1G心以从惯性叮几L7.等(云十算模型的主轴惯件w外.还可汁算出模型相对f157.轴的惯性特性。
此外.重心位钱也可直说缺示出来,如图7-16所示.在币心符号处的球形显示门听选零件的敢心f立片.箭头抬示S,1,%轴的力向除r物理特性外.MI图7-17所示,特性卜中还包括模IV的概要、项II、状态等信L.,川户可报据实际悄况坑叮,方便以后夜询和竹理、生成气维装配模10后.InvrldIIr还可进行干涉检六,4u州7-1R,图7-19所示.模型上的深色!K城tli示出r发生1-涉的部位.if f1l ili r十涉检0报告C丧达视图设计在传统的二维设计,卜.绘制部件的分解表达视图钻很复杂和费时的事.要模拟装配部件的动作过程史是儿.r不'If能的fi,在二维设什环境F .完成这任务是很轻松的,石.,.3直齿圆锥齿轮的传动计算直齿圆柱齿轮的端面参数被定为标准值.但直齿圆锥齿轮的轮齿沿圆锥母线从大端到小端逐渐收缩,故在圆锥齿轮不同端面上.其直径与模数等就有大端和小端之分.为减小测量误差,也为了便于加工及估什机构尺寸,通常取圆锥齿轮的大端参数为标准值,其大端模数按表6-1选取.但是无论大端或者小端.直齿圆锥齿轮不同背锥上的齿顶高系数h;径向齿顶间隙系数c’和压力角。
均相等.其中a=200;一般取h; =l.c'=0.2.标准直齿团锥齿轮的几何尺寸计算公式可参见表6-7.ri L向下的Lt if方法见在装配环境下FN一个主要零件或部件为参考)设O其他零件。
数值备注使用系数K A 1表1动载系数K V 1.38级精度齿间载荷分布K α1K F α=K H α=11.43齿向载荷分布K β 1.1表3齿宽系数ΦR 齿宽b/锥距R 0.330.25~0.35,通常取1/32若已知P(kw)1若已知T(N.mm)9946.88参数小齿轮大齿轮备注齿数z 2448Z2=Z1*u分锥角δ(°)26.5763.43tan δ1=Z1/Z2斜齿轮当量齿数Z v 26.83107.33Zv=Z/cos δ齿形系数Y Fa 2.577 2.152应力矫正系数Y sa 1.58 1.69Y Fa *Y sa 4.08 3.65相配合的齿轮数j 11工作寿命L(h)班次*班时*天数*年限转速n(r/min)960480应力循环次数N 4.15E+09 2.07E+09N=60njL 寿命系数K N 0.90.95表4齿面硬度(HBS)300250疲劳极限σFE 400380表6中ML与MQ 许用应力[σF ]240240.67[σ]=K N *σFE /S,S取1.5Yfa*Ysa/[σF ]0.01700.0151选大的带入计算1.48公式见附录参数小齿轮大齿轮备注应力循环次数N 4.15E+09 2.07E+09N=60njL 寿命系数K N 0.90.95表5齿面硬度(HBS)300250疲劳极限σHlim 620550表7中ML与MQ 许用应力[σH ]558522.5[σ]=KN*σHlim/S,S取1取[σH ]小值取[σH ]小值189.8表846.56公式见附录按齿根弯曲疲劳强度计算最小模数参数与条件载荷分布系数K=K A *K V *K α*K β=传动比u 小齿轮传递功率与转矩2选1输入72000锥齿轮最小模数m 按齿面接触疲劳强度计算最小分度圆522.5弹性影响系数Z E (MPa 1/2)锥齿轮最小分度圆d1开式齿轮m≥ 1.70放大1.1~1.15倍m≥ 1.48d1≥46.56附录 所用公式类别备注许用应力[σF]S取1.5许用应力[σH]S取1说明:1)开式齿轮传动:按齿根弯曲疲劳强度设计公式作齿轮的设计计算,不按齿面接触疲劳强度设计公式计算,也无需用齿面接触疲劳强度校核公式进行校核。
圆锥齿轮参数设计0.概述锥齿轮是圆锥齿轮的简称,它用来实现两相交轴之间的传动,两轴交角S称为轴角,其值可根据传动需要确定,一般多采用90 °锥齿轮的轮齿排列在截圆锥体上,轮齿由齿轮的大端到小端逐渐收缩变小,如下图所示。
由于这一特点,对应于圆柱齿轮中的各有关"圆柱"在锥齿轮中就变成了”圆锥”,如分度锥、节锥、基锥、齿顶锥等。
锥齿轮的轮齿有直齿、斜齿和曲线齿等形式。
直齿和斜齿锥齿轮设计、制造及安装均较简单,但噪声较大,用于低速传动(<5m/s );曲线齿锥齿轮具有传动平稳、噪声小及承载能力大等特点,用于高速重载的场合。
本节只讨论S=90。
的标准直齿锥齿轮传动。
1.齿廓曲面的形成直齿锥齿轮齿廓曲面的形成与圆柱齿轮类似。
如下图所示,发生平面1与基锥2相切并作纯滚动,该平面上过锥顶点0的任一直线OK的轨迹即为渐开锥面。
渐开锥面与以0为球心,以锥长R为半径的球面的交线AK为球面渐开线,它应是锥齿轮的大端齿廓曲线。
但球面无法展开成平面,这就给锥齿轮的设计制造带来很多困难。
为此产生一种代替球面渐开线的近似方法。
2.锥齿轮大端背锥、当量齿轮及当量齿数(1)背锥和当量齿轮下图为一锥齿轮的轴向半剖面,其中DOAA为分度锥的轴剖面,锥长OA称锥距,用R表示;以锥顶O为圆心,以R为半径的圆应为球面的投影。
若以球面渐开线作锥齿轮的齿廓,则园弧bAc为轮齿球面大端与轴剖面的交线,该球面齿形是不能展开成平面的。
为此,再过A作O1A丄OA ,交齿轮的轴线于点01。
设想以OO1为轴线,以O1A为母线作圆锥面O1AA,该圆锥称为锥齿轮的大端背锥。
显然,该背锥与球面切于锥齿轮大端的分度圆。
由于大端背锥母线1A与锥齿轮的分度锥母线相互垂直,将球面齿形的圆弧bAc投影到背锥上得到线段b'Ac',圆弧bAc与线段b'Ac'非常接近,且锥距R与锥齿轮大端模数m之比值愈大(一般R/m>30 ),两者就更接近。
标准直齿圆柱齿轮传动的强度计算工程(一)轮齿的受力分析进行齿轮的强度计算时,首先要知道齿轮上所受的力,这就需要对齿轮传动作受力分析,齿轮传动一般均加以润滑,啮合轮齿间的摩擦力通常很小,计算轮齿受力时,可不予考虑。
沿啮合线作用在齿面上的法向载荷Fn垂直于齿面,为了计算方便,将法向载荷Fn在节点P处分解为两个相互垂直的分力,即圆周力Ft与径向力Fr, 。
由此得Ft=2T1/d1 ;Fr=Fttanα ;Fn=Ft/cosα (a)式中:T1—小齿轮传递的转矩,N·mm;d1—小齿轮的节圆直径,对标准齿轮即为分度圆直径,mm;α—啮合角,对标准齿轮,α=20°。
(二)齿根弯曲疲劳强度计算轮齿在受载时,齿根所受的弯矩最大,因此齿根处的弯曲疲劳强度最弱。
当轮齿在齿顶处啮合时,处于双对齿啮合区,此时弯矩的力臂虽然最大,但力并不是最大,因此弯矩并不是最大。
根据分析,齿根所受的最大弯矩发生在轮齿啮合点位于单对齿啮合区最高点。
因此,齿根弯曲强度也应按载荷作用于单对齿啮合区最高点来计算。
由于这种算法比拟复杂,通常只用于高精度的齿轮传动(如6级精度以上的齿轮传动)。
对于制造精度较低的齿轮传动(如7,8,9级精度),由于制造误差大,实际上多由在齿顶处啮合的轮齿分担较多的载荷,为便于计算,通常按全部载荷作用于齿顶来计算齿根的弯曲强度。
当然,采用这样的算法,齿轮的弯曲强度比拟充裕。
右边动画所示为齿轮轮齿啮合时的受载情况。
动画演示为齿顶受载时,轮齿根部的应力图。
在齿根危险截面AB处的压应力σc仅为弯曲应力σF的百分之几,故可忽略,仅按水平分力pcacosγ所产生的弯矩进行弯曲强度计算。
假设轮齿为一悬臂梁,那么单位齿宽(b=1)时齿根危险截面的弯曲应力为取,并将(a)式代入。
对直齿圆柱齿轮,齿面上的接触线长L即为齿宽b(mm),得令YFa是一个无量纲系数,只与齿轮的齿廓形状有关,而与齿的大小(模数m)无关。