第二章 X射线运动学衍射理论.
- 格式:ppt
- 大小:2.92 MB
- 文档页数:38









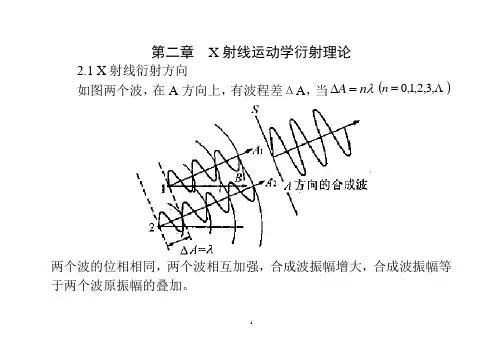
第二章 X 射线运动学衍射理论2.1 X 射线衍射方向如图两个波,在A 方向上,有波程差ΔA ,当λn A =∆() ,3,2,1,0=n两个波的位相相同,两个波相互加强,合成波振幅增大,合成波振幅等于两个波原振幅的叠加。
在B 方向上,波程差λ)2/1(+=∆n B () ,3,2,1,0=n ,两波的位相不同,一个波的波峰与另一个的波谷重叠,合成波振幅为零。
如下图b 。
两波的波程差随方向不同而不同,位相差也有变化。
在A 方向和B 方向之间的方向上,合成波振幅介于前两者之间。
如上图c 。
因此,两个波的波程不同就会产生位相差,随着位相差的变化,其合成波振幅也有变化。
下图是平行的单色X射线以θ角入射到晶面上,在与入射线成2θ角的方向上的散射波。
对于波1和1a,它们在1′和1a′方向上的散射波位相相同,波程差为零。
两波互相加强。
A晶面上该方向的所有散射线均互相加强。
对于波1和2分别被K和L原子散射时,1′和2′的波程差为ML+NL=2d′sinθ,如果波程差2d′sinθ为波长的整数倍,即满足:时,散射波1′和2′的位相相同,两波相互加强。
上式就是布拉格定律。
它是X射线衍射的最基本的定律。
式中n为整数,称为反射级数。
因sinθ≤1,n的大小有一定限制。
n =1时称为第一级反射。
对于一定的λ和d′,存在可以产生衍射的若干个角θ1,θ2,θ3,…,分别对应于n =1,2,3,…。
在满足布拉格定律的方向上,各晶面的散射波位相都相同,其振幅互相加强,散射强度增加,这样,在与入射线成2θ角的方向上就会出现衍射线。
而其他方向上的散射波位相不同,振幅互相抵消,散射强度减弱或完全消除。
X射线衍射和可见光反射有相似的现象,如:入射束、反射面法线、反射束三者处于同一平面,且入射角和反射角相等,但衍射和反射有如下本质的区别:a. X射线不仅被晶体表面的原子散射,而且被晶体内层原子散射,衍射线是晶体中X射线路径上所有原子散射波干涉的结果。