下载文档原格式
试卷一22011/20~1/8较多的地区取其中的较大值。
2屋盖横向支撑以构成几何不变体系。
3刚性45、当实腹6 23 7820mm 2201A(A) 等稳定 (B) 等刚度 (C) 等强度 (D) 计算长度相等 2 A (A) 垫板数不宜少于两个 (B) 垫板数不宜少于一个 (C) 垫板数不宜多于两个 (D) 可不设垫板3 D (A) 支座竖杆中的内力 (B) 下弦杆中的最大内力 (C) 上弦杆中的最大内力 (D) 腹杆中的最大内力4、槽钢檩条的每一端一般用下列哪一项连于预先焊在屋架上弦的B(A) 一个普通螺栓 (B) 两个普通螺栓 (C) 安装焊缝 (D) 一个高强螺栓5、如轻型钢屋架上弦杆的节间距为L(D )。
(A) L (B) 0.8L (C) 0.9L (D) 侧向支撑点间距 6 C (A) 端竖杆处 (B) 下弦中间 (C) 下弦端节间 (D) 斜腹杆处 7 A(A) 可以受压 (B) 只能受拉 (C) 可以受弯 (D) 可以受压和受弯 8、某房屋屋架间距为6m 24m 24m 。
房屋C(A) 上弦横向支撑 (B) 下弦横向支撑 (C) 纵向支撑(D) 垂直支撑9、梯形屋架的端斜杆和受较大节间荷载作用的屋架上弦杆的合理C(A) 等肢角钢相连 (B) 不等肢角钢相连(C) 不等肢角钢长肢相连 (D) 等肢角钢十字相连10 C(A)屋面活荷载 (B)雪荷载(C)屋面活荷载和雪荷载两者中的较大值 (D)屋面活荷载和雪荷载20182636试卷二220123时它0.9L 4度高的连接焊透的k型坡口焊缝5至少两块填板6上玄横向支撑下玄横向支撑下玄纵向支撑竖向支撑系杆201、门式刚架轻型房屋屋面 A区取其中的较大值。
(A) 120—18 (B) 130—18 (C) 120—1 5(D) 130—1 52 B不变体系。
(A) 屋盖纵向支撑 (B) 屋盖横向支撑 (C) 刚性系杆(D) 柔性系杆3C(A) 刚性和柔性 (B) 刚性或柔性 (C) 刚性 (D) 柔性4 AB(A) 2 (B) 3 (C) 4 (D) 55 A(A) (B)不等边角钢短边相(C) (D)等边角钢相连6、屋B(A)10mm (B)20mm (C)30mm (D)40mm7 CA(A)强度 (B)刚度 (C)整体稳定 (D)局部稳定8Q≤30t度l≤6m Al~A5 A的(A) 加强上翼缘 (B) 加强下翼缘 (C) 设制动梁(D) 设制动桁架20182、为何冷弯薄壁构件在其强度和稳定性计算公式中截面特性以63、简述D6试卷三2201件起整体作填板2整体稳定3长度Lox=0.8 L Loy= 1L L为杆件的几何长度。
H 型截面轴心受压柱实验报告学号： 姓名： 任课老师： 实验老师：实验日期：2012年03月30日一、实验目的：1、通过试验掌握钢构件的试验方法，包括试件设计、加载装置设计、测点布置、试验结果整理等方法。
2、通过试验观察十字型截面轴心受压柱的失稳过程和失稳模式。
3、将理论极限承载力和实测承载力进行对比，加深对轴心受压构件稳定系数计算公式的理解。
二、实验原理：1、基本微分方程根据开口薄壁杆件理论，具有初始缺陷的轴心压杆的弹性微分方程为： 2、扭转失稳欧拉荷载H 型截面为双轴对称截面，因其剪力中心和形心重合，有 x 0= y 0 = 0，代入上式可得：''0()0IV IVx EI v v Nv -+= (a)''0()0IV IV y EI u u Nu -+= (b)''''2''''000()()0IV IV t EI GI r N R ωθθθθθθ---+-=(c)说明H 型双轴对称截面轴心压杆在弹性阶段工作时，三个微分方程是相互独立的，可分别单独研究。
在弹塑性阶段，当研究（a ）式时，只要截面上的产于应力对称与 Y 轴，同时又有00u =和00θ=，则该式将始终和其他两式无关，可单独研究。
这样，压杆将只发生Y 方向的位移，整体失稳呈弯曲变形状态，称为弯曲失稳。
这样，式（b ）也是弯曲失稳，只是弯曲失稳的方向不同而已。
对于式（c ），如果残余应力对称与 X 轴和 Y 轴分布，同时假定，00u =和00θ=则压杆将只发生绕 Z 轴的转动，失稳时杆件呈扭转变形状态，称为扭转失稳。
对于理想压杆，则有上面三式可分别求得十字型截面压杆的欧拉荷载为： 绕X 轴弯曲失稳：220xEx xEI N lπ=，绕Y 轴弯曲失稳：220yEy yEI N l π=绕Z 轴扭转失稳：222001()E t EI N GI l r ωθθπ=+ H 字型截面压杆的计算长度和长细比为：绕 X 轴弯曲失稳计算长度：00x x l l μ=，长细比0/x x x l i λ= 绕Y 轴弯曲失稳计算长度：00y y l l μ=，长细比0/y y y l i λ=绕Z 轴扭转失稳计算长度：00l l θθμ=，端部不能扭转也不能翘曲时0.5θμ=，长细比θλ=上述长细比均可化为相对长细比：λ=3、稳定性系数计算公式H 字型截面压杆的弯曲失稳极限承载力：根据欧拉公式22Ew w EA N πλ=得222y Ew w w f Eπσλλ==佩利公式：0(1)2y Excr f εσσ++=再由公式cryf σϕ=可算出轴心压杆的稳定性系数。
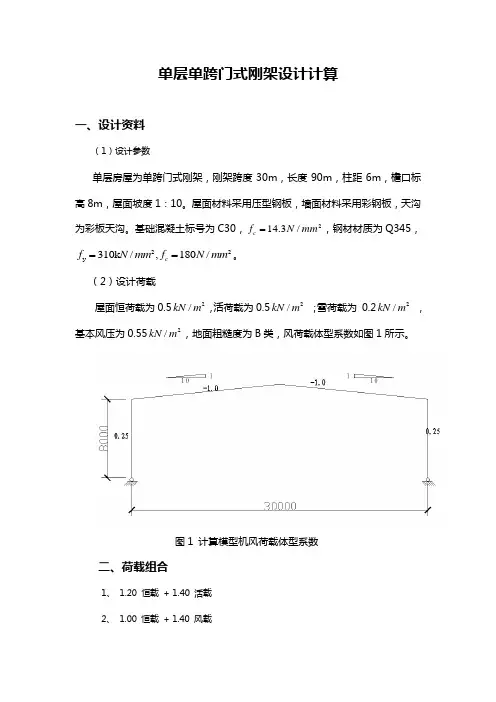
单层单跨门式刚架设计计算一、设计资料（1）设计参数单层房屋为单跨门式刚架，刚架跨度30m ，长度90m ，柱距6m ，檐口标高8m ，屋面坡度1：10。
屋面材料采用压型钢板，墙面材料采用彩钢板，天沟为彩板天沟。
基础混凝土标号为C30，214.3/c f N mm =，钢材材质为Q345，22y 310k /,180/c f N mm f N mm ==。
（2）设计荷载屋面恒荷载为0.52/kN m ，活荷载为0.52/kN m ；雪荷载为 0.22/kN m ，基本风压为0.552/kN m ，地面粗糙度为B 类，风荷载体型系数如图1所示。
图1 计算模型机风荷载体型系数二、荷载组合1、 1.20 恒载 + 1.40 活载2、 1.00 恒载 + 1.40 风载3、1.00 恒载+ 1.40 x 0.90 活载+ 1.40 x 0.90 风载4、1.35 恒载三、内力计算1、计算模型（如图2）图2 节点及单元编号图2、荷载工况荷载工况如图3恒载活载左风右风图3 荷载工况图3、各工况内力恒载、活载、作风和右风作用下的钢架内力如图4—图7。
轴力图（KN）剪力图（KN）弯距图(kN.m)图4 恒载作用下钢架内力图轴力图(kN)剪力图(kN)弯距图(kN.m)图5 活载作用下钢架内力图轴力N图(kN)剪力图(kN)弯距图(kN.m)图6 左风作用下钢架内力图轴力图(kN)剪力图(kN)弯距图(kN.m)图7 右风作用下钢架内力图4、组合内力选取荷载组合1（1.20 恒载+ 1.40 活载）对构件内力值进行验算。
该组合下的构件内力值见表1。
表1 工况1下组合内力表5、构件尺寸和截面特性表2 构件尺寸和截面特性表中：面积和惯性矩的上下行分别指小头和大头的值四、构件截面验算1、宽厚比验算 翼缘板自由外伸宽厚比()2008/29.612.410-=<=，满足规程限值要求。
腹板高厚比80021097.52068-⨯=<=（），满足规程限值要求。
第二章如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图（a ）理想弹性－塑性 （b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅非弹性阶段：'()tan '()tan yyy y f f f E f E σεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？ 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610yf E ε===⨯卸载后残余应变：0c ε= 可恢复弹性应变：0.00114y c εεε=-=（2）B 点：卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f E εε=-= 可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变：0.05869c c E σεε=-= 可恢复弹性应变：0.00131y c εεε=-=试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。
第二章如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图（a ）理想弹性－塑性 （b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅非弹性阶段：'()tan '()tan yyy y f f f E f E σεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？ 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610yf E ε===⨯卸载后残余应变：0c ε= 可恢复弹性应变：0.00114y c εεε=-=（2）B 点：卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f E εε=-= 可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变：0.05869c c E σεε=-= 可恢复弹性应变：0.00131y c εεε=-=试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。
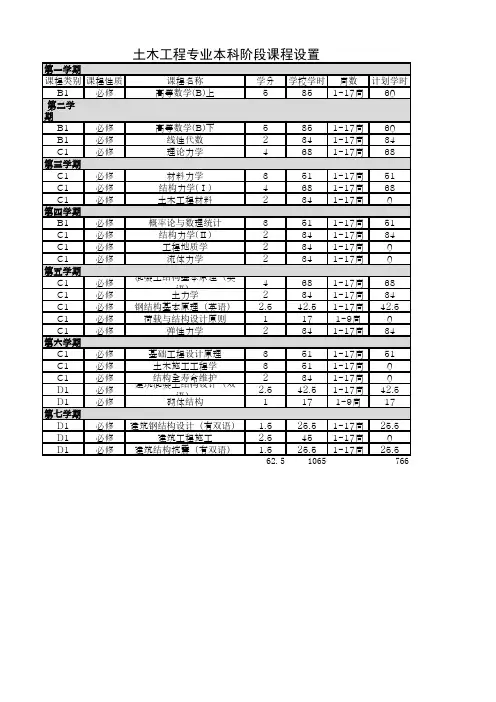
《钢结构基本原理》课程教学大纲课程编号：031126 学分：2.5 总学时：43 实验学时：8（另排）大纲执笔人：罗烈大纲审核人：陈以一一、课程性质与目的《钢结构基本原理》为土木工程专业本科学生的必修课，属于土木工程专业的专业基础课。
钢结构是现代土木工程的基本结构形式之一。
设置本课程的目的，是使学生全面掌握钢结构材料、构件和连接的基础知识，理解钢结构分析的基本原理，为进一步学习各类钢结构与金属结构的设计、制作和建造提供基础。
本课程开设双语教学班。
二、课程面向学生土木工程专业、港口航道与海岸工程专业三、课程基本要求1．了解钢结构的特点、历史、现状及发展前景；2．掌握钢结构材料的基本性能；3．了解钢结构的典型破坏模式、破坏原因和力学分析的基本方法；4．掌握钢结构基本构件及连接的性能、受力分析与设计计算；5．了解钢结构体系的组成原理和典型结构形式的设计要点。
四、实验基本要求通过一次认知实验、二次综合实验、一次自主设计实验，加深对钢结构基本概念和基本理论的理解，了解钢结构构件或连接的实验流程与方法，培养学生的实验技能和创新意识。
详见与本课程同步的《钢结构基本原理实验》课程。
五、课程基本内容1．绪论钢结构的特点及应用；钢结构发展的历史、现状和趋势；钢结构的构件组成和主要结构形式2．钢结构材料钢材在单向均匀受拉时的工作性能；钢材在单轴反复应力作用下的工作性能；钢材在复杂应力作用下的工作性能；钢材抗冲击性能及冷弯性能；影响钢材性能的一般因素；钢材的脆性破坏和延性破坏、疲劳破坏和损伤累积破坏；钢结构防护；钢结构用钢材的分类。
3．钢结构的主要破坏形式整体失稳破坏；板件局部失稳与屈曲后强度；强度破坏与塑性重分布；疲劳；脆性断裂及其机理。
4．钢结构的连接连接的主要类型；对接焊缝构造和计算；角焊缝构造和计算；普通螺栓连接构造和计算；高强螺栓连接构造和计算。
5．受拉构件及索受拉构件的强度，净截面概念；截面效率；拉弯构件的截面强度及强度计算准则；轴力和弯矩的相关关系；索的基本力学性质。
钢结构基本原理自主实验“H型柱受压构件试验”实验报告小组成员：实验教师：杨彬实验时间： 2016.11.8一、实验目的1. 通过试验掌握钢构件的试验方法，包括试件设计、加载装置设计、测点布 置、试验结果整理等方法。
2. 通过试验观察工字形截面轴心受压柱的失稳过程和失稳模式。
3. 将理论极限承载力和实测承载力进行对比，加深对轴心受压构件稳定系数计算公式的理解。
二、实验原理1、轴心受压构件的可能破坏形式轴心受压构件的截面若无削弱，一般不会发生强度破坏，整体失稳或局部失稳总发生在强度破坏之前。
其中整体失稳破坏是轴心受压构件的主要破坏形式。
轴心受压构件在轴心压力较小时处于稳定平衡状态，如有微小干扰力使其偏离平衡位置， 则在干扰力除去后，仍能回复到原先的平衡状态。
随着轴心压力的增加，轴心受压构件会由稳定平衡状态逐步过渡到随遇平衡状态，这时如有微小干扰力使基偏离平衡位置，则在干扰力除去后，将停留在新的位置而不能回复到原先的平衡位置。
随遇平衡状态也称为临界状态，这时的轴心压力称为临界压力。
当轴心压力超过临界压力后，构件就不能维持平衡而失稳破坏。
轴心受压构件整体失稳的破坏形式与截面形式有密切关系，与构件的长细比也有关系。
一般情况下，双轴对称截面如工形截面、H 形截面在失稳时只出现弯曲变形，称为弯曲失稳。
2、基本微分方程（1）钢结构压杆一般都是开口薄壁杆件。
根据开口薄壁杆件理论，具有初始缺陷的轴心压杆的弹性微分方程为：由微分方程可以看出构件可能发生弯曲失稳，扭转失稳，或弯扭失稳。
对于H 型截面的构件来说由于 所以微分方程的变为：由以上三个方程可以看出： 3个微分方程相互独立只可能单独发生绕x 弯曲失稳，或绕y 轴弯曲失稳，或绕杆轴扭转失稳。
()()020000t IV0IV =''-''+''+''-''-''--θθθθθθωR N r u Ny v Nx GI EI ()00IVIV =''+''+-θNy u N u u EI y ()0IV0IV =''-''+-θNx v N v v EI x 000==y x ()()0200t 0IVω=''-''+''-''--θθθθθθR N r GI EI IV ()0IV 0IVy=''+-u N u uEI ()IV0IV x =''+-v N v v EI失稳形式的类型取决于长细比，长细比大的发生。
