圆周角中考题集锦(含答案)

圆周角的练习题初三圆周角是指以圆心为顶点的角，它的度数等于所对弧的度数。

在初三的几何学中，圆周角是一个重要的概念，掌握圆周角的计算方法对于解决几何题目至关重要。

本文将为大家提供一些圆周角的练习题，帮助初三学生巩固和掌握这一知识点。

练习题一：已知直径AB的圆上一点C，连结AC和BC两条弦。

求∠ACB的度数。

解析：根据圆的性质可知，在圆上以弦为底的两个圆周角是等角，所以∠ACB = ∠AEB。

而直径AB是圆上的一条直径，它对应的圆周角为180度。

因此，∠ACB = ∠AEB = 180度。

练习题二：已知弧AC与弧BC分别是圆上的两个等分弧，且∠ACB = 20度。

求弧AC的度数。

解析：根据题目可知，∠ACB为圆周角，而弧AC和弧BC是等分弧，所以它们所对应的圆周角也相等，即∠ACB = ∠AEB。

而∠ACB 已知为20度，所以∠AEB = 20度。

而直径AB上的圆周角为180度，所以弧AC的度数为180度减去∠AEB的度数，即弧AC = 180度 - 20度 = 160度。

练习题三：已知直径AB的圆上一点C与D，连结AC和BD两条弦，交于点E。

若∠AEB = 70度，求证：∠ACD = 35度。

解析：要证明∠ACD = 35度，可以利用等角的性质。

根据题目已知，∠AEB = ∠AED = 70度。

而由圆周角的性质可知，∠ACD =∠AEB = 70度。

又∠ACD和∠ACB是同弦内角和对应的圆周角，所以有∠ACD = 180度 - ∠ACB。

将已知条件带入，∠ACD = 180度 - 70度= 110度。

由此可知，∠ACD的度数为35度。

练习题四：已知弦AB的长为8cm，圆心角∠AOB的度数为60度，求弦AB所对应的弧长。

解析：弦AB所对应的弧可以通过圆心角的度数与圆周长的比例来求解。

已知圆心角∠AOB的度数为60度，而整个圆的圆心角为360度，所以∠AOB所对应的弧所占圆周长的比例为60度/360度= 1/6。

0° 0 中考数学专项练习圆周角定理（含解析）是⊙O 的直径，弦 CD ⊥ AB ，∠ CAB=40 D+ ∠ABD 的度数为〔 〕A. 100°B. 110°C. 120°D. 1502.A 、C 、B 是⊙O 上三点，假设∠ AOC=40°，那么∠ ABC 的度数是 ()A. 1 0°B.C.80°C 的外接圆，∠ OCB=40 °，那么∠ A 的度数等于A. 6B. 5C. 4，连接 BD ， O D. 3.如图，⊙ O 是△ A一】单项选择题 图，那么DD. 304.如图，EF是⊙ O的直径，把∠ A为60°的直角三角板ABC的一条直角边BC放在直线EF上，斜边AB 与⊙ O交于点P，点B与点O 重合．将三角板ABC 沿OE方向平移，使得点B与点E重合为止．设∠ POF＝x°，那么x 的取值范围是( )A. 30≤x≤60B. 30≤x≤90C.30≤x≤120D.60≤x≤1205.如图，圆心角∠ BOC=100°，那么圆周角∠ BAC 的大小是A. 50°B.100°C.130°D.200°6.以下各命题正确的选项是:〔〕A. 假设两弧相等，那么两弧所对圆周角相等B. 有一组对边平行的四边形是梯形.C. 垂直于弦的直线必过圆心 D. 有一边上的中线等于这边一半的三角形是直角三角形.7.某数学研究性学习小组制作了如下的三角函数计算图尺：在半径为 1 的半圆形量角器中，画一个直径为 10的圆，把刻度尺 CA 的 0刻度固定在 刻度尺可以绕点 O 旋转．从图中所示的图尺可读出 sin 〕B.C.D. 【二】填空题 8.如图， P 是⊙ 0 直径那么∠ A 的度数为10.如图，在以 AB 为直径的半圆中，有一个边长为 1 的内接正方形 CF ，那么以 AC 和 BC 的长为两根的一元二次方程是 ___ ．.如图， AB 是⊙的直径，点 C 是半径 OA 的中点，过点 C 作DE ⊥AB ，交 O 于点 D ，E 两点，过点 D 作直径 DF ，连结 AF ，那么∠ DEA= AB 延长线上的点， PC 切⊙0于 C 、假设∠ P=40是半圆 的直径， ，那么 的大小是假设∠ BO ∠BCD ，那么弧 BD 的长为11 A. 半圆的圆 AOB 的o12. 如图，⊙ O的半径为6，四边形ABCD 内接于⊙ O，连接OB，OD，13. __________________________ 如图，AB 是⊙O的直径，C、D、E都是⊙ O上的点，∠ A=55°，∠B=70°，那么∠ E的度数是．14. _____________________________________ 如图，AD 和AC 分别是⊙ O的直径和弦，且∠ CAD=30°，OB⊥A D交AC于点B，假设OB=5，那么BC等于__________________________ ．O 的内接四边形ABCD 中，∠ A=105°，那么∠ BOD 等于【三】解答题16. 如图，在⊙ O 中，AC 与BD 是圆的直径，BE⊥ AC，CF⊥BD，垂足分别为E、F形ABCD 是什么特殊的四边形？请判断并说明理由；2〕求证：BE=CF．17. 如图，AB 是? O的直径，点C在? O上，过点C的直线与AB 的延长线交于点P，AC=PC，∠ COB=2∠PCB.〔1〕求证：PC是? O 的切线；〔2〕求证：BC= AB ；〔3〕点M 是弧AB 的中点，CM 交AB 于点N，假设AB=4 ，求MN ·M C 的值.【四】综合题18. 如图，⊙ O 是△ABC 的外接圆，AB=AC ，P是⊙O 上一点．〔1〕操作：请你只用无刻度的直尺，分别画出图①和图②中∠ P 的平分线；2〕说理：结合图②，说明你这样画的理由．〔1〕⊙D 的半径；〔2〕CE 的长． 【一】单项选择题【考点】垂径定理，圆周角定理 【考点】圆周角定理 【解析】【解答】根据圆周角和圆心角的关系解决问题，由〝一条弧所 对的圆周角等于它所对的圆心角的一半〞解答 . 【分析】此题考查了原周角和圆心角的联系 .【考点】圆周角定理【解析】【解答】解：在△ OCB 中， OB=OC 〔⊙ O 的半径〕，∴∠O BC=∠0CB 〔等边对等角〕；∵∠ OCB=40°，∠ C0B=180°﹣∠ OBC ﹣∠ 0CB ， ∴∠COB=100°； 又∵∠ A= ∠C0B 〔同弧所对的圆周角是所对的圆心角的一半〕 ， ∴∠ A=50 °， 应选 B 、【分析】在等腰三角形 OCB 中，求得两个底角∠ OBC 、∠0CB 的度数，然 后根据三角形的内角和求得∠ COB=100°；最后由圆周角定理求得∠ A 的 度数并作出选择．【考点】圆周角定理【考点】圆周角定理【解析】【分析】∠ BOC ，∠ BAC 是同弧所对的圆周角和圆心角，∠ B OC=2∠ BAC ，因为圆心角∠ BOC=100°，所以圆周角∠ BAC=50°.【点评】此题考查圆周角和圆心角，解此题的关键是掌握同弧所对的圆周 角和圆心角关系，然后根据题意来解答。

初三圆周角练习题圆周角在初三数学中是一个重要的概念，理解和掌握圆周角的性质及计算方法对解题非常关键。

下面给出一系列的圆周角练习题，帮助初三学生加深对这一概念的理解和应用。

题目一：已知半径为5cm的圆上的一条弧所对圆心角的度数是120°，求此弧的长度。

解析：根据圆周角的性质，圆周角的度数等于所对弧的度数，因此所求弧的度数也是120°。

由于圆周角的度数等于所对弧的弧长与半径的比值，设所求弧的弧长为L，则有120/360 = L/(2π×5)。

解方程可得L ≈ 10π/3 cm。

题目二：在半径为8cm的圆中，两条弦长分别为12cm和16cm，求这两条弦所对的圆周角的度数。

解析：根据圆周角的性质，圆周角的度数等于所对弦所对应的弧的度数，而弧长等于弦的长度。

设所求圆周角的度数为x°，根据等式关系12/8 = x/360 和16/8 = x/360，解这两个方程可得x ≈ 180° 和x ≈ 240°。

因此，一条弦所对圆周角的度数为180°，另一条弦所对圆周角的度数为240°。

题目三：一个扇形的圆心角是64°，对应的弧长为10π cm，求此扇形的面积。

解析：根据扇形面积公式，扇形的面积等于扇形所在圆的面积乘以圆心角的度数与360°的比值。

设扇形的面积为S，圆的面积为A，则有S/A = 64°/360° = 64/360。

解方程可得S = (64/360) × π × r^2，代入已知条件，可得S ≈ (64/360) × π × (10/2)^2 = 16π/9 cm^2。

题目四：在半径为3cm的圆中，一条弦的弦长为4cm，这条弦与半径所夹的圆周角的弧度数为1/6π rad，求该弦所对的弧长。

解析：根据圆周角的性质，弧度数等于所对弧的弧长与半径的比值。

圆周角定理专项练习30题（有答案）1．如图AB是⊙O的直径，C是⊙O上的一点，若AC=8cm，AB=10cm，OD⊥BC于点D，求BD的长．2．如图，在⊙O中，直径AB与弦CD相交于点P，∠CAB=40°，∠APD=65°．（1）求∠B的大小；（2）已知AD=6，求圆心O到BD的距离．3．已知AB是⊙O的直径，半径OC⊥AB，D为上任意一点，E为弦BD上一点，且BE=AD，求证：△CDE为等腰直角三角形．4．如图，AB是圆O的直径，AD=DC，∠CAB=30°，AC=2．求AD的长．5．如图，AB，CD是⊙O的两条弦，它们相交于点P，连接AD，BD．已知AD=BD=4，PC=6，求CD的长．6．如图，已知点C、D在以O为圆心，AB为直径的半圆上，且OC⊥BD于点M，CF⊥AB于点F交BD于点E，BD=8，CM=2．（1）求⊙O的半径；（2）求证：CE=BE．7．如图，A是以EF为直径的半圆上的一点，作AG⊥EF交EF于G，又B为AG上一点，EB的延长线交半圆于K，求证：（1）△AEB∽△KEA；（2）AE2=EB•EK．8．如图，BC是⊙O的直径，P为⊙O上一点，点A是的中点，AD⊥BC，垂足为D，PB分别与AD、AC相交于点E、F．（1）若∠BAD=36°，求∠ACB，∠ABP；（2）如果AE=3，求BE．9．如图，△ABC内接于⊙O，AB=AC，弦AD交BC于点E，AE=4，ED=5，（1）求证：AD平分∠BDC；（2）求AC的长；（3）若∠BCD的平分线CI与AD相交于点I，求证：AI=AC．10．如图，AB是⊙O的直径，点C在⊙O上，AB=6，AC=5，求tanA的值．11．如图，AB是⊙O的直径，弦CD与AB相交于点E，∠ACD=60°，∠CEB=100°．求∠ADC的度数．12．已知如图，在⊙O中，弦BC平行于半径OA，AC交BO于M，∠C=25°．求∠AMB的度数．13．如图，⊙O是△ABC的外接圆，∠A=45°，BD是直径，且BD=2，连接CD，求BC的长．14．已知：如图，AD平分∠BAC，DE∥AC，且AB=5cm，求DE的长．15．已知如图，在△ABC中，∠BAC=90°，AB=AC=，D是BC中点，作半径是的圆经过点A和D且交AB于F，交AC于E．求∠ADF的正弦值．16．如图，在△ABC中，AB是⊙O的直径，⊙O与AC交于点D，AB=，∠B=60°，∠C=75°，求∠BOD的度数．17．如图：在⊙O中，AB是直径，∠ACB的平分线交⊙O于点D，AD=5cm．求：BD与⊙O半径的长．18．如图，AB是⊙O的直径，P是弦AC延长线上的一点，且AC=PC，直线PB交⊙O于点D，若∠BDC=30°，求∠P的度数．19．如图，△ABC中，∠B=45°，∠C=60°，AB=cm，以AB为直径的⊙O交BC于点D，求CD的长？20．如图，已知AD是△ABC的高，AE是△ABC的外接圆的直径．（1）求证：AC•AB=AD•AE；（2）若AB=6，AC=5，AD=3，求⊙O的面积．21．如图，⊙0为四边形ABCD的外接圆，AC为⊙0的直径，CD∥AB，点E、F分别在BC和AD上，且EF经过圆心0．求证：OE=OF．22．如图，等腰三角形ABC中，以腰AB为直径的⊙O交底边BC于点D，交AC于点E，连接DE．（1）求证：BD=DE；（2）若⊙O的半径为3，BC=4，求CE的长．23．如图，已知⊙0的半径为5，AB是⊙0的直径，点C、D都在⊙0上，若∠D=30°，求AC的长．24．如下图，已知△ABC内接于⊙O，若∠C=45°，AB=4，求⊙O的面积．25．如图，⊙O的直径AB为4cm，弦AC为3cm，∠ACB的平分线交⊙O于D，求：①BC的长；②AD与BD的长．26．如图，⊙O为四边形ABCD的外接圆，圆心O在AD上，OC∥AB．（1）求证：AC平分∠DAB；（2）若AC=8，AC：CD=2：1，试求⊙O的半径．27．如图，点A、B、C、D在圆上，AB=8，BC=6，AC=10，CD=4，求AD的长．28．如图，AB是⊙O的直径，弦CD与AB相交于点E，∠ACD=50°，∠ADC=45°，求∠CDB及∠CEB的度数．29．如图所示，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D，点E在⊙O上．（1）若∠AOD=54°，求∠DEB的度数；（2）若DC=2，AB=8，求⊙O的直径．30．如图，已知△ABC内接于⊙O，AE平分∠BAC，且AD⊥BC于点D，连接OA．求证：∠OAE=∠EAD．参考答案：1．∵AB是⊙O的直径，∴∠ACB=90°；∵OD⊥BC，∴OD∥AC，又∵AO=OB，∴OD是△ABC的中位线，即BD=BC；Rt△ABC中，AB=10cm，AC=8cm；由勾股定理，得：BC==6cm；故BD=BC=3cm2．（1）∵∠APD=∠C+∠CAB，∴∠C=65°﹣40°=25°，∴∠B=∠C=25°；（2）作OE⊥BD于E，则DE=BE，又∵AO=BO，∴，圆心O到BD的距离为3．3．连接AC、BC，由圆周角定理得∠CBE=∠CAD，∵CO⊥AB，∴点C是弧ABC的中点，∴AC=BC，又∵BE=AD∴△ACD≌△BCE，∴CD=CE．∠ADC=∠BEC，∵AB是直径，∴∠ADB=90°，∵∠BEC=∠DCE+∠CDB，∠ADC=∠ADB+∠CDB，∴∠DCE=∠ADB=90°，即△DCE是等腰直角三角形．4．连接OD；∵D 是的中点，∴OD垂直平分AC；∴∠AOD=90°﹣∠CAB=60°；又∵OA=OD，∴△OAD是等边三角形；∴OA=AD；Rt△ABC中，∠CAB=30°，AC=2；∴AB==4，OA=2；即：AD=OA=2．故AD的长为2．5．连接AC，∵AD=BD，∴=．∵∠C=∠BAD，又∵∠ADP=∠CDA，∴△ADP∽△CDA．∴=，即AD2=CD•DP．∵AD=4，PC=6，设CD=x，则42=x（x﹣6），解得：x1=8，x2=﹣2（不合题意，舍去）∴CD=8．6．1）解：∵OC为⊙O的半径，OC⊥BD，∴；∵DB=8，∴MB=4（1分）设⊙O的半径为r，∵CM=2，∴OM=r﹣2，在Rt△OMB中，根据勾股定理得（r﹣2）2+42=r2，解得r=5；（2）证明：方法一：连接AC、CB，∵AB是直径，∴∠ACB=90°．∴∠ACF+∠FCB=90°．又∵CF⊥AB，∴∠CAF+∠ACF=90°∴∠FCB=∠CAF∵OC为⊙O的半径，OC⊥BD，∴C 是的中点，∴∠CAF=∠CBD．∴∠FCB=∠DBC．∴CE=BE；方法二：如图，连接BC，补全⊙O，延长CF交⊙O于点G；又∵CF⊥AB，AB为直径，∴=．∴OC为⊙O的半径，OC⊥BD．∴C 是的中点，∴=．∴=．∴∠FCB=∠DBC．∴CE=BE．7．（1）连接AK、AF，∴∠K=∠F=90°﹣∠AEF=90°﹣∠AEG．∠EAG=90°﹣∠AEG．∴∠K=∠EAG∠KEA=∠AEB．∴△AEB∽△KEA．（2）由①得△AEB∽△KEA，∴．∴AE2=EB•EK．8．（1）因为BC是⊙O的直径所以∠CAB=90°所以∠ABD+∠ACB=90°因为AD⊥BC所以∠ABD+∠BAD=90°所以∠ACB=∠BAD=36°因为A 是的中点，则所以∠ABP=∠ACB=36°．（2）因为∠ABP=∠ACB，∠BAD=∠ACB所以∠ABP=∠BAD因为AE=3所以BE=3．9．（1）∵AB=AC，∴；∴AD平分∠BDC；解：（2）∵∠ACB=∠ADB，∠CDA=∠ADB，∴∠CDA=∠ACB；∵∠CAE=∠DAC，∴△ACE∽△ADC；∴，即；∴AC=6；证明：（3）∠AIC=∠ADC+∠DCI，∠ACI=∠BCI+∠ACB；∴∠AIC=∠ACI；∴AI=AC．10．∵AB是⊙O的直径，∴∠ACB=90°．在Rt△ABC中，∠ACB=90°，AB=6，AC=5，∴BC===．∴tanA==．11．连接BC．∵AB是⊙O的直径，∴∠ACB=90°，∵∠ACD=60°，∴∠BCE=30°，∵∠CEB=100°，∴∠B=50°，∴∠ADC=∠B=50°．12．∵BC∥OA，∠C=25°，∴∠A=∠C=25°，在⊙O中，∵∠O=2∠C，∴∠O=50°，又∵∠AMB=∠A+∠O，∴∠AMB=75°13．在⊙O中，∵∠A=45°，∠D=45°，∵BD为⊙O的直径，∴∠BCD=90°，∴△BCD是等腰直角三角形，∴BC=BD•sin45°，∵BD=2，∴14．连接AE，BD，∵AD平分∠BAC，∴∠BAD=∠CAD，∵DE∥AC，∴∠ADE=∠CAD，∴∠ADE=∠BAD，∴AE=BD，∴AB=DE，∵AB=5cm，∴DE=5cm15．连接EF，ED（1分）在△ABC中∵AB=AC，∠BAC=90°，BD=CD，∴AD=，∠DAF=∠DCE=45°，∠ADC=90°，∴∠ADE+∠EDC=90°，在⊙O中，∵∠BAC=90°，∴EF是⊙O的直径，（3分）∴∠FDE=90°，∴∠FDA+∠ADE=90°，∴∠EDC=∠FDA，∴△EDC≌△FDA，∴AF=CE，（4分）设AF=x，则CE=x，AE=AC﹣CE=﹣x，∵⊙O 的半径是，∴EF=，在Rt△AEF 中，，解得，∠ADF=∠AEF，（5分）∴当x=1时，sin∠ADF=sin∠AEF==，当x=时，sin∠ADF=sin∠AEF==，∴∠ADF 的正弦值为或．16．在△ABC中，∵∠B=60°，∠C=75°，∴∠A=45°．∵AB是⊙O的直径，⊙O与AC交于点D，∴∠DOB=2∠A=90°．故答案为：90°17．∵∠ACB的平分线交⊙O于点D，∴∠ACD=∠BCD，∴AD=BD，∵AB是直径，∴∠ADB=90°，∵AD=5cm，∴BD=5cm；在Rt△ABD中，2AD2=AB2，∴AB=5cm，∴圆的半径为cm．18．连接BC，∵AB是直径，∴BC⊥AC，（2分）∵AC=CP，∴AB=BP，（3分）∴∠P=∠A，（4分）∵∠A=∠D=30°，（5分）∴∠P=30°．19．连接AD．（1分）∵AB是⊙O的直径．∴∠ADB=90°．（3分）在Rt△ADB中，AD=AB•sinB=2sin45°=2×=2（6分）在Rt△ADC中，CD=，即CD 的长为m．20．（1）证明：连接BE，∵AD是△ABC的高，AE是△ABC的外接圆的直径，∴∠ADC=∠ABE=90°，∵∠C=∠E，∴△ADC∽△ABE．∴AC：AE=AD：AB，∴AC•AB=AD•AE；（2）解：∵AB=6，AC=5，AD=3，∴AE===10，∴OA=5，∴⊙O的面积为：π×52=25π21．∵AC为⊙0的直径，∴∠B=∠D=90°，∵CD∥AB，∴∠B+∠BCD=180°，∴∠BCD=90°，∴∠BCD+∠D=90°，∴AD∥BC，∴∠FAO=∠ECO，在△AOF和△COE中，，∴△AFO≌△CEO（ASA），∴OE=OF22．（1）证明：连接AD，∵AB为圆O的直径，∴AD⊥BC，∵AB=AC，∴D为BC的中点，即BD=CD，∵∠DEC为圆内接四边形ABDE的外角，∴∠DEC=∠B，∵AB=AC，∴∠B=∠C，∴∠DEC=∠C，∴DE=DC，∴BD=DE；（2）解：∵∠DEC=∠B，∠C=∠C，∴△DEC∽△ABC，∴=，即=，则EC=．23．连接BC．∵AB是⊙0的直径，∴∠ACB=90°，在直角△ABC中，∠A=∠D=30°，AB=2×5=10．∴AC=AB•cosA=10×=5．24．连接OA，OB；则OA=OB，∠AOB=2∠C；（2分）∵∠C=45°，∴∠AOB=90°，∴OA2+OB2=AB2；（4分）又∵AB=4，∴2OA2=42，OA2=8；（6分）∴S⊙O=π•OA2=8π．25．①∵AB为直径，∴∠ACB=90°，∵AB=4，AC=3，∴BC===；②∵AB为直径，∴∠ADB=90°，∵CD平分∠ACB，∴∠ACD=∠BCD=45°，∵∠ABD=∠ACD，∠BCD=∠BAD，∴∠DAB=∠DBA=45°，∴AD=DB，∵AD2+BD2=AB2，∴AD=DB=2，26．（1）证明：∵OC∥AB，∴∠OCA=∠CAB，∵OA=OC，∴∠OAC=∠OCA，∴∠OAC=∠CAB，即AC平分∠DAB；（2）解∵AD是⊙O的直径，∴∠ACD=90°，∵AC=8，AC：CD=2：1，∴CD=4，在Rt△ACD中，AD==4，∴OA=AD=2，∴⊙O的半径为2．27．△ABC中，AB=8，BC=6，AC=10，∴AC2=AB2+BC2，∴∠B=90°，∴AC为直径，∴∠D=90°，Rt△ADC中，AD====2．∴AD的长为2．28．连接BC，则∠ACB=90°（圆周角定理），∵∠CBA=∠ADC=45°，∴∠CAB=90°﹣∠CBA=45°（直角三角形的两个锐角互余）；∴∠CEB=∠CAB+∠ACD=45°+50°=95°（外角定理）．∠CDB=∠CAB=45°．综上可得：∠CDB=45°，∠CEB=95°29．（1）∵OD⊥AB∴弧AD=弧BD∴∠DEB=∠AOD=×54°=27°…3分（2）∵OD⊥AB∴AC=AB=×8=4设⊙O的半径为R，则OC=R﹣2在Rt△AOC中，由勾股定理得：42+（R﹣2）2=R2解得：R=5∴⊙O的直径为1030．连接OE，∵AE平分∠BAC，∴∠BAE=∠CAE，∴=，∴OE⊥BC，∵AD⊥BC，∴OE∥AD，∴∠OEA=∠EAD，∵OA=OE，∴∠OEA=∠OAE，∴∠OAE=∠EAD．11。

圆周角定理综合训练一．选择题（共14小题）1．如图，已知⊙O的半径为1，锐角△ABC内接于⊙O，BD⊥AC于点D，OM⊥AB于点M，则sin∠CBD的值等于（）A．OM的长B．2OM的长C．CD的长 D．2CD的长2．如图，已知AB是⊙O的直径，C是⊙O上的一点，连接AC，过点C作直线CD⊥AB交AB于点D．E是OB上的一点，直线CE与⊙O交于点F，连接AF交直线CD于点G，AC=2，则AG•AF是（）A．10 B．12 C．8 D．163．如图，半圆O的直径AB=7，两弦AC、BD相交于点E，弦CD=，且BD=5，则DE等于（）A．B．C．D．4．如图，△ABC为⊙O的内接三角形，AB=1，∠C=30°，则⊙O的内接正方形的面积为（）A．2 B．4 C．8 D．165．如图，四边形ABCD内接于⊙O，它的对角线把四个内角分成八个角，其中相等的角有（）A．2对 B．4对 C．6对 D．8对6．已知，如图弧BC与弧AD的度数之差为20°，弦AB与CD交于点E，∠CEB=60°，则∠CAB等于（）A．50°B．45°C．40°D．35°7．如图，B是线段AC的中点，过点C的直线l与AC成60°的角，在直线L上取一点P，使∠APB=30°，则满足条件的点P的个数是（）A．3个 B．2个 C．1个 D．不存在8．如图，已知∠DEC=80°，弧CD的度数与弧AB的度数的差为20°，则∠DAC的度数为（）A．35°B．45°C．25°D．50°9．如图，⊙O是正五边形ABCDE的外接圆，则正五边形的中心角∠AOB的度数是（）A．72°B．60°C．54°D．36°10．如图，在△ABC中，∠BAC=90°，AB=AC=2，以AB为直径的圆交BC于D，则图中阴影部分的面积为（）A．1 B．2 C．1+D．2﹣11．如图，已知△ABC为等腰直角三角形，D为斜边BC的中点，经过点A、D 的⊙O与边AB、AC、BC分别相交于点E、F、M．对于如下五个结论：①∠FMC=45°；②AE+AF=AB；③；④2BM2=BE•BA；⑤四边形AEMF为矩形．其中正确结论的个数是（）A．2个 B．3个 C．4个 D．5个12．已知：圆内接四边形ABCD中，对角线AC⊥BD，AB＞CD．若CD=4，则AB 的弦心距为（）A．B．2 C．D．13．如图，⊙O中，弦AD∥BC，DA=DC，∠AOC=160°，则∠BCO等于（）A．20°B．30°C．40°D．50°14．如图，在△ABC中，AD是高，△ABC的外接圆直径AE交BC边于点G，有下列四个结论：①AD2=BD•CD；②BE2=EG•AE；③AE•AD=AB•AC；④AG•EG=BG•CG．其中正确结论的个数是（）A．1个 B．2个 C．3个 D．4个二．填空题（共5小题）15．如图，⊙O是正△ABC的外接圆，点D是弧AC上一点，则∠BDC的度数是度．16．如图，点A、B、C是⊙O上的三点，若∠BOC=56°，则∠A=度．17．如图，圆内接四边形ABCD的两条对角线交于点P．已知AB=BC，CD=BD=1，设AD=x，用关于x的代数式表示PA与PC的积：PA•PC=．18．如图所示，在圆O中，弧AB=弧AC=弧CD，AB=3，AE•ED=5，则EC的长为．19．如图，△ABC内接于⊙O，AE是⊙O的直径，AE与BC交于点D，且D是OE 的中点，则tan∠ABC•tan∠ACB=．三．解答题（共7小题）20．如图，AB是⊙O的直径，AC切⊙O于点A，AD是⊙O的弦，OC⊥AD于F 交⊙O于E，连接DE，BE，BD．AE．（1）求证：∠C=∠BED；（2）如果AB=10，tan∠BAD=，求AC的长；（3）如果DE∥AB，AB=10，求四边形AEDB的面积．21．如图，Rt△ABC内接于⊙O，AC=BC，∠BAC的平分线AD与⊙O交于点D，与BC交于点E，延长BD，与AC的延长线交于点F，连接CD，G是C D的中点，连接OG．（1）判断OG与CD的位置关系，写出你的结论并证明；（2）求证：AE=BF；（3）若OG⋅DE=3（2﹣），求⊙O的面积．22．如图，AB是⊙O的直径，C是弧BD的中点，CE⊥AB，垂足为E，BD交CE 于点F．（1）求证：CF=BF；（2）若AD=2，⊙O的半径为3，求BC的长．23．如图，⊙O中，弦AB、CD相交于AB的中点E，连接AD并延长至点F，使DF=AD，连接BC、BF．（1）求证：△CBE∽△AFB；（2）当时，求的值．24．如图，已知AB是⊙O的直径，点C是⊙O上一点，连接BC，AC，过点C作直线CD⊥AB于点D，点E是AB上一点，直线CE交⊙O于点F，连接BF，与直线CD交于点G．求证：BC2=BG•BF．25．如图，点I是△ABC的内心，线段AI的延长线交△ABC的外接圆于点D，交BC边于点E．（1）求证：ID=BD；（2）设△ABC的外接圆的半径为5，ID=6，AD=x，DE=y，当点A在优弧上运动时，求y与x的函数关系式，并指出自变量x的取值范围．26．已知：如图，等边△ABC内接于⊙O，点P是劣弧上的一点（端点除外），延长BP至D，使BD=AP，连接CD．（1）若AP过圆心O，如图①，请你判断△PDC是什么三角形？并说明理由；（2）若AP不过圆心O，如图②，△PDC又是什么三角形？为什么？参考答案与试题解析一．选择题（共14小题）1．如图，已知⊙O的半径为1，锐角△ABC内接于⊙O，BD⊥AC于点D，OM⊥AB于点M，则sin∠CBD的值等于（）A．OM的长B．2OM的长C．CD的长 D．2CD的长【解答】解：连接AO并延长交圆于点E，连接BE．则∠C=∠E，由AE为直径，且BD⊥AC，得到∠BDC=∠ABE=90°，所以△ABE和△BCD都是直角三角形，所以∠CBD=∠EAB．又△OAM是直角三角形，∵AO=1，∴sin∠CBD=sin∠EAB==OM，即sin∠CBD的值等于OM的长．故选：A．2．如图，已知AB是⊙O的直径，C是⊙O上的一点，连接AC，过点C作直线CD⊥AB交AB于点D．E是OB上的一点，直线CE与⊙O交于点F，连接AF交直线CD于点G，AC=2，则AG•AF是（）A．10 B．12 C．8 D．16【解答】解：连接BC，则∠B=∠F，∵CD⊥AB，∴∠ACD+∠CAD=90°，∵AB是直径，∴∠ACB=90°，∠CAB+∠B=90°，∴∠ACG=∠F．又∵∠CAF=∠FAC，∴△ACG∽△AFC，∴AC：AF=AG：AC，即AG•AF=AC2=（2）2=8．故选：C．3．如图，半圆O的直径AB=7，两弦AC、BD相交于点E，弦CD=，且BD=5，则DE等于（）A．B．C．D．【解答】解法一：∵∠D=∠A，∠DCA=∠ABD，∴△AEB∽△DEC；∴=；设BE=2x，则DE=5﹣2x，EC=x，AE=2（5﹣2x）；连接BC，则∠ACB=90°；Rt△BCE中，BE=2x，EC=x，则BC=x；在Rt△ABC中，AC=AE+EC=10﹣3x，BC=x；由勾股定理，得：AB2=AC2+BC2，即：72=（10﹣3x）2+（x）2，整理，得4x2﹣20x+17=0，解得x1=+，x2=﹣；由于x＜，故x=﹣；则DE=5﹣2x=2．解法二：连接OD，OC，AD，∵OD=CD=OC则∠DOC=60°，∠DAC=30°又AB=7，BD=5，∴AD=2，在Rt△ADE中，∠DAC=30°，所以DE=2．故选：A．4．如图，△ABC为⊙O的内接三角形，AB=1，∠C=30°，则⊙O的内接正方形的面积为（）A．2 B．4 C．8 D．16【解答】解：如图，连接BO并延长交圆于点E，连接AE，则∠E=∠C=30°，∠EAB=90°；∴直径BE==2，∵直径是圆内接正方形的对角线长，∴圆内接正方形的边长等于∴⊙O的内接正方形的面积为2．故选：A．5．如图，四边形ABCD内接于⊙O，它的对角线把四个内角分成八个角，其中相等的角有（）A．2对 B．4对 C．6对 D．8对【解答】解：由圆周角定理知：∠ADB=∠ACB；∠CBD=∠CAD；∠BDC=∠BAC；∠ABD=∠ACD；由对顶角相等知：∠1=∠3；∠2=∠4；共有6对相等的角．故选：C．6．已知，如图弧BC与弧AD的度数之差为20°，弦AB与CD交于点E，∠CEB=60°，则∠CAB等于（）A．50°B．45°C．40°D．35°【解答】解：由题意，弧BC与弧AD的度数之差为20°，∴两弧所对圆心角相差20°，∴2∠A﹣2∠C=20°，∴∠A﹣∠C=10°…①；∵∠CEB是△AEC的外角，∴∠A+∠C=∠CEB=60°…②；①+②，得：2∠A=70°，即∠A=35°．故选：D．7．如图，B是线段AC的中点，过点C的直线l与AC成60°的角，在直线L上取一点P，使∠APB=30°，则满足条件的点P的个数是（）A．3个 B．2个 C．1个 D．不存在【解答】解：如图，分别以AC，BC为边，作等边△APC，等边△BP′C，连接BP，依题意，结合等边三角形的性质可知∠APB=∠AP′B=30°，所以满足条件的点P的个数为2个．故选：B．8．如图，已知∠DEC=80°，弧CD的度数与弧AB的度数的差为20°，则∠DAC的度数为（）A．35°B．45°C．25°D．50°【解答】解：∵弧CD的度数与弧AB的度数的差为20°，∴2（∠A﹣∠D）=20°即∠A﹣∠D=10°∵∠DEC=80°∴∠DEC=∠D+∠A=80°∴∠A=45°，∠D=35°．故选：B．9．如图，⊙O是正五边形ABCDE的外接圆，则正五边形的中心角∠AOB的度数是（）A．72°B．60°C．54°D．36°【解答】解：∵⊙O是正五边形ABCDE的外接圆，∴∠AOB=360°÷5=72°．故选：A．10．如图，在△ABC中，∠BAC=90°，AB=AC=2，以AB为直径的圆交BC于D，则图中阴影部分的面积为（）A．1 B．2 C．1+D．2﹣【解答】解：连接AD，OD∵∠BAC=90°，AB=AC=2∴△ABC是等腰直角三角形∵AB是圆的直径∴∠ADB=90°∴AD⊥BC∴点D是BC的中点∴OD是△ABC的中位线∴∠DOA=90°∴△ODA，△ADC都是等腰直角三角形∴两个弓形的面积相等=AD2=1．∴阴影部分的面积=S△ADC故选：A．11．如图，已知△ABC为等腰直角三角形，D为斜边BC的中点，经过点A、D 的⊙O与边AB、AC、BC分别相交于点E、F、M．对于如下五个结论：①∠FMC=45°；②AE+AF=AB；③；④2BM2=BE•BA；⑤四边形AEMF为矩形．其中正确结论的个数是（）A．2个 B．3个 C．4个 D．5个【解答】解：连接AM，根据等腰三角形的三线合一，得AD⊥BC，再根据90°的圆周角所对的弦是直径，得EF、AM是直径，根据对角线相等且互相平分的四边形是矩形，得四边形AEMF是矩形，∴①根据等腰直角三角形ABC的底角是45°，易得∠FMC=45°，正确；②根据矩形和等腰直角三角形的性质，得AE+AF=AB，正确；③连接FD，可以证明△EDF是等腰直角三角形，则③中左右两边的比都是等腰直角三角形的直角边和斜边的比，正确；④根据BM=BE，得左边=4BE2，故需证明AB=4BE，根据已知条件它们之间不一定有这种关系，错误；⑤正确．所以①②③⑤共4个正确．故选C．12．已知：圆内接四边形ABCD中，对角线AC⊥BD，AB＞CD．若CD=4，则AB 的弦心距为（）A．B．2 C．D．【解答】解：如图，设AC与BD的交点为O，过点O作GH⊥CD于G，交AB于H；作MN⊥AB于M，交CD于点N．在Rt△COD中，∠COD=90°，OG⊥CD；∴∠DOG=∠DCO；∵∠GOD=∠BOH，∠DCO=∠ABO，∴∠ABO=∠BOH，即BH=OH，同理可证，AH=OH；即H是Rt△AOB斜边AB上的中点．同理可证得，M是Rt△COD斜边CD上的中点．设圆心为O′，连接O′M，O′H；则O′M⊥CD，O′H⊥AB；∵MN⊥AB，GH⊥CD；∴O′H∥MN，OM∥GH；即四边形O′HOM是平行四边形；因此OM=O′H．由于OM是Rt△OCD斜边CD上的中线，所以OM=O′H=CD=2．故选：B．13．如图，⊙O中，弦AD∥BC，DA=DC，∠AOC=160°，则∠BCO等于（）A．20°B．30°C．40°D．50°【解答】解：连接OD，∵AO=OC=OD，DA=DC，∴△ADO≌△CDO．∴∠COD=∠AOD=∠AOC=80°．∴∠ODC=∠OCD=∠ODA=∠OAD=50°．∴∠CDA=100°．∵AD∥BC，∴∠DCB=180°﹣∠CDA=180°﹣100°=80°．∴∠BCO=∠BCD﹣∠OCD=80°﹣50°=30°．故选：B．14．如图，在△ABC中，AD是高，△ABC的外接圆直径AE交BC边于点G，有下列四个结论：①AD2=BD•CD；②BE2=EG•AE；③AE•AD=AB•AC；④AG•EG=BG•CG．其中正确结论的个数是（）A．1个 B．2个 C．3个 D．4个【解答】解：①若△ABD∽△CAD，则一定有AD：BD=CD：AD，即AD2=BD•CD，而两三角形只有一对角对应相等，不会得到另外的对应角相等，故①不正确；②若△BEG∽△AEB，则一定有BE：EG=AE：BE，即BE2=EG•AE，而两三角形只有一对公共角相等，不会得到另外的对应角相等，故②不正确；③∵∠ABD=∠AEC，∠ADB=∠ACE=90°，∴△ABD∽△AEC，∴AE：AC=AB：AD，即AE•AD=AC•AB，故③正确；∵根据相交弦定理，可直接得出AG•EG=BG•CG，故④正确．故选：B．二．填空题（共5小题）15．如图，⊙O是正△ABC的外接圆，点D是弧AC上一点，则∠BDC的度数是60度．【解答】解：∵△ABC是正三角形，∴∠BAC=60°；由圆周角定理，得：∠BDC=∠A=60°．16．如图，点A、B、C是⊙O上的三点，若∠BOC=56°，则∠A=28度．【解答】解：∵∠BOC=56°∴∠A=∠BOC=28°．17．如图，圆内接四边形ABCD的两条对角线交于点P．已知AB=BC，CD=BD=1，设AD=x，用关于x的代数式表示PA与PC的积：PA•PC=﹣x2+x．【解答】解：根据相交弦定理，可知PA•PC=BP•PD，∵CD=1，BD=2而AB=BC∴∴∠ADB=∠BDC∵∠ABD=∠ACD∴△ADB∽△PDC∴CD：BD=PD：AD而BD=2CD∴PD=x∴BP=BD﹣PD=2﹣x∴PA•PC=BP•PD=（2﹣x）×x=﹣x2+x．18．如图所示，在圆O中，弧AB=弧AC=弧CD，AB=3，AE•ED=5，则EC的长为2．【解答】解：∵弧AB=弧AC=弧CD，∴∠1=∠2=∠3=∠4；∴△AEC∽△BAC；∴CE：AC=AC：BC；∵AC=AB=3，因此CE•BC=3×3=9；∵BC=BE+CE，∴CE（BE+CE）=9，整理得：CE•BE+CE2=9 ①；由根据相交弦定理得，BE•CE=A E•ED=5 ②；②代入①得：5+CE2=9，解得：CE=2（负值舍去）．19．如图，△ABC内接于⊙O，AE是⊙O的直径，AE与BC交于点D，且D是OE 的中点，则tan∠ABC•tan∠ACB=3．【解答】解：连接BE、CE，则∠ABE=∠ACE=90°．∵∠EAC=∠CBE，∠BED=∠ACB，∴△ADC∽△BDE，∴．①同理可由△ADB∽△CDE，得．②①×②，得==3．Rt△AEC中，tan∠AEC=．同理得tan∠AEB=．故tan∠AEC•tan∠AEB==3．∵∠EAC=∠CBE，∠BED=∠ACB，∴tan∠ABC•tan∠ACB=3．三．解答题（共7小题）20．如图，AB是⊙O的直径，AC切⊙O于点A，AD是⊙O的弦，OC⊥AD于F 交⊙O于E，连接DE，BE，BD．AE．（1）求证：∠C=∠BED；（2）如果AB=10，tan∠BAD=，求AC的长；（3）如果DE∥AB，AB=10，求四边形AEDB的面积．【解答】（1）证明：∵AB是⊙O的直径，CA切⊙O于A，∴∠C+∠AOC=90°；又∵0C⊥AD，∴∠OFA=90°，∴∠AOC+∠BAD=90°，∴∠C=∠BAD．又∵∠BED=∠BAD，∴∠C=∠BED．（2）解：由（1）知∠C=∠BAD，tan∠BAD=，∴tan∠C=．在Rt△OAC中，tan∠C=，且OA=AB=5，∴，解得．（3）解：∵OC⊥AD，∴，∴AE=ED，又∵DE∥AB，∴∠BAD=∠EDA，∴，∴AE=BD，∴AE=BD=DE，∴，∴∠BAD=30°，又∵AB是直径，∴∠ADB=90°，∴BD=AB=5，DE=5，在Rt△ABD中，由勾股定理得：AD=，过点D作DH⊥AB于H，∵∠HAD=30°，∴DH=AD=，∴四边形AEDB的面积=．21．如图，Rt△ABC内接于⊙O，AC=BC，∠BAC的平分线AD与⊙O交于点D，与BC交于点E，延长BD，与AC的延长线交于点F，连接CD，G是CD的中点，连接OG．（1）判断OG与CD的位置关系，写出你的结论并证明；（2）求证：AE=BF；（3）若OG⋅DE=3（2﹣），求⊙O的面积．【解答】（1）解：猜想OG⊥CD．证明：如图，连接OC、OD，∵OC=OD，G是CD的中点，∴由等腰三角形的性质，有OG⊥CD．（2）证明：∵AB是⊙O的直径，∴∠ACB=90°，而∠CAE=∠CBF（同弧所对的圆周角相等），在Rt△ACE和Rt△BCF中，∵∠ACE=∠BCF=90°，AC=BC，∠CAE=∠CBF，∴Rt△ACE≌Rt△BCF（ASA）．∴AE=BF．（3）解：如图，过点O作BD的垂线，垂足为H，则H为BD的中点．∴OH=AD，即AD=2OH，又∠CAD=∠BAD⇒CD=BD，∴OH=OG．在Rt△BDE和Rt△ADB中，∵∠DBE=∠DAC=∠BAD，∴Rt△BDE∽Rt△ADB，∴，即BD2=AD•DE．∴．又BD=FD，∴BF=2BD，∴①，设AC=x，则BC=x，AB=，∵AD是∠BAC的平分线，∴∠FAD=∠BAD．在Rt△ABD和Rt△AFD中，∵∠ADB=∠ADF=90°，AD=AD，∠FAD=∠BAD，∴Rt△ABD≌Rt△AFD（ASA）．∴AF=AB=，BD=FD．∴CF=AF﹣AC=．在Rt△BCF中，由勾股定理，得②，由①、②，得，∴x2=12，解得或（舍去），∴，∴⊙O的半径长为．=π•（）2=6π．∴S⊙O22．如图，AB是⊙O的直径，C是弧BD的中点，CE⊥AB，垂足为E，BD交CE 于点F．（1）求证：CF=BF；（2）若AD=2，⊙O的半径为3，求BC的长．【解答】（1）证明：连接AC，如图∵C是弧BD的中点∴∠BDC=∠DBC（1分）又∵∠BDC=∠BAC在△ABC中，∠ACB=90°，CE⊥AB∴∠BCE=∠BAC∠BCE=∠DBC（3分）∴CF=BF；（4分）（2）解：解法一：作CG⊥AD于点G，∵C是弧BD的中点∴∠CAG=∠BAC，即AC是∠BAD的角平分线．（5分）∴CE=CG，AE=AG（6分）在Rt△BCE与Rt△DCG中，CE=CG，CB=CD∴Rt△BCE≌Rt△DCG（HL）∴BE=DG（7分）∴AE=AB﹣BE=AG=AD+DG即6﹣BE=2+DG∴2BE=4，即BE=2（8分）又∵△BCE∽△BAC∴BC2=BE•AB=12（9分）BC=±2（舍去负值）∴BC=2．（10分）解法二：∵AB是⊙O的直径，CE⊥AB ∴∠BEF=∠ADB=90°，（5分在Rt△ADB与Rt△FEB中，∵∠ABD=∠FBE∴△ADB∽△FEB，则，即，∴BF=3EF（6分）又∵BF=CF，∴CF=3EF利用勾股定理得：（7分）又∵△EBC∽△ECA则，则CE2=AE•BE（8分）∴（CF+EF）2=（6﹣BE）•BE即（3EF+EF）2=（6﹣2EF）•2EF ∴EF=（9分）∴BC=．（10分）23．如图，⊙O中，弦AB、CD相交于AB的中点E，连接AD并延长至点F，使DF=AD，连接BC、BF．（1）求证：△CBE∽△AFB；（2）当时，求的值．【解答】（1）证明：∵AE=EB，AD=DF，∴ED是△ABF的中位线，∴ED∥BF，∴∠CEB=∠ABF，又∵∠C=∠A，∴△CBE∽△AFB．（2）解：由（1）知，△CBE∽△AFB，∴，又AF=2AD，∴．24．如图，已知AB是⊙O的直径，点C是⊙O上一点，连接BC，AC，过点C作直线CD⊥AB于点D，点E是AB上一点，直线CE交⊙O于点F，连接BF，与直线CD交于点G．求证：BC2=BG•BF．【解答】证明：∵AB是⊙O的直径，∠ACB=90°，又CD⊥AB于D，∴∠BCD=∠A，又∠A=∠F．∴∠F=∠BCD．在△BCG和△BFC中，，∴△BCG∽△BFC．∴．即BC2=BG•BF．25．如图，点I是△ABC的内心，线段AI的延长线交△ABC的外接圆于点D，交BC边于点E．（1）求证：ID=BD；（2）设△ABC的外接圆的半径为5，ID=6，AD=x，DE=y，当点A在优弧上运动时，求y与x的函数关系式，并指出自变量x的取值范围．【解答】（1）证明：∵点I是△ABC的内心∴∠BAD=∠CAD，∠ABI=∠CBI（2分）∵∠CBD=∠CAD∴∠BAD=∠CBD（3分）∴∠BID=∠ABI+∠BAD，∴∠ABI=∠CBI，∠BAD=∠CAD=∠CBD，∵∠IBD=∠CBI+∠CBD，∴∠BID=∠IBD∴ID=BD；（5分）（2）解：∵∠BAD=∠CBD=∠EBD，∠D=∠D∴△ABD∽△BED（7分）∴∴AD×DE=BD2=ID2（8分）∵ID=6，AD=x，DE=y∴xy=36（9分）又∵x=AD＞ID=6，AD不大于圆的直径10∴6＜x≤10∴y与x的函数关系式是（6＜x≤10）．（10分）说明：只要求对xy=36与6＜x≤10，不写最后一步，不扣分．26．已知：如图，等边△ABC内接于⊙O，点P是劣弧上的一点（端点除外），延长BP至D，使BD=AP，连接CD．（1）若AP过圆心O，如图①，请你判断△PDC是什么三角形？并说明理由；（2）若AP不过圆心O，如图②，△PDC又是什么三角形？为什么？【解答】解：（1）如图①，△PDC为等边三角形．（2分）理由如下：∵△ABC为等边三角形∴AC=BC∵在⊙O中，∠PAC=∠PBC又∵AP=BD∴△APC≌△BDC∴PC=DC∵AP过圆心O，AB=AC，∠BAC=60°∴∠BAP=∠PAC=∠BAC=30°∴∠PBC=∠PAC=30°，∠BCP=∠BAP=30°∴∠CPD=∠PBC+∠BCP=30°+30°=60°∴△PDC为等边三角形；（6分）（2）如图②，△PDC仍为等边三角形．（8分）理由如下：∵△ABC为等边三角形∴AC=BC∵在⊙O中，∠PAC=∠PBC又∵AP=BD∴△APC≌△BDC∴PC=DC∵∠BAP=∠BCP，∠PBC=∠PAC∴∠CPD=∠PBC+∠BCP=∠PAC+∠BAP=60°∴△PDC为等边三角形．（12分）31 / 31。

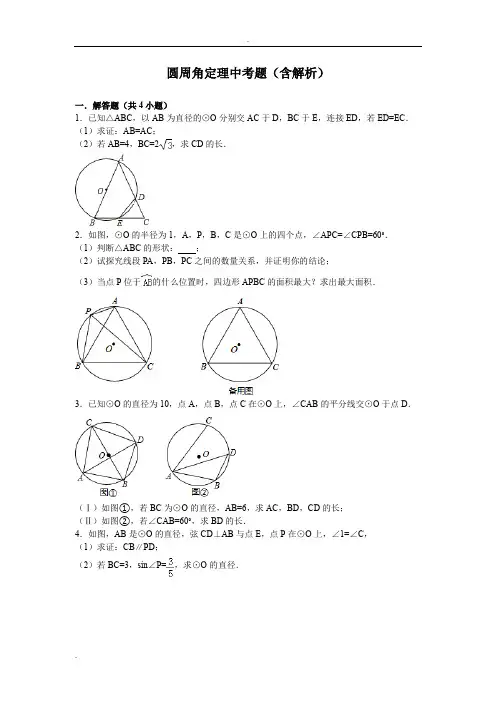
圆周角定理中考题（含解析）一．解答题（共4小题）1．已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED=EC．（1）求证：AB=AC；（2）若AB=4，BC=2，求CD的长．2．如图，⊙O的半径为1，A，P，B，C是⊙O上的四个点，∠APC=∠CPB=60°．（1）判断△ABC的形状：；（2）试探究线段PA，PB，PC之间的数量关系，并证明你的结论；（3）当点P位于的什么位置时，四边形APBC的面积最大？求出最大面积．3．已知⊙O的直径为10，点A，点B，点C在⊙O上，∠CAB的平分线交⊙O于点D．（Ⅰ）如图①，若BC为⊙O的直径，AB=6，求AC，BD，CD的长；（Ⅱ）如图②，若∠CAB=60°，求BD的长．4．如图，AB是⊙O的直径，弦CD⊥AB与点E，点P在⊙O上，∠1=∠C，（1）求证：CB∥PD；（2）若BC=3，sin∠P=，求⊙O的直径．圆周角定理中考题（含解析）参考答案与试题解析一．解答题（共4小题）1．（2016•宁夏）已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED=EC．（1）求证：AB=AC；（2）若AB=4，BC=2，求CD的长．【解答】（1）证明：∵ED=EC，∴∠EDC=∠C，∵∠EDC=∠B，∴∠B=∠C，∴AB=AC；（2）方法一：解：连接AE，∵AB为直径，∴AE⊥BC，由（1）知AB=AC，∴BE=CE=BC=，∵△CDE∽△CBA，∴，∴CE•CB=CD•CA，AC=AB=4，∴•2=4CD，∴CD=．方法二：解：连接BD，∵AB为直径，∴BD⊥AC，设CD=a，由（1）知AC=AB=4，则AD=4﹣a，在Rt△ABD中，由勾股定理可得：BD2=AB2﹣AD2=42﹣（4﹣a）2在Rt△CBD中，由勾股定理可得：BD2=BC2﹣CD2=（2）2﹣a2∴42﹣（4﹣a）2=（2）2﹣a2整理得：a=，即：CD=．2．（2015•德州）如图，⊙O的半径为1，A，P，B，C是⊙O上的四个点，∠APC=∠CPB=60°．（1）判断△ABC的形状：等边三角形；（2）试探究线段PA，PB，PC之间的数量关系，并证明你的结论；（3）当点P位于的什么位置时，四边形APBC的面积最大？求出最大面积．【解答】证明：（1）△ABC是等边三角形．证明如下：在⊙O中∵∠BAC与∠CPB是所对的圆周角，∠ABC与∠APC是所对的圆周角，∴∠BAC=∠CPB，∠ABC=∠APC，又∵∠APC=∠CPB=60°，∴∠ABC=∠BAC=60°，∴△ABC为等边三角形；（2）在PC上截取PD=AP，如图1，又∵∠APC=60°，∴△APD是等边三角形，∴AD=AP=PD，∠ADP=60°，即∠ADC=120°．又∵∠APB=∠APC+∠BPC=120°，∴∠ADC=∠APB，在△APB和△ADC中，，∴△APB≌△ADC（AAS），∴BP=CD，又∵PD=AP，∴CP=BP+AP；（3）当点P为的中点时，四边形APBC的面积最大．理由如下，如图2，过点P作PE⊥AB，垂足为E．过点C作CF⊥AB，垂足为F．∵S△APB=AB•PE，S△ABC=AB•CF，∴S四边形APBC=AB•（PE+CF），当点P为的中点时，PE+CF=PC，PC为⊙O的直径，∴此时四边形APBC的面积最大．又∵⊙O的半径为1，∴其内接正三角形的边长AB=，∴S四边形APBC=×2×=．3．（2014•天津）已知⊙O的直径为10，点A，点B，点C在⊙O上，∠CAB的平分线交⊙O于点D．（Ⅰ）如图①，若BC为⊙O的直径，AB=6，求AC，BD，CD的长；（Ⅱ）如图②，若∠CAB=60°，求BD的长．【解答】解：（Ⅰ）如图①，∵BC是⊙O的直径，∴∠CAB=∠BDC=90°．∵在直角△CAB中，BC=10，AB=6，∴由勾股定理得到：AC===8．∵AD平分∠CAB，∴=，∴CD=BD．在直角△BDC中，BC=10，CD2+BD2=BC2，∴易求BD=CD=5；（Ⅱ）如图②，连接OB，OD．∵AD平分∠CAB，且∠CAB=60°，∴∠DAB=∠CAB=30°，∴∠DOB=2∠DAB=60°．又∵OB=OD，∴△OBD是等边三角形，∴BD=OB=OD．∵⊙O的直径为10，则OB=5，∴BD=5．4．（2013•黔西南州）如图，AB是⊙O的直径，弦CD⊥AB与点E，点P在⊙O上，∠1=∠C，（1）求证：CB∥PD；（2）若BC=3，sin∠P=，求⊙O的直径．【解答】（1）证明：∵∠C=∠P又∵∠1=∠C∴∠1=∠P∴CB∥PD；（2）解：连接AC∵AB为⊙O的直径，∴∠ACB=90°又∵CD⊥AB，∴=，∴∠P=∠CAB，又∵sin∠P=，∴sin∠CAB=，即=，又知，BC=3，∴AB=5，∴直径为5．。

垂径定理圆心角圆周角定理一选择题：1、如图，⊙O是△ABC的外接圆，∠OBC=42°，则∠A的度数是（）A．42°B．48°C．52°D．58°2.如图，A、B、C、D四个点均在⊙O上，∠AOD=50°，AO∥DC，则∠B的度数为( )A．50° B．55° C．60° D．65°3.如图，点B、D、C是⊙O上的点，∠BDC=130°，则∠BOC是（）A．100° B．110° C．120°D．130°4.如图，⊙O的半径为5，弦AB的长为8，点M在线段AB（包括端点A，B）上移动，则OM取值范围是（）A.3≤OM≤5B.3≤OM＜5C.4≤OM≤5 D.4≤OM＜55、如图所示，AB是⊙O的直径，AD=DE，AE与BD交于点C，则图中与∠BCE相等的角有（）A．2个 B．3个 C．4个 D．5个6.将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A、B 的读数分别为86°、30°，则∠ACB的大小为( )A．15°B．28° C.29°D．34°7.如图，C为⊙O直径AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=45°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=x,DE=y,下列中图象中,能表示y与x的函数关系式的图象大致是( )8.如图.⊙O 中，AB、AC是弦，O在∠ABO的内部，，，，则下列关系中，正确的是（）A. B. C． D.9.如图，四边形ABCD内接于⊙O，BC是直径，AD=DC，∠ADB=20º，则∠ACB，∠DBC分别为（）A．15º与30º B．20º与35º C．20º与40º D．30º与35º10.图中∠BOD的度数是（）A．55° B．110° C．125° D．150°11.如图，点I为△ABC的内心，点O为△ABC的外心，∠O=140°，则∠I为（）（A）140°（B）125°（C）130°（D）110°12.如图,弦AB∥CD，E为上一点，AE平分，则图中与相等（不包括）的角共有（）A．3个 B．4个 C．5个 D．6个13、如图，已知的半径为1，锐角内接于，于点，于点，则的值等于（）A．的长 B．的长 C．的长 D．的长14.如图，在直角∠O的内部有一滑动杆AB，当端点A沿直线AO向下滑动时，端点B会随之自动地沿直线OB向左滑动，如果滑动杆从图中AB处滑动到A′B′处，那么滑动杆的中点C所经过的路径是（）A.直线的一部分B.圆的一部分C.双曲线的一部分 D.抛物线的一部分15.如图，AB是⊙O的直径，弦BC=2cm，∠ABC=60°.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动，点Q从A点出发沿着A→C的方向运动，当点P到达点A时，点Q也随之停止运动．设运动时间为t(s)，当△APQ是直角三角形时，t的值为（）A. B. C.或 D.或或16.如图，，在以为直径的半圆上，，在上，为正方形，若正方形边长为1，，，则下列式子中，不正确的是（）A. B. C. D.17.如图，AB是⊙O的直径，AB=8，点M在⊙O上，∠MAB=20°，N是弧MB的中点，P是直径AB上的一动点．若MN=1，则△PMN周长的最小值为（）A．4 B．5 C．6 D．718.如图，在△ABC中，AD是高，AE是直径，AE交BC于G，有下列四个结论：•①AD2=BD·CD；②BE2=EG·AE；③AE·AD=AB·AC；④AG·EG=BG·CG．其中正确结论的有（）A．1个 B．2个 C．3个 D．4个19.如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG，DE，FG，，的中点分别是M，N，P，Q。

提技能·题组训练圆周角定理及其推论1.( 滨州中考 ) 如图 , 在☉ O中, 圆心角∠ BOC=78°, 则圆周角∠ BAC的大小为 ()A.156°B.78 °C.39°【解析】选C.∠BOC是所对的圆心角D.12°, ∠ BAC是所对的圆周角,∴∠ BAC=∠ BOC=39°.2.( 海南中考 ) 如图 , 在☉ O中 , 弦 BC=1,点 A 是圆上一点 , 且∠ BAC=30°, 则☉ O的半径是 ()A.1B.2C.D.【解析】选A. 方法一 : 连接OB,OC.∵∠ BAC=30°, ∴∠ BOC=2∠ BAC=60° ,∵OB=OC,∴△ OBC是等边三角形 ,∴OB=OC=BC =1.方法二 : 作直径 CD,连接 BD.则∠ CBD=90°, ∵∠ BDC=∠ BAC=30°, ∴CD=2BC=2,∴OC=CD=1.3.( 长春中考 ) 如图 , △ABC内接于☉ O,∠ABC=71° , ∠ CAB=53° , 点 D 在上,则∠ ADB的大小为()A.45°B.53 °C.56 °D.71 °【解析】选 C.在△ ABC中, ∵∠ ABC=71° , ∠ CAB=53°,∴∠ C=180°-71 °-53 °=56° , ∴∠ ADB=∠C=56°.D,则∠ BOD=. 4.( 佛山中考 ) 图中圆心角∠ AOB=30° , 弦 CA∥ OB,延长CO与圆交于点【解析】因为圆心角∠ AOB=30°, 弦 CA∥OB,所以∠ AOB=∠CAO=30°,又 OA=OC,所以∠ CAO=∠ ACO=30° , 所以∠ AOD=∠ CAO+∠ ACO=60° =∠ AOB+∠ BOD,所以∠BOD=30°.答案 : 30°5.( 贵阳中考 ) 如图 ,AD,AC 分别为☉ O的直径和弦 , ∠CAD=30°,B 是 AC上一点 ,BO⊥AD,垂足为【解析】在Rt△AOB中 , ∠A=30° ,BO=5cm,∴AO=5cm,∵AD是直径 ,∴AD=10cm,∠C=90°, 在 Rt△ ADC中,∠A=30°,AD=10cm,∴CD=5cm.答案: 56. 如图 , 正方形ABCD的顶点都在☉O上 ,P是弧DC上的一点 , 则∠ BPC=.【解析】连接 BD,则 BD是直径 ,∴△ BCD是等腰直角三角形 ,∴∠ BDC=45°, ∴∠ BPC=∠ BDC=45°.答案 : 45°【知识归纳】圆周角与直径1.当题目中出现了直径时 , 常作辅助线 , 利用直径所对的圆周角是直角解决问题 .2.当出现 90°的圆周角时 , 常连接该圆周角所对的弦 , 则该弦为直径 .7. 如图 , 在☉ O中, 直径 AB与弦 CD相交于点 P, ∠CAB=40°, ∠APD=65° .(1)求∠B 的大小 .(2)已知 AD=6,求圆心 O到 BD的距离 .【解析】 (1) ∵∠ APD=∠C+∠CAB,∴∠ C=65°-40 °=25° .∴∠ B=∠C=25° .(2) 过点 O作 OE⊥ BD于 E, 则 DE=BE.又∵ AO=BO,∴OE= AD= ×6=3.∴圆心 O到 BD的距离为 3.圆内接四边形1. 如图 , 四边形 ABCD内接于☉ O,如果∠ BOD=130°, 则∠ BCD的度数是 ()A.115°B.130°C.65°D.50°【解析】选 A. ∵∠ BOD=130°, ∴∠ A= ∠BOD=65°, ∵∠2.( 莱芜中考 ) 如图 , 在☉ O中 , 已知∠ OAB=22.5°, 则∠C 的度数为 ()A. 135 °B.122.5 °C.115.5°D.112.5 °【解析】选 D.如图, 作所对的圆周角 .∵OA=OB,∴∠ OBA=∠ OAB=22.5° . ∴∠ AOB=180 ° - ∠ OAB-∠ OBA =180° -22.5 ° -22.5 °=135° .∴∠ D= ∠ AOB=×135°=67.5 °.∵四边形 ACBD是圆内接四边形 ,∴∠ C+∠D=180° .∴∠ C=112.5 °.【方法技巧】1. 在圆中 , 求角的度数时 , 常利用圆周角定理和圆内接四边形的对角互补来完成.2.有时需要自己作出与已知角互补的圆周角 , 才能运用圆内接四边形的性质 .3. 四边形 ABCD内接于☉ O,AD∥BC,∠ B=75° , 则∠ C=.【解析】∵AD∥ BC,∴∠ A+∠B=180° ,∴∠ A=180°-75 °=105°,答案 : 75°【变式训练】已知 , 四边形 ABCD内接于☉ O, 且∠ A∶∠ C=1∶2, 则∠ BOD= ° .【解析】∵四边形 ABCD内接于☉ O,∴∠ A+∠C=180°.又∠ A∶∠ C=1∶ 2, 得∠ A=60° .∴∠ BOD=2∠A=120°.答案 : 1204.如图 , △ ABC内接于☉ O,AD为△ ABC的外角平分线 , 交☉ O 于点 D, 连接 BD,CD,判断△DBC的形状 , 并说明理由 .【解析】△DBC为等腰三角形 . 理由如下 :∵四边形 ABCD为☉ O的内接四边形 ,∴∠ DCB+∠DAB=180°,又∠ EAD+∠DAB=180°,∴∠ EAD=∠DCB.又∠ DAC=∠DBC,∠EAD=∠DAC,∴∠ DBC=∠DCB,∴DB=DC,即△ DBC为等腰三角形 .【错在哪？】作业错例课堂实拍A,B 为☉ O上的两点 , ∠ AOB=100° , 若点 C 也在☉ O上, 且点 C不与 A,B 重合 , 求∠ACB的度数 .(1)错因 :____________________________________.(2)纠错 :____________________________________________________________ _________________________________.答案： (1) 点 C也可能在劣弧AB上，需要分情况讨论(2)当 C在优弧AB上时，∠ ACB=1∠AOB=50°，当 C 在劣弧AB上时，∠ ACB=2 180°-50 °=130°。

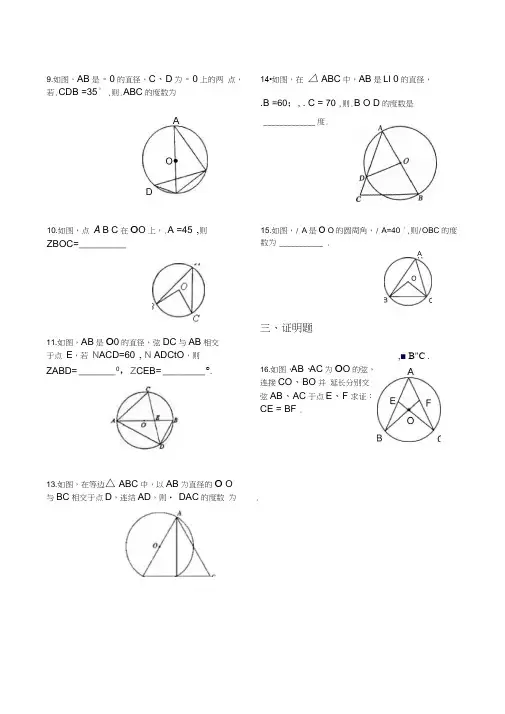
5.如图，已知AB 为O O 的直径，点 C 在O O 上,圆周角中考题集锦/ C=15°,则/ BOC 的度数为（、选择题)B 30C (B)CB P 40O (D) 50 AD )AA CD 45o Ao)oBooAACEDOB填空题CCoO DOBBA6. 上 15o 20o 30o B C D30° A . 上一点，则• D(A) 20 (B ) 25 (D ) 45ACB = 50°，点 D 是 BAC若/ PBO=15),C. 45 ° D . 60 °A 、B 则/ 乙APD =70，则乙B 等于 8.如图，△ ABC 内接于 O O ,AC 是O O 的直径，50°~^CP 为O O 上的点 AOB=( )若若 )1101.如图，O O 中，弦AB 、CD 相交于点P 的内接三角形ABC 是 O O ，则.AOC 的度数等于( B . 130 C . 120 DOA . 15° B. 30Z A =30B C 2.已知：点 且 PA// OB 7.如图，已知BD 是O O 的直径，O O 的弦4.如图，A 、B 、C 是O O 上的三点，已知.O =60则.C =( )3.如图，△ /ABC =70 A . 140 将量角器按如图所示的方式放置在三角形纸板 使点C 在半圆上.点A 、B 的读数分别为86 '，则/ ACB 的大小为 15° 28° 29° 34°AC_ BD 于点 E,若 AOD=60°,则.DBC 的度数为A.30 B. 40° C. 50 D. 60-谅1 q9.如图，AB 是。

0的直径，C 、D 为。

0上的两 点，若.CDB =35° ,则.ABC 的度数为14•如图，在 △ ABC 中，AB 是LI 0的直径，.B =60；, . C = 70 ,则.B O D 的度数是10.如图，点 A B C 在O O 上，.A =45°,则ZBOC= _________15.如图，/ A 是O O 的圆周角，/ A=40 °,则/OBC 的度数为 ___________ .11.如图，AB 是O 0的直径，弦DC 与AB 相交 于点 E ，若 N ACD=60°, N ADCtO ，则ZABD= _______ 0，Z CEB= ________ °.16.如图，AB 、AC 为O O 的弦，连接CO 、BO 并 延长分别交弦AB 、AC 于点E 、F 求证：CE = BF .13.如图，在等边△ ABC 中，以AB 为直径的O O 与BC 相交于点D ，连结AD ，则• DAC 的度数 为._____________ 度.三、证明题A,■ B " C .一、选择题I. C 2. C 3. A 4. C 5. B6. B7. A二、填空题8. 40°9. 55°10. 90°II. 60°,100°13. 30°14. 100 15. 50 °三、证明题16. 证明：'；O B O是O O的半径.OB =OC又；B . BOE "COF .△EOB FOC.OE =OF.CE =BF。

九年级数学上册《圆周角》练习题及答案解析学校:___________姓名：___________班级：______________一、单选题1．如图，在⊙O中，AB＝AC，⊙AOB＝40°，则⊙ADC的度数是（）A．40°B．30°C．20°D．15°2．下列说法正确的是（）A．劣弧一定比优弧短B．面积相等的圆是等圆C．长度相等的弧是等弧D．如果两个圆心角相等，那么它们所对的弧也相等3．如图，⊙O的两条弦AB⊙CD，已知⊙ADC＝35°，则⊙BAD的度数为（）A．55°B．70°C．110°D．130°4．如图，在⊙O中，点A是BC的中点，⊙ADC＝24°，则⊙AOB的度数是（）A．24°B．26°C．48°D．66°5．如图，正五边形ABCDE 和正三角形AMN 都是O 的内接多边形，则BOM ∠的度数是（ ）A ．36︒B ．45︒C ．48︒D ．60︒6．如图，AB 是⊙O 的直径，P A 与⊙O 相切于点A ，⊙ABC ＝25°，OC 的延长线交P A 于点P ，则⊙P 的度数是( )A ．25°B ．35°C ．40°D ．50°7．如图，AB 是O 的直径，C ，D 是O 上的两点，若54ABD ∠=︒，则BCD ∠的度数是（ ）A ．36°B ．40°C ．46°D ．65°8．下列说法正确的是（ ）A ．顶点在圆上的角是圆周角B ．两边都和圆相交的角是圆周角C ．圆心角是圆周角的2倍D ．圆周角度数等于它所对圆心角度数的一半9．下列命题是真命题的是（ ）A ．相等的两个角是对顶角B ．相等的圆周角所对的弧相等C ．若a b <，则22ac bc <D ．在一个不透明的箱子里放有1个白球和2个红球，它们除颜色外其余都相同，从箱子里任意摸出1个球，摸到白球的概率是1310．如图，⊙O 是ABC 的外接圆，AC 是⊙O 的直径，点P 在⊙O 上，若40ACB ∠=︒，则BPC ∠的度数是（ ）A ．40︒B ．45︒C ．50︒D ．55︒11．如图，O 的半径OD ⊥弦AB 于点C ，连接AO 并延长交O 于点E ，连接EB ．若4AB =，1CD =，则EB 的长为（ ）A ．5B ．4C ．3D ．2.512．如图，点A ，B ，C 是O 上的点，连接,,AB AC BC ，且15ACB ∠=︒，过点O 作OD AB ∥交O 于点D ．连接,AD BD ，已知O 半径为2，则图中阴影面积为( )A ．2πB ．3πC ．4πD ．23π 13．如图，ABC ∆中，AB 是O 的直径，AC 交O 于点E ，BC 交O 于点D ，点D 是BC 中点，O 的切线DF 交AC 于点F ，则下列结论中⊙A ABE ∠=∠；⊙BD DE =；⊙AB AC =；⊙F 是EC 中点，正确的个数是（ ）A ．1B ．2C ．3D ．4二、填空题14．如图，点A 、B 、C 、D 、E 在O 上，且弧AB 为50︒，则E C ∠+∠=________．15．如图，A 、B 、C 是⊙O 上的三点，AB ＝2，∠ACB ＝30°，那么⊙O 的半径等于_____．16．如图，AB 是⊙O 的直径，CD 为弦，AB ⊙CD ，若CD =CB ＝2，则阴影部分的面积是______．17．如图，在半径为1的O 上顺次取点A ，B ，C ，D ，E ，连接AB ，AE ，OB ，OC ，OD ，OE ．若65BAE ∠=︒，70COD ∠=︒，则BC 与DE 的长度之和为__________．（结果保留π）．18．如图，ABC内接于⊙O，AB＝BC，⊙BAC＝30°，AD为⊙O的直径，AD＝2，则BD＝________．19．如图，OE、OF分别为⊙O的弦AB、CD的弦心距，如果OE=OF，那么________（只需写一个正确的结论）．20．如图，AB是⊙O的直径，C、D是⊙O上的两点，⊙AOC＝120°，则⊙CDB＝_____°．三、解答题21．如图．AB是⊙O的直径，点C，D在⊙O上，C是BD的中点，连接BD交AC于点E，延长AC至F，使CE＝CF．(1)求证：BF 是⊙O 的切线．(2)若BF ＝3，1sin 3A =，求BD 的长． 22．如图，在⊙AOB 和⊙COD 中，OA ＝OB ，OC ＝OD ，若⊙AOB ＝⊙COD ＝60°．(1)求证：AC ＝BD ．(2)求⊙APB 的度数．23．如图，已知ABCD 是某圆的内接四边形，AB BD =，BM AC ⊥于M ，求证：AM DC CM =+．24．已知AB 是⊙O 的直径，点C 在AB 的延长线上，AB ＝4，BC ＝2，P 是⊙O 上半部分的一个动点，连接OP ，CP ．(1)如图⊙，⊙OPC 的最大面积是________；(2)如图⊙，延长PO 交⊙O 于点D ，连接DB ，当CP ＝DB 时，求证：CP 是⊙O 的切线．25．如图，,,//,//AD DB AE EC FG AB AG BC ==．利用平移或旋转的方法研究图中的线段,,DE BF FC 之间的位置关系和数量关系．参考答案及解析：1．C【详解】先由圆心角、弧、弦的关系求出⊙AOC=⊙AOB=50°，再由圆周角定理即可得出结论．解：⊙在⊙O 中，= ，⊙⊙AOC=⊙AOB ，⊙⊙AOB=40°，⊙⊙AOC=40°， ⊙⊙ADC=12⊙AOC=20°， 故选C ．2．B【分析】根据圆的相关概念、圆周角定理及其推论进行逐一分析判断即可．【详解】解：A.在同圆或等圆中，劣弧一定比优弧短，故本选项说法错误，不符合题意；B.面积相等的圆是等圆，故本选项说法正确，符合题意；C.能完全重合的弧才是等弧，故本选项说法错误，不符合题意；D.必须在同圆或等圆中，相等的圆心角所对的弧相等，故本选项说法错误，不符合题意．故选：B ．【点睛】本题主要考查了圆周角定理及其推论、等弧、等圆、以及优弧和劣弧等知识，解题关键是理解各定义的前提条件是在同圆或等圆中．3．A【分析】根据垂直定义和三角形的两锐角互余进行解答即可．【详解】解：⊙AB ⊙CD ，⊙⊙ADC +⊙BAD =90°，⊙⊙ADC =35°，⊙⊙BAD =90°﹣35°=55°，故选：A ．【点睛】本题考查垂直定义、直角三角形的两锐角互余，熟练掌握直角三角形的两锐角互余是解答的关键．4．C【分析】直接利用圆周角求解．【详解】解：⊙点A 是BC 的中点，⊙AC AB =，⊙⊙AOB =2⊙ADC =2×24°=48°．故选：C ．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．5．C【分析】如图，连接AO ．利用正多边形的性质求出AOM ∠，AOB ∠，可得结论．【详解】解：如图，连接AO ．AMN △是等边三角形，60ANM ∠∴=︒，2120AOM ANM ∠∠∴==︒， ABCDE 是正五边形，360725AOB ∠︒∴==︒，1207248BOM ∠∴=︒-︒=︒．故选：C ．【点睛】本题考查正多边形与圆，等边三角形的性质，圆周角定理等知识，解题的关键是熟练掌握正多边形的性质，属于中考常考题型．6．C【分析】根据圆周角定理可得50AOC ∠=︒，根据切线的性质可得90PAO ∠=︒，根据直角三角形两个锐角互余即可求解．【详解】AC AC =，⊙ABC ＝25°，250AOC ABC ∴∠=∠=︒，AB 是⊙O 的直径，∴90PAO ∠=︒，9040P AOC ∴∠=︒-∠=︒．故选C ．【点睛】本题考查了圆周角定理，切线的性质，掌握圆周角定理与切线的性质是解题的关键．7．A【分析】连接AD ，如图，根据圆周角定理得到⊙ADB =90°，⊙C =⊙A ，然后利用余角的性质计算出⊙A ，从而得到⊙C 的度数．【详解】解：如图，连接AD ，⊙AB 为⊙O 的直径，⊙⊙ADB =90°，⊙⊙A =90°−⊙ABD =90°−54°=36°，⊙⊙C =⊙A =36°．故选：A ．【点睛】本题主要考查了同弦所对的圆周角相等，直径所对的圆周角是直角，解题的关键在于能够熟练掌握相关知识进行求解．8．D【详解】解：顶点在圆上，且与圆有相交的角是圆周角，则A 和B 是错误的；同弧所对的圆周角的度数等于圆心角度数的一半，故选D ．9．D【分析】分别根据对顶角的定义，圆周角定理，不等式的基本性质及概率公式进行判断即可得到答案．【详解】有公共顶点且两条边互为反向延长线的两个角是对顶角，故A 选项错误，不符合题意； 在同圆或等圆中，相等的圆周角所对的弧相等，故B 选项错误，不符合题意；若a b <，则22ac bc ≤，故C 选项错误，不符合题意；在一个不透明的箱子里放有1个白球和2个红球，它们除颜色外其余都相同，从箱子里任意摸出1个球，摸到白球的概率是13，故D 选项正确，符合题意； 故选：D ．【点睛】本题考查了命题的真假，涉及对顶角的定义，圆周角定理，不等式的基本性质及概率公式，熟练掌握知识点是解题的关键．10．C【分析】根据圆周角定理得到90ABC ∠=︒，BPC A ∠=∠，然后利用互余计算出⊙A 的度数，从而得到BPC ∠的度数．【详解】解：⊙AB 是⊙O 的直径，⊙90ABC ∠=︒，⊙90904050A ACB ∠=︒-∠=︒-︒=︒，⊙50BPC A ∠=∠=︒，故选：C ．【点睛】本题考查了圆周角定理，解题的关键是掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半；半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．11．C【分析】设圆O 的半径为r ，则OC =OD -CD =r -1，AE =2OA =2r ，先利用垂径定理得到AC =2，即可利用勾股定理求出半径，从而求出AE 的长，再利用勾股定理即可求出BE ．【详解】解：设圆O 的半径为r ，则OC =OD -CD =r -1，AE =2OA =2r ， 由垂径定理得122AC BC AB ===，在Rt ⊙OAC 中，222OA OC AC =+，⊙()22221r r =+-， ⊙52r =， ⊙AE =5，⊙AE 是圆O 的直径，⊙⊙B =90°，⊙在Rt ⊙ABE 中，3BE ，故选：C ．【点睛】本题主要考查了垂径定理，勾股定理，直径所对的圆周角是直角等等，熟知垂径定理是解题的关键．12．B【分析】根据圆周角定理可得⊙AOB =30°，再由OD AB ∥，可得AOB ADB SS =，从而得到阴影面积等于扇形AOB 的面积，即可求解．【详解】解：⊙15ACB ∠=︒，⊙⊙AOB =30°， ⊙23023603AOB S ππ⨯==扇形， ⊙OD AB ∥，⊙AOB ADB S S =，⊙阴影面积等于扇形AOB 的面积，⊙阴影面积等于3π． 故选：B【点睛】本题考查了圆周角定理、扇形面积公式和同底等高的两个三角形的面积相等等知识，属于常考题型，熟练掌握上述基本知识是解题的关键．13．C【分析】连接连接OD ，AD 、DE ，根据直径所对的圆周角是直角以及等腰三角形的性质可判断结论⊙；根据同圆或等圆中，同弧所对的弦相等可得结论⊙；根据切线的性质以及三角形中位线定理可得结论⊙；因为只有ABE △是等腰直角三角形时，才能满足结论⊙．【详解】解：连接OD，AD、DE．AB是O的直径，∴∠=︒（直径所对的圆周角是直角），ADB90∴⊥，AD BC点D是BC中点，=，故⊙正确；∴∠=∠，AB ACBAD CAD∴BD DE=，∴=，故⊙正确；BD DEDF是O的切线，∴⊥，OD DF=，BD DCAO BO=，∴，OD AC//∴⊥，DF AF∴，DF BE//⊙点D是BC的中点，∴点F是EC的中点，故⊙正确；只有当ABE△是等腰直角三角形时，45∠=∠=︒，BAC ABE故⊙错误，正确的有⊙⊙⊙共3个，故选：C．【点睛】本题考查了圆周角定理，圆切线的性质，等腰三角形的性质，三角形中位线定理的应用，题目难度适中，熟练掌握相关图形的性质定理是解本题的关键．14．155︒【分析】先根据弧的度数与它所对应的圆心角的度数的关系，求得弧AB对应的圆心角的度数，再根据圆周角与圆心角的关系，则可求得E C ∠+∠.【详解】弧的度数等于它所对应的圆心角的度数，由于弧AB 为50︒，所以3=50∠︒ .顶点在圆上且两边都和圆相交的角叫做圆周角，而一条弧所对的圆周角等于它所对的圆心角的一半，所以：112E ∠=∠ ,122C ∠=∠ ， ()()()11112360336050155222E C ∠+∠=∠+∠=︒-∠=︒-︒=︒.【点睛】本题考查弧、圆周角、圆心角的概念，及它们之间的关系.15．2【分析】根据题意和圆周角定理得∠O ＝60°，则△OAB 是等边三角形，根据AB ＝2即可得．【详解】解：∵OA ＝OB ，∠ACB ＝30°，OA =OB ，∴∠O ＝60°，∴△OAB 是等边三角形，∵AB ＝2，∴OA ＝AB ＝2，故答案为：2．【点睛】本题考查了等边三角形的判定与性质，圆周角定理，解题的关键是掌握这些知识点．16．23π【分析】连接OC ，设CD 与AB 的交点为E ，利用垂径定理、勾股定理判定△OBC 是等边三角形，运用扇形的面积减去△OBC 的面积即可．【详解】连接OC ，设CD 与AB 的交点为E ，⊙AB 是⊙O 的直径，AB ⊙CD ，CD =CB ＝2，⊙CE 1BE ==，⊙⊙ECB =30°，⊙CBE =60°，⊙CO =BO ，⊙△OBC 是等边三角形，⊙⊙BOC =60°，OC =OB =2，⊙2602123602S =π⨯⨯-⨯阴影=23π故答案为：23π 【点睛】本题考查了垂径定理，勾股定理，扇形的面积公式，等边三角形的判定和性质，熟练掌握垂径定理，扇形的面积公式是解题的关键．17．13π##3π 【分析】由圆周角定理得2130BOE BAE ∠=∠=︒，根据弧长公式分别计算出BE 与DC 的长度，相减即可得到答案．【详解】解：⊙65BAE ∠=︒，⊙2130BOE BAE ∠=∠=︒又O 的半径为1，BE 的长度=130113=18018ππ⨯，又70COD ∠=︒，⊙DC 的长度=7017=18018ππ⨯， ⊙BC 与DE 的长度之和=13761-==1818183ππππ，故答案为：13π． 【点睛】本题主要考查了计算弧长，圆周角定理，熟练掌握弧长计算公式是解答本题的关键．18【分析】根据AB ＝BC ，可得⊙C =⊙BAC =30°，再由圆周角定理，可得⊙D =30°，然后利用锐角三角函数，即可求解．【详解】解：⊙AB ＝BC ，⊙⊙C =⊙BAC =30°，⊙⊙C =⊙D ，⊙⊙D =30°，⊙AD 为⊙O 的直径，⊙⊙ABD =90°，在Rt ABD △ 中，AD ＝2，⊙D =30°，⊙cos302BD AD =⋅︒==．【点睛】本题主要考查了圆周角定理，锐角三角函数等知识，熟练掌握相关知识点是解题的关键．19．AB =CD （答案不唯一）【分析】根据圆心角、弧、弦、弦心距之间的关系定理的推论可以直接得到所求的结论．【详解】解：⊙OE =OF ，OE 、OF 分别为⊙O 的弦AB 、CD 的弦心距，⊙AB =CD ．故答案为：AB =CD （答案不唯一）【点睛】本题主要考查了圆心角、弧、弦的关系．熟练掌握在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等是解题的关键． 20．30．【分析】先利用邻补角计算出BOC ∠，然后根据圆心周角定理得到CDB ∠的度数．【详解】⊙⊙BOC ＝180°﹣⊙AOC ＝180°﹣120°＝60°，⊙⊙CDB ＝12⊙BOC ＝30°． 故答案为30．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．21．(1)见详解(2)BD=16 3【分析】（1）根据直径所对圆周角得出⊙ACB=90°，根据C是BD的中点，得出DC BC=，利用等弧所对圆周角得出⊙CAB=⊙CBD即可（2）连结OC，交BD于G，根据垂径定理得出OC⊙BD，DG=BG=12BD，由三角函数求出AF=9，利用勾股定理求出ABAB BFBCAF⋅===（1）证明：⊙AB是⊙O的直径，⊙⊙ACB=90°，⊙C是BD的中点，⊙DC BC=，⊙⊙CAB=⊙CBD，⊙CE=CF，BC⊙EF，⊙BE=BF，⊙⊙FBC=⊙CBE，⊙⊙FBC=⊙CBE=⊙CAB，⊙⊙CAB+⊙CBA=90°，⊙⊙FBC+⊙CBA=90°，⊙FB⊙AB，AB为直径，⊙BF为⊙O的切线；，（2）解：连结OC，交BD于G，⊙DC BC=，OC为半径，⊙OC⊙BD，DG=BG=12 BD，⊙BF＝3，1 sin3A=，⊙31sin 3BF A AF AF ===， ⊙AF =9，在Rt △ABF 中AB⊙S △ABF =12BC ·AF =12AB ·BF ，⊙AB BF BC AF ⋅=== ⊙sin A =sin⊙CBG =13CG BC ==，⊙3CG =，在Rt ⊙BCG 中83BG ==， ⊙BD =2BG =163．【点睛】本题考查圆的切线判定，等弧所对圆周角性质，线段线段垂直平分线性质，等腰三角形等腰三角形三线合一性质，勾股定理锐角三角函数，面积等积式，本题难度不大，是中考常考试题，掌握好相关知识是解题关键．22．(1)见解析(2)60°【分析】（1）通过证明⊙AOC ⊙⊙BOD ，即可求证；（2）由（1）可得⊙OAC ＝⊙OBD ，从而得到⊙P AB +⊙PBA ＝⊙OAB +⊙OBA ，利用三角形内角和的性质即可求解．（1）证明：⊙⊙AOB ＝⊙COD ，⊙AOB BOC COD BOC ∠+∠∠+∠＝，即⊙AOC ＝⊙BOD ，在⊙AOC 和⊙BOD 中，OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩，⊙⊙AOC ⊙⊙BOD （SAS ），⊙AC ＝BD ．（2）解：⊙⊙AOC ⊙⊙BOD ，⊙⊙OAC ＝⊙OBD ，⊙⊙PBA ＝⊙ABO +⊙OBD ，⊙OAB =⊙P AB +⊙OAC ，⊙⊙P AB +⊙PBA ＝⊙P AB +⊙ABO +⊙OBD =⊙P AB +⊙OAC +⊙ABO =⊙OAB +⊙OBA ，⊙OA ＝OB ，⊙AOB ＝60°，⊙⊙AOB 是等边三角形，⊙⊙OAB +⊙OBA ＝120°⊙⊙P AB +⊙PBA ＝120°，⊙()180********APB PAB PBA ∠︒-∠+∠︒-︒︒＝＝＝． 【点睛】此题考查了全等三角形的判定与性质，三角形内角和定理，等边三角形的判定和性质，解题的关键是熟练掌握全等三角形的判定和性质．23．见解析【分析】在MA 上截取ME MC =，连接BE ，利用圆周角定理易得()ABE DBC AAS ≅，利用三角形的性质得到AE CD =即可求解．【详解】证明：在MA 上截取ME MC =，连接BE ，BM AC ⊥，BE BC ∴=，BEC BCE ∴∠=∠．AB BD =，∴AB BD =，ADB BAD ∴∠=∠，而ADB BCE ∠=∠，BCE BAD ∴∠=∠．又180BCD BAD ∠+∠=︒，180BEA BCE ∠+∠=︒，BEA BCD ∴∠=∠．BAE BDC ∠=∠，()ABE DBC AAS ∴∆≅∆，AE CD ∴=，AM AE EM DC CM ∴=+=+．【点睛】本题主要考查了圆周角定理，全等三角形的判定和性质，作出辅助线构建三角形全等是解答关键．24．(1)4(2)见解析【分析】（1）因为OC 长度确定，所以当点P 到OC 的距离最大时⊙OPC 的面积最大，当OP ⊙OC 时，当点P 到OC 的距离最大，等于圆O 的半径，求出此时的⊙OPC 的面积即可；（2）连接AP ，BP ，利用同圆中，相等的圆心角所对的弦相等，可得AP =DB ，因为CP ＝DB ，所以AP =CP ，可证⊙APB ⊙⊙CPO （SAS ），得到⊙OPC ＝90°，即可证明CP 是切线．（1）解：⊙AB ＝4，⊙OB ＝2，OC ＝OB +BC ＝4．在⊙OPC 中，设OC 边上的高为h ，⊙S △OPC 12=OC •h ＝2h ， ⊙当h 最大时，S △OPC 取得最大值．作PH ⊙OC ，如图⊙，则PO PH >，当OP ⊙OC 时，PO PH =，此时h 最大，如答图1所示：此时h ＝半径＝2，14242OPC S ⨯⨯＝＝．⊙⊙OPC 的最大面积为4， 故答案为：4．（2）证明：如答图⊙，连接AP ，BP ．⊙⊙AOP ＝⊙BOD ，⊙AP ＝BD ，⊙CP ＝DB ，⊙AP ＝CP ，⊙⊙A ＝⊙C ，在⊙APB 与⊙CPO 中， AP CPA C AB CO=⎧⎪∠=∠⎨⎪=⎩，⊙⊙APB ⊙⊙CPO （SAS ）， ⊙⊙APB ＝⊙OPC ，⊙AB 是直径，⊙⊙APB ＝90°，⊙⊙OPC＝90°，⊙DP⊙PC，⊙DP经过圆心，⊙PC是⊙O的切线．【点睛】本题考查了圆，熟练掌握圆的半径、切线、弦与圆心角的关系等知识是解题的关键．25．DE与BF平行且相等，DE与FC平行且相等，BF与FC相等且在一条直线上【分析】易知DE是△ABC的中位线，则DE∥BC∥AG；由此可知四边形ADEG和四边形DBFE都是平行四边形，故AG＝DE＝BF；由全等三角形可得AG＝FC，故DE＝BF＝FC．【详解】解：线段DE，BF，FC之间的位置关系是DE∥BF，DE∥FC，数量关系是DE＝BF＝FC，∵AG∥BC（已知）∴∠G＝∠EFC（两直线平行，内错角相等）∵∠AEG＝∠FEC（对顶角相等），又AE＝EC（已知）∴△AGE≌△CFE（AAS）；∴AG＝FC，FE＝EG（全等三角形的对应边相等），可以看做△AGE绕点E旋转180°得到△CFE，又∵AD＝DB（已知）∴DE为三角形ABC的中位线，BC，∴DE∥BC，DE=12即DE∥BF，DE∥FC，∵FG∥AB，AG∥BC（已知）∴四边形ABFG是平行四边形∴AG＝BF，BC，∴BF＝FC＝12∴DE＝BF＝FC，可以看做⊙ADE沿直线AE平移得到△EFC，故线段DE，BF，FC之间的位置关系是DE∥BF，DE∥FC，BF与FC在一条直线上，数量关系是DE＝BF＝FC．【点睛】题考查的是三角形中位线定理、平行四边形及全等三角形的判定和性质．三角形的中位线的性质定理，为证明线段相等和平行提供了依据．第21页共21页。

中考数学复习----《圆周角定理》知识点总结与专项练习题（含答案）知识点总结1.圆心角、弦以及弧之间的关系：①定理：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等。

②推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等。

说明：同一条弦对应两条弧，其中一条是优弧，一条是劣弧，而在本定理和推论中的“弧”是指同为优弧或劣弧。

2.圆周角的定义：顶点在圆上，并且两边都与圆相交的角叫做圆周角。

3.圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。

4.圆周角定理的推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径。

5.圆的内接四边形：①定义：四个顶点都在圆上的四边形叫做圆的内接四边形。

②性质：I：圆内接四边形的对角互补。

II：圆内接四边形的任意一个外角等于它的内对角。

练习题1、（2022•襄阳）已知⊙O的直径AB长为2，弦AC长为2，那么弦AC所对的圆周角的度数等于．【分析】首先利用勾股定理逆定理得∠AOC＝90°，再根据一条弦对着两种圆周角可得答案．【解答】解：如图，∵OA＝OC＝1，AC＝，∴OA2+OC2＝AC2，∴∠AOC＝90°，∴∠ADC＝45°，∴∠AD'C＝135°，故答案为：45°或135°．2、（2022•日照）一圆形玻璃镜面损坏了一部分，为得到同样大小的镜面，工人师傅用直角尺作如图所示的测量，测得AB＝12cm，BC＝5cm，则圆形镜面的半径为．【分析】连接AC，根据∠ABC＝90°得出AC是圆形镜面的直径，再根据勾股定理求出AC 即可．【解答】解：连接AC，∵∠ABC＝90°，且∠ABC是圆周角，∴AC是圆形镜面的直径，由勾股定理得：AC＝＝＝13（cm），所以圆形镜面的半径为cm，故答案为：cm．3、（2022•永州）如图，AB是⊙O的直径，点C、D在⊙O上，∠ADC＝30°，则∠BOC＝度．【分析】根据在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半求出∠AOC的度数，根据平角的定义即可得到∠BOC＝180°﹣∠AOC的度数．【解答】解：∵∠ADC是所对的圆周角，∴∠AOC＝2∠ADC＝2×30°＝60°，∴∠BOC＝180°﹣∠AOC＝180°﹣60°＝120°．故答案为：120．4、（2022•苏州）如图，AB是⊙O的直径，弦CD交AB于点E，连接AC，AD．若∠BAC＝28°，则∠D＝°．【分析】如图，连接BC，证明∠ACB＝90°，求出∠ABC，可得结论．【解答】解：如图，连接BC．∵AB是直径，∴∠ACB＝90°，∴∠ABC＝90°﹣∠CAB＝62°，∴∠D＝∠ABC＝62°，故答案为：62．5、（2022•湖州）如图，已知AB 是⊙O 的弦，∠AOB ＝120°，OC ⊥AB ，垂足为C ，OC 的延长线交⊙O 于点D ．若∠APD 是AB ⌒所对的圆周角，则∠APD 的度数是 ．【分析】由垂径定理得出，由圆心角、弧、弦的关系定理得出∠AOD ＝∠BOD ，进而得出∠AOD ＝60°，由圆周角定理得出∠APD ＝∠AOD ＝30°，得出答案．【解答】解：∵OC ⊥AB ，∴，∴∠AOD ＝∠BOD ，∵∠AOB ＝120°，∴∠AOD ＝∠BOD ＝∠AOB ＝60°，∴∠APD ＝∠AOD ＝×60°＝30°，故答案为：30°．6、（2022•徐州）如图，A 、B 、C 点在圆O 上，若∠ACB ＝36°，则∠AOB ＝ ．【分析】利用一条弧所对的圆周角等于它所对的圆心角的一半即可得出结论．【解答】解：∵∠ACB ＝∠AOB ，∠ACB ＝36°，∴∠AOB ＝2×∠ACB ＝72°．故答案为：72°．7、（2022•锦州）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，∠ADC＝130°，连接AC，则∠BAC的度数为．【分析】利用圆内接四边形的性质和∠ADC的度数求得∠B的度数，利用直径所对的圆周角是直角得到∠ACB＝90°，然后利用直角三角形的两个锐角互余计算即可．【解答】解：∵四边形ABCD内接于⊙O，∠ADC＝130°，∴∠B＝180°﹣∠ADC＝180°﹣130°＝50°，∵AB为⊙O的直径，∴∠ACB＝90°，∴∠CAB＝90°﹣∠B＝90°﹣50°＝40°，故答案为：40°．8、（2022•雅安）如图，∠DCE是⊙O内接四边形ABCD的一个外角，若∠DCE＝72°，那么∠BOD的度数为．【分析】根据邻补角的概念求出∠BCD，根据圆内接四边形的性质求出∠A，根据圆周角定理解答即可．【解答】解：∵∠DCE＝72°，∴∠BCD＝180°﹣∠DCE＝108°，∵四边形ABCD内接于⊙O，∴∠A＝180°﹣∠BCD＝72°，由圆周角定理，得∠BOD＝2∠A＝144°，故答案为：144°．9、（2022•甘肃）如图，⊙O是四边形ABCD的外接圆，若∠ABC＝110°，则∠ADC＝°．【分析】根据圆内接四边形的对角互补即可得到结论．【解答】解：∵四边形ABCD内接于⊙O，∠ABC＝110°，∴∠ADC＝180°﹣∠ABC＝180°﹣110°＝70°，故答案为：70．。

北师大版九年级下册 3.4 圆周角与圆心角的关系中考试题精选（含答案）一．选择题（共20小题）1．（2019•营口）如图，BC是⊙O的直径，A，D是⊙O上的两点，连接AB，AD，BD，若∠ADB＝70°，则∠ABC的度数是（）A．20°B．70°C．30°D．90°2．（2019•陕西）如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF＝EB，EF与AB交于点C，连接OF，若∠AOF＝40°，则∠F的度数是（）A．20°B．35°C．40°D．55°3．（2019•沈阳）如图，AB是⊙O的直径，点C和点D是⊙O上位于直径AB两侧的点，连接AC，AD，BD，CD，若⊙O的半径是13，BD＝24，则sin∠ACD的值是（）A．B．C．D．4．（2019•广元）如图，AB，AC分别是⊙O的直径和弦，OD⊥AC于点D，连接BD，BC，且AB＝10，AC＝8，则BD的长为（）A．2B．4 C．2D．4.8 5．（2019•吉林）如图，在⊙O中，所对的圆周角∠ACB＝50°，若P为上一点，∠AOP＝55°，则∠POB的度数为（）A．30°B．45°C．55°D．60°6．（2019•柳州）如图，A，B，C，D是⊙O上的点，则图中与∠A相等的角是（）A．∠B B．∠C C．∠DEB D．∠D 7．（2019•镇江）如图，四边形ABCD是半圆的内接四边形，AB是直径，＝．若∠C ＝110°，则∠ABC的度数等于（）A．55°B．60°C．65°D．70°8．（2019•十堰）如图，四边形ABCD内接于⊙O，AE⊥CB交CB的延长线于点E，若BA 平分∠DBE，AD＝5，CE＝，则AE＝（）A．3 B．3C．4D．2 9．（2019•贵港）如图，AD是⊙O的直径，＝，若∠AOB＝40°，则圆周角∠BPC的度数是（）A．40°B．50°C．60°D．70°10．（2019•宜昌）如图，点A，B，C均在⊙O上，当∠OBC＝40°时，∠A的度数是（）A．50°B．55°C．60°D．65°11．（2019•眉山）如图，⊙O的直径AB垂直于弦CD，垂足是点E，∠CAO＝22.5°，OC ＝6，则CD的长为（）A．6B．3C．6 D．12 12．（2019•安顺）如图，半径为3的⊙A经过原点O和点C（0，2），B是y轴左侧⊙A优弧上一点，则tan∠OBC为（）A．B．2C．D．13．（2019•襄阳）如图，AD是⊙O的直径，BC是弦，四边形OBCD是平行四边形，AC与OB相交于点P，下列结论错误的是（）A．AP＝2OP B．CD＝2OP C．OB⊥AC D．AC平分OB 14．（2019•兰州）如图，四边形ABCD内接于⊙O，若∠A＝40°，则∠C＝（）A．110°B．120°C．135°D．140°15．（2019•天水）如图，四边形ABCD是菱形，⊙O经过点A、C、D，与BC相交于点E，连接AC、AE．若∠D＝80°，则∠EAC的度数为（）A．20°B．25°C．30°D．35°16．（2019•威海）如图，⊙P与x轴交于点A（﹣5，0），B（1，0），与y轴的正半轴交于点C．若∠ACB＝60°，则点C的纵坐标为（）A．+B．2+C．4D．2+2 17．（2019•菏泽）如图，AB是⊙O的直径，C，D是⊙O上的两点，且BC平分∠ABD，AD 分别与BC，OC相交于点E，F，则下列结论不一定成立的是（）A．OC∥BD B．AD⊥OC C．△CEF≌△BED D．AF＝FD 18．（2019•聊城）如图，BC是半圆O的直径，D，E是上两点，连接BD，CE并延长交于点A，连接OD，OE．如果∠A＝70°，那么∠DOE的度数为（）A．35°B．38°C．40°D．42°19．（2019•白银）如图，点A，B，S在圆上，若弦AB的长度等于圆半径的倍，则∠ASB 的度数是（）A．22.5°B．30°C．45°D．60°20．（2019•潍坊）如图，四边形ABCD内接于⊙O，AB为直径，AD＝CD，过点D作DE⊥AB于点E，连接AC交DE于点F．若sin∠CAB＝，DF＝5，则BC的长为（）A．8 B．10 C．12 D．16二．填空题（共20小题）21．（2019•辽阳）如图，A，B，C，D是⊙O上的四点，且点B是的中点，BD交OC于点E，∠AOC＝100°，∠OCD＝35°，那么∠OED＝．22．（2019•娄底）如图，C、D两点在以AB为直径的圆上，AB＝2，∠ACD＝30°，则AD ＝．23．（2019•常州）如图，AB是⊙O的直径，C、D是⊙O上的两点，∠AOC＝120°，则∠CDB＝°．24．（2019•东营）如图，AC是⊙O的弦，AC＝5，点B是⊙O上的一个动点，且∠ABC＝45°，若点M、N分别是AC、BC的中点，则MN的最大值是．25．（2019•宜宾）如图，⊙O的两条相交弦AC、BD，∠ACB＝∠CDB＝60°，AC＝2，则⊙O的面积是．26．（2019•连云港）如图，点A、B、C在⊙O上，BC＝6，∠BAC＝30°，则⊙O的半径为．27．（2019•台州）如图，AC是圆内接四边形ABCD的一条对角线，点D关于AC的对称点E在边BC上，连接AE．若∠ABC＝64°，则∠BAE的度数为．28．（2019•株洲）如图所示，AB为⊙O的直径，点C在⊙O上，且OC⊥AB，过点C的弦CD与线段OB相交于点E，满足∠AEC＝65°，连接AD，则∠BAD＝度．29．（2019•盐城）如图，点A、B、C、D、E在⊙O上，且为50°，则∠E+∠C＝°．30．（2019•凉山州）如图所示，AB是⊙O的直径，弦CD⊥AB于H，∠A＝30°，CD＝2，则⊙O的半径是．31．（2019•湖州）已知一条弧所对的圆周角的度数是15°，则它所对的圆心角的度数是．32．（2018•朝阳）如图，点A，B，C在⊙O上，AC∥OB，∠BAO＝20°，则∠BOC的度数为．33．（2018•辽阳）如图，AB是半圆O的直径，E是半圆上一点，且OE⊥AB，点C为的中点，则∠A＝°．34．（2018•黑龙江）如图，AC为⊙O的直径，点B在圆上，OD⊥AC交⊙O于点D，连接BD，∠BDO＝15°，则∠ACB＝．35．（2018•镇江）如图，AD为△ABC的外接圆⊙O的直径，若∠BAD＝50°，则∠ACB ＝°．36．（2018•北京）如图，点A，B，C，D在⊙O上，＝，∠CAD＝30°，∠ACD＝50°，则∠ADB＝．37．（2018•东莞市）同圆中，已知所对的圆心角是100°，则所对的圆周角是．38．（2018•杭州）如图，AB是⊙O的直径，点C是半径OA的中点，过点C作DE⊥AB，交⊙O于D，E两点，过点D作直径DF，连结AF，则∠DF A＝．39．（2018•无锡）如图，点A、B、C都在⊙O上，OC⊥OB，点A在劣弧上，且OA＝AB，则∠ABC＝．40．（2018•青海）如图，A、B、C是⊙O上的三个点，若∠AOC＝110°，则∠ABC＝．三．解答题（共10小题）41．（2019•南通）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝1，以边AC上一点O为圆心，OA为半径的⊙O经过点B．（1）求⊙O的半径；（2）点P为劣弧AB中点，作PQ⊥AC，垂足为Q，求OQ的长；（3）在（2）的条件下，连接PC，求tan∠PCA的值．42．如图，在⊙O中，B是⊙O上的一点，∠ABC＝120°，弦AC＝2，弦BM平分∠ABC 交AC于点D，连接MA，MC．（1）求⊙O半径的长；（2）求证：AB+BC＝BM．43．（2019•南京）如图，⊙O的弦AB、CD的延长线相交于点P，且AB＝CD．求证：P A ＝PC．44．（2018•鞍山）如图，四边形ABCD内接于⊙O，AC与BD为对角线，∠BCA＝∠BAD，过点A作AE∥BC交CD的延长线于点E．（1）求证：EC＝AC．（2）若cos∠ADB＝，BC＝10，求DE的长．45．（2018•宜昌）如图，在△ABC中，AB＝AC，以AB为直径的圆交AC于点D，交BC于点E，延长AE至点F，使EF＝AE，连接FB，FC．（1）求证：四边形ABFC是菱形；（2）若AD＝7，BE＝2，求半圆和菱形ABFC的面积．46．（2018•无锡）如图，四边形ABCD内接于⊙O，AB＝17，CD＝10，∠A＝90°，cos B ＝，求AD的长．47．（2017•济南）如图，AB是⊙O的直径，∠ACD＝25°，求∠BAD的度数．48．（2016•温州）如图，在△ABC中，∠C＝90°，D是BC边上一点，以DB为直径的⊙O 经过AB的中点E，交AD的延长线于点F，连结EF．（1）求证：∠1＝∠F．（2）若sin B＝，EF＝2，求CD的长．49．（2016•宁夏）已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED＝EC．（1）求证：AB＝AC；（2）若AB＝4，BC＝2，求CD的长．50．（2016•株洲）已知AB是半径为1的圆O直径，C是圆上一点，D是BC延长线上一点，过点D的直线交AC于E点，且△AEF为等边三角形（1）求证：△DFB是等腰三角形；（2）若DA＝AF，求证：CF⊥AB．3.4 圆周角与圆心角的关系参考答案与试题解析一．选择题（共20小题）1．（2019•营口）如图，BC是⊙O的直径，A，D是⊙O上的两点，连接AB，AD，BD，若∠ADB＝70°，则∠ABC的度数是（）A．20°B．70°C．30°D．90°解：连接AC，如图，∵BC是⊙O的直径，∴∠BAC＝90°，∵∠ACB＝∠ADB＝70°，∴∠ABC＝90°﹣70°＝20°．故答案为20°．故选A．2．（2019•陕西）如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF＝EB，EF与AB交于点C，连接OF，若∠AOF＝40°，则∠F的度数是（）A．20°B．35°C．40°D．55°解：连接FB．∵∠AOF＝40°，∴∠FOB＝180°﹣40°＝140°，∴∠FEB＝∠FOB＝70°∵EF＝EB∴∠EFB＝∠EBF＝55°，∵FO＝BO，∴∠OFB＝∠OBF＝20°，∴∠EFO＝∠EBO，∠EFO＝∠EFB﹣∠OFB＝35°，故选B．3．（2019•沈阳）如图，AB是⊙O的直径，点C和点D是⊙O上位于直径AB两侧的点，连接AC，AD，BD，CD，若⊙O的半径是13，BD＝24，则sin∠ACD的值是（）A．B．C．D．解：∵AB是直径，∴∠ADB＝90°，∵⊙O的半径是13，∴AB＝2×13＝26，由勾股定理得AD＝10，∴sin∠B＝＝＝，∵∠ACD＝∠B，∴sin∠ACD＝sin∠B＝，故选D．4．（2019•广元）如图，AB，AC分别是⊙O的直径和弦，OD⊥AC于点D，连接BD，BC，且AB＝10，AC＝8，则BD的长为（）A．2B．4 C．2D．4.8解：∵AB为直径，∴∠ACB＝90°，∴BC＝＝＝6，∵OD⊥AC，∴CD＝AD＝AC＝4，在Rt△CBD中，BD＝＝2．故选C．5．（2019•吉林）如图，在⊙O中，所对的圆周角∠ACB＝50°，若P为上一点，∠AOP＝55°，则∠POB的度数为（）A．30°B．45°C．55°D．60°解：∵∠ACB＝50°，∴∠AOB＝2∠ACB＝100°，∵∠AOP＝55°，∴∠POB＝45°，故选B．6．（2019•柳州）如图，A，B，C，D是⊙O上的点，则图中与∠A相等的角是（）A．∠B B．∠C C．∠DEB D．∠D解：∵∠A与∠D都是所对的圆周角，∴∠D＝∠A．故选D．7．（2019•镇江）如图，四边形ABCD是半圆的内接四边形，AB是直径，＝．若∠C ＝110°，则∠ABC的度数等于（）A．55°B．60°C．65°D．70°解：连接AC，∵四边形ABCD是半圆的内接四边形，∴∠DAB＝180°﹣∠C＝70°，∵＝，∴∠CAB＝∠DAB＝35°，∵AB是直径，∴∠ACB＝90°，∴∠ABC＝90°﹣∠CAB＝55°，故选A．8．（2019•十堰）如图，四边形ABCD内接于⊙O，AE⊥CB交CB的延长线于点E，若BA 平分∠DBE，AD＝5，CE＝，则AE＝（）A．3 B．3C．4D．2解：连接AC，如图，∵BA平分∠DBE，∴∠1＝∠2，∵∠1＝∠CDA，∠2＝∠3，∴∠3＝∠CDA，∴AC＝AD＝5，∵AE⊥CB，∴∠AEC＝90°，∴AE＝＝＝2．故选D．9．（2019•贵港）如图，AD是⊙O的直径，＝，若∠AOB＝40°，则圆周角∠BPC的度数是（）A．40°B．50°C．60°D．70°解：∵＝，∠AOB＝40°，∴∠COD＝∠AOB＝40°，∵∠AOB+∠BOC+∠COD＝180°，∴∠BOC＝100°，∴∠BPC＝∠BOC＝50°，故选B．10．（2019•宜昌）如图，点A，B，C均在⊙O上，当∠OBC＝40°时，∠A的度数是（）A．50°B．55°C．60°D．65°解：∵OB＝OC，∴∠OCB＝∠OBC＝40°，∴∠BOC＝180°﹣40°﹣40°＝100°，∴∠A＝∠BOC＝50°．故选A．11．（2019•眉山）如图，⊙O的直径AB垂直于弦CD，垂足是点E，∠CAO＝22.5°，OC ＝6，则CD的长为（）A．6B．3C．6 D．12解：∵CD⊥AB，∴CE＝DE，∵∠BOC＝2∠A＝2×22.5°＝45°，∴△OCE为等腰直角三角形，∴CE＝OC＝×6＝3，∴CD＝2CE＝6．故选A．12．（2019•安顺）如图，半径为3的⊙A经过原点O和点C（0，2），B是y轴左侧⊙A优弧上一点，则tan∠OBC为（）A．B．2C．D．解：作直径CD，在Rt△OCD中，CD＝6，OC＝2，则OD＝＝4，tan∠CDO＝＝，由圆周角定理得，∠OBC＝∠CDO，则tan∠OBC＝，故选D．13．（2019•襄阳）如图，AD是⊙O的直径，BC是弦，四边形OBCD是平行四边形，AC与OB相交于点P，下列结论错误的是（）A．AP＝2OP B．CD＝2OP C．OB⊥AC D．AC平分OB 解：∵AD为直径，∴∠ACD＝90°，∵四边形OBCD为平行四边形，∴CD∥OB，CD＝OB，在Rt△ACD中，sin A＝＝，∴∠A＝30°，在Rt△AOP中，AP＝OP，所以A选项的结论错误；∵OP∥CD，CD⊥AC，∴OP⊥AC，所以C选项的结论正确；∴AP＝CP，∴OP为△ACD的中位线，∴CD＝2OP，所以B选项的结论正确；∴OB＝2OP，∴AC平分OB，所以D选项的结论正确．故选A．14．（2019•兰州）如图，四边形ABCD内接于⊙O，若∠A＝40°，则∠C＝（）A．110°B．120°C．135°D．140°解：∵四边形ABCD内接于⊙O，∴∠C+∠A＝180°，∴∠C＝180°﹣40°＝140°．故选D．15．（2019•天水）如图，四边形ABCD是菱形，⊙O经过点A、C、D，与BC相交于点E，连接AC、AE．若∠D＝80°，则∠EAC的度数为（）A．20°B．25°C．30°D．35°解：∵四边形ABCD是菱形，∠D＝80°，∴∠ACB＝∠DCB＝（180°﹣∠D）＝50°，∵四边形AECD是圆内接四边形，∴∠AEB＝∠D＝80°，∴∠EAC＝∠AEB﹣∠ACE＝30°，故选C．16．（2019•威海）如图，⊙P与x轴交于点A（﹣5，0），B（1，0），与y轴的正半轴交于点C．若∠ACB＝60°，则点C的纵坐标为（）A．+B．2+C．4D．2+2解：连接P A，PB，PC，过P作PD⊥AB于D，PE⊥OC于E，∵∠ACB＝60°，∴∠APB＝120°，∵P A＝PB，∴∠P AB＝∠PBA＝30°，∵A（﹣5，0），B（1，0），∴AB＝6，∴AD＝BD＝3，∴PD＝，P A＝PB＝PC＝2，∵PD⊥AB，PE⊥OC，∠AOC＝90°，∴四边形PEOD是矩形，∴OE＝PD＝，PE＝OD＝2，∴CE＝＝＝2，∴OC＝CE+OE＝2+，∴点C的纵坐标为2+，故选B．17．（2019•菏泽）如图，AB是⊙O的直径，C，D是⊙O上的两点，且BC平分∠ABD，AD 分别与BC，OC相交于点E，F，则下列结论不一定成立的是（）A．OC∥BD B．AD⊥OC C．△CEF≌△BED D．AF＝FD解：∵AB是⊙O的直径，BC平分∠ABD，∴∠ADB＝90°，∠OBC＝∠DBC，∴AD⊥BD，∵OB＝OC，∴∠OCB＝∠OBC，∴∠DBC＝∠OCB，∴OC∥BD，选项A成立；∴AD⊥OC，选项B成立；∴AF＝FD，选项D成立；∵△CEF和△BED中，没有相等的边，∴△CEF与△BED不全等，选项C不成立；故选C．18．（2019•聊城）如图，BC是半圆O的直径，D，E是上两点，连接BD，CE并延长交于点A，连接OD，OE．如果∠A＝70°，那么∠DOE的度数为（）A．35°B．38°C．40°D．42°解：连接CD，如图所示：∵BC是半圆O的直径，∴∠BDC＝90°，∴∠ADC＝90°，∴∠ACD＝90°﹣∠A＝20°，∴∠DOE＝2∠ACD＝40°，故选C．19．（2019•白银）如图，点A，B，S在圆上，若弦AB的长度等于圆半径的倍，则∠ASB 的度数是（）A．22.5°B．30°C．45°D．60°解：设圆心为O，连接OA、OB，如图，∵弦AB的长度等于圆半径的倍，即AB＝OA，∴OA2+OB2＝AB2，∴△OAB为等腰直角三角形，∠AOB＝90°，∴∠ASB＝∠AOB＝45°．故选C．20．（2019•潍坊）如图，四边形ABCD内接于⊙O，AB为直径，AD＝CD，过点D作DE⊥AB于点E，连接AC交DE于点F．若sin∠CAB＝，DF＝5，则BC的长为（）A．8 B．10 C．12 D．16解：连接BD，如图，∵AB为直径，∴∠ADB＝∠ACB＝90°，∵AD＝CD，∴∠DAC＝∠DCA，而∠DCA＝∠ABD，∴∠DAC＝∠ABD，∵DE⊥AB，∴∠ABD+∠BDE＝90°，而∠ADE+∠BDE＝90°，∴∠ABD＝∠ADE，∴∠ADE＝∠DAC，∴FD＝F A＝5，在Rt△AEF中，∵sin∠CAB＝＝，∴EF＝3，∴AE＝＝4，DE＝5+3＝8，∵∠ADE＝∠DBE，∠AED＝∠BED，∴△ADE∽△DBE，∴DE：BE＝AE：DE，即8：BE＝4：8，∴BE＝16，∴AB＝4+16＝20，在Rt△ABC中，∵sin∠CAB＝＝，∴BC＝20×＝12．故选C．二．填空题（共20小题）21．（2019•辽阳）如图，A，B，C，D是⊙O上的四点，且点B是的中点，BD交OC于点E，∠AOC＝100°，∠OCD＝35°，那么∠OED＝60°．解：连接OB．∵＝，∴∠AOB＝∠BOC＝50°，∴∠BDC＝∠BOC＝25°，∵∠OED＝∠ECD+∠CDB，∠ECD＝35°，∴∠OED＝60°，故答案为60°．22．（2019•娄底）如图，C、D两点在以AB为直径的圆上，AB＝2，∠ACD＝30°，则AD ＝1．解：∵AB为直径，∴∠ADB＝90°，∵∠B＝∠ACD＝30°，∴AD＝AB＝×2＝1．故答案为1．23．（2019•常州）如图，AB是⊙O的直径，C、D是⊙O上的两点，∠AOC＝120°，则∠CDB＝30°．解：∵∠BOC＝180°﹣∠AOC＝180°﹣120°＝60°，∴∠CDB＝∠BOC＝30°．故答案为30．24．（2019•东营）如图，AC是⊙O的弦，AC＝5，点B是⊙O上的一个动点，且∠ABC＝45°，若点M、N分别是AC、BC的中点，则MN的最大值是．解：∵点M，N分别是BC，AC的中点，∴MN＝AB，∴当AB取得最大值时，MN就取得最大值，当AB是直径时，AB最大，连接AO并延长交⊙O于点B′，连接CB′，∵AB′是⊙O的直径，∴∠ACB′＝90°．∵∠ABC＝45°，AC＝5，∴∠AB′C＝45°，∴AB′＝＝＝5，∴MN最大＝．故答案为．25．（2019•宜宾）如图，⊙O的两条相交弦AC、BD，∠ACB＝∠CDB＝60°，AC＝2，则⊙O的面积是4π．解：∵∠A＝∠BDC，而∠ACB＝∠CDB＝60°，∴∠A＝∠ACB＝60°，∴△ACB为等边三角形，∵AC＝2，∴圆的半径为2，∴⊙O的面积是4π，故答案为4π．26．（2019•连云港）如图，点A、B、C在⊙O上，BC＝6，∠BAC＝30°，则⊙O的半径为6．解：∵∠BOC＝2∠BAC＝60°，又OB＝OC，∴△BOC是等边三角形∴OB＝BC＝6，故答案为6．27．（2019•台州）如图，AC是圆内接四边形ABCD的一条对角线，点D关于AC的对称点E在边BC上，连接AE．若∠ABC＝64°，则∠BAE的度数为52°．解：∵圆内接四边形ABCD，∴∠D＝180°﹣∠ABC＝116°，∵点D关于AC的对称点E在边BC上，∴∠D＝∠AEC＝116°，∴∠BAE＝116°﹣64°＝52°．故答案为52°．28．（2019•株洲）如图所示，AB为⊙O的直径，点C在⊙O上，且OC⊥AB，过点C的弦CD与线段OB相交于点E，满足∠AEC＝65°，连接AD，则∠BAD＝20度．解：连接OD，如图：∵OC⊥AB，∴∠COE＝90°，∵∠AEC＝65°，∴∠OCE＝90°﹣65°＝25°，∵OC＝OD，∴∠ODC＝∠OCE＝25°，∴∠DOC＝180°﹣25°﹣25°＝130°，∴∠BOD＝∠DOC﹣∠COE＝40°，∴∠BAD＝∠BOD＝20°，故答案为20．29．（2019•盐城）如图，点A、B、C、D、E在⊙O上，且为50°，则∠E+∠C＝155°．解：连接EA，∵为50°，∴∠BEA＝25°，∵四边形DCAE为⊙O的内接四边形，∴∠DEA+∠C＝180°，∴∠DEB+∠C＝180°﹣25°＝155°，故答案为155．30．（2019•凉山州）如图所示，AB是⊙O的直径，弦CD⊥AB于H，∠A＝30°，CD＝2，则⊙O的半径是2．解：连接BC，如图所示：∵AB是⊙O的直径，弦CD⊥AB于H，∴∠ACB＝90°，CH＝DH＝CD＝，∵∠A＝30°，∴AC＝2CH＝2，在Rt△ABC中，∠A＝30°，∴AC＝BC＝2，AB＝2BC，∴BC＝2，AB＝4，∴OA＝2，即⊙O的半径是2；故答案为2．31．（2019•湖州）已知一条弧所对的圆周角的度数是15°，则它所对的圆心角的度数是30°．解：∵一条弧所对的圆周角的度数是15°，∴它所对的圆心角的度数为2×15°＝30°．故答案为30°．32．（2018•朝阳）如图，点A，B，C在⊙O上，AC∥OB，∠BAO＝20°，则∠BOC的度数为40°．解：∵OA＝OB，∴∠BAO＝∠B＝20°，∵AC∥OB，∴∠CAB＝∠B＝20°，∴∠OAC＝40°，∵OA＝OC，∴∠C＝∠OAC＝40°，∴∠BOC＝∠C＝40°，故答案为40°．33．（2018•辽阳）如图，AB是半圆O的直径，E是半圆上一点，且OE⊥AB，点C为的中点，则∠A＝22.5°．解：连接OC，∵OE⊥AB，∴∠EOB＝90°，∵点C为的中点，∴∠BOC＝45°，∵OA＝OC，∴∠A＝∠ACO＝×45°＝22.5°，故答案为22.5°．34．（2018•黑龙江）如图，AC为⊙O的直径，点B在圆上，OD⊥AC交⊙O于点D，连接BD，∠BDO＝15°，则∠ACB＝60°．解：连接DC，∵AC为⊙O的直径，OD⊥AC，∴∠DOC＝90°，∠ABC＝90°，∵OD＝OC，∴∠ODC＝45°，∵∠BDO＝15°，∴∠BDC＝30°，∴∠A＝30°，∴∠ACB＝60°，故答案为60°．35．（2018•镇江）如图，AD为△ABC的外接圆⊙O的直径，若∠BAD＝50°，则∠ACB＝40°．解：连接BD，如图，∵AD为△ABC的外接圆⊙O的直径，∴∠ABD＝90°，∴∠D＝90°﹣∠BAD＝90°﹣50°＝40°，∴∠ACB＝∠D＝40°．故答案为40．36．（2018•北京）如图，点A，B，C，D在⊙O上，＝，∠CAD＝30°，∠ACD＝50°，则∠ADB＝70°．解：∵＝，∠CAD＝30°，∴∠CAD＝∠CAB＝30°，∴∠DBC＝∠DAC＝30°，∵∠ACD＝50°，∴∠ABD＝50°，∴∠ACB＝∠ADB＝180°﹣∠CAB﹣∠ABC＝180°﹣50°﹣30°﹣30°＝70°．故答案为70°．37．（2018•东莞市）同圆中，已知所对的圆心角是100°，则所对的圆周角是50°．解：弧AB所对的圆心角是100°，则弧AB所对的圆周角为50°．故答案为50°．38．（2018•杭州）如图，AB是⊙O的直径，点C是半径OA的中点，过点C作DE⊥AB，交⊙O于D，E两点，过点D作直径DF，连结AF，则∠DF A＝30°．解：∵点C是半径OA的中点，∴OC＝OD，∵DE⊥AB，∴∠CDO＝30°，∴∠DOA＝60°，∴∠DF A＝30°，故答案为30°39．（2018•无锡）如图，点A、B、C都在⊙O上，OC⊥OB，点A在劣弧上，且OA＝AB，则∠ABC＝15°．解：∵OA＝OB，OA＝AB，∴OA＝OB＝AB，即△OAB是等边三角形，∴∠AOB＝60°，∵OC⊥OB，∴∠COB＝90°，∴∠COA＝90°﹣60°＝30°，∴∠ABC＝15°，故答案为15°40．（2018•青海）如图，A、B、C是⊙O上的三个点，若∠AOC＝110°，则∠ABC＝125°．解：如图，在优弧AC上取点D，连接AD，CD，∵∠AOC＝100°，∴∠ADC＝∠AOC＝55°，∴∠ABC＝180°﹣∠ADC＝125°．故答案为125°．三．解答题（共10小题）41．（2019•南通）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝1，以边AC上一点O为圆心，OA为半径的⊙O经过点B．（1）求⊙O的半径；（2）点P为劣弧AB中点，作PQ⊥AC，垂足为Q，求OQ的长；（3）在（2）的条件下，连接PC，求tan∠PCA的值．解：（1）作OH⊥AB于H．在Rt△ACB中，∵∠C＝90°，∠A＝30°，BC＝1，∴AB＝2BC＝2，∵OH⊥AB，∴AH＝HB＝1，∴OA＝AH÷cos30°＝．（2）如图2中，连接OP，P A．设OP交AB于H．∵＝，∴OP⊥AB，∴∠AHO＝90°，∵∠OAH＝30°，∴∠AOP＝60°，∵OA＝OP，∴△AOP是等边三角形，∵PQ⊥OA，∴OQ＝QA＝OA＝．（3）连接PC．在Rt△ABC中，AC＝BC＝，∵AQ＝QO＝AO＝．∴QC＝AC﹣AQ＝﹣＝，∵△AOP是等边三角形，PQ⊥OA，∴PQ＝1，∴tan∠ACP＝＝＝．42．如图，在⊙O中，B是⊙O上的一点，∠ABC＝120°，弦AC＝2，弦BM平分∠ABC 交AC于点D，连接MA，MC．（1）求⊙O半径的长；（2）求证：AB+BC＝BM．解：（1）连接OA、OC，过O作OH⊥AC于点H，如图1，∵∠ABC＝120°，∴∠AMC＝180°﹣∠ABC＝60°，∴∠AOC＝2∠AMC＝120°，∴∠AOH＝∠AOC＝60°，∵AH＝AC＝，∴OA＝，故⊙O的半径为2．（2）证明：在BM上截取BE＝BC，连接CE，如图2，∵∠MBC＝60°，BE＝BC，∴△EBC是等边三角形，∴CE＝CB＝BE，∠BCE＝60°，∴∠BCD+∠DCE＝60°，∵∠ACM＝60°，∴∠ECM+∠DCE＝60°，∴∠ECM＝∠BCD，∵∠ABC＝120°，BM平分∠ABC，∴∠ABM＝∠CBM＝60°，∴∠CAM＝∠CBM＝60°，∠ACM＝∠ABM＝60°，∴△ACM是等边三角形，∴AC＝CM，∴△ACB≌△MCE，∴AB＝ME，∵ME+EB＝BM，∴AB+BC＝BM．43．（2019•南京）如图，⊙O的弦AB、CD的延长线相交于点P，且AB＝CD．求证：P A ＝PC．证明：连接AC，∵AB＝CD，∴＝，∴+＝+，即＝，∴∠C＝∠A，∴P A＝PC．44．（2018•鞍山）如图，四边形ABCD内接于⊙O，AC与BD为对角线，∠BCA＝∠BAD，过点A作AE∥BC交CD的延长线于点E．（1）求证：EC＝AC．（2）若cos∠ADB＝，BC＝10，求DE的长．（1）证明：∵BC∥AE，∴∠ACB＝∠EAC，∵∠ACB＝∠BAD，∴∠EAC＝∠BAD，∴∠EAD＝∠CAB，∵∠ADE+∠ADC＝180°，∠ADC+∠ABC＝180°，∴∠ADE＝∠ABC，∵∠EAD+∠ADE+∠E＝180°，∠BAC+∠ABC+∠ACB＝180°，∴∠E＝∠ACB＝∠EAC，∴CE＝CA．（2）解：设AE交⊙O于M，连接DM，作MH⊥DE于H．∵∠EAD＝∠CAB，∴＝，∴DM＝BC＝10，∵∠MDE+∠MDC＝180°，∠MDC+∠MAC＝180°，∴∠MDE＝∠CAM，∵∠E＝∠CAE，∴∠E＝∠MDE，∴MD＝ME＝10，∵MH⊥DE，∴EH＝DH，∵∠ADB＝∠ACB＝∠BAD＝∠E，∴cos∠E＝＝，∴EH＝4，∴DE＝2EH＝8．45．（2018•宜昌）如图，在△ABC中，AB＝AC，以AB为直径的圆交AC于点D，交BC于点E，延长AE至点F，使EF＝AE，连接FB，FC．（1）求证：四边形ABFC是菱形；（2）若AD＝7，BE＝2，求半圆和菱形ABFC的面积．（1）证明：∵AB是直径，∴∠AEB＝90°，∴AE⊥BC，∵AB＝AC，∴BE＝CE，∵AE＝EF，∴四边形ABFC是平行四边形，∵AC＝AB，∴四边形ABFC是菱形．（2）设CD＝x．连接BD．∵AB是直径，∴∠ADB＝∠BDC＝90°，∴AB2﹣AD2＝CB2﹣CD2，∴（7+x）2﹣72＝42﹣x2，解得x＝1或﹣8（舍弃）∴AC＝8，BD＝＝，∴S菱形ABFC＝8．∴S半圆＝•π•42＝8π．46．（2018•无锡）如图，四边形ABCD内接于⊙O，AB＝17，CD＝10，∠A＝90°，cos B ＝，求AD的长．解：∵四边形ABCD内接于⊙O，∠A＝90°，∴∠C＝180°﹣∠A＝90°，∠ABC+∠ADC＝180°．作AE⊥BC于E，DF⊥AE于F，则CDFE是矩形，EF＝CD＝10．在Rt△AEB中，∵∠AEB＝90°，AB＝17，cos∠ABC＝，∴BE＝AB•cos∠ABE＝，∴AE＝＝，∴AF＝AE﹣EF＝﹣10＝．∵∠ABC+∠ADC＝180°，∠CDF＝90°，∴∠ABC+∠ADF＝90°，∵cos∠ABC＝，∴sin∠ADF＝cos∠ABC＝．在Rt△ADF中，∵∠AFD＝90°，sin∠ADF＝，∴AD＝＝＝6．47．（2017•济南）如图，AB是⊙O的直径，∠ACD＝25°，求∠BAD的度数．解：∵AB为⊙O直径∴∠ADB＝90°∵相同的弧所对应的圆周角相等，且∠ACD＝25°∴∠B＝25°∴∠BAD＝90°﹣∠B＝65°．48．（2016•温州）如图，在△ABC中，∠C＝90°，D是BC边上一点，以DB为直径的⊙O 经过AB的中点E，交AD的延长线于点F，连结EF．（1）求证：∠1＝∠F．（2）若sin B＝，EF＝2，求CD的长．解：（1）证明：连接DE，∵BD是⊙O的直径，∴∠DEB＝90°，∵E是AB的中点，∴DA＝DB，∵∠B＝∠F，∴∠1＝∠F；（2）∵∠1＝∠F，∴AE＝EF＝2，∴AB＝2AE＝4，在Rt△ABC中，AC＝AB•sin B＝4，∴BC＝＝8，设CD＝x，则AD＝BD＝8﹣x，∵AC2+CD2＝AD2，即42+x2＝（8﹣x）2，∴x＝3，即CD＝3．49．（2016•宁夏）已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED＝EC．（1）求证：AB＝AC；（2）若AB＝4，BC＝2，求CD的长．（1）证明：∵ED＝EC，∴∠EDC＝∠C，∵∠EDC＝∠B，（∵∠EDC+∠ADE＝180°，∠B+∠ADE＝180°，∴∠EDC＝∠B）∴∠B＝∠C，（2）方法一：解：连接AE，∵AB为直径，∴AE⊥BC，由（1）知AB＝AC，∴BE＝CE＝BC＝，∵△CDE∽△CBA，∴，∴CE•CB＝CD•CA，AC＝AB＝4，∴•2＝4CD，∴CD＝．方法二：解：连接BD，∵AB为直径，∴BD⊥AC，设CD＝a，由（1）知AC＝AB＝4，则AD＝4﹣a，在Rt△ABD中，由勾股定理可得BD2＝AB2﹣AD2＝42﹣（4﹣a）2在Rt△CBD中，由勾股定理可得BD2＝BC2﹣CD2＝（2）2﹣a2∴42﹣（4﹣a）2＝（2）2﹣a2整理得a＝，即：CD＝．50．（2016•株洲）已知AB是半径为1的圆O直径，C是圆上一点，D是BC延长线上一点，过点D的直线交AC于E点，且△AEF为等边三角形（1）求证：△DFB是等腰三角形；（2）若DA＝AF，求证：CF⊥AB．解：（1）∵AB是⊙O直径，∴∠ACB＝90°，∵△AEF为等边三角形，∴∠CAB＝∠EF A＝60°∴∠B＝30°，∵∠EF A＝∠B+∠FDB，∴∠B＝∠FDB＝30°，∴△DFB是等腰三角形；（2）过点A作AM⊥DF于点M，设AF＝2a，∵△AEF是等边三角形，∴FM＝EM＝a，AM＝a，在Rt△DAM中，AD＝AF＝2a，AM＝，∴DM＝5a，∴DF＝BF＝6a，∴AB＝AF+BF＝8a，在Rt△ABC中，∠B＝30°，∠ACB＝90°，∴AC＝4a，∵AE＝EF＝AF＝2a，∴CE＝AC﹣AE＝2a，∴∠ECF＝∠EFC，∵∠AEF＝∠ECF+∠EFC＝60°，∴∠CFE＝30°，∴∠AFC＝∠AFE+∠EFC＝60°+30°＝90°，∴CF⊥AB．。

初三数学圆周角试题及答案《圆周角》试题◆随堂检测1.如图，图中圆周角的个数是A.9B.12C.8D. 142.如图，圆∠BOC=100 o，则圆周角∠BAC为A.100 oB.130 oC.50 oD.80o3.如图，AB为⊙O的直径，点C在QO上，∠B=50 o，则∠A等于A.80 oB.60 oC.50 oD.40 o4. 如图，点A、B、C都在⊙O上，连结AB、BC、AC、OA、OB，且∠BAO=25 o，则∠ACB的大小为___________.5. 如图，等腰三角形ABC的底边BC的长为a，以腰AB为直径的⊙O交BC于点D.则BD的长为___________.◆典例分析如图，已知在⊙O中，直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC，AD和BD的长.分析：所要求的三线段BC，AD和BD的长，能否把这三条线段转化为是直角三角形的直角边问题，由于已知AB为⊙O的直径，可以得到△ABC和△ADB都是直角三角形，又因为CD平分∠ACB，所以可得 = ，可以得到弦AD=DB，这时由勾股定理可得到三条线段BC、AD、DB的长.解：∵AB为直径，∴∠ACB=∠ADB=90°.在Rt△ABC中，∵CD平分∠ACB，∴ = .在等腰直角三角形ADB中，点评：利用“直径所对的圆周角是直角”构造直角三角形解题。

◆课下作业●拓展提高1.如图.⊙O中OA⊥BC，∠CDA=25o，则∠AOB的度数为_______.2.如图.AB为⊙O的直径，点C、D在⊙O上，∠BAC=50 o.则∠ADC=_______.3. 如图，AB是半圆O的直径，∠BAC=30 o，D是AC上任意一点，那么∠D的度数是A.150 oB.120 oC.100 oD.90 o4.如图,∆ABC内接于⊙O，AD是⊙O的直径，∠ABC=30o，则∠CAD等于A.30 oB.40 oC.50 oD. 60 o5.如图，∠APC=∠CPB=60 o，请推测△ABC是什么三角形，并证明猜想的正确性.6. 如图，AD是∆ABC的高，AE是∆ABC的外接圆的直径.试说明AB•AC=AE•AD.7. 如图，点A、B、C为圆O上的三个点，∠AOB= ∠BOC, ∠BAC=45 o，求∠ACB的度数.8. 如图，AB是⊙O的直径，C是⊙O上一点，连结AC，过点C作直线CD⊥AB，垂足为点DAD1试说明AC2=AG•AF;2若点E是AD点A、D除外上任意一点，上述结论是否仍然成立?若成立.请画出图形，并给予证明;若不成立，请说明理由.●体验中考1. 2021年温州如图，∠AOB是⊙0的圆心角，∠AOB=80°，则弧所对圆周角∠ACB的度数是A.40°B.45°C.50°D.80°2. 2021年凉山州如图，是的外接圆，已知，则的大小为A.40°B.30°C.45°D.50°3. 2021年山西省如图所示，、、、是圆上的点，则度.4. 2021宁夏已知：如图，为的直径，交于点，交于点 . 1求的度数;2求证： .初三数学《圆周角》试题参考答案：◆随堂检测1.B提示：利用弧来找圆周角2.C提示3.D提示：4. 650提示：5.◆课下作业●拓展提高1. 500 提示：2. 400 提示：连接BC，3. B提示：连接BC，4.D8.1证明：●体验中考1. A提示：2. A3. 300提示：4.感谢您的阅读，祝您生活愉快。

圆周角练习题及答案在平面几何课程中，圆周角是一个非常重要的概念。

学生通过练习圆周角的计算和解题，可以更好地理解和应用该概念。

本文将提供一些圆周角的练习题及其答案，旨在帮助学生加深对圆周角的理解和应用能力。

一、单选题1. 在圆的半径为r的两条弦之间所夹的圆周角是：A. 60度B. 90度C. 180度D. 360度答案：C. 180度2. 在相同圆上的两个圆周角，其中一个是另一个的两倍，那么它们的度数分别是：A. 60度和120度B. 90度和180度C. 120度和240度D. 150度和300度答案：C. 120度和240度二、填空题1. 在相同圆上的两个圆周角，它们的度数之和为________度。

答案：360度2. 在一个圆上，一个圆周角的度数是60度，那么它所对应的弧长为________。

答案：π/3（弧度）三、解答题1. 已知一个圆的半径为8cm，圆心角的度数为60度，求该圆内切正多边形的边长和面积。

解答：首先，由于圆心角度数为60度，所以切割的正多边形是六边形。

其次，由于圆的半径为8cm，因此可以通过正多边形的对称性得知，该六边形的边长为2r=16cm。

最后，可以通过将该六边形切割成等腰三角形，并计算其面积的一半来得到该多边形的面积。

所以，该六边形的边长为16cm，面积为(16*8*sin60°)/2=64√3 cm^2。

2. 若一个正八边形的外接圆的圆周角的度数为x度，求x的值。

解答：在一个正八边形中，通过连接圆心以及相邻的两个顶点，可以将该八边形分割为八个等腰三角形。

由于正八边形的圆心角度数为x 度，而圆心角是等腰三角形的内角，所以每个三角形的内角度数为x/2度。

根据三角形的内角和公式，可得(x/2)*8=180度，解得x=360度。

综上所述，圆周角练习题及答案提供了一些常见的练习题，通过对这些题目的解答，可以帮助学生更好地理解和应用圆周角的概念。

希望本文对学生们的学习有所帮助！。

初三上册圆的圆周角练习题在初三数学的课程中，圆的相关概念和性质是学生们需要掌握的重要内容之一。

其中，圆周角作为圆的一个重要性质，在解题过程中起着至关重要的作用。

本文将为大家提供一些圆周角练习题，帮助大家巩固和提升对圆周角的理解和运用。

1.已知半径为r的圆上有两条弧AB和CD，弧AB对应的圆心角为α，弧CD对应的圆心角为β。

如果α+β=90°，求证：弧AB和弧CD的长度相等。

解答：由于α+β=90°，根据圆周角和的性质可知，弧AB和弧CD所对应的弧度和为π/2，即AB+CD=π/2。

又由于AB和CD是同一圆上的两条弧，因此它们的弧长相等，即AB=CD。

2.已知圆心角θ对应的圆弧长度为s，圆的半径为r。

求证：θ的度数等于s/r的弧度数。

解答：根据圆周等分的原理，360°对应于2π的弧度数。

假设θ对应的弧度数为x，那么x/2π=θ/360°。

根据题目已知条件，s/r=x/2π，两边乘以360°得到s/r=θ。

3.已知直径为d的圆上的两条弧AB和CD，弧AB对应圆心角为α，弧CD对应圆心角为β。

如果α和β的度数之和等于180°，求证：弧AB和弧CD的长度之和等于圆周长的一半。

解答：由题意可知，α+β=180°，根据圆周角和的性质可得，AB+CD=π，即弧AB和弧CD的长度之和等于圆周长的一半。

通过以上的练习题，我们可以更深入地了解和应用圆的圆周角的性质。

在解题过程中，需要灵活运用和转化弧度和度数的关系、圆周角和的性质等概念。

只有真正理解并掌握这些概念，才能在数学问题中正确地运用它们。

圆周角作为圆的一个重要性质，不仅存在于初三数学中，也在实际生活中有着广泛的应用。

比如，在建筑中，为了保证圆形构件的连接稳定，需要正确地计算和设计圆周角。

因此，对圆周角的学习不仅仅是应试的需要，更是培养学生逻辑思维和数学运算能力的重要一环。

通过不断练习和巩固，相信大家在初三数学中的圆的圆周角问题上将能够得心应手，取得良好的成绩。

2.4圆周角知识点一：圆周角概念1.圆周角定义：像图中∠AEB、∠ADB、∠ACB这样的角，它们的顶点在圆上，并且两边都与圆相交的角叫做圆周角．题型一：圆周角的概念【例题1】（2021·全国九年级课时练习）如图，其中圆周角有（）A．1个B．2个C．3个D．4个【答案】B【分析】根据圆周角的定义进行判断，即可得到答案．【详解】解：根据题意，AEP，CPE∠是圆周角，共2个．故选：B．【点睛】本题考查了圆周角的定义，解题的关键是掌握圆周角的定义进行判断．变式训练【变式1-1】（2021·全国九年级课时练习）下列四个图形的角是圆周角的是（）A．B．C．D．知识点管理归类探究【答案】A【分析】根据圆周角的定义：顶点在圆上，并且两边都与圆相交的角叫做圆周角．即可求得答案．【详解】解：A、图中的角是圆周角，故本选项符合题意；B、图中的角不是圆周角，故本选项不符合题意；C、图中的角不是圆周角，故本选项不符合题意；D、图中的角不是圆周角，故本选项不符合题意；故选：A．【点睛】本题考查了圆周角的定义，能熟记圆周角定义的内容是解此题的关键．【变式1-2】（2021·浙江温州·）如图，⊙O的两条弦AB⊙CD，已知⊙ADC＝35°，则⊙BAD的度数为（）A．55°B．70°C．110°D．130°【答案】A【分析】根据垂直定义和三角形的两锐角互余进行解答即可．【详解】解：⊙AB⊙CD，⊙⊙ADC+⊙BAD=90°，⊙⊙ADC=35°，⊙⊙BAD=90°﹣35°=55°，故选：A．【点睛】本题考查垂直定义、直角三角形的两锐角互余，熟练掌握直角三角形的两锐角互余是解答的关键．【变式1-3】（2021·江西九年级期末）如图，AB是O的直径，C为圆内一点，则下列说法中正确的是（）A．AC是O的弦B．BOC是圆心角+<C．C∠是圆周角D．AC OC AB【答案】B【分析】根据弦、圆心角、圆周角的概念可直接进行排除选项．【详解】解：A、点C不在O上，所以AC不是O的弦，故错误，不符合题意；B、因为点O是圆心，所以⊙BOC是圆心角，故正确，符合题意；C、点C不在O上，所以⊙C不是圆周角，故错误，故不符合题意；+<成立，则AC+OC＜OA+OB，D、当点C在圆上时，则OC=OA=OB，若AC OC AB⊙AC＜OA，与题干矛盾，⊙D选项错误，不符合题意；故选B．【点睛】本题主要考查弦、圆心角、圆周角的概念，熟练掌握弦、圆心角、圆周角的概念是解题的关键．【变式1-4】（2021·全国）顶点在圆上，两边都和圆相交的角叫做____________．圆周角的特征：⊙顶点在_____上；⊙两边都和圆_________．【答案】圆周角圆相交圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．题型二：同弧所对圆周角等于圆心角一半【例题2】（2021·湖南长沙市·明德华兴中学九年级开学考试）如图，圆周角⊙ACB的度数为48°，则圆心角⊙AOB的度数为（）A．48°B．24°C．36°D．96°【答案】D【分析】同圆中，同弧所对的圆周角=圆心角的一半．【详解】解：由题意得，圆周角⊙ACB的度数为48°，⨯=︒，圆心角⊙AOB的度数为48°296故选：D．【点睛】本题考查圆周角定理，是重要考点，掌握相关知识是解题关键． 变式训练【变式2-1】（2021·全国九年级课时练习）如图，已知CD 是O 的直径，过点D 的弦DE 平行于半径OA ，若D ∠的度数是50︒，则C ∠的度数是（ ）A ．25︒B ．30C ．40︒D ．50︒【答案】A【分析】根据平行线的性质和圆周角定理计算即可； 【详解】⊙//OA DE ，50D ∠=︒， ⊙50AOD ∠=︒，⊙12C AOD ∠=∠，⊙150225C ︒∠=⨯=︒． 故选A ．【点睛】本题主要考查了圆周角定理、平行线的性质，准确计算是解题的关键．【变式2-2】（2021·黑龙江九年级期末）如图，O 是ABC 的外心，42ABC ∠=︒，72ACB ∠=︒，则BOC ∠=______．【答案】132°【分析】先利用三角形内角和计算出⊙BAC =66°，在利用三角形外心的性质和圆周角定理得到⊙BOC 的度数． 【详解】解：⊙⊙ABC =42°，⊙ACB =72°， ⊙⊙BAC =180°-42°-72°=66°，⊙O 是⊙ABC 的外心，⊙以O 为圆心，OB 为半径的圆是⊙ABC 的外接圆， ⊙⊙BOC =2⊙BAC =132°． 故答案为：132°．【点睛】本题考查了三角形的外接圆与外心：三角形外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心．也考查了圆周角定理．【变式2-3】（2021·全国九年级课时练习）如图，BC 是O 的弦，D 是BC 上一点，DO 交O 于点A ，连接AB ，OC ，若20A ∠=︒，30C ∠=︒，则AOC ∠的度数为________．【答案】100︒【分析】设⊙AOC =x °，根据圆周角定理得到⊙B 的度数，根据三角形的外角的性质列出方程，解方程得到答案．【详解】解：设⊙AOC =x °，则⊙B =12x °， ⊙⊙AOC =⊙ODC +⊙C ，⊙ODC =⊙B +⊙A ， ⊙x =20°+30°+12x ， 解得x =100°．故选A ．【点睛】本题主要考查的是圆周角定理和三角形的外角的性质，掌握一条弧所对的圆周角等于这条弧所对的圆心角的一半是解题的关键． 题型三：同弧所对圆周角【例题3】（2021·江苏盐城·景山中学九年级月考）如图，在⊙O 中，弦AB 、CD 相交于点E ，⊙C ＝40°，⊙AED ＝100°，则⊙D ＝______．【答案】60°【分析】首先根据圆周角定理的推论，得⊙C =⊙ABD ，再根据三角形外角的性质即可求得⊙D 的度数． 【详解】解：⊙⊙C =40°， ⊙⊙C =⊙B =40°． ⊙⊙AED =100°，⊙⊙D =⊙AED -⊙B =100°-40°=60°．故答案是：60°．【点睛】本题考查了圆周角定理，三角形的外角的性质，熟记圆周角定理是解题的关键． 变式训练【变式3-1】（2021·全国九年级课时练习）如图，O 是ABC 的外接圆，65CAB ∠=︒，P 是O 上的一点，则CPB ∠等于________．【答案】65°【分析】根据圆周角定理（同弧所对在圆周角相等）进行解答． 【详解】解：根据同弧所对的圆周角相等，得CPB CAB ∠=∠．⊙65CAB ∠=︒， ⊙65CPB ∠=︒． 故答案为：65°【点睛】本题考查了圆周角定理．注意：圆周角必须满足两个条件：⊙定点在圆上．⊙角的两条边都与圆相交，二者缺一不可．【变式3-2】（2021·北京市陈经纶中学分校九年级月考）如图，点A，B，C，D在⊙O上，CB CD=，⊙CAD ＝30°，⊙ACD＝50°，则⊙ADB＝_____．【答案】70°【分析】直接利用圆周角定理以及结合三角形内角和定理得出⊙ACB=⊙ADB=180°-⊙CAB-⊙ABC，进而得出答案．【详解】解：⊙CB CD=，⊙CAD=30°，⊙⊙CAD=⊙CAB=30°，⊙⊙DBC=⊙DAC=30°，⊙⊙ACD=50°，⊙⊙ABD=50°，⊙⊙ADB=⊙ACB=180°-⊙CAB-⊙ABC=180°-50°-30°-30°=70°．故答案为：70°．【点睛】此题主要考查了圆周角定理以及三角形内角和定理，正确得出⊙ABD度数是解题关键．【变式3-3】（2021·江苏淮安·中考真题）如图，AB是⊙O的直径，CD是⊙O的弦，⊙CAB＝55°，则⊙D的度数是___．【答案】35°【分析】根据直径所对的圆周角是直角推出⊙ACB＝90°，再结合图形由直角三角形的性质得到⊙B＝90°﹣⊙CAB ＝35°，进而根据同圆中同弧所对的圆周角相等推出⊙D ＝⊙B ＝35°． 【详解】解：⊙AB 是⊙O 的直径， ⊙⊙ACB ＝90°， ⊙⊙CAB ＝55°，⊙⊙B ＝90°﹣⊙CAB ＝35°， ⊙⊙D ＝⊙B ＝35°． 故答案为：35°．【点睛】本题主要考查了直径所对的圆周角是直角，同弧所对的圆周角相等，解题的关键在于能够熟练掌握相关知识进行求解.圆周角定理推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径． 题型四：直径所对圆周角是直角【例题4】（2021·江苏九年级期末）如图，AB 是O 的直径，CD 是O 的弦，40BAC ∠=︒，则ADC ∠=________°．【答案】50【分析】连接BC ，则由圆周角定理可以得到⊙ADC =⊙ABC ，再根据直径所对的圆周角是90度，得到⊙ACB =90°，再根据⊙BAC =40°即可求解. 【详解】解：如图所示，连接BC ⊙⊙ADC =⊙ABC ⊙AB 是直径 ⊙⊙ACB =90° ⊙⊙BAC =40°⊙⊙ABC =180°-90°-40°=50° ⊙⊙ADC =⊙ABC =50° 故答案为：50.【点睛】本题主要考查了圆周角定理，直径所对的圆周角是直角，三角形内角和定理，解题的关键在于能够熟练掌握相关知识进行求解.变式训练【变式4-1】（2021·湖南九年级期末）如图，AB是⊙O的直径，C是⊙O上一点，OD BC于点D，8cmAC，BD=，则AB的长为________cm．3cm【答案】10AC＝4cm．然后利用勾股定理求解．【分析】利用圆周角定理和三角形中位线定理求得OD＝12【详解】解：⊙AB是⊙O的直径，⊙⊙ACB＝90°，又⊙OD⊙BC，即⊙ODB＝90°，⊙AC⊙OD，⊙点O是AB的中点，⊙OD是⊙ABC的中位线，AC＝4cm，⊙OD＝12⊙BD＝3cm，⊙OB22+5cm，BD OD⊙AB＝2OB＝10cm．故答案为：10．【点睛】本题主要考查了勾股定理和圆周角定理，根据题意推知OD是⊙ABC的中位线是解题的关键．【变式4-2】（2021·四川九年级期末）如图，A是⊙O上一点，BC是直径，AC＝1，AB＝3，点D在圆O 上且平分BC，则DC的长为__．5【分析】先利用圆周角定理得到⊙A＝⊙D＝90°，再利用勾股定理计算出BC10接着证明⊙BCD为等腰直角三角形，然后根据等腰直角三角形的性质求DC的长．【详解】解：⊙BC是直径，⊙⊙A＝⊙D＝90°，在Rt⊙ACB中，⊙AC＝1，AB＝3，⊙BC22+10，13⊙点D平分BC，即BD＝BC，⊙⊙BCD＝⊙CBD，⊙⊙BCD为等腰直角三角形，⊙DC221055【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．BC OA，连接BO并延【变式4-3】（2021·苏州市立达中学校九年级二模）如图，点A、B、C在O上，//长，交O于点D，连接AC、DC．若24∠的大小为________︒．∠=︒，则DA【答案】42【分析】利用平行线的性质求出⊙ACB ＝24°，再利用圆周角定理求出⊙AOB ＝48°，利用平行线的性质可得⊙CBO ＝48°，再证明⊙DCB ＝90°可得结论． 【详解】解：⊙//BC OA ， ⊙⊙ACB ＝⊙A ＝24°， ⊙⊙AOB ＝2⊙ACB ＝48°， ⊙//BC OA ，⊙⊙CBO ＝⊙AOB ＝48°， ⊙BD 是直径， ⊙⊙DCB ＝90°， ⊙⊙D ＝90°﹣48°＝42°， 故答案为：42．【点睛】本题考查圆周角定理，平行线的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．【变式4-4】（2021·宁夏九年级一模）如图，AB 为O 的直径，CD 为O 的弦，40ACD ∠=︒，则BAD ∠的度数为_______．【答案】50°【分析】由同弧所对的圆周角相等可知40ABD ACD ∠=∠=︒，再由直径所对的圆周角为直角即可得到答案． 【详解】解：连接BD ，⊙40ACD ∠=︒， ⊙40ABD ∠=︒， ⊙AB 为O 的直径， ⊙90ADB ∠=︒， ⊙90BAD ABD ∠+∠=︒， ⊙904050BAD =︒-︒=︒∠， 故答案为：50︒．【点睛】本题考查了同弧所对的圆周角相等，直径所对的圆周角为直角，掌握基础知识是解题的关键． 题型五：90°圆周角所对弦是直径【例题5】（2021·科尔沁左翼中旗教研室）如图，小明同学设计了一个测量圆直径的工具，标有刻度的尺子OA 、OB 在O 点钉在一起，并使它们保持垂直，在测直径时，把O 点靠在圆周上，读得刻度OE ＝8cm ，OF ＝6cm ，则圆的直径为__________【答案】10cm【分析】由题意可知OE OF ⊥，利用90º圆周角所对的弦为直径，确定EF 是该圆的直径，利用勾股定理求该圆的直径即可． 【详解】连结EF ，⊙OA 、OB 在O 点钉在一起，并使它们保持垂直， ⊙OE⊙OF ，即⊙EOF=90º， ⊙EF 为直径，在Rt⊙EOF 中，由勾股定理2222OE +OF =6810EF +=， ⊙圆的直径为10． 故答案为：10．【点睛】本题考查圆周角的性质与勾股定理的应用，掌握圆周角的定理，通过构造直角三角形用勾股定理是解题关键． 变式训练【变式5-1】（2020·山东烟台芝罘中学九年级月考）如图，Rt ABC 中，6AC =，8BC =，点E 是ABC 外接圆上任意一点，点M 是弦AE 的中点，当点E 在ABC 外接圆上运动一周时，点M 运动的路径长为______．【答案】5π【分析】作AB 的中点O ，连接OE 、OM ，M 是弦AE 的中点，可证O 为ABC 外接圆的圆心，OM⊙AE ，可证点M 在以AO 为直径的圆上运动，求出AO 的长度，进而求出点M 的运动路径长度． 【详解】解：作AB 的中点O ，连接OE 、OM ，如图：⊙ABC 是直角三角形，点E 是ABC 外接圆上任意一点， ⊙AB 为ABC 外接圆的直径，（90°圆周角所对的弦是直径）， 点O 为ABC 外接圆的圆心，AE 为ABC 外接圆上的弦， ⊙点M 是弦AE 的中点，⊙OM⊙AE （平分弦的直径垂直于这条弦，注：该弦不是直径）， ⊙点M 在以AO 为直径的圆上运动（90°圆周角所对的弦是直径）， ⊙在Rt ABC 中，6AC =，8BC =， ⊙22226810ABAC BC ，⊙AO＝5，⊙点M运动的路径长为5π．故答案为：5π．【点睛】本题考查了垂径定理、圆周角定理的运用及勾股定理，灵活运用垂径定理的推论是解题关键．【变式5-2】（2018·山东济南·中考真题）如图，⊙O的半径为1，⊙ABC是⊙O的内接等边三角形，点D，E在圆上，四边形BCDE为矩形，这个矩形的面积是（）A．2B．32C3D3【答案】C【分析】连接BD、OC，根据矩形的性质得⊙BCD=90°，再根据圆周角定理得BD为⊙O的直径，则BD=2；由ABC为等边三角形得⊙A=60°，于是利用圆周角定理得到⊙BOC=2⊙A=120°，易得⊙CBD=30°，在Rt⊙BCD中，根据含30°的直角三角形三边的关系得到CD=12BD=1，33解．【详解】连结BD、OC，如图，⊙四边形BCDE为矩形，⊙⊙BCD=90°，⊙BD为⊙O的直径，⊙BD=2，⊙⊙ABC为等边三角形，⊙⊙A=60°，⊙⊙BOC=2⊙A=120°，而OB=OC，⊙⊙CBD=30°，在Rt⊙BCD 中，CD=12BD=1，33 ⊙矩形BCDE 的面积3C ．【点睛】本题考查了圆周角定理、等边三角形的性质和矩形的性质，综合性比较强．合理利用圆的基本性质是解题的关键．【变式5-3】（2021·江苏苏州市·九年级开学考试）如图，在Rt ABC 中，90ACB ∠=︒，30BAC ∠=︒，4AC =，P 是ABC 所在平面内一点，且满足PA PC ⊥，则PB 的最大值为________．221【分析】由于⊙APC=90°，则根据圆周角定理可判断点P 在以AC 为直径的圆上，取AC 的中点O ，连接BO ，然后根据点与圆的位置关系确定PB 的最大值． 【详解】解：⊙⊙ACB=90°,⊙BAC=30°, ⊙AB=2BC ，又AC=4， ⊙()22242BC BC +=， 解得：43⊙PA⊙PC ，即⊙APC=90°， ⊙点P 在以AC 为直径的圆O 上， 如图，当P 、O 、B 三点共线时，PB 最大， 43，OC=12AC=2， 22BC OC +221221，221．【点睛】本题考查了圆周角定理，勾股定理，含30°的直角三角形的性质，利用90°的圆周角所对的弦是直径构造圆O是解题的关键．知识点四：圆内接四边形圆内接四边形：（1）定义: 圆内接四边形：顶点都在圆上的四边形，叫圆内接四边形．（2）性质：圆内接四边形对角互补，外角等于内对角（即它的一个外角等于它相邻内角的对角）．题型六：圆内接四边形【例题6】（2020·温州市实验中学九年级期末）如图，在⊙O中，点B是弧AC上的一点，⊙AOC=140°，则⊙ABC的度数为（）A．70°B．110°C．120°D．140°【答案】B【分析】在优弧AC上取点D，连接AD、CD，由⊙AOC=140︒求出⊙ADC=1702AOC∠=︒，根据四边形ABCD是圆内接四边形，得到⊙ADC+⊙ABC=180︒，即可求出⊙ABC的度数．【详解】在优弧AC上取点D，连接AD、CD，⊙⊙AOC=140︒，⊙⊙ADC=1702AOC∠=︒，⊙四边形ABCD是圆内接四边形，⊙⊙ADC+⊙ABC=180︒，⊙⊙ABC=110 ，故选：B．【点睛】此题考查圆周角定理：同弧所对的圆周角等于圆心角的一半，圆内接四边形的性质：圆内接四边形的对角互补．变式训练【变式6-1】（2021·科尔沁左翼中旗教研室）如图，四边形ABCD内接于⊙O，⊙A＝115°，则⊙BOD＝_______．【答案】130°【分析】先根据圆内接四边形的性质求出⊙C的度数，再由圆周角定理即可得出结论．【详解】解：⊙四边形ABCD内接于⊙O，⊙A=115°，⊙⊙C=180°-⊙A=180°-115°=65°，⊙⊙BOD=2⊙C=130°．故答案为：130°．【点睛】本题考查的是圆内接四边形的性质，熟知圆内接四边形的对角互补是解答此题的关键．【变式6-2】（2021·江苏南京·）如图，点A、B、C、D在⊙O上，B是AC的中点，过点C作⊙O的切线交AB的延长线于点E，若⊙AEC＝87°，则⊙ADC＝__°．【答案】62【分析】连接BD 、BC ，由圆周角定理可得⊙BDC=⊙ADB=12⊙ADC ，再根据圆內接四边形的性质可得⊙EBC=⊙ADC ，由切线的性质得出⊙BCE=⊙BDC=12⊙ADC ，最后根据三角形内角和定理解答即可．【详解】解：连接BD 、BC ， ⊙B 是AC 的中点， ⊙AB BC =⊙⊙BDC=⊙ADB=12⊙ADC ， ⊙四边形ABCD 是圆内接四边形， ⊙⊙EBC=⊙ADC, ⊙EC 是⊙O 的切线， ⊙⊙BCE=⊙BDC=12⊙ADC⊙⊙AEC=87°，⊙AEC+⊙BCE+⊙EBC=180°， ⊙87°+12⊙ADC+⊙ADC=180°，解得⊙ADC=62°．故答案为62°．．【点睛】本题主要考査了圆的切线性质、圆內接四边形的性质、圆周角的定理等知识点，灵活运用圆的相关性质定理是解答本题的关键．【变式6-3】（2020·云梦县实验外国语学校九年级月考）如图，四边形A BCD 是⊙O 的内接四边形，AB AD = ，若72C ∠=︒，则ABD ∠的度数是______．【答案】36°【分析】根据圆内接四边形的性质求出⊙A ，根据等边对等角的性质得到⊙ABD=⊙ADB ，根据三角形内角和定理计算即可．【详解】解：⊙四边形ABCD 是⊙O 的内接四边形， ⊙⊙A ＝180°﹣⊙C ＝108°， ⊙AB ＝AD ， ⊙∠ABD=∠ADB ，⊙⊙ABD ＝()()113180180108622A ⨯=⨯∠︒︒︒=︒--故答案为36°．【点睛】本题考查了圆内接四边形的性质，等边对等角的性质，掌握圆内接四边形的对角互补是解题的关键．【真题1】（2021·江苏南京·）如图，四边形ABCD 是⊙O 的内接四边形，若⊙BOD ＝130°，则⊙A 的度数为（ ）A ．50°B ．65°C ．115°D ．130°【答案】C【分析】先根据圆周角定理求出BCD ∠的度数，再根据圆的内接四边形对角互补的性质求出结果． 【详解】解：⊙130BOD ∠=︒，链接中考⊙1652BCD BOD ∠=∠=︒，⊙四边形ABCD 是⊙O 的内接四边形， ⊙180A BCD ∠+∠=︒， ⊙115A ∠=︒． 故选：C ．【点睛】本题考查圆的内接四边形的性质，解题的关键是掌握圆的内接四边形对角互补的性质．【真题2】（2021·西藏中考真题）如图，⊙BCD 内接于⊙O ，⊙D ＝70°，OA ⊙BC 交⊙O 于点A ，连接AC ，则⊙OAC 的度数为（ ）A ．40°B ．55°C ．70°D ．110°【答案】B【分析】连接OB ，OC ，根据圆周角定理得到⊙BOC ＝2⊙D ＝140°，根据垂径定理得到⊙COA 1702BOC =∠=︒，根据等腰三角形的性质即可得到结论． 【详解】解：连接OB ，OC ， ⊙⊙D ＝70°，⊙⊙BOC ＝2⊙D ＝140°， ⊙OA ⊙BC ，⊙⊙COA 1702BOC =∠=︒，⊙OA ＝OC ， ⊙⊙OAC ＝⊙OCA 12=（180°﹣70°）＝55°， 故选：B ．【点睛】本题考查了三角形的外接圆与外心，垂径定理，等腰三角形性质，三角形的内角和定理，正确的作出辅助线是解题的关键．【真题3】（2021·辽宁鞍山·）如图，AB 为O 的直径，C ，D 为O 上的两点，若54ABD ∠︒＝，则C ∠的度数为（ ）A ．34︒B ．36︒C ．46︒D ．54︒【答案】B 【分析】连接AD ，如图，根据圆周角定理得到90ADB ∠=︒，C A ∠=∠，然后利用互余计算出A ∠，从而得到C ∠的度数．【详解】解：连接AD ，如图，AB 为O 的直径，90ADB ∴∠=︒，90905436A ABD ∴∠=︒-∠=︒-︒=︒，36C A ∴∠=∠=︒．故选B ．【点睛】本题主要考查了同弦所对的圆周角相等，直径所对的圆周角是直角，解题的关键在于能够熟练掌握相关知识进行求解.【真题4】（2021·四川德阳·中考真题）如图，在圆内接五边形ABCDE中，⊙EAB⊙+⊙C+⊙CDE+⊙E＝430°，则⊙CDA＝_____度．【答案】70【分析】先利用多边的内角和得到⊙EAB+⊙B+⊙C+⊙CDE+⊙E=540°，则可计算出⊙B=110°，然后根据圆内接四边形的性质求⊙CDA的度数．【详解】解：⊙五边形ABCDE的内角和为（5-2）×180°=540°，⊙⊙EAB+⊙B+⊙C+⊙CDE+⊙E=540°，⊙⊙EAB+⊙C+⊙CDE+⊙E=430°，⊙⊙B=540°-430°=110°，⊙四边形ABCD为⊙O的内接四边形，⊙⊙B+⊙CDA=180°，⊙⊙CDA=180°-110°=70°．故答案为70．【点睛】本题考查了多边形的内角和与圆内接四边形的性质，运用圆内接四边形的性质是解决问题的关键．【拓展1】（2020·浙江绍兴市·）如图，一块三角尺ABC的斜边AB与量角器的直径恰好重合，点D对应的刻度是46°，则ACD的度数为__________．【答案】67°【分析】首先连接OD，由直角三角板ABC的斜边AB与量角器的直径恰好重合，可得点A，B，C，D共圆，又由点D对应的刻度是46°，利用圆周角定理求解即可求得⊙BCD的度数，继而求得答案．【详解】解：连接OD，满分冲刺⊙直角三角板ABC 的斜边AB 与量角器的直径恰好重合，⊙点A ，B ，C ，D 共圆，⊙点D 对应的刻度是46°，⊙⊙BOD ＝46°，⊙⊙BCD ＝12⊙BOD ＝23°，⊙⊙ACD ＝90°-⊙BCD ＝67°，故答案为：67°．【点睛】此题考查了圆周角定理．注意准确作出辅助线是解此题的关键．【拓展2】（2020·山东烟台芝罘中学九年级月考）如图．在⊙ABC 中，⊙A ＝60°，BC ＝5cm ．能够将⊙ABC 完全覆盖的最小圆形纸片的直径是__________cm ．103 【分析】根据题意作出ABC 的外接圆，然后根据圆的相关知识即可求得⊙ABC 外接圆的直径，本题得以解决．【详解】解：将ABC 完全覆盖的最小覆盖圆就是ABC 的外接圆，如解图，作ABC 的外接圆，作直径BD ，连接CD ，则60D A ∠=∠=︒，BD 是O 的直径，90BCD ∴∠=︒，30DBC ∴∠=︒，⊙BD=2CD ，在Rt BDC 中，2225BD CD -=，⊙22354BD =， ⊙103BD =（取正值）．所以能够将⊙ABC 103cm ． 103 【点睛】本题考查三角形的外接圆和圆周角定理的推论，解答本题的关键是明确题意，作出合适的辅助线，利用数形结合的思想解答．【拓展3】（2017·湖北十堰·中考真题）如图，⊙ABC 内接于⊙O ，⊙ACB =90°，⊙ACB 的角平分线交⊙O 于D ．若AC =6，BD 2，则BC 的长为_____．【答案】8【分析】连接AD ，根据CD 是⊙ACB 的平分线可知⊙ACD=⊙BCD=45°，故可得出AD=BD ，再由AB 是⊙O 的直径可知⊙ABD 是等腰直角三角形，利用勾股定理求出AB 的长，在Rt⊙ABC 中，利用勾股定理可得出BC 的长．【详解】连接AD ，⊙⊙ACB=90°，⊙AB 是⊙O 的直径．⊙⊙ACB 的角平分线交⊙O 于D ，⊙⊙ACD=⊙BCD=45°，2．⊙AB是⊙O的直径，⊙⊙ABD是等腰直角三角形，22+．AD BD⊙AC=6，2222AB AC-=-．106故答案为：8．【点睛】本题考查的是圆周角定理，熟知直径所对的圆周角是直角是解答此题的关键．备考无忧系列26。

圆中考试题集锦一、选择题1．如图，BC 是⊙O 的直径，P 是CB 延长线上一点，PA 切⊙O 于点A ，如果PA ＝3，PB ＝1，那么∠APC 等于 （） （A ）ο15 （B ）ο30 （C ）ο45 （D ）ο602．如果圆柱的高为20厘米，底面半径是高的41，那么这个圆柱的侧面积是 （） （A ）100π平方厘米 （B ）200π平方厘米（C ）500π平方厘米 （D ）200平方厘米3．“圆材埋壁”是我国古代着名的数学菱《九章算术》中的一个问题，“今在圆材，埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺，问径几何”用现在的数学语言表述是：“如图，CD 为⊙O 的直径，弦AB ⊥CD ，垂足为E ，CE ＝1寸，AB ＝10寸，求直径CD 的长”．依题意，CD 长为 （）（A ）225寸 （B ）13寸 （C ）25寸 （D ）26寸 4．已知：如图，⊙O 半径为5，PC 切⊙O 于点C ，PO 交⊙O 于点A ，PA ＝4，那么PC 的长等于 （）（A ）6 （B ）25 （C ）210 （D ）2145．如果圆锥的侧面积为20π平方厘米，它的母线长为5厘米，那么此圆锥的底面半径的长等于 （）（A ）2厘米 （B ）22厘米 （C ）4厘米 （D ）8厘米6．相交两圆的公共弦长为16厘米，若两圆的半径长分别为10厘米和17厘米，则这两圆的圆心距为 （）（A ）7厘米 （B ）16厘米 （C ）21厘米 （D ）27厘米7．如图，⊙O 为△ABC 的内切圆，∠C ＝ο90，AO 的延长线交BC 于点D ，AC＝4，DC ＝1，，则⊙O 的半径等于 （）（A ）54 （B ）45 （C ）43 （D ）65 8．一居民小区有一正多边形的活动场．小区管委会决定在这个多边形的每个顶点处修建一个半径为2米的扇形花台，花台都以多边形的顶点为圆心，以多边形的内角为圆心角，花台占地面积共为12π平方米．若每个花台的造价为400元，则建造这些花台共需资金 （）（A ）2400元 （B ）2800元 （C ）3200元 （D ）3600元9．如图，AB 是⊙O 直径，CD 是弦．若AB ＝10厘米，CD ＝8厘米，那么A 、B 两点到直线CD 的距离之和为 （）（A ）12厘米 （B ）10厘米 （C ）8厘米 （D ）6厘米10．某工件形状如图所示，圆弧BC 的度数为ο60，AB ＝6厘米，点B 到点C 的距离等于AB ，∠BAC ＝ο30，则工件的面积等于 （）（A ）4π （B ）6π （C ）8π （D ）10π11．如图，PA 切⊙O 于点A ，PBC 是⊙O 的割线且过圆心，PA ＝4，PB ＝2，则⊙O的半径等于 （）（A ）3 （B ）4 （C ）6 （D ）812．已知⊙O 的半径为35厘米，⊙O '的半径为5厘米．⊙O 与⊙O '相交于点D 、E ．若两圆的公共弦DE 的长是6厘米（圆心O 、O '在公共弦DE 的两侧），则两圆的圆心距O O '的长为 （）（A ）2厘米 （B ）10厘米 （C ）2厘米或10厘米 （D ）4厘米13．如图，两个等圆⊙O 和⊙O '的两条切线OA 、OB ，A 、B 是切点，则∠AOB 等于 （）（A ）ο30 （B ）ο45 （C ）ο60 （D ）ο9014．如图，AB 是⊙O 的直径，∠C ＝ο30，则∠ABD ＝ （）（A ）ο30 （B ）ο40 （C ）ο50 （D ）ο6015．弧长为6π的弧所对的圆心角为ο60，则弧所在的圆的半径为 （）（A ）6 （B ）62 （C ）12 （D ）1816．如图，在△ABC 中，∠BAC ＝ο90，AB ＝AC ＝2，以AB 为直径的圆交BC 于D ，则图中阴影部分的面积为 （）（A ）1 （B ）2 （C ）1+4π （D ）2－4π 17．已知圆的内接正六边形的周长为18，那么圆的面积为 （）（A ）18π （B ）9π （C ）6π （D ）3π18．如图，点P 是半径为5的⊙O 内一点，且OP ＝3，在过点P 的所有弦中，长度为整数的弦一共有 （）（A ）2条 （B ）3条 （C ）4条 （D ）5条19．如图，正六边形ABCDEF 的边长为a ，分别以C 、F 为圆心，a 为半径画弧，则图中阴影部分的面积是 （）（A ）261a π （B ）231a π （C ）232a π （D ）234a π20．过⊙O 内一点M 的最长的弦长为6厘米，最短的弦长为4厘米，则OM 的长为（）（A ）3厘米 （B ）5厘米 （C ）2厘米 （D ）5厘米21．已知圆锥的底面半径是3，高是4，则这个圆锥侧面展开图的面积是（）（A ）12π （B ）15π （C ）30π （D ）24π22．已知⊙O 的直径AB 与弦AC 的夹角为ο30，过C 点的切线PC 与AB 延长线交P ．PC ＝5，则⊙O 的半径为（）（A ）335 （B ）635 （C ）10 （D ）5 23．如图：PA 切⊙O 于点A ，PBC 是⊙O 的一条割线，有PA ＝32，PB ＝BC ，那么BC 的长是（）（A ）3 （B ）32 （C ）3 （D ）3224．如图，⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离，它们的半径都是1，顺次连结五个圆心得到五边形ABCDE ，则图中五个扇形（阴影部分）的面积之和是（）（A ）π （B ）π （C ）2π （D ）π25．正六边形的半径为2厘米，那么它的周长为（）（A ）6厘米 （B ）12厘米 （C ）24厘米 （D ）122厘米26．一个圆柱形油桶的底面直径为0.6米，高为1米，那么这个油桶的侧面积为（）（A ）π平方米 （B ）π平方米 （C ）平方米 （D ）π平方米27．一个形如圆锥的冰淇淋纸筒，其底面直径为6厘米，母线长为5厘米，围成这样的冰淇淋纸筒所需纸片的面积是（）（A ）66π平方厘米 （B ）30π平方厘米 （C ）28π平方厘米 （D ）15π平方厘米28．在半径为2的⊙O 中，圆心O 到弦AB 的距离为1，则弦AB 所对的圆心角的度数可以是（）（A ）ο60 （B ）ο90 （C ）ο120 （D ）ο15029．将一张长80厘米、宽40厘米的矩形铁皮卷成一个高为40厘米的圆柱形水桶的侧面，（接口损耗不计），则桶底的面积为（）（A ）π1600平方厘米 （B ）1600π平方厘米 （C ）π6400平方厘米 （D ）6400π平方厘米 30．如图，已知AB 是⊙O 的直径，弦CD ⊥AB 于点P ，CD ＝10厘米，AP ∶PB＝1∶5，那么⊙O 的半径是（）（A ）6厘米 （B ）53厘米 （C ）8厘米 （D ）35厘米31．在Rt △ABC 中，已知AB ＝6，AC ＝8，∠A ＝ο90．如果把Rt △ABC 绕直线AC 旋转一周得到一个圆锥，其表面积为S 1；把Rt △ABC 绕直线AB 旋转一周得到另一个圆锥，其表面积为S 2，那么S 1∶S 2等于（）（A ）2∶3 （B ）3∶4 （C ）4∶9 （D ）5∶1232．如图，⊙O 的弦AB ＝8厘米，弦CD 平分AB 于点E ．若CE ＝2厘米．ED 长为（）（A ）8厘米 （B ）6厘米 （C ）4厘米 （D ）2厘米33．如图，四边形ABCD 内接于⊙O ，若∠BOD ＝ο160，则∠BCD ＝（）（A ）ο160 （B ）ο100 （C ）ο80 （D ）ο2034．如图，正方形ABCD 内接于⊙O ，E 为DC 的中点，直线BE 交⊙O 于点F ．若⊙O 的半径为2，则BF 的长为（）（A ）23 （B ）22 （C ）556 （D ）55435．如图，AB 是⊙O 的直径，∠ACD ＝ο15，则∠BAD 的度数为（）（A ）ο75 （B ）ο72 （C ）ο70 （D ）ο6536．已知：点P 直线l 的距离为3，以点P 为圆心，r 为半径画圆，如果圆上有且只有两点到直线l 的距离均为2，则半径r 的取值范围是（）（A ）r ＞1 （B ）r ＞2 （C ）2＜r ＜3 （D ）1＜r ＜537．边长为a 的正方边形的边心距为（）（A ）a （B ）23a （C ）3a （D ）2a 38．如图，以圆柱的下底面为底面，上底面圆心为顶点的圆锥的母线长为4，高线长为3，则圆柱的侧面积为（）（A ）30π （B ）76π （C ）20π （D ）74π39．如图，扇形的半径OA ＝20厘米，∠AOB ＝ο135，用它做成一个圆锥的侧面，则此圆锥底面的半径为（）（A ）厘米 （B ）厘米 （C ）15厘米 （D ）30厘米40．如图，正六边形ABCDEF 中．阴影部分面积为123平方厘米，则此正六边形的边长为（）（A ）2厘米 （B ）4厘米 （C ）6厘米 （D ）8厘米41．已知扇形的弧长是2π厘米，半径为12厘米，则这个扇形的圆心角是（）（A ）ο60 （B ）ο45 （C ）ο30 （D ）ο2042．圆锥的高线长是厘米，底面直径为12厘米，则这个圆锥的侧面积是（）（A ）48π厘米 （B ）24π13平方厘米（C ）48π13平方厘米 （D ）60π平方厘米43．如图，AB 是⊙O 的直径，点P 在BA 的延长线上，PC 是⊙O 的切线，C 为切点，PC ＝26，PA ＝4，则⊙O 的半径等于（） （A ）1 （B ）2 （C ）23 （D ）26 44．已知圆柱的母线长为5厘米，表面积为28π平方厘米，则这个圆柱的底面半径是（）（A ）5厘米 （B ）4厘米 （C ）2厘米 （D ）3厘米45．半径相等的圆内接正三角形、正方形、正六边形的边长之比为（）（A ）1∶2∶3 （B ）3∶2∶1（C ）3∶2∶1 （D ）1∶2∶346．如图，若四边形ABCD 是半径为1和⊙O 的内接正方形，则图中四个弓形（即四个阴影部分）的面积和为（）（A ）（2π－2）厘米 （B ）（2π－1）厘米（C ）（π－2）厘米 （D ）（π－1）厘米47．如图，已知圆心角∠BOC ＝ο100，则圆周角∠BAC 的度数是（）（A ）ο50 （B ）ο100 （C ）ο130 （D ）ο20048．半径为5厘米的圆中，有一条长为6厘米的弦，则圆心到此弦的距离为（）（A ）3厘米 （B ）4厘米 （C ）5厘米 （D ）6厘米49．已知：Rt △ABC 中，∠C ＝ο90，O 为斜边AB 上的一点，以O 为圆心的圆与边AC 、BC 分别相切于点E 、F ，若AC ＝1，BC ＝3，则⊙O 的半径为（）（A ）21 （B ）32 （C ）43 （D ）54 50．已知：如图，E 是相交两圆⊙M 和⊙O 的一个交点，且ME ⊥NE ，AB 为外公切线，切点分别为A 、B ，连结AE 、BE ．则∠AEB 的度数为（）（A ）145° （B ）140° （C ）135° （D ）130°二、填空题1．如图，AB 、AC 是⊙O 的两条切线，切点分别为B 、C ，D 是优弧上的一点，已知∠BAC ＝ο80，那么∠BDC ＝__________度．2．在Rt △ABC 中，∠C ＝ο90，A Ｂ＝3，BC ＝1，以AC 所在直线为轴旋转一周，所得圆锥的侧面展开图的面积是__________．3．如果圆锥母线长为6厘米，那么这个圆锥的侧面积是_______平方厘米4．一种圆状包装的保鲜膜，如图所示，其规格为“20厘米×60米”，经测量这筒保鲜膜的内径1ϕ、外径2ϕ的长分别为厘米、厘米，则该种保鲜膜的厚度约为_________厘米（π取，结果保留两位有效数字）．5．两个点O 为圆心的同心圆中，大圆的弦AB 与小圆相切，如果AB的长为24，大圆的半径OA 为13，那么小圆的半径为___________．6．已知⊙O 中，两弦AB 与CD 相交于点E ，若E 为AB 的中点，CE ∶ED ＝1∶4，AB ＝4，则CD 的长等于___________．7．如图，AB 是⊙O 的直径，四边形ABCD 内接于⊙O ，，，的度数比为3∶2∶4，MN 是⊙O 的切线，C 是切点，则∠BCM 的度数为___________．8．如图，P 是⊙O 的直径AB 延长线上一点，PC 切⊙O 于点C ，PC ＝6，BC ∶AC＝1∶2，则AB 的长为___________．9．如图，四边形ABCD 内接于⊙O ，AD ∥BC ，＝，若AD ＝4，BC ＝6，则四边形ABCD 的面积为__________．10．若一个圆柱的侧面积等于两底面积的和，则它的高h 与底面半径r 的大小关系是__________．11．要用圆形铁片截出边长为4厘米的正方形铁片，则选用的圆形铁片的直径最小要___________厘米．12．圆内两条弦AB 和CD 相交于P 点，AB 长为7，AB 把CD 分成两部分的线段长分别为2和6，那么＝__________．13．△ABC 是半径为2厘米的圆内接三角形，若BC ＝23厘米，则∠A 的度数为________．14．如图，已知OA 、OB 是⊙O 的半径，且OA ＝5，∠AOB ＝15ο，AC ⊥OB 于C ，则图中阴影部分的面积（结果保留π）S ＝_________．15．如图，圆内接正六边形ABCDEF 中，AC 、BF 交于点M ．则ABM S △∶AFM S △＝_________．16．两圆外离，圆心距为25厘米，两圆周长分别为15π厘米和10π厘米．则其内公切线和连心线所夹的锐角等于__________度．17．将两边长分别为4厘米和6厘米的矩形以其一边所在直线为轴旋转一周，所得圆柱体的表面积为_________平方厘米．18．如图，在⊙O 的内接四边形ABCD 中，∠BCD ＝130ο，则∠BOD 的度数是________．19．已知⊙O 的半径为4厘米，以O 为圆心的小圆与⊙O 组成的圆环的面积等于小圆的面积，则这个小圆的半径是______厘米．20．如图，⊙O 1的半径O 1A 是⊙O 2的直径，C 是⊙O 1上的一点，O 1C 交⊙O 2于点B ．若⊙O1的半径等于5厘米，的长等于⊙O 1周长的101，则的长是_________．21．正三角形的内切圆与外接圆面积之比为_________．22．如图，AB ＝8，AC ＝6，以AC 和BC 为直径作半圆，两圆的公切线MN 与AB 的延长线交于D ，则BD 的长为_________．23．圆锥的母线长为5厘米，高为3厘米，在它的侧面展开图中，扇形的圆心角是_________度．24．如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足是G ，F 是CG 的中点，延长AF 交⊙O 于E ，CF ＝2，AF ＝3，则EF 的长是_________．25．在⊙O 中，直径AB ＝4厘米，弦CD ⊥AB 于E ，OE ＝3，则弦CD 的长为__________厘米．26．若圆锥底面的直径为厘米，线线长为5厘米，则它的侧面积为__________平方厘米（结果保留π）．27．如图，AB 为⊙O 的直径，P 点在AB 的延长线上，PM 切⊙O 于M 点．若OA ＝a ，PM ＝3a ，那么△PMB 的周长的__________．28．在半径9厘米的圆中，ο60的圆心角所对的弧长为__________厘米．29．扇形的圆心角为120ο，弧长为6π厘米，那么这个扇形的面积为_________．30．如果圆O 的直径为10厘米，弦AB 的长为6厘米，那么弦AB 的弦心距等于________厘米．31．某种商品的商标图案如图所求（阴影部分），已知菱形ABCD 的边长为4，∠A ＝ο60，是以A 为圆心，AB 长为半径的弧，是以B 为圆心，BC 长为半径的弧，则该商标图案的面积为_________．32．已知，一个直角三角形的两条直角边的长分别为3厘米、4厘米、以它的直角边所在直角线为轴旋转一周，所得圆锥的表面积是__________．33．正六边形的边心距与半径的比值为_________．34．如图，已知扇形AOB 的半径为12，OA ⊥OB ，C 为OA 上一点，以AC 为直径的半圆1O 和以OB 为直径的半圆2O 相切，则半圆1O 的半径为__________．35．如图，PA 、PB 与⊙O 分别相切于点A 、点B ，AC 是⊙O 的直径，PC 交⊙O 于点D ．已知∠APB ＝ο60，AC ＝2，那么CD 的长为________．36．底面半径为2厘米，高为3厘米的圆柱的体积为_________立方厘米（结果保留π）．37．边长为2厘米的正六边形的外接圆半径是________厘米，内切圆半径是________厘米（结果保留根号）．38．如图，PT 是⊙O 的切线，T 为切点，PB 是⊙O 的割线交⊙O 于A 、B 两点，交弦CD 于点M ，已知：CM ＝10，MD ＝2，PA ＝MB ＝4，则PT 的长等于__________．39．如图，扇形OAB 中，∠AOB ＝ο90，半径OA ＝1，C 是线段AB 的中点，CD ∥OA ，交于点D ，则CD ＝________．40．已知扇形的圆心角为150ο，它所对的弧长为20π厘米，则扇形的半径是________厘米，扇形的面积是__________平方厘米．41．如图，AB 是⊙O 直径，CE 切⊙O 于点C ，CD ⊥AB ，D 为垂足，AB ＝12厘米，∠B ＝30ο，则∠ECB ＝__________ο；CD ＝_________厘米．42．如图，DE 是⊙O 直径，弦AB ⊥DE ，垂足为C ，若AB ＝6，CE ＝1，则CD ＝________，OC ＝_________．43．如果把人的头顶和脚底分别看作一个点，把地球赤道作一个圆，那么身高压2米的汤姆沿着地球赤道环道环行一周，他的头顶比脚底多行________米．44．已知：⊙O 的半径为1，M 为⊙O 外的一点，MA 切⊙O 于点A ，MA ＝1．若AB 是⊙O 的弦，且AB ＝2，则MB 的长度为_________．45．如果圆的半径为4厘米，那么它的周长为__________厘米．三、解答题：1．已知：如图，△ABC 内接于⊙O ，过点B 作⊙O 的切线，交CA 的延长线于点E ，∠EBC ＝2∠C ．①求证：AB ＝AC ；②若tan ∠ABE ＝21，（ⅰ）求BC AB 的值；（ⅱ）求当AC ＝2时，AE 的长．2．如图，PA 为⊙O 的切线，A 为切点，⊙O 的割线PBC 过点O 与⊙O 分别交于B 、C ，PA ＝8cm ，PB ＝4cm ，求⊙O 的半径．3．已知：如图，BC 是⊙O 的直径，AC 切⊙O 于点C ，AB 交⊙O 于点D ，若AD ︰DB ＝2︰3，AC ＝10，求AC ︰A B 的值．4．如图，PC 为⊙O 的切线，C 为切点，PAB 是过O 的割线，CD ⊥AB 于点D ，若CD ︰DB ＝21，PC ＝10cm ，求三角形BCD 的面积．5．如图，在两个半圆中，大圆的弦MN 与小圆相切，D 为切点，且MN ∥AB ，MN ＝a ，ON 、CD 分别为两圆的半径，求阴影部分的面积．6．已知，如图，以△ABC 的边AB 作直径的⊙O ，分别并AC 、BC 于点D 、E ，弦FG ∥AB ，S △CDE ︰S △ABC ＝1︰4，DE ＝5cm ，FG ＝8cm ，求梯形AFGB 的面积．7．如图所示：PA 为⊙O 的切线，A 为切点，PBC 是过点O 的割线，PA ＝10，PB ＝5，求：（1）⊙O 的面积（注：用含π的式子表示）；（2）cos ∠BAP 的值．参考答案一、选择题1．B2．B3．D4．D5．C6．C7．A8．C9．D10．B11．A12．B13．C14．D15．D16．A17．B18．C19．C20．B21．B22．A23．A24．B25．B26．D27．D28．C29．A30．B31．A32．A33．B34．C35．A36．D37．B38．B39．B40．B41．C42．D43．A44．C45．B46．C47．A48．B49．C50．C二、填空题1．502．2π3．18π4．4105.7-⨯5．56．57．30°8．99．2510．h ＝r 11．4212．3或413．60°或120°14．8252425-π15．1:216．3017．80π或120π18．100°19．22 20．π21．1:422．123．28824．425．226．15π27．()a 23+28．3π29．27π平方厘米30．431．34 32．24π平方厘米或36π平方厘米33．2334．435．77436．12π37．2，338．13239．213-40．24，240π41．60°，3342．9，443．4π44．1或545．8π三、解答题：1．（1）∵ BE 切⊙O 于点B ，∴ ∠ABE ＝∠C ．∵ ∠EBC ＝2∠C ，即 ∠ABE ＋∠ABC ＝2∠C ，∴ ∠C ＋∠ABC ＝2∠C ，∴ ∠ABC ＝∠C ，∴ AB ＝AC ．（2）①连结AO ，交BC 于点F ，∵ AB ＝AC ，∴ ＝，∴ AO ⊥BC 且BF ＝FC ．在Rt △ABF 中，BFAF ＝tan ∠ABF ， 又 tan ∠ABF ＝tan C ＝tan ∠ABE ＝21，∴ BF AF ＝21， ∴ AF ＝21BF ． ∴ AB ＝22BF AF +＝2221BF BF +⎪⎭⎫ ⎝⎛＝25BF ． ∴ 452==BF AB BC AB ． ②在△EBA 与△ECB 中，∵ ∠E ＝∠E ，∠EBA ＝∠ECB ，∴ △EBA ∽△ECB ．∴ ⎪⎩⎪⎨⎧⋅==EC EA BE BC AB EB EA 2，解之，得516EA 2＝EA ·（EA ＋AC ），又EA ≠0， ∴ 511EA ＝AC ，EA ＝115×2＝1110． 2．设⊙的半径为r ，由切割线定理，得PA 2＝PB ·PC ，∴ 82＝4（4＋2r ），解得r ＝6（cm ）．即⊙O 的半径为6cm ．3．由已知AD ︰DB ＝2︰3，可设AD ＝2k ，DB ＝3k （k ＞0）．∵ AC 切⊙O 于点C ，线段ADB 为⊙O 的割线，∴ AC 2＝AD ·AB ，∵ AB ＝AD ＋DB ＝2k ＋3k ＝5k ，∴ 102＝2k ×5k ，∴ k 2＝10，∵ k ＞0，∴ k ＝10．∴ AB ＝5k ＝510．∵ AC 切⊙O 于C ，BC 为⊙O 的直径，∴ AC ⊥BC ．在Rt △ACB 中，sin B ＝51010510==AB AC ． 4．解法一：连结AC ．∵ AB 是⊙O 的直径，点C 在⊙O 上，∴ ∠ACB ＝90°．CD ⊥AB 于点D ，∴ ∠ADC ＝∠BDC ＝90°，∠2＝90°－∠BAC ＝∠B ．∵ tan B ＝21， ∴ tan ∠2＝21． ∴ CB AC DB CD CD AD ===21． 设AD ＝x （x ＞0），CD ＝2x ，DB ＝4x ，AB ＝5x ．∵ PC 切⊙O 于点C ，点B 在⊙O 上，∴ ∠1＝∠B ．∵ ∠P ＝∠P ，∴ △PAC ∽△PCB ，∴ 21==CB AC PC PA ． ∵ PC ＝10，∴ PA ＝5，∵ PC 切⊙O 于点C ，PAB 是⊙O 的割线，∵ PC 2＝PA ·PB ，∴ 102＝5（5＋5 x ）．解得x ＝3．∴ AD ＝3，CD ＝6，DB ＝12．∴ S △BCD ＝21CD ·DB ＝21×6×12＝36．即三角形BCD 的面积36cm 2．解法二：同解法一，由△PAC ∽△PCB ，得21==CB ACPC PA．∵ PA ＝10，∴ PB ＝20．由切割线定理，得PC 2＝PA ·PB ．∴ PA ＝201022-PB PC ＝5，∴ AB ＝PB －PA ＝15，∵ AD ＋DB ＝x ＋4x ＝15，解得x ＝3，∴ CD ＝2x ＝6，DB ＝4x ＝12．∴ S △BCD ＝21CD ·DB ＝21×6×12＝36．即三角形BCD 的面积36cm 2．5．解：如图取MN 的中点E ，连结OE ，∴ OE ⊥MN ，EN ＝21MN ＝21a ．在四边形EOCD 中，∵ CO ⊥DE ，OE ⊥DE ，DE ∥CO ，∴ 四边形EOCD 为矩形．∴ OE ＝CD ，在Rt △NOE 中，NO 2－OE 2＝EN 2＝22⎪⎭⎫⎝⎛a ．∴ S 阴影＝21π（NO 2－OE 2）＝21π·22⎪⎭⎫ ⎝⎛a ＝28πa ．6．解：∵ ∠CDE ＝∠CBA ，∠DCE ＝∠BCA ，∴ △CDE ∽△ABC ． ∴ 2⎪⎭⎫⎝⎛=∆∆AB DE S S ABCCDE∴ AB DE ＝ABC CDES S ∆∆＝41＝21，即215=AB ，解得 AB ＝10（cm ），作OM ⊥FG ，垂足为M ，则FM ＝21FG ＝21×8＝4（cm ），连结OF ，∵ OA ＝21AB ＝21×10＝5（cm ）．∴ OF ＝OA ＝5（cm ）．在Rt △OMF 中，由勾股定理，得OM ＝22FM OF -＝2245-＝3（cm ）．∴ 梯形AFGB 的面积＝2FG AB +·OM ＝2810⨯×3＝27（cm 2）．7．⎭⎬⎫的割线⊙是的切线⊙是O PBC O PA )1(PA 2＝PB ·PCPC ＝20半径为圆面积为π4225（或π）（平方单位）． ⎭⎬⎫∠=∠∠=∠P P BAP C )2(△ACP ∽△BAP PB PA AB AC =12=AB AC ．解法一：设AB ＝x ，AC ＝2x ，BC 为⊙O 的直径∠CAB ＝90°，则 BC ＝5x ．∵ ∠BAP ＝∠C ，∴ cos ∠BAP ＝cos ∠C ＝55252==x xBC AC解法二：设AB ＝x ，在Rt △ABC 中，AC 2＋AB 2＝BC 2，即 x 2＋（2x ）2＝152，解之得 x ＝35，∴ AC ＝65，∵ ∠BAP ＝∠C ，∴ ∴ cos ∠BAP ＝cos ∠C ＝5521556==BC AC 6．解：∵ ∠CDE ＝∠CBA ，∠DCE ＝∠BCA ，∴ △CDE ∽△ABC ．∴ 2⎪⎭⎫ ⎝⎛=∆∆AB DE S S ABC CDE ∴ AB DE ＝ABCCDE S S ∆∆＝41＝21， 即215=AB ，解得 AB ＝10（cm ）， 作OM ⊥FG ，垂足为M ， 则FM ＝21FG ＝21×8＝4（cm ）， 连结OF ， ∵ OA ＝21AB ＝21×10＝5（cm ）． ∴ OF ＝OA ＝5（cm ）．在Rt △OMF 中，由勾股定理，得OM ＝22FM OF -＝2245-＝3（cm ）．∴ 梯形AFGB 的面积＝2FG AB +·OM ＝2810⨯×3＝27（cm 2）． 7．⎭⎬⎫的割线⊙是的切线⊙是O PBC O PA )1(PA 2＝PB ·PCPC ＝20半径为圆面积为π4225（或π）（平方单位）． ⎭⎬⎫∠=∠∠=∠P P BAP C )2(△ACP ∽△BAP PB PA AB AC =12=AB AC ． 解法一：设AB ＝x ，AC ＝2x ，BC 为⊙O 的直径∠CAB ＝90°，则 BC ＝5x ．∵ ∠BAP ＝∠C ，∴ cos ∠BAP ＝cos ∠C ＝55252==xx BC AC 解法二：设AB ＝x ，在Rt △ABC 中，AC 2＋AB 2＝BC 2，即 x 2＋（2x ）2＝152，解之得 x ＝35，∴ AC ＝65， ∵ ∠BAP ＝∠C ，∴ ∴ cos ∠BAP ＝cos ∠C ＝5521556==BC AC6．解：∵ ∠CDE ＝∠CBA ，∠DCE ＝∠BCA ，∴ △CDE ∽△ABC ．∴ 2⎪⎭⎫ ⎝⎛=∆∆AB DE S S ABC CDE ∴ AB DE ＝ABCCDE S S ∆∆＝41＝21， 即215=AB ，解得 AB ＝10（cm ）， 作OM ⊥FG ，垂足为M ， 则FM ＝21FG ＝21×8＝4（cm ）， 连结OF ， ∵ OA ＝21AB ＝21×10＝5（cm ）． ∴ OF ＝OA ＝5（cm ）．在Rt △OMF 中，由勾股定理，得OM ＝22FM OF -＝2245-＝3（cm ）．∴ 梯形AFGB 的面积＝2FG AB +·OM ＝2810⨯×3＝27（cm 2）． 7． ⎭⎬⎫的割线⊙是的切线⊙是O PBC O PA )1(PA 2＝PB ·PCPC ＝20半径为圆面积为π4225（或π）（平方单位）． ⎭⎬⎫∠=∠∠=∠P P BAP C )2(△ACP ∽△BAP PB PA AB AC =12=AB AC ． 解法一：设AB ＝x ，AC ＝2x ，BC 为⊙O 的直径∠CAB ＝90°，则 BC ＝5x ．∵ ∠BAP ＝∠C ，∴ cos ∠BAP ＝cos ∠C ＝55252==x x BC AC 解法二：设AB ＝x ，在Rt △ABC 中，AC 2＋AB 2＝BC 2，即 x 2＋（2x ）2＝152，解之得 x ＝35，∴ AC ＝65， ∵ ∠BAP ＝∠C ，∴ ∴ cos ∠BAP ＝cos ∠C ＝5521556==BC AC圆是中考中的必考内容，大约占整个分数的百分之30左右，希望大家能够加深练习，提到自己的做题能力。