二面角的求法---三垂线法

用三垂线法求二面角的方法三垂线定理：在平面内的一条直线,如果和穿过这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。

已知：如图, PB 是平面α的斜线, PA 是平面α的垂线, 直线a ⊂平面α,直线a 垂直;射影AB. 求证： a ⊥PB证明：∵PA 是平面α的垂线, 直线a ⊂平面α∴直线a ⊥PA 又∵直线a ⊥AB AB ⋂PA A = ∴直线a ⊥平面PAB 而PB ⊂平面PAB ∴a ⊥PB 总结：定理论述了三个垂直关系，①垂线PA 和平面α垂直;②射影AB 和直线a 垂直;③斜线PB 和直线a 垂直.三垂线定理揭示了一个平面和四条直线所构成的三种垂直关系的内在联系，是线面垂直的性质，在立体几何中有广泛的应用。

求二面角是高考考查的热点，三垂线法是求二面角最常用的方法,应用好定理的关键是实现斜线与其在面内射影垂直关系的转化，因此寻找垂线、斜线及其射影至关重要。

运用三垂线法求二面角的一般步骠：①作：过二面角的其中一个平面上一点作(找)另一个平面的垂线,过垂足作二面角的棱的垂线。

. ②证：证明由①所得的角是二面角的平面角(符合二面角的定义) 。

③求： 二面角的平面角的大小(常用面积相等关系求垂线段长度) 。

1、如右图所示的四面体ABCD 中，AB ⊥平面BCD ，BC CD ⊥且1BC CD ==，AD =①求二面角C ABD --的大小；②求二面角B CD A --的大小；1．解： ①∵AB ⊥面BCD ∴BC AB ⊥ BD AB ⊥∴CBD ∠为二面角C AB D --的平面角 ∵BC CD ⊥且1BC CD ==∴CBD ∠=4π ∴二面角C AB D --的大小为4π ②∵AB ⊥面BCD BC CD ⊥ ∴由三垂线定理得CD AC ⊥∴ACB ∠为二面角B CD A --的平面角 ∵BC CD ⊥∴BD ==∵AB ⊥平面BCD ∴AB BC ⊥ AB BD ⊥∴1AB ==在Rt ABC ∆中，tan 1ABACB BC∠==， ∴二面角B CD A --的大小为4π 方法点拨：本题①的方法是直接运用二面角的定义求解,本题②的关键是找出垂线AB 、斜线AC 及其射影BC,。

二面角的作与求求角是每年高考必考内容之一，可以做为选择题，也可作为填空题，时常作为解答题形式出现，重点把握好二面角，它一般出现在解答题中。

下面就对求二面角的方法总结如下：1、定义法：在棱上任取一点，过这点在两个面内分别引棱的垂线，这两条射线所成的角就是二面角的平面角。

2、三垂线定理及逆定理法：自二面角的一个面上的一点向另一个面引垂线，再由垂足向棱作垂线得到棱上的点。

斜足与面上一点连线，和斜足与垂足连线所夹的角即为二面角的平面角。

3、作棱的垂面法:自空间一点作与棱垂直的平面，截二面角的两条射线所成的角就是二面角的平面角。

4、投影法：利用s投影面=s被投影面θcos 这个公式对于斜面三角形，任意多边形都成立，是求二面角的好方法。

尤其对无棱问题5异面直线距离法： EF 2=m 2+n 2+d 2－2mn θcos例1：若p 是ABC ∆所在平面外一点，而PBC ∆和ABC ∆都是边长为2的正三角形，PA=6,求二面角P-BC-A 的大小。

分析：由于这两个三角形是全等的三角形， 故采用定义法解：取BC 的中点E ，连接AE 、PEAC=AB ，PB=PC ∴AE ⊥ BC ，PE ⊥BC∴PEA ∠为二面角P-BC-A 的平面角在PAE ∆中AE=PE=3，PA=6PCBAE∴PEA ∠=900∴二面角P-BC-A 的平面角为900。

例2：已知ABC ∆是正三角形，⊥PA 平面ABC 且PA=AB=a,求二面角A-PC-B 的大小。

[思维]二面角的大小是由二面角的平面角 来度量的，本题可利用三垂线定理（逆）来作 平面角，还可以用射影面积公式或异面直线上两点 间距离公式求二面角的平面角。

解1：（三垂线定理法）取AC 的中点E ，连接BE ，过E 做EF ⊥PC,连接BF ⊥PA 平面ABC ，PA ⊂平面PAC∴平面PAC ⊥平面ABC, 平面PAC 平面ABC=AC∴BE ⊥平面PAC由三垂线定理知BF ⊥PC∴BFE ∠为二面角A-PC-B 的平面角设PA=1,E 为AC 的中点，BE=23,EF=42∴tan BFE ∠=6=EFBE∴BFE ∠=arctan 6解2：（三垂线定理法）取BC 的中点E ，连接AE ，PE 过A 做AF ⊥PE, FM ⊥PC,连接FMAB=AC,PB=PC ∴AE ⊥BC,PE ⊥BC∴ BC ⊥平面PAE,BC ⊂平面PBC∴平面PAE ⊥平面PBC, 平面PAE 平面PBC=PE由三垂线定理知AM ⊥PCPC BAEF MEPCBAF图1图2∴FMA ∠为二面角A-PC-B 的平面角设PA=1，AM=22,AF=721.=PE AE AP∴sin FMA ∠=742=AM AF ∴FMA ∠=argsin742解3：（投影法）过B 作BE ⊥AC 于E,连结PE ⊥PA 平面ABC ，PA ⊂平面PAC∴平面PAC ⊥平面ABC, 平面PAC 平面ABC=AC∴BE ⊥平面PAC∴PEC ∆是PBC ∆在平面PAC 上的射影设PA=1,则PB=PC=2,AB=141=∆PEC S ,47=∆PBC S由射影面积公式得，77cosarg ,77=∴==∆∆θθPBC PEC S S COS , 解4：（异面直线距离法）过A 作AD ⊥PC,BE ⊥PC 交PC 分别于D 、E 设PA=1,则AD=22,PB=PC=2 ∴BE=PC S PBC 21∆=414,CE=42,DE=42由异面直线两点间距离公式得 AB 2=AD 2+BE 2+DE 2-2ADBE θCOS ,θCOS =77cos arg ,77=∴θ [点评]本题给出了求平面角的几种方法，应很好掌握。

图1二面角计算一 、直接法：即先作出二面角的平面角，再利用解三角形知识求解之。

通常作二面角的平面角的途径有：⑴定义法：在二面角的棱上取一个特殊点，由此点出发在二面角的两个面内分别作棱的垂线；⑵三垂线法：如图1，C 是二面角βα--AB 的面β内的一个点，CO ⊥平面α于O ，只需作OD⊥AB 于D ，连接CD ，用三垂线定理可证明∠CDO 就是 所求二面角的平面角。

⑶垂面法：即在二面角的棱上取一点，过此点作平面γ，使γ垂直于二面角的棱，则γ 与二面角的两个面的交线所成的角就是该二面角的平面角。

例1 如图2，在四棱锥V-ABCD 中，底面ABCD 是正方形，侧面VAD 是正三角形, 平面VAD⊥底面ABCD ． （1）证明AB⊥平面VAD ；（2）求面VAD 与面VDB 所成的二面角的大小． 解：（1）证明：VAD ABCD AB AD AB VADAB ABCD AD VAD ABCD ⊥⎫⎪⊥⎪⇒⊥⎬⊂⎪⎪=⎭平面平面平面平面平面平面 （2）解：取VD 的中点E ，连结AF ，BE ， ∵△VAD 是正三形，四边形ABCD 为正方形， ∴由勾股定理可知，BD VB,===∴AE⊥VD，BE⊥VD，∴∠AEB 就是所求二面角的平面角. 又在Rt△ABE 中，∠BAE=90°，AB ，因此，tan∠AEB=.332=AE AB 即得所求二面角的大小为.332arctan例2 如图3，AB⊥平面BCD ，DC⊥CB，AD 与平面BCD成30°的角，且AB=BC.（1）求AD 与平面ABC 所成的角的大小； （2）求二面角C-AD-B 的大小；（3）若AB=2，求点B 到平面ACD 的距离。

解：(1) ∵AB⊥平面BCD ，∴∠ADB 就是AD 与平面BCD 所成的角,即∠ADB=300,且CD⊥AB， 又∵DC⊥BC，ABBC B =,∴ CD⊥平面ABC ，∴ AD 与平面ABC 所成的角为∠DAC ，设AB=BC=a,则AC=a 2， BD=acot300=a 3,AD=2a, a BC BD CD 222=-=,∴ tan∠DAC=122==aa CDAC , ∴ 045=∠DAC ,即，AD 与平面ABC 所成的角为450. (2)作CE⊥BD 于E ，取AD 的中点F ，连CF ， ∵ AB⊥面BCD ，ABD AB ⊂面， ∴ 面ABD⊥面BCD ， 又∵ 面ABD面BCD=BD ，BCD CE ⊂面，CE⊥BD，∴ CE⊥面ABD ，又∵AC=BC=a 2，AF=FD ，∴AD⊥EF，有三垂线定理的逆定理可知，∠CFE 就是所求二面角的平面角.计算可知, BC CD CE BD ⋅=，2AD a,=12CF AD a ==，∴ CE sin CFE CF ∠==故，所求的二面角为3.略例3如图4，P 是边长为1的正六边形ABCDEF 所在平面外一点，1PA =，P 在平面ABC 内的射影为BF 的中点O.（1）证明PA ⊥BF ；（2）求面APB 与面DPB 所成二面角的大小。

三垂线定理：平面内一条直线，如果和这个平面的一条斜线在平面内的射影垂直，那么这条直线就和这条斜线垂直；已知：,PA PO 分别是平面α的垂线和斜线，AO 是PO 在平面α的射影,,a α⊂a AO ⊥。

求证：a PO ⊥；证明： 说明：（1）线射垂直（平面问题）⇒线斜垂直（空间问题）；（2）证明线线垂直的方法：定义法；线线垂直判定定理；三垂线定理；（3）三垂线定理描述的是PO(斜线)、AO(射影)、a(直线)之间的垂直关系。

（4）直线a 与PO 可以相交，也可以异面。

（5）三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理。

2．写出三垂线定理的逆命题，并证明它的正确性； 命题： 已知： 求证： 证明：例1、判断下列命题的真假：（1）若a 是平面α的斜线，直线b 垂直于a 在平面α内的射影，则 a ⊥b （ ）（2）若 a 是平面α的斜线，平面β内的直线b 垂直于a 在平面α内的射影，则 a ⊥b （ ） （3）若a 是平面α的斜线，直线b ⊂ α且b 垂直于a 在另一平面β内的射影，则a ⊥b （ ） （4）若a 是平面α的斜线,b ∥α,直线 b 垂直于a 在平面α内的射影，则 a ⊥b （ ）例2、已知P 是平面ABC 外一点， PA ⊥平面ABC ，AC ⊥ BC ， 求证： PC ⊥ BC 。

例3、在四面体ABCD 中，已知AB ⊥CD ，AC ⊥BD ，求证：AD ⊥BC 。

PP1.已知P 是平面ABC 外一点，,PA ABC AC BC ⊥⊥。

求证：PC BC ⊥。

2.已知PA ⊥正方形ABCD 所在平面，O 为对角线BD 的中点。

求证：,PO BD PC BD ⊥⊥。

3.在正方体1AC 中，求证：11111,AC B D AC BC ⊥⊥；4.在空间四边形ABCD 中，设,AB CD AC BD ⊥⊥。

求证：（1）AD BC ⊥；（2）点A 在底面BCD 上的射影是BCD ∆的垂心；5.求证:如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上二面角大小的求法的归类分析一、定义法：直接在二面角的棱上取一点（特殊点），分别在两个半平面内作棱的垂线，得出平面角，用定义法时，要认真观察图形的特性；例1 在四棱锥P-ABCD 中，ABCD 是正方形，PA ⊥平面ABCD ，PA=AB=a ，求二面角B-PC —-D 的大小。

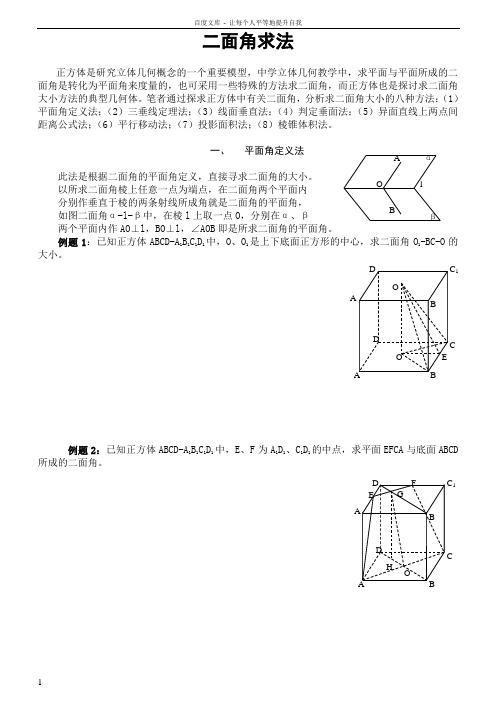
二面角求法正方体是研究立体几何概念的一个重要模型，中学立体几何教学中，求平面与平面所成的二面角是转化为平面角来度量的，也可采用一些特殊的方法求二面角，而正方体也是探讨求二面角大小方法的典型几何体。

笔者通过探求正方体中有关二面角，分析求二面角大小的八种方法：（1）平面角定义法；（2）三垂线定理法；（3）线面垂直法；（4）判定垂面法；（5）异面直线上两点间距离公式法；（6）平行移动法；（7）投影面积法；（8）棱锥体积法。

一、平面角定义法此法是根据二面角的平面角定义，直接寻求二面角的大小。

以所求二面角棱上任意一点为端点，在二面角两个平面内分别作垂直于棱的两条射线所成角就是二面角的平面角，如图二面角α-l-β中，在棱l上取一点O，分别在α、β两个平面内作AO⊥l，BO⊥l，∠AOB即是所求二面角的平面角。

例题1：已知正方体ABCD-A1B1C1D1中，O、O1是上下底面正方形的中心，求二面角O1-BC-O的大小。

例题2：已知正方体ABCD-A1B1C1D1中，E、F为A1D1、C1D1的中点，求平面EFCA与底面ABCD所成的二面角。

二、 利用三垂线定理法此方法是在二面角的一个平面内过一点作另一个面的垂线，再由垂足（或仍是该点）作棱的垂线，连接该点和棱上的垂足（或连两垂足）两点线，即可得二面角的平面角。

如图二面角α-l-β中，在平面α内取一点A ，过A 作AB ⊥平面β，B 是垂足， 由B （或A ）作BO （或AO ）⊥l ，连接AO （或BO ）即得AO 是平面β的斜线， BO 是AO 在平面β中的射影，根据三垂线定理（或逆定理）即得AO ⊥l ，BO ⊥l ， 即∠AOB 是α-l-β的平面角。

例题3：已知正方体ABCD-A 1B 1C 1D 1中，求二面角B-AC-B 1的大小。

例题4：已知正方体ABCD-A 1B 1C 1D 1中，求平面ACD 1与平面BDC 1所成的二面角。

三、 线面垂直法此法利用直线垂直平面即该直线垂直平面内任何直线的性质来寻求二面角的平面角。

空间几何二面角解题技巧练习————————————————————————————————作者：————————————————————————————————日期：ﻩ知识点: 二面角的求法一、思想方法求二面角的大小，是立体几何计算与运用中的一个重点和难点. 直接法的核心是作（或找)出二面角的平面角,间接法可利用投影、异面直线、空间向量等。

常用的方法有以下几种：方法一(定义法）即从二面角棱上一点在两个面内分别引棱的垂线如图１。

方法二（三垂线法)在二面角的一个面上一点P 棱及另一个面分别引垂线ＰA 、PB,连接AB,根据三垂线定理（或逆定理）,∠PAB 为所求的二面角的平面角.如图2。

方法三(作垂面法）作棱的垂直平面，则这个垂面与二面角两个面的交线所夹的角就是二面角的平面角（图３中∠MAN ）.方法四（投影面积法)一个平面α上的图形面积为S,它在另一个平面β上的投影面积为S'，这两个平面的夹角为θ,则S ＇=Sco ｓθ或c ｏs θ=/S S．方法五（异面直线法)如图4中，平面α、β相交成θ角，AC 、B Ｄ分别在α、β上，且与棱垂直.若ＡＣ=m,BD＝n, C Ｄ=d,则有A Ｂ２=m 2+n 2+ｄ2-2mncos θ,故cos θ=22222m n d AB mn++- (1）在已知二面角两个面上两点间距离(即｜AB|)的情况下,可以用此公式来求θ.说明:原来的公式中θ理解为两异面直线间的夹角，只取锐角（或直角)，故根据A 、Ｂ的位置情况公式是AB ２=m 2+n 2＋d 2±2mnc ｏs θ．但二面角可以取钝角,故只需取“-”号得出公式（1）． 方法六（空间向量法)如图5，设12,,n n 是二面角l αβ--的两个半平面的法向量，其方向一个指向内．侧,另一个指向外．侧，则二面角l αβ--的平面角α＝1212arccos ||||n n n n ⋅。

二、例题：例1．在棱长为1的正方体1AC 中，（1)求二面角11A B D C --的大小；(２)求平面1C BD 与底面ABCD 所成二面角1C BD C --的平面角大小例２．如果二面角l αβ--的平面角是锐角,点P 到,,l αβ的距离分别为22,4,42,求二面角的大小(垂面法)。

精品)三垂线法求二面角专题1、已知正方形ABCD，AE=1，BE=3，求证平面ADE⊥平面BCE，求二面角B—AC—E的大小。

证明：由题意，DA⊥平面ABE，且ABCD是正方形，故DA⊥BC，即DA⊥BE。

又因为AE=1，BE=3，AB=2，所以BE⊥EA，即BE垂直于平面ADE。

因此，BE垂直于平面ADE和平面BCE，即平面ADE⊥平面BCE。

求二面角B—AC—E的大小：过点E作EF⊥XXX与F，连接EG并延长交AC于G。

根据三垂线定理可得，XXX。

因此，∠EGF为二面角B—AC—E的平面角。

在直角三角形EFG中，tan(∠EGF)=EF/GF=6/7.因此，∠EGF=arctan(6/7)=arcsin(6/√85)≈57.84°。

2、已知直角梯形ABCD，AB=BC=1，AD=2，PA⊥平面ABCD，PA=1，求点P到CD的距离、证明平面PAC⊥平面PCD，求平面PAB与平面PCD所成二面角的大小。

点P到CD的距离为PC，因为XXX⊥平面ABCD且PC⊥CD。

证明平面PAC⊥平面PCD：因为ABCD是直角梯形，所以AC⊥CD。

又因为XXX⊥平面ABCD，PC⊥CD，且AC与PC的交点为C，所以CD垂直于平面PAC，即平面PAC⊥平面PCD。

求平面PAB与平面PCD所成二面角的大小：延长XXX的延长线于G，连接PG。

XXX⊥平面PAB，所以AH⊥PG。

因此，∠AHD为平面PAB与平面PCD所成二面角的平面角。

根据勾股定理，DG=√5，AG=3/2，AH=√5/2.因此，tan(∠AHD)=2/√5，所以∠AHD=arctan(2/√5)=arcsin(2/3)≈41.81°。

的平面角。

我们可以利用余弦定理求解这个平面角的正切值。

首先，我们需要求出三个边的长度：BE = BC = 1（正方形的边长为1）EC = DE = $\sqrt{2}$（利用勾股定理求解）根据余弦定理：cos $\angle$ BEC = $\frac{BE^2 + EC^2 - BC^2}{2BE\cdot EC}$ = $\frac{1 + 2 - 1}{2\sqrt{2}}$ = $\frac{\sqrt{2}}{2}$ 因此，tan $\angle$ B-DE-C = $\frac{\sqrt{1 - cos^2\angle BEC}}{cos\angle BEC}$ = $\frac{\sqrt{2 -(\frac{\sqrt{2}}{2})^2}}{\frac{\sqrt{2}}{2}}$ = $\sqrt{2}$。

”三垂线法作二面角的平面角的技巧求二面角的大小是考试中经常出现的问题，而用三垂线法作二面角的平面角是求二面角大小的一个重要方法，许多同学在解题过程中由于没有有效地利用三垂线定理(或逆定理)作出二面角的平面角，使得解题受阻．我们把用三垂线定理(或逆定理)作二面角的平面角的方法称为三垂线法，其作图模型为：如图1，在二面角α—l一β中，过平面α内一点A作AO⊥平面β，垂足为O，过点O作OB⊥l于B(过A点作AB⊥于B)，连结AB(或OB)，由三垂线定理(或逆定理)知AB⊥l(或OB⊥l)，则∠ABO为二面角。

α—l—β的平面角．作图过程中，作出了两条垂线AO与OB(或AB)，后连结AB两点(或OB两点)，这一过程可简记为“两垂一连，其中AO为“第一垂线．“第一垂线”能否顺利找到或恰当作出是用三垂线法作二面角的平面角的关键，在具体解题过程中要注意以下几点：1．善于利用图中已有的“第一垂线”例1已知斜三棱柱ABC—A1B1C1中，∠BCA=90°，AC=BC，A1在底面ABC的射影恰为AC的中点M，又知AA1与底面ABC所成的角为60°．(1)求证：BC⊥平面AA1CC1；(2)求二面角B一AA1—C的大小．-可编辑修改-的平面角．设 AC ＝BC ＝ ，正△a AA 1C 的边长为 a ，所以 CN =3a ，在 Rt△” ” 剖析：注意该题的第(1)问，事实上本题已经暗示了 BC 就是我们要寻求的“第一垂线．略解 2 A 1A 与底面 AB 成的角为 60°，所以∠A 1AC ＝60°，又 M 是 AC中点，所以 △AA 1C 是正三角形，作 CN ⊥AA 1 于 N ，点 N 为 A 1A 的中点，连结 BN ，由 BC ⊥平面 AA 1CC 1，BN ⊥AA 1，则∠BNC 为二面角 B 一 AA 1 一 C2BNC 中，tan∠BNC = BC = a = 2 3 ，即∠BNC = arctan 2 3 .NCa 3 332例 2如图 3，在底面是直角梯形的四棱锥 S —ABCD 中，∠ABC ＝90°，SA ⊥面 ABCD ，SA =AB =BC ＝1，AD ＝ 12(1)求四棱锥 S —ABCD 的体积；(2)求面 SCD 与面 SBA 所成的二面角的正切值．剖析：由 SA ⊥面 ABCD 及∠ABC =90°，不难发现，BC 即为“第一垂线，但是，本题要作二面角的平面角，还需首先作出二面角的棱．略解 2 延长 BA 、CD 相交于点 E ，连结 SE ，则 SE 是所求二面角的棱，因为 AD ∥BC ，BC =2AD ，所以 EA =AB =SA ，所以 SE ⊥SB ，因为 SA ⊥面 ABCD ，得面 SEB ⊥面 EBC ，EB 是交线，又 BC ⊥EB ，所以 BC ⊥面 SEB ，故 SB 是CS 在面 SEB 上的射影，所以 CS ⊥SE ，所以∠BSC 是所求二面角的平面角，因为 SB = SA 2+ AB 2= 2 ，BC =1，BC ⊥SB ，因为 tan∠BSC = = BC = 2，即所SB2求二面角的正切值为 2 ．2-可编辑修改-例3如图4，正三棱柱ABC—A1B1C1的底边长为a，侧棱长为2a，DF⊥面A1AB1，即DF为我们要作的“第一垂线．因为D是A1C1中点，A1B1＝a，所以B1F=3a，DF=3a，在Rt△DFG，可2．借助第三个平面，作“第一垂线”2若经过对角线AB1且与对角线BC1平行的平面交上底面一边A1C1于点D．(1)确定点D的位置，并证明你的结论；(2)求二面角A1—AB1—D的大小．剖析：由线面平行的性质定理及三角形中位线性质，易知D是A1C1中点．二面角A1—AB1一D的放置属于非常规位置的图形，但是，容易发现，平面A1B1C1过点D且与平面A1AB1垂直，这样的平面相对于二面角的两个平面而言，我们称为第三个平面．过D作DF⊥A1B1，由面面垂直的性质知，”略解2在平面A1B1C1内，作CF⊥A1B1于F，连DC，由三垂线定理可证AB1⊥DG，∠DGF就是二面角A1—AB1一D的平面角，在正△A1B1C1中，44求得∠DCF=45°．3．利用特殊图形的定义、性质作“第一垂线”-可编辑修改-例4已知：△Rt ABC的斜边BC在平面α内，AB、AC分别与平面。

二面角的找法定义法：在二面角的棱上找一点，在两个半平面内分别作垂直于棱的射线(如图(1))．垂面法：过棱上一点作棱的垂直平面，该平面与二面角的两个半平面产生交线，这两条交线所成的角，即为二面角的平面角(如图(2))．三垂线法：在一个半平面内不同于棱上的点A 向另一个半平面作垂线，垂足为B ，由点B 向二面角的棱作垂线，垂足为O ，连结AO ，则∠AOB 为二面角的平面角(如图（3）)．面积射影法：根据三角形面积(S )与其射影面积(S ′)之间的关系cos θ＝S S '确定面ABC 与面A ′BC 所成的角θ(如图(4))．例题1、已知二面角α-l -β，其大小为90°，A ∈α，B ∈β，线段AB ＝2a ，AB与α成45°的角，与β成30°的角，过A 、B 作l 的垂线AC 、BD ，C 、D 分别是垂足，求二面角C -AB -D 的余弦值．解：定义法：在平面ABD 内，作DF ⊥AB 于F ，在平面ABC 内作FH ⊥AB 于F ，交BC 于点H ，连结DH ．则∠HFD 为二面角C -AB -D 的平面角．∴ AB ⊥面HFD ，∴ AB ⊥HD ．∵ α-l -β是直二面角，∴ AC ⊥l ．∴ AC ⊥平面β．又∵ DH ⊂β，∴ AC ⊥DH ，又∵ AC ∩AB ＝A ，∴ HD ⊥平面ABC ，∵ HF ⊂平面ABC ，∴ HD ⊥HF ，∴ △DHF 为Rt △．∵ AC ⊥β，∴ ∠ABC 为AB 与β所成的角，∴ ∠ABC ＝30°．同理可得，∠BAD ＝45°．在△ABD 中，DF ＝21AB ＝a ， BD ＝2a ，AB ＝2a ，在△ABC 中，BC ＝Ab cos ∠ABC ＝2a cos30°＝3a ， 在△BCD 中，CD ＝a ，DH ＝36=⋅BC BD CD a ．在△DHF 中，HF ＝33a ，∴ cos ∠DFH ＝DF HF ＝33．∴ 二面角C -AB -D 的余弦值为33．三垂线定理法： ∵ α-l -β是直二面角，AC ⊥l ，∴ AC ⊥β．∴ 面ABC ⊥β，且BC 为交线．过D 作DH ⊥BC 于H ，则DH ⊥平面ABC ，过H 作HF ⊥AB 于F ，连结DF ，由三垂线定理，得DF ⊥AB ，∴ ∠HFD 为二面角C -AB -D 的平面角．∵ AC ⊥β，∴ ∠ABC ＝30°．同理可得∠BAD ＝45°．∵ 在△ABD 中，DF ＝21AB ＝a ，BD ＝22AB ＝2a ，在△BCD 中，CD ＝a ，DH ＝36a ，在△DHF 中，HF ＝33a ．∴ cos ∠DFH ＝DF HF ＝33，∴ 二面角C -AB -D 的余弦值为33．2、在所给空间图形中ABCD 是正方形，PD ⊥面ABCD ，PD＝AD ．求平面PAD 和面PBC 所成二面角的大小．解：经P 在面PAD 内作PE ∥AD ，AE ⊥面ABCD ，两线相交于E ，连BE ．∵ BC ∥AD ，则BC ∥面PAD ．∴ 面PBC ∩面PAD ＝PE ．∴ BC ∥PE ．因PD ⊥面ABCD ，BC ⊥CD ，那么BC ⊥PC ，BC ⊥面PDC ，即有PE ⊥面PDC ．PE ⊥PD ，PE ⊥PC ，∠CPD 就是所求二面角的平面角．因PD ＝AD ，而AD ＝DC ，∴ ∠CPD ＝45°．即面PAD 与面PBC 成角为45°．3、如图，几何体中，ABCD 是直角梯形，∠ABC ＝90°，SA ⊥面ABCD ，SA ＝AB ＝BC ＝1，AD ＝21，求面SCD 与面SBA 所成二面角的正切值．解一：因AB 、CD 共面，AD ＝21BC ，故AB 、CD 相交，设其交点为E ．∵ E ∈CD ，CD 面SCD ，∴ E ∈面SCD ，同理E ∈面SAB ．那么E 在面SCD 、面SAB 的交线上．连SE 则面SCD ∩面SAB ＝SE ．由题AE ＝AB ＝SA ，SA ⊥面ABCD ，故SE ⊥SB ，面SEB ⊥面EBC ．又∵ EB ⊥BC ，CB ⊥面SEB ，SB 是SC 在面SEB 内射影，∴ SE ⊥SC ．∠BSC 就是面SCD 与面SBA 所成二面角的平面角．在Rt △SBC 中tan ∠BSC ＝21=SB BC ＝22那么面SCD 与面SBA 所成二面角的正切值为22．解二：分别取SC 及SB 的中点E 、F ，连EF ，则EF21BC ，即EF AD ．故ADEF 为平行四边形，那么DE ∥AF ，即DE ∥面SAB ．经S 在面SCD 内作l ∥DE ，那么l 就是所求二面角的棱．因SA ＝AB 有AF ⊥SB ．又SA ⊥面ABCD ，则面BSA ⊥面ABCD ．又BC ⊥AB ，∴ BC ⊥面SAB ，即BC ⊥AF ．故AF ⊥面SBC ．那么l ⊥面SBC ．l ⊥SB ，l ⊥SC ．∠CSB 就是二面角的平面角．在Rt △CSB 中，tan ∠CSB ＝21=SB BC ＝22．解法三：如图，将题所给几何体“装”入正方体，分别取M 、N 为SE 及GF 中点，连DM ，MN ，DNSC ∩DN ＝O ，连OM ，则面DMN ∥面SAB ．SM ⊥面DMN ，又DM ＝MN ，∴ MO ⊥DN ，有DN ⊥SO ．故∠SOM 为面DMN 与SDC 所成二面角的平面角，也是面SAB 与面SDC 所成二面角的大小．在Rt △SMO 中，tan ∠MOS ＝2221=MO SM ＝22．解法四：还将原几何体“装”入正方体．∵ 面SAB ∥面EHC ，故面SAB 与面SDC 所成二面角等于面EHC 与面SDC 所成二面角，这还是一个无棱二面角问题“找公共点”．延长SD 、EH ，使SD ∩EH ＝G ，连CG ．则CG 就是面EHC 与面SDC 所成二面角的棱．由题正方体棱长为1，AD ＝21．连CE ，则CE ＝2，EG ＝2，CG ＝2．∴ ∠GCE ＝90°，GC ⊥EC ．而SE ⊥面EHC ，故GC ⊥SC ，∠SCE 就是面EHG 与面SDC 所成二面角的平面角．tan ∠ECS ＝21=EC SE ＝22．故面SAB 与面SDC 所成二面角正切值为22． 作辅助面求解．(等价转化)解法五：分别取BC 及SB 的中点M 、N ，连AM ，MN ，AN ，则有MN ∥SC ，MA ∥CD ，故面AMN ∥面SDC ．那么问题就转化为求面SAB 与面AMN 所成二面角，棱为AN ．解法六：同上思路，找面，使之平行于一面而与另一面相交，图形如下：面GDF ∥面SAB面积射影分析：如上图所示两个面，面SAB 及面SDC 所成二面角，若为α，则应有cos α＝SDCASB S S ∆∆其中面SDC 在面SAB 上射影为△SAB ，解三角形可求得 S △SDC ＝21SC ·46)2(22=-SC CDS △ABS ＝21SA ·AB ＝21那么cos α＝364621= 即tan α＝22．解法七：……也许还有好的方法，妙的思路……。

三垂线定理及其逆定理•正射影的概念：自一点向平面引垂线，垂足叫做这一点在平面内的正射影（简称为射影）；平面的斜线的概念：如果一条直线和一个平面相交但不垂直，那么这条直线叫做这个平面的斜线，斜线和平面的交点叫做斜足。

•三垂线定理：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。

三垂线定理的逆定理：如果平面内一条直线和穿过该平面的一条斜线垂直，那么这条直线也垂直于这条斜线在平面内的射影。

•三垂线定理与其逆定理的关系：即：•三垂线定定理的主要应用：证明线线、线面垂直，求点到线的距离、二面角大小。

应用两个定理解题的一般思路：平面内的一条直线，如果和穿过这个平面的一条斜线在这个平面内的射影垂直，那么它也和这条斜线垂直。

三垂线定理的逆定理：如果平面内一条直线和穿过该平面的一条斜线垂直，那么这条直线也垂直于这条斜线在平面内的射影。

证明：1）用线面垂直证明已知：如图，PO在α上的射影OA垂直于a三垂线定理的证明三垂线定理的证明求证：OP⊥a证明：过P做PA垂直于α∵PA⊥α且a⊆α∴a⊥PA又a⊥OAOA∩PA=A∴a⊥平面POA∴a⊥OP（2）用向量证明三垂线定理1.已知：PO，PA分别是平面α的垂线，斜线，OA是PA在α内的射影，向量b包含于α，且向量b垂直于OA，求证：向量b垂直于PA证明：∵PO垂直于α，∴PO垂直于b，又∵OA垂直b，向量PA=（向量PO+向量OA）∴向量PA·向量b=（向量PO+向量OA）·向量b=（向量PO·向量b）+（向量OA·向量b ）=0，∴PA⊥向量b。

2.已知三个平面OAB，OBC，OAC相交于一点O，∠AOB=∠BOC=∠COA=60度，求交线OA与平面OBC所成的角。

解：∵向量OA=（向量OB+向量AB），O是内心，又∵AB=BC=CA，∴OA与平面OBC所成的角是30°。

用途在做图中，做二面角的平面角在证明中，证明线线垂直在计算中，用归纳法归拢已知条件，便于计算口诀线射垂，线斜垂；线斜垂，线射垂。