邱关源《电路》第四版课后第一章答案
- 格式:doc
- 大小:1.02 MB
- 文档页数:22




电路第四版课后习题答案第一章:电路基础1. 确定电路中各元件的电压和电流。
- 根据基尔霍夫电压定律和电流定律,我们可以列出方程组来求解未知的电压和电流值。
2. 计算电路的等效电阻。
- 使用串联和并联电阻的计算公式,可以求出电路的等效电阻。
3. 应用欧姆定律解决实际问题。
- 根据欧姆定律 \( V = IR \),可以计算出电路中的电压或电流。
第二章:直流电路分析1. 使用节点电压法分析电路。
- 选择一个参考节点,然后对其他节点应用基尔霍夫电流定律,列出方程组并求解。
2. 使用网孔电流法分析电路。
- 选择电路中的网孔,对每个网孔应用基尔霍夫电压定律,列出方程组并求解。
3. 应用叠加定理解决复杂电路问题。
- 将复杂电路分解为简单的子电路,然后应用叠加定理计算总的电压或电流。
第三章:交流电路分析1. 计算交流电路的瞬时值、有效值和平均值。
- 根据交流信号的表达式,可以计算出不同参数。
2. 使用相量法分析交流电路。
- 将交流信号转换为复数形式,然后使用复数运算来简化电路分析。
3. 计算RLC串联电路的频率响应。
- 根据电路的阻抗,可以分析电路在不同频率下的响应。
第四章:半导体器件1. 分析二极管电路。
- 根据二极管的伏安特性,可以分析电路中的电流和电压。
2. 使用晶体管放大电路。
- 分析晶体管的共发射极、共基极和共集电极放大电路,并计算放大倍数。
3. 应用场效应管进行电路设计。
- 根据场效应管的特性,设计满足特定要求的电路。
第五章:数字逻辑电路1. 理解逻辑门的工作原理。
- 描述不同逻辑门(如与门、或门、非门等)的逻辑功能和电路实现。
2. 使用布尔代数简化逻辑表达式。
- 应用布尔代数的规则来简化复杂的逻辑表达式。
3. 设计组合逻辑电路。
- 根据给定的逻辑功能,设计出相应的组合逻辑电路。
第六章:模拟集成电路1. 分析运算放大器电路。
- 根据运算放大器的特性,分析电路的增益、输入和输出关系。
2. 设计滤波器电路。

习题一1、 说明图(a)、(b)中:u )(au )(b(1)u 、i 的参考方向是否关联? (2)ui 乘积表示什么功率?(3)如果在图(a )中u>0,i 〈0;图(b )中u 〉0,i>0,元件实际发出还是吸收功率? 解:(1)(a )图u 、i 参考方向关联(b ) 图u 、i 参考方向非关联; (2)(a)图u i 乘积表示吸收功率;(b )图u i 乘积表示发出功率;(3)(a)中u>0,i 〈0则0〈p 元件实际发出功率,图(b)中u>0,i 〉0,则0〉p 元件实际发出功率2、 试校核图中电路所得解答是否满足功率平衡。
60V 20解:0300560〉=⨯=W p A 实际发出功率060160〉=⨯=W P B 实际吸收功率0120260〉=⨯=W P C 实际吸收功率080240〉=⨯=W P D 实际吸收功率 040220〉=⨯=W P E 实际吸收功率 发吸=P P 故功率平衡3、 试求图中各电路的电压U ,并讨论其功率平衡。
)(aRI解:应用KCL 先计算电阻电流R I ,再根据欧姆定律计算电压,从而得出端电压U ,最后计算功率.(a)图A I R 862=+= V I U U R R 16822=⨯=⨯== 所以输入电路的功率为 W U P 322162=⨯=⨯= 电流源发出功率 W U P I 961666=⨯=⨯=电阻消耗功率 W I P R R 12882222=⨯=⨯=显然R I P P P =+,即输入电路的功率和电流源发出的功率都被电阻消耗了.(b)图A I R 426=-= V I U U R R 8422=⨯=⨯== 所以输入电路的功率为 W U P 16282-=⨯-=⨯-= 电流源发出功率 W U P I 48866=⨯=⨯=电阻消耗功率 W I P R R 3242222=⨯=⨯=显然R I P P P =+,即电流源发出的功率都被电阻消耗了32W ,还有16W 输入到了外电路。
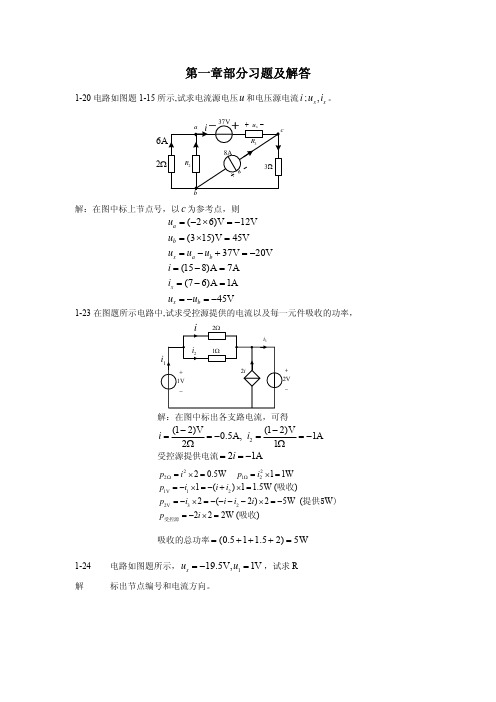
i = = 0.5A, i 2 = =1A 第一章部分习题及解答1-20 电路如图题 1-15 所示,试求电流源电压 u 和电压源电流 i ; u x , i x 。
i+ u2Rb解:在图中标上节点号,以 c 为参考点,则u a = ( 2 ⋅ 6)V = 12V u b = (3⋅15)V = 45V u x = u a u b + 37V = 20V i = (15 8)A = 7A i x = (7 6)A = 1A x b 1-23+解:在图中标出各支路电流,可得(1 2)V (1 2)V 2∧ 1∧受控源提供电流 = 2i = 1Ap 2∧ = i 2 ⋅ 2 = 0.5Wp 1∧ = i 22 ⋅1 = 1Wp 1V = i 1 ⋅1 = (i + i 2 ) ⋅1 = 1.5W (吸收)p 2V = i 3 ⋅ 2 = ( i i 2 2i ) ⋅ 2 = 5W (提供5W ) p 受控源 = 2i ⋅ 2 = 2W (吸收)吸收的总功率 = (0.5 + 1 + 1.5 + 2) = 5W1-24 解电路如图题所示,u s = 19.5V, u 1 = 1V ,试求R标出节点编号和电流方向。
ai +3∧u∧b+ui2∧4∧i+10ucRiiei1 =u11= 1A, u bc = u1 10u1 = 9Vu bc2u ab = i s ⋅ 3 = 10.5Vu ce = u cb + u ba + u s = (9 + 10.5 19.5) = 0V为确定R,需计算i4,u ce = u cd + u de = 0 ® u de = u cd = 10u1 = 10V故1-33 试用支路电流法求解图题所示电路中的支路电流i1, i2 , i3。
a 1∧ci+6Vb解求解三个未知量需要三个独立方程。
由KCL可得其中之一,即i1 + i2 + i3 = 5对不含电流源的两个网孔,列写KVL方程,得网孔badb网孔bdacb2i1 3i2 + 8 = 08 + 3i2 i3 + 6 = 0i 2 = = 4.5A, i s = i 1 + i 2 = 3.5Ai 3 = = 2.5A, i 4 = i s i 3 = ( 3.5 + 2.5)A = 1A整理得: ♦ 2i 1 2 = 8+ 3i ® ♦i 2 = 2A♥♥♣i 1 + i 2 + i 3 = 5 ♣i 1 = 1A ♠ ♠♠3i 2 i 3 = 2 ♠i 3 = 4A♦ i1 + 8i2 3i3 = 9 ® ♦i2 = 1A♥i3 = 1A® ♦♠(R +R)i M2 R1i M 1 R2i M 3 =u ♠♠♠==0♣i M 1 = 24 u® ♦(3 + 4)i M 3 = u ® ♦ ♥i M 3 i M 1 = 8♥ 第二章部分习题及解答2-1试用网孔电流法求图题所示电路中的电流i和电压u ab。
第一章电路模型和电路定律电路理论主要研究电路中发生的电磁现象,用电流i、电压u和功率p等物理量来描述其中的过程。
因为电路是由电路元件构成的,因而整个电路的表现如何既要看元件的联接方式,又要看每个元件的特性,这就决定了电路中各支路电流、电压要受到两种基本规律的约束,即:(1)电路元件性质的约束。
也称电路元件的伏安关系(VCR),它仅与元件性质有关,与元件在电路中的联接方式无关。
(2)电路联接方式的约束(亦称拓扑约束)。
这种约束关系则与构成电路的元件性质无关。
基尔霍夫电流定律(KCL)和基尔霍夫电压定律(KVL)是概括这种约束关系的基本定律。
掌握电路的基本规律是分析电路的基础。
1-1说明图(a),(b)中,(1),u i的参考方向是否关联?(2)ui乘积表示什么功率?(3)如果在图(a)中0u i<>,元件实际发出还是吸收功>iu;图(b)中0,0,0<率?解:(1)当流过元件的电流的参考方向是从标示电压正极性的一端指向负极性的一端,即电流的参考方向与元件两端电压降落的方向一致,称电压和电流的参考方向关联。
所以(a)图中iu,的参考方向为非关联。
u,的参考方向是关联的;(b)图中i(2)当取元件的iu,参考方向为关联参考方向时,定义uip=为元件吸收的功率;当取元件的iu,参考方向为非关联时,定义uip=为元件发出的功率。
所以(a)图中的ui乘积表示元件吸收的功率;(b)图中的ui乘积表示元件发出的功率。
(3)在电压、电流参考方向关联的条件下,带入iu,数值,经计算,若0p,>=ui表示元件确实吸收了功率;若0p,表示元件吸收负功率,实际是发出功率。
(a)图<中,若0,0<>i u ,则0<=ui p ,表示元件实际发出功率。
在i u ,参考方向非关联的条件下,带入i u ,数值,经计算,若0>=ui p ,为正值,表示元件确实发出功率;若0<p ,为负值,表示元件发出负功率,实际是吸收功率。
所以(b )图中当0,0>>i u ,有0>=ui p ,表示元件实际发出功率。
1-2 若某元件端子上的电压和电流取关联参考方向,而170cos(100)u t V π=,7sin(100)i t A π=,求:(1)该元件吸收功率的最大值;(2)该元件发出功率的最大值。
解:()()()170cos(100)7sin(100)595sin(200)p t u t i t t t t W πππ==⨯=(1)当0)200sin(>t π时,0)(>t p ,元件吸收功率;当1)200sin(=t π时,元件吸收最大功率:max 595p W =(2)当0)200sin(<t π时,0)(<t p ,元件实际发出功率;当1)200sin(-=t π时,元件发出最大功率:max 595p W =1-3 试校核图中电路所得解答是否满足功率平衡。
(提示:求解电路以后,校核所得结果的方法之一是核对电路中所有元件的功率平衡,即元件发出的总功率应等于其他元件吸收的总功率)。
解:由题1-3图可知,元件A 的电压、电流为非关联参考方向,其余元件的电压电流均为关联参考方向。
所以各元件的功率分别为:6053000A p W =⨯=>,为发出功率601600B p W =⨯=>,为吸收功率60201200C p W =⨯=>,为吸收功率402800D p W =⨯=>,为吸收功率202400E p W =⨯=>,为吸收功率电路吸收的总功率601208040300B D C E p p p p p W =+++=+++=即,元件A 发出的总功率等于其余元件吸收的总功率,满足功率平衡。
注:以上三题的解答说明,在电路中设电压、电流参考方向是非常必要的。
在计算一段电路或一个元件的功率时,如果不设电流、电压的参考方向,就无法判断该段电路或元件是发出还是吸收功率。
此外还需指出:对一个完整的电路来说,它产生(或发出)的功率与吸收(或消耗)的功率总是相等的,这称为功率平衡。
功率平衡可以做为检验算得的电路中的电压、电流值是否正确的一个判据。
1-4 在指定的电压u 和电流i 参考方向下,写出各元件u 和i 的约束方程(元件的组成关系)。
解:(a )图为线性电阻,其电压、电流关系满足欧姆定律。
需要明确的是:(1)欧姆定律只适用于线性电阻;(2)如果电阻R 上的电流、电压参考方向非关联,欧姆定律公式中应冠以负号,即)()(t Ri t u -=。
由以上两点得(a )图电阻元件u 和i 的约束方程为i i R u 31010⨯-=-=欧姆定律表明,在参数值不等于零、不等于无限大的电阻上,电流与电压是同时存在、同时消失的。
即电阻是无记忆元件,也称即时元件。
(b )图为线性电感元件,其电压、电流关系的微分形式为:dtt di L t u )()(=。
如果电压、电流参考方向为非关联,上式中应冠以负号,所以(b )图电感元件u 和i 的约束方程为 dtdi u 31020-⨯-= 电感元件的电压、电流微分关系表明:(1)任何时刻,其电压与该时刻的电流变化率成正比,显然直流时,电感电压为零,电感相当于短路。
因此,电感是一个动态元件。
(2)当电感上的电压为有限值时,电感中的电流不能跃变,应是时间的连续函数。
(c )图为线性电容元件,其电压、电流关系的微分形式为:dt t du Ct i )()(=。
如果电压、电流的参考方向为非关联,上式中应冠以负号,即dt t du Ct i )()(-=。
所以(b )图电容元件u 和i 的约束方程为 dtdu dt du i 56101010--=⨯= 电容元件的电压。
电流微分关系表明:(1)任何时刻,通过电容的电流与该时刻其上的电压变化率成正比,即电容是一个动态元件。
显然直流时,电容电流为零,电容相当于开路。
(2)当电容上的电流为有限值时,电容上的电压不能跃变,必须是时间的连续函数。
(d )图是理想电压源。
理想电压源的特点为:(1)其端电压与流经它的电流方向、大小无关。
(2)其电压由它自身决定,与所接外电路无关,而流经它的电流由它及外电路所共同决定。
由以上特点得(d )图的约束方程为V u 5-=(e )图是理想电流源。
理想电流源的特点为:(1)其发出的电流)(t i 与其两端电压大小、方向无关。
(2)其输出电流由它自身决定,与所接外电路无关,而它两端电压由它输出的电流和外部电路共同决定。
由以上特点得(e )图的约束方程为A i 2=注:以上五个理想元件是电路分析中常遇到的元件。
元件电压、电流的约束方程,反映了每一元件的特性和确定的电磁性质。
不论元件接入怎样的电路,其特性是不变的,即它的,u i 约束方程是不变的。
因而深刻地理解和掌握这些方程,就是掌握元件的特性,对电路分析是非常重要的。
1-5 图(a )电容中电流i 的波形如图(b )所示现已知0)0(=C u ,试求s t 1=时,s t 2=和s t 4=时的电容电压。
解:已知电容的电流)(t i 求电压)(t u 时,有 0000111()()()()()t t t t t u t i d i d u t i d C C Cξξξξξξ-∞=+=+⎰⎰⎰ 式中)(0t u 为电容电压的初始值。
本题中电容电流)(t i 的函数表示式为⎪⎩⎪⎨⎧>-<≤≤=21020500)(t t t t t i根据,u i 积分关系,有1t s =时 101(1)(0)()C C u u i t dt C=+⎰ V t tdt 25.1)25(21521010210=⨯=+=⎰ s t 2=时 ⎰+=20)(1)0()2(dt t i C u u C C V t tdt 5)25(21521020220=⨯=+=⎰ 4t s =时 ⎰+=42)(1)2()4(dt t i C u u C C V t tdt 5)10(215102154242-=-⨯+=-+=⎰注:电路元件,u i 关系的积分形式表明,t 时刻的电压与t 时刻以前的电流的“全部历史”有关,即电容有“记忆”电流的作用,故电容是有记忆的元件。
因此在计算电容电压时,要关注它的初始值()0c u t ,()0c u t 反映了电容在初始时刻的储能状况,也称为初始状态。
电感元件也具有类似的性质,参见1-6题。
1-6 图(a )中H L 4=,且i ,电压的波形如图(b )所示。
试求当 s t 1=,s t 2=,s t 3=和s t 4=时的电感电流i 。
解:电感元件i u ,关系的积分形式为 001()()()t t i t i t u d L ξξ=+⎰ 上式表明,电感元件有“记忆”电压的作用,也属于记忆元件。
式中)(o t i 为电感电流的初始值,反映电感在初始时刻的储能状况。
本题中电感电压的函数表示式为⎪⎪⎪⎩⎪⎪⎪⎨⎧<<<-<<<<<=t t t t t t t u 40434010320201000)( 应用i u ,积分关系式,有s t 1=时,101(1)(0)()i i u t dt L=+⎰ A t dt 5.2)10(41104101010=⨯=+=⎰ s t 2=时,⎰+=21)(1)1()2(dt t u L i i21112.510 2.5(10)544dt t A =+=+⨯=s t 3=时,⎰+=32)(1)2()3(dt t u L i i A dt 5041532=+=⎰ s t 4=时,⎰+=43)(1)3()4(dt t u L i i 4315(1040) 3.754t dt A =+-=⎰1-7 若已知显像管行偏转线圈中的周期性行扫描电流如图所示,现已知线圈电感为H 01.0,电阻略而不计,试求电感线圈所加电压的波形。
解:电流)(t i 的函数表达式为 ⎪⎩⎪⎨⎧<<-⨯⨯<<⨯=-st t s t t t i μ6460)1064(103μ60010602.1)(656根据电感元件i u ,的微分关系,得电压的函数表达式为 ⎩⎨⎧<<⨯-<<⨯==st s t dt t di t u μ6460103μ600102)(01.0)(32 )(t u 的波形如题解1-7图,说明电感的电压可以是时间的间断函数。
1-8 F μ2电容上所加电压的波形如图所示。
求:(1)电容电流i ;(2)电容电荷q ;(3)电容吸收的功率p 。
解:(1)电压)(t u 的函数表达式为⎪⎪⎩⎪⎪⎨⎧≤≤≤-≤≤≤=m s t m s t t m s t t t t u 4042104201000)(33根据电容元件i u ,的微分关系,得电流)(t i 的函数表达式为:=⨯=-dt t du t i )(102)(6⎪⎪⎩⎪⎪⎨⎧<<<⨯-<<⨯<--ms t ms t ms t t 4042102201020033(2)因为u q C =,所以有 ==)()(t Cu t q ⎪⎪⎩⎪⎪⎨⎧≤≤≤-⨯≤≤⨯≤--m s t m st t m s t t t 4042)104(1022010200363(3)在电压电流参考方向关联时,电容元件吸收的功率为 ==)()()(t i t u t p ⎪⎪⎩⎪⎪⎨⎧≤<<-⨯-<≤≤-m s t m s t t m s t t t 4042)104(1022020033)(),(),(t p t q t i 波形如题解1-8图所示。