含两个绝对值的线性目标函数

处理带有绝对值约束的问题的策略和技巧在数值分析中，处理带有绝对值约束的问题通常需要一些特殊的技术和策略。

绝对值的存在使得问题可能不再是平滑的（即不可导），这增加了求解的复杂性。

以下是一些处理这类问题的方法：1. 转换为线性规划或二次规划问题在某些情况下，如果目标函数和约束都是线性的（或可以近似为线性），并且绝对值出现在约束中，那么可以尝试通过引入额外的变量和约束来将问题转换为标准的线性规划（LP）或二次规划（QP）问题。

例如，考虑以下带有绝对值约束的优化问题：minimize f(x)subject to |g(x)|≤ℎ(x)可以转换为：引入新变量y，使得y=|g(x)|，则原问题变为：minimize f(x)subject to y≥g(x),y≥−g(x),y≤ℎ(x)注意，这里的y是一个额外的决策变量，并且我们需要同时最小化f(x)和确保新约束的满足。

2. 使用罚函数法罚函数法是一种处理约束优化问题的常用技术，也可以用于处理带有绝对值约束的问题。

基本思想是将约束条件通过罚项加入到目标函数中，从而形成一个无约束的优化问题。

对于绝对值约束|g(x)|≤ℎ(x)，可以定义一个罚函数p(x)，例如：p(x)=max(0,|g(x)|−ℎ(x))2然后将原问题转换为：其中λ>0是一个罚参数，用于控制罚项对目标函数的影响。

随着求解过程的进行，可以逐渐增大λ以使解更接近满足原始约束。

3. 光滑化技术对于不可导的绝对值项，可以使用光滑化技术来近似它，从而得到一个可导的目标函数或约束条件。

一种常用的光滑化近似是：|x|≈√x2+ϵ其中ϵ>0是一个小的正数，用于控制近似的平滑度。

这种近似在x=0处是平滑的，并且随着ϵ趋于零，近似越来越接近真实的绝对值函数。

4. 松弛和逼近方法在某些情况下，如果直接处理绝对值约束过于复杂，可以考虑使用松弛或逼近方法来简化问题。

例如，可以将绝对值约束松弛为一个更宽松的约束（如线性约束），或者使用分段线性函数来逼近绝对值函数。

《管理运筹学》期中复习题答案标准化文件发布号：（9312-EUATWW-MWUB-WUNN-INNUL-DQQTY-《管理运筹学》期中测试题 第一部分 线性规划 一、填空题 1．线性规划问题是求一个 目标函数 在一组 约束条件 下的最值问题。

2．图解法适用于含有 两个 _ 变量的线性规划问题。

3．线性规划问题的可行解是指满足 所有约束条件_ 的解。

4．在线性规划问题的基本解中，所有的非基变量等于 零 。

5．在线性规划问题中，基本可行解的非零分量所对应的列向量线性 无 关 6．若线性规划问题有最优解，则最优解一定可以在可行域的 顶点_ 达到。

7．若线性规划问题有可行解，则 一定 _ 有基本可行解。

8．如果线性规划问题存在目标函数为有限值的最优解，求解时只需在其 可行解 的集合中进行搜索即可得到最优解。

9．满足 非负 _ 条件的基本解称为基本可行解。

10．在将线性规划问题的一般形式转化为标准形式时，引入的松驰变量在目标函数中的系数为 正 。

11．将线性规划模型化成标准形式时，“≤”的约束条件要在不等式左_端加入 松弛 _ 变量。

12．线性规划模型包括 决策变量 、目标函数 、约束条件 三个要素。

13．线性规划问题可分为目标函数求 最大 _ 值和 最小 _值两类。

14．线性规划问题的标准形式中，约束条件取 等 _ 式，目标函数求 最大 _值，而所有决策变量必须 非负 。

15．线性规划问题的基本可行解与基本解的关系是 基本可行解一定是基本解，反之不然16．在用图解法求解线性规划问题时，如果取得最值的等值线与可行域的一段边界重合，则 _ 最优解不唯一 。

17．求解线性规划问题可能的结果有 唯一最优解，无穷多最优解，无界解，无可行解 。

18.如果某个约束条件是“ ”情形，若化为标准形式，需要引入一个 剩余 _ 变量。

19.如果某个变量X j 为自由变量，则应引进两个非负变量X j ′ , X j 〞, 同时令X j ＝ X j ′ - X j 〞 j 。

多个绝对值相加求最小值的方法标题：如何求多个绝对值相加的最小值？在日常生活或数学问题中，我们经常会遇到需要求多个绝对值相加的最小值的情况。

当我们需要确定一组数中距离零点最近的数时，或者需要在一组数中找到和最接近某个特定值的数时。

本文将介绍一些方法和技巧，帮助你轻松求解多个绝对值相加的最小值。

1. 定义问题让我们从最基本的开始，明确问题的定义。

我们要求解的是如何求多个数的绝对值相加的最小值。

具体来说，就是给定n个数a1, a2, ..., an，我们要找到一组数x1, x2, ..., xn，使得表达式|x1-a1| + |x2-a2| + ... + |xn-an|的值最小。

这个问题其实可以抽象为一个优化问题，在一定约束条件下找到使目标函数最小化的解。

2. 穷举法一种直观的方法是利用穷举法，列举出所有可能的情况，然后逐一计算出最小值。

但是当n较大时，这个方法的时间复杂度会呈指数级增长，不太适用于大规模问题求解。

3. 贪心算法贪心算法是一种高效的方法，它通常适用于求解最优化问题。

在本问题中，我们可以利用贪心算法来求解多个绝对值相加的最小值。

具体来说，我们可以按照一定规则依次确定每个xi，使得每一步都是对整体最优的选择。

对于求解两个数a和b的绝对值相加的最小值，我们可以根据a和b的大小关系来确定x，使得|x-a|+|x-b|的值最小。

4. 动态规划动态规划是另一种常用的优化算法，它可以帮助我们高效地求解多个数的绝对值相加的最小值。

在本问题中，我们可以借助动态规划的思想，利用子问题的最优解来求解整体问题的最优解。

具体来说，我们可以定义一个二维数组dp，其中dp[i][j]表示前i个数中选取j个数，使得其绝对值相加的和最小。

然后根据动态规划的状态转移方程逐步求解dp数组的值，最终得到最小值。

5. 个人观点和总结在实际应用中，我们可以根据具体问题的特点选择合适的方法来求解多个绝对值相加的最小值。

贪心算法适用于一些特殊情况，而动态规划则更适用于一般情况下的求解。

高中数学 复数 排列组合二次项定理 线性规划素材1．虚数单位数i 满足21i =-，且规定i 可以与实数在一起按实数的运算律进行四那么运算．i 叫做虚数单位．2．形如()a bi a b +∈R 、的数叫做复数．复数全体组成的集合叫做复数集，通常用字母C 表示．实数集R 是复数集C 的真子集，即R C ．定义了复数的加法和乘法运算后的复数集叫做复数系．3．单个复数常常用字母z 表示，即()z a bi a b =+∈R 、．把复数z 表示成a bi +时，叫做复数的代数形式，并规定00i =，0bi bi +=．a 与b 分别叫做复数z a bi =+的实部与虚部．复数z 的实部记作Re z ，复数z 的虚部记作Im z ．当0b =时，复数z a bi a =+=是实数；当0b ≠时，z 叫做虚数；当0a =且0b ≠时，z a bi bi =+=叫做纯虚数；当且仅当0a b ==时，z 是实数0．4．复数相等：两个复数相等，当且仅当它们的实部和虚部分别相等．5．共轭复数：两个复数共轭，当且仅当它们的实部相等，虚部互为相反数，z 的共轭复数记为z ．6．建立了直角坐标系用来表示复数的平面叫做复平面，在复平面内，x 轴叫做实轴，y 轴叫做虚轴．复数z a bi =+所对应的点(),Z a b 到坐标原点的距离叫做复数z 的模〔或绝对值〕，记作z ．z a bi =+7．复数集C 中的元素与复平面上以原点为起始点的向量是一一对应的〔实数0与零向量对应〕，可以把复数z a bi =+看作点(),Z a b 或看作向量OZ ． 8．共轭复数与复数的模的性质：〔1〕2Re z z z +=；〔2〕2Im z z i z -=；〔3〕z z z ∈⇔=R ；〔4〕z z =；〔5〕2z z z ⋅=． 9．四那么运算法那么：加减法：()()()()a bi c di a c b d i +±+=±+± 乘除法：()()()()a bi c di ac bd ad bc i ++=-++2222a bi ac bd bc adi c di c d c d ++-=++++〔以上a b c d 、、、均为实数〕 运算律：1221z z z z +=+，()()123123z z z z z z ++=++，1221z z z z ⋅=⋅，()()123123z z z z z z ⋅⋅=⋅⋅，()1231213z z z z z z z +=+10．共轭复数运算性质：设1212z z z z ±=±，1212z z z z ⋅=⋅，2zz z =，1122z z z z ⎛⎫= ⎪⎝⎭，可推广到n 个复数：1212n n z z z z z z +++=+++，1212n n z z z z z z ⋅⋅⋅=⋅⋅⋅，()nnz z =11．复数模的运算性质：11121222,,z z z z z z z z ==nn z z = 12．实系数一元二次方程()20,,0ax bx c a b c a ++=∈≠R 且在复数集中恒有解．当判别式240b ac ∆=-≥时，方程有实数解1,22b x a-=；当判别式240b ac∆=-<时，方程有一对共轭虚根2b x a =-．1．四个命题：〔1〕,a b ∈R ，那么a b +i 是虚数；〔2〕b ∈R ，那么b i 是纯虚数； 〔3〕z a =不是虚数；〔4〕14z <<，那么z 不是虚数．其中正确命题的个数是〔〕(A)0个 (B)1个 (C)2个 (D)3个2．以下结论中正确的选项是〔〕〔A 〕假设0,0,21222121===+∈z z z z C z z 则且〔B 〕假设,z a =那么 z a =± 〔C 〕22z z =〔D 〕()()1112--=-z z z3．如果α、C ∈β，假设022=+βα，那么 ( )(A) 0==βα (B) βα= (C)0≠=βα (D) αβ=±i排列、组合与概率、统计 1．加法原理和乘法原理加法原理：如果完成一件事有n 类办法，第1类办法中有1m 种不同的方法，第2类办法有2m 种不同的方法，……，在第n 类办法有n m 种不同的方法， 那么完成这件事共有n m m m N +++= 21种不同的方法．乘法原理：如果完成一件事需要n 个步骤，第1步有1m 种不同的方法，第2步有2m 种不同的方法，……，第n 步有n m 种不同的方法， 那么完成这件事共有n m m m N 21=种不同的方法． 2．排列与组合〔1〕从n 个不同的元素中取出)(n m m ≤个元素，按照一定的次序排成一列，叫做从n 个不同的元素中取出m 个元素的一个排列．〔2〕从n 个不同的元素中取出)(n m m ≤个元素的所有排列的个数，叫做从n 个不同的元素中取出m 个元素的排列数，记作mn P ．〔3〕从n 个不同的元素中取出)(n m m ≤个元素组成一组，叫做从n 个不同的元素中取出m 个元素的一个组合．〔4〕从n 个不同的元素中取出)(n m m ≤个元素的所有组合的个数，叫做从n 个不同的元素中取出m 个元素的组合数，记作m n C ． 3．主要公式排列数公式：)!(!)1()2()1(m n n m n n n n P mn -=+-⋅⋅-⋅-⋅= )(n m ≤；!321n n P n n =⨯⨯⨯⨯= ；1!0=．组合数公式：)!(!!321)1()2()1(m n m n m m n n n n C mn -=⋅⋅⋅⋅+-⋅⋅-⋅-⋅=)(n m ≤．组合数性质：〔1〕m n n m n C C -=)(n m ≤；〔2〕11-++=r n r n r n C C C )1(n r ≤≤．性质一的实际模型：六人中选两人和六人中选四人的情况是一样的。

取绝对值的函数人们在数学中经常会遇到一些需要取绝对值的形式，这个过程被称为取绝对值函数，简称abs。

取绝对值的函数是指从一个数值中把它的相反数去掉，以获得一个绝对值，或把一个实数映射到一个非负实数上。

绝对值表示某个数值的总量，忽略它的正负号，例如abs(-4)等于4.一般来说，取绝对值的函数可以分为两类：离散取绝对值函数和连续取绝对值函数。

离散取绝对值函数由一系列数字组成，其中每一个数字都有一个对应的绝对值，比如abs(-2)等于2。

连续取绝对值函数则是由一段连续的函数定义的，用来把实数映射到非负实数上，比如abs(3.14)等于3.14。

取绝对值函数多用于线性代数、凸分析、机器学习等领域，也可用于构建多种凸优化问题，以实现最佳结果。

凸优化问题通常都有凸取绝对值函数为一个约束，其中凸取绝对值函数表示f（x） = |x| = max{x, -x}，其中x为实数。

绝对值函数有各种实现方式，比如C语言中可以使用fabs（x）函数来实现取绝对值，而Python语言中可以使用abs（x）函数来实现取绝对值。

在Python中，取绝对值的函数可以用作内置函数实现，也可以用作自定义函数实现。

例如，在Python中可以使用以下代码实现取绝对值函数：def myabs(x):if x >= 0:return xelse:return -x## 使用print(myabs(-3)) #回3其中myabs()函数首先判断参数x是否大于等于0，如果x大于等于0，则直接返回x；如果x小于0，则返回-x，从而实现取x的绝对值。

此外，取绝对值函数还可以用于求解多变量函数的极值问题。

多变量函数的极值问题指的是，给定一组变量，求这组变量在目标函数中的极值。

求解这种问题的方法之一是使用取绝对值函数，将函数转换为更易于求解的函数。

例如，可以将原函数f（x）=x2 + 5转换为取绝对值函数min {|x2 + 5|, x}，以求解其最小值。

第四章 多目标规划模型多目标决策问题的理论基础之一是向量优化问题，也称多目标优化问题。

这类问题，从方法论的角度看，它是一个目标函数中具有向量值的数学规划问题；从决策论角度看，它又是决策规则中含有各个目标极值的决策问题。

因此，多目标决策问题属于向量优化问题。

向量优化问题的解与标量优化问题的解是不同的。

标量优化问题对任何两个函数的解，只要比较它们的两个函数值的大小，总可以从中找出一个最优解，且能排出它们的顺序；而多目标优化问题的解都是非劣解，且不是唯一的，究竟谁优谁劣，很难直接作出判断。

非劣解的概念是由经济学家pareto 于1896年提出的。

但是发展为向量优化问题的生成非劣解技术，还是在1951年Kuhn-Tucker 非劣性条件发表以后的事。

由于向量优化问题是在标量优化问题的基础上发展起来的，只要通过适当的途径将向量优化问题转化为标量优化问题，就可以利用求解标量优化问题的现有方法，求解具有一定特征的向量优化问题。

本章主要介绍有关向量优化问题的基本理论，如非劣解概念，特征非裂解的标量优化解法及非劣性的充要条件。

其中提到的许多概念和术语，在本书的后继章节中都是很有用的。

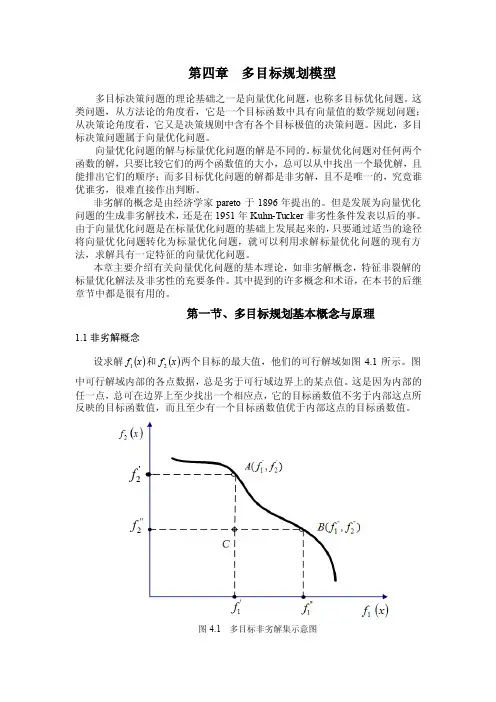
第一节、多目标规划基本概念与原理1.1非劣解概念设求解()x f 1和()x f 2两个目标的最大值，他们的可行解域如图4.1所示。

图中可行解域内部的各点数据，总是劣于可行域边界上的某点值。

这是因为内部的任一点，总可在边界上至少找出一个相应点，它的目标函数值不劣于内部这点所反映的目标函数值，而且至少有一个目标函数值优于内部这点的目标函数值。

图4.1 多目标非劣解集示意图例如，图中的C 点就劣于A 点和B 点之间任一点所反映的目标函数值。

所以，在优选中类似C 点的一些点可以舍去，并将这些可以舍去的解称为劣解。

但是可行域边界上各点所代表的解，就不能直接判断它们的优劣（如A 点、B 点就是这样）。

因为这些点中任一个与其他任一个相比较，总会发现一个目标函数值比其他另一个函数值优越，但又不是两个目标函数值都优越，否则其中的一个作为劣解而舍去。

含绝对值的解与不等式求解绝对值函数在数学中具有重要的应用价值，尤其是在解方程和不等式问题上。

本文旨在探讨含绝对值的解以及如何求解不等式。

一、含绝对值的方程解法对于形如|a|x + b| = c的绝对值方程，需要分别讨论x的取值范围，并找出满足条件的解。

下面将介绍两种常用解法。

1.1 分类讨论法当a为正数时，绝对值函数为增函数，因此可以将方程化简为两个线性方程来求解。

考虑到x的取值情况，可以得到以下两个方程：a*x + b = c x >= 0；-a*x - b = c x < 0。

解出以上两个方程可得到两组解，分别代入原方程中验证，得到最终的解集。

当a为负数时，绝对值函数为减函数。

同样可以将方程化简为两个线性方程来求解，但此时每个方程对应的x的取值范围相反：-a*x + b = c x >= 0；a*x - b = c x < 0。

解出以上两个方程可得到两组解，分别代入原方程中验证，得到最终的解集。

1.2 代数法求解对于一元绝对值方程|a|x + b| = c，可以将方程分解为两个方程：a*x + b = c 或 a*x + b = -c。

解出以上两个方程的解集分别为S1和S2，则原方程的解集为S1 ∪ S2。

二、含绝对值的不等式解法对于形如|a|x + b| < c的绝对值不等式，同样需要根据a的正负情况进行分类讨论。

2.1 分类讨论法当a为正数时，绝对值函数为增函数，可以将不等式化简为两个线性不等式：a*x + b < c x >= 0；-a*x - b < c x < 0。

解出以上两个不等式可得到两个解集，分别为S1和S2。

由于题目要求不等式的解集，因此需要求得S1 ∪ S2的交集。

当a为负数时，绝对值函数为减函数，将不等式化简为以下两个线性不等式：-a*x + b < c x >= 0；a*x - b < c x < 0。

不等式解法1、不等式的基本性质（8条）2、一元二次不等式的解法（注意讨论） 求一元二次不等式20(0)ax bx c ++><或2(0,40)a b ac ≠∆=−>解集的步骤：一化：化二次项前的系数为正数. 二判：判断对应方程的根.三求：求对应方程的根.四画：画出对应函数的图象.五解集：根据图象写出不等式的解集.规律：当二次项系数为正时，小于取中间，大于取两边.3、高次不等式的解法：穿根法.分解因式，把根标在数轴上，从右上方依次往下穿（奇穿偶切），结合原式不等号的方向，写出不等式的解集.4、分式不等式的解法：先移项通分标准化，则()0()()0()()()0()0()0()f x f x g x g x f x g x f x g x g x >⇔⋅>⋅≥ ≥⇔ ≠ （<≤“或”时同理）规律：把分式不等式等价转化为整式不等式求解. 5、含绝对值不等式的解法： ⑴定义法：(0).(0)a a a a a ≥ = −<⑵平方法：22()()()().f x g x f x g x ≤⇔≤ ⑶同解变形法，其同解定理有： ①(0);x a a x a a ≤⇔−≤≤≥ ②(0);x a x a x a a ≥⇔≥≤−≥或 ③()()()()()(()0)f xg x g x f x g x g x ≤⇔−≤≤≥④()()()()()()(()0)f x g x f x g x f x g x g x ≥⇔≥≤−≥或 规律：关键是去掉绝对值的符号.6、含有两个（或两个以上）绝对值的不等式的解法：规律：找零点、划区间、分段讨论去绝对值、每段中取交集，最后取各段的并集.7、无理不等式的解法：转化为有理不等式求解2()0(0)()f x a a f x a ≥ >>⇔ >2()0(0)()f x a a f x a≥ <>⇔ <⑶2()0()0()()0()0()[()]f x f x g x g x g x f x g x > ≥>⇔≥<>或2()0()()0()[()]f x g x g x f x g x ≥<⇔> <()0()0()()f x g x f x g x ≥>⇔≥ >规律：把无理不等式等价转化为有理不等式，诀窍在于从“小”的一边分析求解. 8、指数不等式的解法：⑴当1a >时,()()()()f x g x a a f x g x >⇔> ⑵当01a <<时, ()()()()f x g x aa f x g x >⇔<规律：根据指数函数的性质转化.9、对数不等式的解法 ⑴当1a >时,()0log ()log ()()0()()a a f x f x g x g x f x g x >>⇔> >⑵当01a <<时,()0log ()log ()()0.()()a a f x f x g x g x f x g x >>⇔> <规律：根据对数函数的性质转化.10、含参数的不等式的解法解形如20ax bx c ++>且含参数的不等式时，要对参数进行分类讨论，分类讨论的标准有： ⑴讨论a 与0的大小； ⑵讨论∆与0的大小； ⑶讨论两根的大小. 11、恒成立问题⑴不等式20ax bx c ++>的解集是全体实数（或恒成立）的条件是：①当0a =时 0,0;b c ⇒=>②当0a ≠时00.a > ⇒∆<⑵不等式20ax bx c ++<的解集是全体实数（或恒成立）的条件是：①当0a =时0,0;b c ⇒=<②当0a ≠时00.a < ⇒∆<⑶()f x a <恒成立max ();f x a ⇔<()f x a ≤恒成立max ();f x a ⇔≤⑷()f x a >恒成立min ();f x a ⇔>()f x a ≥恒成立min ().f x a ⇔≥13、线性规划问题目标函数、线性目标函数、可行解、可行域不等式的证明1、几个重要不等式①()222a b ab a b R +≥∈，,（当且仅当a b =时取""=号）. 变形公式：22.2a b ab +≤②（基本不等式）2a b+≥ ()a b R +∈，,（当且仅当a b =时取到等号）.变形公式：a b +≥ 2.2a b ab +≤用基本不等式求最值时（积定和最小，和定积最大），要注意满足三个条件“一正、二定、三相等”.③（三个正数的算术—几何平均不等式）3a b c ++≥()a b c R +∈、、（当且仅当a b c ==时取到等号）.④()222a b c ab bc ca a b R ++≥++∈， （当且仅当a b c ==时取到等号）. ⑤3333(0,0,0)a b c abc a b c ++≥>>> （当且仅当a b c ==时取到等号）.⑥0,2b aab a b >+≥若则（当仅当a=b 时取等号） 0,2b aab a b<+≤−若则（当仅当a=b 时取等号）⑦ba nb n a m a m b a b <++<<++<1 其中(000)a b m n >>>>，，规律：小于1同加则变大，大于1同加则变小. ⑧220;a x a x a x a x a >>⇔>⇔<−>当时，或22.x a x a a x a <⇔<⇔−<<⑨绝对值三角不等式.a b a b a b −≤±≤+2、几个著名不等式①平均不等式：1122a ba b−−+≤≤≤+()a b R+∈，,（当且仅当a b=时取""=号）.（即调和平均≤几何平均≤算术平均≤平方平均）.变形公式：222;22a b a bab++≤≤222().2a ba b++≥②幂平均不等式：222212121...(...).n na a a a a an+++≥+++③二维形式的三角不等式：≥1122(,,,).x y x y R∈④二维形式的柯西不等式：22222()()()(,,,).a b c d ac bd a b c d R++≥+∈当且仅当ad bc=时，等号成立.⑤三维形式的柯西不等式：2222222123123112233()()().a a ab b b a b a b a b++++≥++⑥一般形式的柯西不等式：2222221212(...)(...)n na a ab b b++++++21122(...).n na b a b a b≥+++⑦向量形式的柯西不等式（略）设,αβu r u r是两个向量，则,αβαβ⋅≤u r u r u r u r当且仅当βu r是零向量，或存在实数k，使kαβ=u r u r时，等号成立.⑧排序不等式（排序原理）：设1212...,...n na a ab b b≤≤≤≤≤≤为两组实数.12,,...,nc c c是12,,...,nb b b的任一排列，则12111122......n n n n na b a b a b a c a c a c−+++≤+++1122....n na b a b a b≤+++（反序和≤乱序和≤顺序和）当且仅当12...na a a===或12...nb b b===时，反序和等于顺序和.⑨琴生不等式:（特例:凸函数、凹函数）若定义在某区间上的函数()f x,对于定义域中任意两点1212,(),x x x x≠有12121212()()()()()().2222x x f x f x x x f x f xf f++++≤≥或则称f(x)为凸（或凹）函数.3、不等式证明的几种常用方法（略）常用方法有：比较法、分析法综合法、；比较法：作差比较法、作商比较法分析法：从结论出发分析不等式成立的充分条件，即欲证什么，只需证什么。

第二章目标函数的基本性质及数学分析2.1 目标函数的等值面（线）对于简单的问题，可用等值线或等值面来描述函数的变化趋势，还可以直观地给出极值点的位置。

1）目标函数的等值面，其数学表达式为f(x)=c。

在这种线或面上所有点的函数值均相等，因此，这种线或面就称为函数的等值线或等值面。

当c取一系列不同的常数值时，可以得到一组形态相似的等值线或等值面，称为函数的等值线簇或等值面簇。

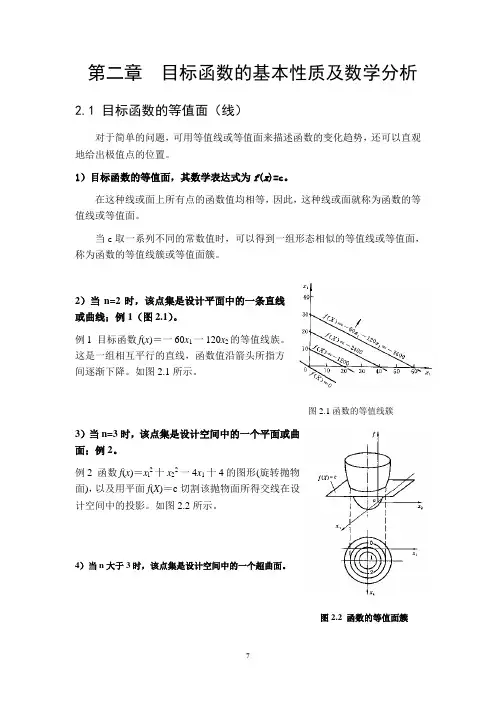
2）当n=2时，该点集是设计平面中的一条直线或曲线；例1（图2.1）。

例1 目标函数f(x)＝一60x1一120x2的等值线族。

这是一组相互平行的直线，函数值沿箭头所指方间逐渐下降。

如图2.1所示。

图2.1函数的等值线簇3）当n=3时，该点集是设计空间中的一个平面或曲面；例2。

例2 函数f(x)＝x l2十x22一4x1十4的图形(旋转抛物面)，以及用平面f(X)＝c切割该抛物面所得交线在设计空间中的投影。

如图2.2所示。

4）当n大于3时，该点集是设计空间中的一个超曲面。

图2.2 函数的等值面簇2.2 目标函数的方向导数和梯度实例：一块长方形的金属板，四个顶点的坐标是(1,1)，(5,1)，(1,3)，(5,3)．在坐标原点处有一个火焰，它使金属板受热．假定板上任意一点处的温度与该点到原点的距离成反比．在(3,2)处有一个蚂蚁，问这只蚂蚁应沿什么方向爬行才能最快到达较凉快的地点？问题的实质：应沿由热变冷变化最骤烈的方向（即梯度方向）爬行．2.2.1方向导数的定义讨论函数),(y x f z =在一点P 沿某一方向的变化率问题．定理 如果函数),(y x f z =在点),(y x P 是可微分的，那末函数在该点沿任意方向L 的方向导数都存在，且有ϕϕsin cos yf x f l f ∂∂+∂∂=∂∂，其中ϕ为x 轴到方向L 的转角．例2.1 求函数 yxe z 2= 在点 )0 ,1(P 处沿从点 )0 ,1(P到点 )1 ,2(-Q 的方向的方向导数.解： 这里方向 l 即为}1 ,1{-=PQ , 故x 轴到方向 l 的转角4πϕ-=.=∂∂)0,1(xz 由 )0,1(2ye=1=∂∂)0,1(yz )0,1(22yxe =2故方向导数=∂∂lz )4sin(2)4cos(1ππ-⋅+-⋅= .22-=2.2.2梯度的定义函数在一点的梯度是这样一个向量, 它的方向与取得最大方向导数的方向一致, 而它的模为方向导数的最大值. 用u ∇定义2.4 以)(x f 的n 个偏导数为分量的向量称为)(x f 在x 处的梯度，记为Tn x x f x x f x x f x f ⎥⎦⎤⎢⎣⎡∂∂∂∂∂∂=∇)(,,)(,)()(21梯度也可以称为函数)(x f 关于向量x 的一阶导数．2.2.3、梯度与方向导数之间的关系(1) 若0)(0<∇P x f T ，则P 的方向是函数)(x f 在点0x 处的下降方向； (2) 若0)(0>∇P x f T ，则P 的方向是函数)(x f 在点0x 处的上升方向． 方向导数的正负决定了函数值的升降，而升降的快慢就由它的绝对值大小决定．绝对值越大，升降的速度就越快，即由此可得如下重要结论(如图2.1所示）： (1)梯度方向是函数值的最速上升方向； (2)函数在与其梯度正交的方向上变化率为零；(3)函数在与其梯度成锐角的方向上是上升的，而在与其梯度成钝角的方向上是下降的；(4)梯度反方向是函数值的最速下降方向．例2.2：求函数y x z y x u 2332222-+++=在点)2,1,1(、)0,21,23(-处的梯度，并问在哪些点处梯度为零？k z u j y u i x u z y x u ∂∂+∂∂+∂∂=∇),,( ,6)24()32(k z j y i x +-++=.1225)2,1,1(k j i u ++=∇ 0)0,21,23(=-∇u例2.3 试求目标函数1)(2221++=x x X f 在点TX ]30[0，=处的最速下降方向，并求沿这个方向移动一个单位长后新点的目标函数值．解 因为221122x x f x x f =∂∂=∂∂，，所以最速下降方向是⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-=∇-==6022)(3021021x x x x X f ．这个方向上的单位向量是⎥⎦⎤⎢⎣⎡-=∇-∇-=10)()(00X f X f e ．故新点是⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡=+=20103001e X X ，2.2.4小结1、方向导数的概念（注意方向导数与一般所说偏导数的区别） 2、梯度的概念（注意梯度是一个向量） 3、方向导数与梯度的关系 思考题：一、讨论函数22),(yx y x f z +==在)0,0(点处的偏导数是否存在？方向导数是否存在？ 答：xf x f xz x ∆-∆=∂∂→∆)0,0()0,(lim)0,0( .||limxx x ∆∆=→∆同理：)0,0(yz ∂∂yy y ∆∆=→∆||lim故两个偏导数均不存在.图2.1沿任意方向},,{z y x l =的方向导数, ρρ)0,0(),(lim)0,0(f y x f lz -∆∆=∂∂→ 1)()()()(lim22220=∆+∆∆+∆=→y x y x ρ故沿任意方向的方向导数均存在且相等.2.3 多元目标函数的泰勒表达式和海赛矩阵2.3.1 海赛（Hesse ）矩阵前面说过，梯度)(x f ∇是)(x f 关于x 的一阶导数，现在要问)(x f 关于x 的二阶导数是什么？定义 ： 如果)(x f 在点0x 处对于自变量x 的各分量的二阶偏导数ji x x x f ∂∂∂)(2（n j i ,,2,1, =）都存在，则称函数)(x f 在点0x 处二阶可导，并且称矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂=∇n n nn nn x x x f x x x f xx x f x x x f x x x f xx x f x x x f x x x f x x x f x f )()()()()()()()()()(02202102202220212021022102110202是)(x f 在点0x 处的Hesse 矩阵．在数学分析中已经知道，当)(x f 在点0x 处的所有二阶偏导数为连续时有．，，，，，n j i x x f x x f ij ji 2122=∂∂∂=∂∂∂因此，在这种情况下Hesse 矩阵是对称的． 例2.4 求目标函数23132221233241432)(x x x x x x x x x X f -+-++=的梯度和Hesse 矩阵． 解 因为，，，3123332122223213112464624x x x x x f x x x x f x x x x x f -+=∂∂+-=∂∂--=∂∂，所以 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-++---=∇3123321222321312464624)(x x x x x x x x x x x X f ．又因为22221213211213222212222331222212462f f f x x x x xx x x x f f f x x x x x x ∂∂∂=-=-=-∂∂∂∂∂∂===-∂∂∂，，，，，，所以⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=∇13213122122642412222212)(x xx x x x x x X f ．例2.5 设1R b R X R a nn∈∈∈，，，求线性函数bX a X f T+=)(在任意点X 处的梯度和Hesse 矩阵．解 设Tn Tn x x x X a a a a ][][2121，，，，，，， ==，则∑=+=ni iin bxa x x x f 121)(，，， ，，，，，，n i a x f i i21==∂∂ （2.2）∴aa a a X f Tn ==∇],,,[)(21 ．由式（2.2）进而知，，，，，，n j i x x fji 2102==∂∂∂∴O X f =∇)(2（n n ⨯阶零矩阵）．2.3.2 多元目标函数的泰勒表达式定理 1 （泰勒(Taylor)中值定理） 如果函数)(x f 在含有0x 的某个开区间(b a ,)内具有直到(1+n )阶的导数，则当任一),(b a x ∈，有++-''+-'+= 200000)(!2)())(()()(x x x f x x x f x f x f)()(!)(00)(x R x x n x fn nn +-, （3）其中 10)1()()!1()()(++-+=n n n x x n fx R ξ，对于n 维向量的xxxf x x xf xf x f Tk T Tk k ∆⋅∇∆+∆⋅∇+≈)(21)()()()(2)()(2.4 目标函数的极值条件2.4.1 无约束问题的极值条件1.必要条件：梯度等于0即： 0)(,,)(,)()(*21*=⎥⎦⎤⎢⎣⎡∂∂∂∂∂∂=∇Txn x x f x x f x x f x f 2.充分条件：海赛矩阵>0 正定，有极小值海赛矩阵<0 负定，有极大值2.4.2 有约束问题的极值条件（1）目标函数的凸性与凸函数研究目标函数的凸性是为了分清目标函数的极小值在什么情况是极大值什么情况是极小值。