普通圆柱蜗杆传动的基本参数及几何尺寸计算
- 格式:doc
- 大小:139.50 KB
- 文档页数:6


普通圆柱蜗杆传动的基本参数及几何尺寸计算1.基本参数:(1)模数m和压力角α:在中间平面中,为保证蜗杆蜗轮传动的正确啮合,蜗杆的轴向模数m a1和压力角αa1应分别相等于蜗轮的法面模数m t2和压力角αt2,即m a1=m t2=mαa1=αt2蜗杆轴向压力角与法向压力角的关系为:tgαa=tgαn/cosγ式中:γ-导程角。
(2)蜗杆的分度圆直径d1和直径系数q为了保证蜗杆与蜗轮的正确啮合,要用与蜗杆尺寸相同的蜗杆滚刀来加工蜗轮。
由于相同的模数,可以有许多不同的蜗杆直径,这样就造成要配备很多的蜗轮滚刀,以适应不同的蜗杆直径。
显然,这样很不经济。
为了减少蜗轮滚刀的个数和便于滚刀的标准化,就对每一标准的模数规定了一定数量的蜗杆分度圆直径d1,而把及分度圆直径和模数的比称为蜗杆直径系数q,即:q=d1/m常用的标准模数m和蜗杆分度圆直径d1及直径系数q,见匹配表。
(3)蜗杆头数z1和蜗轮齿数z2蜗杆头数可根据要求的传动比和效率来选择,一般取z1=1-10,推荐z1=1,2,4,6。
选择的原则是:当要求传动比较大,或要求传递大的转矩时,则z1取小值;要求传动自锁时取z1=1;要求具有高的传动效率,或高速传动时,则z1取较大值。
蜗轮齿数的多少,影响运转的平稳性,并受到两个限制:最少齿数应避免发生根切与干涉,理论上应使z2min≥17,但z2<26时,啮合区显著减小,影响平稳性,而在z2≥30时,则可始终保持有两对齿以上啮合,因之通常规定z2>28。
另一方面z2也不能过多,当z2>80时(对于动力传动),蜗轮直径将增大过多,在结构上相应就须增大蜗杆两支承点间的跨距,影响蜗杆轴的刚度和啮合精度;对一定直径的蜗轮,如z2取得过多,模数m就减小甚多,将影响轮齿的弯曲强度;故对于动力传动,常用的范围为z2≈28-70。
对于传递运动的传动,z2可达200、300,甚至可到1000。
z1和z2的推荐值见下表(4)导程角γ蜗杆的形成原理与螺旋相同,所以蜗杆轴向齿距p a与蜗杆导程p z的关系为p z=z1p a,由下图可知:tanγ=p z/πd1=z1p a/πd1=z1m/d1=z1/q导程角γ的范围为3.5°一33°。



普通圆柱蜗杆传动几何尺寸计算(轴交角90度,已知中心距)啮合中心距: A=95蜗杆轴向模数: m=5蜗杆头数: z1=1蜗杆分度圆直径: d1=40蜗轮齿数: z2=30蜗轮分度圆直径: d2=m*z2= 150蜗杆直径系数: q=d1/m= 8齿数比: u=z2/z1= 30蜗轮变位系数: x2=A/m-0.5*(q+z2)= 0蜗杆分度圆柱导程角: r=atan(z1/q)= 7.125016 法向模数: mn=m*cos(r)= 4.961389蜗杆轴向齿距: px1=pi*m= 15.707963蜗杆螺旋线导程: pz1=px1*m= 78.539816蜗杆轴向齿形角: angle=20蜗杆节圆直径: d'1=(q+2*x2)*m= 40蜗杆节圆柱导程角: r'=z1/(q+2*x2)= 0.125渐开线蜗杆:基圆柱导程角:rb=acos(cos(angle)*cos(r))= 21.182185基圆直径: db1=z1*m/tan(rb)= 12.902668法向基节: pbm=pi*m*cos(rb)= 14.646674蜗杆齿顶高: ha1=m= 5蜗杆齿根高: hf1=1.2*m= 6蜗杆全齿高: h1=ha1+hf1= 11顶隙: c1=0.2*m= 1齿根圆角半径: pf=0.3*m= 1.5蜗杆齿顶圆直径: da1=d1+2*ha1= 50蜗杆齿根圆直径: df1=d1-hf1*2= 28蜗杆齿宽: b1=2.5*m*(z2+1)^0.5=69.597055蜗杆螺牙分度圆轴向弦齿厚: sx1_=0.5*m*pi=7.853982蜗杆螺牙分度圆示向弦齿厚:sn1_=0.5*pi*m*cos(r)= 7.793332蜗杆螺牙法向测齿高度:hcn1_=m+0.5*sn1_*tan(0.5*asin(sn1_*sin(r)^2/d1)) = 5.005840测棒直径: dm=1.67*m= 8.35蜗杆跨棒距:md1=d1-(px1-0.5*pi*m)*cos(r)/tan(angle)+dm*(1/si n(angle)+1)= 51.351762蜗轮分度圆螺旋角:B2=r'= 0.125蜗轮中圆螺旋角:Bm2=r= 7.125016蜗轮分度圆直径:d2=m*z2= 150蜗轮中圆直径:dm2=d2+2*m*x2= 150蜗轮齿顶高:ha2=(1+x2)*m= 5蜗轮齿根高:hf2=(1.2-x2)*m= 6蜗轮全齿高:h2=ha2+hf2= 11蜗轮齿顶圆直径:da2=d2+ha2*2= 160蜗轮齿根圆直径:df2=d2-2*hf2= 138蜗轮外圆直径:de2=da2+m= 165蜗轮齿宽:b2=2*m*(0.5+(q+1)^0.5)= 35蜗轮齿宽包角:xita=2*asin(b2/d1)= 122.089951 蜗轮喉圆半径:rg2=A-0.5*da2= 15db2=d2*cos(angle)= 140.953893端面重合度:ea=(0.5*(da2^2-db2^2)^0.5+m*(1-x2)/sin(angle)-0. 5*d2*sin(angle))/(pi*m*cos(angle))= 1.817161 n1=2000分度圆处滑动速度:vs=pi*d1*n1/(6*10000*cos(r))= 4.221388。

计算项目中心距模数轴截面齿形角传动比变位系数径向间隙头数Z1特性系数q 齿顶高h di 齿根高hg 分度圆直径D fe1节圆直径D je1齿顶圆直径D di1齿根圆直径D g1分度圆螺旋导角λ法向模数m f 轴截面齿距P螺旋导程P Z 螺牙沿分度圆柱上的轴向齿厚S z1螺牙沿分度圆柱上的法向齿厚S f1齿厚测量高度h~齿数Z 2分度圆直径D fe2节圆直径D je2齿根圆直径D g2齿顶圆直径D di2最大外圆直径Dw 2轮缘宽度b 齿顶圆弧半径R 1代 号A M du α螺旋长度L☆蜗 轮圆柱蜗杆传动基本几i ξc蜗杆齿根圆弧半径R 2轮基本几何尺寸计算公式公 式计算结果备注A=0.5M du(Z2+q+2ξ)175.00Mdu=2A/(Z2+q+2ξ) 3.15α=20°20.00i=Z2/Z1=n1/n297.00ξ=(A/Mdu)-0.5(q+z2) 2.06C=0.25Mdu0.79Z1=1,2,4 1.00q=Dfe1/Mdu10.00hdi=Mdu 3.15hg=1.25Mdu 3.94Dfe1=qMdu31.50Dje1=Dfe1+2Mduξ=Mdu(q+2ξ)44.45Ddi1=Mdu(q+2)37.80Dg1=Mdu(q-2.5)23.63λ=arctgZ1/q0.10mf=Mducosλ 3.13L=(12+0.1z2)Mdu68.36Z1=1,2 L=(13+0.1z2)Mdu71.51Z1=4 P=πMdu9.90PZ=πMduZ19.90Sz1=0.45πMdu97.00Sf1=Sz1cosλ96.52h~=Mdu 3.15Z2=iZ197.00Dfe2=MduZ2305.55Dje2=Dfe2=MduZ2305.55Dg2=2(A-0.5Ddi1-0.25Mdu)310.63Ddi2=2(A-0.5Dfe1+Mdu)324.80Dw2=Ddi2+Mdu327.95b=0.65Ddi124.57R1=0.5Dfe1-Mdu12.60R1=0.5Ddi1+0.25Mdu19.69。


普通圆柱蜗杆传动的主要参数及几何尺寸计算普通圆柱蜗杆传动的主要参数及几何尺寸计算如图11 - 13所示,在中间平面上,普通圆柱蜗杆传动就相当于齿条与齿轮的啮合传动。
故在设计蜗杆传动时,均取中间平面上的参数(如模数、压力角等)和尺寸(如齿顶圆、分度圆等)为基准,并沿用齿轮传动的计算关系。
(一)普通圆柱蜗杆传动的主要参数及其选择普通圆柱蜗杆传动的主要参数有模数m、压力角a、蜗杆头数z1.、蜗轮齿数z2及蜗杆的直径d.等。
进行蜗杆传动的设计时,首先要正确地选择参数。
1.模数m和压力角a和齿轮传动一样,蜗杆传动的几何尺寸也以模数为主要计算参数。
蜗杆和蜗轮啮合时,在中间平面上,蜗杆的轴面模数、压力角应与蜗轮的端面模数、压力角相等,即ma1=mt2=maa1=at2ZA蜗杆的轴向压力角仅。
为标准值(200),其余三种(ZN、ZI、ZK)蜗杆的法向压力角口。
为标准值( 200),蜗杆轴向压力角与法向压力角的关系为tanαa=tanαn/cosγ式中,γ为导程角。
2.蜗杆的分度圆直径d1在蜗杆传动中,为了保证蜗杆与配对蜗轮的正确啮合,常用与蜗杆具有同样尺寸的蜗轮滚刀①来加工与其配对的蜗轮。
这样,只要有一种尺寸的蜗杆,就得有一种对应的蜗轮滚刀。
对于同一模数,可以有很多不同直径的蜗杆,因而对每一模数就要配备很多蜗轮滚刀。
显然,这样很不经济。
为了限制蜗轮滚刀的数目及便于滚刀的标准化,就对每一标准模数规定了一定数量的蜗杆分度圆直径d1而把比值称为蜗杆的直径系数。
d.与q已有标准值;常用的标准模数m和蜗杆分度圆直径d,及直径系数q见表11 -2。
如果采用非标准滚刀或飞刀切制蜗轮,d1与q值可不受标准的限制。
3.蜗杆头数z1.蜗杆头数z,可根据要求的传动比和效率来选定。
单头蜗杆传动的传动比可以较大,但效率较低,如要提高效率,应增加蜗杆的头数。
但蜗杆头数过多,又会给加工带来困难。
所以,通常蜗杆头数取为1、2、4、6 04.导程角y蜗杆的直径系数q和蜗杆头数Zl选定之后蜗杆分度圆柱上的导程角γ也就确定了。
蜗杆与蜗轮主要参数及几何计算一、蜗杆与蜗轮的主要参数1. 模数:蜗杆和蜗轮的齿轮尺寸参数之一,用来描述蜗轮齿数与蜗杆齿数的比例关系。
模数的单位通常为毫米(mm),常用的模数有0.5、1、1.5、2等。
2.蜗杆传动比(减速比):蜗杆与蜗轮之间齿轮传动的转速比,一般用i表示。
传动比等于蜗轮的齿数除以蜗杆的齿数,即i=Z2/Z1、蜗杆传动比通常为10至80左右。
3.螺旋线角度:蜗杆的螺旋线与轴线的夹角,通常用θ表示。
螺旋线角度决定了蜗杆的斜度,直接影响到蜗杆与蜗轮传动的效率。
4.蜗杆和蜗轮的材料:由于传动过程中会有相对滑动和高速摩擦,所以蜗杆和蜗轮通常使用耐磨、耐热、耐疲劳的材料,比如高强度合金钢、铜合金等。
5.渐开线角:蜗杆渐开线与垂直于轴线的圆柱面交线的夹角,用α表示。
渐开线角的大小会直接影响到蜗杆与蜗轮的传动效率和噪音。
二、蜗杆与蜗轮的几何计算1.蜗杆的直径计算:蜗杆的直径可以根据承受的转矩和材料的强度来确定。
通常根据公式d=K∛(T/σ)计算,其中d为蜗杆直径,K为一个系数,T为扭矩,σ为所选材料的强度。
2.蜗杆和蜗轮的齿数计算:蜗杆和蜗轮的齿数需要满足传动比和滚动角度等要求。
通常滚动角度为20°时,蜗杆的齿数为4至6;滚动角度为15°时,蜗杆的齿数为6至9、齿数的具体计算可以根据所选的传动比和齿轮的模数来确定。
3. 蜗轮的直径计算:蜗轮的直径需要根据滚动角度和蜗杆直径来确定。
一般来说,蜗轮的直径大于或等于蜗杆的直径。
可以根据公式d2 =d1 + 2mcosα 计算,其中d2为蜗轮的直径,d1为蜗杆的直径,m为模数,α为渐开线角。
4.蜗杆传动比的计算:蜗杆传动比等于蜗轮的齿数除以蜗杆的齿数。
根据所选的传动比和蜗杆的齿数,可以计算出蜗轮的齿数。
以上是蜗杆与蜗轮的主要参数和几何计算的介绍,这些参数和计算方法的正确选择和应用,能够保证蜗杆与蜗轮传动的效率和可靠性。
在实际应用中,还需要考虑到摩擦和磨损等因素,选择适当的润滑方式和材料,以提高传动的效率和寿命。
普通圆柱蜗杆传动承载能力计算(一)蜗杆传动的失效形式、设计准则及常用材料和齿轮传动一样,蜗杆传动的失效形式也有点蚀(齿面接触疲劳破坏)、齿根折断、曲面胶合及过度磨损等。
由于材料和结构上的原因,蜗杆螺旋齿部分的强度总是高于蜗轮轮齿的强度,所以失效经常发生在蜗轮轮齿上。
因此,一般只对蜗轮轮齿进行承载能力计算。
由于蜗杆与蜗轮齿面间有较大的相对滑动,从而增加了产生胶合和磨损失效的可能性,尤其在某些条件下(如润滑不良),蜗杆传动因齿面胶合而失效的可能性更大。
因此,蜗杆传动的承载能力往往受到抗胶合能力的限制。
在开式传动中多发生齿面磨损和轮齿折断,因此应以保证齿根弯曲疲劳强度作为开式传动的主要设计准则。
在闭式传动中,蜗杆副多因齿面胶合或点蚀而失效。
因此,通常是按齿面接触疲劳强度进行设计,而按齿根弯曲疲劳强度进行校核。
此外,闭式蜗杆传动,由于散热较为困难,还应作热平衡核算。
由上述蜗杆传动的失效形式可知,蜗杆、蜗轮的材料不仅要求具有足够的强度,更重要的是要具有良好的磨合和耐磨性能。
蜗杆一般是用碳钢或合金钢制成。
高速重载蜗杆常用15Cr或20Cr,并经渗碳淬火;也可用40、45号钢或40Cr并经淬火。
这样可以提高表面硬度,增加耐磨性。
通常要求蜗杆淬火后的硬度为40~55HRC,经氮化处理后的硬度为55~62HRC。
一般不太重要的低速中载的蜗杆,可采用40或45号钢,并经调质处理,其硬度为220~300HBS。
常用的蜗轮材料为铸造锡青铜(ZCuSnlOPl,ZCuSn5Pb5Zn5)、铸造铝铁青铜(ZCuAl10Fe3)及灰铸铁(HTl5O、HT2OO)等。
锡青铜耐磨性最好,但价格较高,用于滑动速度Vs≥3m/s的重要传动;铝铁青铜的耐磨性较锡青铜差一些,但价格便宜,一般用于滑动速度Vs≤4m/s的传动;如果滑动速度不高(Vs<2m/s),对效率要求也不高时,可采用灰铸铁。
为了防止变形,常对蜗轮进行时效处理。
(二)蜗杆传动的受力分析蜗杆传动的受力分析和斜齿圆柱齿轮传动相似。
圆柱蜗杆传动主要参数及几何计算设计圆柱蜗杆传动时,均取给定平面上的参数和几何尺寸作为主要参数,参考齿轮传动的计算关系进行几何计算。
1. 蜗杆传动主要参数∙普通圆柱蜗杆的基准齿廓普通圆柱蜗杆的基准齿廓是指基准蜗杆在给定截面上的规定齿廓。
在蜗杆的轴平面内基准齿廓的尺寸参数包括:∙齿顶高:Ha = m(正常齿)ha = 0.8m(短齿)∙工作齿高:h’ = 2m(正常齿)h’ = 1.6m(短齿)∙轴向齿距:Px = πm (中线上的齿厚等于齿槽宽)∙顶隙:c = 0.2m,必要时可减小到0.15m或增大到0.35m∙齿根圆角:ρf = 0.3m, 必要时可减小到0.2m或增大到0.4m∙齿形角:阿基米德蜗杆,轴向齿形角αx = 20°,法向直廓蜗杆,法向齿形角αn = 20°,渐开线蜗杆,法向齿形角αn = 20°∙模数、蜗杆分度圆直径和直径特性系数1)模数m 在中间平面上的模数为标准值,即蜗杆的轴向模数mx和蜗轮的端面模数mt为标准值。
2) 蜗杆分度圆直径d1要保证蜗杆与蜗轮的正确啮合,蜗轮加工是用和与该蜗轮相啮合的蜗杆的直径、齿形参数完全相同的滚刀进行切制。
为了减少加工蜗轮的滚刀的规格数量,利于蜗轮滚刀的标准化和系列化,国标规定d1为标准值,且与m有一定的搭配关系。
3) 蜗杆直径特性系数q由于蜗杆分度圆直径d1和蜗杆模数m均为标准值,定义它们的比值为蜗杆直径特性系数,即d1 = mq。
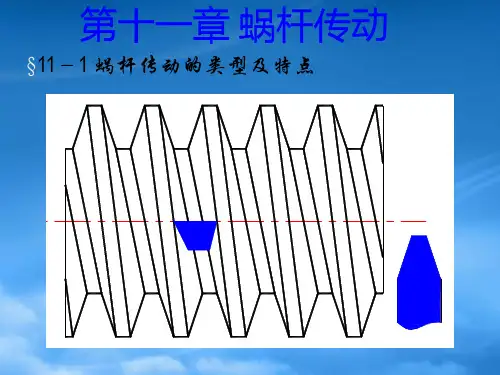
∙蜗杆头数Z1和蜗轮齿数Z2蜗杆头数Z1是指蜗杆圆柱面上连续齿的个数,也就是螺旋线的线数。
常用取值为1,2,4,6。
Z1过多,加工制造的难度增加,精度不易保证;Z1减小,传动效率降低,传动比较大或要求自锁时取Z1=1。
蜗轮齿数Z2根据传动比i和Z1确定。
Z2 = i Z1。
为避免蜗轮轮齿发生根切和保证传动的平稳性,一般取蜗轮齿数Z2>27;同时为避免结构尺寸一定时,模数过小而导致弯曲强度不足或模数一定时,蜗轮直径过大而导致蜗杆轴支撑跨距过大从而刚度降低,蜗轮齿数也不宜过大,一般取Z2<80。
普通圆柱蜗杆传动的基本参数及几何尺寸计算
1.基本参数:
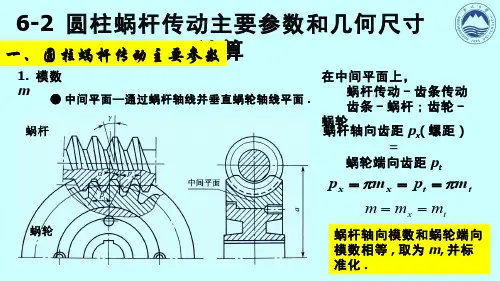
(1)模数m和压力角α:
在中间平面中,为保证蜗杆蜗轮传动的正确啮合,蜗杆的轴向模数m a1和压力角αa1应分别相等于蜗轮的法面模数m t2和压力角αt2,即
m a1=m t2=mαa1=αt2
蜗杆轴向压力角与法向压力角的关系为:
tgαa=tgαn/cosγ
式中:γ-导程角。
(2)蜗杆的分度圆直径d1和直径系数q
为了保证蜗杆与蜗轮的正确啮合,要用与蜗杆尺寸相同的蜗杆滚刀来加工蜗轮。
由于相同的模数,可以有许多不同的蜗杆直径,这样就造成要配备很多的蜗轮滚刀,以适应不同的蜗杆直径。
显然,这样很不经济。
为了减少蜗轮滚刀的个数和便于滚刀的标准化,就对每一标准的模数规定了一定数量的蜗杆分度圆直径d1,而把及分度圆直径和模数的比称为蜗杆直径系数q,即:
q=d1/m
常用的标准模数m和蜗杆分度圆直径d1及直径系数q,见匹配表。
(3)蜗杆头数z1和蜗轮齿数z2
蜗杆头数可根据要求的传动比和效率来选择,一般取z1=1-10,推荐z1=1,2,4,6。
选择的原则是:当要求传动比较大,或要求传递大的转矩时,则z1取小值;要求传动自锁时取z1=1;要求具有高的传动效率,或高速传动时,则z1取较大值。
蜗轮齿数的多少,影响运转的平稳性,并受到两个限制:最少齿数应避免发生根切与干涉,理论上应使z2min≥17,但z2<26时,啮合区显著减小,影响平稳性,而在z2≥30时,则可始终保持有两对齿以上啮合,因之通常规定z2>28。
另一方面z2也不能过多,当z2>80时(对于动力传动),蜗轮直径将增大过多,在结构上相应就须增大蜗杆两支承点间的跨距,影响蜗杆轴的刚度和啮合精度;对一定直径的蜗轮,如z2取得过多,模数m就减小甚多,将影响轮齿的弯曲强度;故对于动力传动,常用的范围为z2≈28-70。
对于传递运动的传动,z2可达200、300,甚至可到1000。
z1和z2的推荐值见下表
(4)导程角γ
蜗杆的形成原理与螺旋相同,所以蜗杆轴向齿距p a与蜗杆导程p z的关系为p z=z1p a,由下图可知:
tanγ=p z/πd1=z1p a/πd1=z1m/d1=z1/q
导程角γ的范围为3.5°一33°。
导程角的大小与效率有关。
导程角大时,效率高,通常γ=15°-30°。
并多采用多头蜗杆。
但导程角过大,蜗杆车削困难。
导程角小时,效率低,但可以自锁,通常γ=3.5°一4.5°
5)传动比I
传动比i=n主动1/n从动2
蜗杆为主动的减速运动中
i=n1/n2=z2/z1 =u
式中:n1 -蜗杆转速;n2-蜗轮转速。
减速运动的动力蜗杆传动,通常取5≤u≤70,优先采用15≤u≤50;增速传动5≤u≤15。
普通圆柱蜗杆基本尺寸和参数及其与蜗轮参数的匹配表。
2 蜗杆传动变位的特点
蜗杆传动变位
标准
正变位
负变位
变位蜗杆传动根据使用场合的不同,可在下述两种变位方式中选取一种。
1)变位前后,蜗轮的齿数不变(z2 '=z2),蜗杆传动的中心距改变(a '≠a),如图9-8a、c所示,其中心距的计算式如下:
a '=a+x2m=(d1+d2+2x2m)/2
2)变位前后,蜗杆传动的中心距不变(a '=a),蜗轮齿数发生变化(z2'≠z2),如图9-8d、e所示,z2' 计算如下:
因a'=a则z2' =z2-2x2
蜗杆传动变位:
3 普通圆柱蜗杆传动的几何尺寸计算
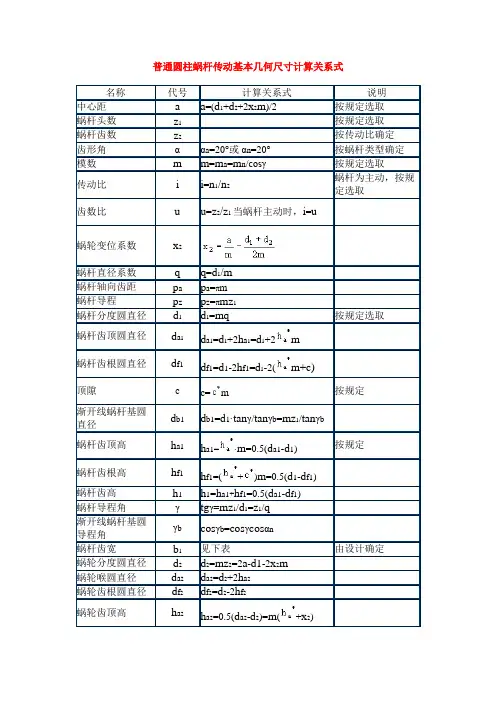
普通圆柱蜗杆传动基本几何尺寸计算关系式:
(end)。