九年级数学上册 1.2《平行四边形的判定》课件2 青岛版
- 格式:ppt
- 大小:555.50 KB
- 文档页数:7

《平行四边形的性质》教案(第1课时)精华版一、内容和内容解析1.内容平行四边形的概念,平行四边形边、角的性质,平行线间的距离.2.内容解析平行四边形作为最基本的几何图形,作为“空间与图形”领域中研究的主要对象,它在实际生产和生活中有着广泛的应用,这不仅表现在日常生活中有很多平行四边形的图案,还包括其性质在生产生活各领域的实际应用.本节内容是平行四边形第一课时,既是本节的重点,又是本章的重点.学习它不仅是对已学的平行线、三角形等知识的综合运用和深化,又为我们接下来类比学习矩形、菱形等特殊四边形奠定了重要基础.此外,平行四边形的性质还是证明线段相等和角相等的重要依据和方法,具有承上启下的作用.本节课的主要内容是平行四边形的概念和平行四边形对边相等、对角相等的性质,之后又引出平行线间的距离的概念.平行四边形是一种特殊的四边形,特殊在两组对边分别平行且相等.由于这个特殊性导致它具有一般四边形不具有的特殊性质,这些特殊的性质有助于我们解决许多实际生活中的问题.所以,本节课的重点是平行四边形对边相等、对角相等的性质.二、目标和目标解析1.目标(1)理解平行四边形的概念.(2)探究并证明平行四边形对边相等、对角相等的性质.2.目标解析达成目标(1)的标志是:理解平行四边形的概念,明确平行四边形和四边形的区别和联系,会用平行四边形的概念进行判断和推理.达成目标(2)的标志是:能够利用平行四边形的概念证明它的边、角的性质,并能初步应用平行四边形的性质进行简单的计算和证明,解决生活中的实际问题,培养学生的观察能力及逻辑推理论证能力,渗透“转化”的数学思想.三、教学问题诊断分析由于学生在前面已接触过平行线和三角形的有关知识,根据学生的年龄特点,运用直观生动的形象,使学生通过动手度量发现性质,并用全等三角形的知识加以证明.学生证明过程中出现的主要困难是添加辅助线,构造全等三角形.教师可以引导学生“要证明两条线段或两角相等,可以通过证明两条线段或两角所在的三角形全等”,由此想到连接平行四边形的对角线,构造全等三角形进行证明.所以本节课的难点是如何添加辅助线将平行四边形问题转化为三角形问题解决的思想方法.四、教学过程设计(一)视频导课:播放视频《平行四边形的性质》(第一课时)导入二,进行导入新课.(多媒体授课)1.看一看欣赏视频与图片:老师播放课件,显示丰富多彩的画面,其中有学生熟悉的校门(伸缩门),楼梯两旁的扶手,窗户在太阳光下的影子等.2.找一找问题:这些精美的画面中,你能找出其中的平行四边形吗?请谈谈你对平行四边形的认识?师生活动:学生积极举手回答后,师引导学生共同归纳: (1)定义:两组对边分别平行的四边形叫做平行四边形. (2)表示:平行四边形用符号“□”来表示.如图,在四边形ABCD 中,AB ∥DC ,AD ∥BC ,那么四边形ABCD 是平行四边形.平行四边形ABCD 记作“□ABCD ”,读作“平行四边形ABCD ”.DCBA①∵AB //DC ,AD //BC ,∴四边形ABCD 是平行四边形(判定). ②∵四边形ABCD 是平行四边形, ∴AB //DC ,AD //BC (性质).平行四边形的概念既可以作为性质,又可以作为判定平行四边形的依据.师强调:平行四边形中对边是指无公共点的边,对角是指不相邻的角,对角线是指连接对角顶点的线,邻边是指有公共端点的边,邻角是指有一条公共边的两个角.而三角形对边是指一个角的对边,对角是指一条边的对角.(结合图形,让学生认识清楚)平行四边形是我们常见的图形,你还能举出平行四边形在生活中应用的例子吗? 学生同桌交流后,师选学生发言.设计意图:通过观察生活中常见的图片,找出图片中平行四边形的原型,从而抽象出平行四边形的定义,让学生在感受美的同时,体会数学源于生活,激发学生学习的兴趣.(二)猜想证明,探究性质(可用微课视频辅助授课)平行四边形是一种特殊的四边形,它除具有四边形的性质和两组对边分别平行外,还有什么特殊的性质呢?我们一起来探究一下.1.做一做:(1)让学生根据平行四边形的定义画一个平行四边形,观察所画的平行四边形,它是中心对称图形吗?如果是,你能找出它的对称中心并验证你的结论吗?师生活动:学生通过动手操作、小组交流、探究验证结论:平行四边形是中心对称图形,两条对角线的交点是它的对称中心.(师课件演示验证结论) (2)平行四边形除具有四边形的性质和两组对边分别平行以外,它的边和角之间有什么关系?度量一下,是不是和你猜想的一致?①由定义知道,平行四边形的对边平行.根据平行线的性质可知,在平行四边形中,相邻的角互为补角.(相邻的角指四边形中有一条公共边的两个角,教学时结合图形使学生分辨清楚.) ②猜想:平行四边形的对边相等、对角相等. ③下面证明这个结论的正确性.已知:如图,四边形ABCD 为平行四边形.求证:AB =CD ,CB =AD ,∠B =∠D ,∠BAD =∠BCD .4321DC BA分析:连接□ABCD的对角线AC,它将平行四边形分成△ABC和△CDA,证明这两个三角形全等即可得到结论.连接对角线是解决四边形问题常用的辅助线,通过作对角线,可以把未知问题转化为已知的关于三角形的问题.证明:连接AC,∵AB∥CD,AD∥BC,∴∠1=∠3,∠2=∠4.又AC=CA,∴△ABC≌△CDA(ASA).∴AB=CD,CB=AD,∠B=∠D.又∠BAD=∠1+∠4,∠BCD=∠2+∠3,∴∠BAD=∠BCD.由此得到:平行四边形性质1:平行四边形的对边相等.平行四边形性质2:平行四边形的对角相等.设计意图:引导学生证明猜想,体会证明思路的分析方法和把四边形问题转化为三角形问题来解决的思想方法.(三)初步应用,巩固知识例求证:(1)夹在两条平行线间的平行线段相等;(2)如果两条直线平行,那么一条直线上各点到另一条直线的距离相等.(1)已知:如图,l1∥l2,A,D是直线l1上的任意两点,过点A,D作AB∥CD,分别交l2于点B,C.求证:AB=CD.l 2l1DCBA师点拨:根据已知l1∥l2,AB∥CD,根据平行四边形的定义可知四边形ABCD是平行四边形,根据平行四边形的性质,那么就能证明AB=CD.(通过课件展示证明过程) 证明:∵AD∥BC,AB∥CD,∴四边形ABCD是平行四边形(平行四边形的定义),∴AB=CD(平行四边形的性质定理1).(2)已知:如图,l1∥l2,A,D是直线l1上的任意两点,AB⊥l2,垂足是B,CD⊥l2,垂足是C.求证:AB=CD.l 2l1DCBA师点拨:根据已知AB⊥l2,CD⊥l2,可知∠ABC=∠DCB=90°,则∠ABC+∠DCB=180°.根据平行线的判定,就能证明AB∥CD.由(1)可知AB=CD.(通过课件展示证明过程)证明:∵AB⊥l2,CD⊥l2,∴∠ABC=90°,∠DCB=90°.∴∠ABC+∠DCB B=180°.∴AB∥CD.由(1)可知AB=CD.设计意图:通过例题的讲解,让学生进一步体会平行四边形的性质.挑战自我:如图,P为□ABCD内的任意一点,连接P A,PB,PC,PD得到△P AB,△PBC,△PCD,△P AD.你发现其中两个不相邻的三角形的面积之和与平行四边形ABCD的面积之间有什么关系?从而你能得到什么结论?证明你的结论.PDCBA如图,假设△P AB ,△PBC ,△PCD ,△PDA 的面积分别是S 1,S 2,S 3,S 4,得出如下结论:S 1+S 3=S 2+S 4=12S □ABCDHG FE S 4S 3S 2S 1P DCBA证明:如图,过点P 分别作边AB ,BC 的平行线,则□ABCD 被分成四个小平行四边形,AP ,BP ,CP ,DP 分别为四个小平行四边形的对角线,把四个小平行四边形分成两个面积相等小三角形.即:S △APE = S △APG ,S △BPG = S △BPF ,S △CPF = S △CPH ,S △DPH = S △DPE .PABPCDS S +=S 1+S 3= S △APG + S △BPG + S △DPH + S △CPH =12S □ABCD PBC PDASS+= S 2+S 4= S △BPF + S △CPF + S △APE +S △DP =E12S □ABCD 所以△P AB 与△PCD 的面积和等于△PBC 与△PDA 的面积和,都等于□ABCD 面积的一半,即:S 1+S 3=S 2+S 4=12S □ABCD . 课堂练习: 在□ABCD 中,(1)已知AB =5,BC =3,求它的周长; (2)已知∠A =38°,求其余各角的度数.师找两名学生板书解题步骤,根据出现的问题进行点拨.也可用几何画板进行动画演示.解:(1)∵四边形ABCD是平行四边形,∴AB=CD,BC=DA.∴□ABCD的周长为AB+CD+BC+DA=2(AB+BC)=16.(2)∵四边形ABCD是平行四边形,∴∠C=∠A,∠B+∠A=180°,∠D=∠B.∵∠A=38°,∴∠C=38°,∠B=180° 38°=142°,∠D=142°.师强调:1.因为平行四边形的对边相等,所以平行四边形的周长=两邻边和的2倍.2.平行四边形的对角相等、邻角互补.设计意图:通过练习巩固平行四边形的性质及运用.(四)课堂小结1.引导学生从对知识的理解,在知识的获得过程中的体验和感受,在解决问题过程中的心得和对数学思想方法的体会等方面进行学习小结,开展交流.(1)平行四边形的概念;(2)平行四边形的性质:①平行四边形是中心对称图形,两条对角线的交点是它的对称中心.②边:对边平行且相等.③角:对角相等、邻角互补.2.鼓励学生对教师的教和同伴、自身的学习行为进行反思和评价,还可以对本节课进行质疑,说出存在的疑惑,谈谈自己不同的见解.设计意图:通过小结,使学生梳理本节所学内容,进一步理解平行线的概念和性质.(五)布置作业1.如图,已知四边形ABCD是平行四边形,∠BCD的平分线CF交边AB于F,∠ADC 的平分线DG交边AB于G.(1)求证:AF=GB;(2)请你在已知条件的基础上再添加一个条件,使得△EFG是等腰直角三角形,并说明理由.G FA BCE设计意图:考查应用平行四边形的概念和性质进行推理的能力. 2.提高题:如图②,将□ABCD (纸片)沿过对角线交点O 的直线EF 折叠,点A 落在点A 1处,点B 落在点B 1处,设FB 1交CD 于点G ,A 1B 1分别交CD ,DE 于点H ,I . 求证:EI =FG .IB 1A 1HGFABCD E设计意图:考查知识的综合应用能力. 作业答案:1.(1)证明:∵四边形ABCD 是平行四边形, ∴AB ∥CD . ∴∠AGD =∠CDG . ∵∠ADG =∠CDG , ∴∠ADG =∠AGD . ∴AD =AG . 同理可证,BC =BF .又∵四边形ABCD 是平行四边形, ∴AD =BC . ∴AG =BF .∴AG -GF =BF -GF . 即AF =GB .(2)可添加条件EF =EG .理由如下:由(1)证明易知∠AGD =∠ADG =21∠ADC ,∠BFC =∠BCF =21∠BCD . ∵AD ∥BC ,∴∠ADC +∠BCD =180°. ∴∠AGD +∠BFC =90°. ∴∠GEF =90°. 又∵EF =EG ,∴△EFG 为等腰直角三角形. 2.65IB 1A 1HGF ABCD E4321证明:∵四边形ABCD 是平行四边形, ∴∠A =∠C ,∠B =∠D .由折叠的性质可得:AE =A 1E ,∠A 1=∠A ,∠B 1=∠B , ∴A 1E =CF ,∠A 1=∠A =∠C ,∠B 1=∠B =∠D . 又∵∠1=∠2, ∴∠3=∠4.∵∠5=∠3,∠4=∠6, ∴∠5=∠6.在△A 1IE 与△CGF 中,1156A C A E CF =⎧⎪=⎨⎪=⎩∠∠,∠∠,,∴△A 1IE ≌△CGF (AAS ). ∴EI =FG .(六)课堂检测1.在□ABCD中,∠A比∠B大30°,则∠A=________,∠D=________.2.在□ABCD中,如果∠A的外角是50°,那么平行四边形的每个内角________.3.若□ABCD的周长是30 cm,AB︰CB=3︰2,则AD=________ cm,CD=________ cm.4.在□ABCD中∠B的平分线将AD分成4 cm和2 cm两段,求□ABCD的周长.课堂检测答案:1.∠A=105°,∠D=75°.2.∠A=130°,∠B=50°,∠C=130°,∠D=50°.3.AD=6 cm,CD=9 cm.4.□ABCD的周长为20 cm或16 cm.。


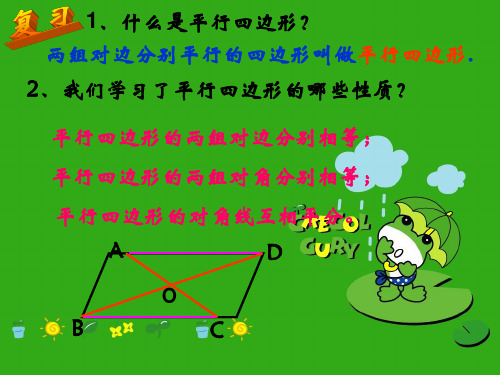
1.2平行四边形的判定【教学目标】1.平行四边形的判定定理及应用.2•会综合运用平行四边形的判定定理和性质定理来解决问题.3•会根据条件来画出平行四边形.4•培养用类比、逆向联想及运动的思维方法来研究问题]【教学重点、难点】【教学过程】一、用类比、逆向思维的方式探索平行四边形的判定方法1 •复习平行四边形的主要性质,两组对边平行,(性质1)边4(b)两组对边相等■(性质2)角:(c )两组对角相等.(性质3)(等价命题:两组邻角互补)对角线:(d)对角线互相平分.(性质4)2 •逆向思维:怎样判定一个四边形是平行四边形?(1 )学生容易由定义得出:两组对边分别平行的四边形是平行四边形(判定方法一)•也就是说,定义既是平行四边形的一个性质,又是它的一个判定方法.(2)观察判定方法一与性质1的关系,寻找逆命题的特征:(3)类比联想,猜想其他性质的逆命题也能判定平行四边形,构造逆命题如下:①两组对边分别相等的四边形是平行四边形(猜想1)(4)证明猜想,得到平行四边形的判定定理 1 •教师引导学生根据平行四边形的定义以及平行线的性质、三角形全等的知识对以上猜想进行证明•实际,让学生利用上述方法得出有关平行四边形判定方法的部分常用(或全部)猜想.(教师也可用判断题的形式让学生思考,从而降低难度)猜想一:一组对边平行且相等的四边形是平行四边形.猜想二:一组对边平行且另一组对边相等的四边形是平行四边形.猜想三:一组对边相等且一组对角相等的四边形是平行四边形.(3)证明猜想成立或举例说明某猜想不成立.以上猜想中正确的是猜想一,猜想二和三的反例图形分别见图4-21 ( a).图4-2]如图4 —21 (a),在四边形ABCD中,AD //BC , 形;在图4-21 ( b)中,AB = AC= DE / B=Z C=Z D,但四边形ABED不是平行四边(4)总结。
平行四边形判定方法,根据题目条件从中灵活选用方法来解决问题.二、判定定理的巩固练习1 •禾U用平行四边形的判定定理及性质定理进行证明.例1已知:如图4 —22, E和F是一-'ABCD寸角钱AC上两点,AE= CF.求证:四边形BFDE是平行四边形.说明:引导学生从条件、结论两方面对题目进行再思考.(1)在此基础上,还可证出什么结论?用到什么方法?如还可证BE兰DF,DE兰BF, / BED=Z BFD等.总结方法:利用平行四边形的性质---- 判定 -- 性质可解决较复杂的几何题目(2)根据运动、类比、特殊化的思维方法,猜想对此题可作怎样的推广?类比例1条件,利用运动变化的观点,让E和F在对角线AC上运动到一些特殊位置,猜想还可得出同样结论如图4-23,但其中的猜想无法证明.缺图4-23猜想一如图4-23 (a),在口ABCC中,E , F为AC上两点,/ ABE=Z CDF求证:四边形BEDF为平行四边形.猜想二如图4—23 ( b),在口ABCD中,E, F为AC上两点,BE//DF .求证:四边形BEDF为平行四边形.AB = DC但四边形ABCD不是平行四边<«)<b)图4-22猜想三如图4-23 ( c),在口ABCD中,E , F为AC上两点,BE = DF.求证:四边形BEDF为平行四边形.求证:四边形BEDF为平行四边形例2已知:如图4 —24(a),在口ABCD中,E,F分别是边AD, BC的中点.求证:EB=DF 说明:(1)分析证明思路,所要证明的两条线段恰为四边形EBFD的一组对边,由图中它们所在的位置来看,可首先判定四边形BEDF为平行四边形,再利用平行四边形的性质来解决.培养学生思维的层次:使用已知平行四边形的性质一一判定新平行四边形一一使用新平行四边形的性质得出结论.(2)弓|导学生适当改变题目的条件、结论,对命题加以引伸和推广.推广一(对结论引伸)已知:如图4-42 ( b),在口ABCD中,E,F分别为AD, BC 的中点,BE交AF于G, EC交DF于H.求证:(1 )四边形EGFH为平行四边形;(2)四边形EGHE为平行四边形猜想四如图4—23 (d),在匚JABCD中, E,F分别是AC上两点,BEX AC 于E, DF丄AC于F.冲E(c)A E DB F c思考:怎样用运动、类比及特殊到一般的方法来改变命题的条件,将命题加以推广推广二已知:如图4-24 ( c),在口ABCD中, E, F为AD, BC上两点,AE= CF.求证:EB= DF.推广三已知:如图4-24 (d),在口ABCD中, E , F为AD, BC上两点,/ ABE=Z CDF求证:EB= DF .推广四已知:如图4-24 (e),在口ABCD中, E, F分别为AD,・BC上两点,BE和DF分别平分/ ABC和/ ADC求证:EB = DF .推广五已知:如图4-24 (f ),在口ABCD中, E, F分别为AD BC上两点,AE± BC于E, CF丄AD于F.求证:BE= DF.四、师生共同归纳小结1 .平行四边形的判定方法有哪些?应从边、角、对角线三方面来进行总结,并指出:性质定理的逆命题如果正确,常常作为判定定理来使用.2•学习了哪些研究问题的思想方法五、作业课本第144页第7〜14题,B组1 , 2, 4题.补充题:1 .如图4-25,在:二ABCD中,AE = CF, BG= DH 求证:AH, BE, CG,DF 围成的四边形MNP 购平行四边形.2.如图4-26,在二ABCD中, E, F, G和H分别是各边中点.求证:四边形EFGH为平行四边形.3 .如图4 —27,在口ABCD中,AC, BD交于0点,AEL BD于E,CG丄BD于G,BH丄AC于H, DFL AC于F.求证:四边形EFGH为平行四边形.。

