《船舶结构力学》0预备知识-弯矩图、剪力图复习
- 格式:ppt
- 大小:773.00 KB
- 文档页数:25
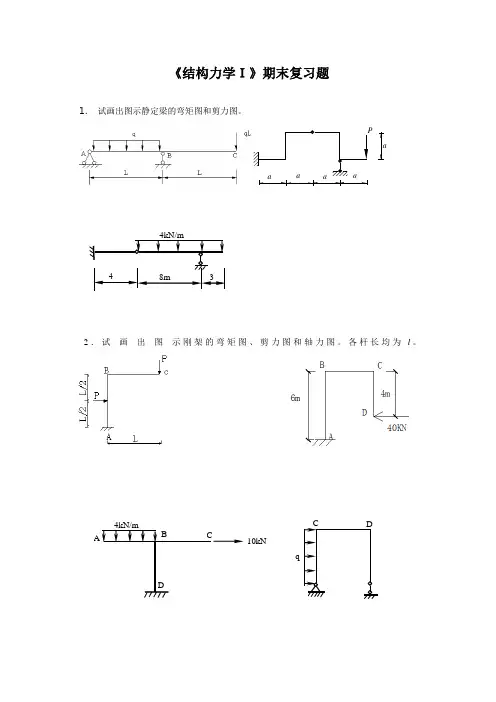
《结构力学I》期末复习题1.试画出图示静定梁的弯矩图和剪力图。
Pa aaa a2.试画出图示刚架的弯矩图、剪力图和轴力图。
各杆长均为l。
DA C4kN/mB10kNDC48m34kN/m3.试求图示桁架各指定杆的轴力。
已知F= 30kN。
三、静定结构的位移计算1.用图乘法计算图示荷载作用下外伸梁C点的竖向位移Δcy。
3×4=12m3F2313m3m4bacFF2×2=4m2×3=6m2F 3Fbac4m4×3=12m2.试画出 图示结构的弯距图。
并求C 点的水平位移和D 点转角。
已知三杆长均为l ,EI 为常数。
3.试绘制图示静定结构的弯矩图,并求A 点的垂直位移和B 点转角。
已知三杆长均为3m 。
各杆EI 均为10000kNm 2。
4.试绘制图示静定结构的弯矩图,并求A 点的垂直位移。
各杆EI 均为5000kNm 2。
5kN四.力法1.试用力法计算图示结构,绘制弯矩图。
已知二杆长均为l,EI为常数。
q2.试用力法计算图示结构,绘制弯矩图。
已知两杆长均为l,EI为常数。
3.试用力法计算图示结构,绘制弯矩图。
已知三杆长均为l,EI为常数。
4.用力法计算并作图示结构M图。
已知二杆长均为l,E I= 常数。
五、位移法1.建立图示结构的方程,求出方程的系数和自由项。
已知三杆长均为l,EI为常数。
2.试用位移法计算图示结构,绘制弯矩图。
已知两杆长均为l,EI为常数。
q3.试用位移法计算图示结构,绘制弯矩图。
已知三杆长均为6米 ,EI 为常数。
4. 位移法作图示刚架的M 图(EI﹦常数)。
5.试 用 最 简 捷 的 方 法 求 图 示 结 构 的 弯 矩 图 , 各 杆 的 长 度 l 均 相同 。
PEIEIEIEI EI 1=ACBD12kN/m6.用位移法作图示结构M 图,EI 常数。
l /2l /2六.力矩分配法1.试用力矩分配法计算图示连续梁,绘制弯矩图。
EI 为常数。

轴,。
以表(a)(b)(c)(1)(2) (3) ≤ (4)以剪力图是平行于轴的直线。
段的剪力为正,故剪力图在轴上方;段剪力为负,故剪力图在轴之下,如图8-12(b )所示。
由式(2)与式(4)可知,弯矩都是的一次方程,所以弯矩图是两段斜直线。
根据式(2)、(4)确定三点,,,由这三点分别作出段与段的弯矩图,如图8-12(c )。
例8-4 简支梁受集度为的均布载荷作用,如图8-13(a )所示,作此梁的剪力图和弯矩图。
x C l x AC x BC x x 0=x 0)(=x M a x =l Fab x M =)(l x =0)(=x M AC BC AB q图8-13解 (1)求支反力 由载荷及支反力的对称性可知两个支反力相等,即(2)列出剪力方程和弯矩方程 以梁左端为坐标原点,选取坐标系如图所示。
距原点为的任意横截面上的剪力和弯矩分别为<< (1) 0≤≤ (2)(3)作剪力图和弯矩图 由式(1)可知,剪力图是一条斜直线,确定其上两点后即可绘出此梁的剪力图(图8-13b )。
由式(2)可知,弯矩图为二次抛物线,要多确定曲线上的几点,才能画出这条曲线。
例如通过这几点作梁的弯矩图,如图8-13(c )所示。
由剪力图和弯矩图可以看出,在两个支座内侧的横截面上剪力为最大值:。
在梁跨度中点横截面上弯矩最大,而在此截面上剪力。
例8-5 图8-14所示简支梁,跨度为,在截面受一集中力偶作用。
试列出梁的剪力方程和弯矩方程,并绘出梁的剪力图和弯矩图。
2ql F F B A ==A x qx ql qx F x F A Q -=-=2)(0x l 22122)(qx x ql x qx x F x M A -=-=x l 2maxql F Q=2max 81ql M =0=Q F l C m )(x F Q )(x M AB图8-14解 (1)求支反力 由静力平衡方程,得(2)列剪力方程和弯矩方程 由于集中力作用在处,全梁内力不能用一个方程来表示,故以为界,分两段列出内力方程段0<≤ (1)0≤< (2) 段≤< (3) ≤≤ (4)(3) 画剪力图和弯矩图 由式(1)、(3)画出剪力图,见图8-14(b );由式(2)(4)画出弯矩图,见图8-14(c )。


《结构力学》课程习题集西南科技大学成人、网络教育学院版权所有习题【说明】:本课程《结构力学》(编号为06014)共有单选题,判断题,计算题1,计算题2,计算题3,计算题4,几何构造分析等多种试题类型,其中,本习题集中有[计算题4]等试题类型未进入。
一、单选题1.弯矩图肯定发生突变的截面是()。
A.有集中力作用的截面;B.剪力为零的截面;C.荷载为零的截面;D.有集中力偶作用的截面。
2.图示梁中C截面的弯矩是()。
4m2m4mA.12kN.m(下拉);B.3kN.m(上拉);C.8kN.m(下拉);D.11kN.m(下拉)。
3.静定结构有变温时,()。
A.无变形,无位移,无内力;B.有变形,有位移,有内力;C.有变形,有位移,无内力;D.无变形,有位移,无内力。
4.图示桁架a杆的内力是()。
A.2P;B.-2P;C.3P;D.-3P。
5.图示桁架,各杆EA为常数,除支座链杆外,零杆数为()。
A.四根;B.二根;C.一根;D.零根。
Pal= aP PP66.图示梁A点的竖向位移为(向下为正)()。
A.)24/(3EIPl; B.)16/(3EIPl; C.)96/(53EIPl; D.)48/(53EIPl。
PEI EIAl/l/2227.静定结构的内力计算与()。
A.EI无关;B.EI相对值有关;C.EI绝对值有关;D.E无关,I有关。
8.图示桁架,零杆的数目为:()。
A.5;B.10;C.15;D.20。
9.图示结构的零杆数目为()。
A.5;B.6;C.7;D.8。
10.图示两结构及其受力状态,它们的内力符合()。
A.弯矩相同,剪力不同;B.弯矩相同,轴力不同;C.弯矩不同,剪力相同;D.弯矩不同,轴力不同。
PPll11. 刚结点在结构发生变形时的主要特征是( )。
A.各杆可以绕结点结心自由转动;B.不变形;C.各杆之间的夹角可任意改变;D.各杆之间的夹角保持不变。
12. 若荷载作用在静定多跨梁的基本部分上,附属部分上无荷载作用,则( )。

结构⼒学弯矩图画弯矩图的基本理论1.1 指定截⾯上的弯矩计算弯矩等于截⾯⼀侧所有外⼒对截⾯形⼼⼒矩的代数和,画在受拉⼀侧。
1.2 荷载、剪⼒、弯矩三者之间的微分关系即:当荷载为常数时,剪⼒图为斜直线,弯矩图为⼆次曲线;当荷载为零时,剪⼒图为平⾏线或为零线,弯矩图为斜直线或为平⾏线、零线。
1.3 区段叠加法区段叠加法是以⼀段梁的平衡为依据,⽐拟相应跨度简⽀梁的计算⽽得到的⽅法:以⼀段梁的两端弯矩值的连线为基线,叠加该段相应简⽀梁的弯矩图。
1.4 刚结点处⼒矩的分配与杆端弯矩的传递利⽤⼒矩分配法中的结点分配和传递的原理,计算出结点的分配系数,将结点的不平衡⼒矩快速分配和传递给其他杆的近端及远端。
1.5 剪⼒分配法的应⽤对于在结点⽔平荷载作⽤下的排架(横梁EA为⽆穷⼤)、框架及框排架结构(横梁EI为⽆穷⼤),可以根据各个柱⼦的侧移刚度,计算出剪⼒分配系数,得到各柱的剪⼒。
在弯矩为零处作⽤该柱的剪⼒,按悬臂柱即可计算其柱端弯矩。
速画弯矩图的基本技巧2.1 单跨静定梁和超静定梁的弯矩图熟练掌握单跨静定梁在简单荷载作⽤下的弯矩图,单跨超静定梁的载常数和形常数。
2.2 集中⼒及约束处弯矩图的特征集中⼒处的弯矩图有尖⾓,尖⾓的⽅向同荷载的指向;集中⼒偶处的弯矩图有突变,突变的幅值等于⼒偶的⼤⼩,突变的变化与⼒偶的效应对应。
例如:对于⽔平杆,弯矩图若从左向右绘制,遇到顺时针转向的⼒偶,有增加右段杆下侧受拉的效应,因此弯矩图形向下突变。
固定端处的弯矩⼀般不为零;⾃由杆端、杆端铰⽀座及铰结点处,若⽆外⼒偶作⽤,该处的弯矩恒等于零;当直线段的中间铰上⽆集中⼒作⽤时,由于中间铰两侧的剪⼒相同,因此,中间铰两侧杆的弯矩图形连续,并且经过中间铰(铰结点处的弯矩恒等零);当直线段的滑动约束上⽆集中⼒作⽤时,由于滑动约束两侧的剪⼒为零,因此,滑动约束两侧杆的弯矩图形为⼀平⾏线;在两杆相连的刚结点处,两杆的杆端弯矩⼤⼩相同、同侧(⾥侧或外侧)受拉;在三杆相连的刚结点处,当已知两杆的杆端弯矩时,另外⼀杆的弯矩值可按结点的⼒矩平衡求得。
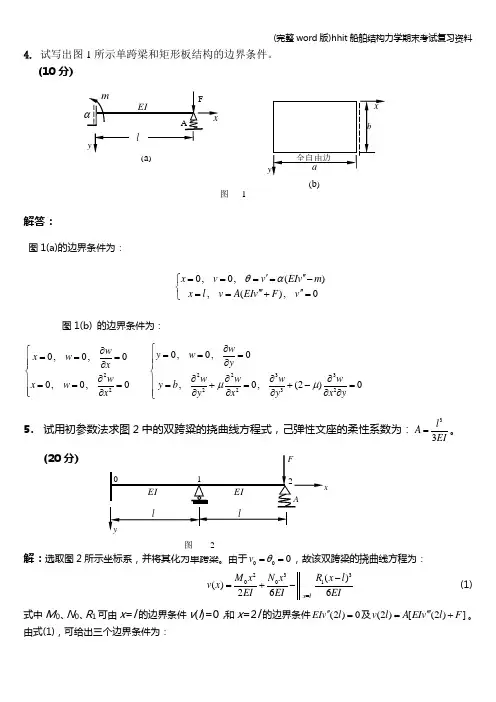
4. 试写出图1所示单跨梁和矩形板结构的边界条件。
(10分)解答:图1(a)的边界条件为:0,0,(),(),0x v v EIv m x l v A EIv F v θα'''====-⎧⎨'''''==+=⎩图1(b) 的边界条件为:22233222320,0,00,0,00,0,0,0,(2)0w w y w x w y x w w w w w x w y b x y x y x y μμ∂⎧∂⎧======⎪⎪∂⎪⎪∂⎨⎨∂∂∂∂∂⎪⎪====+=+-=⎪⎪∂∂∂∂∂∂⎩⎩5. 试用初参数法求图2中的双跨粱的挠曲线方程式,己弹性文座的柔性系数为:33l A EI =。
(20分)解:选取图200233001()()266x lM x N x R x l v x EI EIEI=-=+-(1)式中M 0、N 0、R 1可由x =l 的边界条件v (l )=0,和x =2l 的边界条件(2)0EIv l ''=及(2)[(2)]v l A EIv l F '''=+。
由式(1),可给出三个边界条件为:0000110010262042()363M N lM N l R l R l l M Nl N R F ⎫+=⎪⎪+-=⎬⎪⎪+-=-+⎭(2) 解方程组式(2),得0012610,,111111M Fl N F R F =-==将以上初参数及支反力代入式(1),得挠曲线方程式为:2335()()111133x lFl F Fv x x x x l EI EIEI==-+-- 一. (15分)用初参数法求图示梁的挠曲线方程,已知3l EI α=,36lA EI=,q 均布。
αAqEI ,L解:梁的挠曲线方程为:处的边界条件为: ;处的边界条件:故有:及有二式可解得:;于是梁的挠曲线方程为:三、(20分)用能量法求解如图所示梁的静不定性。

hhit-船舶结构力学-期末考试复习资料处的边界条件:故有:及有二式可解得:;于是梁的挠曲线方程为:三、(20分)用能量法求解如图所示梁的静不定性。
已知图中E 为常数,柔性系数,端部受集中弯矩m 作用,悬臂端的惯性矩是其余部分的2倍。
解:取挠曲线函数为 ,满足梁两端的位移边界条件,即x=0时,3/(12)A l EI LLmx=3L/2时,说明此挠曲线函数满足李兹法的要求,下面进行计算。
(1) 计算应变能。
此梁的应变能包括两部分,一是梁本身的弯曲应变能,二是弹性支座的应变能。
注意到梁是变断面的,故有总的应变能为(2)计算力函数。
此梁的力函数为(3) 计算总位能故梁的挠曲线方程为弹性支座处的挠度为四、(20)用位移法求解下图连续梁的静不定问题。
已知:, , , ,画出弯矩图。
解:设节点1、2、3的转角为,由题意可知。
根据平衡条件有节点1:节点2:其中:将其代入整理,联立求解得:P ql =1223l l l ==1223I I I ==/(6)l EI α=;故:;;;弯矩图:四、(20分)用力法求解下图连续梁的静不定问题。
已知:其中杆件EI为常数,分布力q2P/L,集中弯矩m=PL,画出弯矩图。
解: 本例的刚架为一次静不定结构,现将支座1处切开,加上未知弯矩M1,原来作用于节点1上的外力矩m可考虑在杆0-1上亦可考虑在杆1-2上,今考虑在杆1-2上。
于是得到两根单跨梁如上图所示。
变形连续条件为节点1转角连续,利用单跨梁的弯曲要素表,这个条件给出:解得:弯矩图:6、用位移法计算下面刚架结构的杆端弯矩为了书写方便,将钢架的各节点分别命名为0、1、2和3,如上面右图所示。
解:1、确定未知转角的数目本题0、1、2三个节点都可能发生转动,故有三个未知转角 。
解题时将以上三个节点作刚性固定。
2、计算各杆的固端弯矩M 01 = -qL212M 10 =qL212M 12 =M 13 =M 21 =M 31 =003、计算因转角引起的杆端弯矩M 01 =′4EI 01L θ0+2EI 01Lθ1M 10 =′4EI 01L θ1+2EI 01L θ0M 12 =′4EI 12L θ1+2EI 12L θ2M 21 =′4EI 12L θ2+2EI 12Lθ1θ0θ1θ2、、M 13 =′4EI 13Lθ1M 31 =′2EI 13θ14、对节点0、1、2列出弯矩平衡方程式对“0”节点:M 01M 01′+= -qL24EI 01θ0+2EI 01θ1+= 0= -qL28E L θ0+4E Lθ1+= 0对“1”节点:M 10M 10′+12M 12′+13M 13′+++=qL24EI 01θ1+2EI 01θ0+4EI 12L θ1+2EI 12L θ2+4EI 13L θ1+= 0=0=qL2124Eθ0++32E θ1+6E θ2= 021M21′+对“2”节点:4EI21θ2+2EI21θ1=12Eθ2+6Eθ1== 0 = 0即: -qL28Eθ0+4Eθ1+= 0qL2 124Eθ0++32ELθ1+6ELθ2= 012E L θ2+6ELθ1= 0θ1θ2θ0===11qL3864EqL3216EqL3432E-解得未知转角:5、计算各杆的杆端弯矩M01 = M10 =M01 +M01′M10M10 =′+= -qL24EI01θ0+2EI01θ1 += -qL28ELθ0+4ELθ1 += -qL28EL+4EL+11qL3864EqL3216E-( )=-0.083+0.102-0.0185=0qL2 124EI01θ1+2EI01θ0+=qL2 8Eθ1+4Eθ0 +=qL2 8E+4E+11qL3864EqL3216E-( )=0.083+0.051-0.037 =0.097qL2LM 13 =M 21M 3113M 13 =′ +M 21M 21′+4EI 21L θ2+2EI 21L θ1=12E L +6E ==M 31 =′2EI 13θ1 =M 12 =12M 12 =′ +12E + 6E qL3216E -( )qL3432E= -0.056+0.0139= - 0.042qL2qL3432E qL3216E -( )= 0qL3216E -( )= - 0.056qL2 = 6E qL3216E -( )= - 0.028qL2二、(16分)图1所示结构,已知作用在杆中点的弯矩M , 和EI ,l 用初参数法求单跨梁的挠曲线方程。

xy 船舶海洋结构力学复习1、请用初参数法确定图示单跨梁0-1的挠曲线方程,其中单跨梁的刚度为EI ,跨长为l ,均布载荷q 如图所示。
左端刚性固定,右端弹性支座的柔性系数EIl A 4831=。
2、请用初参数法确定图示单跨梁0-1的挠曲线方程,其中单跨梁的刚度为EI ,跨长为l ,均布载荷q 如图所示。
左右端均为刚性固定。
3、用力法计算图示结构1点的弯矩1M ,已知杆1-2及杆2-3的刚度均为EI ,l l l ==2312。
4、用力法计算图示结构2点的弯矩2M ,已知杆1-2及杆2-3的刚度均为EI ,l l l ==2312,ql P =,且P 作用于杆1-2的跨中。
qx5、请用位移法解如图所示结构,只写出正则方程即可,不必求解。
各杆的长度及刚度均为l 及EI 。
6、请用位移法解如图所示结构,只写出正则方程即可,不必求解。
各杆的长度及刚度均为l 及EI ,P 分别作用于杆1-2及2-3的跨中。
7、如图所示的结构,杆1-2长为l ,刚度为EI ,在右端受有集中力P 的作用。
试用应力能原理求右端在集中力P 作用下的挠度。
8、请用应力能原理计算图示简单钢架的端点1在外力 P 作用下的垂向位移。
已知112l l =,223l l =,各杆的刚度均为EI 。
9、设有一纵骨架式船,船底肋板间距为1.2m,纵骨间距为0.7m ,如要保证船底板的临界应力达到2/240mm N cr =σ,求所需板厚为多少?10、设有一纵骨架式船,船底纵桁为T 型材,断面尺寸为:翼板100⨯102m m ,腹板180⨯82m m 。
请分别计算纵桁翼板和腹板的临界应力cr σ。
11、四周自由支持的矩形板长边cm a 400=, 短边cm b 100=,板受垂直于板面的均布载荷2/05.0mm N q =作用,板厚cm t 8.0=,材料弹性模量为25101.2mm N E ⨯=。
(1)请写出板筒形弯曲的条件。
(2)按筒形弯曲画出本题矩形板的计算模型,并计算板中心的挠度及弯矩。



作为一名又土又木的工程师,离不开弯矩图,现在把它汇总起来,用以怀念当年的苦逼生活……
各种结构弯矩图的绘制及图例:
一、?方法步骤
1、确定支反力的大小和方向(一般情况心算即可计算出支反力)
●悬臂式刚架不必先求支反力;
●简支式刚架取整体为分离体求反力;
●求三铰式刚架的水平反力以中间铰C的某一边为分离体;
●对于主从结构的复杂式刚架,注意“先从后主”的计算顺序;
●对于复杂的组合结构,注意寻找求出支反力的突破口。
2、对于悬臂式刚架,从自由端开始,按照分段叠加法,逐段求作M图(M图画在受拉一侧);对于其它形式的刚架,从支座端开始,按照分段叠加法,逐段求作M图(M图画在受拉一侧)。
二、?观察检验M图的正确性
1、观察各个关键点和梁段的M图特点是否相符
●铰心的弯矩一定为零;
●集中力偶作用点的弯矩有突变,突变值与集中力偶相等;
●集中力作用点的弯矩有折角;
●均布荷载作用段的M图是抛物线,其凹凸方向与荷载方向要符合“弓箭法则”;
2、结构中的链杆(二力杆)没有弯矩;
3、结构中所有结点的杆端弯矩必须符合平衡特点。
各种结构弯矩图例如下:。
一. 判断(每题2分, 共20分) 1. 图示杆AB 与CD 的EI ,l 相等,但A 端的劲度系数(转动刚度)AB S 大于C 端的劲度系数(转动刚度)CD S 。
( )2. 图示刚架可利用力矩分配法求解。
( )3. 梁的绝对最大弯矩表示在一定移动荷载作用下梁某一截面的最大弯矩( )4. 图示结构E Q 影响线的AC 段纵标不为零。
()5. 静定结构及超静定结构的内力影响线都是由直线组成。
()6. 图示梁的绝对最大弯矩发生在距支座A 6.625m 处。
( )7. 图示体系设为自振频率)可如下计算稳态动位移。
33max 27175,6961(/)st st y Pl Pl y y EI EI θω===-8. 体系的动力自由度与质点的个数不一定相等。
9. 单自由度体系如图,,欲使顶端产生水平位移,需加水平力,则体系的自振频率。
10. 结构刚度矩阵是对称矩阵,即有i j ji K K ,这可由位移互等定理得到证明。
11. 图a 对称结构可简化为图b 来计算。
( )12. 图示结构横梁无弯曲变形,故其上无弯矩。
( )13. 位移法未知量的数目与结构的超静定次数有关。
( )14. 位移法的典型方程与力法的典型方程一样,都是变形谐调方程。
( ) 15. 用位移法可以计算超静定结构,也可以计算静定结构。
( ) 16. 图b 为图a 用位移法求解时的基本体系和基本未知量,其位移法典型方程中的自由项,。
( )Z为水平横梁的水平位移,则图应如图b形状。
17.图示结构a用位移法求解时,基本未知量3()18.图示结构在荷载作用下的弯矩图形状是正确的。
( )19.力矩分配法中的分配系数、传递系数与外来因素(荷载、温度变化等)有关。
()20.力矩分配法仅适用于解无线位移结构。
()21.图示体系是几何不变体系。
22.图示体系是几何不变体系。
N为30kN。
()23.图示拱在荷载作用下,DE24.图示结构中的反力2H kN。
船舶结构力学第一篇:船舶结构力学船舶结构力学一、基本概念部分1、坐标系船舶结构力学与工程力学的坐标系比较如下图:yz0y 船舶结构力学的坐标系xz工程力学的坐标系0x2、符号规则船船结构力学与工程力学的符号规则有相同点和不同点,弯矩四要素的符号基本不同,主要是指弯矩、剪力和挠度的符号规则不同,而转角的符号一致,即是以顺针方向的转角为正角。
船舶结构力学的符号规则如下图所示。
MN工程力学的符号规则NMMNN船舶结构力学力法的符号规则MMNNM船舶结构力学位移法的符号规则3、约束与约束力对物体的运动预加限制的其他物体称为约束。
约束施加于被约束物体的力称为约束力或约束反力,支座的约束力也叫支反力。
4、支座的类型及其边界条件支座有四类:简支端(包括固定支座与滚动支座)、刚性固定端、弹性支座与弹性固定端。
各类支座的图示及其边界条件如下图:1)简支端2)刚性固定端边界条件:v = 0,v″ = 0边界条件:v = 0,v′ = 03)弹性支座边界条件:v =-AEIv′′(′支座左端)v = AEIv′′′(支座右端)(A为支座的柔性系数)′′′4)弹性固定端边界条件:v =′αEIv′′(左v =-′αEIv′′(右端)端)(α为固定端的柔性系数)5、什么是静定梁?什么是超静定梁?如何求解超静定梁?梁的未知反力与静平衡方程个数相同时,此梁为静定梁。
反之,如果梁的未知反力多于梁的静平衡方程数目时,此时的梁称为超静定梁。
超静定梁可用力法求解。
6、什么是梁的弯曲四要素,查弯曲要素表要注意哪些事项?梁的剪力、弯矩、转角和挠度称为梁的弯曲四要素。
查弯曲要素表要注意,四个要素的符号,在位移法中查梁的固端弯矩时要注意把梁的左端弯矩值加一个负号。
7、简述两类力法基本方程的内容力法方程有两类:一是“去支座法”。
是以支座反力为未知量,根据变形条件所列的方程。
二是“断面法”。
以支座断面弯矩为未知量,根据变形连续性条件所列的方程。
结构力学知识点总结
第三章
1)剪力图上某点切线的斜率等于该点横向分布荷载的集度,但正负号相反。
2)弯距图上某点切线的斜率等于该点的剪力。
3)弯距图上某点的曲率等于该点的横向分布荷载的集度,但正负号相反。
4)轴力图上某点的斜率等于该点轴向分布荷载的集度 qx ,但正负号相反
因此,若剪力等于0,M 图平行于杆轴;
若剪力为常数,则 M 图为斜直线;
若剪力为 x 的一次函数,即为均布荷载时,M 图为抛物线。
2不同荷载下弯矩图与剪力图的形状特征表
三、分段叠加法作弯矩图
1叠加原理:结构中由全部荷载所产生的内力或变形等于各种荷载单独作用所产生的效果的总和。
2理论依据:力的独立作用原理。
3应用条件:材料服从“虎克定律”,且是小变形。
即:只有线性变形体才适用叠加原理。
4基本步骤:
1)选定控制截面,求控制截面在全部荷载作用下的M 值,将各控制面的M 值按比例画在图上,在各控制截面间连以直线——基线。
控制截面:集中力或者集中力偶作用截面,分布荷载的起点和终点以及梁的左、右端支座截面等。
2)对于各控制截面之间的直杆段,在基线上叠加该杆段作为简支梁时由杆间荷载产生的M图。
3)当控制截面间无荷载时,根据控制截面的弯矩,即可作出直线弯矩图(连接控制截面弯矩的纵坐标顶点)。
值得注意的是:弯矩图的叠加,是指纵坐标(竖距)的叠加,而不是指图形的简单拼合
一、静定多跨梁的构造特征和受力特征
1. 构造特征
静定多跨梁由基本部分和附属部分组成。
组成的次序是先固定基本部分,再固定附属部分。
(1)单悬臂式。