线段和差的最值问题

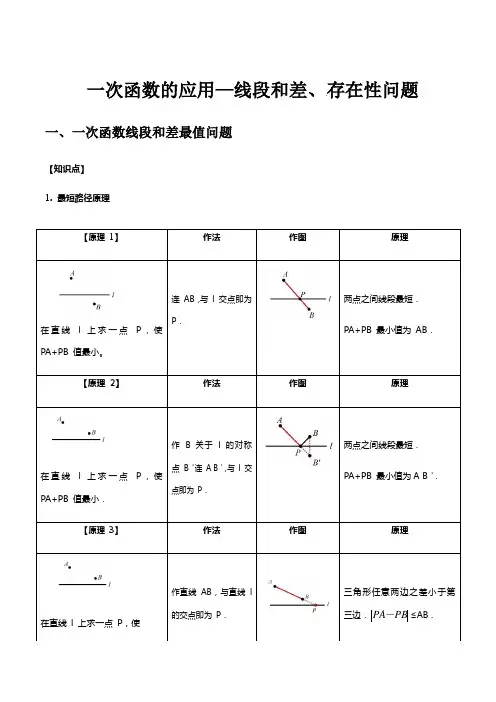
一次函数的应用—线段和差、存在性问题一、一次函数线段和差最值问题【知识点】1. 最短路径原理【原理1】作法作图原理在直线l 上求一点P，使PA+PB 值最小。

连AB，与l 交点即为P．两点之间线段最短．PA+PB 最小值为AB．【原理2】作法作图原理在直线l 上求一点P，使PA+PB 值最小．作 B 关于l 的对称点B＇连A B＇，与l 交点即为P．两点之间线段最短．PA+PB 最小值为A B＇．【原理3】作法作图原理在直线l 上求一点P，使作直线AB，与直线l的交点即为P．三角形任意两边之差小于第三边．≤AB .PBPA－（1）求线段和最小时动点坐标或直线解析式；（2）求三角形周长最小值；（3）求线段差最大时点的坐标或直线解析式。

3. 口诀：“和小异，差大同”（一）一次函数线段和最小值问题【例题讲解】★★☆例题1．在平面直角坐标系xOy中，y轴上有一点P，它到点(4,3)A，(3,1)B 的距离之和最小，则点P的坐标是()A．(0,0)B．4(0,)7C．5(0,)7D．4(0,)5的值最大 .【原理4】作法作图原理在直线l 上求一点P，使的值最大 .作B 关于l 的对称点B＇作直线A B＇，与l交点即为P．三角形任意两边之差小于第三边．≤A B＇ .PB PA－PB PA－PB PA－★★☆练习1．如图，在平面直角坐标系中，已知点(2,3)B-，在x轴上存在点P到A，B两点的A，点(2,1)距离之和最小，则P点的坐标是．★★☆练习2．如图，直线34120+-=与x轴、y轴分别交于点B、A两点，以线段AB为边在第一象限x y内作正方形ABCD．若点P为x轴上的一个动点，求当PC PD+的长最小时点P的坐标．★★☆例题2．在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，3∆的周长最小时，求点E OB=，D为边OB的中点，若E为x轴上的一个动点，当CDEOA=，4的坐标()A ．(3,0)-B ．(1,0)C ．(0,0)D ．(3,0)★★☆练习1．如图，在平面直角坐标系中，点A 、B 的坐标分别为(1,4)和(3,0)，点C 是y 轴上的一个动点，连接AC 、BC ，当ABC ∆的周长最小值时，ABC ∆的面积为 ．★★☆练习2．如图，在平面直角坐标系中，直线122y x =+与x 轴、y 轴分别交于A 、B 两点，以AB 为边 在第二象限内作正方形ABCD ．（1）求点A 、B 的坐标，并求边AB 的长；（2）求点C 和点D 的坐标；（3）在x 轴上找一点M ，使MDB ∆的周长最小，请求出M 点的坐标，并直接写出MDB ∆的周长最小值．（二）一次函数线段差最大值问题【例题讲解】★★☆例题1．已知，如图点(1,1)A，(2,3)B-，点P为x轴上一点，当||PA PB-最大时，点P 的坐标为()A．1(,0)2B．5(,0)4C．1(,0)2-D．(1,0)★★☆练习1．平面直角坐标系中，已知(4,3)A、(2,1)B，x轴上有一点P，要使PA PB-最大，则P点坐标为★★☆练习2．如图，在平面直角坐标系中，点A的坐标为(0,4)，点B的坐标为(6,0)，点P在一次函数1322y x =+的图象上运动，则PB PA -的最大值为( )A ．2B ．233C ．4D ．143【题型知识点总结】一次函数最短路径问题注意事项：1. 根据“和小异，差大同”判断是否需要作对称；2. 作对称时注意要选取动点运动的直线为对称轴作某一定点的对称点。

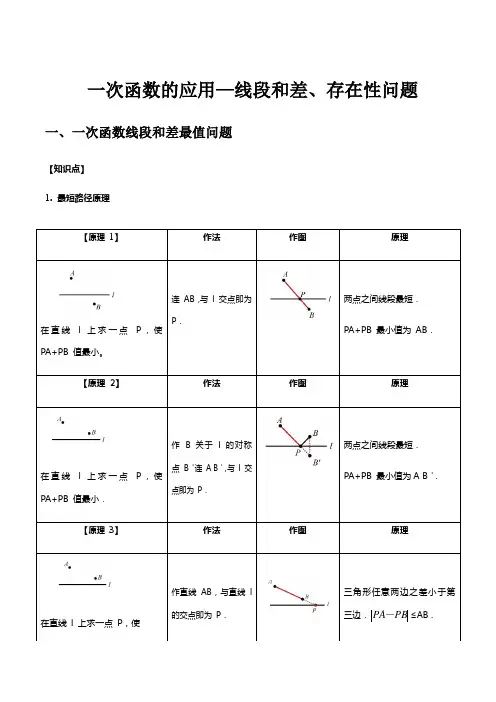
一次函数的应用—线段和差、存在性问题一、一次函数线段和差最值问题【知识点】1. 最短路径原理【原理1】作法作图原理在直线l 上求一点P，使PA+PB 值最小。

连AB，与l 交点即为P．两点之间线段最短．PA+PB 最小值为AB．【原理2】作法作图原理在直线l 上求一点P，使PA+PB 值最小．作 B 关于l 的对称点B＇连A B＇，与l 交点即为P．两点之间线段最短．PA+PB 最小值为A B＇．【原理3】作法作图原理在直线l 上求一点P，使作直线AB，与直线l的交点即为P．三角形任意两边之差小于第三边．≤AB .PBPA－（1）求线段和最小时动点坐标或直线解析式； （2）求三角形周长最小值；（3）求线段差最大时点的坐标或直线解析式。

3. 口诀：“和小异，差大同”（一）一次函数线段和最小值问题【例题讲解】★★☆例题1．在平面直角坐标系xOy 中，y 轴上有一点P ，它到点(4,3)A ，(3,1)B 的距离之和最小，则点P 的坐标是( ) A ．(0,0)B ．4(0,)7C ．5(0,)7D ．4(0,)5【答案】C的值最大 .【原理 4】作法作图原理在直线 l 上求一点 P ，使的值最大 .作 B 关于 l 的对称点 B ＇作直线 A B ＇，与 l 交点即为 P ．三角形任意两边之差小于第三边．≤A B ＇ .PB PA －PB PA －PB PA －【解析】解：作A 关于y 轴的对称点C ，连接BC 交y 轴于P ，则此时AP PB +最小，即此时点P 到点A 和点B 的距离之和最小，(4,3)A ，(4,3)C ∴-，设直线CB 的解析式是y kx b =+，把C 、B 的坐标代入得：3413k bk b =-+⎧⎨-=+⎩，解得：47k =-，57b =，4577y x ∴=-+，把0x =代入得：57y =， 即P 的坐标是5(0,)7，故选：C ．【备注】本题考查了轴对称-最短路线问题，一次函数的解析式，坐标与图形性质等知识点，关键是能画出P 的位置，题目比较典型，是一道比较好的题目．★★☆练习1．如图，在平面直角坐标系中，已知点(2,3)A ，点(2,1)B -，在x 轴上存在点P 到A ，B 两点的距离之和最小，则P 点的坐标是 ．【答案】(1,0)-【解析】解：作A 关于x 轴的对称点C ，连接BC 交x 轴于P ，则此时AP BP +最小，A 点的坐标为(2,3)，B 点的坐标为(2,1)-，(2,3)C ∴-，设直线BC 的解析式是：y kx b =+，把B 、C 的坐标代入得：2123k b k b -+=⎧⎨+=-⎩解得11k b =-⎧⎨=-⎩．即直线BC 的解析式是1y x =--，当0y =时，10x --=，解得：1x =-，P ∴点的坐标是(1,0)-．故答案为：(1,0)-．【备注】本题考查了一次函数图象上点的坐标特征，用待定系数法求一次函数的解析式，轴对称-最短路线问题的应用，关键是能找出P 点，题目具有一定的代表性，难度适中．★★☆练习2．如图，直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点，以线段AB 为边在第一象限内作正方形ABCD ．若点P 为x 轴上的一个动点，求当PC PD +的长最小时点P 的坐标．【答案】详见解析【解析】解：直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点，则点A 、B 的坐标分别为：(0,3)，(4,0)，如图所示，过点C 作CH x ⊥轴交于点H ，90ABO BAO ∠+∠=︒，90ABO CBH ∠+∠=︒，CBH BAO ∴∠=∠，又90AOB CHB ∠=∠=︒，AB BC =，()AOB BHC AAS ∴∆≅∆，4CH OB ∴==，3HB OA ==，故点(7,4)C ，同理可得点(3,7)D ，确定点C 关于x 轴的对称点(7,4)C '-，连接C D '交x 轴于点P ，则此时PC PD +的长最小，将点C '、D 的坐标代入一次函数表达式并解得： 直线CD 的表达式为：116144y x =-+， 当0y =时，6111x =，故点61P，0)．(11【备注】本题考查的是一次函数上坐标点的特征，涉及到点的对称性、正方形性质等，本题的难点在于：通过证明三角形全等，确定点C、D的坐标．★★☆例题2．在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，3OB=，D为边OB的中点，若E为x轴上的一个动点，当CDE∆的周长最小时，求点E OA=，4的坐标()A．(3,0)-B．(1,0)C．(0,0)D．(3,0)【答案】B【解析】解：如图，作点D关于x轴的对称点D'，连接CD'与x轴交于点E，连接DE．若在边OA上任取点E'与点E不重合，连接CE'、DE'、D E''由DE CE D E CE CD D E CE DE CE'+'=''+'>'='+=+，可知CDE∆的周长最小．OB=，D为边OB的中点，42∴=，OD∴，(0,2)D在矩形OACB 中，3OA =，4OB =，D 为OB 的中点，3BC ∴=，2D O DO '==，6D B '=，//OE BC ，Rt ∴△D OE Rt '∽△D BC '，∴OE D OBC D B '=' 即236OE = 1OE =，∴点E 的坐标为(1,0)故选：B ．【备注】此题主要考查轴对称--最短路线问题，解决此类问题，一般都是运用轴对称的性质，将求折线问题转化为求线段问题，其说明最短的依据是三角形两边之和大于第三边．★★☆练习1．如图，在平面直角坐标系中，点A 、B 的坐标分别为(1,4)和(3,0)，点C 是y 轴上的一个动点，连接AC 、BC ，当ABC ∆的周长最小值时，ABC ∆的面积为 ．【答案】3【解析】解：如图，作点A 关于y 轴的对称点A '，连接A B '交y 轴于点C '，此时ABC ∆'的周长最小，设直线A B ' 的解析式为y kx b =+，(1,4)A '-，(3,0)B ，∴430k b k b -+=⎧⎨+=⎩，1k ∴=-，3b =，∴直线A B ' 的解析式为3y x =-+，当0x =时，3y =，(0,3)C ∴'，ABC AA BAA C S SS∆'''∴=-11242122=⨯⨯-⨯⨯ 413=-=．所以ABC ∆'的面积为3．故答案为：3．【备注】本题考查了轴对称、最短路线问题、坐标与图形性质、三角形的面积，解决本题的关键是掌握轴对称的性质．★★☆练习2．如图，在平面直角坐标系中，直线122y x =+与x 轴、y 轴分别交于A 、B 两点，以AB 为边 在第二象限内作正方形ABCD ．（1）求点A 、B 的坐标，并求边AB 的长；（2）求点C 和点D 的坐标；（3）在x 轴上找一点M ，使MDB ∆的周长最小，请求出M 点的坐标，并直接写出MDB ∆的周长最小值．【答案】详见解析【解析】解： （1）对于直线122y x =+， 令0x =，得到2y =；令0y =，得到4x =-，(4,0)A ∴-，(0,2)B ，即4OA =，2OB =， 则224225AB =+=；（2）过D 作DE x ⊥轴，过C 作CF y ⊥轴，四边形ABCD 为正方形，AB BC AD ∴==，90ABC BAD BFC DEA AOB ∠=∠=∠=∠=∠=︒，90FBC ABO ∠+∠=︒，90ABO BAO ∠+∠=︒，90DAE BAO ∠+∠=︒，FBC OAB EDA ∴∠=∠=∠，()DEA AOB BFC AAS ∴∆≅∆≅∆，2AE OB CF ∴===，4DE OA FB ===，即426OE OA AE =+=+=，246OF OB BF =+=+=，则(6,4)D -，(2,6)C -；（3）如图所示，连接BD ，找出B 关于y 轴的对称点B '，连接DB '，交x 轴于点M ，此时BM MD DM MB DB +=+'='最小，即BDM ∆周长最小，(0,2)B ，(0,2)B ∴'-，设直线DB '解析式为y kx b =+，把(6,4)D -，(0,2)B '-代入得：642k b b -+=⎧⎨=-⎩，解得：1k =-，2b =-，∴直线DB '解析式为2y x =--，令0y =，得到2x =-，则M 坐标为(2,0)-， 此时MDB ∆的周长为21062+．【备注】本题属于一次函数综合题，涉及的知识有：待定系数法求一次函数解析式，坐标与图形性质，勾 股定理，全等三角形的判定与性质，正方形的性质，对称性质，以及一次函数与坐标轴的交点，熟练掌握 性质及定理是解本题的关键（二）一次函数线段差最大值问题【例题讲解】★★☆例题1．已知，如图点(1,1)A ，(2,3)B -，点P 为x 轴上一点，当||PA PB -最大时，点P的坐标为( )A ．1(,0)2B ．5(,0)4C ．1(,0)2-D ．(1,0)【答案】A【解析】解：作A 关于x 轴对称点C ，连接BC 并延长交x 轴于点P ， (1,1)A ，C ∴的坐标为(1,1)-，连接BC ，设直线BC 的解析式为：y kx b =+，∴123k b k b +=-⎧⎨+=-⎩， 解得：21k b =-⎧⎨=⎩， ∴直线BC 的解析式为：21y x =-+， 当0y =时，12x =， ∴点P 的坐标为：1(2，0)，当B ，C ，P 不共线时，根据三角形三边的关系可得：||||PA PB PC PB BC -=-<，∴此时||||PA PB PC PB BC -=-=取得最大值．故选：A ．【备注】此题考查了轴对称、待定系数法求一次函数的解析式以及点与一次函数的关系．此题难度较大，解题的关键是找到P 点，注意数形结合思想与方程思想的应用．★★☆练习1．平面直角坐标系中，已知(4,3)A 、(2,1)B ，x 轴上有一点P ，要使PA PB -最大，则P 点坐 标为【答案】(1,0)【解析】解：(4,3)A 、(2,1)B ，x 轴上有一点P ，||PA PB AB ∴-，∴当A ，B ，P 三点共线时，PA PB -最大值等于AB 长，此时，设直线AB 的解析式为y kx b =+，把(4,3)A 、(2,1)B 代入，可得3412k b k b =+⎧⎨=+⎩， 解得11k b =⎧⎨=-⎩， ∴直线AB 的解析式为1y x =-，令0y =，则1x =，P ∴点坐标为(1,0)，故答案为：(1,0)． 【备注】本题主要考查了坐标与图形性质，利用待定系数法求得直线AB 的解析式是解决问题的关键． ★★☆练习2．如图，在平面直角坐标系中，点A 的坐标为(0,4)，点B 的坐标为(6,0)，点P 在一次函数1322y x =+的图象上运动，则PB PA -的最大值为( )A ．2B ．233C ．4D ．143【答案】C【解析】解：如图，作点A 关于直线1322y x =+的对称点K ，连接AK 交直线于H ，连接PK ．AK PH ⊥，(0,4)A ，∴直线AK 的解析式为24y x =-+，由132224y x y x ⎧=+⎪⎨⎪=-+⎩，解得12x y =⎧⎨=⎩， (1H ∴，20，AH KH =，(2,0)K ∴．PB PA PB PK KB ∴-=-，∴当点P 在BK 的延长线上时，P B P K BK '-'=的值最大，最大值为624-=，故选：C ．【备注】本题考查一次函数图象上的点的特征、轴对称等知识，解题的关键是学会利用对称解决最值问题 属于中考常考题型．【题型知识点总结】一次函数最短路径问题注意事项：1. 根据“和小异，差大同”判断是否需要作对称；2. 作对称时注意要选取动点运动的直线为对称轴作某一定点的对称点。

初中几何中线段和差的最大值与最小值典型分析(最全)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN初中几何中线段和（差）的最值问题一、两条线段和的最小值。

基本图形解析：（对称轴为：动点所在的直线上）一）、已知两个定点：1、在一条直线m 上，求一点P ，使PA+PB 最小； （1）点A 、B 在直线m 两侧：（2）点A 、B 在直线同侧：A 、A ’ 是关于直线m 的对称点。

2、在直线m 、n 上分别找两点P 、Q ，使PA+PQ+QB 最小。

（1）两个点都在直线外侧：（2）一个点在内侧，一个点在外侧： （3）两个点都在内侧：mm A Bm B mA Bmnmnnmn（4）、台球两次碰壁模型变式一：已知点A 、B 位于直线m,n 的内侧，在直线n 、m 分别上求点D 、E 点，使得围成的四边形ADEB 周长最短.填空：最短周长=________________变式二：已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二）、一个动点，一个定点： （一）动点在直线上运动：n点B 在直线n 上运动，在直线m 上找一点P ，使PA+PB 最小（在图中画出点P 和点B ） 1、两点在直线两侧：2、两点在直线同侧：（二）动点在圆上运动点B 在⊙O 上运动，在直线m 上找一点P ，使PA+PB 最小（在图中画出点P 和点B ）1、点与圆在直线两侧：2、点与圆在直线同侧：m nmnmnmmm三）、已知A 、B 是两个定点，P 、Q 是直线m 上的两个动点，P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点，使得PA+PQ+QB 的值最小。

(原理用平移知识解)（1）点A 、B 在直线m 两侧：过A 点作AC ∥m,且AC 长等于PQ 长，连接BC,交直线m 于Q,Q 向左平移PQ 长，即为P 点，此时P 、Q 即为所求的点。

初中几何中线段和（差）的最值问题一、两条线段和的最小值。

基本图形解析：（对称轴为：动点所在的直线上）一）、已知两个定点：1、在一条直线m 上，求一点P ，使PA+PB 最小； （1）点A 、B 在直线m 两侧：（2）点A 、B 在直线同侧：A 、A ’ 是关于直线m 的对称点。

2、在直线m 、n 上分别找两点P 、Q ，使PA+PQ+QB 最小。

（1）两个点都在直线外侧：（2）一个点在内侧，一个点在外侧：m m mmABmn m nnmn（3）两个点都在内侧：（4）、台球两次碰壁模型变式一：已知点A 、B 位于直线m,n 的内侧，在直线n 、m 分别上求点D 、E 点，使得围成的四边形ADEB 周长最短.填空：最短周长=________________变式二：已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二）、一个动点，一个定点： （一）动点在直线上运动：点B 在直线n 上运动，在直线m 上找一点P ，使PA+PB 最小（在图中画出点P 和点B ） 1、两点在直线两侧：nnm Bnn2、两点在直线同侧：（二）动点在圆上运动点B 在⊙O 上运动，在直线m 上找一点P ，使PA+PB 最小（在图中画出点P 和点B ） 1、点与圆在直线两侧：2、点与圆在直线同侧：三）、已知A 、B 是两个定点，P 、Q 是直线m 上的两个动点，P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点，使得PA+PQ+QB 的值最小。

(原理用平移知识解) （1）点A 、B 在直线m 两侧：mnmmmmm过A 点作AC ∥m,且AC 长等于PQ 长，连接BC,交直线m 于Q,Q 向左平移PQ 长，即为P 点，此时P 、Q 即为所求的点。

（2）点A 、B 在直线m 同侧： 练习题1．如图，∠AOB =45°，P 是∠AOB 内一点，PO =10，Q 、R 分别是OA 、OB 上的动点，求△PQR 周长的最小值为 ．2、 如图1，在锐角三角形ABC 中，AB=4,∠BAC=45°，∠BAC 的平分线交BC 于点D ，M,N 分别是AD 和AB 上的动点，则BM+MN 的最小值为 ． 3、如图，在锐角三角形ABC 中 ，AB=52，∠BAC=45，BAC 的平分线交BC 于D ，M 、N 分别是AD 和AB 上的动点，则BM+MN 的最小值是多少mABB'EQ PmABQPQ4、如图4所示，等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.若AE=2,EM+CM的最小值为.5、如图3，在直角梯形ABCD中，∠ABC＝90°，AD∥BC，AD＝4，AB＝5，BC＝6，点P是AB 上一个动点，当PC＋PD的和最小时，PB的长为__________．6、如图4，等腰梯形ABCD中，AB=AD=CD=1，∠ABC=60°，P是上底，下底中点EF直线上的一点，则PA+PB的最小值为．7、如图5菱形ABCD中，AB=2，∠BAD=60°，E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值为．8、如图，菱形ABCD的两条对角线分别长6和8，点P是对角线AC上的一个动点，点M、N分别是边AB、BC的中点，则PM+PN的最小值是9、如图，圆柱形玻璃杯，高为12cm，底面周长为18cm，在杯内离杯底3cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为________cm．10、如图，菱形ABCD中，AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为11、如图，正方形ABCD的边长为2，E为AB的中点，P是AC上一动点．则PB+PE的最小值是12、如图6所示，已知正方形ABCD的边长为8，点M在DC上，且DM=2，N是AC上的一个动点，则DN+MN的最小值为．13、如图，正方形ABCD的边长是2，∠DAC的平分线交DC于点E，若点P、Q分别是AD和AE上的动点，则DQ+PQ的最小值为．14、如图7，在边长为2cm的正方形ABCD中，点Q为BC边的中点，点P为对角线AC上一动点，连接PB、PQ，则△PBQ周长的最小值为cm．（结果不取近似值）．15、如图，⊙O的半径为2，点A、B、C在⊙O上，OA⊥OB，∠AOC=60°，P是OB上一动点，则PA+PC的最小值是．16、如图8，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN＝30°，B为AN弧的中点，P是直径MN上一动点，则PA＋PB的最小值为( )(A)2 (B) (C)1 (D)2解答题1、如图9，正比例函数y=x的图象与反比例函数y=（k≠0）在第一象限的图象交于A 点，过A点作x轴的垂线，垂足为M，已知三角形OAM的面积为1.（1）求反比例函数的解析式；（2）如果B为反比例函数在第一象限图象上的点（点B与点A不重合），且B点的横坐标为1，在x轴上求一点P，使PA+PB最小.2、如图，一元二次方程x2+2x-3=0的二根x1，x2（x1＜x2）是抛物线y=ax2+bx+c 与x轴的两个交点B，C的横坐标，且此抛物线过点A（3，6）．（1）求此二次函数的解析式；（2）设此抛物线的顶点为P，对称轴与AC相交于点Q，求点P和点Q的坐标；（3）在x轴上有一动点M，当MQ+MA取得最小值时，求M点的坐标．3、如图10，在平面直角坐标系中，点A的坐标为（1，），△AOB的面积是.（1）求点B的坐标；（2）求过点A、O、B的抛物线的解析式；（3）在（2）中抛物线的对称轴上是否存在点C，使△AOC的周长最小若存在，求出点C的坐标；若不存在，请说明理由；4．如图，抛物线y ＝35x 2－185x ＋3和y 轴的交点为A ，M 为OA 的中点，若有一动点P ，自M点处出发，沿直线运动到x 轴上的某点（设为点E ），再沿直线运动到该抛物线对称轴上的某点（设为点F ），最后又沿直线运动到点A ，求使点P 运动的总路程最短的点E ，点F 的坐标，并求出这个最短路程的长．5．如图，已知在平面直角坐标系xOy 中，直角梯形OABC 的边OA 在y 轴的正半轴上，OC 在x 轴的正半轴上，OA =AB =2，OC =3，过点B 作BD ⊥BC ，交OA 于点D ．将∠DBC 绕点B 按顺时针方向旋转，角的两边分别交y 轴的正半轴、x 轴的正半轴于点E 和F ． （1）求经过A 、B 、C 三点的抛物线的解析式； （2）当BE 经过（1）中抛物线的顶点时，求CF 的长；（3）在抛物线的对称轴上取两点P 、Q （点Q 在点P 的上方），且PQ ＝1，要使四边形BCPQ 的周长最小，求出P 、Q 两点的坐标．6．如图，已知平面直角坐标系，A，B两点的坐标分别为A(2，－3），B(4，－1）若C(a，0)，D(a+3，0)是x轴上的两个动点，则当a为何值时，四边形ABDC的周长最短．7、如图11，在平面直角坐标系中，矩形的顶点O在坐标原点，顶点A、B分别在x 轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点.（1）若E为边OA上的一个动点，当△CDE的周长最小时，求点E的坐标；（2）若E、F为边OA上的两个动点，且EF=2，当四边形CDEF的周长最小时，求点E、F的坐标.v1.0 可编辑可修改二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析：1、在一条直线m 上，求一点P ，使PA 与PB 的差最大； （1）点A 、B 在直线m 同侧：解析：延长AB 交直线m 于点P ，根据三角形两边之差小于第三边，P ’A —P ’B ＜AB ，而PA —PB=AB 此时最大，因此点P 为所求的点。

线段和差最值问题解题技巧
1. 嘿，你知道吗？平移线段有时就像变魔术一样神奇！比如在这个问题里，把这两条线段平移到一起，你看，是不是一下子就找到答案啦！
2. 哇塞，利用对称性质来解决线段和差最值问题，那可真是绝了呀！就像给问题找到了一把万能钥匙。

比如这个图形，通过对称，一下子就柳暗花明了呢！
3. 哎呀呀，有时候转换思维超重要的啦！别死磕一种方法呀，就像走不通的路咱就换一条呗。

像这个例子，转换一下思考角度，答案不就出来啦！
4. 嘿，当遇到难题不要慌，想想三角形三边关系呀！这就好比给你指了一条明路。

比如看到这样的条件，马上想起三边关系，难题迎刃而解咯！
5. 哇哦，构造辅助线简直就是秘密武器呀！就如同给问题搭了一座桥。

像这个情况，构造出合适的辅助线，一下子就突破难关啦！
6. 哈哈，把复杂问题简单化，不就轻松多了吗？就像把一大团乱麻理清楚。

看这个例子，简单化之后，答案显而易见呀！
7. 哟呵，关注特殊点和特殊位置呀，这可是关键呢！如同发现了宝藏的线索。

像这个情况，抓住特殊点，难题瞬间攻克啦！
8. 嘿呀，寻找等量关系也很重要呀，就像在迷宫里找到了正确的路线。

看看这个例子，一旦找到等量关系，答案就水到渠成啦！
9. 最后我想说，掌握了这些解题技巧，遇到线段和差最值问题根本不用怕呀！它们就是我们的得力助手，能让我们在数学的海洋里畅游无阻呀！。

线段和（差）最值问题引例：如图，有一圆形透明玻璃容器，高15cm，底面周长为24cm，在容器内壁柜上边缘4cm 的A处，停着一只小飞虫，一只蜘蛛从容器底部外向上爬了3cm的B处时（B处与A处恰好相对），发现了小飞虫，问蜘蛛怎样爬去吃小飞虫最近？它至少要爬多少路？（厚度忽略不计）．Ⅰ．专题精讲：最值问题是一类综合性较强的问题，而线段和（差）问题，要归归于几何模型：（1）归于“两点之间的连线中，线段最短”凡属于求“变动的两线段之和的最小值”时，大都应用这一模型．（2）归于“三角形两边之差小于第三边”凡属于求“变动的两线段之差的最大值”时，大都应用这一模型．Ⅱ．典型例题剖析:一．归入“两点之间的连线中，线段最短”Ⅰ．“饮马”几何模型：条件：如下左图，A、B是直线l同旁的两个定点．问题：在直线l上确定一点P，使PA＋PB的值最小．模型应用：1．如图，正方形ABCD的边长为2，E为AB的中点，P是AC上一动点．则PB+PE的最小值是．2．如图，⊙O的半径为2，点A、B、C在⊙O上，OA⊥OB，∠AOC=60°，P是OB上一动点，则PA+PC的最小值是．3．如图，在锐角△ABC中，AB＝42，∠BAC＝45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是．第1题第2题第3题第4题5．如图，等腰梯形ABCD 中，AB ＝AD ＝CD ＝1，∠ABC ＝60°，P 是上底，下底中点EF 直线上的一点，则PA +PB 的最小值为 ．6．如图，MN 是半径为1的⊙O 的直径，点A 在⊙O 上，∠AMN ＝30°，B 为AN 弧的中点，P 是直径MN 上一动点，则PA ＋PB 的最小值为 ．7．已知A (－2，3)，B (3，1)，P 点在x 轴上，若P A ＋PB 长度最小，则最小值为 ． 8．已知：如图所示，抛物线y ＝－x 2＋bx ＋c 与x 轴的两个交点分别为A (1，0)，B (3，0)． （1）求抛物线的解析式；（2）设点P 在该抛物线上滑动，且满足条件S △PAB ＝1的点P 有几个？并求出所有点P 的坐标； （3）设抛物线交y 轴于点C ，问该抛物线对称轴上是否存在点M ，使得△MAC 的周长最小？若存在，求出点M 的坐标；若不存在，请说明理由．Ⅱ．台球两次碰壁模型已知点A 位于直线m ，n 的内侧，在直线m 、n 分别上求点P 、Q 点，使PA +PQ +QA 周长最短.变式：已知点A 、B 位于直线m ，n 的内侧，在直线m 、n 分别上求点D 、E 点，使得围成的四边形ADEB 周长最短.第5题 第6题 第7题模型应用：1．如图，∠AOB=45°，P是∠AOB内一点，PO=10，Q、R分别是OA、OB上的动点，求△PQR 周长的最小值．2．如图，已知平面直角坐标系，A，B两点的坐标分别为A(2，－3），B(4，－1）设M，N分别为x轴和y轴上的动点，请问：是否存在这样的点M(m，0），N(0，n),使四边形ABMN的周长最短？若存在，请求出m＝______，n＝______（不必写解答过程）；若不存在，请说明理由．中考赏析：1．著名的恩施大峡谷（A）和世界级自然保护区星斗山（B）位于笔直的沪渝高速公路X同侧，AB=50km、B到直线X的距离分别为10km和40km，要在沪渝高速公路旁修建一服务区P，向A、B两景区运送游客．小民设计了两种方案，图（1）是方案一的示意图（AP与直线X垂直，垂足为P），P到A、B的距离之和S1＝PA＋PB，图（2）是方案二的示意图（点A关于直线X的对称点是A'，连接BA'交直线X于点P），P到A、B的距离之和S2＝P A＋PB．（1）求S1、S2，并比较它们的大小；（2）请你说明S2＝PA＋PB的值为最小；（3）拟建的恩施到张家界高速公路Y与沪渝高速公路垂直，建立如图（3）所示的直角坐标系，B到直线Y的距离为30km，请你在X旁和Y旁各修建一服务区P、Q，使P、A、B、Q组成的四边形的周长最小．并求出这个最小值．2．如图，抛物线y ＝35x 2－185x ＋3和y 轴的交点为A ，M 为OA 的中点，若有一动点P ，自M 点处出发，沿直线运动到x 轴上的某点（设为点E ），再沿直线运动到该抛物线对称轴上的某点（设为点F ），最后又沿直线运动到点A ，求使点P 运动的总路程最短的点E ，点F 的坐标，并求出这个最短路程的长．Ⅲ．已知A 、B 是两个定点，P 、Q 是直线m 上的两个动点，P 在Q 的左侧，且PQ 间长度恒定,在直线m 上要求P 、Q 两点，使得PA +PQ +QB 的值最小．(原理用平移知识解) （1）点A 、B 在直线m 两侧： （2）点A 、B 在直线m 同侧：实战演练：1．如图，已知平面直角坐标系，A，B两点的坐标分别为A(2，－3），B(4，－1）若C(a，0)，D(a+3，0)是x轴上的两个动点，则当a＝______时，四边形ABDC的周长最短．2．如图，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y 轴的正半轴上，OA=3，OB=4，D为边OB的中点.（1）若E为边OA上的一个动点，当△CDE的周长最小时，求点E的坐标；（2）若E、F为边OA上的两个动点，且EF＝2，当四边形CDEF的周长最小时，求点E、F的坐标.3．如图，已知在平面直角坐标系xOy中，直角梯形OABC的边OA在y轴的正半轴上，OC在x 轴的正半轴上，OA=AB=2，OC=3，过点B作BD⊥BC，交OA于点D．将∠DBC绕点B按顺时针方向旋转，角的两边分别交y轴的正半轴、x轴的正半轴于点E和F．（1）求经过A、B、C三点的抛物线的解析式；（2）当BE经过（1）中抛物线的顶点时，求CF的长；（3）在抛物线的对称轴上取两点P、Q（点Q在点P的上方），且PQ＝1，要使四边形BCPQ 的周长最小，求出P、Q两点的坐标．4．如图，已知点A（－4，8）和点B（2，n）在抛物线y＝ax2上．（1）求a的值及点B关于x轴对称点P的坐标，并在x轴上找一点Q，使得AQ＋QB最短，求出点Q的坐标；（2）平移抛物线y＝ax2，记平移后点A的对应点为A′，点B的对应点为B′，点C（－2，0）和点D（－4，0）是x轴上的两个定点．①当抛物线向左平移到某个位置时，A′C＋CB′最短，求此时抛物线的函数解析式；②当抛物线向左或向右平移时，是否存在某个位置，使四边形A′B′CD的周长最短？二．求两线段差的最大值问题(运用三角形两边之差小于第三边)几何模型：在一条直线m上，求一点P，使P A－PB的差最大；（1）点A、B在直线m同侧：（2）点A、B在直线m异侧：模型应用：1. 如图，抛物线y ＝－14x2－x ＋2的顶点为A ，与y 轴交于点B ．(1)求点A 、点B 的坐标；(2)若点P 是x 轴上任意一点，求证：PA －PB ≤AB ； (3)当P A －PB 最大时，求点P 的坐标.2. 如图，已知直线y ＝21x ＋1与y 轴交于点A ，与x 轴交于点D ，抛物线y ＝21x2＋bx ＋c 与直线交于A 、E 两点，与x 轴交于B 、C 两点，且B 点坐标为(1，0)．（1）求该抛物线的解析式；（3）在抛物线的对称轴上找一点M ，使|AM －MC |的值最大，求出点M 的坐标．⊙A经过点B和点O，直线BC交⊙A于点D．（1）求点D的坐标；（2）过O，C，D三点作抛物线，在抛物线的对称轴上是否存在一点P，使线段PO与PD之差的值最大？若存在，请求出这个最大值和点P的坐标．若不存在，请说明理由．4. 已知：如图，把矩形OCBA放置于直角坐标系中，OC＝3，BC＝2，取AB的中点M，连接MC，把△MBC沿x轴的负方向平移OC的长度后得到△DAO．（1）试直接写出点D的坐标；（2）已知点B与点D在经过原点的抛物线上，点P在第一象限内的该抛物线上移动，过点P 作PQ⊥x轴于点Q，连接OP．若以O、P、Q为顶点的三角形与△DAO相似，试求出点P的坐标；TO－TB的值最大？若存在，则求出（3）试问在（2）抛物线的对称轴上是否存在一点T，使得||点T点的坐标；若不存在，则说明理由．好题赏析：（2010•宁德）如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B 点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．（1）求证：△AMB≌△ENB；（2）①当M点在何处时，AM＋CM的值最小；②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；（3）当AM＋BM＋CM的最小值为3＋1时，求正方形的边长．变式：如图四边形ABCD是菱形，且∠ABC＝60，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM，则下列五个结论中正确的是（）①若菱形ABCD的边长为1，则AM＋CM的最小值1；②△AMB≌△ENB；=S四边形ADCM；④连接AN，则AN⊥BE；③S四边形AMBE⑤当AM＋BM＋CM的最小值为23时，菱形ABCD的边长为2．A．①②③B．②④⑤C．①②⑤D．②③⑤。

思维特训(九) 抛物线背景下线段和(差)的最值问题类型一二次函数中的“饮马问题”基本原理：两点之间，线段最短．解题思路：利用抛物线自身的轴对称性找到抛物线上某点关于对称轴的对称点，实现化“折”为“直”，再结合函数的相关知识解决．1．如图9－1，抛物线y＝ax2＋bx＋c 经过A(－1，0)，B(3，0)，C(0，3)三点，直线l 是抛物线的对称轴．(1)求抛物线的解析式；(2)设P 是直线l 上的一个动点，当PA＋PC 最小时，求点P 的坐标．图9－12．如图9－2，抛物线y＝ax2＋bx＋3 经过A(1，0)，B(4，0)两点．(1)求抛物线的解析式．(2)在抛物线的对称轴上是否存在点P，使得四边形PAOC 的周长最小？若存在，求出四边形PAOC 周长的最小值；若不存在，请说明理由．图9－23．如图9－3，已知抛物线y＝ax2＋bx＋c 经过A(－3，0)，B(1，0)，C(0，3)三点，其顶点为D，对称轴是直线l，l 与x 轴交于点H.(1)求该抛物线的解析式；(2)PQ 是该抛物线对称轴l 上的动线段，且PQ＝1，求PC＋QB 的最小值．图9－3类型二二次函数中线段差的最大值问题基本原理：三角形任何两边之差小于第三边．解题思路：先根据原理确定线段差的最值问题时的图形，再根据已知条件进行求解．4．如图9－4，抛物线y＝x2＋bx＋c 过点A(3，0)，B(1，0)，交y 轴于点C，P 是该抛物线上一动点，点P 从点C 沿抛物线向点A 运动(点P 不与点A，C 重合)，过点P 作PD∥y 轴交直线AC 于点D.(1)求抛物线的解析式．(2)当D 在线段AC 上运动时，求点P 在运动的过程中线段PD 长度的最大值．(3)在抛物线的对称轴上是否存在点M，使|MA－MC|的值最大？若存在，请求出点M 的坐标；若不存在，请说明理由．图9－45．2016·眉ft已知：如图9－5，在平面直角坐标系xOy 中，A，B，C 分别为坐标轴上的三个点，且OA＝1，OB＝3，OC＝4，(1)求经过A，B，C 三点的抛物线的解析式．(2)在平面直角坐标系xOy 中是否存在一点P，使得以点A，B，C，P 为顶点的四边形为菱形？若存在，请求出点P 的坐标；若不存在，请说明理由．(3)若M 为该抛物线上一动点，在(2)的条件下，请求出当|PM－AM|取最大值时点M 的坐标，并直接写出|PM－AM|的最大值．图9－56．已知：如图9－6，在平面直角坐标系xOy 中，直线y 3＋6 与x 轴、y 轴的交点＝－4x分别为A，B，将∠OBA 对折，使点O 的对应点H 落在直线AB 上，折痕交x 轴于点C.(1)直接写出点C 的坐标，并求经过A，B，C 三点的抛物线的解析式．(2)若(1)中抛物线的顶点为D，在直线BC 上是否存在点P，使得四边形ODAP 为平行四边形？若存在，求出点P 的坐标；若不存在，说明理由．(3)若把(1)中的抛物线向左平移3.5 个单位长度，则图象与x 轴交于G，N(点G 在点N 的左侧)两点，交y 轴于点E，则在此抛物线的对称轴上是否存在一点Q，使点Q 到E，N 两点的距离之差最大？若存在，请求出点Q 的坐标；若不存在，请说明理由．图9－63 典题讲评与答案详析 1．解：(1)∵抛物线 y ＝ax 2＋bx ＋c 经过 C (0，3)，∴c ＝3.∵抛物线 y ＝ax 2＋bx ＋3 经过 A (－1，0)，B (3，0)，⎧0＝a －b ＋3， ∴⎨ ⎧a ＝－1， 解得⎨⎩0＝9a ＋3b ＋3， ⎩b ＝2，∴抛物线的解析式为 y ＝－x 2＋2x ＋3. (2)∵y＝－x 2＋2x ＋3＝－(x －1)2＋4，∴对称轴为直线 x ＝1.∵A ，B 是抛物线与 x 轴的交点，∴点 A ，B 关于直线 l 对称，∴PA ＋PC 最小时，点 P 就是直线 BC 与直线 l 的交点(如图)．∵B (3，0)，C (0，3)，∴直线 BC 的解析式为 y ＝－x ＋3.∵点 P 在直线 l 上，∴点 P 可设为(1，m )．将(1，m )代入 y ＝－x ＋3，可得 m ＝2，∴P (1，2)．2．解：(1)由已知，得⎧a ＋b ＋3＝0， ⎧a ＝4， ⎨ 解得⎨ 15 ⎩16a ＋4b ＋3＝0， ⎩b ＝－ 4 . ∴抛物线的解析式为 y 3 2 15＋3.＝4x － 4 x(2)∵A ，B 关于对称轴对称，如图，连接 BC ，∴BC 与对称轴的交点即为所求的点 P ，此时 PA ＋PC ＝BC ，∴四边形 PAOC 的周长的最小值为 OC ＋OA ＋BC .∵A (1，0)，B (4，0)，C (0，3)， ∴OA ＝1，OC ＝3，BC ＝ OB 2＋OC 2＝5，∴OC ＋OA ＋BC ＝3＋1＋5＝9，∴在抛物线的对称轴上存在点 P ，使得四边形 PAOC 的周长最小，四边形 PAOC 周长的最小值为 9.3． 解：(1)∵抛物线 y ＝ax 2＋bx ＋c 经过 C (0，3)，∴c ＝3.∵抛物线 y ＝ax 2＋bx ＋3 经过 A (－3，0)，B (1，0)，⎧0＝a ＋b ＋3， ∴⎨ ⎧a ＝－1， ∴⎨⎩0＝9a －3b ＋3， ⎩b ＝－2，∴抛物线的解析式为 y ＝－x 2－2x ＋3.(2)过点 C 作直线 l 的对称点 E ，过点 E 作 EG ⊥AB 于点 G ，过点 Q 作 QF ∥PE ，交 EG 于点 F ，连接 FB ，如图，则有 PC ＝PE ，EF ∥PQ .∵EF ∥PQ ，QF ∥PE ，∴四边形 EFQP 是平行四边形，∴EF ＝PQ ＝1，PE ＝FQ ，∴PC ＝FQ ，∴PC ＋QB ＝FQ ＋QB ，根据两点之间线段最短可得 FQ ＋QB (即 PC ＋QB )的最小值为 FB .∵抛物线 y ＝－x 2－2x ＋3 的对称轴为直线 x ＝－1，C (0，3)，∴点 E 的坐标为(－2，3)， ∴点 F 的坐标为(－2，2)．在 Rt △FGB 中，FG ＝2，GB ＝1－(－2)＝3，根据勾股定理可得 FB ＝ FG 2＋GB 2＝ 13.∴PC ＋QB 的最小值为 13.4．解：(1)∵抛物线 y ＝x 2＋bx ＋c 过点 A (3，0)， B (1，0)， ⎧9＋3b ＋c ＝0， ⎧b ＝－4， ∴⎨ ⎩1＋b ＋c ＝0， 解得⎨ ⎩c ＝3， ∴抛物线的解析式为 y ＝x 2－4x ＋3. (2)令 x ＝0，则 y ＝3，∴点 C (0，3)， 则直线 AC 的解析式为 y ＝－x ＋3. 设点 P (x ，x 2－4x ＋3)．∵PD ∥y 轴， ∴D (x ，－x ＋3)， ∴PD ＝(－x ＋3)－(x 2－4x ＋3)＝－x 2＋3x ＝－(x 3 2 9 ．∵a ＝－1＜0，∴当 x 3 －2) ＋4(0<x <3) PD 的长度有最大值9＝2时，线段 4.(3)∵抛物线的对称轴垂直平分 AB ，∴MA ＝MB .由三角形的三边关系，可知|MB －MC |＜BC ，∴当 M ，B ，C 三点共线时，|MB －MC |的值最大，为 BC 的长度． 设直线 BC 的解析式为 y ＝kx ＋m (k ≠0)，⎧k ＋m ＝0， ⎧k ＝－3， 则⎨ ⎩m ＝3， 解得⎨⎩m ＝3，∴直线 BC 的解析式为 y ＝－3x ＋3.∵抛物线 y ＝x 2－4x ＋3 的对称轴为直线 x ＝2，∴当 x ＝2 时，y ＝－3×2＋3＝－3，∴M (2，－3)，即抛物线的对称轴上存在点 M (2，－3)，使|MA －MC |的值最大．5．解：(1)设抛物线的解析式为 y ＝ax 2＋bx ＋c .3 ⎧ ＝－4， ， ⎨ 由题意易知 A (1，0)，B (0，3)，C (－4，0)，⎧a ＋b ＋c ＝0， ∴⎨c ＝3， ⎩16a －4b ＋c ＝0，⎧a 3 解得⎨b9 ⎩＝－4， c ＝3， ∴经过 A ，B ，C 三点的抛物线的解析式为 y ＝－3 2 9 ＋3.(2)存在．∵OB ＝3，OC ＝4，OA ＝1，∴BC ＝AC ＝5，AB ＝ 10. 如图，当 BP 綊 AC 时，四边形 ACBP 为菱形，∴BP ＝AC ＝5，且点 P 到 x 轴的距离等于 OB ，∴点 P 的坐标为(5，3)．4x －4x当点 P 在第二、三象限时，以点 A ，B ，C ，P 为顶点的四边形只能是平行四边形，不 是菱形，∴当点 P 的坐标为(5，3)时，以点 A ，B ，C ，P 为顶点的四边形为菱形．(3)设直线 PA 的解析式为 y ＝kx ＋m (k ≠0)．∵点 A (1，0)，P (5，3)在直线 PA 上，⎧k ＝ ， ⎧5k ＋m ＝3，4 ∴⎨ ⎩k ＋m ＝0， 解得⎨ ⎩m ＝－3 4 ∴直线 PA 的解析式为 y 3 3＝4x －4.当点 M 与点 P ，A 不在同一直线上时，根据三角形的三边关系，知|PM －AM |<PA ， 当点 M 与点 P ，A 在同一直线上时，|PM －AM |＝PA ，∴当点 M 与点 P ，A 在同一直线上时，|PM －AM |的值最大，即 M 为直线 PA 与抛物线的交点． 3 3 y ＝ x － ， 解方程组 4 4 3 9 ⎩y ＝－4x 2－4x ＋3， ⎧x 1＝1，⎧⎪x 2＝－5， 得⎨ ⎨ 9 ⎩y 1＝0，⎪⎩y 2＝－2， ∴点 M 的坐标为(1，0)或(－59 时，|PM －AM |的值最大．此时|PM －AM |的最大值 为 5.6．解：(1)如图①，连接 CH .，－2)由轴对称的性质，得 CH ⊥AB ，BH ＝BO ，CH ＝CO ，∴在 Rt △CHA 中，由勾股定理，得4 AC 2＝CH 2＋AH 2. ∵直线 y 3 ＋6 与 x 轴、y 轴的交点分别为 A ，B ， ＝－4x ∴当 x ＝0 时，y ＝6，当 y ＝0 时，x ＝8， ∴B (0，6)，A (8，0)， ∴BO ＝6，OA ＝8， 在 Rt △AOB 中，由勾股定理，得 AB ＝10. 设 C (p ，0)，则 OC ＝p ， ∴CH ＝p ，AH ＝4，AC ＝8－p ， ∴(8－p )2＝p 2＋42，解得 p ＝3，∴C (3，0)． 设抛物线的解析式为 y ＝ax 2＋bx ＋c . ⎧a 1 ⎧6＝c ， ＝4， 由题意，得⎨64a ＋8b ＋c ＝0，解得⎨b 11 ⎩0＝9a ＋3b ＋c ， ＝－ ， ⎩c ＝6， ∴抛物线的解析式为 y 1 2 11x ＋6. ＝4x － 41 2 11 1⎛x 11⎫ (2)不存在．理由：如图②，设抛物线对称轴交 x 轴于点 F .∵y ＝4x － 4 x ＋6＝4⎝ － 2 ⎭ 2 25 －16， ∴ 11 25 25 D ( 2 ，－16)，∴DF ＝16. 设直线 BC 的解析式为 y ＝kx ＋b ′，则有 ⎧6＝b ′， ⎨ ⎧k ＝－2， 解得⎨ ⎩0＝3k ＋b ′， ⎩b ′＝6， ∴直线 BC 的解析式为 y ＝－2x ＋6. 设存在点 P 使四边形 ODAP 是平行四边形，P (m ，n )． 过点 P 作 PM ⊥OA 于点 M ， 则∠PMO ＝∠AFD ＝90°，PO ＝DA ，PO ∥DA ， ∴∠POM ＝∠DAF ，∴△OPM ≌△ADF ， ∴PM ＝DF ＝n 25 25 2m ＋6， ＝16，∴16＝－ ∴m 71 ＝32， 但 OM ＝AF ＝8 11 5 71 － 2 ＝2≠32， ∴点 P 不在直线 BC 上，即直线 BC 上不存在满足条件的点 P . (3)由题意得，平移后的抛物线的解析式为 y 1 －2)225 为直线 x ＝2.＝4(x －16，∴平移后抛物线的对称轴1 9∴⎨9当x＝0 时，y＝－16；当y＝0 时，01(x－2)225＝41 9解得x1＝－，x2＝.－16，2 2∵点G 在点N 的左侧，∴G(19 9－2，0)，E(0，－16)，N(2，0)．如图③，连接EG，直线EG 交直线x＝2 于点Q，则此时点Q 到E，N的距离之差最大．设直线EG 的解析式为y＝k0x＋b0，则⎧0＝－2k0＋b0，⎧k0＝－8，⎨9 解得⎨9⎩b0＝－16，⎩b0＝－16，∴直线EG 的解析式为y＝－9 9⎧y 9 9 8x－16，⎧x＝2，⎪＝－8x－16，⎪解得⎨ 45⎪⎩x＝2，∴Q(2 45 ．⎪⎩y＝－16，，－16)。

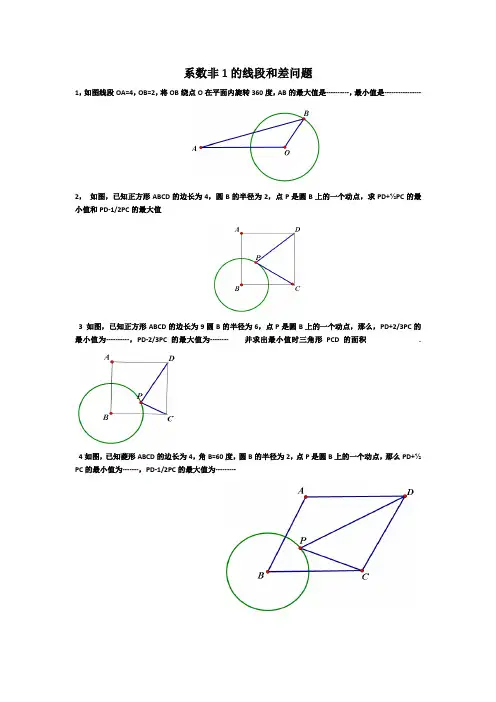
系数非1的线段和差问题
1，如图线段OA=4，OB=2，将OB绕点O在平面内旋转360度，AB的最大值是----------，最小值是----------------
2，如图，已知正方形ABCD的边长为4，圆B的半径为2，点P是圆B上的一个动点，求PD+½PC的最小值和PD-1/2PC的最大值
3 如图，已知正方形ABCD的边长为9圆B的半径为6，点P是圆B上的一个动点，那么，PD+2/3PC的最小值为----------，PD-2/3PC的最大值为-------- 并求出最小值时三角形PCD的面积.
4如图，已知菱形ABCD的边长为4，角B=60度，圆B的半径为2，点P是圆B上的一个动点，那么PD+½ PC的最小值为-------，PD-1/2PC的最大值为---------
5，二次函数y=ax²-2x+c的图像与x轴交于A，C两点，点C（3,0），与y轴交于点B（0，-3）（1）a=-----------，c= ---------
（2）如图，p是x轴上一动点，点D（0,1）在y轴上，连接PD，求PD+PC的最小值
（3）如图2，点M在抛物线上，若三角形MBC的面积等于3，求点M的坐标。

中考复习专题之线段(和差)最值问题之对称对称问题，指的是通过对称的方式求得线段(和差)最值的问题类型，包含一次对称即将军饮马问题、二次对称、过河修桥问题等. 1.将军饮马问题“白日登山望烽火，黄昏饮马傍交河”，这是唐代诗人李颀《古从军行》里的一句诗。

而由此却引申出一系列非常有趣的数学问题，通常称为“将军饮马”。

如图，将军在图中点A 处，现在他要带马去河边喝水，之后返回军营，问：将军怎么走能使得路程最短？如图，在直线上找一点P 使得PA+PB 最小？这个问题的难点在于PA+PB 是一段折线段，通过观察图形很难得出结果，关于最小值，我们知道“两点之间，线段最短”、“点到直线的连线中，垂线段最短”等，所以此处，需转化问题，将折线段变为直线段．作点A 关于直线的对称点A'，连接PA'，则PA'=PA ，所以PA+PB=P A'+PB当A'、P 、B 三点共线的时候，PA'+PB =A'B ，此时为最小值（两点之间线段最短） 作端点（点A 或点B ）关于折点（上图P 点）所在直线的对称，化折线段为直线段．2.二次对称问题在OA 、OB 上分别取点M 、N ，使得△PMN 周长最小．AB 将军军营河A'AP 折点端点A 'P A此处M 、N 均为折点，分别作点P 关于OA （折点M 所在直线）、OB （折点N 所在直线）的对称点，化折线段PM +MN +NP 为P'M +MN +NP ’’，当P'、M 、N 、P''共线时，△PMN 周长最小． 3.过河修桥问题已知人在图中点A 村庄，现要过河去往B 村，桥必须垂直于河岸建造，问：桥建在何处能使路程最短？考虑MN 长度恒定，只要求AM +NB 最小值即可．问题在于AM 、NB 彼此分离，所以首先通过平移，使AM 与NB 连在一起，将AM 向下平移使得M 、N 重合，此时A 点落在A ’位置．问题化为求A'N +NB 最小值，显然，当A'、N 、B 共线时，AM+MN+BN 的值最小，并得出桥应建的位置． 【问题扩展1】已知将军在图中点A 处，现要过两条河去往B 点的军营，桥必须垂直于河岸建造，问：桥建在何处能使路程最短？MP'NMBPOOPB考虑PQ 、MN 均为定值，所以路程最短等价于AP +QM +NB 最小，对于这彼此分离的三段，可以通过平移使其连接到一起．AP 平移至A'Q ，NB 平移至MB ’，化AP +QM +NB 为A'Q +QM +MB'．当A'、Q 、M 、B ’共线时，A'Q +QM +MB'取到最小值，再依次确定P 、N 位置． 【问题扩展1】如图，将军在A 点处，现在将军要带马去河边喝水，并沿着河岸走一段路，再返回军营，问怎么走路程最短？已知A 、B 两点，MN 长度为定值，求确定M 、N 位置使得AM +MN +NB 值最小？【分析】考虑MN 为定值，故只要AM +BN 值最小即可．将AM 平移使M 、N 重合，AM =A'N ，将AM +BN 转化为A'N +NB ．构造点A 关于MN 的对称点A''，连接A''B ，可依次确定N 、M 位置，可得路线．军营将军河河QA B MNPB'A'QABMNPPNMBAQA'B'M将军A军营河A'AA''MNAA'练习题1.如图，点P 是∠AOB 内任意一点，∠AOB =30°，OP =8，点M 和点N 分别是射线OA 和射线OB 上的动点，则△PMN 周长的最小值为___________．2. 如图，正方形ABCD 的边长是4，M 在DC 上，且DM =1， N 是AC 边上的一动点，则△DMN 周长的最小值是___________．3.如图，在Rt △ABO 中，∠OBA =90°，A （4,4），点C 在边AB 上，且AC :CB =1:3，点D 为OB 的中点，点P 为边OA 上的动点，当点P 在OA 上移动时，使四边形PDBC 周长最小的点P 的坐标为( ) A ．(2,2)B ．5(2，5)2C ．8(3，8)3D ．(3,3)4.如图，在△ABC 中，AC =BC ，∠ACB =90°，点D 在BC 上，BD =3，DC =1，点P 是AB 上的动点，则PC +PD 的最小值为( )A ．4B ．5C ．6D ．7P OBAMNNMD CBAyPO D CBA PDCBA5.如图，在等边△ABC 中，AB =6， N 为AB 上一点且BN =2AN ， BC 的高线AD 交BC 于点D ，M 是AD 上的动点，连结BM ，MN ，则BM +MN 的最小值是___________．6. 如图，在Rt △ABD 中，AB =6，∠BAD =30°，∠D =90°，N 为AB 上一点且BN =2AN ， M 是AD 上的动点，连结BM ，MN ，则BM +MN 的最小值是___________．7.如图，在Rt △ABC 中，∠ACB =90°，AC =6．AB =12，AD 平分∠CAB ，点F 是AC 的中点，点E 是AD 上的动点，则CE +EF 的最小值为( ) A ．3B ．4C ．33D ．238.如图，在锐角三角形ABC 中，BC =4，∠ABC =60°， BD 平分∠ABC ，交AC 于点D ，M 、N 分别是BD ，BC 上的动点，则CM +MN 的最小值是( )A 3B ．2C ．23D ．49.如图，在菱形ABCD 中，AC =62BD =6，E 是BC 的中点，P 、M 分别是AC 、AB 上的动点，N MDBA A BCDMNE AFCDBNMDCBA连接PE 、PM ，则PE +PM 的最小值是( )A ．6B ．33C ．26D ．4.510.如图，矩形ABOC 的顶点A 的坐标为（-4,5），D 是OB 的中点，E 是OC 上的一点，当△ADE 的周长最小时，点E 的坐标是( ) A ．4(0,)3B ．5(0,)3C ．(0,2)D ．10(0,)311.如图，在矩形ABCD 中，AB =6，AD =3，动点P 满足13PAB ABCD S S ∆=矩形，则点P 到A 、B 两点距离之和P A +PB 的最小值为( ) A ．213B ．210C ．35D 4112.如图，矩形ABCD 中，AB =10，BC =5，点E 、F 、G 、H 分别在矩形ABCD 各边上，且AE =CG ，BF =DH ，则四边形EFGH 周长的最小值为( ) A ．5B ．105C ．103D ．15313.如图，∠AOB =60°，点P 是∠AOB 内的定点且OP =3，若点M 、N 分别是射线OA 、OB 上异EPDCAMEOD C B AyDCBAPH FGEDCB A于点O 的动点，则△PMN 周长的最小值是( )A ．362B ．332C ．6D ．314. 如图，∠AOB 的边OB 与x 轴正半轴重合，点P 是OA 上的一动点，点N （3,0）是OB 上的一定点，点M 是ON 的中点，∠AOB =30°，要使PM +PN 最小，则点P 的坐标为 ．15. 如图，已知正比例函数y =kx （k >0）的图像与x 轴相交所成的锐角为70°，定点A 的坐标为（0，4），P 为y 轴上的一个动点，M 、N 为函数y =kx （k >0）的图像上的两个动点，则AM +MP +PN 的最小值为____________．16.如图，在平面直角坐标系中，矩形ABCD 的顶点B 在原点，点A 、C 在坐标轴上，点D 的坐标为（6，4），E 为CD 的中点，点P 、Q 为BC 边上两个动点，且PQ =2，要使四边形APQE 的周长最小，则点P 的坐示应为______________．17.如图，矩形ABCD 中，AD =2，AB =4，AC 为对角线，E 、F 分别为边AB 、CD 上的动点，且EF ⊥AC 于点M ，连接AF 、CE ，求AF +CE 的最小值．ABOPNNMPOBAyPAMN Oy Ey xB ()Q ACD OP18. 如图，在平面直角坐标系中，Rt△OAB 的直角顶点A 在x 轴的正半轴上，顶点B 的坐标为(3，3 )，点C 的坐标为(12，0)，点P 为斜边OB 上一动点，则PA+PC 的最小值为___________．19.如图，△ AOB=30 °，点M 、 N 分别在边 OA 、OB 上，且 OM=1 ，ON=3，点P 、Q 分别在边 OB 、OA 上，则 MP+PQ+QN 的最小值 _________20.如图，在矩形ABCD 中，AB=4，BC=8，E 为CD 边的中点．若P ，Q 为BC 边上的两动点，且PQ=2，则当BP=___时，四边形APQE 的周长最小．21.如图在河的两侧有两个村庄，A 离河为60米，B 离河是30米，AB 的水平距离为120米，河的宽度为30米，问桥修在何处会使得从A 经过桥到B 的路程最小，最小值为多少？参考答案1.82.63.C4.B5.276.277.C8.C9.C 10.BAB CDEFMyx PCBAO QPED C BA11.A 12.B 13.D14.3(,3)215.2316.8(,0)317.5 18.3121020.622217+21.180。